下载文档原格式
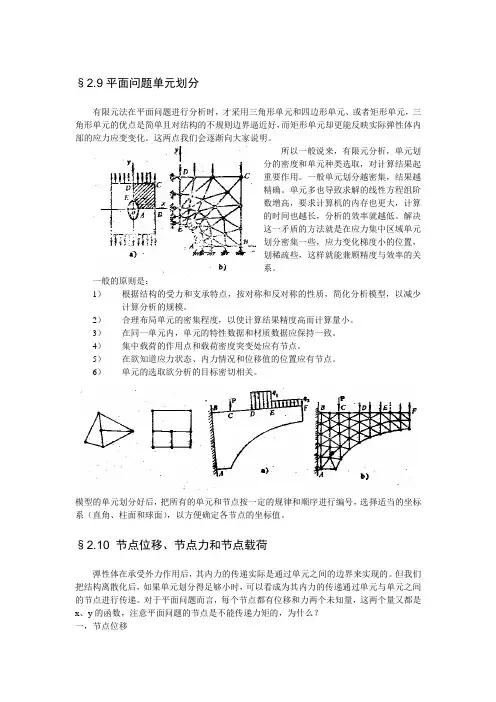
§2.9平面问题单元划分有限元法在平面问题进行分析时，才采用三角形单元和四边形单元、或者矩形单元，三角形单元的优点是简单且对结构的不规则边界逼近好，而矩形单元却更能反映实际弹性体内部的应力应变变化。
这两点我们会逐渐向大家说明。
所以一般说来，有限元分析，单元划分的密度和单元种类选取，对计算结果起重要作用。
一般单元划分越密集，结果越精确。
单元多也导致求解的线性方程组阶数增高，要求计算机的内存也更大，计算的时间也越长，分析的效率就越低。
解决这一矛盾的方法就是在应力集中区域单元划分密集一些，应力变化梯度小的位置，划稀疏些，这样就能兼顾精度与效率的关系。
一般的原则是：1）根据结构的受力和支承特点，按对称和反对称的性质，简化分析模型，以减少计算分析的规模。
2）合理布局单元的密集程度，以使计算结果精度高而计算量小。
3）在同一单元内，单元的特性数据和材质数据应保持一致。
4）集中载荷的作用点和载荷密度突变处应有节点。
5）在欲知道应力状态、内力情况和位移值的位置应有节点。
6）单元的选取欲分析的目标密切相关。
模型的单元划分好后，把所有的单元和节点按一定的规律和顺序进行编号，选择适当的坐标系（直角、柱面和球面），以方便确定各节点的坐标值。
§2.10 节点位移、节点力和节点载荷弹性体在承受外力作用后，其内力的传递实际是通过单元之间的边界来实现的。
但我们把结构离散化后，如果单元划分得足够小时，可以看成为其内力的传递通过单元与单元之间的节点进行传递。
对于平面问题而言，每个节点都有位移和力两个未知量，这两个量又都是x、y的函数，注意平面问题的节点是不能传递力矩的，为什么？一，节点位移对三节点三角形单元而言，因有三个节点，每个节点的位移都有x ，y 两个分量，所以一共有6个自由度。
单元节点位移向量可表示为：{}[]Tm m j j i ie v u v u v u =δ二，节点力所谓节点力，就是单元对节点或节点对单元作用的力，它是弹性体内部的作用力，也就是我们常说的内力。
