当前位置：文档之家 › 位似图形与坐标

位似图形与坐标

  • 格式：doc
  • 大小：974.50 KB
  • 文档页数：3

下载文档原格式

  / 3

合集下载

位似图形的坐标变化规律-课件

位似图形的坐标变化规律-课件
是 (－2，0)或(34，32) ．
14．(14 分)如图正方形 ABCD，以 A 为位似中心，把正方形 ABCD 缩小 为原来的一半，得正方形 A′B′C′D′，画出图形并写出 B′，C′，D′的坐标．
解：图略，∵A(1，0)，B(3，0)，∴AB＝BC＝CD＝DA＝2， ∴C(3，2)，D(1，2)．∵正方形ABCD，以A为位似中心，把正方形 ABCD缩小为原来的一半，得正方形A′B′C′D′，有两种情况：①B′(2， 0)，C′(2，1)，D′(1，1)；②B′(0，0)，C′(0，－1)，D′(1，－1)．
A．y＝4x B．y＝34x C．y＝－34x D．y＝1x8
11．如图，△ABC 中，A，B 两个顶点在 x 轴的上方，点 C 的坐标是(－1， 0)，以点 C 为位似中心，在 x 轴的下方作△ABC 的位似图形△A′B′C′，并把 △ABC 的边长放大到原来的 2 倍，设点 B 的对应点 B′的横坐标是 a，则点 B 的横坐标是( D )
•
14、意志坚强的人能把世界放在手中 像泥块 一样任 意揉捏 。2021年2月27日星期 六2021/2/272021/2/272021/2/27
•
15、最具挑战性的挑战莫过于提升自 我。。2021年2月2021/2/272021/2/272021/2/272/27/2021
•
16、业余生活要有意义，不要越轨。2021/2/272021/2/27Februar y 27, 2021
A．(2，5) B．(2.5，5) C．(3，5) D．(3，6) 2．(4 分)(2015·十堰)在平面直角坐标系中，已知点 A(－4，2)，B(－6，
－4)，以原点 O 为位似中心，相似比为12，把△ABO 缩小，则点 A 的对应点

数学九年级下册位似—两个位似图形坐标之间的关系课件PPT公开课

数学九年级下册位似—两个位似图形坐标之间的关系课件PPT公开课
（4）若五边形ABCDE与五边形A1B1C1D1E1位似，则其中⊿ABC与⊿A1B1C1也是位似图形. 利用位似中心将△ABC三边扩大为原来的2倍 1、在△ABC外任取一点P 作出下列位似图形的位似中心
1、在△ABC外任取一点P 如果两个图形不仅是相似图形，而且对应顶点的连线相交于一点，像这样的两个图形叫位似图形，这个点叫做位似中心，这时的相似 比又叫位似比。
H
如4、图依，次D连，接ED分D、别EA、B，F AC上的点. E
把一个图形变换成一个与原来的图形的形状和大小都相同的图形。
2作、出判下断列位位似似图图形形时的要位注似意中首心先它们必须是相似形，其次每一对对应点所在直线都经过同一点。O
()
( B)
DE BC
F
C
B
G C
2.如图所示,四边形OABC与四边形OA1B1C1 是位似图形, AB与A1B1一定平行吗?为什么?
（3）两个位似图形若全等，则位似中心在两个图形之间； １．位似图形的对应点和位似中心在同一条直线上
利用位似，可以将一个图形放大或缩小
❖ 如图，将四边形ABCD缩小为原来的一半。
A D
C B
练习
❖ 1、教材第2题 ❖ 2、将下列图形放大一倍，使位似中心在图形
内：
❖ 将下列图形放大一倍：
课堂小结
应用位似图形概念作图
利用位似中心作图将△ABC的三边缩小为原来的1/2
A
1、在△ABC外任取一点P D
C
2、分别连接PA、PB、PC
F
P
3、分别取PA、PB、PC的中点D、E、EF
B
4、依次连接D、E、F
小 结
实际上△ABC与△DEF是位似图形，位似中心是点P

位似对应点坐标公式

位似对应点坐标公式

位似对应点坐标公式位似对应点坐标公式，这可是个在数学世界里有点小神秘但又超级实用的家伙！咱先来说说位似是啥。

想象一下，有两个图形，它们不仅形状相同，而且对应顶点的连线相交于一点，对应边互相平行，这就是位似啦。

就好比两个相似的双胞胎，只不过一个大一点，一个小一点，但是五官比例啥的都一样。

位似对应点坐标公式呢，就是用来描述这两个相似图形中对应点坐标之间关系的神奇公式。

比如说，如果位似中心是坐标原点 O ，原图形上一点的坐标是（x，y），位似比为 k ，那么位似图形对应点的坐标就是（kx，ky）或者（-kx，-ky）。

记得有一次，我给学生们讲这个知识点。

当时有个小同学瞪着大眼睛，一脸迷茫地问我：“老师，这公式有啥用啊？”我笑着跟他说：“孩子，你想想啊，假如你是个建筑师，要设计一个大楼的模型，是不是得根据实际大楼和模型的比例关系来确定模型上每个点的位置呀？这公式就能帮你算出来！”那孩子似懂非懂地点点头。

在实际解题中，这个公式能帮咱们省不少事儿。

比如说，给你一个三角形，告诉你位似中心和位似比，让你求位似后的三角形顶点坐标。

这时候，只要把原来顶点的坐标按照公式一计算，答案就出来啦。

不过，同学们在运用这个公式的时候可别马虎。

一定要搞清楚位似中心的位置，还有位似比是正数还是负数。

有一次考试，有个题给出的位似比是 -2 ，好多同学都忘了还有负数这回事，结果全做错啦，那叫一个可惜哟！其实啊，数学里的每个公式就像是一把钥匙，能帮我们打开知识的大门。

位似对应点坐标公式这把钥匙，能让我们更轻松地探索图形的奥秘。

大家在学习的时候，多做几道练习题，把这个公式用熟了，以后遇到相关的问题就能轻松应对啦。

就像骑自行车，刚开始可能摇摇晃晃，但练得多了，就能自由自在地在路上飞驰啦！希望大家都能和位似对应点坐标公式成为好朋友，让数学学习变得更有趣、更轻松！。

图形的位似变换与坐标

图形的位似变换与坐标
放大后对应点的坐标分别是多少?
A′( 4 ,6 ), B′( 4 ,2 ), C′( 12 ,4 )
y
A'
6
4 A
3
2
B'
C
1
B
o
2
4
6
还有其他办法吗?
C'
x
12
在平面直角坐标系中, △ABC三个顶点的坐标分别 为A(2,3),B(2,1),C(6,2),以原点O为位似中心,相 似比为2,将△ABC放大.
（2）一般情况下，画已知图形的位似图形的结果不唯一； （3）将一个图形放大或缩小而保持形状不变.
复习回顾
如何把三角形ABC放大为原来的2倍?
E
B
O
C
F
D
A
D
B
O
C
F
A
E
对应点连线都交于_位__似___中__心____ 对应线段___平___行__或__在___一__条__直___线__上_________
放大后对应点的坐标分别是多少?
A′( -4 ,-6 ), B′( -4 ,-2 ), C′( -12 ,-4 )
y
A
C
B
x
o
B”
A”
例题.在平面直角坐标系中, 四边形ABCD的四个顶点的坐
标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出它的一个以 原点O为位似中心,相似比为1/2的位似图形.
y
A(5,4)
A’(10,4)
C(5,1)
C’
0
B(3,0) B’
D(5,-1)
x
D'
E(4,-2)
E’(8,-2)

人教版九年级下册位似—两个位似图形坐标之间的关系课件

人教版九年级下册位似—两个位似图形坐标之间的关系课件

A
y
D
A′
B
D′
B′
C
C′ o
x
A′( -3,3 ), B′( -4,1 ), C′( -2,0 ), D′( -1,2 )
A′′ (3,-3 ), B′′ ( 4,-1 ), C′′ ( 2,0 ), D′′ ( 1,-2 )
A
y
D
B
C ′′
Co
x
B ′′
D ′′
A ′′
巩固训练
1. 在平面直角坐标系中，四边形 OABC 的顶点 坐标分别为 O (0，0)，A (6，0)，B (3，6)，C (－3，3). 以原点 O 为位似中心，画出四边形 OABC 的位似图形，使它与四边形 OABC 的相 似是 2 : 3.
A′(-3,3)，B′(-4,1)，C′(-2,0)，D′(-1,2).
或 A′′(3,-3)，B′′(4,-1)，C′′(2,0)，D′′ (1,-2).
例题.在平面直角坐标系中, 四边形ABCD的四个顶点的
坐标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出
它的一个以原点O为位似中心,位似比为1:2的位似图形.
投影—“动” 悉重难点
解：画法一：将四边 形 OABC 各顶点的坐
标都乘 2 ；在平面 3
直角坐标系中描点O
(0，0)，A' (4，0)，B'
(2，4)，C′ (－2，2)，
用线段顺次连接O，
A'，B'，C'.
y 6
4 C
C' 2
－4
O
－2
－4
B B'
A' A 6x

在平面直角坐标系中画位似图形

在平面直角坐标系中画位似图形

(1)相似比为
1 2
;
y
z ( 1,4 )
y ( 5,4 )
S( 2,2 )
W ( 1,1 )
x ( 5,1 )
o
x
• 不经历风雨，怎么见彩虹 • 没有人能随随便便便成功!
复习回顾
如何把三角形ABC放大为原来的2倍?
E
B
O
C
F
D
A
D
B
O
C
F
A
E
对应点连线都交于_位__似___中__心____ 对应线段___平___行__或__在___一__条__直___线__上_________
探索1:
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为 位似中心,相似比为1:3,把线段AB缩小.
y A′(2,1), B′(2,0)
A
A'
x
o
B'
B
观察对应点之间的坐标的变化,你有什么发现?
在平面直角坐标系中,有两点A(6,3),B(6,0),以原 点O为位似中心,相似比为1:3,把线段AB缩小.
A′(2,1),B′(2,0) y
A〞(-2,-1),B(-2,0)
A
A'
B〞
x
o
B变化,你有什么发现?
在平面直角坐标系中,如果位似变换是以原点 为位似中心,相似比为k,那么位似图形对应点 的坐标的比等于k或-k.
探索2:
在平面直角坐标系中, △ABC三个顶点的坐标分别为 A(2,3),B(2,1),C(6,2),以原点O为位似中心,相似比 为2画它的位似图形.
放大后对应点的坐标分别是多少?
A′( 4 ,6 ), B′( 4 ,2 ), C′( 12 ,4 )

两个位似图形坐标之间的关系

两个位似图形坐标之间的关系
以原点为位似中心，画出一个与原图
形位似的图形，使它与原图形的相似 比为k，那么与原图形上的点(x，y)对 应的位似图形上的点的坐标为(kx，ky) 或(-kx，-ky).
(教材例题)如图所示，△ABO三个顶点的坐标分别为A(-2，4)，
B(-2，0)，O(0，0)，以原点O为位似中心，画一个三角形，使它
倍得到△A1B1C1(顶点均在格点上)，它们是以P点 为位似中心的位似图形，则P点的坐标是( D )
A.(-3，-3) B.(-3，-4) C.(-4，-4) D.(-4，-3)
解析:∵△ABC的三边分别扩大 一倍得到△A1B1C1(顶点均在格 点上)，它们是以P点为位似中 心的位似图形，根据位似图形 的性质，对应点的连线相交于 一点，连接BB1，CC1，交点即 是P点，如图所示，∴P点的坐 标为(-4，-3).故选D.
就这一个图形 吗？
平移、旋转、轴对称、位似四种变换的异同
我们已经学习了平移、轴对称、旋转和位似等 图形的变化方式，你能在下图所示的图案中找 到它们吗?四种变换有什么异同?
【四种变换的异同】 图 形经过平移、旋转、轴对 称后，图形的位置虽然改 变了，但是图形的大小和 形状没有改变，即两个图 形是全等的;而图形经过 位似变换后，图形是相似
坐标为
;
(2)以原点O为位似中心，在第一象限内将△ABC放大为原来的2倍，画
-4
变化,你有什么发现?
-6
A"
-8
A/
A
C' 2 4 C 6 8 9 101112
在平面直角坐标系中，以原点为位似中心,将一个图形点的坐标比为k; 当新图形与原图形在原点的异侧，这时新旧图形上对应点的坐标比为-k。
总结 一般地，在平面直角坐标系中，如果

两个位似图形坐标之间的关系

两个位似图形坐标之间的关系

A'（ 4 ，－ 4 ），B ' （ 8 ， － 10 ），C ' （ 10 ，－4 ），
A" （－ 4 ， 4 ），B" （－ 8 ， 10 ），C" （－10 ，4 ），
图片欣赏：
至此，我们已经学习了四种变换：平移、轴对称、旋转和位似，你能 说出它们之间的异同吗？在图所示的图案中，你能找到这些变换吗？
B′′ -2
A B′ B
24
C′
C
6 8 10 12 x
C′′
-4
A′ ′ -6
在平面直角坐标系中，如果位似变换是以原点为位似中心，
相似比为k，那么位似图形对应点的坐标的比等于k或－k．
与原图形上的点P(x，y)对应点P'坐标为 （__k_x_,_k_y_）__或__（__-_k_x_,_-_k_y_）______．
填一填： 平面直角坐标系中任意一点P（x，y）
平移：点P向右平移a(a>0)，对应点P'坐 标为（ x+a, y ）向上平移b（b>0）个 单位，对应点P''坐标为（ x , y+b ） 轴对称：点P关于x轴对称点 P'（ x ， -y ），关于y轴对称点 P''（ -x ， y ） 中心对称：点P（x，y）关于原点的对称 的对应点P'坐标为（ -x ，-y）
小试牛刀：
59．如图，在平面直角坐标系中，矩形 OABC 的顶点 O 在坐标原点， 边 OA 在 x 轴上，OC 在 y 轴上，如果矩形 OA′B′C′与矩形 OABC 关于 点 O 位似，且矩形 OA′B′C′的面积等于矩形 OABC 面积的14，那 么点 B′的坐标是( D ) A．(－2，3) B．(2，－3) C．(3，－2)或(－2，3) D．(－2，3)或(2，－3)

位似图形的点的坐标变化规律难点

位似图形的点的坐标变化规律难点

教 材 习 题 27.3
复习巩固
1.如图，如果虚线图形与实线图形是位似图形， 求它们的相似比并找出位似中心.
2.如图，以点P为位似中心，将五角星的边长
缩小为原来的 1 .
2
3.△ABC三个顶点的坐标分别为A(2，2)，B(4，2)， C(6，4). 以原点O为位似中心，将△ABC缩小得到 △DEF，使△DEF与△ABC对应边的比为1:2，这时 △DEF各个顶点的坐标分别是多少？
1.如图表示△AOB和把它缩小后得到的△OCD， 求△AOB与△COD的相似比。
解：相似比为OB:OD=5：2. A
5
C B
D5
2.如图，△ABO三个顶点的坐标分别为A(4,-5), B(6,0), O(0,0). 以原点O为位似中心，把这个三角形 放大为原来的2倍，得到△A′B′O′.写出△A′B′O′三 个顶点的坐标.
以y轴为对称轴则对应点的纵坐标相等横坐标互为相反数一个图形绕原点旋转180则旋转前后两个图形对应点的横坐标与纵坐标都互为相反数当以原点为位似中心时变换前后两个图形对应点的横坐标纵坐标之比的绝对值等于相似比随堂演练基础巩固1
位似图形的点的坐标变化规律难点
位似图形y在直角
坐标系中又有什 么规律呢？
新课导入
随堂演练
基础巩固
1.某学习小组在讨论“变化的鱼”时, 知道大
鱼与小鱼是位似图形(如图所示), 则小鱼上的
点(a, b)对应大鱼上的点( )
A.(-2a, -2b)
B.(A-a, -2b)
C.(-2b, -2a)
D.(-2a, -b)
2.△ABC三个顶点坐标分别为A(-2，-2)，B(-4，-2)，
3．发展 (1)原因： ①甲午战争以后列强激烈争夺在华铁路的 修。筑权 ②修路成为中国人 救的亡强图烈存愿望。 (2)成果：1909年 京建张成铁通路车；民国以后，各条商路修筑 权收归国有。 4．制约因素 政潮迭起，军阀混战，社会经济凋敝，铁路建设始终未入 正轨。

第2课时 位似图形的坐标变化规律

第2课时 位似图形的坐标变化规律
【知识网络】
提纲挈领，重点突出.
【教学反思】
①[授课流程反思]
在教授本课时，以复习学过的图形和坐标变换为例，引出本节课的位似坐标变换，效果较好；在探究新知过程中，利用点的坐标变换规律的特征进行作图，培养学生的数形结合思想，学生能够更好地理解内容.
②[讲授效果反思]
本节课中，让学生自己通过观察、动手操作画出变换后的图形，向学生提供充分从事数学活动的机会，帮助他们在自主探索和合作交流的过程中真正理解和掌握基本的数学知识与技能、数学思想与方法，获得广泛的数学活动经验.
1.通过对问题的探究，提高学生的观察能力、分析解决问题的能力，加强小组活动的效果，培养学生的作图能力和语言表达能力，拓宽学生的思维，让学生总结解决问题的方法，使学生获得成功的体验，增强学习的信心.
活动
二：
实践
探究
交流
新知
3.探究四种变换之间的区别和联系：
师生活动：师生共同总结位似、平移、轴对称、旋转等图形变换的基本变换规律：
情感态度
通过经历对位似图形的认识、操作、归纳等过程，激发学生探究问题的兴趣，得到解决问题的成功体验，培养学生之间的交流合作意识.
教学
重点
用图形中的点的坐标变化来表示图形的位似变换．
教学
难点
对平面直角坐标系下位似图形的点的坐标变化规律的归纳．
授课
类型
新授课
课时
教具
多媒体
教学活动
教学
步骤
师生活动
设计意图
你有什么发现？
利用解答问题的形式，探寻点的坐标规律，能提高学生的学习兴趣.
活动
二：
实践
探究
交流
新知
1.探究位似图形的坐标变化规律：

画相似图形、位似图形及图形与坐标知识点

画相似图形、位似图形及图形与坐标知识点

画相似图形及图形与坐标
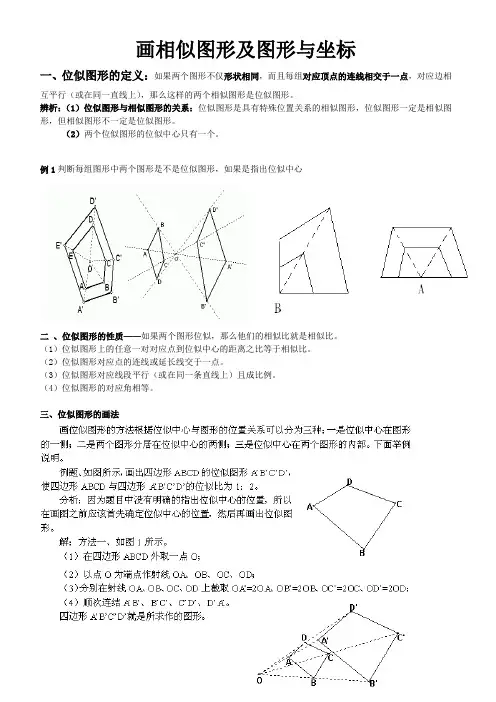
一、位似图形的定义：如果两个图形不仅形状相同，而且每组对应顶点的连线相交于一点，对应边相
互平行（或在同一直线上），那么这样的两个相似图形是位似图形。

辨析：（1）位似图形与相似图形的关系：位似图形是具有特殊位置关系的相似图形，位似图形一定是相似图形，但相似图形不一定是位似图形。

（2）两个位似图形的位似中心只有一个。

例1判断每组图形中两个图形是不是位似图形，如果是指出位似中心
二、位似图形的性质——如果两个图形位似，那么他们的相似比就是相似比。

（1）位似图形上的任意一对对应点到位似中心的距离之比等于相似比。

（2）位似图形对应点的连线或延长线交于一点。

（3）位似图形对应线段平行（或在同一条直线上）且成比例。

（4）位似图形的对应角相等。

三、位似图形的画法
四、确定物体位置的方法
方法1：用坐标确定位置。

先选取某点为坐标原点，建立平面直角坐标系，然后用一对有序实数来表示一个点的位置，即为某物体的位置。

方法2：用一个角度和距离确定点的位置。

先选定某个参照物和某个方向，然后用一个角度和距离来表示一个点的位置，即为某物体的位置。

这种方法在军事和地理中经常用到。

注意：用此方法确定点的位置时，角度与距离二者缺一不可。

五、图形的变换与坐标
1.在平移过程中(1)左右移,横坐标变,纵坐标不变.
(2)上下移,纵坐标变,横坐标不变.
2.关于x轴对称的图形对应点的横坐标不变，纵坐标互为相反数；
关于y轴对称的图形对应点的纵坐标不变，横坐标互为相反数.
3.位似中心是原点的位似变换中,坐标扩大或缩小相同的倍数.。

人教版九年级数学课件《位似图形的坐标变化规律》

人教版九年级数学课件《位似图形的坐标变化规律》

(2，-3)
x轴对称的点的坐标是_______，关于y轴对称的点的坐标是
(-2，3)
(-2，-3)
_______，关于原点对称的点的坐标是________.
复习回顾
类似地，位似也可
以用两个图形坐标
之间的关系来表示.
人教版数学九年级下册
知识精讲
人教版数学九年级下册
在平面直角坐标系中，有两点A(6，3)，B(6，0).以原点
的坐标变化的规律. (重点、难点)
3.了解四种图形变换 (平移、轴对称、旋转和位似) 的异同，并能在复杂图形中找出这些变换.
复习回顾
人教版数学九年级下册
∽
1.如图，若AB∥CD，则△OAB___△OCD，△OAB与△OCD是
位似中心
_____图形，点O是它们的_________；
位似
2.在平面直角坐标系中，若点A的坐标为(2，3)，则点A关于
(1)若点F的坐标为(4.5, 3),直接写出点A和点C的坐标;
(2)若正方形BEFG的边长为6，求点C的坐标.
解:(2)∵正方形ABCD与正方形BEFG是以原点
O为位似中心的位似图形，相似比是1:3，正方
形BEFG的边长为6
∴正方形ABCD的边长为2，OB:0E=1:3
∴0B:(0B+6)=1:3,解得0B=3
且相似比为2:1 (A1的对应点为A2,B1的对应点为B2);
解:如图，线段A2B2即为所求;
5 2
3
(3)连接AA2、BB2交于C点，则AC=_____.
THE END!
祝各位同学们学业进步、天天向上！
2.如图，△ABO三个顶点的坐标分别为A(4，-5)，B(6，
0)O(0，0).以原点O为位似中心，把这个三角形放大为原

第2课时 位似图形与坐标

第2课时 位似图形与坐标

·数学
探究点二:平面直角坐标系中的位似变换 【例2】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4), C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是
;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比
(1)以O点为位似中心在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比 为2),画出图形;
解:(1)如图.
·数学
(2)分别写出B,C两点的对应点B′,C′的坐标; (3)如果△OBC内部一点M的坐标为(x,y),写出M的对应点M′的坐标.
解:(2)B′(-6,2),C′(-4,-2). (3)M′(-2x,-2y).
为2∶1,点C2的坐标是
;
(3)△A2B2C2的面积是 平方单位.
·数学
【导学探究】 1.把△ABC向下平移4个单位长度则各顶点的 纵 2.点A2在线段BA的延长线上且BA2等于 2 BA.
解:(1)如图所示,C1(2,-2). (2)如图所示,C2(1,0).
(3)因为 A2 C22 =20,B2 C22 =20,A2 B22 =40, 所以△A2B2C2 是等腰直角三角形,
所以△A2B2C2 的面积是 1 × 20 × 20 =10.
2
坐标减去 4 .
·数学
1. 如图,已知△ABC三个顶点的坐标分别为(1,2),(-2,3),(-1,0),把它们的横 坐标和纵坐标都扩大到原来的2倍,得到点A′,B′,C′.下列说法正确的是 ( B) (A)△A′B′C′与△ABC位似,位似中心是点(1,0) (B)△A′B′C′与△ABC位似,位似中心是点(0,0) (C)△A′B′C′与△ABC相似,但不位似 (D)△A′B′C′与△ABC不相似

两个位似图形坐标之间的关系

两个位似图形坐标之间的关系
解析:根据以原点为位似图形的坐标特征，可得C，D点横、 纵坐标为A，B点横、纵坐标的同一个倍数的只有D.故选D.
3.如图所示，原点O是△ABC和△A1B1C1的位似中心，点A(1，0)与A1(-2，0)
是对应点，△ABC的面积是
3 2
，则△A1B1C1的面积是
6
.
解析:∵原点O是△ABC和△A1B1C1的位似中心，点
-4
变化,你有什么发现?
-6
A"
-8
A/
A
C' 2 4 C 6 8 9 101112
在平面直角坐标系中，以原点为位似中心,将一个图形按照相似比k放大或缩小， 当新图形与原图形在原点的同侧，这时新旧图形上对应点的坐标比为k; 当新图形与原图形在原点的异侧，这时新旧图形上对应点的坐标比为-k。
总结 一般地，在平面直角坐标系中，如果
以原点为位似中心，画出一个与原图
形位似的图形，使它与原图形的相似 比为k，那么与原图形上的点(x，y)对 应的位似图形上的点的坐标为(kx，ky) 或(-kx，-ky).
(教材例题)如图所示，△ABO三个顶点的坐标分别为A(-2，4)，
B(-2，0)，O(0，0)，以原点O为位似中心，画一个三角形，使它
• 练习 课本50页 1、2 • 作业 课本51页 3、5
思考
如图所示，正方形OEFG和正方形ABCD是位似图形，点F的 坐标为(-1，1)，点C的坐标为(-4，2)，求这两个正方形位似
中心的坐标.
【分析】 (1)两个位似图形的特征是什么?
(每对对应点与位似中心共线;对应线段 平行或在同一条直线上)
与△ABO的相似比为 3 .
2
分析：由于要画的图形是三角

位似图形对应点坐标变化规律及拓展

位似图形对应点坐标变化规律及拓展

位似图形对应点坐标变化规律及拓展
归纳图形点移动规律，可概括为“双曲线关于原点的对称性规律”。

即，点的水平（x）坐标无论如何变化，纵（y）坐标却要遵循特定的函数关系式。

按照此原理，绘制图形时可先
确定点的水平位置，再利用其他函数确定点的纵坐标，即可完成图形的绘制。

接下来要拓展的是，如果双曲线的曲率系数不定，那么可以由双曲线方程得出点移动规律。

例如，假设双曲线曲率系数是k，那么，
x^2=k*y^2
y^2=k^(-1) * x^2
可以看出，当k > 0时，在直角坐标系上，横坐标和纵坐标要做相反的运动，当k < 0时，横坐标和纵坐标要做相同的运动，而当k=0时，反而得到的是一条平行于横轴的直线。

另外，双曲线的能量关系也可以用来求解双曲线上特定点的位置机制：
能量关系式为：E = k*(x^2 + k^(-1)*y^2)
可以从中求得位置关系式：
x^2 = (E/k)*(1-k^(-1)*y^2)
以此类推，可以把这种求解机制扩展到定义域内的任意多边形上，按照多边形各顶点及其
位置属性计算出点移动规律，此类规律更为灵活，可以用于更多的图形绘制形式。

总之，双曲线点移动规律可概括为“双曲线关于原点的对称性规律”，通过其灵活性，可用
于绘制多边形，得出特定点的移动机制，并可以从能量方程上求解双曲线上特定点的位置
机制。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

九 年 级 数 学 导 学 案 年级 九 班级
学科 数 学 课题 位似图形与坐标 第 课时 总 课时 编制人 审核人 课型 新授课 使用者
教 学 内 容
学习目标：
1、 了解平面直角坐标系下位似变换图形坐标的特点.
2、 能够熟练准确地利用坐标变化将一个图形放大或缩小. 学习过程
一.复习回顾
1、把一个图形变成另一个图形，并保持图形形状不变的几何变换叫做_________.
2、如果两个图形不仅相似，而且每组对应点所在的直线__________，那么这样的几何变换叫做___________，这样的两个图形叫做___________．
3、图形在平面直角坐标系中作平移变换时坐标的变化规律是(h>0)： 向左平移h 个单位→),(b a (_ _,b)，向右平移h 个单位→),(b a (____,b)； 向上平移h 个单位,(),(a b a →___)，向下平移h 个单位,(),(a b a → __).
二.学习新课
阅读课本115-117页，回答下列问题：
1、在平面直角坐标系中，如果位似变换是以原点O 为位似中心，相似比为K （K ＞0），原图形上点的坐标为（x,y ），那么同向位似图形对应点的坐标为___________（K ＞0）.
2、在平面直角坐标系中，在作),(),(by ax y x →变换时，当0≠=b a 时为相似变换；当b a ≠时便不是相似变换，我们称之为___________ ．
3、在问题1中若K ＜0，则与K ＞0时的变换结果有什么不同？
4．如图，△ ABC 三个顶点坐标分别为A(2,3)，B(2,1)，C(6,2).
（1）将△ ABC 向左平移三个单位得到△ A 1B 1C 1，写出三点的坐标；
（2）写出△ ABC 关于x 轴对称的△ A 2B 2C 2三个顶点A 2、B 2、C 2的坐标；
（3）将△ ABC 绕点O 旋转180°得到△ A 3B 3C 3，写出三点的坐标．[来
三.尝试应用
1.如图，ABC ∆三个顶点坐标分别为()2,3A ()2,1B ()3,1C ，以点O 为位似中心，相似比为２，将ABC ∆放大，观察对应顶点坐标的变化，你有什么发现？
归纳：在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于；
四.达标测试
一、选择题
1．如图，以点O为位似中心，将△ABC缩小后得到△A′B′C′，已知
OB=3OB′，则△A′B′C′与△ABC的面积比为（）
A．1：3 B．1：4 C．1：5 D．1：9
2．如图，在平面直角坐标系中，已知点A（﹣3，6），B（﹣9，﹣3），以原点O为位似中心，相似比为，把△ABO缩小，则点A的对应点A′的坐
标是（）
A．（﹣1，2）
B．（﹣9，18）
C．（﹣9，18）或（9，﹣18）
D．（﹣1，2）或（1，﹣2）
二、解答题：
3.已知：如图△ABC三个顶点的坐标分别为A（0，﹣3）、B（3，﹣2）、C （2，﹣4），正方形网格中，每个小正方形的边长是1个单位长度．
（1）画出△ABC向上平移6个单位得到的△A1B1C1；
（2）以点C为位似中心，在网格中画出△A2B2C2，使△A2B2C2与△ABC位似，且△A2B2C2与△ABC的位似比为2：1，并直接写出点A2的坐标．
教后
反思。