选择、填空9

操作系统选择、填空、判断题（含答案）1.当每类资源只有⼀个个体时，下列说法中哪⼀个不正确(A )。

A.有循环等待必死锁B.死锁不⼀定有循环等待C.死锁必有循环等待D.被锁必在循环等待中2.作业调度的关键在于( C )。

A.选择恰当的进程管理程序B.⽤户作业准备充分C.选择恰当的作业调度算法D.有⼀个较好的操作环境3.下列关于进程与线程的叙述何者正确( A )。

A.⼀个进程可拥有多个线程B.⼀个线程只拥有⼀个进程C.⼀个进程只拥有⼀个线程D.⼀个线程可拥有多个进程4.系统抖动是指(B )。

A.使⽤机器时，屏幕闪烁的现象B.被调出的页⾯⼜⽴刻被调⼊所形成的频繁调⼊调出现象C.系统盘有问题，致使系统不稳定的现象D.由于主存分配不当，偶然造成主存不够的现象5.SPOOLing技术可以实现设备的( C )分配。

A.独占B.共享C.虚拟D.物理6.避免死锁的⼀个著名的算法是( D )。

A.先⼈先出算法B.优先级算法C.资源按序分配法D.银⾏家算法7.操作系统中利⽤信号量和P、V操作，(C )。

A.只能实现进程的互斥B.只能实现进程的同步C.可实现进程的互斥和同步D.可完成进程调度8.当进程因时间⽚段⽤完⽽让出处理时，该进程应转变为( B )状态。

A.等待B.就绪C.运⾏D.完成9.设计批处理多道系统，⾸要考虑是( A )。

A.系统效率与吞吐量B.灵活性和适应性C.实时性与可靠性D.交互性与响应时间10.⽂件系统中⽤( D )管理⽂件。

A.指针B.页表C.堆栈结构D.⽬录⼆、填空题（每空2分，共20分，请将答案填写在答题纸上，否则不予给分）1.多道批处理系统的优缺点:__资源利⽤率⾼____、_系统吞吐量⼤_____、平均周转时间长、⽆交互能⼒。

2.操作系统基本特征:并发、共享、__异步____、_虚拟______。

3.同步机制都应遵循的准则:空闲让进、忙则等待、___有限等待___、_让权等待_____。

4.在连续分配⽅式中，可通过紧凑来减少内存零头，但此时必须将有关程序和进⾏移动；⽽___动态重定位______是⼀种允许作业在运⾏过程中，在内存中进⾏移动的技术。

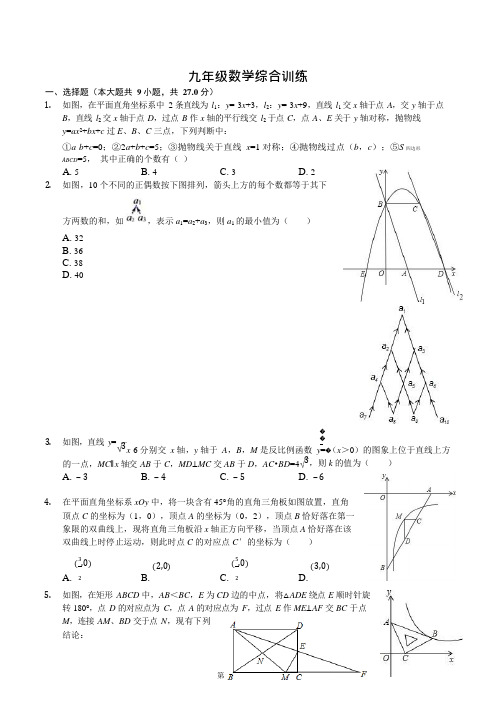
九年级数学综合训练一、选择题（本大题共9 小题，共27.0 分）1.如图，在平面直角坐标系中2 条直线为l1：y=-3x+3，l2：y=-3x+9，直线l1交x 轴于点A，交y 轴于点B，直线l2交x 轴于点D，过点B 作x 轴的平行线交l2于点C，点A、E 关于y 轴对称，抛物线y=ax2+bx+c 过E、B、C 三点，下列判断中：①a-b+c=0；②2a+b+c=5；③抛物线关于直线x=1 对称；④抛物线过点（b，c）；⑤S 四边形ABCD=5，其中正确的个数有（）A. 5B. 4C. 3D. 22.如图，10 个不同的正偶数按下图排列，箭头上方的每个数都等于其下方两数的和，如，表示a1=a2+a3，则a1的最小值为（）A.32B.36C.38D.403.如图，直线y= ��x -6 分别交x 轴，y 轴于A，B，M 是反比例函数y=�（x＞0）的图象上位于直线上方的一点，MC∥x 轴交AB 于C，MD⊥MC 交AB 于D，AC•BD=43，则k 的值为（）A. ‒ 3B. ‒ 4C. ‒ 5D. ‒ 64.在平面直角坐标系xOy 中，将一块含有45°角的直角三角板如图放置，直角顶点C 的坐标为（1，0），顶点A 的坐标为（0，2），顶点B 恰好落在第一象限的双曲线上，现将直角三角板沿x 轴正方向平移，当顶点A 恰好落在该双曲线上时停止运动，则此时点C 的对应点C′的坐标为（）(3,0) (2,0) (5,0) (3,0)A. 2B.C. 2D.5.如图，在矩形ABCD 中，AB＜BC，E 为CD 边的中点，将△ADE 绕点E 顺时针旋转180°，点D 的对应点为C，点A 的对应点为F，过点E 作ME⊥AF 交BC 于点M，连接AM、BD 交于点N，现有下列结论：35 ①AM =AD +MC ；②AM =DE +BM ；③DE 2=AD •CM ；④点 N 为△ABM 的外心． 其中正确的个数为（）A. 1 个B. 2 个C. 3 个D. 4 个6. 规定：如果关于 x 的一元二次方程 ax 2+bx +c =0（a ≠0）有两个实数根，且其中一个根是另一个根的 2倍，则称这样的方程为“倍根方程”．现有下列结论：①方程 x 2+2x -8=0 是倍根方程；②若关于 x 的方程 x 2+ax +2=0 是倍根方程，则 a =±3；③若关于 x 的方程 ax 2-6ax +c =0（a ≠0）是倍根方程，则抛物线 y =ax 2-6ax +c 与 x 轴的公共点的坐标是 （2，0）和（4，0）； 4 ④若点（m ，n ）在反比例函数 y =x 的图象上，则关于 x 的方程 mx 2+5x +n =0 是倍根方程． 上述结论中正确的有（ ）A. ①②B. ③④C. ②③D. ②④7. 如图，六边形 ABCDEF 的内角都相等，∠DAB =60°，AB =DE ，则下列结论成立的个数是（） ①AB ∥DE ；②EF ∥AD ∥BC ；③AF =CD ；④四边形 ACDF 是平行四边形；⑤六边形 ABCDEF 既是中心对称图形，又是轴对称图形．A. 2B. 3C. 4D. 58. 如图，在 Rt △ABC 中，∠C =90°，以△ABC 的一边为边画等腰三角形，使得它的第三个顶点在△ABC 的其他边上，则可以画出的不同的等腰三角形的个数最多为（ ）A. 4B. 5C. 6D. 79. 如图，矩形 ABCD 中，AE ⊥BD 于点 E ，CF 平分∠BCD ，交 EA 的延长线于点 F ，且 BC =4，CD =2，给出下列结论：①∠BAE =∠CAD ；4②∠DBC =30°；③AE =5 5；④AF =2 ，其中正确结论的个数有（ ）A. 1 个B. 2 个C. 3 个D. 4 个二、填空题（本大题共 10 小题，共 30.0 分）10.如图，在Rt△ABC 中，∠BAC=30°，以直角边AB 为直径作半圆交AC 于点D，以AD 为边作等边△ADE，延长ED 交BC 于点F，BC=2 3，则图中阴影部分的面积为．（结果不取近似值）11.如图，在6×6 的网格内填入1 至6 的数字后，使每行、每列、每个小粗线宫中的数字不重复，则a×c=．12.如图，正方形ABCD 中，BE=EF=FC，CG=2GD，BG 分别交AE，AF 于M，N．下列结论：4 �M 3 1①AF⊥BG；②BN=3NF；③M G=8；④S 四边形CGNF=2S 四边形ANGD．其中正确的结论的序号是．13.已知：如图，在△AOB 中，∠AOB=90°，AO=3cm，BO=4cm．将△AOB 绕顶点O，按顺时针方向旋转到△A1OB1处，此时线段OB1与AB 的交点D 恰好为AB 的中点，则线段B1D= cm．14.如图，边长为4 的正六边形ABCDEF 的中心与坐标原点O 重合，AF∥x 轴，将正六边形ABCDEF 绕原点O 顺时针旋转n 次，每次旋转60°．当n=2017 时，顶点A 的坐标为．15.如图，在Rt△ABC 中，BC=2，∠BAC=30°，斜边AB 的两个端点分别在相互垂直的射线OM、ON 上滑动，下列结论：①若C、O 两点关于AB 对称，则OA=2 3；②C、O 两点距离的最大值为4；③若AB 平分CO，则AB⊥CO；�④斜边AB 的中点D 运动路径的长为2；其中正确的是（把你认为正确结论的序号都填上）．16.如图，∠AOB 的边OB 与x 轴正半轴重合，点P 是OA 上的一动点，点N（3，0）是OB 上的一定点，点M 是ON 的中点，∠AOB=30°，要使PM+PN 最小，则点P 的坐标为．17.在一条笔直的公路上有A、B、C 三地，C 地位于A、B 两地之间，甲车从A地沿这条公路匀速驶向C 地，乙车从B 地沿这条公路匀速驶向A 地，在甲车出发至甲车到达C 地的过程中，甲、乙两车各自与C 地的距离y（km）与甲车行驶时间t（h）之间的函数关系如图所示．下列结论：①甲车出发2h 时，两车相遇；②乙车出发1.5h 时，两车相距170km；③乙车出5发27h 时，两车相遇；④甲车到达C 地时，两车相距40km．其中正确的是（填写所有正确结论的序号）．�18.如图，在平面直角坐标系中，OA=AB，∠OAB=90°，反比例函数y=x（x＞0）的图象经过A，B 两点．若点A 的坐标为（n，1），则k 的值为．19.如图，在平面直角坐标系中，△ABC 的顶点坐标分别为A（-1，1），B（0，-2），C（1，0），点P（0，2）绕点A 旋转180°得到点P1，点P1绕点B 旋转180°得到点P2，点P2绕点C 旋转180°得到点P3，点P3绕点A 旋转180°得到点P4，…，按此作法进行下去，则点P2017的坐标为．答案和解析1.【答案】C【解析】解：∵直线l1：y=-3x+3 交x 轴于点A，交y 轴于点B，∴A（1，0），B（0，3），∵点A、E 关于y 轴对称，∴E（-1，0）．∵直线l2：y=-3x+9 交x 轴于点D，过点B 作x 轴的平行线交l2 于点C，∴D（3，0），C 点纵坐标与B 点纵坐标相同都是3，把y=3 代入y=-3x+9，得3=-3x+9，解得x=2，∴C（2，3）．∵抛物线y=ax2+bx+c 过E、B、C 三点，∴，解得，∴y=-x2+2x+3．①∵抛物线y=ax2+bx+c 过E（-1，0），∴a-b+c=0，故①正确；②∵a=-1，b=2，c=3，∴2a+b+c=-2+2+3=3≠5，故②错误；③∵抛物线过B（0，3），C（2，3）两点，∴对称轴是直线x=1，∴抛物线关于直线x=1 对称，故③正确；④∵b=2，c=3，抛物线过C（2，3）点，∴抛物线过点（b，c），故④正确；⑤∵直线l1∥l2，即AB∥CD，又BC∥AD，∴四边形ABCD 是平行四边形，∴S 四边形ABCD=BC•OB=2×3=6≠5，故⑤错误．综上可知，正确的结论有3个．故选：C．根据直线l1的解析式求出A（1，0），B（0，3），根据关于y 轴对称的两点坐标特征求出E（- 1，0）．根据平行于x 轴的直线上任意两点纵坐标相同得出C 点纵坐标与B 点纵坐标相同都是3，再根据二次函数图象上点的坐标特征求出C（2，3）．利用待定系数法求出抛物线的解析式为y=-x2+2x+3，进而判断各选项即可．本题考查了抛物线与x 轴的交点，一次函数、二次函数图象上点的坐标特征，关于y 轴对称的两点坐标特征，平行于x 轴的直线上任意两点坐标特征，待定系数法求抛物线的解析式，平行四边形的判定及面积公式，综合性较强，求出抛物线的解析式是解题的关键．2.【答案】D【解析】解：∵a1=a2+a3=a4+a5+a5+a6=a7+a8+a8+a9+a8+a9+a9+a10=a7+3（a8+a9）+a10，∴要使a1 取得最小值，则a8+a9 应尽可能的小，取a8=2、a9=4，∵a5=a8+a9=6，则a7、a10 中不能有6，若a7=8、a10=10，则a4=10=a10，不符合题意，舍去；若a7=10、a10=8，则a4=12、a6=4+8=12，不符合题意，舍去；若a7=10、a10=12，则a4=10+2=12、a6=4+12=16、a2=12+6=18、a3=6+16=22、a1=18+22=40，符合题意；综上，a1的最小值为40，故选：D．由a1=a7+3（a8+a9）+a10 知要使a1 取得最小值，则a8+a9 应尽可能的小，取a8=2、a9=4，根据a5=a8+a9=6，则a7、a10 中不能有6，据此对于a7、a8，分别取8、10、12 检验可得，从而得出答案．本题主要考查数字的变化类，根据题目要求得出a1取得最小值的切入点是解题的关键．3.【答案】A【解析】解：过点D 作DE⊥y 轴于点E，过点C 作CF⊥x 轴于点F，令x=0 代入y= x-6，∴y=-6，∴B（0，-6），∴OB=6，令y=0 代入y= x-6，∴x=2 ，∴（2 ，0），∴OA=2 ，∴勾股定理可知：AB=4 ，∴sin∠OAB= = ，cos∠OAB= =设M（x，y），∴CF=-y，ED=x，∴sin∠OAB= ，∴AC=- y，∵cos∠OAB=cos∠EDB= ，∴BD=2x，∵AC•BD=4，∴- y×2x=4 ，∴xy=-3，∵M 在反比例函数的图象上，∴k=xy=-3，故选（A）过点D 作DE⊥y 轴于点E，过点C 作CF⊥x 轴于点F，然后求出OA 与OB 的长度，即可求出∠OAB 的正弦值与余弦值，再设M（x，y），从而可表示出BD 与AC 的长度，根据AC•BD=4列出即可求出k 的值．本题考查反比例函数与一次函数的综合问题，解题的关键是根据∠OAB 的锐角三角函数值求出BD、AC，本题属于中等题型．4.【答案】C【解析】解：过点B 作BD⊥x 轴于点D，∵∠ACO+∠BCD=90°，∠OAC+∠ACO=90°，∴∠OAC=∠BCD，在△ACO 与△BCD 中，∴△ACO➴△BCD（AAS）∴OC=BD，OA=CD，∵A（0，2），C（1，0）∴OD=3，BD=1，∴B（3，1），∴设反比例函数的解析式为y= ，将B（3，1）代入y= ，∴k=3，∴y= ，∴把y=2 代入y= ，∴x= ，当顶点A 恰好落在该双曲线上时，此时点A 移动了个单位长度，∴C 也移动了个单位长度，此时点C 的对应点C′的坐标为（，0）故选：C．过点B 作BD⊥x 轴于点D，易证△ACO➴△BCD（AAS），从而可求出B 的坐标，进而可求出反比例函数的解析式，根据解析式与 A 的坐标即可得知平移的单位长度，从而求出 C 的对应点．本题考查反比例函数的综合问题，涉及全等三角形的性质与判定，反比例函数的解析式，平移的性质等知识，综合程度较高，属于中等题型．5.【答案】B【解析】解：∵E 为CD 边的中点，∴DE=CE，又∵∠D=∠ECF=90°，∠AED=∠FEC，∴△ADE➴△FCE，∴AD=CF，AE=FE，又∵ME⊥AF，∴ME 垂直平分AF，∴AM=MF=MC+CF，∴AM=MC+AD，故①正确；如图，延长CB 至G，使得∠BAG=∠DAE，由AM=MF，AD∥BF，可得∠DAE=∠F=∠EAM，可设∠BAG=∠DAE=∠EAM=α，∠BAM=β，则∠AED=∠EAB=∠GAM=α+β，由∠BAG=∠DAE，∠ABG=∠ADE=90°，可得△ABG∽△ADE，∴∠G=∠AED=α+β，∴∠G=∠GAM，∴AM=GM=BG+BM，由△ABG∽△ADE，可得= ，而AB＜BC=AD，∴BG＜DE，∴BG+BM＜DE+BM，即AM＜DE+BM，∴AM=DE+BM 不成立，故②错误；∵ME⊥FF，EC⊥MF，∴EC2=CM×CF，又∵EC=DE，AD=CF，∴DE2=AD•CM，故③正确；∵∠ABM=90°，∴AM 是△ABM 的❧➓圆的直径，∵BM＜AD，∴当BM∥AD 时，= ＜1，∴N 不是AM 的中点，∴点N 不是△ABM 的❧心，故④错误．综上所述，正确的结论有2 个，故选：B．根据全等三角形的性质以及线段垂直平分线的性质，即可得出AM=MC+AD；根据△ABG∽△ ADE，且AB＜BC，即可得出BG＜DE，再根据AM=GM=BG+BM，即可得出AM=DE+BM 不成立；根据ME⊥FF，EC⊥MF，运用射影定理即可得出EC2=CM×CF，据此可得DE2=AD•CM 成立；根据N 不是AM 的中点，可得点N 不是△ABM 的❧心．本题主要考查了相似三角形的判定与性质，全等三角形的判定与性质，矩形的性质以及旋转的性质的综合应用，解决问题的关键是运用全等三角形的对应边相等以及相似三角形的对应边成比例进行推导，解题时注意：三角形❧➓圆的圆心是三角形三条边垂直平分线的交点，叫做三角形的❧心，故❧心到三角形三个顶点的距离相等．6.【答案】C【解析】解：①由x2-2x-8=0，得（x-4）（x+2）=0，解得x1=4，x2=-2，∵x1≠2x2，或x2≠2x1，1 1 ∴方程 x 2-2x-8=0 不是倍根方程． 故①错误；②关于 x 的方程 x 2+ax+2=0 是倍根方程，∴设 x 2=2x 1，∴x 1•x 2=2x 2=2，∴x 1=±1，当 x 1=1 时 ，x 2=2，当 x 1=-1 时 ，x 2=-2，∴x 1+x 2=-a=±3，∴a=±3，故②正确；③关于 x 的方程 ax 2-6ax+c=0（a≠0）是倍根方程，∴x 2=2x 1，∵抛物线 y=ax 2-6ax+c 的对称轴是直线 x=3，∴抛物线 y=ax 2-6ax+c 与 x 轴的交点的坐标是（2，0）和（4，0），故③正确；④∵点（m ，n ）在反比例函数 y= 的图象上，∴mn=4，解 mx 2+5x+n=0 得 x 1=- ，x 2=- ，∴x 2=4x 1，∴关于 x 的方程 mx 2+5x+n=0 不是倍根方程；故选：C ．①通过解方程得到该方程的根，结合“倍根方程”的定义进行判断；②设 x 2=2x 1，得到 x 1•x 2=2x 2=2，得到当 x 1=1 时，x 2=2，当 x 1=-1 时，x 2=-2，于是得到结论；③根据“倍根方程”的定义即可得到结论；④若点（m，n）在反比例函数y= 的图象上，得到mn=4，然后解方程mx2+5x+n=0 即可得到正确的结论；本题考查了反比例函数图象上点的坐标特征，根与系数的关系，正确的理解倍根方程的定义是解题的关键．7.【答案】D【解析】解：∵六边形ABCDEF 的内角都相等，∴∠EFA=∠FED=∠FAB=∠ABC=120°，∵∠DAB=60°，∴∠DAF=60°，∴∠EFA+∠DAF=180°，∠DAB+∠ABC=180°，∴AD∥EF∥CB，故②正确，∴∠FED+∠EDA=180°，∴∠EDA=∠ADC=60°，∴∠EDA=∠DAB，∴AB∥DE，故①正确，∵∠FAD=∠EDA，∠CDA=∠BAD，EF∥AD∥BC，∴四边形EFAD，四边形BCDA 是等腰梯形，∴AF=DE，AB=CD，∵AB=DE，∴AF=CD，故③正确，连➓CF 与AD 交于点O，连➓DF、AC、AE、DB、BE．∵∠CDA=∠DAF，∴AF∥CD，AF=CD，∴四边形AFDC 是平行四边形，故④正确，同法可证四边形AEDB 是平行四边形，∴AD 与CF，AD 与BE 互相平分，∴OF=OC，OE=OB，OA=OD，∴六边形ABCDEF 既是中心对称图形，故⑤正确，故选D．根据六边形ABCDEF 的内角都相等，∠DAB=60°，平行线的判定，平行四边形的判定，中心对称图形的定义一一判断即可．本题考查平行四边形的判定和性质、平行线的判定和性质、轴对称图形、中心对称图形等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．8.【答案】D【解析】解：如图：故选：D．①以B 为圆心，BC 长为半径画弧，交AB 于点D，△BCD 就是等腰三角形；②以A 为圆心，AC 长为半径画弧，交AB 于点E，△ACE 就是等腰三角形；③以C 为圆心，BC 长为半径画弧，交AC 于点F，△BCF 就是等腰三角形；④以C 为圆心，BC 长为半径画弧，交AB 于点K，△BCK 就是等腰三角形；⑤作AB 的垂直平分线交AC 于G，则△AGB 是等腰三角形；➅作BC 的垂直平分线交AB 于I，则△BCI 和△ACI 是等腰三角形．本题考查了等腰三角形的判定的应用，主要考查学生的理解能力和动手操作能力．9.【答案】C【解析】解：在矩形ABCD 中，∵∠BAD=90°，∵AE⊥BD，∴∠AED=90°，∴∠ADE+∠DAE=∠DAE+∠BAE=90°，∴∠BAE=∠ADB，∵∠CAD=∠ADB，∴∠BAE=∠CAD，故①正确；∵BC=4，CD=2，∴tan∠DBC= = ，∴∠DBC≠30°，故②错误；∵BD= =2 ，∵AB=CD=2，AD=BC=4，∵△ABE∽△DBA，∴，即，∴AE= ；故③正确；∵CF 平分∠BCD，∴∠BCF=45°，∴∠ACF=45°-∠ACB，∵AD∥BC，∴∠DAC=∠BAE=∠ACB，∴∠EAC=90°-2∠ACB，∴∠EAC=2∠ACF，∵∠EAC=∠ACF+∠F，∴∠ACF=∠F，∴AF=AC，∵AC=BD=2 ，∴AF=2 ，故④正确；故选C．根据余角的性质得到∠BAE=∠ADB，等量代换得到∠BAE=∠CAD，故①正确；根据三角函数的定义得到tan∠DBC= = ，于是得到∠DBC≠30°，故②错误；由勾股定理得到BD==2 ，根据相似三角形的性质得到AE= ；故③正确；根据角平分线的定义得到∠BCF=45°，求得∠ACF=45°-∠ACB，推出∠EAC=2∠ACF，根据❧角的性质得到∠EAC=∠ACF+∠F，得到∠ACF=∠F，根据等腰三角形的判定得到AF=AC，于是得到AF=2 ，故④正确．本题考查了矩形的性质，相似三角形的判定和性质，三角形的❧角的性质，角平分线的定义，熟练掌握相似三角形的判定和性质是解题的关键．10.【答案】3【解析】3 3-2π解：如图所示：设半圆的圆心为O，连➓DO，过D 作DG⊥AB 于点G，过D 作DN⊥CB 于点N，∵在Rt△ABC 中，∠BAC=30°，∴∠ACB=60°，∠ABC=90°，∵以AD 为边作等边△ADE，∴∠EAD=60°，∴∠EAB=60°+30°=90°，可得：AE∥BC，则△ADE∽△CDF，∴△CDF 是等边三角形，∵在Rt△ABC 中，∠BAC=30°，BC=2 ，∴AC=4 ，AB=6，∠DOG=60°，则AO=BO=3，故DG=DO•sin60°=，则AD=3 ，DC=AC-AD= ，故DN=DC•sin60°=×= ，则S 阴影=S△ABC-S△AOD-S 扇形DOB-S△DCF= ×2 ×6- ×3×- - × ×=3 - π．故答案为：3 - π．根据题意结合等边三角形的性质分别得出AB，AC，AD，DC 的长，进而利用S 阴影=S△ABC-S△AOD-S 扇形DOB-S△DCF 求出答案．此题主要考查了扇形面积求法以及等边三角形的性质和锐角三角函数关系等知识，正确分割图形是解题关键．11.【答案】2【解析】解：对各个小宫格编号如下：先看己：已经有了数字3、5、6，缺少1、2、4；观察发现：4 不能在第四列，2 不能在第五列，而2 不能在第六列；所以2 只能在第六行第四列，即a=2；则b 和c 有一个是1，有一个是4，不确定，如下：观察上图发现：第四列已经有数字2、3、4、6，缺少1 和5，由于5 不能在第二行，所以5 在第四行，那么1 在第二行；如下：再看乙部分：已经有了数字1、2、3，缺少数字4、5、6，观察上图发现：5 不能在第六列，所以5在第五列的第一行；4 和6 在第六列的第一行和第二行，不确定，分两种情况：①当4 在第一行时，6 在第二行；那么第二行第二列就是4，如下：再看甲部分：已经有了数字1、3、4、5，缺少数字2、6，观察上图发现：2 不能在第三列，所以2 在第二列，则6 在第三列的第一行，如下：观察上图可知：第三列少1 和4，4 不能在第三行，所以4 在第五行，则1 在第三行，如下：观察上图可知：第五行缺少1 和2，1 不能在第1 列，所以1 在第五列，则2 在第一列，即c=1，所以b=4，如下：观察上图可知：第六列缺少1 和2，1 不能在第三行，则在第四行，所以2 在第三行，如下：再看戊部分：已经有了数字2、3、4、5，缺少数字1、6，观察上图发现：1 不能在第一列，所以1 在第二列，则6 在第一列，如下：观察上图可知：第一列缺少3 和4，4 不能在第三行，所以4 在第四行，则3 在第三行，如下：观察上图可知：第二列缺少5 和6，5 不能在第四行，所以5 在第三行，则6 在第四行，如下：观察上图可知：第三行第五列少6，第四行第五列少3，如下：所以，a=2，c=1，ac=2；②当6 在第一行，4 在第二行时，那么第二行第二列就是6，如下：再看甲部分：已经有了数字1、3、5、6，缺少数字2、4，观察上图发现：2 不能在第三列，所以2 在第2 列，4 在第三列，如下：观察上图可知：第三列缺少数字1 和6，6 不能在第五行，所以6 在第三行，则1 在第五行，所以c=4，b=1，如下：观察上图可知：第五列缺少数字3 和6，6 不能在第三行，所以6 在第四行，则3 在第三行，如下：观察上图可知：第六列缺少数字1 和2，2 不能在第四行，所以2 在第三行，则1 在第四行，如下：观察上图可知：第三行缺少数字1 和5，1 和5 都不能在第一列，所以此种情况不成立；综上所述：a=2，c=1，a×c=2；故答案为：2．粗线把这个数独分成了6 块，为了便于解答，对各部分进行编号：甲、乙、丙、丁、戊、己，先从各部分中数字最多的己出发，找出其各个小方格里面的数，再根据每行、每列、每小宫格都不出现重复的数字进行推算．本题是六阶数独，比较复杂，关键是找出突破口，先推算出一个区域或者一行、一列，再逐步的进行推算．12.【答案】①③【解析】解：①∵四边形ABCD 为正方形，∴AB=BC=CD，∵BE=EF=FC，CG=2GD，∴BF=CG，∵在△ABF 和△BCG 中，，∴△ABF➴△BCG，∴∠BAF=∠CBG，∵∠BAF+∠BFA=90°，∴∠CBG+∠BFA=90°，即AF⊥BG；①正确；②∵在△BNF 和△BCG 中，，∴△BNF∽△BCG，∴ = = ，∴BN= NF；②错误；③作EH⊥AF，令AB=3，则BF=2，BE=EF=CF=1，AF= = ，∵S△ABF= AF•BN=AB•BF，∴BN= ，NF= BN= ，∴AN=AF-NF= ，∵E 是BF 中点，∴EH 是△BFN 的中位线，∴EH= ，NH= ，BN∥EH，∴AH= ， = ，解得：MN= ，∴BM=BN-MN= ，MG=BG-BM= ，∴ = ；③正确；④连➓AG，FG，根据③中结论，则NG=BG-BN= ，∵S 四边形CGNF=S△CFG+S△GNF= CG•CF+NF•NG=1+= ，S 四边形ANGD=S△ANG+S△ADG= AN•GN+AD•DG= + = ，∴S 四边形CGNF≠S 四边形ANGD，④错误；故答案为①③．①易证△ABF➴△BCG，即可解题；②易证△BNF∽△BCG，即可求得的值，即可解题；③作EH⊥AF，令AB=3，即可求得MN，BM 的值，即可解题；④连➓AG，FG，根据③中结论即可求得S 四边形CGNF 和S 四边形ANGD，即可解题．本题考查了全等三角形的判定和性质，考查了相似三角形的判定和对应边成比例的性质，本题中令AB=3 求得AN，BN，NG，NF 的值是解题的关键．13.【答案】1.5【解析】解：∵在△AOB 中，∠AOB=90°，AO=3cm，BO=4cm，∴AB= =5cm，∵点D 为AB 的中点，∴OD= AB=2.5cm．∵将△AOB 绕顶点O，按顺时针方向旋转到△A1OB1 处，∴OB1=OB=4cm，∴B1D=OB1-OD=1.5cm．故答案为1.5．先在直角△AOB 中利用勾股定理求出AB= =5cm，再利用直角三角形斜边上的中线等于斜边的一半得出OD= AB=2.5cm．然后根据旋转的性质得到OB1=OB=4cm，那么B1D=OB1-OD=1.5cm．本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了直角三角形斜边上的中线等于斜边的一半的性质以及勾股定理．14.【答案】（2，2 3）【解析】解：2017×60°÷360°=336…1，即与正六边形ABCDEF 绕原点O 顺时针旋转1 次时点A 的坐标是一样的．当点A 按顺时针旋转60°时，与原F 点重合．连➓OF，过点F 作FH⊥x 轴，垂足为H；由已知EF=4，∠FOE=60°（正六边形的性质），∴△OEF 是等边三角形，∴OF=EF=4，∴F（2，2 ），即旋转2017 后点A 的坐标是（2，2 ），故答案是：（2，2 ）．将正六边形ABCDEF 绕原点O 顺时针旋转2017 次时，点A 所在的位置就是原F 点所在的位置．此题主要考查了正六边形的性质，坐标与图形的性质-旋转．此题难度适中，注意掌握辅助线的作法，注意数形结合思想的应用．15.【答案】①②③【解析】解：在Rt△ABC 中，∵BC=2，∠BAC=30°，∴AB=4，AC= =2 ，①若C、O 两点关于AB 对称，如图1，∴AB 是OC 的垂直平分线，则OA=AC=2 ；所以①正确；②如图1，取AB 的中点为E，连➓OE、CE，∵∠AOB=∠ACB=90°，∴OE=CE= AB=2，当OC 经过点E 时，OC 最大，则C、O 两点距离的最大值为4；所以②正确；③如图2，同理取AB 的中点E，则OE=CE，∵AB 平分CO，∴OF=CF，∴AB⊥OC，所以③正确；④如图3，斜边AB 的中点D 运动路径是：以O 为圆心，以2 为半径的圆周的，则：=π．所以④不正确；综上所述，本题正确的有：①②③；故答案为：①②③．①先根据直角三角形30°的性质和勾股定理分别求AC 和AB，由对称的性质可知：AB 是OC 的垂直平分线，所以OA=AC；②当OC 经过AB 的中点E 时，OC 最大，则C、O 两点距离的最大值为4；③如图2，根据等腰三角形三线合一可知：AB⊥OC；④如图3，半径为2，圆心角为90°，根据弧长公式进行计算即可．本题是三角形的综合题，考查了直角三角形30°的性质、直角三角形斜边中线的性质、等腰三角形的性质、轴对称的性质、线段垂直平分线的性质、动点运动路径问题、弧长公式，熟练掌握直角三角形斜边中线等于斜边一半是本题的关键，难度适中．3 316.【答案】（2， 2 ）【解析】解：作N 关于OA 的对称点N′，连➓N′M 交OA 于P，则此时，PM+PN 最小，∵OA 垂直平分NN′，∴ON=ON′，∠N′ON=2∠AON=60°，∴△NON′是等边三角形，∵点M 是ON 的中点，∴N′M⊥ON，∵点N（3，0），∴ON=3，∵点M 是ON 的中点，∴OM=1.5，∴PM= ，∴P（，）．故答案为：（，）．作N 关于OA 的对称点N′，连➓N′M 交OA 于P，则此时，PM+PN 最小，由作图得到ON=ON′，∠N′ON=2∠AON=60°，求得△NON′是等边三角形，根据等边三角形的性质得到N′M⊥ON，解直角三角形即可得到结论．本题考查了轴对称-最短路线问题，等边三角形的判定和性质，解直角三角形，关键是确定P 的位置．17.【答案】②③④【解析】解：①观察函数图象可知，当t=2 时，两函数图象相交，∵C 地位于A、B 两地之间，∴交点代表了两车离C 地的距离相等，并不是两车相遇，结论①错误；②甲车的速度为240÷4=60（km/h），乙车的速度为200÷（3.5-1）=80（km/h），∵（240+200-60-170）÷（60+80）=1.5（h），∴乙车出发1.5h 时，两车相距170km，结论②正确；③∵（240+200-60）÷（60+80）=2 （h），∴乙车出发2 h 时，两车相遇，结论③正确；④∵80×（4-3.5）=40（km），∴甲车到达C 地时，两车相距40km，结论④正确．综上所述，正确的结论有：②③④．故答案为：②③④．①观察函数图象可知，当t=2 时，两函数图象相交，结合交点代表的意义，即可得出结论①错误；②根据速度=路程÷时间分别求出甲、乙两车的速度，再根据时间=路程÷速度和可求出乙车出发1.5h 时，两车相距170km，结论②正确；③根据时间=路程÷速度和可求出乙车出发2 h 时，两车相遇，结论③正确；④结合函数图象可知当甲到C 地时，乙车离开C 地0.5 小时，根据路程=速度×时间，即可得出结论④正确．综上即可得出结论．本题考查了一次函数的应用，根据函数图象逐一分析四条结论的正误是解题的关键．18.【答案】【解析】5 ‒ 1 2解：作AE⊥x 轴于E，BF⊥x 轴于F，过B 点作BC⊥y 轴于C，交AE 于G，如图所示：则AG⊥BC，∵∠OAB=90°，∴∠OAE+∠BAG=90°，∵∠OAE+∠AOE=90°，∴∠AOE=∠GAB ，在△AOE 和△BAG 中，，∴△AOE ➴△BAG （AAS ），∴OE=AG ，AE=BG ，∵点 A （n ，1），∴AG=OE=n ，BG=AE=1，∴B （n+1，1-n ），∴k=n×1=（n+1）（1-n ），整理得：n 2+n-1=0，解得：n= ∴n=，（负值舍去）， ∴k=故答案为： ；．作 AE ⊥x 轴于 E ，BF ⊥x 轴于 F ，过 B 点作 BC ⊥y 轴于 C ，交 AE 于 G ，则 AG ⊥BC ，先求得△ AOE ➴△BAG ，得出 AG=OE=n ，BG=AE=1，从而求得 B （n+1，1-n ），根据 k=n×1=（n+1）（1-n ）得出方程，解方程即可．本题考查了全等三角形的判定与性质、反比例函数图象上点的坐标特征、解方程等知识；熟练掌握反比例函数图象上点的坐标特征，证明三角形全等是解决问题的关键．19.【答案】（-2，0）【解析】解：如图所示，P 1（-2，0），P 2（2，-4），P 3（0，4），P 4（-2，-2），P 5（2，-2），P 6（0，2），发现 6 次一个循环，∵2017÷6=336…1，∴点 P 2017 的坐标与 P 1 的坐标相同，即 P 2017（-2，0），故答案为（-2，0）．画出P1～P6，寻找规律后即可解决问题．本题考查坐标与图形的性质、点的坐标等知识，解题的关键是循环探究问题的方法，属于中考常考题型．“”“”At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。

选择填空练习题1. 魏晋时期，丞相才任命的从九品官员称为____________。

A. 御史B. 主簿C. 前将军D. 中书令2. 中国古代四大美女之一的貂蝉是哪个时期的人物？A. 春秋时期B. 三国时期C. 汉朝D. 唐朝3. 以下哪位是中国五代十国时期的皇帝？A. 李世民B. 宋太祖C. 刘表D. 刘宗元4. 《红楼梦》是中国古代四大名著之一，它的作者是____________。

B. 李白C. 施耐庵D. 曹雪芹5. 魏晋时期，以下哪位作家是长篇小说的代表作家？A. 柳宗元B. 陆游C. 陶渊明D. 蔡东藩6. 被称为中国古代文学史上“文学骑士”的作家是____________。

A. 杜甫B. 李清照C. 苏轼D. 辛弃疾7. 以下哪位是中国唐代的文学家？A. 王羲之B. 王勃D. 王维8. 以下哪部作品被誉为中国古代文学中最早的长篇小说？A. 《西游记》B. 《水浒传》C. 《红楼梦》D. 《三国演义》9. 以下诗句中，描述了“世界美”的是：A. 春风十里不如你B. 千山鸟飞绝，万径人踪灭C. 春花秋月何时了D. 满地都是黄金10. 以下哪个不是中国古代文学典籍中的作品？A. 《礼记》B. 《左传》C. 《秋水共长天一色》D. 《史记》11. 以下哪位是中国唐代的诗人？A. 杜牧B. 陆游C. 辛弃疾D. 王昌龄12. 以下哪个是中国古代五大笔记小说之一？A. 《水浒传》B. 《红楼梦》C. 《聊斋志异》D. 《三国演义》13. 以下哪位是中国古代文学史上以诗人身份著称的政治家？A. 苏轼B. 李商隐C. 杜牧D. 陆游14. 下列哪个选项是描写雪的古诗？A. 万物生光辉，华夏尽可笑B. 读书破万卷，下笔如有神C. 白日依山尽，黄河入海流D. 日暮乡关何处是，烟波江上使人愁15. 中国古代诗词之父被誉为：A. 杜甫B. 苏轼C. 李白D. 白居易16. 以下哪位不是中国唐代的名将？A. 岳飞B. 李靖C. 郭子仪D. 杨广17. 以下哪位是中国古代文学史上以词人身份著称的文学家？A. 李白B. 杜牧C. 辛弃疾D. 陆游18. 以下哪部作品被誉为中国古代文学中的杰作？A. 《庐山谣》B. 《把酒问月》C. 《徐霞客游记》D. 《水调歌头》19. “梅花香自苦寒来”出自以下哪位诗人的作品？A. 王维B. 王之涣C. 陆游D. 白居易20. 以下哪位是中国明代的文学家？A. 羊欢B. 袁宏道C. 贾仲明D. 高星煊注意：文章只包含选择题，选项和答案并未给出。

专题 09 阅读理解问题例 1．我们把 1，1，2， 3，5，8，13， 21， 这组数称为斐波那契数列，为了进一步研究，挨次以这列数为半径作 90°圆弧 PP ，PP ，PP ， 获得斐波那契螺旋线，而后按序连接， ， ， 获得螺旋折线（如图） ，已知点 P （0， 1）， PP PP PPP （－ 1，0），（ 0，－ 1），则该折线上的点 的坐标为（ ）P PA ．（－ 6，24）B ．（－ 6，25）C ．（－ 5，24）D ．（－ 5，25） 同类题型 1.1 定义 [x]表示不超出实数 x 的最大整数，如 [1.8] ＝1，[－ 1.4]＝－12，[－3]＝－ 3．函数 y ＝[x] 的图象以下图，则方程[x] ＝ x 的解为（）2A ．0 或 2B ．0 或 2C ．1 或－ 2D ． 2或－ 2同类题型 1.2 nmn ﹣1m ﹣1对于函数 y ＝ x ＋ x ，我们定义y'＝ nx ＋ mx （ m 、 n 为常数）．比如 y ＝x 4＋x 2，则 y'＝4x 3＋2x ．已知： y ＝1x 3＋（ m ﹣1）x 2＋m 2x ．3（1）若方程 y ′＝0 有两个相等实数根，则 m 的值为 ；（2）若方程 y ′＝m ﹣1有两个正数根，则 m 的取值范围为．4例 2．将一枚六个面的编号分别为 1，2，3，4，5，6 的质地平均的正方体骰子先后扔掷两次，记第一次掷出的点数为 a ，第二次掷出的点数为 b ，则使对于x ，y 的方程组 {ax ＋by ＝3)有正数解的概率为 ___．x ＋2y ＝2同类题型 2.1 六个面上分别标有1，1，2，3， 4， 5 六个数字的平均立方体的表面睁开图以下图，掷这个立方体一次，记向上一面的数为平面直角坐标系 中某个点的横坐标，朝下一面的数为该点的纵坐标．则获得的坐标落在抛物线y ＝2x －x 上的概率是（ ）A ．2 B ．1C ．1D ．13639同类题型 2.2 把一枚六个面编号分别为 1，2，3， 4，5， 6 的质地平均的正方体骰子先后扔掷 2 次，若两个正面向上的编号分别为m 、n ，则二次函数 y ＝x ＋mx ＋n 的图象与 x 轴没有公共点的概率是 ________．同类题型2.3 如图，正方形ABCD的边长为2，将长为2 的线段QR 的两头放在正方形的相邻的两边上同时滑动．假如点Q 从点A 出发，沿图中所示方向按A →B →C →D →A 滑动到A 止，同时点R 从点 B 出发，沿图中所示方向按B →C →D →A →B 滑动到B 止．点N 是正方形ABCD内任一点，把N 点落在线段 QR 的中点M 所经过的路线围成的图形内的概率记为P ，则P ＝（）4－ππ 1π－1A ．B ．C ．D ．4444同类题型 2.4 从－ 1， 1， 2 这三个数字中，随机抽取一个数，记为 a ，那么，使对于 x 的一次函数 y ＝2x ＋a 的图象与 x 轴、 y 轴围成的三角形的面积为1，4且使对于 x 的不等式组 {x ＋2 ≤a 有解的概率为 _________．－)1 x ≤2a例 3．若 f （n ）为的各位数字之和，如 ＋1＝197，1＋9 ＋ （是随意正整数）14 n 1 n＋7＝17，则 f （ 14）＝ 17，记 （ n ）＝ f （n ）， ＝（f （n ）），k 是任 f f ＝ （（）） f f f nf意正整数则f（8）＝（）A．3 B ．5 C．8 D．11同类题型 3.1 将 1，2，3，，100 这100 个自然数，随意分为50 组，每组两个数，现将每组的两个数中任一数值记作a，另一个记作b，代入代数式1(|a－2b|＋a＋b)中进行计算，求出其结果，50 组数代入后可求得50 个值，则这 50 个值的和的最大值是 ____________．同类题型 3.2 规定： [x]表示不大于 x 的最大整数，（x）表示不小于x 的最小整数， [x）表示最靠近x 的整数（ x≠n＋ 0.5，n 为整数），比如： [2.3] ＝2，（2.3）＝3，[2.3）＝ 2．则以下说法正确的选项是 ________．（写出全部正确说法的序号）①当 x＝1.7 时， [x]＋（ x）＋ [x）＝ 6；②当 x＝－ 2.1 时， [x] ＋（ x）＋ [x）＝－ 7；③方程 4[x]＋3（x）＋ [x）＝ 11 的解为 1＜x＜1.5；④当－ 1＜ x＜ 1 时，函数 y＝[x] ＋（ x）＋ x 的图象与正比率函数有两个交点．y＝ 4x 的图象同类题型 3.3 设[x]表示不大于 x 的最大整数， { x} 表示不小于 x 的最小整数，＜x＞表示最靠近 x 的整数（ x≠n＋ 0.5， n 为整数）．比如 [3.4] ＝3，{3.4} ＝4，＜3.4 ≥3．则方程 3[x]＋2{x} ＋＜ x≥ 22（）A ．没有解B．恰巧有 1 个解C．有 2 个或 3 个解D．有无数个解同类题型 3.4 对于实数 p， q，我们用符号min{ p，q} 表示 p， q 两数中较小的数，如 min{1 ，2} ＝1，所以， min{ －，} ＝ ______；若 min{ （－， }2 －3 ）xx 1＝1，则 x＝____________．例4．已知点 A 在函数y＝－1（x＞0）的图象上，点 B 在直线y＝ kx＋1＋k（k x为常数，且 k≥0）上．若 A，B 两点对于原点对称，则称点 A， B 为函数y，y图象上的一对“友好点”．请问这两个函数图象上的“友好点”对数的状况为（）A．有 1 对或 2 对B．只有 1 对C．只有 2 对D．有 2 对或3 对同类题型 4.1 在平面直角坐标内A，B 两点知足：①点 A，B 都在函数 y＝f（x）的图象上；②点 A，B 对于原点对称，则称A，B 为函数 y＝f（x）的一个“黄金点对”．|x＋4|，x ≤0则函数 f（x）＝1的“黄金点对”的个数为（）{－，x＞0 )xA．0 个 B ．1 个C．2 个D．3 个同类题型 4.2 定义：在平面直角坐标系 xOy 中，把从点 P 出发沿纵或横方向抵达点Q（至多拐一次弯）的路径长称为 P，Q 的“实质距离”．如图，若 P（－1， 1）， Q（ 2，3），则 P， Q 的“实质距离”为 5，即 PS＋ SQ＝ 5 或 PT＋ TQ＝5．环保低碳的共享单车，正式成为市民出行喜爱的交通工具．设A，B，C 三个小区的坐标分别为 A（3， 1），B（5，－ 3），C（－ 1，－ 5），若点 M 表示单车停放点，且知足 M 到 A， B， C 的“实际距离”相等，则点 M 的坐标为____________．同类题型 4.3 经过三边都不相等的三角形的一个极点的线段把三角形分红两个小三角形，假如此中一个是等腰三角形，此外一个三角形和原三角形相像，那么把这条线段定义为原三角形的“和睦切割线”．如图，线段CD 是△ABC 的“和谐切割线”，△ACD 为等腰三角形，△CBD 和△ABC 相像，∠A＝ 46°，则∠ACB 的度数为__________．专题 09 阅读理解问题例 1．我们把 1，1，2， 3，5，8，13， 21， 这组数称为斐波那契数列，为了进一步研究，挨次以这列数为半径作 90°圆弧 PP ，PP ，PP ， 获得斐波那契螺旋线，而后按序连接， ， ， 获得螺旋折线（如图） ，已知点 P （0， 1），PP PP PPP （－ 1，0），（ 0，－ 1），则该折线上的点 的坐标为（ ）P PA ．（－ 6，24）B ．（－ 6，25）C ．（－ 5，24）D ．（－ 5，25）解：由题意， P 在 P 的正上方，推出 P 在 P 的正上方，且到P 的距离＝ 21＋ 5＝26，所以 P 的坐标为（－ 6，25）， 选 B ．同类题型 1.1 定义 [x]表示不超出实数 x 的最大整数，如 [1.8] ＝1，[－ 1.4]＝－ 2，[－3]＝－ 3．函数 y ＝[x] 的图象以下图，则方程[x] ＝ 1 的解为（ ）2 xA ．0 或 2B ．0 或 2C ．1 或－ 2D ． 2或－ 2解：当 1≤x＜2 时，1＝1，解得＝ 2 ，；2xx＝－ 2x1当 x＝0，x＝0，x＝0；21当－ 1≤x＜0时，2x＝－ 1，方程没有实数解；1当－ 2≤x＜－ 1 时，2x＝－ 2，方程没有实数解；1所以方程 [x]＝2x的解为 0 或 2．选A．同类题型 1.2 对于函数nm n﹣1m﹣1y＝ x ＋ x ，我们定义y'＝ nx ＋ mx （ m、 n 为常数）．比如 y＝x4＋x2，则 y'＝4x3＋2x．已知： y＝1x3＋（ m﹣1）x2＋m2x．3（1）若方程y′＝0 有两个相等实数根，则m 的值为；（2）若方程y′＝m﹣1有两个正数根，则4m 的取值范围为．解：依据题意得y′＝x2＋2（m﹣1）x＋m2，（1）∵方程x2﹣2（m﹣1）x＋m2＝0 有两个相等实数根，∴△＝ [ ﹣2（m﹣1）]2﹣4m2＝0，1解得： m＝；（2）y′＝m﹣1，即 x2＋2（m﹣1）x＋m2＝m﹣1，4 41化简得： x2＋2（m﹣1）x＋m2﹣m＋＝0，4∵方程有两个正数根，2(m－1)＜0∴m2－m＋＞ 0 {[－2(m－1)]2－4(m2－m＋) )，≥03 1解得： m≤且 m≠ ．4 2例2．将一枚六个面的编号分别为 1，2，3，4，5，6 的质地平均的正方体骰子先后扔掷两次，记第一次掷出的点数为a，第二次掷出的点数为b，则使对于＋＝ax by 3)有正数解的概率为 ___．x，y的方程组 {x＋2y＝2解：①当 2a－b＝0 时，方程组无解；②当 2a－b≠0时，方程组的解为由 a、b 的实质意义为1， 2， 3， 4，5， 6 可得．易知 a，b 都为大于 0 的整数，则两式结合求解可得＝6－2b，2a－3，－y ＝－x2a b2a b∵使 x、y 都大于 0 则有6－2b＞0，＝2a－3＞0，＝－x －y2a b 2a b∴解得 a＜1.5，b＞3 或许 a＞1.5，b＜3，∵a，b 都为 1 到 6 的整数，∴可知当 a 为 1 时 b 只好是 4， 5， 6；或许 a 为 2， 3， 4， 5， 6 时 b 为 1 或2，这两种状况的总出现可能有3＋10＝13 种；（1， 4）（1，5）（ 1，6）（2，1）（ 3，1）（4，1）（ 5，1）（6，1）（2，2）（3，2）（4，2）（5，2）（6，2）又掷两次骰子出现的基本领件共6×6＝36 种状况，故所求概率为＝13．36同类题型 2.1 六个面上分别标有 1，1，2，3， 4， 5 六个数字的平均立方体的表面睁开图以下图，掷这个立方体一次，记向上一面的数为平面直角坐标系中某个点的横坐标，朝下一面的数为该点的纵坐标．则获得的坐标落在抛物线y＝2x－x 上的概率是（）A ．2B ．1C ．1D ．13639解：掷一次共出现 6 种状况，依据图形可知 1，2，3 所对应的数分别是 1，5，4，在抛物线上的点为：（ 1，1），只有两种状况，所以概率为：2＝1． 6 3选 C ．同类题型 2.2 把一枚六个面编号分别为1，2，3， 4，5， 6 的质地平均的正方体骰子先后扔掷 2 次，若两个正面向上的编号分别为m 、n ，则二次函数 ＝ ＋xy mx ＋n 的图象与 x 轴没有公共点的概率是 ________． 解：∵二次函数 y ＝x ＋mx ＋n 的图象与 x 轴没有公共点， ∴△＜ 0，即 m －4n ＜0， ∴m ＜4n ，列表以下：m 、 n 1234561 1，1 1，2 1，3 1，4 1，5 1，6 2 2，1 2，2 2，3 2，4 2，5 2，6 3 3，1 3，2 3，3 3，4 3，5 3，6 44 ， 1 ， 2 ， 3 ， 4 ，5 4 ， 64 4 4 45 5，1 5，2 5，3 5，4 5，5 5，6 66，16，26，36，46，56，6共有 36 种等可能的结果，此中知足 m ＜4n 占 17 种，17所以二次函数y＝x＋mx＋n 的图象与 x 轴没有公共点的概率＝．同类题型 2.3 如图，正方形 ABCD 的边长为 2，将长为 2 的线段 QR 的两头放在正方形的相邻的两边上同时滑动．假如点Q 从点 A 出发，沿图中所示方向按A→B→C→D→A 滑动到 A 止，同时点R 从点 B 出发，沿图中所示方向按B→C→D→A→B 滑动到 B 止．点 N 是正方形 ABCD 内任一点，把 N 点落在线段 QR 的中点 M 所经过的路线围成的图形内的概率记为 P，则 P＝（）－ B ．πC．1 －A．4πD．π14 4 4 4解：依据题意得点M 到正方形各极点的距离都为1，点M 所走的运动轨迹为以正方形各极点为圆心，以 1 为半径的四个扇形，∴点 M 所经过的路线围成的图形的面积为正方形ABCD 的面积减去 4 个扇形的面积．而正方形ABCD 的面积为2×2＝4，4 个扇形的面积为90π×14 ×＝π，360∴点∴把M 所经过的路线围成的图形的面积为4－π，N 点落在线段QR 的中点 M 所经过的路线围成的图形内的概率记为P，则4－π．P＝ 4选A．同类题型 2.4 从－ 1， 1， 2 这三个数字中，随机抽取一个数，记为a，那么，使对于 x 的一次函数 y＝2x＋a 的图象与 x 轴、 y 轴围成的三角形的面积为1，4且使对于 x 的不等式组{x ＋2 ≤a)有解的概率为 _________． 1－x ≤2a1解：当 a ＝－ 1 时， y ＝2x ＋a 可化为 y ＝ 2x － 1，与 x 轴交点为 （， 0），与 y轴 2交点为（ 0，－ 1），三角形面积为1 1 12 × ×1＝ ；241，0），与 y 轴交点当 a ＝ 1 时， y ＝2x ＋ a 可化为 y ＝ 2x ＋1，与 x 轴交点为 （－2为（ 0，1），三角形的面积为 1 1 1 2 × ×1＝ ；2 4当 a ＝2 时， y ＝2x ＋2 可化为 y ＝ 2x ＋ 2，与 x 轴交点为（－ 1，0），与 y 轴交点为（ 0，2），三角形的面积为 1×2×1＝1（舍去）；2当 a ＝－ 1 时，不等式组{x ＋2 ≤a 可化为 x ＋2 ≤－1，不等式组的解集为){)1－x ≤2a1－x ≤－2x ≤－3 ，无解；{ x ≥3 )x ＋2 ≤ax ＋2 ≤1 x ≤－1 当 a ＝ 1 时，不等式组1－x ≤2a可化为1－x ≤2 ，解得 －x ≤1)，解集为{){ ) {－≤ 1，解得 x ＝－ 1．{－)x ≥ 1使对于 x 的一次函数 y ＝2x ＋a 的图象与 x 轴、 y 轴围成的三角形的面积为1，4且使对于 x 的不等式组 {x ＋2 ≤a 有解的概率为1．)3＝1－x ≤2a P例 3．若 f （n ）为 ＋ （是随意正整数） 的各位数字之和，如 ＋1＝197，1＋ 914n 1 n ＋7＝17，则 f （ 14）＝ 17，记 （ n ）＝ f （n ）， ＝（f （n ）），k 是任 f f ＝ （（）） f f f nf意正整数则 f （8）＝（）A ．3B ．5C ．8D ．11解：∵ 8＋1＝65，∴ f （8）＝ f （8）＝ 6＋5＝11，同理，由 11＋1＝122 得 f （8）＝ 1＋ 2＋2＝ 5；由 5＋ 1＝26，得 f （8）＝ 2＋ 6＝8，可得f （8）＝6＋5＝11＝f （8）， （8）， ，f （8）＝f ∴ f （8）＝f （8）对随意 k ∈ N 建立又∵ 2016＝3×672，∴ f （8）＝f （8）＝f （8）＝ ＝f （8）＝ 8．选 C ．同类题型3.1 将 1，2，3， ，100 这100 个自然数，随意分为50 组，每组两个数，现将每组的两个数中任一数值记作a ，另一个记作b ，代入代数式1(|a －2b|＋a ＋b)中进行计算，求出其结果，50 组数代入后可求得50 个值，则这50 个值的和的最大值是 ____________．解：①若 a ≥b ，则代数式中绝对值符号可直接去掉，∴代数式等于 a ，②若 b ＞a 则绝对值内符号相反，∴代数式等于 b因而可知输入一对数字，能够获得这对数字中大的那个数（这跟谁是a 谁是b没关）既然是乞降，那就要把这五十个数加起来还要最大，我们能够列举几组数，找找规律，假如 100 和 99 一组，那么 99 就被浪费了，由于输入 100 和 99 这组数字，获得的不过 100，假如我们取两组数字 100 和 1 一组， 99 和 2 一组，则这两组数字代入再乞降是 199，假如我们这样取100 和 99 2 和 1，则这两组数字代入再乞降是102，这样，能够很显然的看出，应防止大的数字和大的数字相遇这样就能够使最后的和最大，由此一来，只需100 个自然数里面最大的五十个数字从51 到 100 随意俩个数字不一样组，这样最后求得五十个数之和最大值就是五十个数字从51 到 100 的和，51＋52＋53＋＋100＝3775．同类题型 3.2 规定： [x]表示不大于 x 的最大整数，（x）表示不小于x 的最小整数， [x）表示最靠近x 的整数（ x≠n＋ 0.5，n 为整数），比如： [2.3] ＝2，（2.3）＝3，[2.3）＝ 2．则以下说法正确的选项是 ________．（写出全部正确说法的序号）①当 x＝1.7 时， [x]＋（ x）＋ [x）＝ 6；②当x＝－ 2.1 时， [x] ＋（ x）＋ [x）＝－ 7；③方程 4[x]＋3（x）＋ [x）＝ 11 的解为 1＜x＜1.5；④当－ 1＜ x＜ 1 时，函数 y＝[x] ＋（ x）＋ x 的图象与正比率函数 y＝ 4x 的图象有两个交点．解：①当 x＝1.7 时，[x]＋（ x）＋ [x）＝[1.7] ＋（ 1.7）＋ [1.7）＝1＋2＋2＝5，故①错误；②当 x＝－ 2.1 时，[x]＋（ x）＋ [x）＝[－2.1]＋（－ 2.1）＋ [ －2.1）＝（－ 3）＋（－ 2）＋（－ 2）＝－ 7，故②正确；③4[x] ＋3（x）＋ [x）＝ 11，7[x]＋3＋[x）＝ 11，7[x]＋[x）＝ 8，1＜x＜1.5，故③正确；④∵－ 1＜x＜1 时，∴当－ 1＜x＜－ 0.5 时， y＝[x] ＋（ x）＋ x＝－ 1＋0＋x＝x－1，当－ 0.5＜x＜0 时， y＝[x] ＋（ x）＋ x＝－ 1＋0＋x＝x－1，当x＝0 时， y＝[x] ＋（ x）＋ x＝0＋0＋0＝0，当0＜x＜0.5 时， y＝[x]＋（ x）＋ x＝0＋1＋x＝x＋1，当0.5＜x＜1 时， y＝[x]＋（ x）＋ x＝0＋1＋x＝x＋1，∵y＝4x，则x－ 1＝4x 时，得x＝－ 1；x＋1＝4x3 时，得x＝1；当3x＝ 0 时， y＝4x＝0，∴当－ 1＜ x＜ 1 时，函数y＝[x] ＋（ x）＋ x 的图象与正比率函数y＝ 4x 的图象有三个交点，故④错误，答案为②③．同类题型 3.3 设[x]表示不大于 x 的最大整数， { x} 表示不小于 x 的最小整数，＜x＞表示最靠近 x 的整数（ x≠n＋ 0.5， n 为整数）．比如 [3.4] ＝3，{3.4} ＝4，＜3.4 ≥3．则方程A ．没有解C．有 2 个或3[x]＋2{x} ＋＜ x≥ 22（）B．恰巧有 1 个解3 个解D．有无数个解】解：当 x＝ 3 时， 3[x]＋ 2{ x} ＋＜ x≥3×3＋2×3＋ 3＝ 18，当 x＝ 4 时， 3[x] ＋ 2{x} ＋＜ x≥ 3×4＋2×4＋4＝24，∴可得 x 的大概范围为 3＜x＜4，①3＜x＜3.5 时， 3[x] ＋2{ x} ＋＜ x≥3×3＋2×4＋3＝20，不切合方程；②当3.5＜x＜4 时， 3[x]＋2{ x} ＋＜ x≥3×3＋2×4＋4＝21，不切合方程．选A．同类题型 3.4 对于实数 p， q，我们用符号min{ p，q} 表示 p， q 两数中较小的数，如 min{1 ，2} ＝1，所以， min{ －，} ＝ ______；若 min{ （－， }2 －3 ）xx 1＝1，则 x＝____________．解： min{ －2，－ 3} ＝－ 3，∵min{ ， } ＝1，（－）xx 1当 x＝0.5 时，，不行能得出，最小值为1，x＝（x－1）∴当 x＞0.5 时，（－）＜，x 1 x则（x－1）＝1，x－1＝±1，x－1＝1，x－1＝－ 1，解得：x＝2，x＝0（不合题意，舍去），当x＜0.5 时，（x－1）＞x，则x＝1，解得：x＝1（不合题意，舍去），x＝－ 1，综上所述： x 的值为： 2 或－ 1．例4．已知点 A 在函数y＝－1（x＞0）的图象上，点 B 在直线y＝ kx＋ 1＋ k（k x为常数，且 k≥0）上．若 A，B 两点对于原点对称，则称点 A， B 为函数y，y图象上的一对“友好点”．请问这两个函数图象上的“友好点”对数的状况为（）A．有 1 对或 2 对B．只有 1 对C．只有2 对D．有2 对或3 对解：设 A （a ，－1），a1由题意知，点 A 对于原点的对称点B （－ a ，）在直线 y ＝kx ＋1＋k 上， a则1＝－ ak ＋1＋k ， a整理，得： ka －（ k ＋1）a ＋1＝0 ①，即（ a －1）（ka －1）＝ 0，∴a －1＝0 或 ka －1＝0，则 a ＝1 或 ka －1＝0，若 k ＝0，则 a ＝1，此时方程①只有 1 个实数根，即两个函数图象上的 “友善点 ” 只有 1 对； 若 k ≠0，则 a ＝1 或1，此时方程①有 2 个实数根，即两个函数图象上的 “友a ＝k好点 ”有 2 对，综上，这两个函数图象上的 “友善点 ”对数状况为 1 对或 2 对，选 A ．同类题型 4.1 在平面直角坐标内A ，B 两点知足：①点 A ，B 都在函数 y ＝f （x ）的图象上；②点 A ，B 对于原点对称，则称 A ，B 为函数 y ＝f （x ）的一个 “黄金点对 ”．|x ＋4|，x ≤0则函数 f （x ）＝ {1 )的“黄金点对 ”的个数为（ ） － ，x ＞0xA ．0 个B ．1 个C ．2 个D ．3 个解：依据题意： “黄金点对 ”，可知，作出函数y＝－1（x＞0）的图象对于原点对称的图象，x同一坐标系里作出函数y＝|x＋4|，x≤0的图象如右图：察看图象可得，它们在x≤0时的交点个数是3．即f（x）的“黄金点对”有： 3个．选 D．同类题型 4.2 定义：在平面直角坐标系xOy 中，把从点 P 出发沿纵或横方向到达点 Q（至多拐一次弯）的路径长称为P，Q 的“实质距离”．如图，若P（－1， 1）， Q（ 2，3），则 P， Q 的“实质距离”为 5，即 PS＋ SQ＝ 5 或 PT＋ TQ＝5．环保低碳的共享单车，正式成为市民出行喜爱的交通工具．设A，B，C 三个小区的坐标分别为 A（3， 1），B（5，－ 3），C（－ 1，－ 5），若点 M 表示单车停放点，且知足 M 到 A， B， C 的“实际距离”相等，则点 M 的坐标为____________．解：若设 M（x，y），则由题目中对“实质距离”的定义可得方程组： 3－x＋1－y＝y＋5＋x＋1＝5－x＋3＋y，解得， x＝1，y＝－ 2，则 M（1，－ 2）．同类题型 4.3 经过三边都不相等的三角形的一个极点的线段把三角形分红两个小三角形，假如此中一个是等腰三角形，此外一个三角形和原三角形相像，那么把这条线段定义为原三角形的“和睦切割线”．如图，线段CD 是△ABC 的“和睦切割线”，△ACD 为等腰三角形，△CBD 和△ABC 相像，∠ A＝ 46°，则∠ ACB 的度数为 __________．解：∵△ BCD∽△ BAC，∴∠ BCD＝∠ A＝46°，∵△ ACD 是等腰三角形，∵∠ ADC＞∠ BCD，∴∠ ADC＞∠ A，即 AC≠CD，1①当 AC＝AD 时，∠ACD＝∠ADC＝（180°－46°）＝ 67°，∴∠ ACB＝67°＋46°＝113°，②当 DA＝DC 时，∠ ACD＝∠ A＝46°，∴∠ ACB＝46°＋46°＝92°，故答案为 113°或 92°．。

填空题1．土方工程的施工往往具有（工程量大、工期长、劳动强度高、施工条件复杂）等特点。

2．土方施工中，按照（土的坚硬程度和开挖特征）划分，土可分为松软土、普通土、坚土、砂砾坚土、软石、次坚石、坚石、特坚石八类。

3．土方施工中要考虑土的可松性，是由于土方工程量是以（自然状态的体积）来计算的，土的可松性用（可松性系数）来表示。

4．最佳设计平面既能使土方工程量最小又能保证填挖方量相等，一般可用最小二乘法原理方法求解。

5．影响土方边坡稳定的因素主要有土质、开挖深度、施工工期、地下水水位、坡顶荷载、气候条件因素6．计算水井系统时，水井可分成（承压完整井、承压非完整井、无压完整井、无压非完整井）7．一般轻型井点的管路系统包括（滤管、井点管、弯联管、总管）8．填土的压实方法有碾压法、夯实法、震动法其中（夯实、震动压实）适用于非粘性土9．防治流砂的方法：抢挖法、冻结法、水下挖土法、井点降水、枯水期施工、加设支护结构。

10．挖掘机根据工作装置可分成正铲、反铲、抓铲、拉铲等类型。

2．钻孔灌注桩成孔施工时，泥浆作用是保护孔壁、防止塌孔、携渣、冷却钻头。

3．钢筋混凝土预制桩的打桩顺序一般有逐段打设、自中部向四周打设和由中间向两侧打设4．打桩桩锤一般可分几类落锤、蒸汽锤和柴油锤、液压锤。

5．桩锤重量可按哪几个因素来选择土质、桩的规格、打桩方法。

6．预制打入桩垂直度偏差应控制在 1% 以内。

入土深度控制对摩擦桩应以桩尖设计标高为主，以贯入度作为参考，端承桩应以标高为主。

7．钻孔灌注桩钻孔时的泥浆循环工艺有正循环和反循环两种，其中反循环工艺的泥浆上流速度高，携土能力大。

8.当摩擦型桩采用锤击沉管桩时，沉管入土深度控制是以___桩尖设计标高___为主，以____贯入度____为参考。

9．灰土垫层施工时，当灰土地基高度不同时，应做成__阶梯形__，每阶宽度不少于__0.5__m。

1．滑模组成包括操作平台系统，液压系统，滑板系统三个系统。

专题9 二次函数的实际应用问题例题精讲例1.定义符号min{a，b}的含义为：当a＞b时min{a，b}=b；当a＜b时min{a，b}=a．如：min{1，-3}=﹣3，min{﹣4，﹣2}=﹣4，则min{﹣x2+2，﹣x}的最大值是（）A. ﹣1B. ﹣2C. 1D. 0【答案】C【解析】【解答】联立解得，所以min{﹣x2+2，﹣x}的最大值是1故答案为：C例2.如图，有一块边长为6cm的正三角形纸板，在它的三个角处分别截去一个彼此全等的筝形，再沿图中的虚线折起，做成一个无盖的直三棱柱纸盒，则该纸盒侧面积的最大值是（）A. cm2B. cm2C. cm2D. cm2【答案】C【解析】【解答】解：∵△ABC为等边三角形∴∠A=∠B=∠C=60°，AB=BC=AC∵筝形ADOK≌筝形BEPF≌筝形AGQH∴AD=BE=BF=CG=CH=AK∵折叠后是一个三棱柱∴DO=PE=PF=QG=QH=OK，四边形ODEP、四边形PFGQ、四边形QHKO都为矩形∴∠ADO=∠AKO=90°连结AO，在Rt△AOD和Rt△AOK中∴Rt△AOD≌Rt△AOK（HL）∴∠OAD=∠OAK=30°设OD=x，则AO=2x，由勾股定理就可以求出AD= x∴DE=6﹣2x∴纸盒侧面积=3x（6﹣2x）=﹣6x2+18x=﹣6（x﹣）2+∴当x= 时，纸盒侧面积最大为故答案为：C例3.图2是图1中拱形大桥的示意图，桥拱与桥面的交点为O，B，以点O为原点，水平直线OB为轴，建立平面直角坐标系，桥的拱形可以近似看成抛物线，桥拱与桥墩AC的交点C 恰好在水面，有AC⊥轴。

若OA=10米，则桥面离水面的高度AC为（）A. 米B. 米C. 米D. 米【答案】B【解析】【解答】根据题意，由AC⊥x轴，OA=10米，可知点C的横坐标为-10，然后把x=-10代入函数的解析式=- ，即C点为（-10，- ），因此可知桥面离水面的高度AC为m. 故答案为：B例4.一座石拱桥的桥拱是近似的抛物线形，建立如图所示的平面直角坐标系，其函数关系式为y=- ，当水面离桥拱顶的高度OC是4m时，水面的宽度AB为________m．【答案】16【解析】【解答】解：根据题意B的纵坐标为-4把y=-4代入y=- x2得x=±8∴A（-8，-4），B（8，-4）∴AB=16m即水面宽度AB为16m故答案为：16例5.若关于x的方程x2+2mx+m2+3m-2=0有两个实数根x1、x2，则x1(x1+x2)+x22的最小值为________【答案】【解析】【解答】设关于的方程的两根是：、∴，∴=====∴当时，有最小值为：习题精炼1.如图为一座抛物线型的拱桥，AB、CD分别表示两个不同位置的水面宽度，O为拱桥顶部，水面AB宽为10米，AB距桥顶O的高度为12.5米，水面上升2.5米到达警戒水位CD位置时，水面宽为（）米．A. 5B. 2C. 4D. 82.图（1）是一个横断面为抛物线形状的拱桥，当水面在l时，拱顶（拱桥洞的最高点）离水面2m，水面宽4m．如图（2）建立平面直角坐标系，则抛物线的关系式是（）A.y=﹣2x2B.y=2x2C.y=﹣x2D.y= x23.绍兴是著名的桥乡，如图，圆拱桥的拱顶到水面的距离CD为8m，桥拱半径OC为5m，则水面宽AB为（）A. 4mB. 5mC. 6mD. 8m4.如图，一农户要建一个矩形花圃，花圃的一边利用长为12m的住房墙，另外三边用25m长的篱笆围成，为方便进出，在垂直于住房墙的一边留一个1m宽的门，花圃面积为80m2，设与墙垂直的一边长为xm （已标注在图中），则可以列出关于x的方程是（）A. x（26﹣2x）=80B. x（24﹣2x）=80C. （x﹣1）（26﹣2x）=80D. x（25﹣2x）=805.如图，某中学准备在校园里利用围墙的一段，再砌三面墙，围成一个矩形花园ABCD (围墙MN最长可利用25m)，现在已备足可以砌50m长的墙的材料，若设计一种砌法，使矩形花园的面积为300m2．则AB长度为（）A. 10B. 15C. 10或15D. 12.56.如图所示是由截面为同一种矩形的墙砖粘贴的部分墙面，其中三块横放的墙砖比一块竖放的墙砖高10cm，两块横放的墙砖比两块竖放的墙砖低40cm，则每块墙砖的截面面积是（）A. 425cm2B. 525cm2C. 600cm2D. 800cm27.如图，从某建筑物10m高的窗口A处用水管向外喷水，喷出的水成抛物线状（抛物线所在平面与墙面垂直）．如果抛物线的最高点M离墙1m，离地面m，则水流落地点B离墙的距离OB是（）A. 2mB. 3mC. 4mD. 5m8.某广场有一喷水池，水从地面喷出，如图，以水平地面为x轴，出水点为原点，建立平面直角坐标系，水在空中划出的曲线是抛物线y＝－x2＋4x（单位：米）的一部分，则水喷出的最大高度是( )A. 4米B. 3米C. 2米D. 1米9.某幢建筑物，从10米高的窗口A用水管向外喷水，喷出的水流呈抛物线状(抛物线所在平面与墙面垂直，如图)．若抛物线的最高点P离墙一米，离地面米，则水流落地点B离墙的距离OB是( )A. 2米B. 3米C. 4米D. 5米10.某地要建造一个圆形喷水池，在水池中央垂直于地面安装一个柱子OA，O恰为水面中心，安置在柱子顶端A处的喷头向外喷水，水流在各个方向上沿形状相同的抛物线路径落下.在过OA的任一平面上，建立平面直角坐标系（如图），水流喷出的高度y（m）与水平距离x（m）之间的关系式是，则下列结论：（1）柱子OA的高度为3m；（2）喷出的水流距柱子1m处达到最大高度；（3）喷出的水流距水平面的最大高度是4m；（4）水池的半径至少要3m才能使喷出的水流不至于落在池外.其中正确的有（）A. 1个B. 2个C. 3个D. 411.某公园草坪的防护栏是由100段形状相同的抛物线形组成的．为了牢固起见，每段护栏需要间距0.4m加设一根不锈钢的支柱，防护栏的最高点距底部0.5m（如图），则这条防护栏需要不锈钢支柱的总长度至少为（）A. 50mB. 100mC. 160mD. 200m12.如图，庄子大桥有一段抛物线形的拱梁，抛物线的表达式为y=ax2+bx，小强骑自行车从拱梁一端O沿直线匀速穿过拱梁部分的桥面OC，当小强骑自行车行驶10秒时和26秒时拱梁高度相同，则小强骑自行车通过拱梁部分的桥面OC共需（）A. 18秒B. 36秒C. 38秒D. 46秒13.一种包装盒的设计方法如图所示，四边形ABCD是边长为30cm的正方形硬纸片，切去阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起，使得A，B，C，D四点重合于图中的点O，形成一个底面为正方形的长方体包装盒．设BE=CF=xcm，要使包装盒的侧面积最大，则x应取( )A. 12.5cmB. 10cmC. 7.5cmD. 5cm14. 如图1，点E为矩形ABCD边AD上一点，点P，点Q同时从点B出发，点P沿BE→ED→DC 运动到点C 停止，点Q沿BC运动到点C停止，它们运动的速度都是1cm/s，设P，Q出发t秒时，△BPQ的面积为ycm2，已知y与t的函数关系的图形如图2（曲线OM为抛物线的一部分），则下列结论：①AD=BE=5cm；②当0＜t≤5时，；③直线NH的解析式为；④若△ABE与△QBP相似，则t=秒。

8.选择、填空题选择题和填空也是有机化学常见的习题类型，覆盖面广，出题灵活，答题客观；可以考查到有机化学知识的方方面面，如有机物的物理性质，常见反应的反应历程、反应速度、难易程度、反应物的活性等等，还有有机物的酸性强弱、碱性强弱、芳香性、物质的同分异构现象、命名、有机实验、有机化学的基础理论等等。

8.1综合练习(1) 下列化合物沸点最高的是（）。

(2) 下列三种杂化态碳原子中电负性最大的是（）。

(3) 反应前后碳原子的杂化状态有变化的是（D ）。

(4) 按照优先次序规则，下列基团中最优先的是（A ）。

A. CH 2ClB. CH 2OHC. CH(OH) CH 3D. CHO(5) 正丁烷的优势构象是（ C ）。

A. CH 3CH 2COOHB. CH 3COCH 3C. CH 3CH 2CH 2OHD. CH 3OCH 2CH 3A. spB. sp 2C. sp 3A. CH 3CH 3CCH3Cl 2CH 3CH 3C CH3ClB.+Br 2CCl 4Br —CH 2—CH 2—CH 2—Br C.CH 3CHO NH 2OH CH 3CH=NOHD.CH CH + HClCH 2=CH —ClA 333333B C D(6) 既能使KMnO 4溶液褪色,又能使溴的四氯化碳溶液褪色的化合物为（C ）。

A. 乙醛B. 环丙烷C. 环己烯D.环己醇(7) 下面这个化合物的名称是（C ）。

H 3C C CCH 3Cl H A. 反-2-氯-2-丁烯 B. 顺-3-氯-2-丁烯 氯-2-丁烯 D. Z-2-氯-2-丁烯(8) 烯烃起亲电加成反应最活泼的是( A )。

A. (CH 3)2C=CHCH 3B. CH 3CH=CHCH 3C.CH 2=CH —CF 3D. CH 2=CHCl(9) 下列化合物不具有芳香性的是( D )。

(10) 能将正丁醇、仲丁醇和叔丁醇鉴别开来的一种试剂是（ B ）。

一、单项选择题（17道小题，共20分）1、以下叙述中正确的是( C )。

（1分）A、 C语言比其他语言高级B、 C语言可以不用编译就能被计算机识别执行C、 C语言以接近英语国家的自然语言和数学语言作为语言的表达形式D、 C语言出现的最晚，具有其他语言的一切优点2、以下说法正确的是( C )。

（1分）A、C语言程序总是从第一个函数开始执行B、在C语言程序中，要调用函数必须在main()函数中定义C、C语言程序总是从main()函数开始执行D、C语言程序中的main()函数必须放在程序的开始部分3、下列可用于C语言用户标识符的一组是( B )。

（1分）A、 void define WORDB、 a3_b3 _123 CarC、 For abc caseD、 2a DO sizeof4、设int a=3,b=4,c=5;表达式(a+b)>c&&b==c的值是( C ) 。

（1分）A、2B、-1C、0D、15、以下关于循环体的描述中，( C )是错误的。

（2分）A、循环体中可以出现break语句B、循环体中还可以出现循环语句C、循环体中不能出现continue语句D、循环体中可以出现switch语句6、While(x)中的x相当于( D )。

（2分）A、x==0B、x==1C、x!=1D、x!=07、以下关于switch语句和break描述中 , ( A ) 是正确的。

（2分）A、在switch语句中,可以根据需要使用或不使用break语句B、switch语句中必须用break语句C、break语句只能用于switch语句D、break语句是switch语句必须的一部分8、以下对C语言函数的有关描述中，正确的是( B )。

（1分）A、在C中，调用函数时，只能把实参的值传送给形参，形参的值不能传送给实参B、C函数既可以嵌套调用又可以递归调用C、函数必须有返回值，否则不能使用函数D、C程序中有调用关系的所有函数必须放在同一个源程序文件中、9、在下面的函数声明中，存在着语法错误的是( A )。

九年级上册英语第一单元测试卷及答案免费九年级上册英语第一单元测试卷I. 选择填空。

(15分)( )1. It’s not polite to speak in public.A. loudB. loudlyC. louderD. loudlier( ) 2.I haven’t seen the movie and my brother hasn’t,____.A. tooB. eitherC. alreadyD. yet( ) 3. _________ should not be allowed to go out at night.A. Twelve-years-oldB. Twelve-year-oldsC. Twelve year oldD. Twelve years olds( ) 4.---- They have a lot of rules at their house.----_________A. so do IB. So we doC. So have ID. So I have( ) 5. I don’t know _________.A. what to do itB. how to do itC. what to doD. to do what( ) 6. This question is ______ easy, all the students can answer the question.A. too muchB. too manyC. much tooD. many to( ) 7. I have ever ____ the Great Wall twice. It is an _____ place.A. been to; excitedB. gone to; excitingC. been to; excitingD. gone to; excited( ) 8 ------Could you tell me __________________?------Sorry, I don’t know.A. When does the train arriveB. When the train arrivesC. When arrives the trainD. The train when arrives( ) 9. He ______ be a history teacher.A. used toB. be used toC. use to beD. be use to( ) 10. _______ lovely weather it is!A. WhatB. What aC. How aD. How( )11.Jack said to me: “You look worried today.”Jack told me that ____worried _____.A. he looks; todayB. you look; todayC. we looked; that dayD. I looked; that day( )12. He is too tired ________ any longer.A. not to walkB. to walkC. walkingD. not walking( ) 13. _____ he was tired , he still went on with his homework .A. BecauseB. ThoughC. SinceD. As( ) 14.----Have you _______ spoken to an Englishman?----No, I’ve _______ met a foreigner.A. ever; everB. never; neverC. ever; neverD. never, ever( ) 15. It is hard______ the work today .A. to finishB. finishedC. finishesD. finishII. 完形填空 (10分)阅读下面短文，然后从各题所给的四个选项中，选出最佳选项。

一、判断题1. 顺序表和一维数组一样，都可以按下标随机（或直接）访问。

（√）2. 数据的逻辑结构是指各数据元素之间的逻辑关系，是用户根据应用需要建立的。

（√）3. 只有用面向对象的计算机语言才能描述数据结构算法。

（×）4. 在对双向循环链表做删除一个结点操作时，应先将被删除结点的前驱结点和后继结点链接好再执行删除结点操作。

（√）5. 数据元素是数据的最小单位。

（×）6. 算法和程序都应具有下面一些特征：输入，输出，确定性，有穷性，可行性。

（√）7. 插入与删除操作是数据结构中最基本的两种操作，因此这两种操作在数组中也经常被使用。

（×）8. 线性表若采用链式存储表示, 在删除时不需要移动元素。

（√）9. 用一组地址连续的存储单元存放的元素一定构成线性表。

（×）10. 线性表的逻辑顺序与物理顺序总是一致的。

( × )11. 线性表的顺序存储表示优于链式存储表示。

( × )12.链表的每个结点中都恰好包含一个指针。

（×）二、填空题1. 若经常需要对线性表进行查找操作，则最好采用 (顺序)存储结构。

2.(循环)链表从任何一个结点出发，都能访问到所有结点。

3.若经常需要对线性表进行插入与删除操作，该线性表最好采用(链式)存储结构。

4.通常用时间复杂度和(空间复杂度)两种方法衡量算法的效率5.已知一顺序存储的线性表，每个元素占用k个存储单元，若第一个元素的地址为Loc1，则第i个元素的地址为( Loc1+(i-1)*k )。

6.在以L为头指针的带头结点的单链表和单循环链表中，判断链表是否为空的条件分别为(L->next==NULL和_L->next==L)。

7.顺序表中逻辑上相邻的元素的物理位置(相邻)，单链表中逻辑上相邻的元素的物理位置(不一定相邻)。

8.数据的逻辑结构包括集合、(线性结构)、树形结构和图状结构四种类型。

9.已知有实现同一功能的两个算法，其时间复杂度分别为O(log2n)和O(n)，哪个算法的效率更高？( O（log2n）)10.在一个单链表L中，若要在指针q所指结点的后面插入一个由指针p所指向的结点，则应进行的操作序列为：( p->next=q->next),q一>next=p。

9的分解和组成练习题单一、填空题1. 9可以分解为1和________的和。

2. 9可以分解为2和________的和。

3. 9可以分解为3和________的和。

4. 9可以分解为4和________的和。

5. 9可以分解为5和________的和。

6. 9可以分解为6和________的和。

7. 9可以分解为7和________的和。

8. 9可以分解为8和________的和。

二、选择题1. 下列哪个数字可以与9组成10？A. 1B. 2C. 3D. 82. 下列哪个数字与9相加等于18？A. 8B. 9C. 10D. 113. 下列哪个数字与9相减等于0？A. 9B. 8C. 7D. 64. 下列哪个数字与9相乘等于81？A. 8B. 9C. 10D. 11三、判断题1. 9可以分解为2和7的和。

（）2. 9可以分解为4和5的和。

（）3. 9与6相加等于15。

（）4. 9与3相乘等于27。

（）四、连线题请将下列数字与它们对应的分解方式连线：1. 9 A. 1和82. 9 B. 2和73. 9 C. 3和64. 9 D. 4和5五、简答题1. 请写出9的四种分解方式。

2. 请写出9的四种组成方式（与另一个数字相加或相减）。

六、应用题1. 小明有9个苹果，他想把这些苹果分给两个朋友，每个朋友能得到几个苹果？请写出所有可能的分配方案。

2. 小红有9元钱，她想买一些糖果，每颗糖果1元，她最多可以买几颗糖果？请写出所有可能的数量。

七、匹配题1. 18 A. 9 + 92. 27 B. 9 + 8 + 103. 36 C. 9 + 9 + 94. 45 D. 9 + 7 + 9八、填空题（数字分解）1. 18可以分解为9和________的和。

2. 27可以分解为9和________的和。

3. 36可以分解为9和________的和。

4. 45可以分解为9和________的和。

九、填空题（数字组成）1. 10可以由9和________组成。

选择题：( )1. I get up _______ about seven fifty -five .A. inB. onC. atD. for( )2. Why are you looking at _______like that?A. IB. mineC. myD. me( )3. I want _______ a map of China .A. buyB. is buyingC. to buyD. am buying( )4. Is it a picture ______ your school ？A. ofB. toC. andD. with( )5. Do you like _______ ?A. swimB. swimmingC. are swimmingD. swim, too( )6. The man ______ a book in his hand is my uncle .A. andB. ofC. withD. for( )7. Who's the lady ______ blue ?A. inB. onC. atD. with( )8. We usually stay _____ home ____ Saturday afternoon .A. at…inB. at…onC. in…atD. on…on( )9. A: It's a white shirt , is it yours ? B: No, ____ is yellow .A. IB. MyC. MineD. Me( )10. ______ any men in the room ?A. Is thereB. Are thereC. There aren'tD. There isn't( )11. The bed ______ the right is yours .A. onB. inC. atD. of( )12. Look at _______ picture .A. oneB. the oneC. firstD. the first( )13. These books are my _______ .A. studentsB. students'sC. students'D. students of( )14. My parents often tell me ______ your family .A. aboutB. fromC. forD. by( )15. ______ any food in the fridge ？A. Are thereB. Is thereC. HaveD. Has( )16．He often helps with English.A．her，her B．she，her C．her，she D．she，she ( )17．How many are there in your school?A．woman teacher B．women teacher C．woman teachersD．women teachers( )18．"Are you ?""Yes，we are brothers."A．twin，twin B．twins，twins C．twins，twinD．twin，twins( )19．David goes to school every day.A．by a bike B．by his bike C．on his bike D．on bike ( )20．Are in the same class?A．you，he and I B．you，I and he C．he，you and ID．I，you and he( )21．There's "u" in the word "use".A．a B．an C．the D．×( )22．" your brother's number?" "4".A．What's B．How many C．How D．How old( )23．That's bus.A．English B．his C．Japanese D．he( )24．"Thank you very much."" ".A．That's right. B．Thank you. C．Oh，yes，all rightD．That's all right.( )25． a bird. name is Polly.A．Its，Its B．It's，Its C．It's，It's D．Its，It's用所给的动词的适当形式填空：1. Look ! My sister _________ ( play ) with the toy cars .2. I _______ ( get ) up at 6:30 every morning .3. Do they like ________ (swim) ?4. Tom's mother _______ (have) a nice jacket .5. Can you _______ (make ) a paper plane for me ?联词成句：1. the, read, in, don't, sun, please _________________________________2. sisters, brothers, you, any, or, got, have? _________________________________3. black, all, like, I, at, don't _________________________________4. can, do, I, for, what, you? _________________________________5. drink, like, something, you, to, would? __________________________________根据句意填入合适的词：1．"Where are my pen and pencil?"" in your desk."2．Ask that woman. I think it's picture.3．four plus three? It's seven.4．is that? That's Miss Gao.5．Lucy and Lily look same.完型填空：My name is 1 . My 2 name is Joy. 3 twelve. 4 school is NO.1 Middle School. I'm in 5 . I'm in Row 2. 6 Li is my Englishteacher. Her name is Sue. She's a 7 .Liu Yang isn't here today.I think he is 8 . Liu Yang is my friend. I have seven 9 at school.They are in Grade 1，10 .( )1．A．Zhengxiao Fang B．Zheng xiao fangC．Zheng Xiao Fang D．Zheng Xiaofang( )2．A．Chinese B．English C．Japanese D．English's( )3．A．Am B．I C．I'm D．Am I( )4．A．His B．Her C．Their D．My( )5．A．Grade One，Class One B．Class One，Grade OneC．Grade one，Class one D．Class one，Grade one( )6．A．Mr B．Mrs C．mr D．mrs( )7．A．man B．boy C．woman D．girl( )8．A．in home B．at home C．at school D．at a home( )9．A．friend B．friend's C．friends' D．friends( )10．A．and B．or C．too D．two选择填空:( )1. May ____ got a Chinese book.a. isb. hasc. have( )2. This is Mr Li's room. _____ room is clean.a. Heb. Hisc. The( )3. ____ any bags in the locker.a. There areb. Is therec. There aren't( )4. ____ , is this Park School?a. Pardonb. Sorryc. Excuse me( )5. I'm in _______ room.a. heb. mec. our( )6. A: Where's John? B:____________.a. He's over there.b. Which one?c. Oh, she's in the classroom.( )7. There is a letter ______ your grandma.a. inb. forc. to( )8. How many ____ are there in the classroom?a. boyb. girlc. girls and boys( )9. A:_____ is your phone number?B: My phone number is 59811678.a. Whichb. Whatc. Who( )10. A:_____ is your brother? B: He's 20 years old.a. Whatb. Whoc. How old( )11. Is there _______ paper in the desk?a. someb. anyc. a( )12. Mary has got _______ red apples.a. someb. anyc. an( )13. He's got _______ brother.a. someb. ac. an( )14. A: Have you got any books? B:_______________.a. Yes, I have got.b. No, I haven't.c. Yes, I am.( )15. Can you do some washing?a. Yes, please.b. Sure.c. Thank you.( )1. The students in our class__________ different primary schools.A. is fromB. are come fromC. comes fromD. are from ( )2. We go to school__________ Monday ________ Friday.A. from … andB. both …andC. from … toD. and…and ( )3. Would you ________ a cup of tea?A. likeB. toC. atD. for( )4. Do they get__________________ school early?Yes, they do.A. onB. toC. atD. for( )5. They live ____________ the _________ floor.A. in...five B. in...fifth C. on ...fifth D. on (iv)( )6. He usually goes to school_________ underground.A. onB. inC. byD. to( )7. Do you live far___________ school?No, I don't. I live near here.A. forB. to C .at D. from( )8. I get up very early____________ weekdays.A. onB. inC. atD. to( )9. _________ do you go to work? On foot.A. WhatB. HowC. WhereD. What time( )10. What's your favourite book?I like books ________ animals.A. toB. forC. aboutD. in( )1. There's _________ apple tree in our garden.Under _________ tree, there is ________ young man.A. a; the; aB. an; the; theC. an; the; aD. the; the; a ( )2. ---Whose watch is this?---Is it a black _________?A. itB. oneC. thisD. that ( )3. There aren't _______ pears _______the tree.A. some; onB. any; inC. some; inD. any; on ( )4. ---What can you see in the bag?---_________. Oh, they are pencil-boxes.A. All rightB. No, I can'tC. ThanksD. Let me see ( )5. ---Excuse me, do you have any erasers?---__________________.A. It's my pleasureB. Sorry, I can'tC. OK, here you areD. Yes, here you are( )6. There __________ some books and a clockon the desk. The clock ________three hands.A. are; isB. is; hasC. are; hasD. have; has( )7. ---____________ is your shirt?---It's black and white.A. WhatB. What colourC. WhichD. Where( )8. It's time ______________.A. play basketballB. to go to bedC. playing gamesD. for the supper( )9. Here's a letter ______ Kate. She's ill _____ home.A. to; inB. from; forC. for; atD. at; from ( )10. ---Is this computer ______________?---No, it's not _____________.It's my _____________.A. yours; my; brotherB. your; mine; brotherC. his; hers; brother'sD. yours; mine; brother's( )1. Classes begin seven fifty-five.A. inB. onC. atD. for( )2. They often help .A. IB. mineC. myD. me( )3. I want a map of China .A. buyB. is buyingC. to buyD. am buying( )4. Is it a picture your school?A. ofB. toC. andD. with( )5. Do you like ?A. swimB. swimmingC. are swimmingD. swim, too ( )6. The man a stick(手杖)is my grandpa.A. andB. ofC. withD. for( )7. Who's the lady blue?A. inB. onC. atD. with( )8. We usually stay home Saturday afternoon.A. at...inB. at...onC. in...atD. on...on( )9. A: It's a white shirt, is it yours? B: No, is yellow.A. IB. MyC. MineD. Me( )10. any men in the room?A. Is thereB. Are thereC. There aren'tD. There isn't( )11. The bed the right is yours.A. onB. inC. atD. of( )12. Look at picture.A. oneB. the oneC. firstD. the first( )13. These books are my .A. studentsB. students'sC. students'D. students of ( )14. My parents often tell me China.A. aboutB. fromC. forD. by( )15. any food in the fridge?A. Are thereB. Is thereC. HaveD. Has( )1. I like English. How you?A. areB. doC. about( )2. Does Su Hai have hobbies?A. someB. anyC. all( )3. The girl usually plays the violin Sunday morning.A. atB. inC. on( )4. He to school from Monday to Friday.A. goB. goesC. going( )5. am your English teacher. Please listen to .A. I, mineB. I, meC. you, my( )6. Kate blue eyes. Her hair brown.A. has, isB. has, areC. have, is( )7. The boy draws .A. carefulB. carefullyC. be careful( )8. Put your hands your head and turn left and right.A. on, /B. on, toC. with, /( )9. This is Ben. He is from . He speaks .A. the USA, AmericanB. American, EnglishC. the USA, English( )10. Give me orange,please. I want big orange.A. an, anB. a,anC. an,a( )1. Ben _______ morning exercises now.A. doB. doesC. doingD. is doing( )2. _______ you like watching TV? Yes, I do.A. AreB. doC. doesD. Can( )3. He usually _______ breakfast at 6:30.A. hasB. haveC. doD. does( )4. The boy is good ______ drawing.A. onB. atC. inD. are( )5. My cousin ___ _____ Paris next Spring Festival.A. visitsB. is visitingC. visitD. will visit( )6. The girl often ________ home at 5:00.A. goB. go toC. goesD. is going( )7. They go to school ___ ___.A. by footB. on footC. on bikeD. take bike( )8. Do you play the piano ?A. badlyB. badC. goodD. nice( )9. There ________ some milk in the bottle.A. hasB. areC. haveD. is( )10. Whose present is it? It's ___ .A. IB. meC. myD. mine( )11. We often _______ games after school.A. playingB. playsC. playD. do( )12. What would you like? I'd like _ ________.A. two piece of breadB. two piece of breadsC. two pieces of breadD. two pieces of breads( )14. ________ does your first class begin? At 8.00.A. WhatB. WhenC. WhereD. Why( )15. My hobby is ________ pets.A. keepingB. keepC. keepingD. to keep。

一、选择题1、我国规范采用（A、）强度作为混凝土各种力学指标的代表值。

A、立方体抗压B、轴心抗压C、轴心抗拉D、劈拉2、混凝土的弹性系数反映了混凝土的弹塑性性质，定义(A)为弹性系数A、弹性应变与总应变的比值B、塑性应变与总应变的比值C、弹性应变与塑性应变的比值D、塑性应变与弹性应变的比值3、结构的（D）是：结构在规定的时间内，在规定的条件下，完成预定功能的能力。

A、安全性B、适用性C、耐久性D、可靠性4、可变荷载中作用时间占设计基准期内总持续时间超过50%的荷载值，称为（D）。

A、长期荷载效应组合B、标准荷载C、短期荷载效应组合D、可变荷载准永久值5、当楼面均布活荷载大于或等于4kN/m2时，取γQ（C）。

A、1.0B、1.2C、1.3D、1.46、在截面设计时，满足下列条件（D）则为第二类T形截面。

A、f y A s≤f c b'f h'fB、M≤f c b'f h'f(h o-h'f/2)C、f y A s>f c b'f h'fD、M>f c b'f h'f(h o-h'f/2)7、梁的破坏形式为受拉钢筋先屈服，然后混凝土受压破坏，则称为（B）。

A、少筋梁B、适筋梁C、平衡配筋梁D、超筋梁8、受弯构件正截面承载能力极限状态设计的依据是适筋梁正截面破坏的（C）。

A、第Ⅰ阶段末的应力状态B、第Ⅱ阶段末的应力状态C、第Ⅲ阶段末的应力状态9、双筋矩形截面梁，正截面承载力计算公式的第二个适用条件x≥2a'的物理意义是（C）。

A、防止出现超筋破坏B、防止出现少筋破坏C、保证受压钢筋达到规定的抗压设计强度D、保证受拉钢筋达到规定的抗拉设计强度10、钢筋混凝土梁的截面尺寸和材料品种确定后(D)。

A、梁裂缝出现前瞬间受拉钢筋应力与配筋率无关B、梁开裂后的受拉钢筋应力与配筋率无关C、配筋率越大，正截面抗弯强度也越大D、当满足条件ρmin≤ρ≤ρmax时，配筋率越大，正截面抗弯强度也越大11、承受以集中荷载为主的简支梁，当剪跨比λ(B)时，无腹筋梁发生剪压破坏。

1．填空题（1）综合布线系统就是用数据和通信电缆、光缆、各种软电缆及有关连接硬件构成的通用布线系统，它能支持语音、数据、影像和其他控制信息技术的标准应用系统。

（2）综合布线系统是集成网络系统的基础，它能满足数据、语音及图像的传输要求，是智能大厦的实现基础。

（3）在GB 50311—2007《综合布线系统工程设计规范》国家标准中规定，在智能建筑工程设计中宜将综合布线系统分为基本型、增强型、及综合型三种常用形式。

（4）综合布线系统包括7个子系统，分别是工作区子系统、水平子系统、管理间子系统、垂直子系统、设备间子系统和建筑群子系统，进线间子系统。

（5）在工作区子系统中，从RJ—45插座到计算机等终端设备间的跳线一般采用双绞线电缆，长度不宜超过 5 m。

（6）安装在墙上或柱上的信息插座应距离地面30 cm以上。

（7）水平子系统主要由信息插座，跳线和配线架等组成。

（8）水平子系统通常由4 对非屏蔽双绞线组成，如果有磁场干扰时可用屏蔽双绞线。

（9）垂直子系统负责连接管理间子系统到设备间子系统，实现主配线架与中间配线架的连接。

（10）管理间子系统就是连接垂直子系统和水平干线子系统的设备，其配线对数由管理的信息点数来决定。

2．选择题（部分为多选题）(1)GB50311—2007《综合布线系统工程设计规范》中，将综合布线系统分为（ C ）子系统。

A、5 B、6 C、7 D8(2)工作区子系统又称服务区子系统，它是由跳线与信息插座所连接的设备组成。

其中信息插座包括以下哪些类型？（ABC ） A、墙面型 B、地面型 C、桌面型 D、吸顶型(3)常用的网络终端设备包括（ABD）。

A、计算机 B、电话机和传真机 C、汽车 D、报警探头和摄像机(4)设备间入口采用外开双扇门，门宽一般不应小于（ B）。

A、2m B、1．5m C、1m D、0．9m(5)在网络综合布线工程中，大量使用网络配线架，常用标准配线架有（BD ）。

重点:掌握分离过程的特征，分离因子和固有分离因子的区别，平衡分离和速率分离的原理。

难点：用分离因子判断一个分离过程进行的难易程度，分离因子与级效率之间的关系。

•1、说明分离过程与分离工程的区别？•2、实际分离因子与固有分离因子的主要不同点是什么?•3、怎样用分离因子判断分离过程进行的难易程度？•4、比较使用ESA与MSA分离方法的优缺点。

•5、按所依据的物理化学原理不同,传质分离过程可分为那两类?•6、分离过程常借助分离剂将均相混合物变成两相系统,举例说明分离剂的类型.1、下列哪一个是机械分离过程（）（1）蒸馏(2）吸收(3）膜分离（4)离心分离2、下列哪一个是速率分离过程( )（1）蒸馏（2)吸附（3)膜分离（4)沉降3、下列哪一个是平衡分离过程( ）（1)蒸馏（2)热扩散（3）膜分离（4）离心分离1、分离技术的特性表现为其（）、（)和（）。

2、分离过程是(混合过程）的逆过程,因此需加入（）来达到分离目的。

3、分离过程分为（)和（）两大类4、分离剂可以是(）或（),有时也可两种同时应用。

5、若分离过程使组分i及j之间并没有被分离,则（)。

6、可利用分离因子与1的偏离程度,确定不同分离过程分离的（）。

7、平衡分离的分离基础是利用两相平衡（组成不等）的原理，常采用()作为处理手段，并把其它影响归纳于（）中。

8、传质分离过程分为（)和（）两类.9、速率分离的机理是利用溶液中不同组分在某种（）作用下经过某种介质时的（）差异而实现分离。

10、分离过程是将一混合物转变为组成(）的两种或几种产品的哪些操作。

11、工业上常用（）表示特定物系的分离程度,汽液相物系的最大分离程度又称为()。

12、速率分离的机理是利用传质速率差异,其传质速率的形式为（）、（)和（).13、绿色分离工程是指分离过程（)实现.14、常用于分离过程的开发方法有（）、(）。

1、分离过程是一个()a。

熵减少的过程；b.熵增加的过程;c。

熵不变化的过程；d. 自发过程2、组分i、j之间不能分离的条件是（）a。

一、填空题1、软件对象可以这样定义：所谓的软件对象，是一种将状态和行为有机结合起来形成的软件构造模型，它可以用来描述现实世界中的一个对象。

2、类是具有相同属性和操作的一组对象的组合，即抽象模型中的“类”描述了一组相似对象的共同特征，为属于该类的全部对象提供了统一的抽象描述。

3、面向对象程序的基本特征是抽象、封装、继承和多态。

4、在UML中主要包括的视图为静态视图、用例视图、交互视图、状态机视图、活动视图、物理视图和模型管理视图。

5、UML图包括：用例图、类图、状态图、序列图、活动图、构件图和部署图。

6、用例图描述了系统的参与者与系统进行交互的功能，是参与者所能观察和使用到的系统功能的模型图。

一个用例是系统的一个功能单元，是参与者与系统之间进行的一次交互作用。

7、状态机视图是通过对象的各种状态建立模型来描述对象随时间变化的动态行为，并且它是以独立的对象为中心进行描述的。

8、用例图的主要目的是帮助开发团队以一种可视化的方式理解系统的功能需求，包括基于基本流程的“角色”关系，以及系统内用例之间的关系。

9、在UML中定义了4种基本的面向对象的事物，分别是结构事物、行为事物、分组事物和注释事物等。

10、使用Rational Rose建立的Rose模型中包括4种视图，分别是用例视图、逻辑视图、构件视图和部署视图。

11、在用例视图中包括了系统中的所有参与者、用例和用例图，必要时还可以在用例视图中添加顺序图、协作图、活动图和类图等。

12、逻辑视图关注系统如何实现用例中所描述的功能，主要是对系统功能性需求提供支持，即系统应该提供的功能。

13、构件视图用来描述系统中的各个实现模块以及它们之间的依赖关系，包含模型代码库、执行文件、运行库和其他构件等信息。

14、部署视图显示的是系统的实际部署情况，它是为了便于理解系统如何在一组处理节点上的物理分布，而在分析和设计中使用的构架视图。

15、Rational统一过程以一种能够被大多数项目和开发组织适应的形式建立起来，其所包含的6项最佳实践为：迭代式软件开发、需求管理、基于构件的架构应用、建立可视化的软件模型、软件质量验证、软件变更控制。

三．选择题1.高岭石的矿物实验式〔C 〕。

A、Al2O3·SiO2·2H2OB、Al2O3·2SiO2·H2OC、Al2O3·2SiO2·2H2OD、3Al2O3·2SiO22.钾长石的矿物实验式为〔 C 〕A、K2O·Al2O3·2SiO2B、K2O·Al2O3·4SiO2C、K2O·Al2O3·6SiO2D、K2O·2Al2O3·6SiO23.化学式为3Al2O3·2SiO2的化合物是〔D〕A、铝硅尖晶石B、脱水高岭石C、堇青石D、莫来石4.石质瓷瓷胎的相构成是-------------------。

〔B 〕A、石英－长石－高岭石B、石英－方石英－莫来石－玻璃相C、石英－莫来石－玻璃相D、石英－方石英－玻璃相5.粘土按成因可分为------------------------。

( C )A、原生粘土与一次粘土B、原生粘土与耐火粘土C、原生粘土与次生粘土D、次生粘土与高塑性粘土6.粘土风化后残留在原地的粘土称为〔 B 〕A、强可塑性粘土B、一次粘土C、高岭土D、二次粘土7.坯料中的SiO2可由-------------------引入。

〔D 〕A、石英B、粘土C、长石D、以上三者均可8.吸水后产生很大的体积膨胀的粘土矿物是〔 D 〕A、高岭石B、伊利石C、叶蜡石D、蒙脱石9.已知某种粘土的阳离子交换能力强，吸附能力大，吸水性强，吸水后体积膨大5～16倍，初步认定该粘土类型是----------------------。

〔C〕A、高岭石B、伊利石C、蒙脱石D、叶蜡石10.预先煅烧块状石英的目的是-----------------------------( A )A、利于粉碎B、促进晶型转变C、减少收缩11.自然界中的石英多数以〔 B 〕存在。