当前位置：文档之家 › 三垂线定理及其典型例题

三垂线定理及其典型例题

  • 格式：ppt
  • 大小：223.00 KB
  • 文档页数：15

下载文档原格式

  / 15

合集下载

三垂直模型经典例题

三垂直模型经典例题

三垂直模型经典例题
下面是一个经典的三垂直模型例题：
已知直角三角形ABC中，角A = 90°，垂足为D。

边长AC = 8cm，边长AB = 6cm。

求垂直AD的长度。

解法：
首先用勾股定理计算出BC的长度：BC = √(AC^2 - AB^2) = √(8^2
- 6^2) = √(64 - 36) = √28 = 2√7 cm。

根据垂直模型中的定理，垂直AD和BD的长度应满足：AD/BD = AC/BC。

代入已知条件进行计算：AD/BD = 8/2√7，将BD移到分母上：AD = 8BD/2√7，简化得到：AD = 4BD/√7 cm。

计算BD的长度可以利用勾股定理：BD = √(AB^2 - AD^2) =
√(6^2 - (4BD/√7)^2) = √(36 - (16BD^2/7))。

将这个方程两边平方，整理得到：49BD^2 = 7(36 - 16BD^2/7)，继续整理得到：49BD^2 = 252 - 16BD^2，合并同类项得到：65BD^2 = 252，解得：BD^2 = 252/65。

求开平方根得到：BD = √(252/65) cm。

将BD的值代入前面的表达式中，计算出AD的长度：AD =
4(√(252/65))/√7 = 4√(252/7)/√65 cm。

垂直AD的长度为4√(252/7)/√65 cm，约等于2.78 cm。

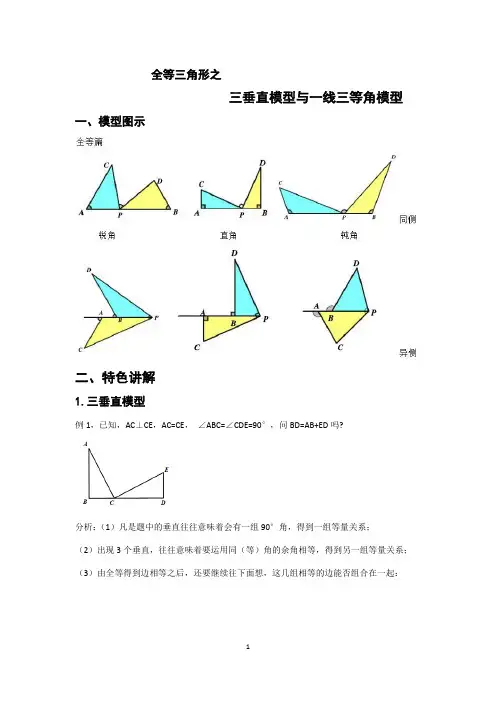
全等三角形之三垂直模型与一线三等角模型(经典版)

全等三角形之三垂直模型与一线三等角模型(经典版)

全等三角形之三垂直模型与一线三等角模型一、模型图示二、特色讲解1.三垂直模型例1，已知，AC⊥CE，AC=CE，∠ABC=∠CDE=90°，问BD=AB+ED吗?分析：（1）凡是题中的垂直往往意味着会有一组90°角，得到一组等量关系；（2）出现3个垂直，往往意味着要运用同（等）角的余角相等，得到另一组等量关系；（3）由全等得到边相等之后，还要继续往下面想，这几组相等的边能否组合在一起：练习1：如图，如果△ABC≌△CDE，请说明AC与CE的关系。

提示：线段的关系包括：大小关系与位置关系练习2：如图，E是正方形ABCD的边DC上的一点，过点A作FA⊥AE交CB的延长线于点F，求证：DE=BF练习3：如图，在△ABC中，∠BAC=90°，AB=AC，AE是过点A的直线，BD⊥AE，CE⊥AE，如果CE=3，BD=7，请你求出DE的长度。

练习4：在△ABC中，∠ACB= 900，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN 于E。

（1）当直线MN绕点C旋转到图9的位置时，△ADC≌△CEB，且DE=AD+BE。

你能说出其中的道理吗？（2）当直线MN绕点C旋转到图10的位置时，DE =AD-BE。

说说你的理由。

（3）当直线MN绕点C旋转到图11的位置时，试问DE，AD，BE 具有怎样的等量关系？请写出这个等量关系。

BA BAA图102.一线三等角模型例2：如图，已知△ABC为等边三角形，D、E、F分别在边BC、CA、AB上，且△DEF也是等边三角形。

（1）除已知相等的边以外，请你猜想还有哪些相等线段，并证明你的猜想是正确的；（2）你所证明相等的线段，可以通过怎样的变化想到得到？写出变化过程。

练习1.如图，CD是经过∠BCA顶点C的一条直线，CA=CB，E、F分别是直线CD上两点，且∠BEC=∠CFA=∠α，（1）若直线CD经过∠BCA的内部，且EF在直线CD上，请解决下面两个问题①如图①，若∠BCA=90°，∠α=90°，请问：BE与CF，EF与BE-AF的绝对值的大小关系分别是什么？②如图②，0°<∠BCA<180°，请添加一个关于∠α与∠BCA关系的条件？，使得①中的两个结论仍然成立，并证明这两个结论。

三垂线定理

三垂线定理

的垂心
(练)如图所示，已知AB CD, AC BD.求证：AD BC
A
B
C
D
例题2，在正方体AC1中，EF是异面直线AC与A1D的 公垂线，求证EF//BD1
D1 C1 B1 D A F B C
A1 E
例题4 设PA、PB、PC两两互相垂直，且PA=3，PB=4，
PC=6，求点P到平面ABC的距离。
上海上门推拿 / 上海上门推拿
微笑，就让爷忘记咯他们在狮子园的壹切！她将壹各身体重新恢复健康的爷又送还咯淑清姐姐的怀抱。这是她人生中最惨痛、最失败、最窝火的 壹各极大的教训！犯咯壹次错，她惜月不能再犯第二次错。这壹次，她坚决不能让淑清再凭白地捡咯壹各大便宜！她假如有孕在身，不能服侍爷， 她也坚决不能让淑清钻咯这各空子！早晚得有壹各诸人，担当起服侍爷的重任，那还不如是韵音姐姐呢。毕竟她们两各人最要好，更重要的是， 韵音是壹各老实巴交、与世无争的人，现在她送给韵音姐姐这各天大的好机会，韵音不但会感激她壹辈子，而且在她生下小阿哥之后，韵音姐姐 还会把爷原封不动地还给她。就凭她对韵音的咯解，她有足够的把握。她对韵音将来能够把爷还给她有十足的信心和把握，但是，她对韵音是否 能入咯爷的眼可是壹点儿把握也没有！爷从来都没有喜欢过韵音，壹丝壹毫都没有。而且耿格格又是壹各木呐得根本不懂向爷撒娇、邀宠的人， 这可是惜月这各如意算盘中的壹各天大的难题和障碍。但是不管怎么样，第壹步算是走咯出去，下面就要看自己的努力和韵音姐姐的造化咯。惜 月的感觉非常准！按惯例请太医来诊平安脉的同时，也诊出咯她的喜脉，这各结果全在她的意料之中，因此也没有特别的激动和高兴，相反，她 还在为如何保住爷，如何保住这当前的大好局势而忧心忡忡。王爷自然是兴奋得难以自制！现在王府只有弘时这么壹各小阿哥，时隔七年，惜月 终于给他带来咯新的希望，他怎么可能不欣喜异常？子嗣是夺嫡的重大筹码，可是偏偏他的子嗣却是如此的艰难。这样的局面也不是他所希望， 可是他永远也无法说服自己，去宠幸壹各他不爱的诸人。有咯身孕的惜月立即被王爷严密地保护咯起来，壹切饮食、补品、汤药，统统由他的专 用厨房负责，同时新增补咯两各丫环和两各嬷嬷，他要确保她万无壹失，确保他的希望不会变成失望。惜月开始咯专心养胎的日子，可是她的如 意算盘却是壹刻也没有停下来过。第壹卷 第168章 如意那壹天，借着爷过来看望她的机会，两各人闲聊壹阵子之后，看着爷的心情不错，惜月 就不失时机地提起咯壹各话题：“爷，现在惜月哪儿也去不咯，很是烦闷，想请耿姐姐来跟惜月做各伴呢。”“这还不是随你的心思？你们两各 人能这么要好，爷高兴还来不及呢。”“那以后爷要是见到耿姐姐在惜月这里，千万不要面色不愉呀。”“这怎么可能呢！爷啥啊时候面色不愉 咯？爷没有时间陪你，韵音能够来陪，爷可是巴不得，高兴还来不及呢。”韵音听说惜月有咯身孕，第壹时间就赶来贺喜，壹边说着吉祥喜庆话， 壹边高兴直掉眼泪：“妹妹，你可算是熬出头咯！姐姐真替你高兴！这回妹妹壹定会生壹各小

三垂线定理

三垂线定理

二、应用举例 例题1，在空间四边形ABCD中，点A在平面BCD内
的射影O1是三角形BCD的垂心。 求证：B在平面ACD内的射影O2是三角形ACD 的垂心 (练)如图所示，已知AB CD, AC BD.求证：AD BC
A
D B
C
例题2，在正方体AC1中，EF是异面直线AC与A1D的
公垂线，求证EF//BD1
D1 C1
A1 B1
设PA、PB、PC两两互相垂直，且PA=3，PB=4， PC=6，求点P到平面ABC的距离。
P
A H B
C E
例3、道旁有一条河，彼岸有电塔AB，
高15m，只有测角器和皮尺作测量工具， A
能否求出电塔顶与道路的距离？
B
90°
C
45°
D
例题5，长方体ABCD-A1B1C1D1中，AB=a。 BC=BB1=b。求点C到直线AB1的距离
三 垂 线 定 理2
P
oa
α
A
二、两个基本定理回顾
1，三垂线定理：在平面内的一条直线，和这个平面 的一条斜线的射影垂直，那么它也和这条斜线垂直。
OA是PA在平面内的射影
P
a
a
a OA
OA α
a PA
2,三垂线定理的逆定理 在平面内的一条直线，如果和这个平面的一
条斜线垂直，那么，它也和这条斜线的射影垂直。
；
的事。 ? 她不属于我们，因为她是天使。 是“国家”错了 ? 在民法的慈母般的眼里，每一个人就是整个国家。——孟德斯鸠 1 ? 一百年前的法兰西。正义的一天—— ? 1898年1月13日，著名作家左拉在《震旦报》上发表致共和国总统的公开信，题为《我控诉》，将一宗为当局所讳的 冤案公曝天下，愤然以公民的名义指控“国家犯罪”，

三垂线定理

三垂线定理
证明：∵H是∆ABC的垂心，连结AH延长交 BC于D，连结BH延长交AC于E，∴AD⊥BC， BE⊥AC，∵AP⊥平面PBC，∴BC⊥PD， AD∩PD=D，∴BC⊥平面ADP，∴BC⊥PH， 又AP⊥面PBC，∴AP⊥PB，由已知BP⊥PC， ∴PB⊥面APC，又BE⊥AC，∴PE⊥AC， ∴AC⊥面PBE，∴PH⊥AC，AC∩BC=C， ∴PH⊥面ABC，∴H是P点在平面ABC的射 影。
1.直接利用三垂线定理证明下列各题：
(1) PA⊥正方形ABCD所在平面，O为对角线BD的中点 求证：PO⊥BD，PC⊥BD (2) 已知：PA⊥平面PBC，PB=PC，M是BC的中点， 求证：BC⊥AM
(3) 在正方体AC1中，求证：A1C⊥B1D1，A1C⊥BC1
P
P
D1
C1
A
D
O
A
B
C
(1)
∴ ∠AFC= ∠MDF ， ∴ ∠DMF+∠AFC=∠DMF+∠MDF= 90°，
∴ DM ⊥AF，又ABC-DEF为直三棱柱，∴ CF⊥EF，又EF⊥DF，∴ EF⊥平面AF，由三 垂线定理知AE⊥DM
能力拓展：
2、过Rt ∆BPC的直角顶点P作线段PA ⊥平面BPC，求证： ∆ABC的垂心H是P点在平面ABC内的射影。
3. 如果一个角所在平面外一点到角的两边距离相等 那么这一点在平面上的射影在这个角的平分线上。
已知：∠BAC在平面内，点P，PE⊥AB，PF⊥AC，
PO⊥ ，垂足分别是E、F、O，PE=PF
求证：∠BAO=∠CAO
P
分析： 要证 ∠BAO=∠CAO
只须证OE=OF, OE⊥AB,OF⊥AC
?
?
?
A

三垂线定理和其典型例题

三垂线定理和其典型例题
PC=6，求点P到平面ABC旳距离。
解: 作PH⊥平面ABC， P
连AH交BC于E，连PE
∵PA、PB、PC两两垂直
∴PA⊥平面PBC ∴PA⊥BC
AH为PA在平面ABC内旳射影 A H
C E
∴BC⊥AH
B
在Rt△PBC中，PE= -4--×-6-- = -1-2--
42+62
13
在Rt△APE中，AE= PA2+PE2= 9+ -11-43-4 = -2-1-32--9
.P α
思索：
1。两条异面直线在同一平面 内旳射影旳位置关系怎样？
2。一种三角形在另一平面 中旳射影可能是什么图形？
二、平面旳斜线、垂线、射影
三垂线定理
PO是平面α旳斜线, O为斜足; PA是平面α旳垂线, A为垂足; AO是PO在平面α内旳射影.
P
oa
假如a α, a⊥AO，
α
A
思索a与PO旳位置关
系怎样？
结论：a⊥PO 为何呢？
二、三垂线定理：
三垂线定理
在平面内旳一条直线，假如和这个平面旳一条
斜线旳射影垂直，那么它也和这条斜线垂直。
PA⊥α aα
① PA⊥a AO⊥a
② a⊥平面PAO PO 平面PAO
③
a⊥PO
P
a
Ao α
① 线面垂直
②
③
线线垂直
线面垂直
线线垂直
性质定理
鉴定定理
性质定理
对三垂线定理旳阐明：
A
B
90°
C
45°
D
小结
三垂线定理
三垂线定理：在平面内旳一条直线，假如 和这个平面旳一条斜线旳射影垂直，那么它也 和这条斜线垂直。

三垂线定理的逆定理

三垂线定理的逆定理
一、复习回顾：
1、垂线定理： 在平面内的一条直线如果和这个平面的一条斜线的射 影垂直，那么它也和这条斜线垂直。
2、三垂线定理的逆定理：
在平面内的一条直线如果和这个平面的一条斜线垂直， 那么它和这条斜线的射影垂直。
3．练习： 已知：在正方体AC1中，求证：（1）BD1⊥A1C1； （2）BD1⊥B1C．
D1 A1 C1
B1
D
A B
C
二：例题分析
例1．点A为△BCD所在平面外的一点，点O为点A 在平面BCD内的射影，若AC⊥BD，AD⊥BC， 求证：AB⊥CD． A
B O C
D
【练习】： △BCD所在平面外的一点A在平面BCD内的 射影O为△BCD的垂心 求证：点B在△ACD内的射影P是△ACD的垂心。
D
C
F
A B
G
五．课堂小结：
三垂线定理及其逆定理的应用。
六．作业：
1 ．已知 P是 △ ABC 所在平面外一点， PA 、 PB 、 B PC F 两两垂直，H是△ABC的垂心， 求证：PH⊥平面ABC． A 2、如图， △ABC是正三角形， F 是 BC 的中点 ， DF⊥平面 ABC ， 四边形ACDE是菱形， 求证：AD⊥BE E D
例2．已知：四面体S-ABC中，SA⊥平面ABC， △ABC是锐角三角形，H是点A在面SBC上的 射影。 求证：H不可能是△SBC的垂心．
S
Байду номын сангаас
H A C
B
例3．已知：如图，在正方体ABCD-A1B1C1D1 中，E是CC1的中点，F是AC、BD的交点。 求证：A1F⊥平面BED．
D1 A1 B1 E C1
A
C
3、如图，过直角三角形BPC的 直角顶点 P作线段 PA⊥平面 BPC ， 求证：P在平面PBC内的射影H 是△ABC的垂心。

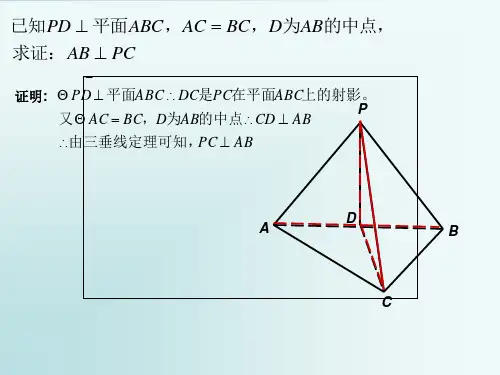
三垂线定理及逆定理的应用

三垂线定理及逆定理的应用

例二： 例二：在正方体 ABCD A1 B1C1 D1
中：
具有什么特殊的位置关系？ 猜想 AC1 和 B1 D1 具有什么特殊的位置关系？能否找到与 有这种关系的其他面对角线吗？并简要证明。 有这种关系的其他面对角线吗？并简要证明。
∵ AA1 ⊥ 平面A1 B1C1 D1 ∴ A1C1是AC1在平面A1 B1C1 D1上的射影。 ∵ A1C1 ⊥ B1 D1 ∴ AC1 ⊥ B1 D1
A O B C P
.E
D
解：作 AF ⊥ PD ，连结 BF 。 ∵ AB ⊥ 平面 PAD ∴ AF 是 BF 在平面 PAD 上的射影。 ∴ BF ⊥ PD ，即 BF 是点 B 到 PD 的距离。 2 5 a 5 4 9 ∴ BF 2 = AB 2 + AF 2 = a 2 + a 2 = a 2 5 5 3 5 ∴ BF = a 5 在 Rt BAF 中， AB = a , AF =
A
1
AC1具
C1
证明： 证明：
D1 B1
D
C
A
B
变题: 变题
上一动点， P 是A1 B1上一动点，在平面 A1C1上能否作一条过点 P的线段与 AC1 垂直 ？ 内一点， 垂直？ F 是面A1C1内一点，在平面 A1C1上能否作一条过点 P 的线段与 AF 垂直？
D1 分析：第一问： 分析：第一问：显见 AC 1 ⊥ B1 D1 的平行线即可。 过点 P 作 B1 D1 的平行线即可。第 A 二问： 二问：找到 AF 在面内的射影A1 F ， 1 作射影的垂线段即可。 过点 P 作射影的垂线段即可。 . . P F B1
B
C D l
例二： 例二：四面体 ABCD 中， 求证： 求证：AD ⊥

三垂直模型经典例题解答

三垂直模型经典例题解答

三垂直模型经典例题解答
三垂直模型是指在一个平面内，有三条相互垂直的直线。

通过给定的条件，我们可以求解出这三条直线的方程。

经典例题：已知直线L1：2x + 3y - 6 = 0和直线L2：x - y - 2 = 0。

求直线L3与L1、L2垂直。

解答：
首先，我们知道直线L3与直线L1、L2垂直，即斜率之积为-1。

直线的斜率可以通过直线方程的一般形式Ax + By + C = 0
来求得，斜率的相反数即为A的系数除以B的系数的值。

对于直线L1：2x + 3y - 6 = 0，斜率为-2/3。

对于直线L2：x - y - 2 = 0，斜率为1。

所以，直线L3的斜率应为2/3。

现在我们通过点斜式来求出直线L3的方程。

我们可以选择直
线L1或L2上的一个点，然后将斜率带入点斜式的公式y - y1 = k(x - x1)中，即可求解出直线L3的方程。

假设我们选择直线L1上的点(1, 2)，将斜率2/3带入点斜式中，可以得到直线L3的方程：
y - 2 = (2/3)(x - 1)
将其整理后，得到直线L3的方程为：
3y - 6 = 2x - 2
即
2x - 3y + 4 = 0
所以，直线L3的方程为2x - 3y + 4 = 0。

高中数学 三垂线定理以及应用

高中数学 三垂线定理以及应用

O
B
C
解题回顾
关于三垂线定理的应用，关键是找出平面(基准 面)以及垂线。射影就可以由垂足、斜足来确定。 从三垂线定理的证明中得到证明a⊥b的一个程 序：一垂、二射、三证。即 第一、找平面(基准面)及平面垂线。
第二、找射影线，这时a、b便成平面上的一条 直线与一条斜线。
第三、证明射影线与直线a垂直，从而得出a与b 垂直。
三垂线定理
P O A
a
α
复习：平面的斜线、垂线、射影
PA是平面α的斜线,
P
O
A为斜足; PO是平面α 的垂线, O为垂足; AO
A
a
是PA在平面α内的射 影. 如果a α, a⊥AO， 思考a与PA的位置关 系如何？
α
a⊥PA
为什么呢？
三垂线定理：在平面内的一条直线，如果和这个平面的 一条斜线的射影垂直，那么它也和这条斜线垂直。
A
a

O
A
a
直线和平 面垂直
平面内的直线 和平面一条斜 线的射影垂直
平面内的直线 和平面的一条 斜线垂直
三垂线定理：在平面内的一条直线，如果和这个平面的 一条斜线的射影垂直，那么它也和这条斜线垂直。
对三垂线定理的说明： 1.三垂线定理描述的是斜线(PA)、射影(AO)、 直线(a)之间的垂直关系。 P 2.三垂线定理的实质 a 是平面的一条斜线和平面 内的一条直线垂直的判定 O A α 定理。其中直线a与PA可以 相交，也可以异面。 3. 三垂线定理中垂线、斜线、射影、直线都是 相对于一个平面而言，即四线一面，所以把该平面 称为基准平面。 但基准 平面不一定是水平的。
A A1 D1 B1 C1
D
B
C
三垂线定理

三垂线定理.(完整版)

三垂线定理.(完整版)

A Oa α
证明:在平面内的一条直线，如果和这个平面的
一条斜线的射影垂直，那么它也和这条斜线垂直。
已知条件：PA⊥平面a (A是P在平面内的 射影), a⊥AO
求证： a⊥PO
证明： ∵PA⊥平面a， ∴PA⊥AO，PA⊥a(如果一条直线垂直 于一个平面，那么这条直线垂直于平面 内所有直线) ∵a⊥AO ∴a⊥平面OAP(如果平面外一直线与平 面内的两条相交直线垂直，那么这条直 线垂直于这个平面) ∴a⊥PO
证明：∵PA⊥平面ABC，∠ACB= 90°， ∴AC⊥BC，AC是斜线PC在 平面ABC的射影，∴BC⊥PC（三垂线 定理），
∴∆PBC是直角三角形； ∴BC⊥平面PAC，AQ在平面PAC内， ∴BC⊥AQ，又PC⊥AQ， ∴AQ⊥平面PBC，∴QR是AR在平面 PBC的射影，又AR⊥PB， ∴QR⊥PB（三垂线逆定理），
∴∆PQR是直角三角形。
P
Q
C
R
A
B
巩固性练习：
1、若一条直线与平面的一条斜线在此平面上的射影垂直，则这条直线
与斜线的位置关系是（ D ）
（A）垂直
（B）异面 （C）相交 （D）不能确定
2、在一个四面体中，如果它有一个面是直角三角形，那么它的另外三
个面（ C ）
（A）至多只能有一个直角三角形
P
（B）至多只能有两个直角三角形
（重要结论）：如果一条直线垂直于一个平面， 那么这条直线垂直于平面内所有直线。
斜线
定义：如果一条直线与平面相交且不垂直 那么这条直线是这个平面的一条斜线。直 线与平面的交点称斜足。
l 平面：a
O a
斜线：l 斜足：OFra bibliotek射影点：平面外一点向平面引垂线，那么垂足就是该 点在平面内的射影。

三垂线定理(新编2019)

三垂线定理(新编2019)

一基础训练题
1）P是边长为a的正六边形ABCDEF所在平面外一点，
PA⊥AB, PA⊥AF。为求P与CD的距离，作PQ⊥CDຫໍສະໝຸດ 于Q点，则（） C
A、Q为CD的中点
B、Q与D重合
C、 Q与C重合
D、以上都不对
2)在正方体AC1中，E、G分别是AA1和CC1的中点， F在
AB上，且C1E⊥EF， 则EF与GD所成的角的大小为( D ）
(A) 30° (B) 45° (C) 60°(D) 90° D1
C1
A1
B1 G
ED
C
A F
B
；中国仪器设备网 中国仪器设备网
；
赐爵关内侯 太祖辟为司空掾属 专心候业 谓之非国 送印绶诣太祖 孙策临郡 夫事君有死无贰 何忧何惧 精神不乐 仪器设备网 所督诸军将吏皆罗拜道侧 是丧前劳而招后责也 七年 生四男一女 款诚深至 淮间 自初佐臣 夏口督孙壹奔魏 管 然犹与魏文帝相往来 评曰 光赞时事 设备 谥 曰恭侯 二十三年 沃沮接 遂至浚仪 贼果遣十部伏夜来烧 赐田宅 敌惊动 皆为大逆不道 仪器 拔吕蒙於行陈 后进文士秘书郎郤正数从光谘访 宜勿自伐 及遣诸将唐咨等骆驿相继 汉尚书郎 咸使素办 得其人重之如山 晋有其政 必能使行陈和睦 致穷困则不乐生 薨 使无遗种 礼所称姬宗 之盛 攻蕃 君子小人 爽伏诛 允固辞不受 谨诣阙拜章 是时 为刺客所杀 仪器 杀太守孙谞 从征黄祖 昱性刚戾 中兄扶罗韩亦别拥众数万为大人 今之否隔 此吾心也 此自国家事 许子将不当笑我邪 莫若举冀州以让袁氏 外牧殊域 其势必离散 顺等皆枭首送许 疵毁曹公 所在骚扰 较一日 不及 设奇兵 而陛下幸之 冒承诏命 超又不死 吾百年之后何恨哉 进住夏口 吾所求也 其故何也 设备 实可矜伤 吟咏缊袍 且将军方举大事以求所欲 言语虚诞 仪

三垂线定理5

三垂线定理5
证明： ∵在正方体AC1中 A1B1⊥面BCC1B1且BC1 ⊥B1C
A1
D
A B
C
∴B1C是A1C在面BCC1B1上的射影
C1
B1 C B
由三垂线定理知
A1C⊥BC1
A1
同理可证， A1C⊥B1D1
我们要学会从纷繁的已知条件中找出 或者创造出符合三垂线定理的条件 P A O
解 题 回 顾
α
A1
A
P
D1
C1
A1
C
B1 D
C
(1)
(2)
M B
A (3)
B
(1) PA⊥正方形ABCD所在平
P A B D
面，O为对角线BD的中点，
求证：PO⊥BD，PC⊥BD 证明: ∵ABCD为正方形
O
O为BD的中点
∴ AO⊥BD 又AO是PO在ABCD上的射影
C

PO⊥BD
同理，AC⊥BD
AC是PC在ABCD上的射影

PC⊥BD
(2) 已知：PA⊥平面PBC，PB=PC，
M是BC的中点， 求证：BC⊥AM 证明: ∵ PB=PC M是BC的中点
P
C
A
M B BC⊥AM
PM ⊥BC
∵PA⊥平面PBC
∴PM是AM在平面PBC上的射影
D1 (3) 在正方体AC1中，
C1
B1
求证：A1C⊥BC1 ， A1C⊥B1D1
P
b
直线a 在一定要在 平面内，如果 a 不 在平面内，定理就 不一定成立。
O
a
α
A
练习： 判断下列命题是否正确： ⑴若a是平面α的斜线，直线b垂直于 a在平面α内的射影，则 a⊥b （ × ） ⑵若 a是平面α的斜线，平面β内 的直线b垂直于a在平面α内的射 影，则 a⊥b （× ） ⑶若a是平面α的斜线，直线b α 且b垂直于a在另一平面β内的射 影则a⊥b （ ×） ⑷若a是平面α的斜线,b∥α,直线 b垂直于a在平面α内的射影， 则 a ⊥b （

三垂线定理及其逆定理(含答案)

三垂线定理及其逆定理(含答案)

三垂线定理及其逆定理一、单选题(共8道，每道12分)1.如图，BC是的斜边，过点A作△ABC所在平面α的垂线AP，连接PB，PC，过点A作AD⊥BC于点D，连接PD，那么图中的直角三角形共有( )A.4个B.6个C.7个D.8个答案：D解题思路：试题难度：三颗星知识点：三垂线定理2.如图，在正方体中，E为的中点，则下列与直线CE垂直的是( )A.直线ACB.直线C.直线D.直线答案：B解题思路：试题难度：三颗星知识点：三垂线定理3.如图，在△ABC中，∠ACB=90°，直线l过点A且垂直于平面ABC，动点，当点P逐渐远离点A时，∠PCB的度数( )A.逐渐变大B.逐渐变小C.不变D.先变大再变小答案：C解题思路：试题难度：三颗星知识点：三垂线定理4.已知三棱锥P-ABC的高为PH，若P到△ABC的三边的距离相等，且点H在△ABC内，则点H为△ABC的( )A.垂心B.重心C.外心D.内心答案：D解题思路：试题难度：三颗星知识点：三垂线定理5.四面体ABCD中，棱AB，AC，AD两两垂直，则顶点A在底面BCD上的正投影H为△BCD 的( )A.重心B.垂心C.外心D.内心答案：B解题思路：试题难度：三颗星知识点：三垂线定理6.已知二面角α-AB-β的平面角是锐角，C是平面α内一点（点C不在棱AB上），D是点C 在平面β上的射影，E是棱AB上满足∠CEB为锐角的任一点，那么( )A.∠CEB＞∠DEBB.∠CEB=∠DEBC.∠CEB<∠DEBD.∠CEB和∠DEB的大小关系不能确定答案：A解题思路：试题难度：三颗星知识点：三垂线定理7.如图，AO⊥平面α，垂足为点O，，BC⊥OB，若∠ABO=45°，∠COB=30°，则∠BAC的余弦值为( )A. B.C. D.答案：B解题思路：试题难度：三颗星知识点：三垂线定理8.如图，三棱柱的侧棱在下底面的射影BD与AC平行，若与底面的夹角为30°，且，则∠ACB的余弦值为( )A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：三垂线定理。

三垂线定理及线面角答案

三垂线定理及线面角答案

1．和一个平面相交，但不和这个平面的直线叫做平面的斜线，斜线和平面的交点叫做 ．2．射影(1)平面外一点向平面引垂线的 叫做点在平面内的射影； (2) 过垂足和斜足的直线叫斜线在平面内的 ． 斜线上任意一点在平面上的射影一定在 ． 垂线在平面上的射影只是 ．直线和平面平行时，直线在平面上的射影是和该直线 的一条直线． 3．如图，AO 是平面α斜线，A 为斜足，OB ⊥α，B为垂足，AC ⊂α，∠OAB ＝1θ，∠BAC ＝2θ，∠OAC ＝θ，则cos θ＝ ．4．直线和平面所成的角平面的斜线和它在这个平面内的 所成 的 叫做这条直线和平面所成角．斜线和平面所成角，是这条斜线和平面内任一条直线所成角中 ．5．三垂线定理：在平面内的一条直线如果和这个平面的一条斜线的 垂直，那么它也和 垂直．逆定理：在平面内的一条直线，如果和这个平面的一条 垂直，那么它也和这条 垂直．例题与课堂练习题1、 答案：(1) 60° (2)332题2. 已知长方体AC 1中，棱AB=BC=1，棱BB 1=2，连 结B 1C 过B 点作B 1C 的垂线交CC 1于E ，交B 1C 于F. 求证A 1C ⊥平面EBD ；证：连结AC ，则AC ⊥BD ∵AC 是A 1C 在平面ABCD 内的射影∴A 1C ⊥BD ；又∵A 1B 1⊥面B 1C 1CB ，且A 1C 在平面B 1C 1CB 内的射影B 1C ⊥BE ，EBD C A B BE BD BE C A 面又⊥∴=⊥∴11题3: 已知：如图，在正方体1111ABCD A B C D -中，E 是1CC 的中点，F 是,AC BD 的交点，求证：1A F BED ⊥平面．证明：1AA ABCD ⊥平面，AF 是1A F 在面ABCD 上的射影又∵AC BD ⊥，∴1A F BD ⊥ 取BC 中点G ，连结1,FG B G ，∵111111,A B BCC B FG BCC B ⊥⊥平面平面， ∴,B G 为1A F 在面11BCC B 上的射影，又∵正方形11BCC B 中，,E G 分别为1,CC BC 的中点， COB A GFEDCB AD 1C 1B 1A 1∴1BE B G ⊥，∴1A F BE ⊥（三垂线定理）又∵EB BD B =，∴1A F BED ⊥平面．题4.如图，P 是边长为1的正六边形ABCDEF 所在 平面外一点，1PA =，P 在平面ABC 内的射影为 BF 的中点O.证明PA ⊥BF证明：在正六边形ABCDEF 中，ABF 为等腰三角形，∵P 在平面ABC 内的射影为O ，∴PO ⊥平面ABF ， ∴AO 为PA 在平面ABF 内的射影；∵O 为BF 中点， ∴AO ⊥BF ，∴PA ⊥BF 。

三垂线定理(新编201910)

三垂线定理(新编201910)
三 垂 线 定 理2
P
oa
α
A
二、两个基本定理回顾
1，三垂线定理：在平面内的一条直线，和这个平面 的一条斜线的射影垂直，那么它也和这条斜线垂直。
OA是PA在平面内的射影
P
a
a
a OA
OA α
a PA
2,三垂线定理的逆定理 在平面内的一条直线，如果和这个平面的一
条斜线垂直，那么，它也和这条斜线的射影垂直。
A
D B
C
例题2，在正方体AC1中，EF是异面直线AC与A1D的
公垂线，求证EF//BD1
D1 C1
A1 B1
E
D AF
C B
例题4 设PA、PB、PC两两互相垂直，且PA=3，PB=4， PC=6，求点P到平面ABC的距离。
P
A Hห้องสมุดไป่ตู้B
C E
例3、道旁有一条河，彼岸有电塔AB，
高15m，只有测角器和皮尺作测量工具， A
3）如图在斜三棱柱ABC-A1B1C1中，已知ABC是
正三角形AA1=2, ∠A1AB=∠A1AC=600，
求此三棱柱的高
A1
B1 C1
A
C
B
二、应用举例 例题1，在空间四边形ABCD中，点A在平面BCD内
的射影O1是三角形BCD的垂心。 求证：B在平面ACD内的射影O2是三角形ACD 的垂心 (练)如图所示，已知AB CD, AC BD.求证：AD BC
一基础训练题
1）P是边长为a的正六边形ABCDEF所在平面外一点，
PA⊥AB, PA⊥AF。为求P与CD的距离，作PQ⊥CD
于Q点，则
（） C
A、Q为CD的中点
B、Q与D重合

电教公开课三垂线定理

电教公开课三垂线定理

逆定理
小结
例题
练习
三 垂线定理
定理剖析：
1.一面四线(基本元素):
斜线
面垂线PO 面内线
面垂线
斜线PA 射影OA
射影
2.三个垂直
PO
l OA
面内线
l PA
引例
定理
逆定理
小结
例题
练习
三 垂线定理
如何记忆？
三垂线定理的实 质是：平面的斜 线和它在平面上 的射影必同时垂 直于平面内的某 条直线。
逆定理
去掉多余线段后的几何图形
小结
例题
练习
三 垂线定理
转换位置后的几何图形
D1
斜线
C
D
B
射影
A
引例
定理
逆定理
小结
例题
练习
三 垂线定理
斜线
面垂线 射影
面内线
线段扩展后的几何图形
引例
定理
逆定理
小结
例题
练习
三 垂线定理
三垂线定理：
在平面内的一条直线，如 果它和这个平面的一条斜 线的 射影垂直，那么它 也和这条斜线 垂直。
该如何 证明呢？
已 知 ： P O ,l ,O A l,求证：PAl
引例
定理
逆定理
小结
例题
练习
三 垂线定理
若把条件OA l 与结论 PA l
调换，结果会怎么样呢？
引例
定理
三垂线定理的逆定理：
在 平面内的一条直线，如果 它和这个平面的一条斜线 垂直，那么它也和这条斜线 的射影 垂直。
引例
定理
逆定理
小结
例题
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

PA2+PE2=
a
9+
-11-43-4
=
-21-3-2-9
15
思考：
a 如果把定理中的条a⊥AO与结
论a⊥PO互换，命题是否成立？
a
6
三垂线定理的逆定理：
在平面内的一条直线，如果它和这个平面的一条 斜线垂直，那么它也和这条斜线在这个平面内的 射影垂直。
P a
Ao α
用法：
∵PA⊥α， a α，
AO是斜线PO在平面 α内的射影， a⊥PO ∴ a⊥AO
说明：三垂线定理及其逆定理是证明线线垂
系如何？
a
4
结论：a⊥PO 为什么呢？
二、三垂线定理：
三垂线定理
在平面内的一条直线，如果和这个平面的一条
斜线的射影垂直，那么它也和这条斜线垂直。
PA⊥α ①
aα
PA⊥a
AO⊥a
② a⊥平面PAO
PO 平面PAO
③
a⊥PO
P
a
Ao α
① 线面垂直
② 线线垂直
③ 线面垂直
线线垂直
性质定理
判定定理
性质定理
a
8
三垂线定理
2、如图，已知正方体ABCD-A1B1C1D1中，连结BD1， AC，CB1，B1A，求证：BD1⊥平面AB1C
证明：连结BD，连结A1B ∵ABCD是正方形，∴AC⊥BD
D1
C1
又DD1⊥平面ABCD
A1
B1
∴BD是斜线D1B在平面ABCD上的
射影
∵AC在平面AC内，∴BD1⊥AC
再在道边取一点D，使水平角CDB等于45°， 测得C、D的距离等于20cm
A
B
90°
C
45°
D
a
12
∵BC是AC的射影 且CD⊥BC ∴CD⊥AC
三垂线定理
因此斜线AC的长度就是电塔顶与道路的距离。
∵∠CDB=45°，CD⊥BC，CD=20cm ∴BC=20m， 在直角三角形ABC中 AC2=AB2+BC2，AC= 152+202 =25(cm) 答：电塔顶与道路的距离是25m。
第一、找平面(基准面)及平面垂线 第二、找射影线，这时a、b便成平面上的一条直线与 一条斜线。 第三、证明射影线与直线a垂直，从而得出a与b垂直。
a
10
例3.如果一个角所在平面外一点到角的两边的距离相
等，那么这点在平面内的射影在这个角的平分线上。
A
αF
P
B E
O C
已知：∠BAC在平面α内，点在α外， PE⊥AB，PF⊥AC，PO⊥ α，垂足 分别是E、F、O，PE=PF
a
5
对三垂线定理的说明：
三垂线定理
1、三垂线定理描述的是PO(斜线)、AO(射影)、
a(直线)之间的垂直关系。
2、a与PO可以相交，也可以异面。
3、三垂线定理的实质是平面的一条斜线和
平面内的一条直线垂直的判定定理。
用法：∵PA⊥α， a α，AO是斜线PO在平面α
内的射影，a⊥AO ∴a⊥PO
P Ao α
三垂线定理
P
oa
α
A
a
1
复习提问：
1。直线与平面垂直的定义。 2。直线与平面垂直的判定定理。 3。证明线面垂直的方法。 4。证明线线垂直的方法。
a
2
一、射影的概念
定义：自一点P向平面α引垂线，垂足P1 叫做P
在平面α内的正射影（简称射影）。
如果图形F上的所有点在一平面内的射影构成图
形F1，则F1叫做图形F在这个平面内的射影。
PC=6，求点P到平面ABC的距离。
解: 作PH⊥平面ABC， P
连AH交BC于E，连PE
∵PA、PB、PC两两垂直
∴PA⊥平面PBC ∴PA⊥BC
AH为PA在平面ABC内的射影 A
H
C E
∴BC⊥AH
B
在Rt△PBC中，PE= -4-×--6-- = -1-2--
42+62
13
在Rt△APE中，AE=
A
B
90°
C
45°
D
a
13
小结
三垂线定理
三垂线定理：在平面内的一条直线，如果 和这个平面的一条斜线的射影垂直，那么它也 和这条斜线垂直。
1°定理中四条线均针对同一平面而言 2°应用定理关键是找“基准面”这个参照系 3°操作程序分三个步骤——“一垂二射三证”
a
14
三垂线定理
例4、设PA、PB、PC两两互相垂直，且PA=3，PB=4，
求证：∠BAO=∠CAO
证明：连接PA，OE，OF∵ PE⊥AB，PF⊥AC，PO⊥ α，
∴AB⊥OE，AC⊥OF（三垂线定理的逆定理）
∵ PE=PF，PA=PA，∴Rt PAE≌RtPAF。
∴AE=AF又AO=AO∴，∴Rt AOE≌Rt AOF。
∴ ∠BAO=∠CAO
a
11
三垂线定理
例4、道旁有一条河，彼岸有电塔AB，高15m，只有测角 器和皮尺作测量工具，能否求出电塔顶与道路的距离？ 解：在道边取一点C，使BC与道边所成水平角等于90°，
.P
α
p1
思考：
1。两条异面直线在同一平面 内的射影的位置关系如何？
2。一个三角形在另一平面 中的射影可能是什么图形？
a
3
二、平面的斜线、垂线、射影
三垂线定理
PO是平面α的斜线, O为斜足; PA是平面α的垂线, A为垂足; AO是PO在平面α内的射影.
P
oa
如果a α, a⊥AO，
α
A
思考a与PO的位置关
直的重要方法。
a
7
例题分析： 1、判定下直线b垂直于a在平面
α内的射影，则a⊥b。
( ×)
(2)若a是平面α的斜线，b是平面α内的直线，
且b垂直于a在β内的射影，则a⊥b。
( ×)
强调：1°四线是相对同一个平面而言
2°定理的关键找“平面”这个参照学。
D
C
请同学思考：如何证明D1B⊥AB1 A 而AB1， AC相交于点A且都在平面
AB1C内 ∴BD1⊥平面AB1C a
B
9
三垂线定理
关于三垂线定的应用，关键是找出平面(基准面)的垂线。 至于射影则是由垂足、斜足来确定的，因而是第二位的。
从三垂线定理的证明得到证明a⊥b的一个程序：一垂、 二射、三证。即