分子对称性和分子点群-结构化学课件

(c)满足缔合性： Cˆ2σˆvσˆv Cˆ2σˆv σˆv σˆvσˆv Eˆ
Cˆ2σˆvσˆv Cˆ2 σˆvσˆv Cˆ2Cˆ2 Eˆ
(d)有逆元素： Cˆ21 Cˆ2 ,σˆv1 σˆv ,
0.0
22
(2) 群的乘法表
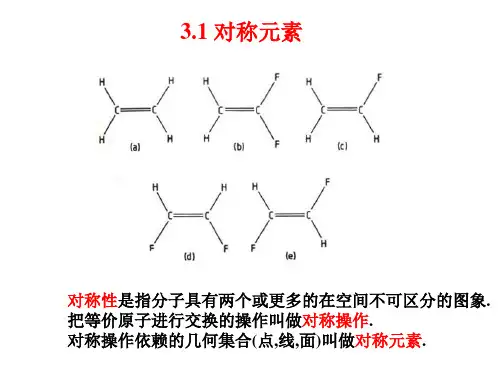
假若有一个有限群的h个元素的完全而不重复的名单，并
作时分子中至少有一点不动；(2) 分子的全部对称元
素至少通过一个公共点。 0.0
19
以H2O为例来说明： H2O分子的对称操作的完全集合为
G Eˆ,Cˆ2 ,σˆV ,σˆV
0.0
20
Cˆ 2
σv
C2
σˆ v σ v
σˆ v
σ v
0.0
21
(a)满足封闭性：如：Cˆ2σˆv σˆv
(b)有恒等元素：恒等操作 Eˆ
的夹角的对称面；
0.0
9
(2) 对称面和反映
H2O
σv
C2
0.0
σv
10
C2轴
主轴C4轴 σd σh
C2轴
0.0
11
C2(z)
d'
d
C2(x)
C2(y)
0.0
12
(3) 对称中心和反演
分子中若存在一点,将每个原子通过这一点引连线 并延长到反方向等距离处而使分子复原,这一点就是对 称中心 i ,这种操作就是反演.
一个偶数次的旋转轴C2n可以产生2n个对称操作：
Cˆ2n ,Cˆ22n ,Cˆ23n ,,Cˆ2nn ,,Cˆ22nn1 ,Cˆ22nn E
而
Cˆ
n 2n
n 0.220πn
2π 2
Cˆ 2
29
x, y, z

X射线晶体学需要制备晶体样品，通过X射线照射晶 体并记录衍射数据，再通过计算机软件分析衍射数 据，最终得到分子的晶体结构。
X射线晶体学对于理解分子结构和性质具有重要意义 ，尤其在化学、生物学和材料科学等领域中广泛应 用。
分子光谱方法
分子光谱方法是研究分子对称 性的另一种实验方法。通过分 析光谱数据，可以确定分子的 振动、转动和电子等运动状态 ，从而推断出分子的对称性。
04
分子的点群
点群的分类
80%
按照对称元素类型分类
分子点群可按照对称元素类型进 行分类，如旋转轴、对称面、对 称中心等。
100%
按照对称元素组合分类
分子点群可按照对称元素的组合 进行分类，如Cn、Dn、Sn等。
80%
按照分子形状分类
分子点群可按照分子的形状进行 分类，如线性、平面、立体等。
点群的判断方法
分子没有对称元素，如 NH3。
分子有一个对称元素， 如H2O。
分子有两个对称元素， 如CO2。
分子有多个对称元素， 如立方烷。
02
分子的对称性
对称面和对称轴
对称面
将分子分成左右两部分的面。
对称轴
将分子旋转一定角度后与原分子重合的轴。
对称中心
• 对称中心：通过分子中心点，将分子分成互为镜像的两部分。
具有高对称性的分子往往表现出较弱的磁性，因为它们具有较低的轨道和自旋分 裂能。相反，对称性较低的分子可能表现出较强的磁性，因为它们的轨道和自旋 分裂能较高。
对称性与化学反应活性
总结词
分子对称性对化学反应活性也有重要影响，可以通过对称性 分析来预测和解释分子的化学反应行为。
详细描述
具有高对称性的分子往往具有较低的反应活性，因为它们的 电子云分布较为均匀，难以发生化学反应。相反，对称性较 低的分子可能具有较高的反应活性，因为它们的电子云分布 较为不均匀，容易发生化学反应。

(2) 若分子中仅有一个镜面，则DM必在面上。 例如：Cs点群分子
(3) 若分子中对称元素交于一线，则DM必在交线上。 例如：Cnv点群分子
(4) 若分子中对称元素交于一点，则DM为零。 (5) 除Cn、 Cs、 Cnv 、 C1、点群分子以外都无偶极矩。
4
§4.3.2分子的旋光性
1、手性分子的特点：分子不能和其镜像分子通过旋 转或平移等第一类操作相重叠，即两个对映体不能 完全重叠。
8
3.分子的手性与旋光性的关系
将分子与其镜象的旋光度分别记作R与R’，则
(1) 无论对手性或非手性分子，都有R’=-R；
(2) 对非手性分子，又有R’=R .
结论：非手性分子没有旋光性，手性分子可能具有旋光
性。
例如：分子各基团差别小，以致于分子旋光性小而观察不到。
A
B CC
D
A=CH2CH3
B=(CH2)2CH3 C=(CH2)3CH3 D=(CH2)5CH3
委员处。 12
分子中含有不对称C原子
分子具有旋光性
CH3H O H NC
CN H O H CH3
11
有手性C，无旋光性，内消旋。
作业 4.1、4.2、4.8、4.9、4.10、4.12、
4.16（3-7）、4.20
请课代表或学习委员收齐作业后 于下次上课前交到讲桌上。再次 提醒：上课后将不再收作业。请 下次上课有可能请假或迟到的同 学提前将作业交到课代表或学习
5
2. 分子手性与对称性的关系 结论1：具有σ、i或S4n的分子,可通过实际操
作与其镜象完全迭合，称为非手性分子。
旋转反映
(具有Sn的)分子 反映
镜象
分子 旋转
6

NH3分子，它有一个C3轴和3个σv反映面，属 于C3V点群，类似的如CHCl3, NF3等。
ppt课件完整
28
2.2.2 主要点群
点群是作用在分子上的所有对称操作的完全集合，原则上可以组 合得到无数个可能的点群。但只需大约40个重要的点群就足以用 来描述各类分子，一下例举的只是其中的几个重要实例。
H2O2分子属于C2点群。 ppt课件完整
30
3. Cs点群
仅含有一个镜面σ。如：HOCl为一与水类似的弯曲 分子，只有一个对称面即分子平面，所以它属于Cs点群。
ppt课件完整
31
4. Cnv点群
含有一个Cn轴和n个通过Cn轴的对称面。如：H2O分
子具有一个C2轴和两个包含该轴的相互垂直的对称面，
ppt课件完整
44
9. Td点群(四面体点群)
对称元素有4个C3轴，3个C2轴，3个S4 轴(与3个C高度对称的分子点群，但由于形象特殊， 常常可从形象上加以确定。 例如：CH4、CCl4、Ni(CO)4、SO42-、MnO4-等 分子和离子的构型均属于Td点群。
平面正三角或三角双锥分子
乙烷重叠型
ppt课件完整
40
D4h群：XeF4
D6h群：苯
Dh群： I3-
ppt课件完整
41
XeF4为平面四边形，属于D4h点群； CO32-离子为平面正三角形，含有对称元素， C3, 3C2, 3σv, σh, S3, E , 属于D3h点群； C6H6为平面正六边形，属于D6h点群； 平面乙烯属于D2h群； 环戊二烯是平面正五边形，为D5h点群； 以上统属于Dnh点群。此点群的特点是具有一 个Cn轴和n个垂直于主轴的C2轴，同时有σh面。
内容提要：

②第二步，进行右上角的乘法， 分子进行 反映，N和H1保持不变，H2与H3互换位置，
再绕 轴旋转120度，则N还是不变，H2到H1 位置，H1到H2位置，H3回到原位置，两个操 作的净结果，相当于一个 镜面反映……可
写出右上角的九个结果。
③同理也可写出左下角的九个结果。旋转操 作和反映操作相乘，得到的是反映操作；两 个旋转操作相乘和两个反映操作相乘得到的 是旋转操作。
学时安排 学时----- 4学时
第四章.分子的对称性
对称 是一种很常见的现象。在自然界
我们可观察到五瓣对称的梅花、桃花，六瓣 的水仙花、雪花、松树叶沿枝干两侧对称， 槐树叶、榕树叶又是另一种对称……在人工 建筑中，北京的古皇城是中轴线对称。在化 学中，我们研究的分子、晶体等也有各种对 称性，有时会感觉这个分子对称性比那个分 子高，如何表达、衡量各种对称？数学中定 义了对称元素来描述这些对称。
I1 S2 i
S1
I
2
I2 S1
S2 I1 i
I3
S
6
C3
i
S3
I
6
C3
I4 S4
S4
I
4
I5 S10 C5 i
S5 I10 C5
I6 S3 C3 S6 I3 C3 i
负号代表逆操作，即沿原来的操作退回去的操作。
S4 S6
对称元 素符号
E Cn
I1n=iC1n 4.1.5.映轴和旋转反映操作
映轴S1n的基本操作为绕轴转3600/n， 接着按垂直于轴的平面进行反映，是C1n和 σ相继进行的联合操作：
S1n=σC1n
如果绕一根轴旋转2/n角度后立即对垂直于这根轴的一 平面进行反映，产生一个不可分辨的构型，那么这个轴就

分子对称性的意义
预测和解释分子的物理和化学性质
分子对称性与分子的电子结构和化学键有关，因此可以用来预测和解释分子的性质，如稳 定性、反应活性等。
确定分子的点群
分子的点群是根据分子的对称性进行分类的，通过确定分子的点群可以更好地理解分子的 结构和性质。
指导药物设计和材料科学
分子对称性在药物设计和材料科学中具有重要意义，例如在药物设计中，可以利用分子对 称性来设计具有特定性质的化合物。
分子对称性在化学反应中的实例分析
以烷烃为例，烷烃的对称性越高，其化学反应选择性越低，因为它们具有更稳定的 分子结构。
以烯烃为例，烯烃的对称性较低，因此它们在加成反应中表现出较高的反应活性。
以芳香族化合物为例，由于芳香族化合物具有较低的对称性，它们在取代反应中表 现出较高的反应活性。
05
CATALOGUE
02
CATALOGUE
分子点群的基本概念
分子点群的分 类
01
02
03
04
第一类点群
包括1个线性群和3个二面体群。
第二类点群
包括4个四面体群、6个三方 柱群和1个六方柱群。
第三类点群
包括4个四方锥群、4个三角 锥群、2个八面体群、1个五 方双锥群和1个三方偏方面体
群。
第四类点群
包括1个二十面体群。
02
分子对称性是分子结构的一个重 要属性，它决定了分子的物理和 化学性质。
分子对称性的分类
01
02
03
点对称性
分子在三维空间中具有一 个或多个对称中心，这些 对称中心可以将分子分成 若干个相同的部分。
轴对称性
分子具有一个或多个对称 轴，这些对称轴可以将分 子分成若干个相同的部分。

(2) 甲烷具有S4，只有C2 与S4共轴，但C4和与之垂直 的σ并不独立存在.
CH4中的映轴S4与旋转反映操作
注意: C4和与之垂直的σ都不独立存在
环辛四烯衍生物中的 S4
分子中心是S4的图形符号
丙二烯
对称操作与对称元素
旋转是真操作, 其它对称操作为虚操作.
两个或多个对称 操作的结果，等效于 某个对称操作.
D2h群：乙烯
D3h 群
D3h 群 ： C2H6
D3h群分子多呈平面正三角形、正三棱柱或三角双锥结构
D4h群：XeF4
D6h群：苯
同核双原子分子，具有对称中心的线型分子，属于Dh群
Dh群： I3-
Dnd: 在Dn基础上, 增加了n个包含主轴且平分二次副轴
夹角的镜面σd.
D2d : 丙二烯
D2d : B2Cl4
3.偶次旋转轴和与它垂直的对称面的组合 一个偶次轴与一个垂直于它的对称面组合，必定在交
点上出现对称中心。 C2σh = S2 = i
3.2 点群
3.2.1定义一种称之为“乘
法”的运算，如果满足下列条件，则集合G构成群。
1）封闭性：集合G 中任何两个元素相“乘”（或称之为 组合），其结果仍然是G 中元素，也就是说，A、B分别 属于G，AB＝C 也属于G。即 A∈G， B∈G， 则 AB＝ C∈G
（2）二面体群：包括Dn、Dnh、Dnd . 这类点群的共同特点是
旋转轴除了主轴Cn外，还有与之垂直的n条C2副轴.
（a）Dn 群: 除主轴Cn外，还有与之垂直的n条C2副轴( 但没有 镜面).（ Cn + nC2⊥ Cn ）
D2 群
主轴C2垂直于荧光屏
D ： 3 这种分子比较少见，其对称元素也不易看出.

例: D3={e,d,f,a,b,c}在三维空间的表示
1 0 0 A(e) 0 1 0
0 0 1
A (e) 3
A(d
)
cos 2
3
sin 2
sin 2
3
cos 2
0
0
A(
f
)
cos 4
3
sin 4
sin 4
3
cos 4
0
0
3
3
3
3
0
0 1
0
0 1
A
(d
)
1
2
cos
2
7. Dnh群
有一个Cn轴, n个垂直于该轴的C2轴, 1
个垂直于该轴的对称面h
D3h
H2为Dh
8. Td点群 有4个C3轴, 3个 C2轴, 6个对称面 d. 正四面体对称群.
9. O h点群 有3个C4轴, 4个C3轴, 3个 h , 6个对称面 d, 对称中心 i. 正八面体对称群.
3.4 群的表示
规则二. 点群中所有不可约表示的维数的平方和等于群的阶 n. l12 l22 lk 2 n
在 D3中, l12 l22 l32 6
从而 l1 l2 1, l3 2
规则三. 点群中不可约表示特征标间的正交关系:
k
h j r (R j ) * s (R j ) n rs
j 1
对不可约表示: (R) 2 n
A(c) A(a) A( f ) 0 1
0
0
001
cos 4
3
sin 4
3 0
sin 4
3
cos 4
3 0
0 0
cos 4

完整版课件
38
3.3.1. 群的表示
例：SO2属于C2v群，对称元素有E，C2， v(xz)，v(yz)。
现让SO2分子沿y方向平移一个单位长度：
Ty
让C2v群的各个对称操作轮
流对Ty作用。
用（＋1）表示没有变化，用（－1）表 示改变了方向。
完整版课件
39
E(Ty)＝ (+1)(Ty) ， C2(Ty)＝(-1)(Ty) (yz)(Ty)= (+1)(Ty)， (xz)(Ty)= (-1)(Ty)
4C3
6σ
4C3， 3S4，6σ，3完C整2版，课件E，属于Td点群
35
Td点群属于高度对称的分子点群，但由于形象 特殊，常常可从形象上加以确定。
例如：CH4、CCl4、Ni(CO)4、SO42-、MnO4-等分子 和离子的构型均属于Td点群；
完整版课件
36
8. Oh点群(八面体点群)
3C4， 4C3， 6C2， 9σ，i，3S4，4S6， E，属于
完整版课件
2
对称元素和对称操作
元素符号
E C
σ
i
S
I
元素名称 单位元素 旋转轴
镜面 对称中心
映轴
反轴
操作符号
Ê
Ĉ σ∧
∧
i
Ŝ
Î
完整版课件
对称操作
恒等操作
绕中心旋转 2π/n
通过镜面反映
按分子中心反 演 绕中心旋转 2π/n 再镜面 对映 绕中心旋转 2π/n 再反演
下一页
3
分子点群的种类
点群
Cn群 C1 Cnv群 C2v Cnh群 C1h Dn群 D3 Dnh群 D2h Dnd群 D2d Sn群 S2 Td群 Td Oh群 Oh