个C2轴的对称面
3.1.3. 对称中心, i (反演)
i2 = I
3.1.4 n 重旋转反映轴, Sn
Sn = h Cn = Cn h
Sn = h C n 由于S1 = h C1 = , S2 = h C2 = i 所以S1 和S2无意义.
3.1.5 恒等元素, E 或 I
当n为偶数时, 当n为奇数时,
nCn I Sn n h n 2n n n 2n 2n Sn n h C n h , Sn h C n I
3.2 群的定义和基本性质
3.2.1 群的定义与分类
• 定义: 群 G 是一个不同元素的集合{A,B,…,R,…}, 对于一定的乘法规则, 满足以下四个条件: • 1) 封闭性 群中任意两个元素R和S的乘积等于集合中另一个元素, T=RS • 2) 结合律 A(BC)=(AB)C • 3) 有唯一的恒等元素 E,使得对任意群元素 R, 有 RE=ER=R • 4) 每个元素 R 必有逆元素 R-1, 使得 RR-1 =R-1 R=E •性质: 1) 若 AB=AC 则 B=C
3.1.1
n 重对称轴, Cn (转动)
转角
2 / n
2 3 n Cn , Cn , Cn ,....,Cn I
I 为恒等操作
主轴: n 最大的轴。 产生 n-1 个转动。
3.1.2
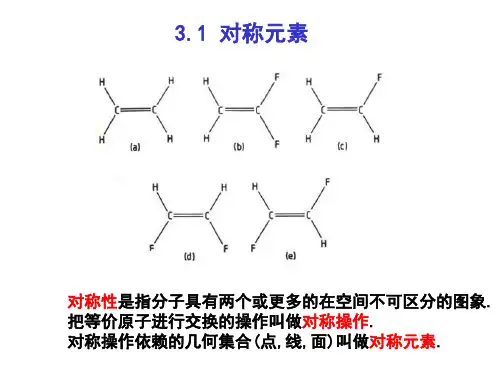
对称面, (反映) 2 = I h : 垂直于主轴的对称面 v :包含主轴的对称面 d :包含主轴且平分两
共轭元素的性质
x 取遍所有的群元素}
(1)每个元素与其自身共轭 A1 AA A (2)若A与B共轭,则B与A共轭 (3)传递性:若A与B及C共轭,则B与C共轭
1 X AX B 1 Y AY C