第七章_金属和半导体的接触
- 格式:ppt
- 大小:1.11 MB
- 文档页数:82







第7章 金属-半导体接触本章讨论与pn 结特性有很多相似之处的金-半肖特基势垒接触。
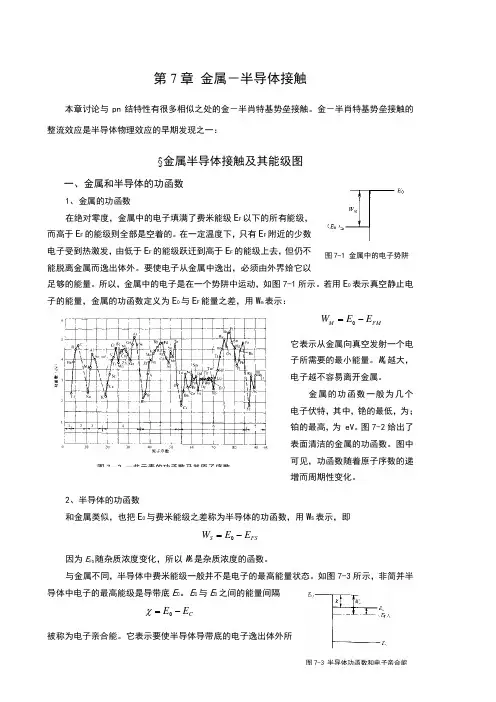
金-半肖特基势垒接触的整流效应是半导体物理效应的早期发现之一:§金属半导体接触及其能级图一、金属和半导体的功函数1、金属的功函数在绝对零度,金属中的电子填满了费米能级E F 以下的所有能级,而高于E F 的能级则全部是空着的。
在一定温度下,只有E F 附近的少数电子受到热激发,由低于E F 的能级跃迁到高于E F 的能级上去,但仍不能脱离金属而逸出体外。
要使电子从金属中逸出,必须由外界给它以足够的能量。
所以,金属中的电子是在一个势阱中运动,如图7-1所示。
若用E 0表示真空静止电子的能量,金属的功函数定义为E 0与E F 能量之差,用W m 表示: FM M E E W -=0它表示从金属向真空发射一个电子所需要的最小能量。
W M 越大,电子越不容易离开金属。
金属的功函数一般为几个电子伏特,其中,铯的最低,为;铂的最高,为 eV 。
图7-2给出了表面清洁的金属的功函数。
图中可见,功函数随着原子序数的递增而周期性变化。
2、半导体的功函数和金属类似,也把E 0与费米能级之差称为半导体的功函数,用W S 表示,即FS S E E W -=0因为E FS 随杂质浓度变化,所以W S 是杂质浓度的函数。
与金属不同,半导体中费米能级一般并不是电子的最高能量状态。
如图7-3所示,非简并半导体中电子的最高能级是导带底E C 。
E C 与E 0之间的能量间隔C E E -=0χ被称为电子亲合能。
它表示要使半导体导带底的电子逸出体外所图7-1 金属中的电子势阱图7-2 一些元素的功函数及其原子序数图7-3 半导体功函数和电子亲合能需要的最小能量。
利用电子亲合能,半导体的功函数又可表示为)(FS C S E E W -+=χ式中,E n =E C -E FS 是费米能级与导带底的能量差。
表7-1 几种半导体的电子亲和能及其不同掺杂浓度下的功函数计算值 (eV)二、有功函数差的金属与半导体的接触把一块金属和一块半导体放在同一个真空环境之中,二者就具有共同的真空静止电子能级,二者的功函数差就是它们的费米能级之差,即W M -W S =E FS -E FM 。
第七章金属和半导体的接触金属—半导体接触指由金属和半导体互相接触而形成的结构,简称M-S 接触。
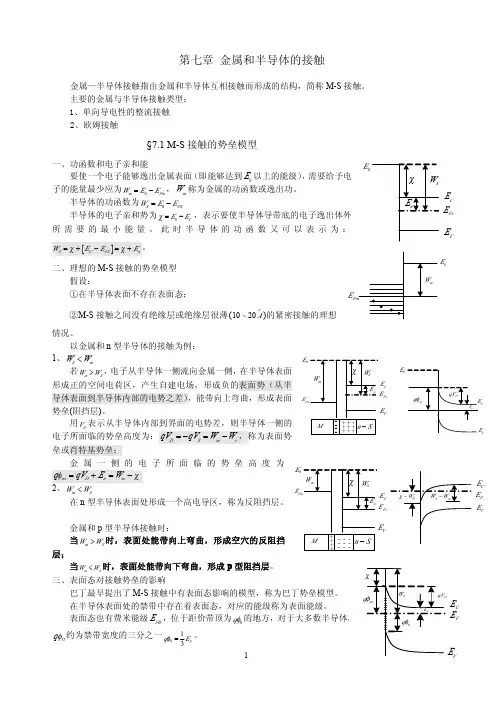
主要的金属与半导体接触类型:1、单向导电性的整流接触2、欧姆接触§7.1M-S 接触的势垒模型一、功函数和电子亲和能要使一个电子能够逸出金属表面(即能够达到0E 以上的能级),需要给予电子的能量最少应为0m Fm W E E =−,m W 称为金属的功函数或逸出功。
半导体的功函数为0S FSW E E =−半导体的电子亲和势为0C E E χ=−,表示要使半导体导带底的电子逸出体外所需要的最小能量。
此时半导体的功函数又可以表示为:[]S C FS n W E E E χχ=+−=+。
二、理想的M-S 接触的势垒模型假设:①在半导体表面不存在表面态;②M-S 接触之间没有绝缘层或绝缘层很薄(1020o~A )的紧密接触的理想情况。
以金属和n 型半导体的接触为例:1、S mW W <若m S W W >,电子从半导体一侧流向金属一侧,在半导体表面形成正的空间电荷区,产生自建电场,形成负的表面势(从半导体表面到半导体内部的电势之差),能带向上弯曲,形成表面势垒(阻挡层)。
用D V 表示从半导体内部到界面的电势差,则半导体一侧的电子所面临的势垒高度为:D S m s qV qV W W =−=−,称为表面势垒或肖特基势垒;金属一侧的电子所面临的势垒高度为ns D n m q qV E W φχ=+=−2、m SW W <在n 型半导体表面处形成一个高电导区,称为反阻挡层。
金属和p 型半导体接触时:当m S W W >时,表面处能带向上弯曲,形成空穴的反阻挡层;当m S W W <时,表面处能带向下弯曲,形成p 型阻挡层。
三、表面态对接触势垒的影响巴丁最早提出了M-S 接触中有表面态影响的模型,称为巴丁势垒模型。
在半导体表面处的禁带中存在着表面态,对应的能级称为表面能级。


第7章 金属-半导体接触本章讨论与pn 结特性有很多相似之处的金-半肖特基势垒接触。
金-半肖特基势垒接触的整流效应是半导体物理效应的早期发现之一:§7.1金属半导体接触及其能级图一、金属和半导体的功函数1、金属的功函数在绝对零度,金属中的电子填满了费米能级E F 以下的所有能级,而高于E F 的能级则全部是空着的。
在一定温度下,只有E F 附近的少数电子受到热激发,由低于E F 的能级跃迁到高于E F 的能级上去,但仍不能脱离金属而逸出体外。
要使电子从金属中逸出,必须由外界给它以足够的能量。
所以,金属中的电子是在一个势阱中运动,如图7-1所示。
若用E 0表示真空静止电子的能量,金属的功函数定义为E 0与E F 能量之差,用W m 表示:FM M E E W -=0它表示从金属向真空发射一个电子所需要的最小能量。
W M 越大,电子越不容易离开金属。
金属的功函数一般为几个电子伏特,其中,铯的最低,为1.93eV ;铂的最高,为5.36 eV 。
图7-2给出了表面清洁的金属的功函数。
图中可见,功函数随着原子序数的递增而周期性变化。
2、半导体的功函数和金属类似,也把E 0与费米能级之差称为半导体的功函数,用W S 表示,即图7-1 金属中的电子势阱图7-2 一些元素的功函数及其原子序数FS S E E W -=0因为E FS 随杂质浓度变化,所以W S 是杂质浓度的函数。
与金属不同,半导体中费米能级一般并不是电子的最高能量状态。
如图7-3所示,非简并半导体中电子的最高能级是导带底E C 。
E C 与E 0之间的能量间隔C E E -=0χ被称为电子亲合能。
它表示要使半导体导带底的电子逸出体外所需要的最小能量。
利用电子亲合能,半导体的功函数又可表示为)(FS C S E E W -+=χ式中,E n =E C -E FS 是费米能级与导带底的能量差。
材料χ (eV) W S (eV)N D (cm-3)N A (cm-3)10141015 1016 1014 1015 1016 Si 4.05 4.37 4.31 4.25 4.87 4.93 4.99 Ge 4.13 4.43 4.37 4.31 4.51 4.57 4.63 GaAs4.074.294.234.175.205.265.32二、有功函数差的金属与半导体的接触把一块金属和一块半导体放在同一个真空环境之中,二者就具有共同的真空静止电子能级,二者的功函数差就是它们的费米能级之差,即W M -W S =E FS -E FM 。