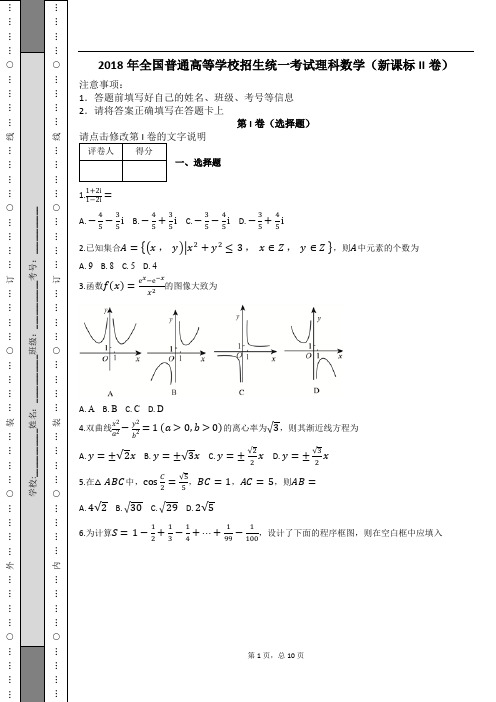
第1页，总10页…………○…………：___________班级：________…………○…………2018年全国普通高等学校招生统一考试理科数学（新课标II 卷）注意事项：1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上第I 卷（选择题）一、选择题1.1+2i1−2i = A. −45−35i B. −45+35i C. −35−45i D. −35+45i2.已知集合A={(x ， y)|x 2+y 2≤3 ， x ∈Z ， y ∈Z }，则A 中元素的个数为 A. 9 B. 8 C. 5 D. 4 3.函数f (x )=e x −e −x x 2的图像大致为A. AB. BC. CD. D 4.双曲线x 22−y 2b2=1 (a >0, b >0)的离心率为√3，则其渐近线方程为A. y=±√2x B. y =±√3x C. y =±√22x D. y =±√32x5.在△ABC 中，cosC 2=√55，BC =1，AC =5，则AB =A. 4√2B. √30C. √29D. 2√5 6.为计算S=1−12+13−14+⋯+199−1100，设计了下面的程序框图，则在空白框中应填入答案第2页，总10页……○…………线…………○题※※……○…………线…………○A. i =i +1B. i =i +2C. i =i +3D. i =i +47.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果．哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”，如30=7+23．在不超过30的素数中，随机选取两个不同的数，其和等于30的概率是 A. 112 B. 114 C. 115 D. 118 8.若f(x)=cosx −sinx 在[−a, a]是减函数，则a 的最大值是A. π4B. π2C. 3π4D. π9.已知f(x)是定义域为(−∞, + ∞)的奇函数，满足f(1−x)=f(1+x)．若f(1)=2，则f(1)+f(2)+f(3) +⋯+f(50)= A. −50 B. 0 C. 2 D. 50 10.已知F 1，F 2是椭圆C ： x 2a 2+y 2b 2=1 (a >b >0)的左，右焦点，A 是C 的左顶点，点P 在过A 且斜率为√36的直线上，△PF 1F 2为等腰三角形，∠F 1F 2P =120°，则C 的离心率为A. 23B. 12C. 13D. 14第II 卷（非选择题）请点击修改第II 卷的文字说明二、填空题（题型注释）11.曲线y=2ln(x +1)在点(0, 0)处的切线方程为__________，12.若x, y 满足约束条件{x +2y −5≥0 ，x −2y +3≥0 ，x −5≤0 ， 则z =x +y 的最大值为__________，13.已知sinα+cosβ=1，cosα+sinβ=0，则sin(α+β)=__________，第3页，总10页○…………订…………○……班级：___________考号：___________○…………订…………○……14.已知圆锥的顶点为S ，母线SA ，SB 所成角的余弦值为78，SA 与圆锥底面所成角为45°，若△SAB 的面积为5√15，则该圆锥的侧面积为__________，三、解答题（题型注释）15.记S n 为等差数列{a n }的前n 项和，已知a 1=−7，S 3=−15，，1）求{a n }的通项公式；，2）求S n ，并求S n 的最小值．16.下图是某地区2000年至2016年环境基础设施投资额y （单位：亿元）的折线图．为了预测该地区2018年的环境基础设施投资额，建立了y 与时间变量t 的两个线性回归模型．根据2000年至2016年的数据（时间变量t 的值依次为1, 2, ⋯, 17）建立模型①，y ̂=−30.4+13.5t ；根据2010年至2016年的数据（时间变量t 的值依次为1, 2, ⋯, 7）建立模型②，ŷ=99+17.5t ， ，1）分别利用这两个模型，求该地区2018年的环境基础设施投资额的预测值； ，2）你认为用哪个模型得到的预测值更可靠？并说明理由． 17.设抛物线C ： y 2=4x 的焦点为F ，过F 且斜率为k(k >0)的直线l 与C 交于A ，B 两点，|AB| =8，（1）求l 的方程；（2）求过点A ，B 且与C 的准线相切的圆的方程． 18.已知函数f(x)=e x −ax 2，（1）若a =1，证明：当x ≥0时，f(x)≥1， （2）若f(x)在(0, + ∞)只有一个零点，求a ， 19.[选修4，4：坐标系与参数方程]在直角坐标系xOy 中，曲线C 的参数方程为{x =2cosθ,y =4sinθ（θ为参数），直线l 的参数方程为{x =1+tcosα,y =2+tsinα（t 为参数）.（1）求C 和l 的直角坐标方程；（2）若曲线C 截直线l 所得线段的中点坐标为(1, 2)，求l 的斜率．20.[选修4，5：不等式选讲]设函数f(x)=5 −|x +a|−|x −2|，（1）当a =1时，求不等式f(x)≥0的解集；答案第4页，总10页（2）若f(x)≤1，求a 的取值范围．第5页，总10页参数答案1.D【解析】1.分析：根据复数除法法则化简复数，即得结果. 详解：∵1+2i 1−2i=(1+2i)25=−3+4i 5∴选D.2.A【解析】2.分析：根据枚举法，确定圆及其内部整点个数. 详解： ∵x 2+y 2≤3,∴x 2≤3,∵x ∈Z,∴x =−1,0,1， 当x =−1时，y =−1,0,1； 当x =0时，y =−1,0,1； 当x =−1时，y =−1,0,1； 所以共有9个，选A. 3.B【解析】3.分析：通过研究函数奇偶性以及单调性，确定函数图像. 详解：∵x ≠0,f(−x)=e −x −e x x =−f(x)∴f(x)为奇函数，舍去A, ∵f(1)=e −e −1>0∴舍去D; ∵f ′(x)=(e x +e −x )x 2−(e x −e −x )2xx 4=(x−2)e x +(x+2)e −xx 3∴x >2,f ′(x)>0，所以舍去C ；因此选B. 4.A【解析】4.分析：根据离心率得a,c 关系，进而得a,b 关系，再根据双曲线方程求渐近线方程，得结果. 详解：∵e =c a=√3,∴b 2a 2=c 2−a 2a 2=e 2−1=3−1=2,∴b a=√2,因为渐近线方程为y=±b ax ，所以渐近线方程为y =±√2x ，选A.5.A【解析】5.分析：先根据二倍角余弦公式求cosC,再根据余弦定理求AB. 详解：因为cosC =2cos 2C 2−1=2×(√55)2−1=−35,所以c 2=a 2+b 2−2abcosC =1+25−2×1×5×(−35)=32∴c =4√2，选A. 6.B【解析】6.分析：根据程序框图可知先对奇数项累加，偶数项累加，最后再相减.因此累加量为隔项. 详解：由S=1−12+13−14+⋯+199−1100得程序框图先对奇数项累加，偶数项累加，最后再相减.因此在空白框中应填入i =i +2，选B.7.C答案第6页，总10页【解析】7.分析：先确定不超过30的素数，再确定两个不同的数的和等于30的取法，最后根据古典概型概率公式求概率.详解：不超过30的素数有2，3，5，7，11，13，17，19，23，29，共10个，随机选取两个不同的数，共有C 102=45种方法，因为7+23=11+19=13+17=30，所以随机选取两个不同的数，其和等于30的有3种方法，故概率为345=115，选C. 8.A【解析】8.分析：先确定三角函数单调减区间，再根据集合包含关系确定a 的最大值 详解：因为f(x)=cosx −sinx =√2cos(x +π4)，所以由0+2kπ≤x +π4≤π+2kπ,(k ∈Z)得−π4+2kπ≤x ≤3π4+2kπ,(k ∈Z)因此[−a,a]⊂[−π4,3π4]∴−a <a,−a ≥−π4,a ≤3π4∴0<a ≤π4，从而a 的最大值为π4，选A.9.C【解析】9.分析：先根据奇函数性质以及对称性确定函数周期，再根据周期以及对应函数值求结果. 详解：因为f(x)是定义域为(−∞, + ∞)的奇函数，且f(1−x)=f(1+x)， 所以f(1+x)=−f(x −1)∴f(3+x)=−f(x +1)=f(x −1)∴T =4,因此f(1)+f(2)+f(3)+⋯+f(50)=12[f(1)+f(2)+f(3)+f(4)]+f(1)+f(2)， 因为f(3)=−f(1)，f(4)=−f(2)，所以f(1)+f(2)+f(3)+f(4)=0，∵f(2)=f(−2)=−f(2)∴f(2)=0，从而f(1)+f(2)+f(3)+⋯+f(50)=f(1)=2，选C.10.D【解析】10.分析：先根据条件得PF 2=2c,再利用正弦定理得a,c 关系，即得离心率. 详解：因为△PF 1F 2为等腰三角形，∠F 1F 2P =120°，所以PF 2=F 1F 2=2c,由AP 斜率为√36得，tan∠PAF 2=√36,∴sin∠PAF 2=√13，cos∠PAF 2=√12√13，由正弦定理得PF2AF 2=sin∠PAF 2sin∠APF2, 所以2c a+c=113sin(π3−∠PAF 2)113√32⋅√12√13−12⋅1√1325∴a =4c,e =14，选D. 11.y=2x【解析】11.分析：先求导数，再根据导数几何意义得切线斜率，最后根据点斜式求切线方程. 详解：∵y ′=2x+1∴k =20+1=2∴y =2x12.9第7页，总10页……○…………线…………_______……○…………线…………【解析】12.分析：先作可行域，再平移直线，确定目标函数最大值的取法. 详解：作可行域，则直线z=x +y 过点A(5,4)时z 取最大值9.13.−12【解析】13.分析：先根据条件解出sinα，cosβ，再根据两角和正弦公式化简求结果. 详解：因为sinα+cosβ=1，cosα+sinβ=0，所以(1−sinα)2+(−cosα)2=1,∴sinα=12,cosβ=12， 因此sin(α+β)=sinαcosβ+cosαsinβ=12×12−cos 2α=14−1+sin 2α=14−1+14=−12.14.40√2π【解析】14.分析：先根据三角形面积公式求出母线长，再根据母线与底面所成角得底面半径，最后根据圆锥侧面积公式求结果.详解：因为母线SA ，SB 所成角的余弦值为78，所以母线SA ，SB 所成角的正弦值为√158，因为△SAB 的面积为5√15，设母线长为l,所以12×l2×√158=5√15∴l 2=80，因为SA 与圆锥底面所成角为45°，所以底面半径为lcos π4=√22l,因此圆锥的侧面积为πrl=√22πl 2=40√2π.15.（1）a n =2n –9，（2）S n =n 2–8n ，最小值为–16，【解析】15.分析：（1）根据等差数列前n 项和公式，求出公差，再代入等差数列通项公式得结果，（2）根据等差数列前n 项和公式得S n 的二次函数关系式，根据二次函数对称轴以及自变量为正整数求函数最值.详解：，1）设{a n }的公差为d ，由题意得3a 1+3d =–15， 由a 1=–7得d =2，答案第8页，总10页所以{a n }的通项公式为a n =2n –9，，2）由（1）得S n =n 2–8n =，n –4，2–16，所以当n =4时，S n 取得最小值，最小值为–16，16.（1）利用模型①预测值为226.1，利用模型②预测值为256.5，（2）利用模型②得到的预测值更可靠．【解析】16.分析：（1）两个回归直线方程中无参数，所以分别求自变量为2018时所对应的函数值，就得结果，（2）根据折线图知2000到2009，与2010到2016是两个有明显区别的直线，且2010到2016的增幅明显高于2000到2009，也高于模型1的增幅，因此所以用模型2更能较好得到2018的预测. 详解：，1）利用模型①，该地区2018年的环境基础设施投资额的预测值为 y ̂=–30.4+13.5×19=226.1（亿元）．利用模型②，该地区2018年的环境基础设施投资额的预测值为 y ̂=99+17.5×9=256.5（亿元）．，2）利用模型②得到的预测值更可靠． 理由如下：，i ）从折线图可以看出，2000年至2016年的数据对应的点没有随机散布在直线y =–30.4+13.5t 上下，这说明利用2000年至2016年的数据建立的线性模型①不能很好地描述环境基础设施投资额的变化趋势．2010年相对2009年的环境基础设施投资额有明显增加，2010年至2016年的数据对应的点位于一条直线的附近，这说明从2010年开始环境基础设施投资额的变化规律呈线性增长趋势，利用2010年至2016年的数据建立的线性模型ŷ=99+17.5t 可以较好地描述2010年以后的环境基础设施投资额的变化趋势，因此利用模型②得到的预测值更可靠．，ii ）从计算结果看，相对于2016年的环境基础设施投资额220亿元，由模型①得到的预测值226.1亿元的增幅明显偏低，而利用模型②得到的预测值的增幅比较合理，说明利用模型②得到的预测值更可靠． 以上给出了2种理由，考生答出其中任意一种或其他合理理由均可得分．17.(1) y =x –1,(2)(x −3)2+(y −2)2=16或(x −11)2+(y +6)2=144，【解析】17.分析：(1)根据抛物线定义得|AB|=x 1+x 2+p ，再联立直线方程与抛物线方程，利用韦达定理代入求出斜率，即得直线l 的方程；（2）先求AB 中垂线方程，即得圆心坐标关系，再根据圆心到准线距离等于半径得等量关系，解方程组可得圆心坐标以及半径，最后写出圆的标准方程. 详解：，1）由题意得F ，1，0，，l 的方程为y =k ，x –1，，k >0，， 设A ，x 1，y 1，，B ，x 2，y 2，， 由{y =k(x −1)y 2=4x得k 2x 2−(2k 2+4)x +k 2=0，Δ=16k 2+16=0，故x 1+x 2=2k 2+4k2，所以|AB |=|AF |+|BF |=(x 1+1)+(x 2+1)=4k 2+4k2，由题设知4k 2+4k2=8，解得k =–1（舍去），k =1，因此l 的方程为y =x –1，，2）由（1）得AB 的中点坐标为（3，2），所以AB 的垂直平分线方程为y −2=−(x −3)，即y =−x +5，设所求圆的圆心坐标为（x 0，y 0），则第9页，总10页{y 0=−x 0+5，(x0=(y 0−x 0+1)22+16.解得{x 0=3，y 0=2 或{x 0=11，y 0=−6.因此所求圆的方程为(x −3)2+(y −2)2=16或(x −11)2+(y +6)2=144，18.（1）见解析（2）e 24【解析】18.分析：(1)先构造函数g(x)=(x 2+1)e −x −1，再求导函数，根据导函数不大于零得函数单调递减，最后根据单调性证得不等式，(2)研究f(x)零点，等价研究ℎ(x)=1−ax 2e −x 的零点，先求ℎ(x)导数：ℎ′(x)=ax(x −2)e −x ，这里产生两个讨论点，一个是a 与零，一个是x 与2，当a ≤0时，ℎ(x)>0，ℎ(x)没有零点；当a >0时，ℎ(x)先减后增，从而确定只有一个零点的必要条件，再利用零点存在定理确定条件的充分性，即得a 的值.详解：（1）当a =1时，f(x)≥1等价于(x 2+1)e −x −1≤0， 设函数g(x)=(x 2+1)e −x −1，则g′(x)=−(x 2−2x +1)e −x =−(x −1)2e −x ，当x ≠1时，g′(x)<0，所以g(x)在(0,+∞)单调递减， 而g(0)=0，故当x ≥0时，g(x)≤0，即f(x)≥1， （2）设函数ℎ(x)=1−ax 2e −x ，f(x)在(0,+∞)只有一个零点当且仅当ℎ(x)在(0,+∞)只有一个零点， （i ）当a ≤0时，ℎ(x)>0，ℎ(x)没有零点； （ii ）当a >0时，ℎ′(x)=ax(x −2)e −x ，当x ∈(0,2)时，ℎ′(x)<0；当x ∈(2,+∞)时，ℎ′(x)>0， 所以ℎ(x)在(0,2)单调递减，在(2,+∞)单调递增， 故ℎ(2)=1−4a e 2是ℎ(x)在[0,+∞)的最小值，①若ℎ(2)>0，即a <e 24，ℎ(x)在(0,+∞)没有零点； ②若ℎ(2)=0，即a =e 24，ℎ(x)在(0,+∞)只有一个零点； ③若ℎ(2)<0，即a >e 24，由于ℎ(0)=1，所以ℎ(x)在(0,2)有一个零点，由（1）知，当x>0时，e x>x 2，所以ℎ(4a)=1−16a 3e 4a=1−16a 3(e 2a )2>1−16a 3(2a)4=1−1a>0，故ℎ(x)在(2,4a)有一个零点，因此ℎ(x)在(0,+∞)有两个零点， 综上，f(x)在(0,+∞)只有一个零点时，a=e 24，19.（1）当cosα≠0时，l 的直角坐标方程为y=tanα⋅x +2−tanα，当cosα=0时，l 的直角坐标方程为x =1，（2）−2【解析】19.分析：(1)根据同角三角函数关系将曲线C 的参数方程化为直角坐标方程，根据代入消元法将直线l 的参数方程化为直角坐标方程，此时要注意分cosα≠0 与cosα=0两种情况.(2)将直线l 参数方程代入曲线C 的直角坐标方程，根据参数几何意义得sinα,cosα之间关系，求得tanα，即得l 的斜率．详解：（1）曲线C 的直角坐标方程为x 24+y216=1，答案第10页，总10页当cosα≠0时，l 的直角坐标方程为y =tanα⋅x +2−tanα， 当cosα=0时，l 的直角坐标方程为x =1，（2）将l 的参数方程代入C 的直角坐标方程，整理得关于t 的方程 (1+3cos 2α)t 2+4(2cosα+sinα)t −8=0，，因为曲线C 截直线l 所得线段的中点(1,2)在C 内，所以①有两个解，设为t 1，t 2，则t 1+t 2=0，又由①得t 1+t 2=−4(2cosα+sinα)1+3cos 2α，故2cosα+sinα=0，于是直线l 的斜率k =tanα=−2，20.（1）{x|−2≤x ≤3},(2)(−∞,−6]∪[2,+∞)【解析】20.分析：（1）先根据绝对值几何意义将不等式化为三个不等式组，分别求解，最后求并集，（2）先化简不等式为|x +a|+|x −2|≥4，再根据绝对值三角不等式得|x +a|+|x −2|最小值，最后解不等式|a +2|≥4得a 的取值范围． 详解：（1）当a =1时，f(x)={2x +4,x ≤−1,2,−1<x ≤2,−2x +6,x >2.可得f(x)≥0的解集为{x|−2≤x ≤3}， （2）f(x)≤1等价于|x +a|+|x −2|≥4，而|x +a|+|x −2|≥|a +2|，且当x =2时等号成立．故f(x)≤1等价于|a +2|≥4， 由|a +2|≥4可得a ≤−6或a ≥2，所以a 的取值范围是(−∞,−6]∪[2,+∞)，。
