张量分析第一章
- 格式:pptx
- 大小:1.54 MB
- 文档页数:91









附录I 张量分析近代力学在电子计算机的辅助下冲破了数学求解上的重重困难,取得了突飞猛进的发展,力求对复杂的物理现象和工程问题做出更为系统和真实的描述和研究。
张量分析能以简洁的表达形式和清晰的推导过程来有效地描述复杂问题的本质,已被近代力学文献和教科书普遍采用。
作为入门,此处着重介绍笛卡儿坐标系和正交曲线坐标系中的张量。
I.1 矢量和张量的记法,求和约定力学中常用的量可以分成三类:只有大小没有方向性的物理量称为标量。
例如温度T 、密度ρ、时间t 等。
既有大小又有方向性的物理量称为矢量,常用黑体(或加箭头)表示,为与课堂讲述一致,此处选择用上加箭头表示矢量。
例如矢径r 、位移u 、速度v 、力f 等。
具有多重方向性的更为复杂的物理量称为张量,常用黑体(或加下横)表示,为与课堂讲述一致,此处选择用下加横线表示矢量。
例如一点的应力状态要用应力张量来表示,它是具有二重方向性的二阶张量,记为σ。
矢量可以在参考坐标系中分解。
例如图1 中P 点的位移u 在笛卡儿坐标系()321,,x x x 中分解为∑==++=31332211i i i e u e u e u e u u (I.1)其中1u 、2u 、3u 是位移的三个分量,1e 、2e 、3e是沿坐标轴的三个单位基矢量。
由此引出矢量(可推广至张量)的三种记法: ( l )实体记法:把矢量或张量的整个物理实体用一个黑体字母或上加箭头来表示。
例如把位移记为u 。
( 2 )分解式记法:同时写出矢量或张量的分量和相应分解方向的基矢量。
例如用式(I.1)表示位移u 。
( 3 )分量记法:把矢量或张量用其全部分量的集合来表示,省略相应的基矢量。
例如用三个位移分量()3,2,1=i u i 的集合表示位移u 。
下面详细讨论后两种记法中广泛采用的指标符号。
对于一组性质相关的n 个量可以采用指标符号来表示。
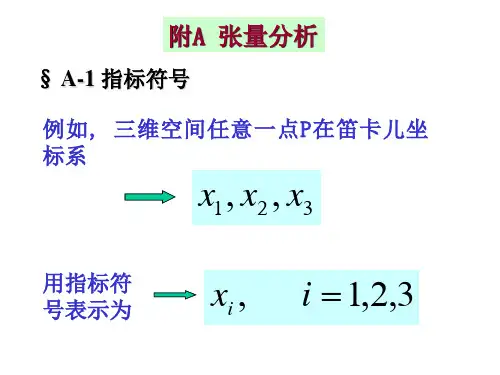
例如,n 维空间中矢量a 的n 个分量1a ,2a ,…,n a 可缩写成()n i a i ,,2,1 =。
各章要点第一章:矢量和张量指标记法:哑指标求和约定 :同一项中出现一对相同的协、逆变指标则对该指标求和 自由指标规则:同一项中只能出现一次,不同项中保持在同一水平线上 协变基底和逆变基底:ki k i i x ∂∂==∂ξ∂ξr g e j j i i ⋅=δg giik k x∂ξ=∂g e123 ===g g g 张量概念i i'i'i =βg g i'i'ii =βg g i k i k j j''''ββ=δ i'i'i i v v =β ii 'i 'iv v =β i 'j'i 'j'k l ij ..k 'l'i j k 'l'..kl T T =ββββ i i i i v v ==v g g ..kl ij ijk l T =⊗⊗⊗T g g g g 度量张量ij i i i j i i g =⊗=⊗=⊗G g g g g g g⋅=⋅=⋅=⋅=v G G v v T G G T T.j kj i ik T T g =张量的商法则lm ijk T(i,j,k,l,m)S U = ijk...lmT(i,j,k,l,m)T = 置换符号312n 1n123n i i i i i 123n 1n i i i ...i A a a a ......a a e -- i j k Lmnijk .L.m .n a a a e e A = i j k .L .m .n ijk Lmn a a a e e A =置换张量i j k ijk ijk i j k =ε⊗⊗=ε⊗⊗εg g g g g gijk i j k ()e ε=⋅⨯=g g gijk ijk i j k ()ε=⋅⨯=g g gi j k ijk ijk i j k a b a b ()::()⨯=ε=ε=⊗=⊗a b g g a b εεa b广义δ符号i ii r s tj j j ijk ijk ijk r s t rst rst rst k k k r s te e δδδδδδ==εε=δδδδijk j k j k jk ist s t t s st δ=δδ-δδδijk k ijt t 2δ=δijk ijk 6δ=性质:是张量重要矢量等式:()()()⨯⨯=⋅-⋅a b c a c b a b c第二章: 二阶张量重要性质:T =T.u u.T 主不变量i 1.i Tr()T ζ==T i j l m2l m .i .j 1T T 2ζ=δ 3det()ζ=T1()()(())(())()⋅⋅⨯⋅⋅⨯⋅⨯⋅=ζ⋅⨯T u v w +u T v w +u v T w u v w2)[)][()(]()[()]()⋅⋅⋅⨯⋅⋅⨯⋅⋅⋅⨯⋅=ξ⋅⨯T u (T v w +u T v T w)+T u (v T w u v w ( ()[()()]det()()⋅⋅⋅⨯⋅=⋅⨯T u T v T w T u v w 标准形1. 特征值、特征向量⋅=λT v v ()-λ⋅=T G v 0 321230λ-ζλ+ζλ-ζ= 2. 实对称二阶张量标准形i 123i 112233=⋅⊗=λ⊗+λ⊗+λ⊗N N g g g g g gg g 3. 正交张量(了解方法)12112233(cos()sin())(sin()cos())=ϕ+ϕ⊗+-ϕ+ϕ⊗+⊗R e e e e e e e e4. 反对称二阶张量的标准形21123=μ⊗-μ⊗=μ⨯Ωe e e e e G⋅=⨯Ωu ωu31:2=-=μ⨯ωεΩe u=-⋅Ωεω5. 正则张量极分解=⋅=⋅T R U V R第三章 张量函数概念:各项同性张量函数、解析函数 计算 e T , sin()T 重要定理:1. Hamilton-Cayley 定理:32321231230λ-ζλ+ζλ-ζ=⇒-ζ+ζ-ζ=T T T G 0 2.对称各向同性张量函数表示定理:2012f ()k k k ==++H N G N N ;其中T T ;==H H N N ;而系数i k 是N 的主不变量的函数。
一 爱因斯坦求和约定1.1指标变量的集合:n n y y y x x x ,...,,,...,,2121表示为:n j y n i x j i ...,3,2,1,,...,3,2,1,==写在字符右下角的 指标,例如xi 中的i 称为下标。
写在字符右上角的指标,例如yj 中的j 称为上标;使用上标或下标的涵义是不同的。
用作下标或上标的拉丁字母或希腊字母,除非作了说明,一般取从1到n 的所有整数,其中n 称为指标的范围。
1.2求和约定若在一项中,同一个指标字母在上标和下标中重复出现,则表示要对这个指标遍历其范围1,2,3,…n 求和。
这是一个约定,称为求和约定。
例如:333323213123232221211313212111bx A x A x A b x A x A x A bx A x A x A =++=++=++筒写为:ijijbx A =j——哑指标i——自由指标,在每一项中只出现一次,一个公式中必须相同遍历指标的范围求和的重复指标称为“哑标”或“伪标”。
不求和的指标称为自由指标。
1.3 Kronecker-δ符号(克罗内克符号)和置换符号Kronecker-δ符号定义j i ji ij ji ≠=⎩⎨⎧==当当01δδ置换符号ijkijk e e =定义为:⎪⎩⎪⎨⎧-==的任意二个指标任意k j,i,当021)(213,132,3的奇置换3,2,1是k j,i,当112)(123,231,3的偶置换3,2,1是k j,i,当1ijk ijke ei,j,k 的这些排列分别叫做循环排列、逆循环排列和非循环排列。
置换符号主要可用来展开三阶行列式:231231331221233211231231133221332211333231232221131211a a a a a a a a a a a a a a a a a a a a a a a a a a a a ---++==因此有:ijmjimii i i jijAA aa a a a ==++=δδδδδ332211kijjkiijkkjiikjjikijkee e e e e e ==-=-=-=同时有:ijjijij iiiijijijkj ikilkljkijjjiiijijijkjikiie e aa aa a a a aa δδδδδδδδδδδδδδδδδδδ=⋅=++=========++=332211332211331001010100131211232221333231321333222111321321321-=====δδδδδδδδδδδδδδδδδδδδδδδδδδδe e k j i k j i k j i k k k j j j i i i ijk333222111321321321r q p r q p r q p k k k j j j i i i pqr ijke e δδδδδδδδδδδδδδδδδδ⋅=ipp i p i p i p i δδδδδδδδδ==++11332211krkqkpjrjqjpiriqippqrijke e δδδδδδδδδ=jqirjriqjrjqiriqkqrijke e kp δδδδδδδδ-===321321322311332112312213322113312312332211333231232221131211k j i ijkkjiijkaa a e a a a e aa a a a a a a a a a a a a a a a a aaaa a aaa a A ==---++==Kronecker-δ和置换符号符号的关系为:itjsjtiskstkije e δδδδ-=二 张量代数2.1张量的加法(减法)两个同阶、同变异(结构) 的张量可以相加(或相减)。