重量重心计算

物体重心公式嘿，咱们来聊聊物体重心公式这事儿！在咱们的生活中啊，物体重心可是个相当重要的概念。

比如说，你看那杂技演员表演走钢丝，他们得时刻掌握好身体的重心，才能稳稳地在钢丝上行走，不至于摔下来。

这就跟咱们要探讨的物体重心公式有着密切的关系。

先来说说什么是物体的重心。

简单来讲，重心就是物体所受重力的作用点。

那怎么确定这个重心的位置呢？这就得靠物体重心公式啦。

对于质量分布均匀，形状规则的物体，重心就在它的几何中心上。

就像一个质地均匀的正方体，它的重心就在正方体的正中心。

可要是物体的质量分布不均匀，或者形状不规则，那确定重心可就没那么简单喽。

这时候，物体重心公式就能派上用场啦。

对于一个由多个质点组成的系统，其重心的位置可以通过公式计算得出。

假设这些质点的质量分别为 m1、m2、m3……，坐标分别为 (x1, y1, z1)、(x2, y2, z2)、(x3,y3, z3)……，那么重心的坐标(x_c, y_c, z_c) 就可以通过以下公式计算：x_c = (m1 * x1 + m2 * x2 + m3 * x3 + …… ) / (m1 + m2 + m3 + ……) y_c = (m1 * y1 + m2 * y2 + m3 * y3 + …… ) / (m1 + m2 + m3 + ……) z_c = (m1 * z1 + m2 * z2 + m3 * z3 + …… ) / (m1 + m2 + m3 + ……)看起来是不是有点复杂？别担心，咱们来举个例子。

比如说有一个由两块不同质量的木板拼接成的不规则形状的物体。

一块木板质量是 3 千克，坐标是 (1, 2, 3) ，另一块木板质量是 5 千克，坐标是 (4, 5, 6) 。

那咱们来算算这个物体的重心位置。

先算 x 坐标：x_c = (3 * 1 + 5 * 4) / (3 + 5) = (3 + 20) / 8 = 23 / 8再算 y 坐标：y_c = (3 * 2 + 5 * 5) / (3 + 5) = (6 + 25) / 8 = 31 / 8最后算 z 坐标：z_c = (3 * 3 + 5 * 6) / (3 + 5) = (9 + 30) / 8 = 39 / 8这样咱们就求出了这个不规则物体的重心坐标。

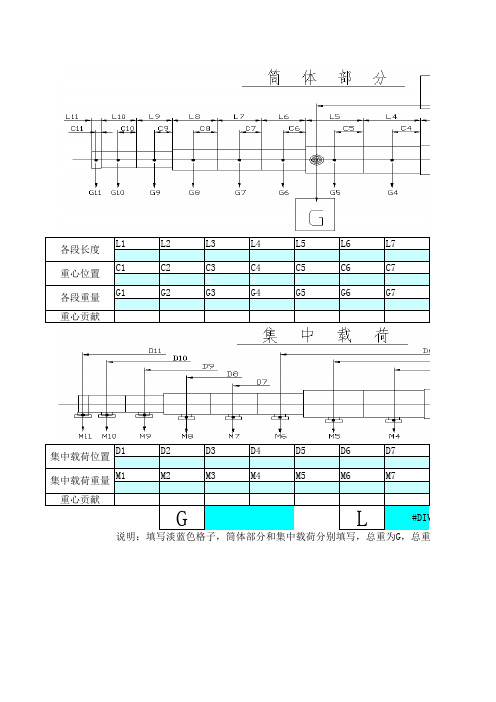
L1L2L3L4L5L6L7
C1C2C3C4C5C6C7
0000000
G1G2G3G4G5G6G7

重心贡献0000000

D1D2D3D4D5D6D7
M1M2M3M4M5M6M7
重心贡献0000000

说明：填写淡蓝色格子，筒体部分和集中载荷分别填写，总重为G，总重心L，计算后不

集中载荷位置

L各段长度重心位置各段重量G
0#DIV/0

集中载荷重量
L8L9L10L11
C8C9C10C11
0000
G8G9G10G11

0000

D8D9D10D11
M8M9M10M11
0000

总重心为L，计算后不要保存。
DIV/0!

总重量、总指数和重心位置之间的关系在绝大多数“飞机的重量与平衡”教学资料中，都没有对总重量、指数和重心位置之间的关系，以及如何用平衡图来表示的原理做详细的解释。

笔者因此撰文对此部分进行补充。

1. 引入符号CG(%MAC)以%MAC为单位的重心位置（重心与MAC前缘的相对距离）x Ref平衡基准点（参考点）站位x CG重心站位x LEMAC MAC前缘站位L MAC MAC长度M力矩M0基本重量的力矩M i第i个重量的力矩（i = 1, 2, …）P重量IND指数（无量纲）IND BW基本重量指数IND0指数附加项K常数（力矩量纲）Σ代表对其后面的量求和（代数和）2. 推导由重心计算公式x CG=x Ref+∑M ∑CG(%MAC)=x CG−x LEMACMAC∙100和指数定义式IND BW=M0K +IND0，IND i=M iKΣIND=IND BW+ΣIND i=M0+∑MiK+IND0=∑MK+IND0导出ΣP、ΣIND和CG(%MAC)的关系：ΣP=A∙(ΣIND−IND0)其中A与CG(%MAC)有关，即A=100∙K L MAC⁄CG(%MAC)−x Ref−x LEMACL MAC∙1003. 结论（参见下图）（1）ΣP和ΣIND的关系为线性关系，在ΣP-ΣIND坐标系中为直线，A为直线的斜率。

（2）斜率A与CG(%MAC)有关，A随CG(%MAC)增加而增加；不同CG(%MAC)的直线均交于同一点：（ΣIND = IND0，ΣP = 0）。

（3）当重心位于参考点时，即x CG = x Ref（CG(%MAC) = x Ref−x LEMACL MAC∙100），斜率为无限大；当重心位于参考点右侧时，x CG > x Ref，斜率为正；位于左侧时，x CG < x Ref，斜率为负。

（4）在实际的平衡图中，横轴上移到虚线位置。

ΣPΣIND0ΣIND x CG Ref CG Ref。

一、整车重心及轴荷分配计算：
1.车辆各部件重心位置
2.部件重心位置列表
x,y——部件重心位置
m——部件重量
3.重心位置及轴荷验算：
轴荷计算：
公式：G
2=∑m
ix
i/L
G
2——中、后轴轴荷kg
m
i，x
i——部件重量和部件重心水平位置
L——汽车轴距+650㎜
将列表数据带入公式（1）
G
2=18900㎏前轴G
1=6100㎏（24.4%）
按汽车厂提供数据，前轴允许载荷6500㎏,中，后轴允许载荷19000㎏
结论：满足使用条件。

汽车重心纵向位置计算：
公式：L
1=G
2L/G L
2=G
1L/G
G——汽车总质量
代入数据：L
1=3780㎜L
2=1220㎜
满载时汽车重心高度计算：
公式：h=∑m
iy
i/G (2)1）（
y
i——部件重心高度h——汽车重心高度
将列表数据代入公式（2）
h=1770㎜
空载时汽车重心高度计算：
仍用公式（2），减去垃圾重量
hg=1174㎜
二、汽车侧翻条件验算：
公式：tgβ=B/2h (3)
β——汽车侧倾稳定角B——汽车轮距B=1860㎜
代入数据：tgβ=0.792β=38.3°≥32°
结论：满足使用条件。

三、危险工况校核计算：
该车在垃圾箱满载，用拉臂钩将垃圾箱拉上车，垃圾箱后轮临界脱离地面时，以汽车不翘头（即前轴负荷≥0）为安全。

物体重心坐标公式在我们的日常生活和学习中，经常会遇到与物体重心相关的问题。

比如说，你在玩跷跷板的时候，为什么有的时候能轻松地一上一下，有的时候却怎么都不平衡呢？这其实就和物体的重心有着密切的关系。

那什么是物体的重心呢？简单来说，重心就是物体各部分所受重力的合力的作用点。

想象一下，一个均匀的球体，它的重心就在球心；而对于一个不均匀的物体，比如一块形状奇怪的木头，它的重心就没那么好找啦。

接下来咱们聊聊物体重心坐标公式。

这公式看起来可能有点复杂，但别怕，我来给您慢慢解释。

假设一个由n 个质点组成的物体系统，每个质点的质量分别为m1、m2、m3……mn，它们在空间中的坐标分别为（x1，y1，z1）、（x2，y2，z2）、（x3，y3，z3）……（xn，yn，zn）。

那么，这个物体系统的重心坐标（x_c，y_c，z_c）可以通过以下公式计算得出：x_c = （m1*x1 + m2*x2 + …… + mn*xn）/ （m1 + m2 + …… + mn）y_c = （m1*y1 + m2*y2 + …… + mn*yn）/ （m1 + m2 + …… + mn）z_c = （m1*z1 + m2*z2 + …… + mn*zn）/ （m1 + m2 + …… + mn）听起来是不是有点晕乎？咱们来举个例子。

比如说有一个由三个质点组成的系统，第一个质点质量是 2 千克，坐标是（1，2，3）；第二个质点质量是 3 千克，坐标是（4，5，6）；第三个质点质量是 5 千克，坐标是（7，8，9）。

那先算 x 坐标：x_c = （2×1 + 3×4 + 5×7）/ （2 + 3 + 5）= （2 + 12 + 35）/ 10= 49 / 10= 4.9y 坐标：y_c = （2×2 + 3×5 + 5×8）/ 10= （4 + 15 + 40）/ 10= 59 / 10= 5.9z 坐标：z_c = （2×3 + 3×6 + 5×9）/ 10= （6 + 18 + 45）/ 10= 69 / 10= 6.9所以这个系统的重心坐标就是（4.9，5.9，6.9）。

重心名词解释重心，是力学概念中的一个术语，指物体所受的重力所作用的中心点。

重心的位置取决于物体形状和密度分布，它是物体所具有平衡稳定性和运动状态的一个重要参数。

下面将对重心的相关概念和应用进行详细解释。

一、重心的概念：重心，也称质心或重心中心，是指物体所受的重力所作用的中心点。

在物理学中，重心的概念常常与物体的平衡和稳定性有关。

重心的位置通常用数学表达式进行描述，表示为物体各部分质量的加权平均值的点。

在不同的物体中，重心的位置可能会有所变化，但它总是位于物体的中心，对物体的运动和平衡状态起到至关重要的作用。

二、重心的计算方法：计算物体的重心位置通常需要考虑物体的形状和密度分布。

在一般情况下，重心的位置可以通过求解物体各部分质心的坐标来确定。

对于连续分布的物体，可以使用积分的方法进行求解。

三、重心的应用：重心在物理学和工程领域有着广泛的应用，它可以用来解决许多与平衡和稳定性有关的问题。

下面是重心在某些领域的具体应用。

1. 建筑工程中的应用：在建筑物设计中，重心的位置通常需要考虑设计的稳定性和抗风能力。

对于高层建筑，重心位置的计算和控制是非常重要的。

2. 汽车设计中的应用：在汽车设计中，重心的位置对于行驶稳定性、转弯半径和悬挂系统的设计都有重要影响。

为了提高汽车的安全性能，需要减少汽车重心的高度。

3. 船舶设计中的应用：对于船舶，重心的位置对于船体的稳定性、承重能力和最大载重量都有很大的影响。

在船舶设计中，需要合理安排货物的位置和分布以控制船体的重心。

4. 航空工程中的应用：在航空工程中，重心位置的计算和控制对于飞机的飞行稳定性、起飞和着陆能力都有着至关重要的作用。

对于不同类型的飞机，需要采用不同的重心控制策略。

总的来说，重心作为物体平衡和稳定性的重要参数，在各种工程领域都有着广泛的应用。

它对于提高工程设施的安全性能和使用效能，具有十分重要的意义。