平行四边形面积的计算典型例题

高中数学竞赛平面几何题典型例题一、高中数学竞赛平面几何题那点事儿高中数学竞赛里的平面几何题啊，就像是一群神秘的小怪兽，有的看着简单，其实暗藏玄机，有的一上来就张牙舞爪，让你不知所措。

不过别怕，咱今儿个就来好好唠唠典型例题。

平面几何题里，三角形可是个大明星。

比如说有这么一道题：在三角形ABC中，AB = AC，角A = 120°，D是BC中点，DE垂直AB于E，求AE与BE的长度比。

这题啊，就考你等腰三角形的性质。

你看啊，因为AB = AC，角A = 120°，那角B和角C就都是30°。

D是BC中点，那AD就垂直BC。

再看三角形ADE，角AED = 90°，角A = 120°，那角ADE就是30°。

根据30°所对直角边是斜边一半这个性质，设AE = x，那AD就是2x。

又因为三角形ABD是直角三角形，角B = 30°，所以AB = 4x，那BE就等于3x，所以AE与BE的长度比就是1:3啦。

还有圆相关的平面几何题也很常见。

像有个圆O，半径为5，AB 是圆的一条弦，AB = 8，C是圆上一点，角ACB = 30°，求圆心O 到弦AB的距离。

这时候就得用到圆的性质和三角函数啦。

连接OA，OB，过O作OD垂直AB于D。

因为OD垂直AB，D就是AB中点，所以AD = 4。

在直角三角形AOD中，OA = 5，AD = 4，根据勾股定理就能算出OD = 3，这就是圆心到弦的距离。

再比如说四边形里的平面几何题。

有个平行四边形ABCD，对角线AC和BD相交于O点，E是AB中点，OE = 3，求平行四边形ABCD 的周长。

这题就需要利用平行四边形对角线互相平分的性质。

因为平行四边形对角线互相平分，所以O是AC中点。

又因为E是AB中点，所以OE是三角形ABC的中位线。

中位线长度是底边的一半，所以BC = 6。

因为平行四边形对边相等，所以AB = CD，AD = BC，那周长就是2×(AB + BC) = 2×(6 + 6)= 24。

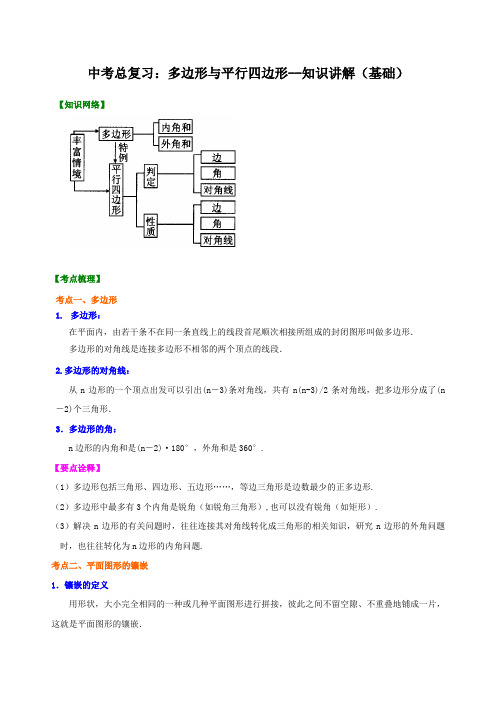
中考总复习：多边形与平行四边形--知识讲解（基础）【知识网络】【考点梳理】考点一、多边形1.多边形：在平面内，由若干条不在同一条直线上的线段首尾顺次相接所组成的封闭图形叫做多边形．多边形的对角线是连接多边形不相邻的两个顶点的线段．2.多边形的对角线：从n边形的一个顶点出发可以引出(n－3)条对角线，共有n(n-3)/2条对角线，把多边形分成了(n －2)个三角形．3．多边形的角：n边形的内角和是(n－2)·180°，外角和是360°.【要点诠释】（1）多边形包括三角形、四边形、五边形……，等边三角形是边数最少的正多边形.（2）多边形中最多有3个内角是锐角（如锐角三角形）,也可以没有锐角（如矩形）.（3）解决n边形的有关问题时，往往连接其对角线转化成三角形的相关知识，研究n边形的外角问题时，也往往转化为n边形的内角问题.考点二、平面图形的镶嵌1．镶嵌的定义用形状，大小完全相同的一种或几种平面图形进行拼接，彼此之间不留空隙、不重叠地铺成一片，这就是平面图形的镶嵌．2．平面图形的镶嵌(1)一个多边形镶嵌的图形有：三角形，四边形和正六边形；(2)两个多边形镶嵌的图形有：正三角形和正方形，正三角形和正六边形，正方形和正八边形，正三角形和正十二边形；(3)三个多边形镶嵌的图形一般有：正三角形、正方形和正六边形，正方形、正六边形和正十二边形，正三角形、正方形和正十二边形.【要点诠释】能镶嵌的图形在一个拼接点处的特点：几个图形的内角拼接在一起时，其和等于360°,并使相等的边互相重合.考点三、三角形中位线定理1．连接三角形两边中点的线段叫做三角形的中位线.2．定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半.考点四、平行四边形的定义、性质与判定1．定义：两组对边分别平行的四边形是平行四边形．2．性质：(1)平行四边形的对边平行且相等；(2)平行四边形的对角相等，邻角互补；(3)平行四边形的对角线互相平分；(4)平行四边形是中心对称图形，对角线的交点是它的对称中心．3．判定：(1)两组对边分别平行的四边形是平行四边形；(2)两组对边分别相等的四边形是平行四边形；(3)一组对边平行且相等的四边形是平行四边形；(4)两组对角分别相等的四边形是平行四边形；(5)对角线互相平分的四边形是平行四边形．4．两条平行线间的距离：定义：夹在两条平行线间最短的线段的长度叫做两条平行线间的距离．性质：夹在两条平行线间的平行线段相等．【要点诠释】1.平行四边形的面积=底×高；2.同底（等底）同高（等高）的平行四边形面积相等．【典型例题】类型一、多边形与平面图形的镶嵌1．如图，在五边形ABCDE中，∠A+∠B+∠E=300°，DP、CP分别平分∠EDC、∠BCD，则∠P的度数是（）A．60° B．65° C．55° D．50°【思路点拨】根据五边形的内角和等于540°，由∠A+∠B+∠E=300°，可求∠BCD+∠CDE的度数，再根据角平分线的定义可得∠PDC与∠PCD的角度和，进一步求得∠P的度数．【答案】A【解析】解：∵五边形的内角和等于540°，∠A+∠B+∠E=300°，∴∠BCD+∠CDE=540°﹣300°=240°，∵∠BCD、∠CDE的平分线在五边形内相交于点O，∴∠PDC+∠PCD=（∠BCD+∠CDE）=120°，∴∠P=180°﹣120°=60°．故选：A．【总结升华】本题主要考查了多边形的内角和公式，角平分线的定义，熟记公式是解题的关键．注意整体思想的运用．举一反三：【变式】如图，小林从P点向西直走12米后，向左转，转动的角度为α，再走12米，如此重复，小林共走了108米回到点P，则α=_________.【答案】40°.2．现有边长相同的正三角形、正方形和正六边形纸片若干张，下列拼法中不能镶嵌成一个平面图案的是( )A．正方形和正六边形 B．正三角形和正方形C．正三角形和正六边形 D．正三角形、正方形和正六边形【思路点拨】注意各正多边形的内角度数.【答案】A.【解析】正方形和正六边形的每个内角分别为90°和120°，要镶嵌则需要满足90°m＋120°n＝360°，但是m、n没有正整数解，故选A.【总结升华】能镶嵌的图形在一个拼接点处的特点：几个图形的内角拼接在一起时，其和等于360°,并使相等的边互相重合.举一反三：【变式】现有四种地面砖，它们的形状分别是：正三角形、正方形、正六边形、正八边形，且它们的边长都相等．同时选择其中两种地面砖密铺地面，选择的方式有( )A．2种 B．3种 C．4种 D．5种【答案】 B.类型二：平行四边形及其他知识的综合运用3．如图，已知在▭ABCD中，对角线AC、BD相交于点O，AE⊥BD，BM⊥AC、DN⊥AC，CF⊥BD垂足分别是E、M、N、F，求证：EN∥MF．【思路点拨】连接ME，FN，由四边形ABCD为平行四边形，得到对角线互相平分，利用AAS得到三角形AOE与三角形COF全等，利用全等三角形对应边相等得到OE=OF，同理得到三角形BOM与三角形DON全等，得到OM=ON，进而确定出四边形MEFN为平行四边形，利用平行四边形的对边平行即可得证．【答案与解析】证明：连接ME，FN，∵四边形ABCD为平行四边形，∴OA=OC，OB=OD，∵AE⊥BD，CF⊥BD，在△AOE和△COF中，，∴△AOE≌△COF（AAS），∴OE=OF，同理△BOM≌△DON，得到OM=ON，∴四边形EMFN为平行四边形，∴EN∥MF．【总结升华】此题考查了平行四边形的判定与性质，熟练掌握平行四边形的判定与性质是解本题的关键．4.如图所示，△ABC中，∠BAC=90°，延长BA到D，使，点E、F分别为边BC、AC 的中点.（1）求证：DF=BE；（2）过点A作AG∥BC，交DF于G，求证：AG=DG.【思路点拨】（1）E、F分别为BC、AC中点，则EF为△ABC的中位线，所以EF∥AB，.而.则EF=AD.从而易证△DAF≌△EFC, 则DF=CE=BE.(2) AG与DG在同一个三角形中,只需证∠D=∠DAG即可.【答案与解析】（1）∵点E、F分别为BC、AC的中点，∴ EF是△ABC的中位线.∴ EF∥AB，.又∵，∴ EF=AD.∵ EF∥AB，∴∠EFC=∠BAC=90°，∵∠BAC=90°，∴∠DAF=90.又∵ F是AC的中点，∴AF=CF，∴△DAF≌△EFC.∴DF=EC=BE.（2）由(1)知∵△DAF≌△EFC，∴∠D=∠FEC.又∵ EF∥AB，∴∠B=∠FEC.又∵ AG∥BC，∴∠DAG=∠B，∴∠ DAG=∠FEC∴∠D=∠DAG.∴AG=DG.【总结升华】三角形中位线定理的作用：位置关系——可以证明两条直线平行；数量关系——可以证明线段的相等或倍分.此外应注意三角形共有三条中位线，并且它们又重新构成一个新的三角形.举一反三：【变式】如图，已知P、R分别是长方形ABCD的边BC、CD上的点，E、F分别是PA、PR的中点，点P在BC上从B向C移动，点R不动，那么下列结论成立的是（）A．线段EF的长逐渐增大B．线段EF的长逐渐变小C．线段EF的长不变D．无法确定【答案】C.5．如图：六边形ABCDEF中，AB平行且等于ED，AF平行且等于CD，BC平行且等于FE，对角线FD ⊥BD．已知FD=4cm，BD=3cm．则六边形ABCDEF的面积是_________cm2．【思路点拨】连接AC交BD于G，AE交DF于H．根据一组对边平行且相等的四边形是平行四边形，得平行四边形AEDB和AFDC．易得AC=FD，EH=BG．计算该六边形的面积可以分成3部分计算，即平行四边形AFDC的面积+三角形ABC的面积+三角形EFD的面积．【答案与解析】连接AC交BD于G，AE交DF于H．∵AB平行且等于ED，AF平行且等于CD，∴四边形AEDB是平行四边形，四边形AFDC是平行四边形，∴AE=BD，AC=FD，∵FD⊥BD，∴∠GDH=90°，∴四边形AHDG是矩形，∴AH=DG∵EH=AE-AH，BG=BD-DG∴EH=BG．∴六边形ABCDEF的面积=平行四边形AFDC的面积+三角形ABC的面积+三角形EFD的面积=FD•BD=3×4=12cm2．故答案为：12.【总结升华】注意求不规则图形的面积可以分割成规则图形，根据面积公式进行计算．6 .已知平行四边形ABCD，对角线AC和BD相交于点O，点P在边AD上，过点P作PE⊥AC，PF⊥BD，垂足分别为E、F，PE=PF．（1）如图，若3，EO=1，求∠EPF的度数；（2）若点P是AD的中点，点F是DO的中点，BF=BC+32-4，求BC的长．【思路点拨】（1）连接PO，利用解直角三角形求出∠EPO=30°，再利用“HL”证明△PEO和△PFO全等，根据全等三角形对应角相等可得∠FPO=∠EPO，从而得解；（2）根据三角形中位线定理可得PF∥AO，且PF=12AO，然后根据两直线平行，同位角相等可得∠AOD=∠PFD=90°，再根据同位角相等，两直线平行可得PE∥OD，所以PE也是△AOD的中位线，然后证明四边形ABCD是正方形，根据正方形的对角线与边长的关系列式计算即可得解．【答案与解析】（1）如图，连接PO，∵PE⊥AC，PE=3，EO=1，∴tan∠EPO=3 EOPE=，∴∠EPO=30°，∵PE⊥AC，PF⊥BD，∴∠PEO=∠PFO=90°，在Rt△PEO和Rt△PFO中，PO PO PE PF=⎧⎨=⎩，∴Rt△PEO≌Rt△PFO（HL），∴∠FPO=∠EPO=30°，∴∠EPF=∠FPO+∠EPO=30°+30°=60°；（2）如图，∵点P是AD的中点，点F是DO的中点，∴PF ∥AO ，且PF=12AO ， ∵PF ⊥BD ，∴∠PFD=90°， ∴∠AOD=∠PFD=90°，又∵PE ⊥AC ，∴∠AEP=90°，∴∠AOD=∠AEP ，∴PE ∥OD ，∵点P 是AD 的中点，∴PE 是△AOD 的中位线，∴PE=12OD ， ∵PE=PF ，∴AO=OD ，且AO ⊥OD ，∴平行四边形ABCD 是正方形，设BC=x ，则x+12x ，∵ -4，∴x ， 解得x=4，即BC=4．【总结升华】 本题考查了平行四边形的性质，三角形的中位线定理，正方形的判定与性质，（2）中判定出平行四边形ABCD 是正方形是解题的关键．举一反三：【变式】如图1，已知正比例函数和反比例函数的图象都经过点M （－2，－1），且P （－1，－2）是双曲线上的一点，Q 为坐标平面上的一动点，PA ⊥x 轴，QB ⊥y 轴，垂足分别为A 、B ．（1）写出正比例函数和反比例函数的关系式；（2）当点Q 在直线MO 上运动时，是否可以使△OBQ 与△OAP 面积相等？（3）如图2，点Q 在第一象限中的双曲线上运动时，作以OP 、OQ 为邻边的平行四边形OPCQ ，求平行四边形OPCQ周长的最小值．图1 图2【答案】（1）正比例函数解析式为，反比例函数解析式为．（2）当点Q在直线MO上运动时，设点Q的坐标为，，解得.所以点Q的坐标为和．（3）因为P（，），由勾股定理得OP＝，平行四边形OPCQ周长=．因为点Q在第一象限中的双曲线上，所以可设点Q的坐标为，由勾股定理可得，通过图形分析可得：OQ有最小值2，即当Q为第一象限中的双曲线与直线的交点时，线段OQ的长度最小．所以平行四边形OPCQ周长的最小值：．。

第十五讲 图形面积姓名：学校： 年级：【学习目标】图形面积【知识要点】1． 长方形的面积=底×高 2． 正方形的面积=边长×边长 3． 平行四边形的面积=底×高 4． 三角形的面积=底×高÷2 5． 梯形的面积=（上底+下底）×高÷2 6． 求地面铺地砖总块数的方法：（1）用房间地面的面积÷每块地砖的面积=所铺地砖的块数 （2）每平方米铺的块数×房间总面积=所铺地砖的块数【典型例题】例1．右图为一面墙，这面墙每平方米需要60块砖，砌这面墙需要多少块砖？例2、求下图的面积。

（单位：分米）例3．求下图，图形的面积。

681515 153245°例4. 如下图是两个正方形组成的，已知大正方形边长12分米，小正方形的边长8分米，求阴影部分的面积。

例5.小丽家装修需要30块木板，木板的形状如下图。

（1）一块木板的面积是多少？（2）如果每块木板需要15元，那么小丽需要花多少钱？脑筋急转弯【课堂练习】一、 填空。

猜一猜1、天热爬上树梢，总爱大喊大叫，明明啥也不懂，偏说知道知道。

2、栖息沼泽和田头，随着季节南北走，队列排成人字形，纪律自觉能遵守。

30cm48cm72cm60cm你是敢于尝试的勇士，心动不如行动，继续努力吧，相信自己。

老师知道你是最棒的！⑴ 三角形的面积=（ ），字母表示为（ ）。

平行四边形的面积=（ ），字母表示为（ ）⑵ 一个直角三角形，它的两条直角边分别是6cm 和8cm ，它的面积是（ ）cm 2。

⑶ 一个梯形的上底是6厘米，下底是10厘米，高是0.4分米，它的面积是（ ）平方厘米。

⑷ 一个平行四边形的底是21分米，高是底的2倍，平行四边形的面积是（ ）平方米。

⑸ 一个等腰梯形的面积是20平方米，高是4米，下底是3米，上底是（ ）米。

与它等底等高的三角形的面积是（ ）平方厘米。

⑹ 一个平行四边形面积60平方厘米，底10厘米，高（ ）厘米。

完整版)五年级奥数平面图形面积计算五年级奥数第六讲——平面图形面积的计算一、知识要点1.基本平面图形特征及面积公式正方形：特征：四条边相等，四个角都是直角，有四条对称轴。

面积公式：S=边长的平方长方形：特征：对边相等，四个角都是直角，有二条对称轴。

面积公式：S=长×宽平行四边形：特征：两组对边平行且相等，对角相等，相邻的两个角之和为180°，容易变形。

面积公式：S=底边×高三角形：特征：两边之和大于第三条边，两边之差小于第三条边，三个角的内角和是180°，具有稳定性。

面积公式：S=底边×XXX÷2梯形：特征：只有一组对边平行，中位线等于上下底和的一半。

面积公式：S=(上底+下底)×高÷22.基本解题方法：由两个或多个简单的基本几何图形组合成的组合图形，要计算这样的组合图形面积，先根据图形的基本关系，再运用分解、组合、平移、割补、添辅助线等几种方法将图形变成基本图形分别计算。

典型例题】例1】已知平行四边形的面积是28平方厘米，求阴影部分的面积。

例2】求图中阴影部分的面积。

例3】如图所示，甲三角形的面积比乙三角形的面积大6平方厘米，求CE的长度。

例4】两条对角线把梯形ABCD分割成四个三角形。

已知两个三角形的面积（如图所示），求另两个三角形的面积各是多少？练与拓展】1.计算下面图形的面积。

2.下面的梯形中，阴影部分面积是150平方厘米，求梯形的面积。

3.正方形ABCD的边长是12厘米，已知DE是EC长度的2倍，求三角形DEF的面积和CF的长。

4.平行四边形ABCD的边长BC=10厘米，直角三角形BCE的直角边EC长8厘米，已知阴影部分的面积比三角形EFG的面积大10平方厘米，求CF的长。

5.正方形ABCD的面积是100平方厘米，AE=8厘米，请计算以下图形的面积。

1.在一块长80米、宽30米的长方形地上，修了宽为2米和3米的两条小路，求草地的面积。

《平行四边形的性质》典型例题例1一个平行四边形的一个内角是它邻角的3倍，那么这个平行四边形的四个内角各是多少度？例2已知：如图，ABCD的周长为60cm，对角线AC、BD相交于点O，∆的周长多8cm，求这个平行四边形各边的长.AOB∆的周长比BOC例3 已知：如图，在ABCD中，BDAC、交于点O，过O点作EF交AB、CD于E、F，那么OE、OF是否相等，说明理由.例4 已知：如图，ABCD 的周长是cm 36，由钝角顶点D 向AB ，BC 引两条高DE ，DF ，且cm DE 34=，cm DF 35=.求这个平行四边形的面积.例5 如图，已知：ABCD 中，BC AE ⊥于E ，CD AF ⊥于F ，若︒=∠60EAF ，cm BE 2=，cm FD 3=.求：AB 、BC 的长和ABCD 的面积.《平行四边形的判定》典型例题例1如图，△DAB、△EBC、△FAC都是等边三角形，试说明四边形AFED是平行四边形．例2如图，E、F分别是ABCD边AD和BC上的点，并且AE=CF，AF和BE相交于G，CE和DF相交于H、EF与GH是否互相平分，请说明理由．例3如图，在平行四边形ABCD中，A1、A2、A3、A4和B1、B2、B3、B4分别是AB和DC 的五等分点，C1、C2和D1、D2分别是AD和BC的三等分点，若四边形C1A4D2B1的面积为1，求S平行四边形ABCD.例4已知：如图，E，F分别为ABCD的边CD，AB上一点，AE∥CF，BE，CF分别交CF，AE于H，G.求证：EG=FH.例5如图，已知：四边形ABCD中，AE⊥BD，CF⊥BD，E，F为垂足，且AE=CF，∠BAC=∠DCA.求证：四边形ABCD是平行四边形.平行四边形的面积一，导入今天，我把一位老朋友带来了，（课件出示一副七巧板）对，七巧板！用七巧板可以拼出各种不同的图案，下面大家要边观察边想，说一说你的发现！（课件分别出示四幅图案）师：谁来说一说你的发现！生1：我发现它们的形状各不相同。

五年级多边形面积计算知识点及重难点简析I. 知识点总结A. 平行四边形部分1. 平行四边形面积的计算公式沿着平行四边形任意一条边上的高，将平行四边形分成两部分，再经过平移或者旋转，可以将平行四边形转化成长方形。

通过观察发现，长方形的长是原平行四边形的底，长方形的宽是原平行四边形的高。

通过长方形的面积公式，我们可以得到平行四边形的面积公式，如果用S表示平行四边形的面积，用a和h分别表示平行四边形的底和高，可以得到平行四边形的面积为：S=a×h。

2. 平行四边形面积公式的应用平行四边形的面积公式：S=a×h，经过变形得到：a=S÷h，h=S÷a。

在已知平行四边形的底、高和面积中任意两个量时，可求出第三个量。

B. 三角形部分1. 三角形面积的计算公式用两个完全相同的三角形，可以拼成一个平行四边形。

三角形的面积等于拼成的平行四边形的一半。

观察可以发现，平行四边形的底和三角形的底相同，平行四边形的高和三角形的高相同。

通过平行四边形的面积公式，可以推导出三角形的面积公式。

如果S表示三角形的面积，用a和h分别表示三角形的底和高，三角形的面积公式为：S=a×h÷2。

2. 三角形面积公式的应用三角形的面积公式：S=a×h÷2，经过变形得到：a=2S÷h，h=2S÷a。

在已知三角形的底、高和面积三个量中任意两个量，都可以求出第三个量。

C. 梯形部分1. 梯形面积的计算公式两个完全相同的梯形可以拼成一个平行四边形，梯形的面积等于拼成的平行四边形面积的一半。

通过观察可以发现，拼成的平行四边形的底等于梯形的上底、下底之和，平行四边形的高等于梯形的高。

根据平行四边形面积公式，可以推导出梯形的面积公式。

用S表示梯形的面积，a、b 和h分别表示梯形的上底、下底和高，梯形的面积公式为：S=(a+b)×h÷2。

2. 梯形面积公式的应用梯形的面积公式：S=(a+b)×h÷2，经过变形得到：h=2S÷(a+b)，a=2S÷h-b，b=2S÷h-a。

教师：学生：时间：_ 2016 _年_ _月日段第__ 次课
ABCD中，延长
随堂练习三：
．若平行四边形的两邻边的长分别为
17在ABCD中，AB比AD大2，∠DAB的角平分线AE交CD于E，∠ABC的角平分线BF交CD于F，若平行四边形ABCD的周长为24，求CE、FD、EF的长
19已知：如图，ABCD中，E、F分别是AC上两点，且BE⊥AC于E，DF⊥AC于F．求证：四边形BEDF 是平行四边形．
20、如图，□ABCD的对角线AC、BD交于O，EF过点O交AD于E，交BC于F，G是OA的中点，H是OC的中点，四边形EGFH是平行四边形吗？说明理由.
21.如图，平行四边形ABCD中，M、N分别为AD、BC的中点，连结AN、DN、BM、CM，且AN、BM交于点P，CM、DN交于点Q.四边形MGNP是平行四边形吗？为什么？
22．如图，△ABC为等边三角形，D、F分别是BC、AB上的点，且CD=BF，以AD•为边作等边△ADE．（1）求证：△ACD≌△CBF；
（2）当D在线段BC上何处时，四边形CDEF为平行四边形，且∠DEF=30°？•证明你的结论．
23已知：如图，E、F、G、H分别是AB、BC、CD、DA的中点．
求证：四边形EFGH是平行四边形．。

巨人学校四年级新华数吴瀚霖第3讲直线形计算一——面积公式的应用长方形与正方形面积计算 Contents1 平行四边形面积计算2三角形面积计算3知识回顾：⏹正方形面积=边长×边长⏹长方形面积=长×宽下面让我们来看看如何运用这两个公式.例题1.如图,由16个同样大小的正方形组成了一个“5”字.如果这个图形的周长是102cm,那么它的面积是多少平方厘米？例题2.如图,用两块长方形纸片和一块小正方形纸片拼成了一个大正方形纸片,其中小正方形纸片的面积是49平方厘米,其中一个长方形的面积是28平方厘米,那么最后拼成的大正方形面积是多少平方厘米？4928③②①练习1.如图,阴影部分是一个长方形花坛.它的四周是用相同的正方形瓷砖砌成的边框.已知边框的总面积是80平方米,那么花坛（不包括边框）的面积是多少平方米？花坛平行四边形：两组对边平行的四边形叫平行四边形.我们把一个平行四边形剪成两块,然后拼成一个长方形。

从图中可以看出,这个四边形的面积与拼成的长方形面积相同,都等于长方形的长乘以宽.长方形的长和宽在平行四边形中都可以找到对应线段.在平行四边形中,这两条线段分别叫做底和高.于是我们有：试一试：⏹下面有4个平行四边形,每个平行四边形都指定了一条边作为底,请针对每条底画出从平行四边形的一个顶点出发的高.底底底底例题3.如图所示,小、中、大三个正方形从左到右依次紧挨着摆放,边长分别是3、7、9.图中两个阴影平行四边形的面积分别是多少？973试一试：⏹下图中的平行四边形的面积都是72.请求出未知的底或高.?12？8 ?6例题4.（本题学生版有典型例题示范）如图,从梯形ABCD 中分出两个平行四边形ABEF 和CDFG.其中ABEF 的面积等于60平方米,且AF 的长度为10米,FD 的长度为4米.平行四边形CDFG 的面积等于多少平方米？G DFE BAC练习3.如图所示,上面的正方形长是3cm,下面的长方形长为8cm,宽为3cm,那么图中阴影平行四边形的面积等于多少？338练习4.两个正方形一左一右如图摆放,图中阴影平行四边形的面积为24平方厘米,而右侧大正方形的边长为6cm,那么左侧小正方形的面积等于多少平方厘米？和平行四边形类似,三角形中也有底和高的概念.试一试：⏹下面指定了一条边为底,请分别作出它的高：底底底三角形面积计算三角形面积计算例题5.如图,把大小两个正方形拼在一起,它们的边长分别是8cm 和6cm,那么左图和右图中阴影部分的面积分别是多少平方厘米？6868例题6.【★】如图所示,AB=24cm,长方形BDEF 中的EF=15cm,阴影三角形BCE 的面积是60cm 2.请问：(1)BC 长多少厘米？(2)三角形DCE 的面积是多少平方厘米？EFD CBA练习5.【★】如图所示,两个正方形的边长分别为10cm和6cm,那么图中阴影三角形的面积为多少平方厘米？思考题某商场大厅的主楼楼梯如图所示,1楼到2楼共12级台阶,每级台阶高15cm,每级台阶进深25cm,已知楼梯宽3m,要在1楼到2楼的楼梯上铺设每平方米80元的地毯,则买地毯至少要多少元?巨人学校THANK YOU吴瀚霖。