机械振动中的特征值问题
- 格式:doc
- 大小:142.50 KB
- 文档页数:4

振动力学与结构动力学研究振动力学和结构动力学是机械工程领域中非常重要的研究方向。
本文将介绍振动力学和结构动力学的基本概念、研究内容和应用领域。
一、引言振动力学是研究物体在受到外力作用时如何振动的学科。
它包括自由振动、受迫振动和阻尼振动等内容。
振动力学的研究对于理解物体振动的特性以及对其进行控制和优化具有重要意义。
结构动力学是研究物体在受到外力作用时的动力响应的学科。
它主要包括结构的自由振动、受迫振动和响应谱分析等内容。
结构动力学在工程设计中起着至关重要的作用,可以评估结构的安全性、稳定性和舒适性等方面的参数。
二、振动力学研究1. 自由振动自由振动是指物体在没有外界干扰的情况下以自身固有频率振动的现象。
通过分析物体的固有频率和振型,可以了解物体的振动特性以及其对外界干扰的敏感程度。
在振动力学研究中,常用的方法包括模态分析和频率响应分析。
模态分析是通过测量物体在不同频率下的振动模态,获得其固有频率、振型和阻尼比等参数。
频率响应分析则是通过施加不同频率的外力,观察物体的振动响应,以获取其频率响应函数和阻尼参数。
受迫振动是指物体在外界施加周期性力或非周期性力的情况下产生的振动现象。
在振动力学研究中,受迫振动被广泛应用于机械系统的振动控制和信号分析。
受迫振动的研究包括强迫振动和共振现象。
强迫振动是指物体在受到周期性外力作用后的振动响应。
共振是指物体在受到特定频率的外力作用时,振幅增大到最大值的现象。
3. 阻尼振动阻尼振动是指物体在振动过程中由于阻力的存在而逐渐减小振幅的现象。
阻尼对振动系统的稳定性和动态响应有重要影响。
在振动力学研究中,常用的阻尼模型包括线性阻尼、非线性阻尼和阻尼比等。
通过分析阻尼对振动系统的影响,可以优化结构的设计和减小振动的能量损耗。
三、结构动力学研究1. 自由振动在结构动力学的研究中,自由振动是一个重要的内容。
通过分析结构的固有频率和振型,可以了解结构的振动特性和稳定性。
自由振动的研究方法包括模态分析和有限元分析。

第四节 特征值和特征向量问题(教材6.13)一、特征值和特征向量问题多自由度系统的无阻尼自由振动的运动微分方程为[]{}[]{}{}0M x k x += (6-54)若系统自由度为n ,则质量矩阵[]M 和刚度矩阵[]k 都是 n ×n 的对称方阵,位移向量{}x 和加速度向量{}x 都是n 维列向量。
由二自由度系统知,多自由度系统的无阻尼自由振动是按相同的频率和相同的相位作简谐振动。
即系统作同步振动。
故可设方程(6-54)的解为{}{}1212sin sin ()()n n n n x u x u x u x t t u ωϕωϕ⎧⎫⎧⎫⎪⎪⎪⎪⎪⎪⎪⎪=⎨⎬⎨⎬⎪⎪⎪⎪⎪⎪⎪⎪⎩⎭⎩⎭=+=+则{}{}2sin()nn x u t ωωϕ=-+将位移向量{}x 和加速度向量{}x 代入方程(6-54),得[][](){}{}2sin()0n n k M u t ωωϕ-+=因为sin()n t ωϕ+不能恒等于零,故有[][](){}{}20n k M u ω-= (6-55)这是一个广义特征值问题,2n ω是特征值,{}u 是特征向量。
令[][][]2n B k M ω=-则矩阵[]B 称为特征矩阵。
因为方程(6-55)是一个齐次方程组,其有非零解的充要条件为特征矩阵[]B 的行列式等于零,即[][]20n k M ω-=这就是特征方程。
从特征方程可以解出特征值2n ω,则ω就是系统的固有频率。
对于n 自由度系统,特征方程是2n ω的n次代数方程,则系统有n 个固有频率12,,,n n nn ωωω将求得的第i 阶固有频率ni ω(i=1,2,,n)代入方程(6-55), 就可以求得相应的振型向量{}(i=1,2,,n)i u 。
则{}i u 就是对应于第i 阶固有频率ni ω的振型向量,它是一个n 维列向量。
将求得的n 个振型向量{}i u 依次排列构成一个n ×n 的矩阵:[]{}{}{}12n n nu u u u ⨯⎡⎤=⎣⎦则[]u 称为振型矩阵。

关于振动单位峰峰值mm和速度值mm/s之间的区别和联系【物理课本】峰峰值是指振幅,速度是指速度的最大值,还有一个是加速度,也就是速度的变化的快慢.位移对时间的导数是速度,速度对时间的导数就是加速度2π×频率×振动位移值=振动速度值(3000r/min对应50HZ,振动稳定时,该公式差不多)就EPRO系统而讲。
瓦振在正常校验卡件时所用是速度传感器。
其测量出是振幅的特征值。
如物理公式。
设振动运动方程是正弦波。
A=asinwt则速度为V=awsinwt它们的特征值相差如上楼所说。
所以一般TSI厂家校验振动探头时给出速度传感器的灵敏度。
而后根据卡件的量程设定算出应该的正弦波有效值。
不仔细说了。
总之在相同的有效电压输入下,频率低则峰峰值高。
而且现场带度传感器过来的信号不能简单地用万用表测量。
它们可能分为不同的倍频进行问题分析。
大多数电厂都不引进分析系统。
所以振动专家也不容易呀。
对于轴振则不用非常考虑频率的问题。
但新的数字卡件也引入了很多这方面的功能。
这太深了。
知道上述问题也就可以在电厂够应用了。
mm/s是振动速度值,一般采用10~1KHz范围内的均方根值,也就是说的振动烈度。
7丝就是70um,是振动位移值。
一般衡量汽机或者大型设备采用振动位移标准来衡量设备振动情况,普通的电机或者泵采用振动速度值,详见国标10086。
mm是振动幅值,用户,特别是电厂,考核的是振动幅值。
mm/s是振动速度,电机的国家标准考核的就是振动速度。
mm/(s^2)是振动加速度,一般用于高速电机的振动评定。
在实际应用中,有可能振动幅值合格,但振动速度不合格;也有可能振动速度合格,但振动幅值不合格,在实际应用中出现过这种情况的。
一般电机厂用的测振动的仪器有三档,分别测振幅、振动速度和振动加速度。
mm、mm/s、mm/(s^2)是不可能相互转换的。
mm是距离单位;mm/s是速度单位;mm/(s^2)是加速度单位。
mm振动位移:一般用于低转速机械的振动评定;mm/s振动速度:一般用于中速转动机械的振动评定;mm/(s^2)振动加速度:一般用于高速转动机械的振动评定。


材料力学特征值问题材料力学特征值问题什么是材料力学特征值问题?•材料力学特征值问题是指在材料力学领域中,通过解特定方程或方程组来求解材料的特征值和特征向量的问题。
•特征值是指在一定条件下,材料力学问题所具有的一些固有的特性或性质,例如材料的弹性模量、刚度等。
•特征向量是与特征值相关联的向量,描述了材料力学问题在不同特征值下的特定形态或模式。
材料力学特征值问题的应用领域•材料的振动分析:通过求解材料力学特征值问题,可以确定材料在振动状态下的固有频率和振动模式。
•结构的稳定性分析:通过求解材料力学特征值问题,可以判断结构在承受外力时的稳定性和破坏模式。
•材料的热传导分析:通过求解材料力学特征值问题,可以获得材料的热传导性质和热扩散模式。
材料力学特征值问题的数学表示•材料力学特征值问题可以通过线性代数中的矩阵特征值问题来表达。
•给定一个具有n个未知数的线性方程组A x=λx,其中A是一个n×n的矩阵,x是一个n维的向量,λ是一个标量。
•求解该方程组的特征值和特征向量,即求解方程λx=A x。
•这将产生n个特征值和相应的n个特征向量。
求解材料力学特征值问题的方法•直接求解法:通过将特征值问题转化为特征值方程,并求解该方程来获得特征值和特征向量。
•迭代求解法:通过迭代计算来逐步逼近特征值和特征向量的解。
•数值求解法:利用计算机数值计算的方法来求解特征值问题,例如特征值分解、Jacobi迭代等。
总结•材料力学特征值问题是在材料力学领域中非常重要的一个问题,涉及到材料的固有特性和性质。
•通过求解特征值问题,可以获得材料在不同特征值下的特定形态和模式。
•求解特征值问题的方法有直接求解法、迭代求解法和数值求解法等。
•在实际应用中,我们可以利用这些方法来分析材料的振动、稳定性和热传导等问题。
材料力学特征值问题的影响因素•材料的性质:特征值问题的解取决于材料的力学性质,如材料的弹性模量、密度、几何形状等。
•外部条件:特征值问题的解还受到外部条件的影响,如材料受到的外力、温度等。
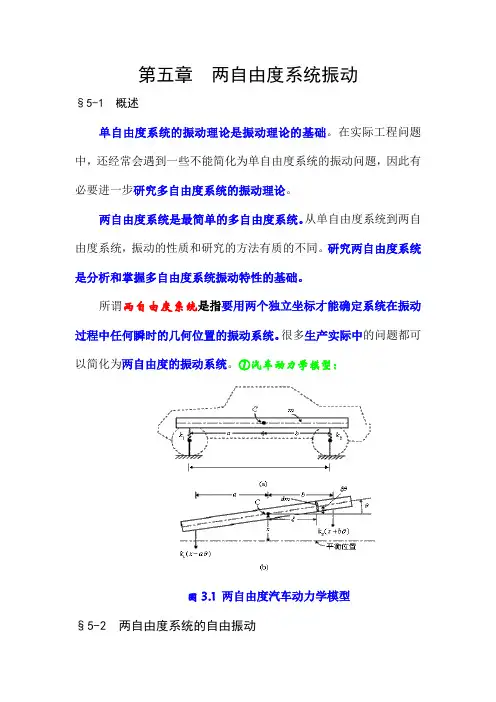
第五章两自由度系统振动§5-1 概述单自由度系统的振动理论是振动理论的基础。
在实际工程问题中,还经常会遇到一些不能简化为单自由度系统的振动问题,因此有必要进一步研究多自由度系统的振动理论。
两自由度系统是最简单的多自由度系统。
从单自由度系统到两自由度系统,振动的性质和研究的方法有质的不同。
研究两自由度系统是分析和掌握多自由度系统振动特性的基础。
所谓两自由度系统是指要用两个独立坐标才能确定系统在振动过程中任何瞬时的几何位置的振动系统。
很多生产实际中的问题都可以简化为两自由度的振动系统。
①汽车动力学模型:图3.1两自由度汽车动力学模型§5-2 两自由度系统的自由振动一、系统的运动微分方程②以图3.2的双弹簧质量系统为例。
设弹簧的刚度分别为k 1和k 2,质量为m 1、m 2。
质量的位移分别用x 1和x 2来表示,并以静平衡位置为坐标原点,以向下为正方向。
(分析)在振动过程中的任一瞬间t ,m 1和m 2的位移分别为x 1及x 2。
此时,在质量m 1上作用有弹性恢复力()12211x x k x k -及,在质量m 2上作用有弹性恢复力()122x x k -。
这些力的作用方向如图所示。
应用牛顿运动定律,可建立该系统的振动微分方程式:()()⎭⎬⎫=-+=--+00122221221111x x k x m x x k x k xm (3.1)令2212121,,m k c m k b m k k a ==+=则(3.1)式可改写成如下形式:()()⎭⎬⎫=-+=--+00122221221111x x k x m x x k x k xm⎭⎬⎫=+-=-+00212211cx cx xbx ax x(3.2) 这是一个二阶常系数线性齐次联立微分方程组。
(分析)在第一个方程中包含2bx -项,第二个方程中则包含1cx -项,称为“耦合项”(coupling term )。
这表明,质量m 1除受到弹簧k 1的恢复力的作用外,还受到弹簧 k 2的恢复力的作用。

机械振动中的特征值问题机械振动是指系统在某一位置(通常是静平衡位置,简称平衡位置)附近所作的往复运动。
显然这是一种特殊形式的机械运动。
人类的大多数活动都包括这样或那样的机械振动。
例如,我们能听见周围的声音是由于鼓膜的振动;我们能看见周围的物体是由于光波振动的结果;人的呼吸与肺的振动紧密相关;行走时人的腿和手臂也都在作机械振动;我们能讲话正是喉咙(和舌头)作机械振动的结果。
早期机械振动研究起源于摆钟与音乐。
至20世纪上半叶,线性振动理论基本建立起来。
欧拉(Euler)于1728年建立并求解了单摆在阻尼介质中运动的微分方程。
1739年他研究了无阻尼简谐强迫振动,从理论上解释共振现象。
1747年他对n个等质量质点由等刚度弹簧连接的系统列出了微分方程组并求出精确解,从而发现系统的振动是各阶简谐振动的叠加。
1760年拉格朗日(Lagrange)建立了离散系统振动的一般理论。
最早研究的连续系统是弦线。
1746年达朗伯(d’Alembert)用片微分方程描述弦线振动而得到波动方程并求出行波解。
1753年伯努利(Bernoulli)用无穷多个模态叠加的方法得到弦线振动的驻波解。
1759年拉格朗日从驻波解推得性波解,但严格的数学证明直到1811年傅里叶(Fourier)提出函数的级数展开理论才完成。
一个振动系统本质上是一个动力系统,这是由于其变量如所受到的激励(输入)和相应(输出)都是随时间变化的。
一个振动系统的响应一般来说是依赖于初始条件和外部激励的。
大多数实际振动系统都十分复杂,因而在进行数学分析时把所有的细节都考虑进来是不可能的。
为了预测在指定输入下振动系统的行为,通常只是考虑那些最重要的特性。
也会经常遇到这样的情况,即对一个复杂的物理系统,即使采用一个比较简单的模型也能够大体了解其行为。
对一个振动系统进行分析通常包括以下步骤。
步骤1,建立数学模型。
建立数学模型的目的是揭示系统的全部重要特性,从而得到描述系统动力学行为的控制方程。
一个系统的数学模型应该包括足够多的细节,能够用方程描述系统的行为但又不致使其过于复杂。
根据基本元件行为的属性,一个振动系统的数学模型可以是线性的,也可以是非线性的。
线性模型处理简单,容易求解。
但是非线性模型有时能够揭示线性模型不能够预测到的某些系统特性。
所以需要对实际系统做大量的工程判断以得到振动系统比较合理的模型。
有时为了得到更准确的结果,需要对系统的数学模型不断进行完善。
此时可以先用一个比较粗略的模型,以便能够较快地对系统的大体属性有所了解。
之后再通过增加更多的元件和细节对模型不断改进,以便进一步分析系统的动力学行为。
步骤2,推导控制方程。
一旦有了系统的数学模型,就可以利用动力学定律推导系统响应变化规律的运动微分方程。
系统的运动微分方程可以通过作每一个质量块的受力分析图方便地得到。
每一个质量块的受力分析图可以通过分离该质量块并加上其所受的全部主动力、反作用力和惯性力得到。
一个振动系统的运动微分方程对于离散系统来说,通常是一个常微分方程组;对于连续系统来说,通常是一个偏微分方程组。
根据基本元件行为的属性,一个振动系统的运动微分方程(组)可以是线性的,也可以是非线性的。
以下几种方法经常用来推导系统的控制方程:牛顿第二运动定律、达朗贝尔原理和能量守恒原理。
步骤3,求控制方程的解。
为了得到振动系统响应的规律,必须求解控制方程。
根据问题具体特点,可以采取下述方法之一:求解微分方程的常规方法,拉普拉斯变换方法、矩阵方法和数值计算方法。
如果控制方程是非线性的,则很少能够得到其封闭形式的解。
另外,求解偏微分方程的情况也远比求解常微分方程的情况多。
利用计算机的数值计算方法求解微分方程是非常便捷的,但欲根据数据计算结果得到关于系统行为的一般结论却是困难的。
步骤4,结果分析。
虽然控制方程的解给出系统中不同质量块的振动位移、速度和加速度的表达式,但是这些结果还必须就某些目的做进一步分析,以期分析结果可能揭示对设计的某些指导意义。
振动系统可以分成两大类,离散系统和连续系统。
连续系统具有连续分布的参量,但可通过适当方式化为离散系统。
按自由度划分,振动系统可分为有限多自由度系统和无限多自由度系统。
前者与离散系统相对应,后者与连续系统相对应。
尽管大部分的振动系统模型(微分方程或偏微分方程)都是不可解得,但人们为了更好的理解振动系统的实质,仍然希望获得解析解。
而获得解析解,必须求解方程的特征值。
其中最有代表性就在处理连续系统的振动问题时,采用的分离变量法。
单自由度系统的自由振动问题包含无阻尼和有阻尼两种情况。
所谓自由振动是指系统受初始扰动后,仅靠弹性恢复力来维持的运动。
其运动方程通常是一个二阶常微分方程,对于无阻尼的情况,方程一般为:0mxkx += ; 可以推出其特征方程:20m s k +=;特征值:12n k s iw m ⎛⎫=±-=± ⎪⎝⎭; 方程通解:()12cos sin n n x t A w t A w t =+;n w 为固有圆频率;可推出系统的固有频率和固有周期;对于有阻尼的情况,如黏性阻尼,方程一般为:0mxcx kx ++= 同样可以推出特征方程:20m s cs k ++=;该特征方程的根为:1,22c s m=-±;方程通解:()2212cc t t m m x t C e C e⎧⎧⎪⎪--⎨⎨⎪⎪⎩⎩=+。
单自由度系统在简谐激励下的振动,无阻尼的情况下,方程一般为:0cos m x kx F w t += ;齐次解可以表示为:()12cos sin h n n x t C w t C w t =+,其中,特征值()12n w k m =为系统的固有频率。
有阻尼的情况下,方程多出一个一阶导数项,方程求解类似;单自由度系统在一般激励下的振动,方程一般为:011cos sin 2jjj j a m x cxkx ajw t bjw t ∞∞==++=++∑∑ ;根据叠加原理,可求出其稳态解。
二自由度系统的振动问题,以一个含黏性阻尼的二自由度弹簧质量系统为例,其方程一般为:()()()()t t t t ++=m x cxkx F ,式中,m ,c ,k 分别为质量矩阵,阻尼矩阵和刚度矩阵,具体形式如下:1200m m ⎡⎤=⎢⎥⎣⎦m ,122223c c c c c c +-⎡⎤=⎢⎥-+⎣⎦c ,122223k k k k k k +-⎡⎤=⎢⎥-+⎣⎦k ()t x 和()t F 分别为位移向量和力向量,具体形式如下:()()()12x t t x t ⎧⎫⎪⎪=⎨⎬⎪⎪⎩⎭x ,()()()12F t t F t ⎧⎫⎪⎪=⎨⎬⎪⎪⎩⎭F其中,在无阻尼自由振动的情况下,其特征方程或频率方程为:()()2112222223d e tm w k k k k m w k k ⎡⎤-++-=⎢⎥--++⎣⎦ 方程的两个根是:()()()()()()1222312212121221222311223212121,2142k k m k k m w w m m k k m k k m k k k k k m m m m +++⎧⎫=⎨⎬⎩⎭⎡⎤⎧⎫+++++-⎧⎫⎪⎪⎢⎥-⎨⎬⎨⎬⎢⎥⎪⎪⎩⎭⎩⎭⎣⎦这表明当w 等于1w 或2w 时,系统具有非零简谐解是可能的。
1w 和2w 成为系统的固有频率。
它决定了振幅比,模态向量(也叫主振型)等。
大多数实际系统都是连续的,具有有限多个自由度。
连续系统的振动分析要求解偏微分方程,这是非常困难的。
实际上对于许多偏微分方程并不存在解析解。
另一方面,多自由度系统的振动分析只要求一组常微分方程,这相对来说要简单的多。
因此,为了分析的简化,连续系统经常近似为多自由度系统。
利用拉格朗日方程可以推导得出以矩阵形式表示的多自由度系统的运动微分方程:,1,2,i i i id T T VF i n dt x x x ⎛⎫∂∂∂-+== ⎪∂∂∂⎝⎭其中,i F 是相对于第i 个广义坐标i x 的非保守广义力;i x是i x 对时间的导数(广义速度)。
多自由度系统的动量和势能以矩阵的形式可以表示为:1212TT V ==Tx m x x kx,其中,x 为广义坐标的列向量,即{}x x =12n x x x ⎧⎫⎪⎪⎪⎪=⎨⎬⎪⎪⎪⎪⎩⎭x经矩阵变换可得矩阵形式的方程+=m x kx F;其中12n F F F ⎧⎫⎪⎪⎪⎪=⎨⎬⎪⎪⎪⎪⎩⎭F 。
若系统是保守的,则不存在非保守力i F ,则运动微分方程为:0+=m x kx通过令特征矩阵的行列式为零来求多自由度系统的固有频率和主振型,通常多个固有频率。
尽管这种方法很精确,但当系统自由度较大时,特征矩阵的展开以及彼此得到的n 次代数方程的求解会变得很繁琐。
目前可以通过数值方法,如邓克莱法、瑞利法、霍尔茨法、李兹法、矩阵迭代法、雅克比法和子空间迭代法。
以上讨论的离散系统都是假定质量、阻尼、弹簧仅出现在系统的某些离散点处。
有许多连续系统的例子,它们不能视离散质量、阻尼或弹簧,因此必须考虑它们的连续分布,同时假定系统的无限个点是能够振动的,这就是为什么连续系统那个也称为无限自由度系统的原因。
根据实际问题,有三类方程典型方程,弦振动方程:()()22122,,,,1,2,3.n u a u f t x x x n t∂=∆+==∂x x ;热传导方程:2(,,,),u a u f t x y z t∂=∆+∂其中222222xyz∂∂∂∆=++∂∂∂为三维拉普拉斯算子;泊松方程:21(,,),u f x y z a∆=-当(,,)0f x y z ≡时,就是调和方程。
其基本解法有行波解法、分离变量法、积分变换法。
行波法是通过找到一种变量代换将齐次波动方程化为很容易求解的二阶偏微分方程,从而求出方程的通解,进而根据初始条件求出方程的特解。
这在整体思路上与求解二阶线性常微分方程是一致的。
但一般而言,偏微分方程的通解不容易求, 这就使得行波法有相当大的局限性, 所以通常只用它求解波动问题,分离变量法和付里叶法变换法有一个共同特点:都是将偏微分方程化为常微分方程,只不过化成常微分方程的方法不同而已。
分离变量法是直接求特解的一种方法,是解数理方程的重要方法之一,适用于解大量的、各种各样的有界问题,因而是一个比较普适的方法。
而对于无界区域或半无界区域的问题,用积分变换法比较方便,并且在解数理方程时不象分离变量法那样区分齐次和非齐次方程,对齐次和非齐次方程都是按同样的步骤解。
当然用积分变换法时,作逆变换过程中求积分有时会很困难,此外作积分变换时,要求所出现的函数满足一定的条件,否则不能作积分变换。
总之,这三种解法各有特点,应根据实际问题选用合适的方法。