由一道课本习题引发的思考

由一道课本习题的思考
王琳
【期刊名称】《数学大世界（教师适用）》
【年(卷),期】2012(000)004
【摘要】数学学习的核心是发展思维能力。

通过对一道习题的引申、改编，同学们不仅对课本知识的掌握和应用更为熟练，而且对培养发散思维和创造性思维能力大有裨益。

【总页数】1页(P53-53)
【作者】王琳
【作者单位】江苏省泰州市海军中学
【正文语种】中文
【中图分类】O1-4
【相关文献】
1.让教材中典型习题散发出火热的美丽——课本中一道习题的探究与思考
2.挖掘课本习题功能,拓宽数学思维空间r——一道课本习题的延伸与拓展
3.挖掘课本习题功能探究高考命题趋势--一道解三角形课本习题的探究
4.一道课本习题教学的实践与思考——关于例、习题教学有效性的探讨
5.由一道课本习题所引发的思考——课本习题的价值到底有多大
因版权原因，仅展示原文概要，查看原文内容请购买。

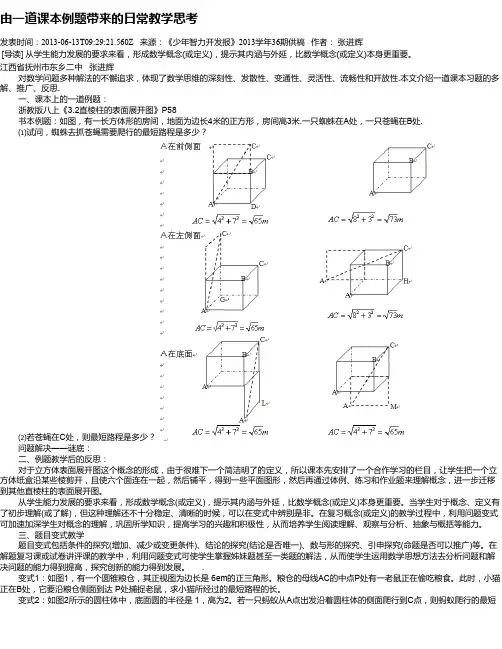
由一道课本例题带来的日常教学思考发表时间：2013-06-13T09:29:21.560Z 来源：《少年智力开发报》2013学年36期供稿作者：张进辉[导读] 从学生能力发展的要求来看，形成数学概念(或定义)，提示其内涵与外延，比数学概念(或定义)本身更重要。

江西省抚州市东乡二中张进辉对数学问题多种解法的不懈追求，体现了数学思维的深刻性、发散性、变通性、灵活性、流畅性和开放性.本文介绍一道课本习题的多解、推广、反思.一、课本上的一道例题：浙教版八上《3.2直棱柱的表面展开图》P58书本例题：如图，有一长方体形的房间，地面为边长4米的正方形，房间高3米.一只蜘蛛在A处，一只苍蝇在B处.⑴试问，蜘蛛去抓苍蝇需要爬行的最短路程是多少？⑵若苍蝇在C处，则最短路程是多少？问题解决——谜底：二、例题教学后的反思：对于立方体表面展开图这个概念的形成，由于很难下一个简洁明了的定义，所以课本先安排了一个合作学习的栏目，让学生把一个立方体纸盒沿某些棱剪开，且使六个面连在一起，然后铺平，得到一些平面图形，然后再通过体例、练习和作业题来理解概念，进一步迁移到其他直棱柱的表面展开图。

从学生能力发展的要求来看，形成数学概念(或定义)，提示其内涵与外延，比数学概念(或定义)本身更重要。

当学生对于概念、定义有了初步理解(或了解)，但这种理解还不十分稳定、清晰的时候，可以在变式中辨别是非。

在复习概念(或定义)的教学过程中，利用问题变式可加速加深学生对概念的理解，巩固所学知识，提高学习的兴趣和积极性，从而培养学生阅读理解、观察与分析、抽象与概括等能力。

三、题目变式教学题目变式包括条件的探究(增加、减少或变更条件)、结论的探究(结论是否唯一)、数与形的探究、引申探究(命题是否可以推广)等。

在解题复习课或试卷讲评课的教学中，利用问题变式可使学生掌握姊妹题甚至一类题的解法，从而使学生运用数学思想方法去分析问题和解决问题的能力得到提高，探究创新的能力得到发展。

V 〇1.51 N 〇.4Apr .2022+k 糾f教■学参考间题争鸣不能忽略的一组弹性碰撞结论------道习题拓展引发的思考张永武(山东省沂水县第一中学山东沂水276400)文章编号：1002-218X (2022)04-0049-02中图分类号：G632. 4文献标识码：B摘要：通过对一道常见习题的拓展与讨论，发现在平时的物理教学中一般不涉及弹性碰撞模型的另一组解，导致学生在分析实际问题出现困惑或错误；用数学知识导出弹性碰撞的另一组表达 式，并用其解决相应类型的问题。

关键词：弹性碰撞；物理情境；结论公式；动量守恒―、题目及其特点分析1. 原题呈现如图1所示，小车的上面固定一个光滑弯曲圆 管道，整个小车（含管道）的质量为，原来静止在光滑的水平面上。

现有一个可以 W /W W "从""""""W a v "" 看做质点的小球，质量为图1半径略小于管道半径，以水平速度I 从左端滑上小 车。

小球恰好能到达管道的最高点，然后从管道左 端滑离小车。

关于这个过程，下列说法中正确的是 (重力加速度为J ?) ()A . 小球滑离小车时，小车回到原来的位置B . 小球滑离小车时相对小车的速度大小为tC . 运动过程中小车（含管道）和小球的总动能不变D .车上管道中心线最高点离小车上表面的竖 直高度为f2. 分析与解该题以小球与轨道（小车）的相互作用为背景， 综合考查系统的动量守恒与机械能守恒的应用。

依据物理情境，选择合理的模型知识列方程求解；对于二者分离时的速度大小，可用弹性碰撞结论直 接求解。

解析小球恰好到达管道的最高点，说明在最高点时小球和管道之间相对速度为〇。

小球从滑进管道到滑到最高点的过程中，由水平方向动量守 恒及系统机械能守恒定律有mv = {m ~\~2m)v®mgH = -^-mv 2 — +得H = 故选项C 错误，选项D 正确。

题目 (人教A 版《数学》选择性必修一课本P38第2题)PA ，PB ，PC 是从点P 出发的三条射线，每两条射线的夹角均为60 ，那么直线PC 与平面PAB 所成角的余弦值为（ ）A.12B. 22 C. 33 D. 36几何问题通性通法通性通法是具有普遍意义的方法和相关知识，因为问题中PA ，PB ，PC 的长度没有给出，需要用一般的量来表示解决问题，体现对数学本质的思考．解法1 在PC 上任取一点D 并作DO APB ⊥平面,则 DPO 即为直线PC 与平面PAB 所成的角．过点O 作OE PA ,OF PB ,垂足分别为E F ,．因为DO APB 平面，所以DE PA ,DF PB ,所以△△DEP DFP Ｑ．所以EP FP =,所以△△OEP OFP Ｑ．因为 APB =60 ,所以 OPE OPF ==30 ．设OE b =，所以OP b PF b PD b =2,=3,=23,所以cos === DPO OP PD 一道课本习题的多种解法及反思王希红ABC DE FPO由n nPA PB,,则n a b c a⋅=++⋅PA x y z()=+⋅+⋅x y za b a c a2=+a x aby212+=012acz, n a b c b⋅=++⋅PB x y z()⋅++⋅x y za b b c b2=+12abx b y bcz2+=012．取x b y a=,=,则z=−3abc，所以n a b c=+−b a3abc,n a b c c⋅+−⋅PC b a3abc⋅+⋅−b aa cbc c3abc2=+−=−1122abc abc abc abc32,||n===6ab, cos<,>nPC=||||nn⋅PCPC==设直线PC与平面PAB所成角为θ，则sin=|cos<,>|=θPCn36．因为θ∈0,π2，所以cos1sinθθ=−=233．所以 x z y z −=−=00，，取z =1，则x y ==1,所以平面PAB 的一个法向量n =(1,1,1)．则cos ,<>===n PC |||| PCPC ⋅n n 23¨263．设直线PC 与平面PAB 所成角为θ，则sin |cos ,|θ=<>=nPC 36．因为θ∈0,π2，所以cos 1-sin θθ==233．直线PC 与平面PAB 所成角的余弦值为33． （王希红，山东省聊城第一中学）第34页参考答案：1.P 到直线C D 11的距离即为PC 1，在面BCC B 11中，动点P 到定点C 1的距离与到定直线BC 的距离之比为2，因此点P 轨迹所在曲线是离心率为2的双曲线，选C.2.设侧面PAB 与底面ABC 所成的二面角大小为θ，过M 作MO 垂直于底面ABC 于O ，过O 作OD 垂直于AB 于D ，则∠MDO 即为θ，所以MO MD =sin θ，即MDMP=sin θ.因为θθ∈π∈(0,),sin (0,1]，当0sin 1<<θ时M 所在曲线为椭圆；当sin 1θ=时M 所在曲线为抛物线．故选BD.第44页参考答案：证明：（法1）记不等式左边为A ，构造A 的对偶式：B =...+a a a a a a a a 122311a a ++++2122+++a a 322n n n −n ，同例3的方法可证明．（法2）由柯西不等式，设a a 1+1=n ，知不等式左边∑i =n1a a i i +aii 2+1≥=∑i =n1()()∑aa =n1ii a +i 2+112.（本题由于数列平方因子出现，显然直接用柯西不等式最简单．）。

学法指导由一道几何题引起的思考■应位峰摘要：数学的课堂难免会出现意外。

这样的意外是学生积极参与，探索思考的结果。

我们善于利用，对自己、对学生、对课堂都大有裨益。

本文从九年级课堂教学中的一道习题出发，通过学生给出的解法，谈谈一些自己在教学时的思考。

关键词：教师；解题数学教学尤其是几何教学总能引发学生们思维的火花碰撞，有的会让我们老师得到意外的收获。

因此，教师的主导不能代替学生的主体，引导学生，积极思维，敢于表达和质疑往往使学生对于知识的掌握更到位。

下面谈谈九年级数学圆周角一课讲到的一个习题时，遇到的意外收获。

一、题目呈现如图，AB 是⊙O 的直径，D 是弦AC 延长线上的一点，且CD=AC ，DB 的延长线交⊙O 于点E 。

问CD 与CE 相等吗？为什么？二、师生解法对比该题教师给出的解法：连接BC 。

由于AB 是圆O 的直径，可得∠ACB =90°，即BC ⊥AD 。

根据已知条件CD=AC ，由“三线合一”得到BA=BD ，再由“等边对等角”得到∠A=∠D 。

由于∠A 与∠E 是同弧所对的圆周角，所以∠A=∠E 。

再等量代换即得到∠E=∠D ，再通过“等角对等边”得到CE=CD 。

学生给出的优解：连接AE ，由于AB ⊙圆O 的直径，因此∠AEB =90°。

因为CD=AC ，所以C 是斜边AD 的中点。

根据直角三角形斜边上的中线等于斜边的一半，可得CE =12AD ，即CE=CD 。

相对而言，两者选择的角度不同，对于教师来说，一般比较喜欢用分析法，从结论出发，要证边相等，就要证角相等，于是要证∠E=∠D 。

因为∠A=∠E ，所以只要证∠A=∠D ，那么就要证BA=BD ，就会向证中垂线的方向去证，因此过程相对就多了一点，但是像这样，从结论出发，往前推逐步跟已知条件联系，对于解任何一道几何题都能行得通，因为思维上比较容易。

而学生方法的最大的优点就是简便，巧妙地运用直径构造另外一个直角，加上中点，使得直角三角形的性质发挥作用。

课本习题引发的思考【摘要】高考是源于课本而高于课本，本文主要通过课本习题引发的思考，来总结高中数学中几个常见的构造法模型的应用。

【关键字】：构造法函数几何图形高考命题组的总结”相当数量的试题都源于课本的例题、习题或稍加改造，或做拼合，或稍做提高，是常规题型、常见思路、常用的方法在试卷占了主题地位。

突出了基础知识、基本技能和基本方法的考查。

“正因为很多高考源于课本而高于课本，而在教学的过程中对于课本上的题会好，很多练模拟卷上的题都和课本上的题有很大的相似之处，可以说有很多题都是课本的习题的变式，尤其是在书后探究拓展、思考运用部分出现的频率更高，所以本人通过课本习题归纳总结一些常见问题的构造法。

在苏教版必修2第一章立体几何部分（第62页）章末复习题第18题【原题】设p、a、b、c是球o 表面上的四点；pa、pb、pc两两互相垂直，且pa=pb=pc=1，求球的表面积及体积。

对于此题本身由于大部分同学对于空间立体的想象比较欠缺，解决起来有一定的困难，由于求本身就是空间的图形不好在平面上画出，还要在还要里面还几条互相垂直的线，不容易找到球心与一已知量之间的关系。

因而很多同对于此只能望而却步，但如果我们能从题目本身的特点和条件入手构造常见的图行从而很容易解决此问题。

上面的问题就用到了常见的数学方法构造法。

下面从以下几个方面谈一下构造法如何在高中数学中很好的运用。

2.1构造图形法构造图形法主要是在原来已知图形、函数，等式的基础上进一步探讨分析，主要也就是数形结合，通过对图形的认识、数形转化，以提高思维的灵活性、形象性、直观性使问题化难为易，化抽象为具体。

它包含”以形助数”和”以数辅形”两个方面。

华罗庚教授对此有精辟的概述：”数无形，少直观；形无数，难入微。

”本人就以开始课本上的习题为例具体说明【原题1】设p、a、b、c是球o 表面上的四点；pa、pb、pc两两互相垂直，且pa=pb=pc=1，求球的表面积及体积。

一道数学题引发的思考数学，是一门极具逻辑性和抽象性的学科，它不仅是一种工具，更是一种思维方式。

数学题在引发我们思考的也促使我们发现问题的本质，培养逻辑推理和解决问题的能力。

下面，我们来谈一谈数学题引发的思考过程。

最近，我在解题时遇到了这样一道题目：已知 a + b = 10，a - b = 6，求 a 和 b 的值。

一般情况下，我们可能会采用代数方法来解这道题，即通过联立方程来求解。

在我解题的过程中，我突然想到了另外一种方法，那就是直接归纳和推理。

我们不妨假设 a 和 b 都是整数。

那么根据题目条件可知 a 和 b 的关系，我们可以通过列举可能的整数对来求解。

当 a = 8, b = 2 时满足条件，因为 8 + 2 = 10，8 - 2 = 6；当 a = 7, b = 3 时也满足条件，因为 7 + 3 = 10，7 - 3 = 4；当 a = 6, b = 4 时满足条件，因为 6 + 4 = 10，6 - 4 = 2。

通过以上列举，我们可以发现，对于 a 和 b 来说，只有一组整数满足条件。

所以，我们得出结论：a = 8，b = 2。

通过这道数学题，我深深地思考到了数学问题解决的多种思路，更加深刻地理解到了数学问题的本质。

数学题并不仅仅是为了考验我们的计算能力，更是考验我们的逻辑思维和解决问题的能力。

在这个过程中，我还意识到了数学的自然美和逻辑美。

每一个数学问题都是一个独立的思维世界，我们可以通过不同的途径来发现和解决问题。

这种美妙的思维方式，远不止局限于数学领域，它更是一种全面的思维能力的培养。

数学题还能引发我们对抽象思维的锤炼。

在解题的过程中，我们需要将问题抽象成符号和方程式，并通过逻辑推理来解决问题。

这种抽象思维的过程，可以帮助我们更好地理解问题的本质，培养我们在解决实际问题时的抽象能力。

数学题还能激发我们对新领域的探索和思考。

在解决数学题的过程中，我们可能会涉及到其他学科的知识，比如物理、化学、计算机等，这些跨学科的思维过程，可以引发我们对新领域的兴趣和探索，帮助我们更好地拓展自己的思维空间。

由一道练习题引发的对学生数学思维品质的思考作者：代秀红来源：《速读·中旬》2018年第03期什么是数学思维品质？如何在小学数学教学中培养学生的数学思维品质？我想大部分数学教师在教学过程中会紧紧围绕如何解决问题来锻炼学生的思维能力，但对数学思维品质的培养就知之甚少了，下面我就结合人教版《小学数学五年级上》第三单元《小数除法》——《商的近似数》一课中的一道练习题来谈谈我对数学思维品质的理解和思考。

《小学数学五年级上》第41页11题：一种瓶装橙子粉重450g，，每冲一杯需要16g橙子粉和9g方糖。

冲完这瓶橙子粉，大约需要多少克方糖？这道题出现在学生已学习了用“四舍五入法”、“进一法”和“去尾法”解决问题后的练习九中，在求“可以冲多少杯？”这一问题时用450÷16=28.125（杯），计算出的结果是小数，而冲出的杯数必须是整数，因此要取计算结果的近似值。

在取近似值时，不能机械地使用“四舍五入法”，要根据具体情况确定“舍”还是“入”。

人教版《小学数学五年级上教师用书》中指出：一般方法是先求可以冲多少杯，450÷16≈28（杯），再求28杯需要多少克方糖，但也可能会有学生提出用“进一法”，450÷16≈29（杯），再求29杯需要多少克方糖，理由是可以将橙子粉冲淡一些，从解决实际问题的角度也是可以的。

对此，引发了我对培养学生数学思维品质的思考。

思维是人的理性认识过程。

所谓数学思维，是指人关于数学对象的理性认识过程。

思维能力的高低，直接影响到数学学习的效果，因此，培养学生的数学思维能力是提高数学教学效率的关键。

良好的数学思维品质主要包括思维的严谨性、广阔性、深刻性、灵活性和批判性，下面就结合本题对培养学生的数学思维品质进行讨论。

一、培养数学思维的严谨性思维的严谨性是指考虑问题的严密、有据。

首先要求学生要按步思维，思路清晰，就是要培养学生按照一定的逻辑顺序进行思考问题。

其次要求学生要全面、周密地思考问题，做到推理论证要有充分的理由作根据。

一道题引出的思考当我们在解答问题出现错误时不能仅仅认为是审题不够深刻、思路不够清析、方法不够灵活造成的，有时应从深层次去考虑出现错误的原因.大家都知道这个答案是错误的，为什么在一阶导数的基础上求出的二阶导数是错误的呢？原因是这样的，引例所给的函数不是显函数形式，而是参数方程形式，在求一阶导数时是对x求导的，在求二阶导数时也应该对x求导，而上述解答中是对t求导的，因此才造成这样的错误.正确的解答是：其实，不能把这种错误简单归结为学生对这类题型的解题方法不熟练或者认为学生对求导方法掌握得不够全面、灵活.笔者认为产生上述错误的真正原因却来源于教师和教材这两个因素.一、教师的指导不当上面提到的例1，绝大部分教师给学生的答案乃至各种类型考试试题的参考答案都是：二、教材的编排不妥上述例题所涉及的题型属于参数方程形式的函数的导数问题，参数方程形式的函数的导数求解最关键的是把导数理解成微商（形式是dydx）.然而绝大部分高等数学教材中，从导数的概念、导数的基本公式、导数的四则运算规则以及复合函数的求导规则的学习中，导数的形式都习惯记为y′或者f ′（x），dydx只是作为一种记号在导数概念学习时简单提了一下，由于写法繁琐一般不常用.更为重要的是绝大部分高等数学教材的编写都是把参数方程形式的函数的导数问题讨论放在微分概念之前，试想在没有学习微分概念之前，怎么可能把导数理解为微商形式呢？因此笔者认为高等数学教材《导数与微分》章节中应该在导数的概念和基本求导公式之后就安排微分概念的学习，然后再讨论各种类型的导数问题更为科学合理.因此当我们在解答问题出现错误时不能仅仅认为是审题不够深刻、思路不够清析、方法不够灵活造成的，有时应从深层次去考虑出现错误的原因.这样还有可能得到解题之外许多收获.[江苏省泰州学院数理信息学院（225300）]。

由一道数学题引发的思考数学，是一门奇妙的科目.正如一句名言：条条大路通罗马.在数学的世界里，不同人的思维就像是一条条修好的路，有的很短，有的通向死胡同，有的迂回曲折却通往正确的终点.然而，数学的魅力正在于此，因为到达同一目的地的路不同，所以领略的风景不同，在与同伴分享风景的过程中所迸发的思维火花是极其炫彩夺目的.高中数学老师应该引领学生寻找终点，而不是要求他们走同一条路，当有数学题可以多解，且方法巧妙时，便足以可以引发我的思考.高二时，一次周五大课间，有位学生来找我，拿着我今天早上才讲的卷子.顿时，我心生疑惑：一向数学很好的学生难道听不懂我讲的课吗？所以在疑惑中我和他开始交谈.原来，他是为那道我做了很长时间，通过冗长计算得出结果的解析几何题而来的.看着他信心满满的样子，我分析了他的解题过程.∵点P在椭圆内部，直线l与椭圆恒有两个交点，∴点M的轨迹方程为：3x（x-1）+4y（y-1）=0对于数学老师来说，面对很熟悉的解析几何题，要保证全班学生都能接受自己的做法，一般都会采用设点的坐标和直线方程，与椭圆方程联立之后运用韦达定理，再根据题目求解，消除未知数，得到正确答案.而且在大型考试中，过程很重要，按照按步给分原则，联立所设方程与椭圆、双曲线或者抛物线方程，根据韦达定理得出式子就可以得到一半的分数，所以在讲课做题的过程中所采用的方法普遍都是这个通用保险但繁琐的联立韦达法.看了这位同学的方法后，我觉得甚是惭愧.按部就班的方法固然比较安全，但是技术含量低、思维量小而运算量大.诚然，点差法无疑是解决含有中点问题的最好的方法.这道解析几何题涉及弦AB的中点坐标，且弦AB的斜率等于MP的斜率，所以点差法可以大大减少运算量，并且减少计算错误，提高正确率，达到事半功倍的效果.这道数学题让我思考了很多，其中有数学思维方面的，也有教学方面的.在数学思维方面，通过这道题，我认为墨守成规只能坐吃山空.凡事都要试一试，多向几个方向走走，就算碰壁，也会很有收获，至少比照猫画虎强.思维，尤其是数学思维，更多的是练，只有一次又一次地练习才能开阔自己的思维，才能注意到别人注意不到的细节，想到别人想不到的联系，这有可能正是解题的关键.就像刚刚那道解析几何，题目中涉及中点和斜率，在表示形式上很相近，而要表示出坐标差的关系同时用到中点的意义，只有两式相减，运用公式转化成我们所期盼的形式，这就是运用点差法解这道题的思维过程.当这种思维慢慢开始形成，并在一次次尝试中取得成效时，就会变成经验，经过总结，成为方法.同时，在思考过程中，在思维碰撞的过程中，那种数学带来的欢愉、兴奋和满足感也是不可替代的.所以，在看到一道数学题时，多联想，特别是在平时的练习中，时间和精力都是充沛的，也不害怕错误，所以我们要尽可能地发散自己的思维；在考试的时候，碰到不熟悉的题目，可以先尝试用自己的所谓简便方法，若是看不到希望，就果断放弃，为了节省时间再用常规方法试着解题.总而言之，思维的广泛性和灵活性对于数学这门学科是很重要的，而这种东西不是与生俱来的天赋，而是需要反复不断尝试和练习才会拥有的本领.作为高中数学老师，我认为我更应该在学生思维的基础上发散自己的思维，用自己的思考带给学生更美更神奇的数学世界.在教学方面，通过这道题，我认为身为数学老师，引领学生往深处想是我的职责.不要用自己的想法禁锢学生的想法，应该鼓励学生有问题或者有什么好的解题方法多和老师交流.老师在课堂上与同学们一起分享，便于拓展全班同学的数学思维，提高学生对数学的探索兴趣.鼓励一题多解，让老师和同学们在一起分享、一起思考的氛围中学数学.同时，在备课期间对待数学题，也要自己多想想，不要自认为自己的知识足以教学生，一定要准备充足，让班级里不同层次的学生都能获得知识.刚刚提到的那道解析几何题，我的普通方法完全满足不了能力很好的学生的知识需求，如果我多想想，备课再充分一些，在用普通方法解题满足一般学生的知识需求之后，再用点差法等更有技术含量的方法解题，用来满足能力好的学生知识需求，提高普通学生的数学能力，这样的数学教学才是令人满意的.原地踏步不是一个合格的老师应有的态度，人们常说老师是学生的精神领袖，我认为学生也是老师的精神宝藏.那位学生用这道解析几何题的不同解法提醒了我，并由一道数学题引发了我关于数学思维和数学教学的思考.思维是数学的基础，教学是我作为老师的职责和把之前千百年来的数学家和我自己的思维精华传递给下一代的方式.作为高中数学老师，我们应该发散自己的数学思维，提高教学质量和改变教学理念，只有同时做好这三点，才能够真正将知识传输到学生脑袋里，利用一题多解和分层次的方法解答，让数学不再一成不变.。