沪科版八年级上15.1全等三角形练习

沪科版八年级上册数学第14章全等三角形含答案一、单选题(共15题，共计45分)1、下列判断正确的是（）A.等边三角形都全等B.面积相等的两个三角形全等C.腰长对应相等的两个等腰三角形全等D.直角三角形和钝角三角形不可能全等2、如图，正方形ABCD中，点P在AC上，PE⊥AB，PF⊥BC，垂足分别为E、F，EF=3，则PD的长为（）A.1.5B.2C.2.5D.33、如图，直线l上有三个正方形a，b，c，若a，c的面积分别为5和12，则b的面积为（）A.4B.17C.16D.554、如图，∠BAC=∠DAF=90°，AB=AC，AD=AF，点D、E为BC边上的两点，且∠DAE=45°，连接EF、BF，则下列结论：①△AED≌△AEF②△AED为等腰三角形③BE+DC＞DE④BE2+DC2=DE2，其中正确的有（）个．A.4B.3C.2D.15、如图，若，则下列结论错误的是（）A. B. C. D.6、如图，Rt△ABC中，∠ACB＝90°，∠BAC＝30°，∠BAC的平分线交BC于点D，过点D作DE⊥AB，垂足为E，连接CE交AD于点F，则以下结论：①AB＝2CE；②AC＝4CD；③CE⊥AD；④△DBE与△ABC的面积比是：1：（）其中正确结论是（）A.①②B.②③C.③④D.①④7、用尺规作已知角的平分线的理论依据是（）A.SASB.AASC.SSSD.ASA8、如图，AB＝AC，点D，E分别在AB，AC上，补充下列一个条件后，不能判断△ABE≌△ACD的是（）A.∠B＝∠CB.AD＝AEC.∠BDC＝∠CEBD.BE＝CD9、下列命题是真命题的是（）A.有一个角为60°的三角形是等边三角形B.底边相等的两个等腰三角形全等C.有一个角是40°，腰相等的两个等腰三角形全等D.两直线平行，内错角相等的逆命题是真命题10、如图，正方形 ABCD中AB= 3,点B在边CD上,且 CD＝3DE. 将△ADE沿AE 对折至△AFE，延长EF交边BC 于点G，连接AG,CF下列结论:①点G是BC的中点；②FG=FC；③ GAE=45º；④GE=BG+DE.其中正确的是( )A.①②B.①③④C.②③D.①②③④11、如图，点B、C、E在同一条直线上，△ABC与△CDE都是等边三角形，则下列结论不一定成立的是（）A.△ACE≌△BCDB.△BGC≌△AFCC.△DCG≌△ECFD.△ADB≌△CEA12、如图是两个全等三角形，图中的字母表示三角形的边长，则∠1等于（）A.60°B.54°C.56°D.66°13、如图，用直尺和圆规作一个角等于已知角，能得出的依据是（）A.（SAS）B.（SSS）C.（ASA）D.（AAS）14、如图，∠ACB=90°，CD⊥AB，垂足为点D，下列结论错误的是（）A.∠A=∠2B.∠1和∠B都是∠A的余角C.∠1=∠2D.图中有3个直角三角形15、如图，△ABC的顶点A、B、C都在小正方形的顶点上，在格点F、G、H、I 中选出一个点与点D、点E构成的三角形与△ABC全等，则符合条件的点共有（）A.1个B.2个C.3个D.4个二、填空题(共10题，共计30分)16、如图，已知BC=EC，∠BCE=∠ACD，要使△ABC≌△DEC，则应添加的一个条件为________.（答案不唯一，只需填一个）17、如图，正方形ABCD中，AB=6，点E在边CD上，且CE=2DE．将△ADE沿AE 对折至△AFE，延长EF交边BC于点G，连结AG、CF．下列结论：=3.6．其中正确结①△ABG≌△AFG；②BG=GC；③EG=DE+BG；④AG//CF；⑤S△FGC论是________．18、空调安装在墙上时，一般会用如图所示的三角形支架固定在墙上，这种方法应用的数学知识是________.19、如图，，，是内过顶点的一条射线，作，，垂足分别为，，将和分别沿直线，翻折得到和，已知，，则的长度是________．20、如图，方格纸上有一个格点三角形和一条格点线段AB．在这个格点纸上找一点C，使得△ABC与这个格点三角形全等，这样的C点可以找到________个．21、如图，Rt△ABC中，∠ABC＝90°，AB＝BC，直线l1、l2、l3分别通过A、B、C三点，且l1∥l2∥l3．若l1与l2的距离为4，l2与l3的距离为6，则Rt△ABC的面积为________．22、如图，过点的直线交轴于点，，，曲线过点，将点沿轴正方向平移个单位长度恰好落在该曲线上，则的值为________．23、如图，CB=CA，∠ACB=90°，点D在边BC上（与B、C不重合），四边形ADEF为正方形，过点F作FG⊥CA，交CA的延长线于点G，连接FB，交DE于点Q，给出以下结论：①AC=FG；②S△FAB ：S四边形CBFG=1：2；③∠ABC=∠ABF；④AD2=FQ•AC，其中正确的结论的个数是________．24、如图，点D、E分别在线段AB、AC上，BE、CD相交于点Ｏ，AE＝AD要使△ABE≌△ACD，需添加一个条件是________（只要写一个条件）．25、已知：如图，四边形中，与相交于点O，则图中全等的三角形共有________对．三、解答题(共5题，共计25分)26、如图，已知∠ACB=∠DCE=90°，AC=BC=6，CD=CE，AE=3，∠CAE=45°，求AD的长．27、如图，是CD上一点，BE交AD于点求证：．28、如图，，，，且，求证：．29、如图，在平行四边形ABCD中，E、F是对角线BD上的两点，且BF=DE．求证：AE∥CF．30、如图，△ABC中，∠CAB的平分线与BC的垂直平分线DG相交于D，过点D 作DE⊥AB，DF⊥A C，求证：BE＝CF．参考答案一、单选题(共15题，共计45分)1、D2、D3、B4、B5、D7、C8、D9、D10、B11、D12、D13、B14、C15、B二、填空题(共10题，共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题，共计25分)28、29、。

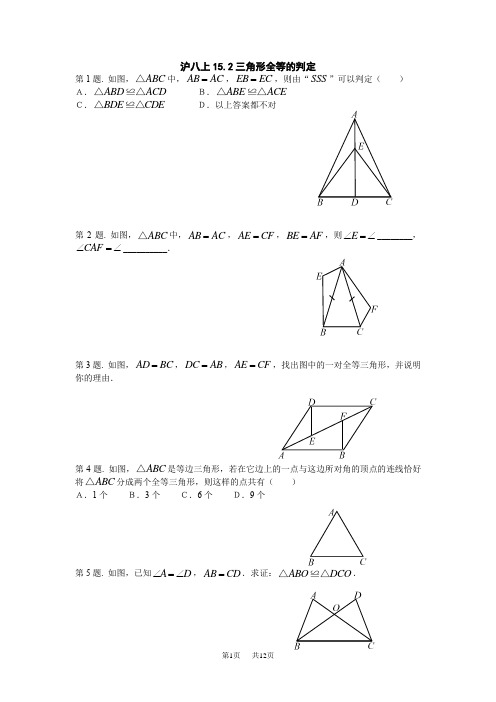
沪八上15.2三角形全等的判定第1题. 如图，ABC △中，AB AC =，EB EC =，则由“SSS ”可以判定（ ） Ａ．ABD ACD △≌△ Ｂ．ABE ACE △≌△ Ｃ．BDE CDE △≌△ Ｄ．以上答案都不对第2题. 如图，ABC △中，AB AC =，AE CF =，BE AF =，则E ∠=∠________，CAF ∠=∠__________．第3题. 如图，AD BC =，DC AB =，AE CF =，找出图中的一对全等三角形，并说明你的理由．第4题. 如图，ABC △是等边三角形，若在它边上的一点与这边所对角的顶点的连线恰好将ABC △分成两个全等三角形，则这样的点共有（ ） Ａ．1个 Ｂ．3个 Ｃ．6个 Ｄ．9个 第5题. 如图，已知A D ∠=∠，AB CD =．求证：ABO DCO △≌△．第6题. 如图，点D E ，分别在AB AC ，上，且AD AE =，BDC CEB ∠=∠． 求证：BD CE =．第7题. 已知AE 交BC ，垂足为D ，123∠=∠=∠，AB AD =． 求证：（1）ADC ABE ∠=∠； （2）DC BE =．第8题. 如图，已知ABC △为等边三角形，QR AB ⊥，垂足为R ，PQ AC ⊥，垂足为Q ，RP BC ⊥，垂足为P ，且AR BP CQ ==．求证：RPQ △为等边三角形．1 23 4第9题. 如图，已知点A C ，在EF 上，AD BC =，AD BC ∥，DE BF ∥． 求证：DE BF =．第10题. 如图，在ABC △和DEF △中，已知AB DE =，BC EF =，根据（SAS ）判定ABC DEF △≌△，还需的条件是（ ）Ａ．A D ∠=∠Ｂ．B E ∠=∠ Ｃ．C F ∠=∠Ｄ．以上三个均可以第11题. 若按给定的三个条件画一个三角形，图形惟一，则所给条件不可能是（ ） Ａ．两边一夹角 Ｂ．两角一夹边 Ｃ．三边 Ｄ．三角第12题. 如图，已知AB BD ⊥，垂足为B ，ED BD ⊥，垂足为D ，AB CD =，BC DE =，则ACE ∠＝___________．第13题. 如图，已知AB AC =，AD AE =，BAC DAE ∠=∠． 求证：BD CE =．Ａ．如果两个三角形面积不相等，那么这两个三角形不可能全等 Ｂ．如果两个三角形不全等，那么这两个三角形面积一定不相等Ｃ．如果MNP EFG △≌△，MNP E F G ''''''△≌△，那么MNP △与EFG △的面积的和等于M N P '''△与E F G '''△面积的和Ｄ．如果MNP EFG △≌△，MNP E F G ''''''△≌△，那么MNP M N P EFG E F G ''''''△+△≌△+△第15题. 如图，已知AF BE =，A B ∠=∠，AC BD =． 求证：F E ∠=∠．第16题. 如图，点P 是AOB ∠的平分线上的一点，作PD OA ⊥，垂足为D ，PE OB ⊥垂足为E ，DE 交OC 于点F ．（1）你能找到几对全等三角形？请说明理由； （2）你能确定图中共有几个直角吗？请说明理由．第17题. 如图，已知AD BC =，AB CD =，O 是BD 中点，过O 作直线交BA 的延长线于E ，交DC 的延长线于F ． 求证：OE OF =．第18题. 如图，已知AB CD =，AE DF =，CE BF =． 求证：AF DE =．第19题. 对于下列各组条件，不能判定ABC A B C '''△≌△的一组是（ ）Ａ．A A '∠=∠，B B '∠=∠，AB A B ''= Ｂ．A A '∠=∠，AB A B ''=，AC A C ''= Ｃ．A A '∠=∠，AB A B ''=，BC B C ''= Ｄ．AB A B ''=，AC A C ''=，BC B C ''=第20题. 如图，把两根钢条AA '，BB '的中点O 连在一起，可以做成一个测量工件内槽宽的工具（工人把这种工具叫卡钳）只要量出A B ''的长度，就可以知道工件的内径AB 是否符合标准，你能说出工人这样测量的道理吗？ 第21题. 如图，已知在ABC △和A B C '''△中，AM 与A M ''分别是BC B C ''，上的中线，AB A B ''=，AC A C ''=，AM A M ''=． 求证：ABC A B C '''△≌△．第22题. 如图，已知在ABC △中，AB AC =，12∠=∠． 求证：AD BC ⊥，BD DC =．第23题. 如图，平面内有一个ABC △，O 为平面内的一点，延长AO 到A '，使OA AO '=，延长BO 到B '，使OB BO '=，延长CO 到C '，使OC CO '=，得到A B C '''△，A B C '''△与ABC △是否全等？这两个三角形的对应边是否平行？为什么？第24题. 如图，在ABC △中，90C ∠=，D E ，分别为AC AB ，上的点，且AD BD =，21 3 4AE BC =，DE DC =． 求证：DE AB ⊥．第25题. 如图，AB AC =，要使△ABE ≌△ACD，应添加的条件是 ，（添加一个条件即可）第26题. 如图，四边形ABCD 中，AC 垂直平分BD ，垂足为点O ． （1）图中有多少对全等三角形？请把它们都写出来；（2）任选（1）中的一对全等三角形加以证明．第27题. 在△ABC 和△DEF 中，已知C D ∠=∠，B E ∠=∠，要判定这两个三角形全等，还需要条件（ ）A ．AB ED = B ．AB FD =C ．AC FD = D ．A F ∠=∠第28题. 小明用四根竹棒扎成如图所示的风筝框架，已知AB CD =，AD CB =，你认为小明的风筝两脚大小相同吗（即B ∠，D ∠相等吗）？请说明理由．A DB OECABDCOAB DO第29题. 小民用五根木条钉成了如图所示的两个三角形，且AB AC =，BD CD =，若ABD △为锐角三角形，则ACD △中的最大角α的取范围是（ ） Ａ．3060<α≤ Ｂ．4560<α≤Ｃ．4590<α≤Ｄ．6090<α≤第30题. 已知：ABC △的三边分别为a b c ，，，A B C '''△的三边分别为a b c '''，，，且有222222222a a b b c c ab bc ca ''''''+++++=++，则ABC △与A B C '''△（ ） Ａ．一定全等 Ｂ．不一定全等 Ｃ．一定不全等 Ｄ．无法确定第31题. 如图，已知12∠=∠，34∠=∠． 求证：BE CD =．第32题. 你见过形如图所示的风筝吗？开始制作时，AB CD =，AC DB =，后来为了加固，又过点O 加了一根竹棒EF ，分别交AB CD ，于点E F ，，且AOE DOF ∠=∠，你认为OE OF ，相等吗？请说明理由．第33题. 如图，AD BC ，相交于点O ，OA OD =，OB OC =． 求证：AOB DOC △≌△．1 23 4第34题. 如图，已知12∠=∠，ABC DCB ∠=∠，AC DB =． 求证：ABC DCB △≌△．第35题. 在ABC △和A B C ''△中，①AB A B ''=；②BC B C ''=；③AC A C ''=；④A A '∠=∠；⑤B B '∠=∠则下列条件中不能保证ABC A B C '''△≌△的是（ ） Ａ．①②③ Ｂ．①②⑤ Ｃ．②④⑤ Ｄ．①③⑤第36题. 在ABC △和A B C 111△中，已知1A A ∠=∠，11AB A B =，在下列说法中，错误的是（ ）Ａ．如果增加条件11AC A C =，那么111ABC A B C △≌△（SAS ） Ｂ．如果增加条件11BC B C =，那么111ABC A B C △≌△（SAS ） Ｃ．如果增加条件1B B ∠=∠，那么111ABC A B C △≌△（ASA ） Ｄ．如果增加条件1C C ∠=∠，那么111ABC A B C △≌△（AAS ）第37题. 如图，AB AC BE =，与CF 交于点O ，EC FB 与相等吗？为什么？第38题. 如图，AB DC AB DC AC BD =∥，，与相交于点O，你能找出两对全等的三角21形吗？你能说明其中的道理吗？第39题. 已知：如图，D 是△ABC 的边AB 上一点，AB FC ∥，DF AC E 交于点，DE FE =．AE CE =求证:．第40题. 如图，给出五个等量关系：①AD BC =、②AC BD =、③CE DE =、④D C ∠=∠、⑤DAB CBA ∠=∠． 已知：求证：证明：第41题. 如图，A B ，两点分别位于池塘两端，小明和同伴用下面的方法测量AB 间的距离：先在地上取一个可以直接到达A 点和B 点的点C ，连接AC 并延长到D ，使CD AC =，连接BC 并延长到E ，使CE BC =，连接DE ，那么量出DE 的长，就是A B ，的距离，小明和同伴的测量方法对不对？为什么？ADB C F E A B C E D第42题. 如图，要测量河两岸相对的两点A，B的距离，可以在AB的垂线BF上取两点C D，，使CD BC=，再定出BF的垂线DE，使A C E，，在一条直线上，这时测得的DE的长就是AB的长，为什么？第43题. 如图A B，两个建筑分别位于河的两岸，要测得它们之间的距离，可以从B出发沿河岸画一条射线BF，在BF上截取BC CD=，过D作DE AB∥，使E C A，，在同一条直线上，则DE的长就是A B，之间的距离．请你说明道理．你还能想出其他方法吗？第44题. 如图，已知90B D∠=∠=，AB AD=．求证：BC DC=．第45题. 如图，已知AD AF，分别是两个钝角ABC△和ABE△的高，如果AD AF=，AC AE=．求证：BC BE=．第11页共12页第46题. 使两个直角三角形全等的条件是（）Ａ．一个锐角对应相等Ｂ．两个锐角对应相等Ｃ．一条边对应相等Ｄ．两条直角边对应相等第47题. 如图，有一正方形窗架，盖房时为了稳定，在上面钉了两个等长的木条GF与GE E F，，分别是AD BC，的中点，G是AB的中点吗？第48题. 如图，已知A F E B，，，四点共线，AC CE⊥，BD DF⊥，AE BF=，AC BD=．求证：ACF BDE△≌△．第49题. 判定两个直角三角形全等的方法有Ａ．两条直角边对应相等Ｂ．斜边和一锐角对应相等Ｃ．斜边和一条直角边对应相等D．两个面积相等其中不正确的为（）第50题. 将一张矩形纸片沿对角线剪开，得到两张三角形纸片，再将这两张三角形纸片摆放成如下右图的形式，使点B，F，C，D在同一条直线上．（1）求证：AB ED⊥；（2）若PB BC=，请找出图中与此条件有关的一对．．全等三角形，并给予证明．AE PNA CBFE第12页共12页。

轧东卡州北占业市传业学校沪八年级上1三角形全等的判定第1题. 如图，ABC △中，AB AC =，EB EC =，那么由“SSS 〞可以判定〔〕Ａ．ABD ACD △≌△ Ｂ．ABE ACE △≌△ Ｃ．BDE CDE △≌△Ｄ．以上答案都不对第2题. 如图，ABC △中，AB AC=，AE CF =，BE AF =，那么E ∠=∠________，CAF ∠=∠__________．第3题. 如图，ADBC =，DC AB =，AE CF =，找出图中的一对全等三角形，并说明你的理由．第4题. 如图，ABC △是等边三角形，假设在它边上的一点与这边所对角的顶点的连线恰好将ABC△分成两个全等三角形，那么这样的点共有〔 〕 Ａ．1个Ｂ．3个Ｃ．6个Ｄ．9个第5题. 如图，A D ∠=∠，AB CD =．求证：ABO DCO △≌△．第6题. 如图，点D E ，分别在AB AC ，上，且AD AE =，BDC CEB ∠=∠．求证：BD CE =．第7题.AE 交BC ，垂足为D ，123∠=∠=∠，AB AD =．求证：〔1〕ADC ABE ∠=∠；〔2〕DCBE =．第8题. 如图，ABC △为等边三角形，QR AB ⊥，垂足为R ，PQ AC ⊥，垂足为Q ，RP BC ⊥，垂足为P ，且AR BP CQ ==求证：RPQ △为等边三角形． 第9题. 如图，点A C ，在EF 上，AD BC =，AD BC ∥，DE BF ∥．AEB D CE D C123 4AR BPCQ求证：DE BF =．第10题. 如图，在ABC△和DEF△中，AB DE=，BC EF=，根据〔SAS 〕判定ABC DEF △≌△，还需的条件是〔〕Ａ．A D ∠=∠ Ｂ．B E ∠=∠ Ｃ．CF ∠=∠Ｄ．以上三个均可以第11题. 假设按给定的三个条件画一个三角形，图形惟一，那么所给条件不可能是〔 〕 Ａ．两边一夹角Ｂ．两角一夹边Ｃ．三边Ｄ．三角第12题. 如图，AB BD ⊥，垂足为B ，ED BD ⊥，垂足为D ，AB CD =，BC DE =，那么ACE ∠＝___________． 第13题. 如图，AB AC =，AD AE =，BAC∠=∠求证：BD CE =．第14题.Ａ．如果两个三角形面积不相等，那么这两个三角形不可能全等Ｂ．如果两个三角形不全等，那么这两个三角形面积一定不相等Ｃ．如果MNP EFG △≌△，M N P E F G ''''''△≌△，那么MNP △与EFG △的面积的和等于M N P '''△与E F G '''△面积的和Ｄ．如果MNP EFG△≌△，M N P E F G ''''''△≌△，那么MNP M N P EFG E F G ''''''△+△≌△+△第15题. 如图，AF BE =，A B ∠=∠，AC BD =．求证：FE ∠=∠．C BA E DBC第16题. 如图，点P 是AOB ∠的平分线上的一点，作PD OA ⊥，垂足为D ，PE OB ⊥垂足为E ，DE 交OC 于点F ．〔1〕你能找到几对全等三角形？请说明理由； 〔2〕你能确定图中共有几个直角吗？请说明理由． 第17题. 如图，AD BC =，AB CD =，O 是BD 中点，过O 作直线交BA 的延长线于E ，交DC的延长线于F ． 求证：OEOF =．第18题. 如图，AB CD =，AE DF =，CE BF =．求证：AF DE =．第19题. 对于以下各组条件，不能判定ABC A'△≌△Ａ．A A '∠=∠，B B '∠=∠，AB A B ''=Ｂ．A A '∠=∠，AB A B ''=，AC A C ''= Ｃ．A A '∠=∠，AB A B ''=，BC B C ''=Ｄ．AB A B ''=，AC A C ''=，BC B C ''=第20题. 如图，把两根钢条AA '，BB '的中点O 连在一起，可以做成一个测量工件内槽宽的工具〔工人把这种工具叫卡钳〕只要量出A B ''的长度，就可以知道工件的内径AB 是否符合HY ，你能说出工人这样测量的道理吗？第21题. 如图，在ABC △和A B C '''△中，AM与A M ''分别是BCBC ''，上的中线，AB A B ''=，AC A C ''=，AM A M ''=．求证：ABC A B C '''△≌△． 第22题. 如图，在ABC △中，AB AC =，12∠=∠．求证：AD BC ⊥，BD DC =．B第23题. 如图，平面内有一个ABC △，O 为平面内的一点，延长AO 到A '，使OA AO '=，延长BO 到B '，使OB BO '=，延长CO 到C'，使OC CO '=，得到A B C '''△，A B C'''△与ABC △是否全等？这两个三角形的对应边是否平行？为什么？ 第24题.如图，在ABC △中，90C∠=，D E ，分别为AC AB ，上的点，且AD BD =，AE BC =，DE DC =．求证：DE AB ⊥． 第25题. 如图，ABAC =，要使△ABE ≌△ACD第26题. 如图，四边形ABCD 中，AC 垂直平分BD 〔1〕图中有多少对全等三角形？请把它们都写出来；〔2〕任选〔1〕中的一对全等三角形加以证明．第27题. 在△ABC 和△DEF 中，C D ∠=∠，B E ∠=∠件〔 〕A ．AB ED = B ．AB FD =C ．AC FD = D ．A F ∠=∠第28题. 小明用四根竹棒扎成如下列图的风筝框架，AB CD =，AD CB =大小相同吗〔即B ∠，D ∠相等吗〕？请说明理由． 第29题. 小民用五根木条钉成了如下列图的两个三角形，且AB AC =，BD CD =，假设ABD △为锐角三角形，那么ACD △中的最大角α的取范围是〔 〕 Ａ．3060<α≤ Ｂ．4560<α≤ Ｃ．4590<α≤Ｄ．6090<α≤第30题. ：ABC △的三边分别为a b c ，，，A B C '''△的三边分别为a b c '''，，，且有AB C D2 13 4C BDCBDC222222222a a b b c c ab bc ca ''''''+++++=++，那么ABC △与A B C '''△〔〕Ａ．一定全等Ｂ．不一定全等Ｃ．一定不全等Ｄ．无法确定第31题. 如图，12∠=∠，34∠=∠． 求证：BECD =．第32题. 你见过形如下列图的风筝吗？开始制作时，AB=O 加了一根竹棒EF ，分别交AB CD ，于点EF ，，且AOE DOF∠=∠，你认为OE OF ，相等吗？请说明理由．第33题. 如图，AD BC ，相交于点O ，OA OD =，OB =求证：AOB DOC △≌△． 第34题. 如图，12∠=∠，ABC DCB ∠=∠，AC DB =．求证：ABC DCB △≌△．第35题. 在ABC △和A B C ''△中，①AB A B ''=；②BC B C ''=；③AC A C ''=；④A A '∠=∠；⑤B B '∠=∠那么以下条件中不能保证ABC A B C '''△≌△的是〔 〕Ａ．①②③Ｂ．①②⑤Ｃ．②④⑤Ｄ．①③⑤第36题. 在ABC △和A B C 111△中，1A A ∠=∠，11AB A B =，在以下说法中，错误的选项是〔 〕Ａ．如果增加条件11AC AC =，那么111ABC A B C △≌△〔SAS 〕Ｂ．如果增加条件11BC B C =，那么111ABC A B C △≌△〔SAS 〕 Ｃ．如果增加条件1B B ∠=∠，那么111ABC A B C △≌△〔ASA 〕 Ｄ．如果增加条件1C C ∠=∠，那么111ABC A B C △≌△〔AAS 〕第37题. 如图，ABAC BE =，与CF 交于点O ，EC FB 与相等吗？为什么？第38题. 如图，AB DC AB DC AC BD =∥，，与相交于点O ，你能找出两对全等的三角形吗？2 A DCB1 ABCFEO你能说明其中的道理吗？ 第39题. ：如图，D 是△ABC 的边AB 上一点，AB FC ∥，DF AC E 交于点，DE FE =．AE CE =求证:．第40题. 如图，给出五个等量关系：①AD BC =、②AC=C ∠、⑤DAB CBA ∠=∠．： 求证： 证明：第41题. 如图，A B ，两点分别位于池塘两端，小明和同伴用下面的方法测量AB 间的距离：先在地上取一个可以直接到达A 点和B 点的点C ，连接AC 并延长到D ，使CD AC =，连接BC 并延长到E ，使CEBC =，连接DE ，那么量出DE 的长，就是A B ，的距离，小明和同伴的测量方法对不对？为什么？第42题. 如图，要测量河两岸相对的两点A ，B 的距离，可以在AB 的垂线BF 上取两点CD ，，使CD BC =，再定出BF 的垂线DE ，使A C E ，，在一条直线上，这时测得的DE 的长就是AB 的长，为什么？第43题. 如图A B ，两个建筑分别位于河的两岸，要测得它们之间的距离，可以从B 出发沿河岸画一条射线BF ，在BF 上截取BC CD =，过D 作DE AB ∥，使E C A ，，在同一条直线上，那么DE的长就是A B ，之间的距离．请你说明道理．你还能想出其他方法吗？第44题. 如图，90B D ∠=∠=，AB AD =．求证：BCDC =．第45题. 如图，AD AF ，分别是两个钝角ABC △和ABE △的高，如果AD AF =，AC AE =．求证：BCBE =．BA B A CDB A DCBE第46题. 使两个直角三角形全等的条件是〔 〕 Ａ．一个锐角对应相等 Ｂ．两个锐角对应相等 Ｃ．一条边对应相等Ｄ．两条直角边对应相等第47题. 如图，有一正方形窗架，盖房时为了稳定，在上面钉了两个等长的木条GF 与GE E F ，，分别是AD BC ，的中点，G 是AB 的中点吗？第48题. 如图，A F E B ，，，四点共线，AC CE ⊥，BD DF ⊥，AE BF =，AC BD =．求证：ACFBDE △≌△．第49题. 判定两个直角三角形全等的方法有 Ａ．两条直角边对应相等 Ｂ．斜边和一锐角对应相等 Ｃ．斜边和一条直角边对应相等 D ．两个面积相等 其中不正确的为〔 〕第50题. 将一张矩形纸片沿对角线剪开，得到两张三角形纸片，再将这两张三角形纸片摆放成如下右图的形式，使点B ，F ，C ，D 在同一条直线上． 〔1〕求证：AB ED ⊥；〔2〕假设PBBC =，请找出图中与此条件有关的一对．．全等三角形，并给予证明．BF CDBDF参考答案1. 答案：Ｂ2. 答案：F ，ABE3. 答案：答案不惟一．如ADC CBA △≌△．理由：根据“SSS 〞即AD CB =，DC BA =，AC CA =．4. 答案：Ｂ5. 答案：在ABO △和DCO △中6. 答案：180ADC BDC ∠+∠=，180BEC AEB ∠+∠=，又BDC CEB ADC AEB ∠=∠∴∠=∠AB AD AC AE ∴-=-，即BD CE =．7. 答案：〔1〕42ADC ∠=∠+∠，43ABE ∠=∠+∠又23∠=∠ADC ABE ∴∠=∠〔2〕在ADC △和ABE△中ADC ABE∠=∠〔已证〕，AD AB=〔〕，12∠=∠〔〕ASA ADC ABE ∴△≌△()DC BE ∴=．8. 答案：ABC △是等边三角形．60A B C ∴∠=∠=∠=，又QR AB ⊥，PQ AC ⊥，RP BC ⊥90ARQ BPR CQP ∴∠=∠=∠= 又AR BP CQ ==，根据ASA 证AQR BRP CPQ △≌△≌△得PQPR QP ==RPQ ∴△为等边三角形．9. 答案：由AD BC∥得CADACB ∠=∠，根据等角的补角相等得EAD FCB ∠=∠，又由DE BF ∥得E F ∠=∠，又AD BC =，根据AAS 证ADE CBF △≌△得DE BF =．10. 答案：B 11. 答案：Ｄ 12. 答案：9013. 答案：先证BAD CAE ∠=∠，再根据SAS 证ABD ACE △≌△，得BD CE =．14. 答案：Ａ 15. 答案：先证：ADBC =，再根据SAS 证ADF BCE △≌△，得F E ∠=∠．16. 答案：〔1〕有三对全等三角形．由“AAS 〞可知ODP OEP △≌△，又由“SAS 〞可知：ODF OEF △≌△，PDF PEF △≌△〔2〕共有八个直角，由〔1〕中的ODF OEF△≌△可知：OFD OFE∠=∠，而180OFD OFE ∠+∠=，因此OF ED ⊥．这样以F 为顶点有四个直角，另有的四个直角，共计八个直角．17. 答案：在ABD △和CDB △中，ABD CDB ∴∠=∠〔全等三角形对应角相等〕O 是BD 中点，BO DO ∴=()OE OF ∴=全等三角形对应边相等．18. 答案：BF CE =BF EF CE EF ∴+=+BE CF ∴=又AB CD =，AE DF=，根据“SSS 〞证ABE DCF △≌△．BC∴∠=∠，又AB CD =，BF CE =，根据SAS 证ABF DCE △≌△AF DE ∴=．19. 答案：C20. 答案：此工具是根据三角形全等制作而成的．由O 是AA '，BB '的中点，可得AO A O '=，BO B O '=，又由于AOB ∠与A OB ''∠是对顶角，可知AOB A OB ''∠=∠，于是根据“SAS 〞有AOB A OB ''△≌△，从而A B AB ''=，只要量出A B ''的长度，就可以知道工作的内径AB 是否符合HY ．21. 答案：延长AM 到N 使2AN AM=，延长A M ''至N '使A N ''2A M ''=，连接BN ，B N ''先证ACM NBM △≌△，得BN AC =，N CAN∠=∠同理可证B N AC ''''=，N C A N ''''∠=∠．利用SSS证ABN A B N '''△≌△．BAN B A N '''∴∠=∠，N N '∠=∠．BAC B A C '''∴∠=∠，根据SAS 证ABC A B C '''△≌△．22. 答案：在ABD △和ACD △中，SAS ABD ACD ∴△≌△()． BD CD ∴=，34∠=∠．又34180∠+∠=，即23180∠=，390∴∠=，AD BC ∴⊥．23. 答案：A B C ABC '''△≌△，AB A B ''∥，AC A C ''∥，BC B C ''∥，理由略．24. 答案：在ADE △和BDC △中， 25. 答案：答案不惟一，如BC ∠=∠等．26. 答案：解：〔1〕图中有三对全等三角形： △COB ≌△COD ，△AOB ≌△AOD ，△ABC ≌△ADC ．〔2〕证明△ABC ≌△ADC ．证明：AC ∵垂直平分BD ，AB AD =∴，CB CD =．又AC AC =∵，∴△ABC ≌△ADC ．27. 答案：C28. 答案：相等．可以连接AC ，由SSS 可知ABC △CDA ≌△B D ∴∠=∠．29. 答案：Ｄ 30. 答案：Ａ31. 答案：34∠=∠，AD AE ∴=，又1324∠+∠=∠+∠ 即ADCAEB ∠=∠，又A A ∠=∠根据ASA 证ABE ACD △≌△，BE CD ∴=．32. 答案：相等．可以连接BC ，首先由“SSS 〞可知：ABC DCB △≌△，因此A D ∠=∠，同理可得B C ∠=∠，又由“ASA 〞可知ABO DCO △≌△，因此AO DO =．最后可由“ASA 〞得AOE DOF △≌△，所以OE OF =．33. 答案：在AOB △和DOC △中(SAS)AOB DOC ∴△≌△．34. 答案：：ABC DCB ∠=∠ ，12∠=∠，DBC ACB ∴∠=∠，即ACB DBC ∠=∠，又ABC DCB ∠=∠，AC DB =，BC CB =，ABC DCB ∴△≌△．35. 答案：D36. 答案：B37. 答案：不一定．EC 与FB 可能相等,也可能不相等．直观地解释：E F AC AB ，在，上的位置不定，因此BF EC 与的关系也不定．逻辑地解释：BF CE 与所在的两个三角形，无法确定其是否全等，因此BF CE 与的关系不一定．38. 答案：事实上有四对全等的三角形．理由分别是：AOB COD △≌△的理由：“角边角〞，即CAB ACD AB CD ABD CDB ∠=∠⎧⎪=⎨⎪∠=∠⎩AOD COB △≌△的理由．“边角边〞，即()()AO CO AOB COD AOD COB DO BO AOB COD =⎧⎪∠=∠⎨⎪=⎩由△≌△所得由△≌△所得 ABC CDA △≌△的理由：“边角边〞．即AB CD BAC DCA AC CA =⎧⎪∠=∠⎨⎪=⎩ADB CBD △≌△的理由：“边角边〞．即AB CD ABD CDB BD DB =⎧⎪∠=∠⎨⎪=⎩39. 答案：证明：AB FC ∵∥，ADE CFE ∠=∠∴．又AEDCEF ∠=∠∵，DE FE =， ∴ △AED ≌△CEF ．∴AE CE =．40. 答案：情况一：：AD BC AC BD ==， 求证：CEDE =〔或D C ∠=∠或DAB CBA ∠=∠〕 证明：在△ABD 和△BAC 中∴△ABD ≌△BAC即CEED =． 情况二：：D C DAB CBA ∠=∠∠=∠，求证：AD BC =〔或AC BD =或CE DE =〕 证明：在△ABD 和△BAC 中D C ∠=∠，DAB CBA ∠=∠∴△ABD ≌△BAC ∴AD BC =．41. 答案：小明和同伴的测量方法是正确的．由于在ABC △和DEC △中，AC DC =〔测得〕，ACB DCE ∠=∠〔对顶角相等〕，BC EC =〔测得〕，于是()ABC DEC SAS △≌△，因而可得AB DE =，所以量出DE 的长，就是A B ，两点间的距离．42. 答案：由AB BF ⊥，DE BF ⊥，可得90ABC EDC ∠=∠=，又由于直线BF 与AE 交于点C ，可知ACB ECD ∠=∠〔对顶角相等〕，再加上条件CD BC =，根据“ASA 〞有ABC EDC △≌△，从而AB ED =，即测得DE 的长就是A B ，两点间的距离．43. 答案：〔1〕B EDC BC DC BCA DCE ∠=∠⎧⎪=⎨⎪∠=∠⎩ABC EDC →→△≌△AB DE =．〔2〕新方法：如图：从B 出发沿河岸作射线BF ，且使BF AB ⊥，在BF 上截取BC CD =，过D 作DE BF ⊥，使E C A ，，在一条直线上，那么DE 的长就是A B ，之间的距离.道理同上．44. 答案：因为AB AD =，AC AC =，根据“HL 〞证Rt Rt ACD ACB △≌△ ，CD BC ∴=．45. 答案：根据“HL 〞证Rt Rt ADC AFE △≌△，CD EF ∴=，再根据“HL 〞证Rt Rt ABD ABF △≌△，BD BF ∴=，BD CD BF EF ∴-=-，即BC BE =．46. 答案：Ｄ47. 答案：G 是AB 的中点．48. 答案：证明：AC CE ⊥，BD DF ⊥〔〕90ACE BDF ∴∠=∠=〔垂直的定义〕 在Rt ACE △和Rt BDF △中，A B ∴∠=∠〔全等三角形的对应角相等〕AE EF BF EF∴-=-〔等式性质〕 即AF BE =SAS ACF BDE ∴△≌△()．49. 答案：D50. 答案：〔1〕证明：由题意得90A B A D ∠+∠=∠=∠，，90∴．∠+∠=D B∴⊥．AB DE=，那么有Rt△ABC≌Rt△DBP．〔2〕假设PB BC∵，，，B B A D BP BC∠=∠∠=∠=∴ Rt△ABC≌Rt△DBP．说明：图中与此条件有关的全等三角形还有如下几对：Rt△APN≌ Rt△DCN、Rt△DEF≌ Rt△DBP、Rt△EPM≌ Rt△BFM．从中任选一对给出证明，只要正确的都对．BF C D。

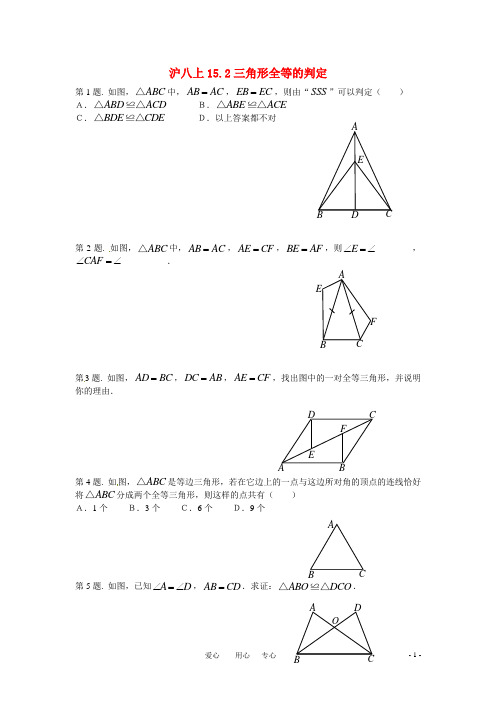
沪八上15.2三角形全等的判定第1题. 如图，ABC △中，AB AC =，EB EC =，则由“SSS ”可以判定（ ） Ａ．ABD ACD △≌△ Ｂ．ABE ACE △≌△ Ｃ．BDE CDE △≌△ Ｄ．以上答案都不对第2题. 如图，ABC △中，AB AC =，AE CF =，BE AF =，则E ∠=∠________，CAF ∠=∠__________．第3题. 如图，AD BC =，DC AB =，AE CF =，找出图中的一对全等三角形，并说明你的理由．第4题. 如图，ABC △是等边三角形，若在它边上的一点与这边所对角的顶点的连线恰好将ABC △分成两个全等三角形，则这样的点共有（ ） Ａ．1个 Ｂ．3个 Ｃ．6个 Ｄ．9个 第5题. 如图，已知A D ∠=∠，AB CD =．求证：ABO DCO △≌△．AE B D CA C FD EB第6题. 如图，点D E ，分别在AB AC ，上，且AD AE =，BDC CEB ∠=∠． 求证：BD CE =．第7题. 已知AE 交BC ，垂足为D ，123∠=∠=∠，AB AD =． 求证：（1）ADC ABE ∠=∠； （2）DC BE =．第8题. 如图，已知ABC △为等边三角形，QR AB ⊥，垂足为R ，PQ AC ⊥，垂足为Q ，RP BC ⊥，垂足为P ，且AR BP CQ ==求证：RPQ △为等边三角形．第9题. 如图，已知点A C ，在EF 上，AD BC =，AD BC ∥，DE BF ∥．E D C 1 23 4A RBPCQ求证：DE BF =．第10题. 如图，在ABC △和DEF △中，已知AB DE =，BC EF =，根据（SAS ）判定ABC DEF △≌△，还需的条件是（ ）Ａ．A D ∠=∠ Ｂ．B E ∠=∠ Ｃ．C F ∠=∠Ｄ．以上三个均可以第11题. 若按给定的三个条件画一个三角形，图形惟一，则所给条件不可能是（ ） Ａ．两边一夹角 Ｂ．两角一夹边 Ｃ．三边 Ｄ．三角第12题. 如图，已知AB BD ⊥，垂足为B ，ED BD ⊥，垂足为D ，AB CD =，BC DE =，则ACE ∠＝___________．第13题. 如图，已知AB AC =，AD AE =，BAC DAE ∠=∠． 求证：BD CE =．第14题. 下列各命题中，真命题是（ ）Ａ．如果两个三角形面积不相等，那么这两个三角形不可能全等 Ｂ．如果两个三角形不全等，那么这两个三角形面积一定不相等Ｃ．如果MNP EFG △≌△，M N P E F G ''''''△≌△，那么MNP △与EFG △的面积的和等于M N P '''△与E F G '''△面积的和 Ｄ．如果M N P △≌△，M N P E F G ''''''△≌△，那么FCDEAA E DB CMNP M N P EFG E F G ''''''△+△≌△+△第15题. 如图，已知AF BE =，A B ∠=∠，AC BD =． 求证：F E ∠=∠．第16题. 如图，点P 是AOB ∠的平分线上的一点，作PD OA ⊥，垂足为D ，PE OB ⊥垂足为E ，DE 交OC 于点F ．（1）你能找到几对全等三角形？请说明理由； （2）你能确定图中共有几个直角吗？请说明理由．第17题. 如图，已知AD BC =，AB CD =，O 是BD 中点，过O 作直线交BA 的延长线于E ，交DC 的延长线于F ． 求证：OE OF =．第18题. 如图，已知AB CD =，AE DF =，CE BF =． 求证：AF DE =．第19题. 对于下列各组条件，不能判定ABC A B C '''△≌△的一组是（ ） Ａ．A A '∠=∠，B B '∠=∠，AB A B ''=C D A BE FO E B A C DFPBBＢ．A A '∠=∠，AB A B ''=，AC A C ''= Ｃ．A A '∠=∠，AB A B ''=，BC B C ''= Ｄ．AB A B ''=，AC A C ''=，BC B C ''=第20题. 如图，把两根钢条AA '，BB '的中点O 连在一起，可以做成一个测量工件内槽宽的工具（工人把这种工具叫卡钳）只要量出A B ''的长度，就可以知道工件的内径AB 是否符合标准，你能说出工人这样测量的道理吗？ 第21题. 如图，已知在ABC △和A B C '''△中，AM 与A M ''分别是BC B C ''，上的中线，AB A B ''=，AC A C ''=，AM A M ''=． 求证：ABC A B C '''△≌△．第22题. 如图，已知在ABC △中，AB AC =，12∠=∠． 求证：AD BC ⊥，BD DC =．第23题. 如图，平面内有一个ABC △，O 为平面内的一点，延长AO 到A '，使OA A O '=，延长BO 到B '，使O B B O '=，延长CO 到C '，使O C C O '=，得到A B C '''△，A B C '''△与ABC △是否全等？这两个三角形的对应边是否平行？为什么？第24题. 如图，在ABC △中，90C ∠=，D E ，分别为AC AB ，上的点，且AD BD =，' A B C 21 3 4 O AB C C 'A 'B 'AE BC =，DE DC =． 求证：DE AB ⊥．第25题. 如图，AB AC =，要使△ABE ≌△ACD ，应添加的条件是 ，（添加一个条件即可）第26题. 如图，四边形ABCD 中，AC 垂直平分BD ，垂足为点O ． （1）图中有多少对全等三角形？请把它们都写出来；（2）任选（1）中的一对全等三角形加以证明．第27题. 在△ABC 和△DEF 中，已知C D ∠=∠，B E ∠=∠等，还需要条件（ ）A ．AB ED =B ．AB FD =C ．AC FD = D ．A F ∠=∠第28题. 小明用四根竹棒扎成如图所示的风筝框架，已知AB CD =，AD CB =，你认为小明的风筝两脚大小相同吗（即B ∠，D ∠相等吗）？请说明理由．B CBDB D第29题. 小民用五根木条钉成了如图所示的两个三角形，且AB AC =，BD CD =，若ABD △为锐角三角形，则ACD △中的最大角α的取范围是（ ） Ａ．3060<α≤ Ｂ．4560<α≤Ｃ．4590<α≤Ｄ．6090<α≤第30题. 已知：ABC △的三边分别为a b c ，，，A B C '''△的三边分别为a b c '''，，，且有222222222a a b b c c ab bc ca ''''''+++++=++，则ABC △与A B C '''△（ ） Ａ．一定全等Ｂ．不一定全等Ｃ．一定不全等Ｄ．无法确定第31题. 如图，已知12∠=∠，34∠=∠． 求证：BE CD =．第32题. 你见过形如图所示的风筝吗？开始制作时，AB CD =，AC DB =，后来为了加固，又过点O 加了一根竹棒EF ，分别交AB CD ，于点E F ，，且AOE DOF ∠=∠，你认为OE OF ，相等吗？请说明理由．第33题. 如图，AD BC ，相交于点O ，OA OD =，OB OC =． 求证：AOB DOC △≌△．A CD第34题. 如图，已知12∠=∠，ABC DCB ∠=∠，AC DB =． 求证：ABC DCB △≌△．第35题. 在ABC △和A B C ''△中，①AB A B ''=；②BC B C ''=；③AC A C ''=；④A A '∠=∠；⑤B B '∠=∠则下列条件中不能保证ABC A B C '''△≌△的是（ ） Ａ．①②③ Ｂ．①②⑤ Ｃ．②④⑤ Ｄ．①③⑤第36题. 在ABC △和A B C 111△中，已知1A A ∠=∠，11AB A B =，在下列说法中，错误的是（ ）Ａ．如果增加条件11AC AC =，那么111ABC A B C △≌△（SAS ） Ｂ．如果增加条件11BC B C =，那么111ABC A B C △≌△（SAS ） Ｃ．如果增加条件1B B ∠=∠，那么111ABC A B C △≌△（ASA ） Ｄ．如果增加条件1C C ∠=∠，那么111ABC A B C △≌△（AAS ）第37题. 如图，AB AC BE =，与CF 交于点O ，EC FB 与相等吗？为什么？第38题. 如图，AB DC AB DC AC BD =∥，，与相交于点O ，你能找出两对全等的三角形吗？你能说明其中的道理吗？2 A DCB 1 A BC FEO第39题. 已知：如图，D 是△ABC 的边AB 上一点，AB FC ∥，DF AC E 交于点，DE FE =．AE CE =求证:．第40题. 如图，给出五个等量关系：①AD BC =、②AC BD =、③CE DE =、④D C ∠=∠、⑤DAB CBA ∠=∠． 请你以其中两个为条件，另三个中的一个为结论，推出一个正确的命题（只需写出一种情况），并加以证明． 已知：求证：证明：第41题. 如图，A B ，两点分别位于池塘两端，小明和同伴用下面的方法测量AB 间的距离：先在地上取一个可以直接到达A 点和B 点的点C ，连接AC 并延长到D ，使CD AC =，连接BC 并延长到E ，使CE BC =，连接DE ，那么量出DE 的长，就是A B ，的距离，BA B小明和同伴的测量方法对不对？为什么？第42题. 如图，要测量河两岸相对的两点A ，B 的距离，可以在AB 的垂线BF 上取两点C D ，，使C D B C =，再定出BF 的垂线DE ，使A C E ，，在一条直线上，这时测得的DE的长就是AB 的长，为什么？第43题. 如图A B ，两个建筑分别位于河的两岸，要测得它们之间的距离，可以从B 出发沿河岸画一条射线BF ，在BF 上截取BC CD =，过D 作DE AB ∥，使E C A ，，在同一条直线上，则DE 的长就是A B ，之间的距离．请你说明道理．你还能想出其他方法吗？第44题. 如图，已知90B D ∠=∠=，AB AD =．求证：BC DC =．第45题. 如图，已知AD AF ，分别是两个钝角ABC △和ABE △的高，如果AD AF =，AC AE =．求证：BC BE =．A BCCD FE A BA C DB ADC B第46题. 使两个直角三角形全等的条件是（ ）Ａ．一个锐角对应相等 Ｂ．两个锐角对应相等Ｃ．一条边对应相等 Ｄ．两条直角边对应相等第47题. 如图，有一正方形窗架，盖房时为了稳定，在上面钉了两个等长的木条GF 与GE E F ，，分别是AD BC ，的中点，G 是AB 的中点吗？第48题. 如图，已知A F E B ，，，四点共线，AC CE ⊥，BD DF ⊥，AE BF =，AC BD =．求证：ACF BDE △≌△．第49题. 判定两个直角三角形全等的方法有Ａ．两条直角边对应相等Ｂ．斜边和一锐角对应相等Ｃ．斜边和一条直角边对应相等D ．两个面积相等其中不正确的为（ ）第50题. 将一张矩形纸片沿对角线剪开，得到两张三角形纸片，再将这两张三角形纸片摆放成如下右图的形式，使点B ，F ，C ，D 在同一条直线上．（1）求证：AB ED ⊥；（2）若PB BC =，请找出图中与此条件有关的一对．．全等三角形，并给予证明． A BF E DG A F D E BC参考答案1. 答案：Ｂ2. 答案：F ，ABE3. 答案：答案不惟一．如AD C C B A △≌△．理由：根据“SSS ”即A D C B =，DC BA =，AC CA =．4. 答案：Ｂ5. 答案：在ABO △和DCO △中 ()()()A D AOB DOC AB DC ∠=∠⎧⎪∠=∠⎨⎪=⎩已知对顶角相等已知(AAS)ABO DCO ∴△≌△6. 答案：180ADC BDC ∠+∠=，180BEC AEB ∠+∠=， 又BDC CEB ADC AEB ∠=∠∴∠=∠()()()A A ADC AEB AD AE ADC AEB ∠=∠⎧⎪=⎨⎪∠=∠⎩公共角已知已证在△和△中， (ASA)ADC AEB AB AC ∴∴=△≌△AB AD AC AE ∴-=-，即BD CE =．7. 答案：（1）42ADC ∠=∠+∠，43ABE ∠=∠+∠又23∠=∠ADC ABE ∴∠=∠（2）在A D C △和ABE △中ADC ABE ∠=∠（已证），AD AB =（已知），12∠=∠（已知）ASA ADC ABE ∴△≌△()DC BE ∴=．8. 答案：ABC △是等边三角形．60A B C ∴∠=∠=∠=，又QR AB ⊥，PQ AC ⊥，RP BC ⊥90ARQ BPR CQP ∴∠=∠=∠=又AR BP CQ ==，根据ASA 证AQR BRP CPQ △≌△≌△得PQ PR QP ==RPQ ∴△为等边三角形．9. 答案：由AD BC ∥得CAD ACB ∠=∠，根据等角的补角相等得EAD FCB ∠=∠，又由DE BF ∥得E F ∠=∠，又AD BC =，根据AAS 证ADE CBF △≌△得DE BF =．10. 答案：B11. 答案：Ｄ12. 答案：9013. 答案：先证BAD CAE ∠=∠，再根据SAS 证ABD ACE △≌△，得BD CE =．14. 答案：Ａ15. 答案：先证：AD BC =，再根据SAS 证ADF BCE △≌△，得F E ∠=∠．16. 答案：（1）有三对全等三角形．由“AAS ”可知ODP OEP △≌△，又由“SAS ”可知：ODF OEF △≌△，PDF PEF △≌△（2）共有八个直角，由（1）中的ODF OEF △≌△可知：OFD OFE ∠=∠，而180OFD OFE ∠+∠=，因此OF ED ⊥．这样以F 为顶点有四个直角，另有已知的四个直角，共计八个直角． 17. 答案：在ABD △和CDB △中，()()()AB CD AD CB BD DB =⎧⎪=⎨⎪=⎩已知已知公共边SSS ABD CDB ∴△≌△()ABD CDB ∴∠=∠（全等三角形对应角相等） O 是BD 中点，BO DO ∴=()()()ABO CDO BOE DOF BO DO BOE DOF ∠=∠⎧⎪=⎨⎪∠=∠⎩已证于是在和中已证对顶角相等△△， ASA BOE DOF ∴△≌△()()OE OF ∴=全等三角形对应边相等．18. 答案：BF CE =BF EF CE EF ∴+=+BE CF ∴=又AB CD =，AE DF =，根据“SSS ”证ABE DCF △≌△．B C ∴∠=∠，又AB CD =，BF CE =，根据SAS 证ABF DCE △≌△AF DE ∴=．19. 答案：C20. 答案：此工具是根据三角形全等制作而成的．由O 是AA '，BB '的中点，可得AO AO '=，BO B O '=，又由于AOB ∠与A OB ''∠是对顶角，可知AOB A OB ''∠=∠，于是根据“SAS ”有AOB A OB ''△≌△，从而A B AB ''=，只要量出A B ''的长度，就可以知道工作的内径AB 是否符合标准．21. 答案：延长AM 到N 使2AN AM =，延长A M ''至N '使A N ''2A M ''=，连接BN ，B N ''先证ACM NBM △≌△，得BN AC =，N CAN ∠=∠同理可证B N A C ''''=，N C A N ''''∠=∠．利用SSS 证ABN A B N '''△≌△．BAN B A N '''∴∠=∠，N N '∠=∠．BAC B A C '''∴∠=∠，根据SAS 证ABC A B C '''△≌△．22. 答案：在ABD △和ACD △中，()12()()AB AC AD AD =⎧⎪∴∠=∠⎨⎪=⎩已知已知公共边SAS ABD ACD ∴△≌△()．BD CD ∴=，34∠=∠．又34180∠+∠=，即23180∠=，390∴∠=，AD BC ∴⊥．23. 答案：A B C ABC '''△≌△，AB A B ''∥，AC A C ''∥，BC B C ''∥，理由略．24. 答案：在ADE △和BDC △中，()()()AE BC AD BD ED CD =⎧⎪=⎨⎪=⎩已知已知已知SSS ()90()90ADE BDC C AED C AED DE AB ∴∴∠=∠∠=∴∠=∴全等三角形对应角相等已知垂直定义△≌△()⊥()25. 答案：答案不惟一，如B C ∠=∠等．26. 答案：解：（1）图中有三对全等三角形：△COB ≌△COD ，△AOB ≌△AOD ，△ABC ≌△ADC ．（2）证明△ABC ≌△ADC ．证明：AC ∵垂直平分BD ，AB AD =∴，CB CD =．又AC AC =∵，∴△ABC ≌△ADC ．27. 答案：C28. 答案：相等．可以连接AC ，由SSS 可知ABC △CDA ≌△B D ∴∠=∠．29. 答案：Ｄ30. 答案：Ａ31. 答案：34∠=∠，AD AE ∴=，又1324∠+∠=∠+∠即ADC AEB ∠=∠，又A A ∠=∠根据ASA 证ABE ACD △≌△，BE CD ∴=．32. 答案：相等．可以连接BC ，首先由“SSS ”可知：ABC DCB △≌△，因此A D ∠=∠，同理可得B C ∠=∠，又由“ASA ”可知ABO DCO △≌△，因此AO DO =．最后可由“ASA ”得AOE DOF △≌△，所以OE OF =．33. 答案：在AOB △和DOC △中()()()OA OD AOB DOC OB OC =⎧⎪∠=∠⎨⎪=⎩已知对顶角相等已知(SAS)AOB DOC ∴△≌△．34. 答案：：ABC DCB ∠=∠ ，12∠=∠，DBC ACB ∴∠=∠，即ACB DBC ∠=∠，又ABC DCB ∠=∠，AC DB =，BC CB =，ABC DCB ∴△≌△． 35. 答案：D36. 答案：B37. 答案：不一定．EC 与FB 可能相等,也可能不相等．直观地解释：E F AC AB ，在，上的位置不定，因此BF EC 与的关系也不定．逻辑地解释：BF CE 与所在的两个三角形，无法确定其是否全等，因此BF CE 与的关系不一定．38. 答案：事实上有四对全等的三角形．AOB COD AOD COB ABC CDA ADB CBD △≌△；△≌△；△≌△；△≌△． 理由分别是：AOB COD △≌△的理由：“角边角”，即CAB ACDAB CD ABD CDB∠=∠⎧⎪=⎨⎪∠=∠⎩AOD COB △≌△的理由．“边角边”，即()()AO CO AOB COD AOD COBDO BO AOB COD =⎧⎪∠=∠⎨⎪=⎩由△≌△所得由△≌△所得ABC CDA △≌△的理由：“边角边”．即ABCDBAC DCA AC CA=⎧⎪∠=∠⎨⎪=⎩ADB CBD △≌△的理由：“边角边”．即AB CDABD CDB BD DB=⎧⎪∠=∠⎨⎪=⎩39. 答案：证明：AB FC ∵∥，ADE CFE ∠=∠∴．又AED CEF ∠=∠∵，DE FE =，∴ △AED ≌△CEF ．∴AE CE =．40. 答案：情况一：已知：AD BC AC BD ==，求证：CE DE =（或D C ∠=∠或DAB CBA ∠=∠）证明：在△ABD 和△BAC 中AD BC AC BD ==∵，AB BA =∴△ABD ≌△BAC∴CAB DBA ∠=∠ A E B E =∴∴AC AE BD BE -=-即CE ED =．情况二：已知：D C DAB CBA ∠=∠∠=∠，求证：AD BC =（或AC BD =或CE DE =）证明：在△ABD 和△BAC 中D C ∠=∠，DAB CBA ∠=∠A B A B=∵ ∴△ABD ≌△BAC∴AD BC =．41. 答案：小明和同伴的测量方法是正确的．由于在ABC △和DEC △中，AC DC =（测得），ACB DCE ∠=∠（对顶角相等），BC EC =（测得），于是()ABC DEC SAS △≌△，因而可得AB DE =，所以量出DE 的长，就是A B ，两点间的距离．42. 答案：由AB BF ⊥，DE BF ⊥，可得90ABC EDC ∠=∠=，又由于直线BF 与AE 交于点C ，可知ACB ECD ∠=∠（对顶角相等），再加上条件CD BC =，根据“ASA ”有ABC EDC △≌△，从而AB ED =，即测得DE 的长就是A B ，两点间的距离．43. 答案：（1）B EDC BC DCBCA DCE ∠=∠⎧⎪=⎨⎪∠=∠⎩ABC EDC →→△≌△AB DE =． （2）新方法：如图：从B 出发沿河岸作射线BF ，且使BF AB ⊥，在BF 上截取B C C D =，过D 作DE BF ⊥，使E C A ，，在一条直线上，则DE 的长就是A B ，之间的距离.道理同上．44. 答案：因为AB AD =，AC AC =，根据“HL ”证Rt Rt ACD ACB △≌△ ，CD BC ∴=．45. 答案：根据“HL ”证Rt Rt ADC AFE △≌△，CD EF ∴=，再根据“HL ”证Rt Rt ABD ABF △≌△，BD BF ∴=，BD CD BF EF ∴-=-，即BC BE =． 46. 答案：Ｄ47. 答案：G 是AB 的中点．48. 答案：证明：AC CE ⊥，BD DF ⊥（已知）90ACE BDF ∴∠=∠=（垂直的定义）在Rt ACE △和Rt BDF △中，()()AE BF AC BD =⎧⎨=⎩已知已知 Rt HL ACE Rt BDF ∴△≌△()A B ∴∠=∠（全等三角形的对应角相等）()AE BF =已知AE EF BF EF ∴-=-（等式性质）即AF BE = A B CF E D()()()AF BE ACF BDE A B AC BD =⎧⎪∠=∠⎨⎪=⎩已证在和中已证已知△△，SAS ACF BDE ∴△≌△()．49. 答案：D50. 答案：（1）证明：由题意得90A B A D ∠+∠=∠=∠，，90D B ∠+∠=∴．AB DE ∴⊥．（2）若PB BC =，则有Rt △ABC ≌Rt △DBP ．B B A D BP BC ∠=∠∠=∠=∵，，，∴ Rt △ABC ≌Rt △DBP ．说明：图中与此条件有关的全等三角形还有如下几对：Rt △APN ≌ Rt △DCN 、Rt △DEF ≌ Rt △DBP 、Rt △EPM ≌ Rt △BFM ． 从中任选一对给出证明，只要正确的都对．B D。

沪科版八年级上册数学第14章全等三角形含答案一、单选题(共15题，共计45分)1、如图，要测量河两岸相对的两点A、B的距离，先在AB的垂线BF上取两点C、D，使BC=CD，再作出BF的垂线DE，使点A、C、E在同一条直线上（如图所示），可以说明△ABC≌△EDC，得AB=DE，因此测得DE的长就是AB的长，判定△ABC≌△EDC，最恰当的理由是（）A.边角边B.角边角C.边边边D.边边角2、如图，AC和BD相交于O点，若OA=OD，用“SAS”证明△AOB≌△DOC还需（）A.AB=DCB.OB=OCC.∠C=∠DD.∠AOB=∠DOC3、某同学把一块三角形的玻璃打碎成三块（如图所示），在要到玻璃店去配一块完全一样的玻璃，应带第（）块去配．A.①B.②C.③D.①②③都不可以4、如图：AB=AD，AE平分∠BAD，则图中有（）对全等三角形。

A.2B.3C.4D.55、两个直角三角形中，如果有一条直角边对应相等．则：①若斜边上的高对应相等．那么这两个直角三角形全等；②若直角的平分线相等，那么这两个直角三角形全等；③若斜边上的中线对应相等，那么这两个直角三角形全等；④两个直角三角形都有一个锐角是30°，那么这两个直角三角形全等．其中正确命题的个数有（）A.1个B.2个C.3个D.4个6、如图所示，已知AB∥CD，AD∥BC，那么图中共有全等三角形（）A.1对B.2对C.4对D.8对7、下列结论是正确的是（）A.全等三角形的对应角相等B.对应角相等的两个三角形全等C.有两条边和一角对应相等的两个三角形全等D.相等的两个角是对顶角8、下列说法正确的是（）A.顺次连接任意一个四边形四边的中点，所得到的四边形一定是平行四边形 B.平行四边形既是中心对称图形，又是轴对称图形 C.对角线相等的四边形是矩形 D.只要是证明两个直角三角形全等，都可以用“HL”定理9、如图，△ABC中，AD⊥BC于D，BE⊥AC于E，AD与BE相交于F，若BF=AC，那么∠ABC的大小是( )A.40°B.45°C.50°D.60°10、如图，在Rt△ABC中，AC＝BC＝2，将△ABC绕点A逆时针旋转60°，连接BD，则图中阴影部分的面积是（）A.2 ﹣2B.2C. ﹣1D.411、如图所示，AB∥CD，AD∥BC，BE＝DF，则图中全等三角形共有( )对．A.2B.3C.4D.512、如图，已知AB=12，AB⊥BC于B，AB⊥AD于A，AD=5，BC=10．点E是CD 的中点，则AE的长为（）A.6B.C.5D.13、如图，在△ABC和△DEF中，满足AB＝DE，∠B＝∠E，如果要判定这两个三角形全等，添加的条件错误的是（）A. BC＝EFB. AC＝DFC.∠ A＝∠ DD.∠ C＝∠ F14、如图所示，为了测量出A，B两点之间的距离，在地面上找到一点C，连接BC，AC，使∠ACB=90°，然后在BC的延长线上确定D，使CD=BC，那么只要测量出AD的长度也就得到了A，B两点之间的距离，这样测量的依据是（）A.AASB.SASC.ASAD.SSS15、如图，在△ABC中，AB=AC，∠BAC=54°，∠BAC的平分线与AB的垂直平分线交于点O，将∠C沿EF（E在BC上，F在AC上）折叠，点C与点O恰好重合，有如下五个结论：①AO⊥ BC；②OD=OE；③△OEF是等边三角形；④△OEF≌△CEF;⑤∠OEF=54°则上列说法中正确的个数是（）A. 2B. 3C. 4D. 5二、填空题(共10题，共计30分)16、阅读后填空：已知：如图，∠A＝∠D＝90°，AC＝DB，AC、DB相交于点O.求证：OA＝OD.分析：要证OA＝OD，可证ABO≌ DCO；要证ABO≌ DCO，可先证ABC≌ DCB得出AB＝DC这个结论；而用________可证ABC≌ DCB（填SAS或AAS或HL）.17、如图，在Rt△ABC中，∠ACB = 90°，，点D、E分别在边AB上，且AD = 2，∠DCE = 45°，那么DE =________．18、如图，△ABC的顶点分别为A（0，3），B（﹣4，0），C（2，0），且△BCD与△ABC全等，则点D坐标可以是________.19、如图，A，D，F，B在同一直线上，AE=BC，且AE∥BC．添加一个条件________ ，使△AEF≌△BCD．20、如图，在△ABC中，AB=AC，∠ABC、∠ACB的平分线BD，CE相交于O点，且BD交AC于点D，CE交AB于点E，某同学分析图形后得出以下结论，上述结论一定正确的是________（填代号）．①△BCD≌△CBE；②△BAD≌△BCD；③△BDA≌△CEA；④△BOE≌△COD；⑤△ACE≌△B CE．21、如图的三角形纸片中，AB=8cm，BC=6cm，AC=5cm.沿过点B的直线折叠三角形，使点C落在AB边的点E处，折痕为BD.则△AED的周长为________cm.22、如图，，，．点，为线段上两点．现存在以下条件：① ；② ；③；④ ．请在以上条件中选择一个条件，使得一定和全等，则这个条件可以为________．（请写出所有正确的答案）23、如图，已知∠ACB=∠DBC,请增加一个条件,使△ABC≌△DCB,你添加的条件为________．24、如图，△ABC与△AEF中，AB=AE，BC=EF，∠B=∠E，AB交EF于D.给出下列结论：⑴∠AFC=∠AFE⑵BF=DE⑶∠BFE=∠BAE⑷∠BFD=∠CAF.其中正确的结论是________（填写所正确结论的序号），25、如图，AC，BD相交于点O，AC＝BD，AB＝CD，写出图中两对相等的角________．三、解答题(共5题，共计25分)26、如图，点D是AB上一点，DF交AC于点E，DE=FE，FC∥AB，AB=6，FC=4，求线段DB的长．27、如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD、等边△ABE．已知∠BAC＝30º，EF⊥AB，垂足为F，连结DF．（1）求证：AC＝EF；（2）求证：四边形ADFE是平行四边形．28、如图，分别以△ABC的两边AB和AC为边向外作正方形ANMB和正方形ACDE，连接NC、BE交于点P．探究：试判断BE和CN的位置关系和数量关系，并说明理由．应用：Q是线段BC的中点，若BC=6，求PQ29、已知：在矩形中，是对角线，于点，于点．求证：30、已知：AD是△ABC中BC边上的中线，延长AD至E，使DE＝AD，连接BE，求证：△ACD≌△EBD．参考答案一、单选题(共15题，共计45分)1、B2、B3、C4、B5、D6、C7、A8、A9、B10、C11、B12、B13、B14、B15、B二、填空题(共10题，共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题，共计25分)26、28、30、。

14.1 全等三角形课程标准学习目标①理解全等三角形的概念，能识别全等三角形中的对应边、对应角；②掌握全等三角形的性质． 1.了解全等形的概念，能判断两个图形是不是全等形．2.理解全等三角形的有关概念，掌握确定对应元素的方法．3.掌握全等三角形的性质，能够利用全等三角形的性质进行计算和证明．知识点01全等的概念·全等形：能够完全重合的两个图形，叫做全等形【即学即练1】（23-24八年级上·安徽阜阳·阶段练习）1．下列说法中正确的是（ ）A ．两个面积相等的图形，一定是全等图形B ．若两个图形周长相等，则它们一定是全等图形C ．两个等边三角形一定是全等图形D ．能够完全重合的两个图形是全等图形知识点02 全等三角形的有关概念·能够完全重合的两个三角形；·符号表示:全等符号“≌”，△ABC ≌△111A B C ；·对应元素：对应顶点、对应角、对应边；【即学即练2】2．如图，ABC DCB △≌△，其中AC 与DB 是对应边，那么BAC Ð的对应角是（ ）A ．ABDÐB ．ACB ÐC ．BDC ÐD ．CDBÐ【即学即练3】3．如图，ABC BAD V V ≌，请指出两个全等三角形的对应边和对应角．【即学即练4】4．如图，已知ABC DEF ≌△△，点A 与点D ，点B 与点E ，点C 与点F 是对应顶点．写出这两个三角形的对应边和对应角．知识点03 全等三角形的性质（1）对应角相等；（2）对应边相等；（3）对应周长、面积相等；（4）对应角平分线、中线、高线相等．【即学即练5】5．下列说法正确的是（ ）①全等三角形的对应边相等，对应角相等；②全等三角形的周长相等，面积相等；③面积相等的三角形全等；④周长相等的三角形全等A ．②③B ．③④C ．①②D ．①②③【即学即练6】6．已知下图中的两个三角形全等，则a Ð等于( )A ．72°B ．60°C ．58°D ．50°【即学即练7】（23-24八年级上·安徽合肥·期末）7．如图，ABC ADE △≌△，70B Ð=°，30C Ð=°，35DAC Ð=°，则CAE Ð的度数为（ ）A ．50°B ．45°C ．40°D ．35°【即学即练8】（23-24八年级上·安徽阜阳·阶段练习）8．如图，ABC CDE △≌△，点C ，A ，D 在同一条直线上.(1)求证：AB CE ∥；(2)当7CE =，12AB =时，求线段AD 的长.·全等三角形中的对应关系：根据全等三角形的表示找对应线段和对应角关键：对应点在全等表示中的位置也对应相等案例：ABC ADE △≌△ABC ADE △≌△中的对应关系：·线段AB 与线段AD 对应，线段BC 与线段DE 对应，线段AC 与线段AE 对应·∠ABC 与∠ADE 对应，∠BCA 与∠DEA 对应，∠CAB 与∠EAD 对应【题型一：全等三角形的性质与角度等量代换】例1．（24-25八年级上·安徽合肥·阶段练习）9．如图，ABC DEC ≌△△，过点A 作AF CD ^，垂足为点F ，若65BCE Ð=°，则CAF Ð的度数为（ ）A ．25°B ．30°C ．35°D ．40°变式1.（23-24八年级上·安徽铜陵·阶段练习）10．如图，ABC DEC ≌△△，75ABC Ð=°，点E 在线段AB 上，过点B 作BF CE ^，且与DE 交于点F ，则BFD Ð的度数为（ ）A ．150°B ．155°C ．160°D ．165°例2.（23-24八年级上·安徽马鞍山·期中）11．如图，已知11ABC A B C V V ≌，若11150,45,60A A B C ACB Ð=°Ð=°Ð=°，则a Ð的度数是（ ）A ．15°B ．20°C ．25°D ．10°变式2.12．如图所示，ABC ADE △△≌，且1025120，,CAD D EAB Ð=°Ð=°Ð=°，求DFB Ð和DGBÐ的度数．【方法技巧与总结】灵活运用外角的性质、三角形的内角和、直角三角形两锐角互余、平行线的性质、角平分线进行角度等量代换．【题型二：利用全等三角形的性质求线段长】例3．（24-25八年级上·安徽合肥·阶段练习）13．如图，A ，C ，E 三点在同一直线上，且ABC DAE △△≌．若2CE DE ==，则BC = ．变式3-1．（23-24八年级上·安徽阜阳·阶段练习）14．如图，ABC CDE △≌△，点C ，A ，D 在同一条直线上.(1)求证：AB CE ∥；(2)当7CE =，12AB =时，求线段AD 的长.变式3-2．（22-23八年级上·安徽滁州·阶段练习）15．如图，ABC DBE ≌△△，点D 在边AC 上，BC 与DE 交于点P ，已知162ABE Ð=°，30DBC Ð=°， 2.5AD DC ==，4BC =．(1)求CBE Ð的度数．(2)求CDP △与BEP △的周长和．【题型三：全等三角形的性质与图形综合】例4．16．如图，已知ABC DEB △△≌，点E 在AB 上，DE 与AC 相交于点F ．(1)若8DE =，5BC =，则线段AE 的长是 ；(2)已知35D Ð=°，60C Ð=°，求AFD Ð的度数．【题型四：全等三角形与坐标】例5．17．如图，在平面直角坐标系中，已知AOB COD V V ≌，则点C 的坐标是 ．变式5.（22-23八年级上·安徽蚌埠·阶段练习）18．如图，直线1l ：y ax b =+（常数0a <，0b >）与x 轴、y 轴分别交于A ，B 两点，直线2l ：y ca d =+（常数0c >，0d >）与x 轴、y 轴分别交于C ，D 两点，直线1l 与直线2l 交于点E ，且△≌△A O B C O D ．(1)求证AB CD^(2)若2a =-，4b =，求ADE V 的面积．一、选择题（23-24八年级上·安徽淮南·期中）19．已知ABC DEF ≌△△，80A Ð=°，40B Ð=°，则F Ð的度数是（ ）A ．40°B ．50°C ．60°D ．80°（23-24八年级上·江苏南通·期中）20．如图，ABC FDE ≌△△，50C Ð=°，100F Ð=°，则B Ð的度数为（ ）A ．20°B ．30°C ．35°D ．40°（16-17八年级上·云南红河·期末）21．如图，ABC DCB △≌△，若7AC =，5BE =，则DE 的长为（ ）A ．2B ．3C ．4D ．5（23-24八年级上·安徽安庆·期末）22．下列命题中，是假命题的是（ ）A ．两点确定一条直线B ．对顶角相等C ．同旁内角互补D ．全等三角形的面积相等（23-24八年级上·安徽亳州·期末）23．如图，已知ABC ADE △△≌，55BAC Ð=°，100Ð=°ADE ，则C Ð的度数为（ ）A ．55°B ．45°C ．35°D ．25°（20-21八年级上·安徽阜阳·阶段练习）24．下列关于全等三角形的说法中，正确的有（ ）①全等三角形的形状相同、大小相等；②全等三角形的对应边相等、对应角相等；③面积相等的两个三角形是全等三角形；④全等三角形的周长相等、面积相等．A ．1个B ．2个C ．3个D ．4个（24-25八年级上·安徽安庆·阶段练习）25．如图，在ABC V 中，AD BC ^于点D ，点E 在AD 上，且CED ABD V V ≌．若14DE DC +=，2DA DB -=，则DE 的长为（ ）A ．6B ．7C ．8D ．9二、填空题（22-23八年级上·江苏南通·期末）26．如图，ABC ADE △≌△，42B Ð=°，30C Ð=°，50BAD Ð=°，则BAE Ð=（23-24八年级上·安徽合肥·期末）27．已知ABC DEF ≌△△，其中6AC =，则DF = ．（16-17八年级下·江西抚州·期中）28．如图，两个全等的直角三角形重叠在一起，将其中的一个三角形沿着点B 到C 的方向平移到DEF V 的位置，10AB =，4DO =，平移距离为6，则阴影部分面积为 ．三、解答题（2023上·河北沧州·八年级校考阶段练习）29．如图，已知ABC DEB @△△，点E 在AB 上，DE 与AC 相交于点F ，若10DE =，6BC =，30D Ð=°，70C Ð=°．(1)求线段AE 的长；(2)求DBC Ð的度数．（21-22八年级上·安徽安庆·期末）30．如图，已知ABC DEB V V ≌，点E 在AB 上，AC 与BD 交于点F ．(1)若6AB =，3BC =，求AE 的长；(2)若25A Ð=°，55C Ð=°，求AED Ð的度数．（23-24八年级上·安徽淮南·阶段练习）31．如图，A 、D 、E 三点在同一条直线上，且ABD CAE ≌V V ．(1)若5BD =，3CE =，求DE ；(2)若BD CE ∥，求BAC Ð．（22-23八年级上·安徽六安·期末）32．如图，直线l ：122y x =-+与x 轴、y 轴分别交于A 、B 两点，在y 轴上有一点()0,4C ，动点M 从A 点以每秒1个单位的速度沿x 轴向左移动，移动了t 秒．(1)求A 、B 两点的坐标．(2)当t 为何值时，COM AOB △△≌，并求此时M 点的坐标．33．如图，在四边形ABCD 中，50B C Ð=Ð=°， 2.5AB =，6BC =，动点E ，F 分别在线段BC ，DC 上，连接AE ，EF ，AF ．(1)若70BAE Ð=°，60AEF Ð=°，求EFC Ð的度数；(2)若V V ≌ABE AFE ，100BAF Ð=°，求AEB Ð的度数；(3)若ABE V 与ECF △全等，点B 与点C 为对应点，求BE 的长．34．综合与实践（1）【探索发现】在ΔABC 中. AC BC =，ACB a Ð=，点D 为直线BC 上一动点（点D 不与点B ，C 重合），过点D 作//DF AC 交直线AB 于点F ，将AD 绕点D 顺时针旋转a 得到ED ，连接BE ．如图（1），当点D 在线段BC 上，且90a =°时，试猜想：①AF 与BE 之间的数量关系：______；②ABE Ð=______．（2）【拓展探究】如图（2），当点D 在线段BC 上，且090a °<<°时，判断AF 与BE 之间的数量关系及ABE Ð的度数，请说明理由．（3）【解决问题】如图（3），在ΔABC 中，AC BC =，4AB =，ACB a Ð=，点D 在射线BC 上，将AD 绕点D 顺时针旋转a 得到ED ，连接BE ．当3BD CD =时，直接写出BE 的长．【分析】根据全等三角形的定义进行判断作答即可．【详解】解：两个面积相等的图形，不一定是全等图形，A 错误，故不符合要求；若两个图形周长相等，则它们不一定是全等图形，B 错误，故不符合要求；两个等边三角形不一定是全等图形，C 错误，故不符合要求；能够完全重合的两个图形是全等图形，D 正确，故符合要求；故选：D ．【点睛】本题考查了全等三角形的定义．解题的关键在于对知识的熟练掌握．2．D【分析】本题主要考查了全等三角形的性质，熟练掌握全等三角形的对应边相等，对应角相等是解题的关键．【详解】解：∵ABC DCB △≌△，其中AC 与BD 是对应边，∴A 和D 、B 和C 是对应点，∴BAC CDB =∠∠．故选：D ．3．对应边：AB 与BA ，BC 与AD ，AC 与BD ；对应角：CAB Ð与DBA Ð，ABC Ð与BAD Ð，C Ð与DÐ【分析】根据全等三角形中能够互相重合的边是对应边，能够互相重合的角是对应角，再解答即可．【详解】解：∵ABC BAD V V ≌，∴对应边：AB 与BA ，BC 与AD ，AC 与BD ；对应角：CAB Ð与DBA Ð，ABC Ð与BAD Ð，C Ð与D Ð．【点睛】本题考查的是全等三角形的概念，掌握全等三角形的对应边与对应角的含义是解本题的关键．4．见解析【分析】根据对应顶点，写出对应边和对应角即可．【详解】解：∵ABC DEF ≌△△，点A 与点D ，点B 与点E ，点C 与点F 是对应顶点，∴这两个三角形的对应边是：BC 和EF ，AB 和DE ，AC 和DF ；对应角是：ABC Ð和DEF Ð，ACB Ð和DFE Ð，BAC Ð和EDF Ð．【点睛】本题考查全等三角形的性质．正确的找出对应边和对应角，是解题的关键．【分析】理清全等三角形的判定及性质，即可熟练求解此题．【详解】解：①全等三角形的对应边相等，对应角相等，正确；②全等三角形的周长相等，面积相等，正确；③面积相等的三角形形状不一定相同，故错误；④周长相等的三角形形状不一定相同，故错误．所以①②正确，故选：C ．【点睛】本题主要考查了全等三角形的判定及性质，能够掌握并熟练运用是解题的关键．6．D【分析】本题考查了全等三角形的性质．由全等三角形的性质即可求得结果．【详解】解：由全等三角形的性质得：a Ð是边a 和c 的夹角，∴50a Ð=°，故选：D ．7．B【分析】本题主要考查全等三角形的性质和三角形内角和定理，由题意得对应角相等，利用三角形内角和定理得80DAE BAC Ð=Ð=°，结合CAE DAE CAD Ð=Ð-Ð即可求得答案．【详解】解：∵ABC ADE △≌△，∴ABC ADE Ð=Ð，C E Ð=Ð，BAC DAE Ð=Ð，∵70B Ð=°，30C Ð=°，∴80DAE BAC Ð=Ð=°，∵35DAC Ð=°，∴45CAE DAE CAD Ð=Ð-Ð=°，故选：B ．8．(1)见解析(2)5【分析】（1）根据三角形全等的性质得到BAC DCE Ð=Ð，再根据内错角相等两直线平行即可得出结论；（2）根据三角形全等的性质得到12CD AB ==，7AC CE ==，根据AD CD AC =-即可求出最后结果．【详解】（1）证明：ABC CDE Q ≌△△，BAC DCE \Ð=Ð，AB CE \∥；（2）ABC CDE Q ≌△△，12CD AB \==，7AC CE ==，1275AD CD AC \=-=-=．【点睛】本题考查了全等三角形的性质，平行线的判定，熟练掌握三角形全等的性质是解答本题的关键．9．A【分析】本题考查了三角形全等的性质，直角三角形的两个锐角互余．根据三角形全等的性质可得ACB DCE Ð=Ð，进而可得BCE ACD Ð=Ð，根据直角三角形的两个锐角互余，即可求得CAF Ð的度数．【详解】解：Q ABC DEC ≌△△，\ACB DCE Ð=Ð，ACB ACE DCE ACE\Ð-Ð=Ð-Ð即BCE ACD Ð=Ð，Q AF CD ^，65BCE Ð=°，9025CAF ACD \Ð=°-Ð=°，故选：A ．10．D【分析】本题考查了全等三角形的性质，垂直的定义，直角三角形的两锐角互余，邻补角，熟练掌握全等三角形的性质是解题的关键．根据全等三角形的性质得出75ABC DEC Ð=Ð=°，根据垂直的定义，直角三角形的两锐角互余，得出 15EFB Ð=°，根据邻补角即可求解．【详解】ABC DEC Q △≌△，75ABC Ð=°，75ABC DEC \Ð=Ð=°，BF CE ^Q ，9015EFB FEC \Ð=°-Ð=°，180165BFD EFB \Ð=°-Ð=°．故选：D ．11．C【分析】本题考查了全等三角形的性质，三角形的内角和等知识．根据11ABC A B C V V ≌得到45ABC Ð=°，根据三角形内角和求出85ACB Ð=°，即可求出125BCB Ð=°，问题得解．【详解】解：∵11ABC A B C V V ≌，∴1145A B C ABC ÐÐ=°=，∵50A Ð=°，∴180180504585ACB A ABC Ð=°-Ð-Ð=°-°-°=°，∵160ACB Ð=°，∴11856025BCB ACB ACB Ð=Ð-Ð=°-°=°即25a Ð=°．故选：C12．9065，DFB DGB Ð=°Ð=°【分析】本题主要考查三角形全等的性质，找到相应等量关系的角是解题的关键，做题时要结合图形进行思考．由ABC ADE △△≌，可得()12DAE BAC EAB CAD Ð=Ð=Ð-Ð，根据三角形外角性质可得DFB FAB B Ð=Ð+Ð，可得DFB Ð的度数；根据三角形内角和定理可得90DGB D Ð=°-Ð，即可得DGB Ð的度数．【详解】解：∵ABC ADE △△≌，∴()()11120106522DAE BAC EAB CAD Ð=Ð=Ð-Ð=´°-°=°，25B D Ð=Ð=°，\652590＝DFG FAB B Ð=Ð+Ð=°+°°，∴90DFB DFG Ð=Ð=°，在Rt DCG △中，90902565DGB D Ð=°-Ð=°-°=°．13．4【分析】本题考查全等三角形的性质，根据全等三角形的对应边相等，得到AC DE =，BC AE =，再利用线段的和差关系，求出AE 的长即可．【详解】解：∵ABC DAE △△≌，∴AC DE =，BC AE =，∵2CE DE ==，∴2AC =，∴4BC AE AC CE ==+=；故答案为：4．14．(1)见解析(2)5【分析】（1）根据三角形全等的性质得到BAC DCE Ð=Ð，再根据内错角相等两直线平行即可得出结论；（2）根据三角形全等的性质得到12CD AB ==，7AC CE ==，根据AD CD AC =-即可求出最后结果．【详解】（1）证明：ABC CDE Q ≌△△，BAC DCE \Ð=Ð，AB CE \∥；（2）ABC CDE Q ≌△△，12CD AB \==，7AC CE ==，1275AD CD AC \=-=-=．【点睛】本题考查了全等三角形的性质，平行线的判定，熟练掌握三角形全等的性质是解答本题的关键．15．(1)66°(2)15.5【分析】（1）根据全等三角形的性质得到ABC DBE Ð=Ð，计算即可；（2）根据全等三角形的性质求出BE 、DE ，根据三角形的周长公式计算即可．【详解】（1）解：∵162ABE Ð=°，30DBC Ð=°，∴132ABD CBE Ð+Ð=°，∵ABC DBE ≌△△，∴ABC DBE Ð=Ð，∴132266ABD CBE Ð=Ð=°¸=°，即CBE Ð的度数为66°；（2）解：∵ABC DBE ≌△△，∴5DE AC AD DC ==+=，4BE BC ==，∴CDP △与BEP △的周长和为DC DP PC BP PE BE+++++DC DE BC BE=+＋＋2.5544=+++15.5=．【点睛】本题主要考查全等三角形的性质，熟练掌握全等三角形的对应角相等，对应边相等是解本题的关键．16．(1)3(2)130°【分析】（1）根据全等三角形的性质得到8A B D E ==，5BE BC ==，结合图形计算，得到答案；（2）根据全等三角形的性质得到60DBE C Ð=Ð=°，35A D Ð=Ð=°，根据三角形内角和定理求出ABC Ð，计算即可．【详解】（1）解：∵ABC DEB △△≌，8DE =，5BC =，∴8A B D E ==，5BE BC ==，∴853AE AB BE =-=-=；（2）解：∵ABC DEB △△≌，35D Ð=°，60C Ð=°，∴60DBE C Ð=Ð=°，35A D Ð=Ð=°，ABC DEB Ð=Ð，∴18085ABC A C Ð=°-Ð-Ð=°，∴85DEB Ð=°，∴95AED Ð=°，∴3595130AFD A AED Ð=Ð+Ð=°+°=°．【点睛】本题考查了全等三角形的性质，三角形的内角和定理，三角形外角的性质，熟练掌握全等三角形的性质是解题的关键．17．()0,1【分析】此题考查了全等三角形的性质，根据点A 的坐标推出1OA =，结合全等三角形对应边相等，即可解答【详解】解：∵()1,0A ，∴1OA =，∵AOB COD V V ≌，∴1OC OA ==，∴C (0,1)，故答案为：(0,1)．18．(1)证明见解析；(2)365．【分析】（1）利用全等三角形的性质，得到ABO CDO Ð=Ð，再根据对顶角相等，得到DCO BCE Ð=Ð，进而得到90ABO BCE Ð+Ð=°，即可证明结论；（2）利用直线1l ：24y x =-+，求出A 、B 两点坐标，得到2OA =，4OB =，再利用全等三角形的性质，得到2OC OA ==，4OD OB ==，进而得到C 、D 两点坐标，从而求出直线2l ：122y x =+，联立方程组，求出点E 坐标，即可求出ADE V 的面积．【详解】（1）证明：AOB COD QV V ≌，ABO CDO \Ð=Ð，DCO BCE Ð=ÐQ ，90CDO DCO ABO BCE \Ð+Ð=Ð+Ð=°，()18090BEC ABO BCE \Ð=°-Ð+Ð=°，AB CD \^；（2）解：2a =-Q ，4b =，\直线1l ：24y x =-+，令0x =，得4y =；令0y =，得240x -+=，解得2x =，()2,0A \，()0,4B ，2OA \=，4OB =，AOB COD QV V ≌，2OC OA \==，4OD OB ==，()0,2C \，()4,0D -，240d c d =ì\í-+=î，解得：122c d ì=ïíï=î，\直线2l ：122y x =+，联立方程组12224y x y x ì=+ïíï=-+î，解得：45125x y ì=ïïíï=ïî，\点E 的坐标为412,55æöç÷èø，ADE \V 的面积为()111236242255E AD y ×=´+´=．【点睛】本题考查了全等三角形的性质，一次函数与坐标轴交点，待定系数法求一次函数解析式，两直线交点与二元一次方程组的解等知识，熟练掌握一次函数性质和全等三角形的性质是解题关键．19．C【分析】本题考查了三角形内角和定理，全等三角形性质的应用，主要考查学生的推理能力，难度不大．根据三角形内角和定理求出C Ð，根据全等三角形性质推出F C Ð=Ð，即可得出答案．【详解】解：80A Ð=°Q ，40B Ð=°，18060C A B \Ð=°-Ð-Ð=°，ABC DEF QV V ≌，60F C \Ð=Ð=°，故选：C ．20．B【分析】本题考查全等三角形的性质，三角形内角和定理．直接利用全等三角形的性质得出对应角相等进而得出答案．【详解】解：∵ABC FDE ≌△△，50C Ð=°，100F Ð=°，∴100BAC F Ð=Ð=°，∴1801005030B Ð=°-°-°=°．故选：B ．21．A【分析】根据全等三角形的对应边相等推知7BD AC ==，然后根据线段的和差即可得到结论．【详解】解：ABC DCB QV V ≌，7BD AC \==，5BE =Q ，2DE BD BE \=-=，故选：A ．【点睛】本题考查了全等三角形的性质，仔细观察图形，根据已知条件找准对应边是解决本题的关键．22．C【分析】本题主要考查真假命题，利用对顶角的性质、平行线的性质、全等三角形的性质及确定直线的条件即可确定正确的选项．【详解】解：A 、两点确定一条直线， 该命题是真命题，故本选项不符合题意；B 、对顶角相等，该命题是真命题，故本选项不符合题意；C 、两直线平行，同旁内角互补，故原命题是假命题，故本选项符合题意；D 、全等三角形的面积相等，该命题是真命题，故本选项不符合题意；故选：C ．23．D【分析】先根据“全等三角形对应角相等”得出100B ADE Ð=Ð=°，再根据三角形内角和定理即可求出C Ð的度数．本题主要考查了全等三角形的性质和三角形内角和定理，熟练掌握以上知识是解题的关键．【详解】∵ABC ADE △△≌，100B ADE \Ð=Ð=°，在ABC V 中，55BAC Ð=°，100B Ð=°，180C BAC B\Ð=°-Ð-Ð18055100=°-°-°25=°．故选：D24．C【分析】根据全等三角形的概念、性质定理和判定定理判断即可．【详解】解：①全等三角形的形状相同、大小相等，故①正确；②全等三角形的对应边相等、对应角相等，故②正确；③面积相等的两个三角形不一定是全等三角形，故③错误；④全等三角形的周长相等、面积相等，故④正确．故选：C ．【点睛】本题考查的是全等三角形的判定和性质，掌握全等三角形的概念和判定定理是解题的关键．25．A【分析】本题考查了全等三角形的性质，二元一次方程组的应用．由全等三角形的性质求得==AD CD y ，BD DE x ==，根据题意得到方程组，解之即可求解．【详解】解：设DE x =，CD y =，∵CED ABD V V ≌，∴==AD CD y ，BD DE x ==，∵14DE DC +=，2DA DB -=，∴14x y +=①，2y x -=②，-①②得212x =，解得6x =，即6DE =，故选：A ．26．58°##58度【分析】此题考查三角形内角和定理和全等三角形的性质等知识，根据三角形内角和定理得到180108BAC B C Ð=-Ð-Ð=°°，由全等三角形的性质得到108DAE BAC Ð=Ð=°，作差即可求出BAE Ð.【详解】解：∵42B Ð=°，30C Ð=°，∴180108BAC B C Ð=-Ð-Ð=°°，∵ABC ADE △≌△，∴108DAE BAC Ð=Ð=°，∴1085058BAE DAE BAD Ð=Ð-Ð=°-°=°．故答案为：58°．27．6【分析】本题考查了全等三角形的性质，理解性质“全等三角形对应边相等．”是解题关键．【详解】解：Q ABC DEF ≌△△，6AC DF \==，故答案：6．28．48【分析】本题考查的是全等三角形的性质、平移的性质，掌握全等形的面积相等是解题的关键．根据平移的性质分别求出BE 、DE ，根据题意求出OE ，根据全等三角形的性质、梯形的面积公式计算，得到答案．【详解】解：由平移的性质知，6BE =，10DE AB ==，1046OE DE DO \=-=-=，ABC DEF QV V ≌，ABC DEF S S \=△△，()()1110664822ODFC ABEO S S AB OE BE \==+×=´+´=四边形梯形，故答案为4829．(1)4AE =(2)10DBC Ð=°【分析】（1）由全等三角形的性质可得10AB DE \==，6BE BC ==，即可求解；（2）由全等三角形的性质可得30BAC Ð=°，70DBE Ð=°，再利用三角形内角和定理求得80ABC Ð=°，即可求解．【详解】（1）解：ABC DEB @Q △△，10DE =，6BC =，10AB DE \==，6BE BC ==，4AE AB BE \=-=；（2）解：ABC DEB @Q △△，30D Ð=°，70C Ð=°，30BAC D °\Ð=Ð=，70DBE C Ð=Ð=°，180180307080ABC A C \Ð=°-Ð-Ð=°-°-°=°，807010DBC ABC DBE °°°\Ð=Ð-Ð=-=.【点睛】本题考查全等三角形的性质、三角形内角和定理，熟练掌握全等三角形的性质是解题的关键．30．(1)3AE =(2)80AED Ð=°【分析】本题主要考查了全等三角形的性质，三角形内角和的定理．（1）利用全等的性质即可求出3BE BC ==，然后根据线段的和差即可求出AE ．（2）利用全等的性质求出ABC DEB Ð=Ð，然后根据三角形的内角和定理即可求出100ABC DEB Ð=Ð=°，然后利用角的和差即可求出AED Ð．【详解】（1）（1）∵ABC DEB V V ≌，3BC =，∴3BE BC ==，∴633AE AB BE =-=-=．（2）∵ABC DEB V V ≌，∴ABC DEB Ð=Ð．∵25A Ð=°，55C Ð=°，∴1801802555100ABC A C Ð=°-Ð-Ð=°-°-°=°，∴100DEB Ð=°，∴180********AED DEB Ð=°-Ð=°-°=°.31．(1)2(2)90°【分析】此题考查了全等三角形的性质，熟练掌握全等三角形的对应边相等和对应角相等是解题的关键．（1）根据全等三角形的性质得到3AD CE ==，5AE BD ==，即可得到答案；（2）根据平行线的性质得到BDE CEA Ð=Ð，根据全等三角形的性质得到ADB CEA Ð=Ð，ABD CAE Ð=Ð，则ADB BDE Ð=Ð，由平角的定义及等量代换即可得到BAC Ð的度数．【详解】（1）解：∵ABD CAE △△≌，5BD =，3CE =，3\==AD CE ，5AE BD ==，2DE AE AD \=-=；（2）∵BD CE ∥，BDE CEA \Ð=Ð，∵ABD CAE △△≌，ADB CEA \Ð=Ð，ABD CAEÐ=ÐADB BDE \Ð=Ð，180ADB BDE Ð+Ð=°Q ，90ADB \Ð=°，90ABD BAD \Ð+Ð=°，90BAC BAD CAE BAD ABD \Ð=Ð+Ð=Ð+Ð=°．32．(1)()40A ，，()02B ，；(2)当2t =时，COM AOB △△≌，此时M 的坐标是()20，；或6t =时，COM AOB △△≌，此时M 的坐标是()20-，．【分析】（1）由直线l 的函数解析式，令0y =求A 点坐标，0x =求B 点坐标；（2）若COM AOB △△≌，则2OM OB ==，分情况求出t 值，并得到M 点坐标．【详解】（1）解：122y x =-+，当0x =时，2y =．当0y =时，1202x -+=，解得4x =．所以()40A ，，()02B ，；（2）解：因为COM AOB △△≌，所以2OM OB ==．当04x <<时，42OM t =-=，所以2t =，当>4x 时，42OM t =-=．所以6t =，即当2t =时，COM AOB △△≌，此时M 的坐标是()20，；或6t =时，COM AOB △△≌，此时M 的坐标是()20-，．【点睛】此题考查了一次函数的图象和性质，三角形面积计算，全等三角形的性质等，正确分类讨论是解题的关键．33．(1)70°(2)80°(3)3或3.5【分析】（1）根据三角形内角和算出60AEB Ð=°，再根据平角定义算出60,FEC Ð=°最后再运用三角形内角和即可求解；（2）根据V V ≌ABE AFE 得出150,2BAE EAF BAF Ð=Ð=Ð=°再由三角形内角和即可求解；（3）根据ABE ECF ≌△△和ABE FCE △≌△分类讨论即可求解；【详解】（1）50,70B BAE Ð=°Ð=°Q ，180,B BAE AEB Ð+Ð+Ð=°60AEB \Ð=°，60,AEF Ð=°Q 180AEB AEF FEC Ð+Ð+Ð=°，60,FEC \Ð=°50,C Ð=°Q 180FEC C CFE Ð+Ð+Ð=°，70EFC \Ð=°；（2）∵,100ABE AFE BAF Ð=°V V ≌，150,2BAE EAF BAF \Ð=Ð=Ð=°180B BAE AEB Ð+Ð+Ð=°Q ，180505080AEB \Ð=°-°-°=°．（3）当ABE ECF ≌△△时，则2,5AB EC ==，6,BC =Q 6 2.5 3.5,BE BC EC \=-=-=当ABE FCE △≌△时，则BE CE =，6BC BE CE ==+Q ，1 3.2BE CE BC \===综上可得：BE 为3或3.5．【点睛】该题主要考查了三角形内角和定理以及全等三角形的性质，解题的关键是分类讨论思想的运用．34．（1）①AF BE =；②90°；（2）AF BE =，ABE a Ð=．理由见解析；（3）BE 的长为1或2．【分析】（1）由“SAS”△ADF ≌△EDB ，可得AF=BE ，再利用“8字型”字母∠OBE=∠ADO=90°即可解决问题；（2）结论：AF=BF ，∠ABE=a ．由“SAS”△ADF ≌△EDB ，即可解决问题；（3）分当点D 在线段BC 上和当点D 在BC 的延长线上两种情形讨论，利用平行线分线段成比例可求解．【详解】解：（1）如图1中，设AB 交DE 于O ．∵∠ACB=90°，AC=BC ，∴∠ABC=45°，∵DF ∥AC ，∴∠FDB=∠C=90°，∴∠DFB=∠DBF=45°，∴DF=DB ，∵∠ADE=∠FDB=90°，∴∠ADF=∠EDB ，且DA=DE ，DF=DB∴△ADF ≌△EDB （SAS ），∴AF=BE ，∠DAF=∠E ，∵∠AOD=∠EOB ，∴∠ABE=∠ADO=90°故答案为AF=BE ，90°．（2）AF BE =，ABE a Ð=.理由：∵//DF AC ，∴FDB ACB a Ð=Ð=，CAB DFB Ð=Ð.∵AC BC =，∴ABC CAB Ð=Ð.∴ABC DFB Ð=Ð.∴DB DF=∵ADE FDB a Ð==Ð，ADF ADE FDE Ð=Ð-Ð，EDB FDB FDE Ð=Ð-Ð，∴ADF EDB Ð=Ð.又∵AD DE =，∴ADF EDB D @D .∴AF BE =，AFD EBD Ð=Ð.∴AFD ABC FDB Ð=Ð+Ð，DBE ABD ABE Ð=Ð+Ð，∴ABE FDB a Ð=Ð=.（3）1或2.解：当点D 在线段BC 上时，过点D 作//DF AC 交直线AB 于点F ，如图（1）.∵//DF AC ，∴3BF BD AF CD==.∵4AB BF AF =+=，∴1AF =.∵//DF AC ，∴BDF C ADE a Ð=Ð=Ð=，DFB CAB Ð=Ð.∵ADF ADE FDE Ð=Ð-Ð，EDB FDB FDE Ð=Ð-Ð，∴ADF EDB Ð=Ð.∵AC BC =，∴CAB CBA Ð=Ð.∴DFB DBF Ð=Ð.∴DF DB =.又AD DE =，∴ADF EDB D @D ，1BE AF ==.当点D 在线段BC 的延长线上时，过点D 作//DF AC ¢交BA 的延长线于点F ¢，如图（2）.∵//DF AC ¢，∴2AB BC AF CD==¢.∴24AB AF ¢==.∴2AF ¢=.同理可得2BE AF ¢==.综上可得，BE 的长为1或2.【点睛】本题考查几何变换综合题、等腰三角形的性质、全等三角形的判定和性质、平行线分线段成比例定理等知识，解题的关键是正确寻找全等三角形解决问题，属于中考压轴题．。