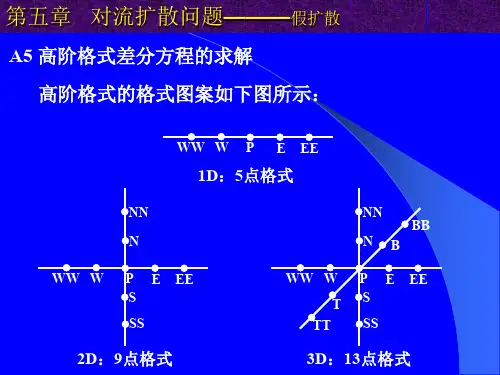
第五章 对流-扩散方程的离散格式
- 格式:ppt
- 大小:8.36 MB
- 文档页数:121


主讲陶文铨西安交通大学能源与动力工程学院热流中心CFD-NHT-EHT CENTER 2007年11月29日, 西安热流问题数值计算第五章有回流的流动与换热第流场数值计算概述5.1.1两类主要流动与两类数值解法5.1.4两种构造对流项离散格式的方法1.两类主要流动2.两类数值求解方法5.1 流场数值计算概述5.1.2强制对流的涡量方程5.1.3一维模型方程5.1.1 两类主要流动与两类数值解法回流型,其基本区别在于是否存在漩涡(vortex)vorticity) 的区别漩涡是一种宏观的流动形态,特点是流体速度发生反转;涡量是粘性流体的基本特性,只要是粘性流体流动中必有涡量。
动力工程中大多为回流型(椭圆型)流动。
本章仅介绍回流型流动的数值解法。
2. 两类数值求解方法数值求解回流型的流动可以大别为原始变量法与涡量流函数法。
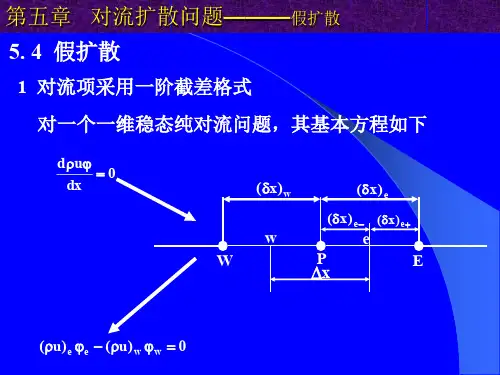
原始变量法u,v,p为求解变量,由于不可压缩流体没有关于压力的独立的方程,数值求解时需要做特殊处理;5.1.3一维模型方程为研究离散格式基本特点又不使过程复杂化,5.1.4两种构造对流项离散格式的方法1. Taylor控制容积积分法-给出界面上被求函数的插值方式对同一种格式,如控制容积积分法得可以认为是控制容积内导数积分中5.2.1 中心差分5.2.2 迎风差分5.2.3 混合格式5.2.4 指数格式5.2.5 乘方格式5.2对流扩散方程的离散格式本节中通过将一维模型方程在取分段线性型线,经整理可得:()eexδΓ+−EaWa做如下变化:()e e x δΓ++为保证代数方程迭代求解的收敛性,我们要求计算中质量守恒一定要满足,于是下列两点边值问题:Pe 随当当当得出结果如右。
,4P =100,W φ=5.5.2 一维对流-扩散方程的迎风控制容积法的定义-界面上未知函数永远取上游Patankar教授提出一种专门符号表示FORTRAN 的Max:,X Y,于是有:(),0,0e P e E eu F Fρφφφ=−−类似地有:(),0,0w W w P wu F Fρφφφ=−−3.对流项一阶迎风、扩散项中心差分的离散方程P P E E W Wa a aφφφ=+,0E e ea D F=+−()P E W e wa a a F F=++−,0W w wa D F=+由于0,0E W a a ≥≥因此FUD 总可以得出物理上合理的解(physically plausible solution ),自五十年代提出以来,半个世纪中得到广泛地采用。


流体仿真与应用第八讲二、对流-扩散问题的有限体积法◆中心差分格式(例子)节点增加到20个结果◆离散格式的性质在数学上,一个离散格式必须要引起很小的误差(包括离散误差和舍入误差)才能收敛于精确解,即要求离散格式必须要稳定或网格必须满足稳定性条件。
在物理上,离散格式所计算出的解必须要有物理意义,对于得到物理上不真实的解的离散方程,其数学上精度再高也没有价值。
通常,离散方程的误差都是因离散而引起,当网格步长无限小时,各种误差都会消失。
然而,在实际计算中,考虑到经济性(计算时间和所占的内存)都只能用有限个控制容积进行离散。
因此,格式需要满足一定的物理性质,计算结果才能令人满意。
主要的物理性质包括:守恒性、有界性和迁移性。
◆离散格式的性质——守恒性满足守恒性的离散方程不仅使计算结果与原问题在物理上保持一致,而且还可以使对任意体积(由许多个控制容积构成的计算区域)的计算结果具有对计算区域取单个控制容积上的格式所估计的误差。
◆离散格式的性质——迁移性③当Pe 为有限大小时,对流和扩散同时影响一个节点的上、下游相邻节点。
随着Pe 的增加,下游受的影响逐渐增大,而上游受的影响逐渐变小。
①,即纯扩散,无对流。
②,即纯对流,无扩散。
0=Pe ∞=Pe◆迎风格式迎风格式(Upwind Differencing Scheme )在确定控制容积界面上的值时就考虑了流动的方向性,其思想为:在控制容积界面上对流项的取上游节点处的值,称之为第二类迎风格式。
中心差分格式的缺点是,它不能识别流动的方向,控制容积界面上的值取相邻上、下游节点的平均值。
当对流作用较强时,这样的处理就与其物理特征(某点的值受上游的影响,而不受下游的影响)不一致了。
φφφ◆迎风格式◆迎风格式在控制容积界面上对流项的取其上游节点处的值EW →φWw φφ=Pe φφ=()()W P w P E e W w P e D D F F φφφφφφ−−−=−()()[]()Ee W w w P w e e w w D F D F F D F D φφφ++=−+++WE →Pw φφ=Ee φφ=()()[]()Ee e W w Pw e e e w F D D F F F D D φφφ−+=−+−+◆迎风格式通用形式WW E E P P a a a φφφ+=()w e E W P F F a a a −++=EW →ww W F D a +=eE D a =W E →w W D a =ee E F D a −=◆迎风格式的特点迎风格式满足守恒性。



对流方程及其解法对流方程是描述流体运动的最基本方程之一,涉及热、动量、物质等的传递现象,对于各种物理问题的研究都具有重要意义。
本文将从对流方程的基本形式和意义出发,探讨其常见解法及相关应用。
一、对流方程的基本形式与意义对流方程是描述流体中质量、热量和动量传递的方程,其基本形式可以写作:$$ \frac{\partial\phi}{\partial t} + (\mathbf{v}\cdot\nabla)\phi =\nabla\cdot(\Gamma\nabla\phi) $$其中,$\phi$为描述流体量的变量,如温度、密度、浓度等;$\mathbf{v}$为流体的流速,$\Gamma$为扩散系数。
对该方程的解析求解较为困难,故通常采用数值方法进行求解。
下面介绍几种常见的数值解法。
二、有限差分法有限差分法是在连续方程的基础上,利用有限差分代替导数,将微分方程变为代数方程组,从而利用计算机求解的方法。
其基本思想是将求解区域划分为有限个网格,对每个网格内的量用差分代替导数,从而得到有限差分方程。
以简单的二维对流扩散为例,其对流方程为:$$ \frac{\partial\phi}{\partial t} + u\frac{\partial\phi}{\partial x} + v\frac{\partial\phi}{\partial y} = \Gamma\frac{\partial^2\phi}{\partial x^2} + \Gamma\frac{\partial^2\phi}{\partial y^2} $$其中,$u$和$v$分别代表$x$和$y$方向的流速。
对该方程进行离散,假设$\phi_{i,j}$为$x=i\Delta x$,$y=j\Delta y$处的$\phi$值,则可以得到:$$ \frac{\phi^{k+1}_{i,j} - \phi^k_{i,j}}{\Delta t} +u\frac{\phi^k_{i+1,j} - \phi^k_{i-1,j}}{2\Delta x} +v\frac{\phi^k_{i,j+1} - \phi^k_{i,j-1}}{2\Delta y} $$$$ = \frac{\Gamma\Delta t}{(\Delta x)^2}(\phi^k_{i+1,j} -2\phi^k_{i,j} + \phi^k_{i-1,j}) + \frac{\Gamma\Delta t}{(\Deltay)^2}(\phi^k_{i,j+1} - 2\phi^k_{i,j} + \phi^k_{i,j-1}) $$其中,$k$为时刻,$\Delta x$和$\Delta y$分别为$x$和$y$方向的网格间距。

对流扩散方程解析解对流扩散方程(Convection-DiffusionEquation)是流体动力学领域里一个基本的求解方程,它表示物理系统的流体流动特征,可用于模拟和分析气体的湍流流动、热力学和传热运算等问题。
新的求解方法对对流扩散方程的解析解具有重要意义。
对流扩散方程的一般形式为:$$frac{partial c}{partial t}+ucdotabla c-DDelta c=f$$其中,u表示大尺度的流体速度,D表示流体扩散系数,f表示质量源期(如,物质沉积或物质释放),c表示浓度。
一般情况下,形式如上的对流扩散方程是无法求解的,因其难以确定恰当的初始条件。
在这种情况下,研究者们提出了不同的解析解算法,其目的是通过特定的分析步骤来求解该方程。
为此,研究者们将对流扩散方程分解成多个子方程,以便更容易的进行解析解析。
其中有许多不同的解析方法,这些方法大多建立在以下基础之上:1.量分离:将变量从原始方程分离出来,然后重新组合,使方程具有更好的求解性。
2.分替换:通过将复杂的积分变换成容易求解的形式,从而更容易求解对流扩散方程。
3.征方程:由于对流扩散方程的变量分离及积分替换,可以将其转换为简单的特征方程,从而可以更快地求出解析解。
4.值方法:这种方法采用计算机进行数值计算,可以从多个精度接近系统中求出解析解。
上述方法都可以用来求出对流扩散方程的解析解,但也存在一些潜在的问题,如数值误差、边界条件不易计算等。
对流扩散方程的解析解技术可以用来分析流体流动特性,模拟和分析气体湍流流动、热力学和传热运算等问题。
有了这些技术,研究者们可以更好地模拟或理解物理系统的流体特性,从而更好地解决实际中存在的问题。
例如,研究者可以利用对流扩散方程的解析解算法来分析汽车的空气动力学运动特性,有效改善汽车的燃油经济性和可靠性;或者用来研究空气流动的特性、助力涡轮机的性能改善;或者用来研究飞行器在进入大气时的热阻力特性,提高航天设备的安全性,等等。
五种离散格式储运与建筑工程学院能源与动力工程系计算传热学课程大作业报告作业题目:五种对流离散项的对比研究学生姓名:宋龙学号:6030221专业班级:能动-班2017年 11 月 3 日目录1 计算题目 (1)2 数学物理模型 (2)3 计算区域及方程离散 (3)3.1 区域离散 (3)3.2 方程离散 (3)3.2.1 中心差分格式 (3)3.2.1 迎风差分格式 (4)3.2.3 混合格式 (4)3.2.4 指数格式 (5)3.2.5 指数格式 (6)3.2.6 五种格式格式系数aEDe的表达式 (6)4 数值方法及程序流程 (7)5 计算结果验证及网格独立性考核 (8)5.1 计算结果验证 (8)5.1 网格独立性考核 (11)6 结果分析与讨论 (14)7 参考资料 (15)附录 (16)附录A:计算环境及源程序 (16)1计算题目对于有源项的一维稳态空气对流-扩散传热方程:d dx ρuT=ddxλcdTdx+S设源项S=0.5-100x,利用中心差分格式,一阶迎风格式,混合格式,指数格式,乘方格式求解在不同流速情况下,温度T的一维分布。
2数学物理模型物理模型:一维,稳态,有内热源,常物性控制方程:ddx ρuT=ddxλcdTdx+Sλc=Γ物理条件:ρ,Γ=const s=0.5-100x边界条件:x=0 T=300K;x=1 T=500K由于在常物性均分网格的情况下网格贝克勒数与流速成正比,所以在流速不同的情况下求温度场即在网格贝克勒数不同的情况下求温度场。
3计算区域及方程离散3.1区域离散3.2 方程离散3.2.1 中心差分格式由控制方程:ddx ρuT=ddxΓdTdx+S对一维模型方程在P控制容积内做积分,取分段线性型线,经整理可得:(ρuT)e?ρuT w=ΓdTdx eΓdTdx w+S PΔx P(ρu)e T E+T Pρu wT P+T W=ΓeeT E?T P?ΓwwT P?T W+S PΔx P整理可得:a P T P=a E T E+a W T W+S PΔx P 其中:a E=D e?1F e=D e(1?1P?e) D e=ΓeeF e=(ρu)ea W=D w+1F w=D w(1+1P?w) D w=ΓwwF w=(ρu)wa P=a E+a W+F e?F w为保证代数方程迭代求解的收敛性,我们要求计算中质量守恒一定要满足,于是:F e?F w=0 a P=a E+a W3.2.1 迎风差分格式控制容积法定义:界面上未知函数永远取上游节点之值紧凑形式:(ρuT)e=T P[F e,0]?T E[?F e,0](ρuT)w=T W[F w,0]?T P[?F w,0]带入控制方程,化简得:a P T P=a E T E+a W T W+S PΔx P其中:a E=D e+?F e,0=D e(1+?P?e,0)a W=D w+F w,0=D w(1+P?w,0)a P=a E+a W+F e,0+?F w,0??F e,0?F w,0=a E+a W+F e?F w为保证代数方程迭代求解的收敛性,我们要求计算中质量守恒一定要满足,于是:F e?F w=0 a P=a E+a W3.2.3混合格式紧凑定义:a E D e =[ ?P?e,1?12P?e,0]a W D w =[0,1+12P?w,P?w]3.2.4指数格式含义:根据一维模型的精确解相对应的离散方程构成的一种格式。