因式分解：完全平方公式_课件

=3a(x+y)2
=(a+b-6)2
分解因式：
(1) ax2+2a2x+a3
(2) -3x2+6xy-3y2
(3) (x+y)2-12x-12y+36
解：(1)原式= a(x2+2ax+a2)
(2)原式= -3(x2-2xy+y2)
=a(x+a)2
=-3(x-y)2
(3)原式=(x+y)2-12(x+y)+36
A. x2-y2= (x+y) (x-y)
B. x2+6x+9= (x+3)2
C. x2+xy=x (x+y)
D. x2+y2= (x+y)2
5.若x2- 2(k+1)x+4是完全平方式，则k的值为( A )
A.1或-3
B. -1或3
C.±1
D.±3
6.已知 = + 2，则代数式32 − 6 + 3 2 + 2022的值为（ D ）
±
10．若x2﹣8x+m2＝(x﹣4)2，那么m＝_____．
11．若 2 + (3 − ) + 9可以用完全平方式来分解因式，则m的值为
−或9
__________．
12．分解因式：
(1) − 22 + 3 ；
(2)3 − 102 + 25；
(3) 2 − 5
(4)(2 + 2 − 2 )2 −42 2 .
例3.分解因式：
(1) 3ax2+6axy+3ay2

a2 2• a •bb2
(1)、解：16x2 24x 9
方法：当一个式子满足完全
(4x)2 2 4x 3 32
平方式的所有特征时，可直 接分解因式。结果为这两平
4x 32
方项底数和或差的平方，是
和是差看中间项的符号
分析：- x2 4xy 4 y2 - x2 2 • x • 2 y 2 y2
• 学习重点：
运用完全平方公式分解因式．
学习难点：综合运用提公因式和公式法分解
因式
复习引入
问题一：大家还记得什么是因式分解吗?
因式分解就是将一个多项式化成几个整式的 积的形式
即： 和
积
问题二：我们已经学习了分解因式的哪
些方法？
1、提公因式法 2、公式法
平方差公式 a2 b2 a ba b
即：两个数的平方差等于 这两个数的和与差的积
方法：若式子有整体满足完全平方 式可直接进行因式分解，需注意中 间项的符号
练习2 将下列多项式分解因式：
1 25a3 ax2 10a2x
2 12x3 12x2 2 y 1- 3x2y -12
答案：
1 a5a x2
a b2 b a2
2 - 3x2 y 1 2x2
或 - 32x 2 y 12
你对因式分解的方法有什么新的发现？请尝试概括 你的发现.
把整式的乘法公式——完全平方公式 倒过来 就得到因式分解的完全平 方公式：
a2 2ab+b2 =（a b）2
首2 2 首 尾 尾2 首 尾2
即两个数的平方和加上（或减去）这两个 数的积的2倍，等于这两个数的和（或差） 的平方
1、在下面括号ቤተ መጻሕፍቲ ባይዱ填空
14.3.2.2 利用完全平方公式因式分解

5.如果x2+mxy+9y2是一个完全平方式，那么m的值为（ B ） A.6 B.±6 C.3 D.±3
6.已知a、b、c是三角形的三边,请你判断a2-b2-c2-2bc的值的正负.
7.说明无论a、b为何值，代数（a+b)²+2(a+b)+5 的值均为正值.
8.若a+b=1,a+c=2,b+c=3,利用因式分解求值： a2+b2+c2+ab+ac+bc.
自 学 检 查
1.下列各式是不是完全平方式？
（1）a2-ab+b2 × （2）a2-4a+4 =a2 -4a +22 √ （3）x2+4xy+4y2=x2+4xy + (2y)2√ （4）x2-6x-9 =x2-6x-32 ×
2.按照完全平方公式填空：
（1）a2-10a+( 25 )=( a-5 )2
(4)原式=(2x +y-3) 2
总结:①因式分解的一般思路: 一提（提公因式法） 二套（套用公式法）
②整体思想，例如：把 2x＋y 看做一个整体。
巩固练习
1.(1)若x2＋2kx＋9是一个完全平方式，则k＝ ___±___3__ (2)若x2＋8x＋k2是一个完全平方式，则k＝ __±___4___．
（ （23））1(a2-y2()+r2s)a+yr+21s2==((
ay+1)2
½ - rs)2
4
自 3.把下列各式因式分解 1 x2 12x 36 2 2xy x2 y2
学 (3) 3ax2﹢6axy﹢3ay2
检 查

（1）a2－4a+4; （3）4b2+4b-1; 是 不是 （2）1+4a² ; 不是 （4）a2+ab+b2; 不是
分析： （2）因为它只有两项；
（ 3） 4b² 与-1的符号不统一；
（4）因为ab不是a与b的积的2倍.
P118 例2 分解因式：
（1）16x2+24x+9； （2）-x2+4xy-4y2.
2
P118 例6 分解因式：
(1)3ax2+6axy+3ay2 ； (2)(a+b)2－12(a+b)+36.
分析：(1)中有公因式3a,应先提出公因式,再进一步分解因式； (2)中将a+b看成一个整体,设a+b=m,则原式化为m2－12m+36.
解: (1)原式=3a(x2+2xy+y2) =3a(x+y)2 (2)原式=(a+b)2－2· (a+b) · 6+62
=(x2－6－3)2 =(x2－9)2 =[(x＋3)(x－3)]2 =(x＋3)2(x－3)2
1. 把下列各式分解因式.
2. 因式分解：x4－8x2y2+16y4．
解：原式=(x2)2－2· x2· 4y2 +(4y2)2
=(x2－4y2)2
=[(x＋2y)(x－2y)]2
=(x＋2y)2(x－2y)2
（2）每个多项式的第一项和第三项有什么特征？
这两项都是数或式的平方，并且符号相同
（3）中间项和第一项，第三项有什么关系？
是第一项和第三项底数的积的±2倍
a 2 2ab b 2
完全平方式的特点： 1.必须是三项式（或可以看成三项的）； 2.有两个同号的数或式的平方； 3.中间有两底数之积的±2倍.

方式.
完全平方式的条件：(1)多项式是二次三项式；(2)首末
两项是两个数(或式子)的平方且符号相同，中间项是这
两个数(或式子)的积的2 倍，符号可以是“＋”，也可以
是“－”.
感悟新知
知5－讲
2. 完全平方公式
两个数的平方和加上(或减去)这两个数
的积的2 倍，等于这两个数的和(或差)的平方.
即：a2±2ab＋b2＝(a±b)2 .
知4－讲
3. 运用平方差公式分解因式的步骤
一判：根据平方差公式的特点，判断是否为平方差，若负
平方项在前面，则利用加法的交换律把负平方项放在后面；
二定：确定公式中的a和b，除a和b是单独一个数或字母外，
其余不管是单项式还是多项式都必须用括号括起来，表示
一个整体；三套：套用平方差公式进行分解；四整理：将
(2)确定另一个因式，另一个因式即多项式除以公因式所
得的商；
(3)写成积的形式.
感悟新知
知3－讲
特别解读
1. 提公因式法实质上是逆用乘法的分配律.
2. 提公因式法就是把一个多项式分解成两个因式的积的形
式，其中的一个因式是各项的公因式，另一个因式是多
项式除以这个公因式所得的商.
感悟新知
知3－练
例 5 把下列多项式分解因式：
感悟新知
例 3 仔细阅读下面例题，解答问题：
知1－练
例题：已知把x2－4x＋m分解因式后有一个因式是x
＋3，求其另一个因式及m的值.
解：设另一个因式为x＋n，则x2－4x＋m＝(x＋3)(x
＋n)，即x2－4x＋m＝x2＋(n＋3)x＋3n.
＝－，
＋＝－，
所以
解得
＝－.

做一做
用两数和的完全平方公式计算(填空):
(1)(a + 1)2=(a )2+2(a )(1 )+ ( 1)2
(a + b)2 = a2 + 2 a b + b2
(2)(2a+3b)2= ( 2a)2 + 2(2a )( 3b ) + ( 3b )2
自主探索
你能用两数和的完全平方公式 来计算(a−b)2吗?
完全平方公式
(a+b)2=a2+2ab+b2 (a−b)2=a2−2ab+b2
两个数的和（或差）的平方，等 于它们的平方和，加上（或减去）它 们的积的2倍。
请先计算下列各题：
(1) (a 2)(a 2) _____a_2__4______; (2) (3 x)(3 x) _____9___x_2_____;
我来做一做
一块方巾铺在正方形 的茶几上，四周刚好都垂 下15cm，如果设方巾的 边长为a，怎样求茶几的 面积？结果怎样用关于a 的多项式表示？如果 a=100cm，茶几的面积是 多少cm2?
想一想
(1)用简便的方法计算: 1.23452+0.76552+2.469×0.7655 (2)已知(a+b)2=11,ab=1,求(a-b)2的 值.
(3) (4k 3)(4k 3) (4) (1 x)( x 1)
(5)
1 2
x
y
1 4
x
y
快速计算:例2 用平方差公式计算
(1) 103×97 (2) 59.8×60.2 5678×5680-56792
(2+1)(22+1)(24+1)(28+1)+1

1、想要体面生活，又觉得打拼辛苦；想要健康身体，又无法坚持运动。人最失败的，莫过于对自己不负责任，连答应自己的事都办不到，又何必抱怨这个世界都和你作对？人生的道理很简单，你想要什么，就去付出足够的努力。 2、时间是最公平的，活一天就拥有24小时，差别只是珍惜。你若不相信努力和时光，时光一定第一个辜负你。有梦想就立刻行动，因为现在过的每一天，都是余生中最年轻的一天。 3、无论正在经历什么，都请不要轻言放弃，因为从来没有一种坚持会被辜负。谁的人生不是荆棘前行，生活从来不会一蹴而就，也不会永远安稳，只要努力，就能做独一无二平凡可贵的自己。 4、努力本就是年轻人应有的状态，是件充实且美好的事，可一旦有了表演的成分，就会显得廉价，努力，不该是为了朋友圈多获得几个赞，不该是每次长篇赘述后的自我感动，它是一件平凡而自然而然的事，最佳的努力不过是：但行好事，莫问前程。愿努力，成就更好的你！ 5、付出努力却没能实现的梦想，爱了很久却没能在一起的人，活得用力却平淡寂寞的青春，遗憾是每一次小的挫折，它磨去最初柔软的心智、让我们懂得累积时间的力量；那些孤独沉寂的时光，让我们学会守候内心的平和与坚定。那些脆弱的不完美，都会在努力和坚持下，改变模样。 6、人生中总会有一段艰难的路，需要自己独自走完，没人帮助，没人陪伴，不必畏惧，昂头走过去就是了，经历所有的挫折与磨难，你会发现，自己远比想象中要强大得多。多走弯路，才会找到捷径，经历也是人生，修炼一颗强大的内心，做更好的自己！ 7、“一定要成功”这种内在的推动力是我们生命中最神奇最有趣的东西。一个人要做成大事，绝不能缺少这种力量，因为这种力量能够驱动人不停地提高自己的能力。一个人只有先在心里肯定自己，相信自己，才能成就自己！ 8、人生的旅途中，最清晰的脚印，往往印在最泥泞的路上，所以，别畏惧暂时的困顿，即使无人鼓掌，也要全情投入，优雅坚持。真正改变命运的，并不是等来的机遇，而是我们的态度。 9、这世上没有所谓的天才，也没有不劳而获的回报，你所看到的每个光鲜人物，其背后都付出了令人震惊的努力。请相信，你的潜力还远远没有爆发出来，不要给自己的人生设限，你自以为的极限，只是别人的起点。写给渴望突破瓶颈、实现快速跨越的你。 10、生活中，有人给予帮助，那是幸运，没人给予帮助，那是命运。我们要学会在幸运青睐自己的时候学会感恩，在命运磨练自己的时候学会坚韧。这既是对自己的尊重，也是对自己的负责。 11、失败不可怕，可怕的是从来没有努力过，还怡然自得地安慰自己，连一点点的懊悔都被麻木所掩盖下去。不能怕，没什么比自己背叛自己更可怕。 12、跌倒了，一定要爬起来。不爬起来，别人会看不起你，你自己也会失去机会。在人前微笑，在人后落泪，可这是每个人都要学会的成长。 13、要相信，这个世界上永远能够依靠的只有你自己。所以，管别人怎么看，坚持自己的坚持，直到坚持不下去为止。 14、也许你想要的未来在别人眼里不值一提，也许你已经很努力了可还是有人不满意，也许你的理想离你的距离从来没有拉近过......但请你继续向前走，因为别人看不到你的努力，你却始终看得见自己。 15、所有的辉煌和伟大，一定伴随着挫折和跌倒；所有的风光背后，一定都是一串串揉和着泪水和汗水的脚印。 16、成功的反义词不是失败，而是从未行动。有一天你总会明白，遗憾比失败更让你难以面对。 17、没有一件事情可以一下子把你打垮，也不会有一件事情可以让你一步登天，慢慢走，慢慢看，生命是一个慢慢累积的过程。 18、努力也许不等于成功，可是那段追逐梦想的努力，会让你找到一个更好的自己，一个沉默努力充实安静的自己。 19、你相信梦想，梦想才会相信你。有一种落差是，你配不上自己的野心，也辜负了所受的苦难。 20、生活不会按你想要的方式进行，它会给你一段时间，让你孤独、迷茫又沉默忧郁。但如果靠这段时间跟自己独处，多看一本书，去做可以做的事，放下过去的人，等你度过低潮，那些独处的时光必定能照亮你的路，也是这些不堪陪你成熟。所以，现在没那么糟，看似生活对你的亏欠， 其实都是祝愿。

什么关系？ 3.两个完全平方式的积中不同的是哪一项？与 a，
b有什么关系？它的符号与什么有关？
数学课堂教学课件设计
新课讲解
想一想：下面各式的计算是否正确？如果不正确，
应当怎样改正？
(1)(x+y)2=x2 +y2
×
(2)(x -y)2 =x2 -y2
×
(x +y)2 =x2+2xy +y2 (x -y)2 =x2 -2xy +y2
a
b
ab
(a−b)2 = a2 −ab −b(a−b) = a2−2ab+b2 .
a
差的完全平方公式： （a-b)2= a2-2ab+b2 .
数学课堂教学课件设计
新课讲解
问题4：观察下面两个完全平方式，比一比，回答下
列问题： (a+b)2= a2+2ab+b2，
(a-b)2=a2-2ab+b2.
1.说一说积的次数和项数. 2.两个完全平方式的积有相同的项吗？与a，b有
新课讲解
【练习】计算：(1)(a－b＋c)2； (2)(1－2x＋y)(1＋2x－y)．
解：(1)原式＝[(a－b)＋c]2 ＝(a－b)2＋2(a－b)c＋c2 ＝a2－2ab＋b2＋c2＋2ac－2bc.
(2)原式＝[1－(2x－y)][1＋(2x－y)] ＝12－(2x－y)2 ＝1－4x2＋4xy－y2.
（a+b)2= a2+2ab+b2 ；（a-b)2= a2-2ab+b2 .
数学课堂教学课件设计
新课讲解
（a+b)2= a2+2ab+b2 ， （a-b)2= a2-2ab+b2 . 也就是说，两个数的和（或差）的平方，等于 它们的平方和，加上（或减去）它们的积的2倍.这 两个公式叫做（乘法的）完全平方公式. 简记为： “首平方，尾平方，积的2倍放中间”.

第十四章 整式的乘法与因式分解 第10课时完全平方公式
预习导学
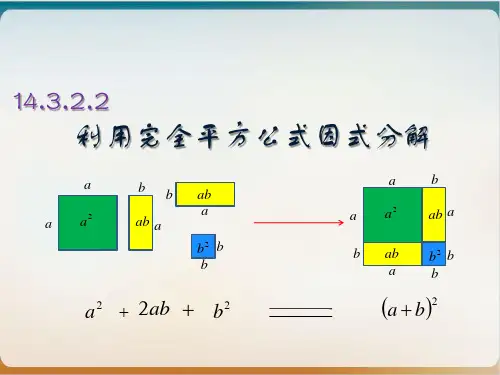
完全平方公式：(a±b)²=
a² ± 2ab + b²_。于它们的 平方和_,加(或减)它们的 积的两倍
A 组基础夯实
知识点1 用完全平方公式计算
1.计算(a+b)²的正确结果是(C )
A.a²+b² C.a²+b²+2ab
A.—6 C.3
5. 已知(x-p²=x²+mx+36,
B.—3 D.6
则 m= ±12
A 组基础夯实 6.计算：(1)(2a+3b)²; 解：(1)原式=(2a)²+2×2a-3b+(3b)² =4a²+12ab+9b2. (2)(—a+5b)².
解：(2)原式=a²—10ab+25b².
A组基础夯实
=40401.
B组思想方法
考向2 利用完全平方公式变形后整体代入求值 12 . 若ab=—2,a²+b²=5, 则 (a—b)²的值为 9 . 13 . 若x(x—2)=3, 则(x—1)²的值是 4 .
B组思想方法
14. 已知A是关于x的多项式，且A—(x—2)²=x(x+7). (1)求多项式A; 解：(1)∵A—(x—2)²=x(x+7), ∴A=(x—2)²+x(x+7)=2x²+3x+4. (2)若一2x²—3x+1=0, 求多项式A的值。 解：(2)∵—2x²—3x+1=0,
哪个等式( C )
A.x²—y²=(x—y)(x+y) B.(x—y)²=x²—2xy+y² C.(x+y)²=x²+2xy+y² D.(x—y)²+4xy=(x+y)²

4.3 用乘法公式分解因式
勤反思
小结
完 全 平 方 公 式
特征
运用完全平方公式分解因式
运用完全平方公式简化运算
4.3 用乘法公式分解因式
反思
判断下面分解因式的过程是否正确，若不正确，请改正．
a3b－2a2b＋ab＝ab(a2－2a＋1)．
解：不正确．改正：a3b－2a2b＋ab＝ab(a2－2a＋1)＝ab(a－1)2.
4.3 用乘法公式分解因式
筑方法
类型一 用完全平方公式分解因式
例1 教材例3变式题用完全平方公式进行因式分解：
(1)9m2＋24mn＋16n2；(2)(x2－4x＋4)－4(x－2)＋4.
解： (1)9m2＋24mn＋16n2＝(3m＋4n)2.
(2)(x2－4x＋4)－4(x－2)＋4＝(x－2)2－4(x－2)＋4＝(x－2－2)2＝(x－4)2.
解：(1)x3－2x2＋x＝x(x2－2x＋1)＝x(x－1)2. (2)16a4－8a2＋1＝(4a2)2－2×4a2×1＋12＝(4a2－1)2＝(2a＋1)2(2a－1)2.
4.3 用乘法公式分解因式
【归纳总结】因式分解的一般步骤 (1)观察多项式是否存在公因式； (2)若提取公因式后的式子是两项或三项，则考虑是否符合平 方差公式或完全平方公式的特点； (3)检查每个因式是否分解彻底．
第4章
4.3
分解因式
用乘法公式分解因式
第4章 因式分解
第2课时
用完全平方公式 分解因式
学知识 筑方法
勤反思
4.3 用乘法公式分解因式
学知识
知识2ab＋b2＝(a＋b)2，a2－2ab＋b2＝(a－b)2.
平方和 ，加上(或者减去)这两数的积的2倍，等于这两数 即两数的________

完全平方公式(gōngshì) 的几何意
义差的完全平方(píngfāng)公式：
b ab b²
a
a² ab
(a-b)²
ab
(ab)2 a 2 ababb2
12/9/2021
a22abb2 第六页，共十五页。
归 纳 完全平方公式(gōngshì)的结构特点：
(a+b)2＝a2 +2ab+b2 (a-b)2＝a2 -2ab + b2 ①等号左边(zuǒ bian)两个数的和（或差）的平方 ②等号右边是等号左边(zuǒ bian)两个数的平方和加上 （或减去）这两个数的乘积的2倍 口诀： 完全平方有3项，首平方，尾平方， 首尾乘积2倍在中央，中央符号同前方
mn
a
2
3y223y•xx2 m n22•m n•aa2
9y26xyx2
练习2：
m 2n22am na2
①-5x+2y2 12/9/2021
②-4y-142
第十页，共十五页。
总结：
① 4 m + n 2 正+正
② x - 2 y 2 正正
③ - x + 3 y 2 负+正
正正3 y x 2
教学 课件 (jiāo xué)
数学 七年级 下册 (niánjí) 青岛版
12/9/2021
第一页，共十五页。
第12章 乘法(chéngfǎ)公式与因式分解
12.2 完全平方公式
12/9/2021
第二页，共十五页。
探索发现
请用多项式的乘法(chéngfǎ)法则计算：(a+b)2
(a+b)2=(a+b)(a+b)=a2+ab+ab+b2=a2+2ab+b2 由此得到(dédào)完全平方公式，即：