当前位置：文档之家 › 全等三角形的判定总复习ppt课件

全等三角形的判定总复习ppt课件

  • 格式：ppt
  • 大小：1.33 MB
  • 文档页数：26

下载文档原格式

  / 26

合集下载

人教版八年级上册 12.2 三角形全等的判定 复习课课件 (共38张PPT)

人教版八年级上册 12.2 三角形全等的判定 复习课课件 (共38张PPT)

B
证明：连接AD， ∵AC=DC
∴∠CAD= ∠CDA
同理， ∠BAD= ∠BDA
∴ ∠BAC= ∠BDC
∵ AC=DC
∠A= ∠D
AB=DB
∴△ABC≌ △DBC（SAS）
A C
如图所示，
△ABC≌△DBC ，那么 B 边边边定理得证。
三角形的判定定理四
D
在两个三角形中，
如果有三条边相等，
AC=DC
求证：OE=OF 证明 在△AOB和△COD中
E
A
B
OB=OD
∠AOB=∠COD
O
OA=OC ∴△AOB≌△COD （SAS） ∴∠B=∠D （全等三角形的对应角相等） D 在△BOE和△DOF中
∠B=∠D
C F
OB=OD ∠BOE=∠COF ∴△BOE≌△DOF （ASA） ∴OE=OF （全等三角形的对应边相等）
1、如右图：已知，∠ABE=∠CBD, ∠BCE=∠DBA,EC=AD 求证：AB=BE,BC=DB
2、如右图：已知，AD, EF,BC交于O，且AO=OD，BO=OC， EO=OF 求证：△AEB≌△DFC
全等三角形的判定（三）
AAS（角角边定理）
定理的引入:
如图在△ABC和△DEF中，∠A=∠D，
那么这两个三角形全 等。
AB=DB
△ABC≌ △DBC（SSS）
BC=BC
例1：如图，已知AB=CD，BC=DA。
说出下列判断成立的理由： （1）△ABC≌△CDA A
D
（2）∠B=∠D
解（1）在△ABC和△CDA中 B
C
AB=CD（已知）
BC=DA（已知）
AC=CA（公共边）

完整版-全等三角形总复习PPT教学课件

完整版-全等三角形总复习PPT教学课件

AC=BC
∠BCE=∠DCA
DC=EC
∴ △ACD≌△BCE (SAS)
∴ BE=AD
2024/3/9
29
6. 如图A、B、C在一直线上，△ABD，△BCE都是等边 三角形，AE交BD于F，DC交BE于G，求证：BF＝BG。
AB
＝
DB
∠ABE ＝ ∠ DBC
BE＝BC ∴△ABE≌△DBC(SAS)
D
C
2
1
A
B
思路3： 已知一边一角（边与角相邻）：
找夹这个角的另一边
AD=CB （SAS）
找夹这条边的另一角
∠ACD=∠CAB（ASA）
找边的对角
∠D=∠（B AAS）
15
如图，已知∠B= ∠E，要识别△ABC≌ △AED，需 要添加的一个条件是--------------
A
D
C
E
思路4：
找夹边
AB=AE (ASA)
∴ △ADC ≌ △EDB
D
C
∴ AC = EB
在△ABE中，AE < AB+BE＝AB+AC
E
即 2AD < AB+AC
∴ AD 1 (AB AC) 2
2024/3/9
35
12.如图,已知AC∥BD，EA、EB分别平分∠CAB和∠DBA， CD过点E，则AB与AC+BD相等吗？请说明理由。
C A
∵ QD⊥OA，QE⊥OB，QD＝QE（已知）． ∴点Q在∠AOB的平分线上．（到角的两边的距
离相等的点在角的平分线上）
2024/3/9
10
2.如图, △ABC的角平分线BM,CN相交于点P, 求证：点P到三边AB、BC、CA的距离相等

人教版《三角形全等的判定》PPT全文课件

人教版《三角形全等的判定》PPT全文课件
知识回顾
问题探究
课堂小结
随堂检测
活动2
0
探究一：探索三角形全等的条件
建立模型，探索发现
只给定一条边相等：
只给定一个角相等：
3cm
3cm
3cm
30°
30°
30°
满足一个条件相等时，两个三角形不一定全等.
知识回顾
问题探究
课堂小结
随堂检测
活动3
0
探究一：探索三角形全等的条件
问题：两个三角形满足六个条件中的两个条件，两个三角形全等吗？两个条件有几种情况?
证明：连接AC，
【解题过程】
如图, 在四边形ABCD中, AB=AD, CB=CD, 求证:∠B=∠D.
∴∠B=∠D．(全等三角形对应角相等)
【思路点拨】先连接AC, 由于AB=AD, CB=CD, AC=AC, 利用SSS可证△ABC≌△ADC, 于是∠B=∠D. 要求学生从“形”思维到“质”的思维飞跃, 实现将“文字语言”, “图形语言”转化为“符号语言”.
∥
∵BC=DE, ∴BC+CD=DE+CD. 即BD=CE.
【数学思想】 数形结合思想，分类讨论思想.
∴ ∠ADB＝∠FEC，AD=EF (全等三角形对应角相等) ∴AD∥EF(同位角相等，两直线平行)
在△ABD和△FCE中
∴△ABD≌△FCE (SSS).
知识回顾
问题探究
课堂小结
随堂检测
例4
0
探究三：利用三角形全等的判定“SSS”解决问题
△ABC是一个钢架，AB=AC，AD是连接点A与BC中点D的支架，请问AD⊥BC吗？请说明理由．
在△ABD和△ADC中，
∴△ABD≌△ACD (SSS).

三角形全等的判定(复习)

三角形全等的判定(复习)
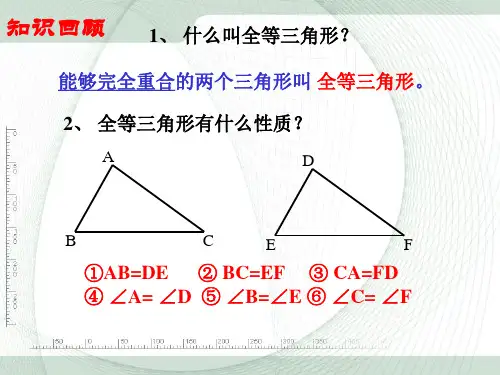
（1）：全等三角形的对应边相等、对应角相等。 （2）：全等三角形的周长相等、面积相等。 （3）：全等三角形的对应边上的对应中线、角平分线、高线分别相等。
SSS、SAS、ASA、AAS、HL(RT△)
方法指引
证明两个三角形全等的基本思路：
（1）：已知两边----
找第三边
(SSS)
找夹角
（SAS)
例3：如图，OB⊥AB,OC⊥AC,垂足为B,C,OB=OC AO平分∠BAC吗？为什么？
O
C
B
A
答： AO平分∠BAC
理由：∵ OB⊥AB,OC⊥AC ∴ ∠B=∠C=90° 在Rt△ABO和Rt△ACO中 OB=OC AO=AO ∴ Rt△ABO≌Rt△ACO （HL） ∴ ∠BAO=∠CAO ∴ AO平分∠BAC
E
C
A
B
2
1
D
(2)怎样变换△ABC和△AED中的一个位置,可使它们重合?
(3)观察△ABC和△AED中对应边有怎样的位置关系?
例6：如图所示，AB与CD相交于点O, ∠A=∠B，OA=OB 添加条件 所以 △AOC≌△BOD 理由是
A
O
D
C
B
∠C=∠D
∠AOC=∠BOD
图6
知识应用：
1.已知△ABC和△DEF,下列条件中,不能保证△ABC和△DEF全等的是( ) AB=DE,AC=DF,BC=EF ∠A= ∠ D, ∠ B= ∠ E,AC=DF C.AB=DE,AC=DF, ∠A= ∠D D.AB=DE,BC=EF, ∠ C= ∠ F
F
E
D
C
B
A
例9：如图，已知AC∥EF,DE∥BA,若使△ABC≌△EDF,还需要补 充的条件可以是

三角形的全等的复习课件

三角形的全等的复习课件

综合练习题
总结词
综合运用知识
示例题目
在两个直角三角形中，一个直角边和一个斜边分别对应相 等，请证明这两个三角形全等。
详细描述
综合练习题要求学生能够综合运用三角形全等的知识解决 一些实际问题或涉及多个知识点的复杂问题，以提高学生 的综合运用能力和解题技巧。
答案
根据直角三角形全等的判定定理——斜边直角边（HL） 定理，如果两个直角三角形的斜边和一直角边对应相等， 则这两个直角三角形全等。
示例题目
已知两个三角形ABC和DEF中，AB=DE, BC=EF, ∠A=∠D，请证明这两个三角形全等。
详细描述
提高练习题要求学生能够运用三角形全等的判定 定理解决一些较为复杂的问题，如证明两个三角 形全等或寻找全等的条件。
答案
根据角边角（ASA）定理，如果两个三角形的两 角和一边相等，则这两个三角形全等。因为 ∠A=∠D和AB=DE是两边，且∠B=∠E是一角，所 以根据ASA定理，三角形ABC和DEF全等。
02
在实际生活中，三角形全等可以 用来解决一些实际问题，如测量 、建筑设计和机械制造等领域。
02
三角形全等的判定方法
边边边相等（SSS）
01
02
03
04
总结词
三边对应相等的两个三角形全 等。
详细描述
如果两个三角形的三组对应边 分别相等，则这两个三角形全
等。
证明方法
通过构造两个三角形，并证明 它们的三组对应角分别相等。
计算面积
全等三角形具有相同的面积。因此，通过比较两个三角形的 面积，可以解决一些面积计算问题。
在证明问题中的应用
证明角度相等
如果两个三角形在某些角度或边 长上相等，则可以通过三角形全 等证明其他角度或边长也相等。

三角形全等专题复习ppt课件

三角形全等专题复习ppt课件

B
C
已知：
AB=DC,AC=BD. 求证： △ABC≌△DCB
图中隐藏条件二 ------ 公共角
A
B
C
E
D
已知： AB=AC,∠D=∠E.
求证： △ABD≌△ACE
图中隐藏条件三 --- 对顶角
C
OB A
已知：
D
AO=BO,CO=DO.
求证：△AOC≌△BOD
转化条件一 ------ 部分公共边
知识点回顾：
1、三角形全等有哪些判定方法？
2、如何从题目中找到三角形全等的条件？
直接条件
图中隐藏条件
转化条件
图中隐藏条件 一 ---- 公共边
B
A
A
D
A
C
D
已知： AB=AD,∠BAC=∠DAC. 求证：△ABC≌△ADC
BC D
已知：在RT△ACB和 RT△ACD中 AB=AD. 求证：△ABC≌△ADC
A
B
D
E
C
如图，∠B＝∠E，AB＝EF，BD＝EC，那么 AC=FD吗？AC∥FD吗？为什么？
F
B
C 42 13 D
E
A
点拨： 证明两条线段相等或两个角相等的思路通常是证明它所在的两个三角形全等。
谈谈本节课有何收获？
A
A
BE CF
A D
F
B
C
E
已知：
D
AB=DF,∠B=∠F,
BE=CF.
求证：
△ABC≌△DFEBE源自CF已知：
AB=DE,AC=DF,BE=CF.
求证：△ABC≌△DEF
D
已知：
AB=DE,AC=DF,BF=CE. 求证：△ABC≌△DEF

用全等三角形的判定总复习ppt课件

用全等三角形的判定总复习ppt课件

7.如图（5）∠CAE=∠BAD，∠B=∠D，
AC=AE，△ABC与△ADE全等吗？为什么？
B
解：∵ ∠CAE=∠BAD(已知)
E
D
∴ ∠CAE+∠BAE=∠BAD+∠BAE
C
A
(等量加等量，和相等) 即∠BAC=∠DAE
在△ABC和△ADE中，
∠B=∠D(已知)
∠BAC=∠DAE(已证)
AC=AE(已知)
典型例题:
例1 :如图,点B在AE上, ∠CAB=∠DAB,要使 ΔABC≌ΔABD,可补充的 一个条件是∠ACB=B=∠AEA=DC∠D.BEA
C
A
B E
D
分析：现在我们已知 A→∠CAB=∠DAB
S→ AB=AB(公共边) .
①用SAS,需要补充条件 AB=AC, ②用ASA,需要补充条件 ∠CBA=∠DBA, ③用AAS,需要补充条件 ∠C=∠D, ④此外,补充条件 ∠CBE=∠DBE也可以(?)
要使△ABD≌△ACD， • 根据“SAS”需要添加条件 AB=AC ； • 根据“ASA”需要添加条件∠BDA=∠CDA • 根据“AAS”需要添加条件 ∠B=∠C
D
C
； ；
友情提示：添加条件的题目.首先要 找到已具备的条件,这些条件有些是 题目已知条件 ,有些是图中隐含条件.
8
认 识 到 了 贫 困户贫 困的根 本原因 ，才能 开始对 症下药 ，然后 药到病 除。近 年来国 家对扶 贫工作 高度重 视，已 经展开 了“精 准扶贫 ”项目
12
D
E
M
N
B
C
创造条件！ ？ 6
认 识 到 了 贫 困户贫 困的根 本原因 ，才能 开始对 症下药 ，然后 药到病 除。近 年来国 家对扶 贫工作 高度重 视，已 经展开 了“精 准扶贫 ”项目

完整版三角形全等的判定ppt课件

完整版三角形全等的判定ppt课件
12.5 三角形全等的判定
初二（5、6）班
1
1、 什么叫全等三角形？
能够重合的两个三角形叫 全等三角形。
2、 已知△ABC ≌△ DEF，找出其中相等的边与角
A
D
①AB=DE ④ ∠A= ∠D
② BC=EF ⑤ ∠B=∠E
③ CA=FD ⑥ ∠C= ∠F
B
CE
F
全等三角形性质：
全等三角形的对应边相等，对应角相等。
40
例 如图，有一池塘，要测池塘两端A、B的距离，
可先在平地上取一个不经过池塘可以直接到达点A 和B
的点C，连接AC并延长至D，使CD =CA，连接BC 并延
长至E，使CE =CB，连接ED，那么量出DE的长就是A，
B的距离．为什么？
A
B
1
C
2
E
D
41
证明：在△ABC 和△DEC 中，
AC = DC（已知），
(4) 两角一边 ?
27
3.角边角公理(ASA)：
两角和它们的夹边分别相等的两个三角形全等.简 写成“角边角”或“ASA ”
A
几何语言：
在△ABC 和△ A′B′ C′中，
B
∠A =∠A′
AB = A′B′
∠B =∠B′
∴ △ABC ≌△ A′B′ C′（ASA）． B′
C A′
C′
28
4.角角边公理(AAS)：
AB =AC ，
∵ BD =CD ， B
D
C
AD =AD ，
∴ △ABD ≌ △ACD （ SSS ）．
32
证明的书写步骤：
①准备条件：证全等时要用的条件要先证好； ②三角形全等书写三步骤：

全等三角形的判定一ppt课件

全等三角形的判定一ppt课件
在△ABH和△ACH中
∵AB=AC，BD=CD，AD=AD ∴△ABD≌△ACD（SSS）；
在△ABH和△ACH中
D B HC
∵BD=CD，BH=CH，DH=DH
∴△DBH≌△DCH（SSS）
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
练一练
1.已知AC=FE，BC=DE，点A，D，B，F在一条直 线上，AD=FB（如图），要用“边边边”证明 △ABC ≌△ FDE，除了已知中的AC=FE，BC=DE 以外，还应该有什么条件？怎样才能得到这个条件？
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
30°50° ③两边：
2cm 4cm
30°
30°
可以发现按这 些条件画的三 30° 50° 角形都不能保 证一定全等。
2cm 4cm
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
动手操作，验证猜想
探究新知
由此可以得到以下基本事实，用它可以判 定两个三角形全等：
三边对应相等的两个三角形全等（可 以简写为“边边边”或“SSS”）。
A
用 数学语言表述：
在△ABC和△ DEF中
{ AB=DE BCC ≌△ DEF（SSS） E
F
判断两个三角形全等的推理过程，叫做证明三角形 全等。
应用所学，例题解析

全等三角形的判定PPT课件共34张

全等三角形的判定PPT课件共34张
24
2024/1/30
06
判定全等三角形的注意事项
25
准确理解全等三角形的定义和性质
2024/1/30
全等三角形的定义
两个三角形如果三边及三角分别对应 相等，则称这两个三角形全等。
全等三角形的性质
全等三角形的对应边相等，对应角相 等；全等三角形的周长、面积相等； 全等三角形的对应边上的中线、高线 、角平分线分别相等。
结论
三边分别相等的两个三角 形全等，简称“SSS”。
16
SAS判定法的证明
已知条件
两边和它们的夹角分别相 等的两个三角形。
2024/1/30
证明过程
将其中一个三角形旋转至 与另一个三角形两边重合 ，由于夹角相等，因此两 个三角形全等。
结论
两边和它们的夹角分别相 等的两个三角形全等，简 称“SAS”。
示例
若三角形ABC和三角形DEF中，∠A=∠D，∠B=∠E ，BC=EF，则三角形ABC全等于三角形DEF。
2024/1/30
14
2024/1/30
04
判定方法的证明与推导
15
SSS判定法的证明
01
02
03
已知条件
三边分别相等的两个三角 形。
2024/1/30
证明过程
通过平移或旋转其中一个 三角形，使得两个三角形 的三边分别重合，从而证 明两个三角形全等。
2024/1/30
在计算三角形面积时，如果知道两个三角形全等，那么可以直接得出它们的面积相 等。
9
2024/1/30
03
全等三角形的判定方法
10
边边边判定法（SSS）
定义
三边分别相等的两个三角形全等 。

直角三角形全等的判定ppt课件

直角三角形全等的判定ppt课件
分
析 锐角和任意一边对应相等判断两个直角三角形全等的方法
是“AAS”或“ASA”.
相等，故只需找另外两个条件即可.
17.4 直角三角形全等的判定
返回目录
对点典例剖析
考
点
典例
如图，四边形 ABCD 是一条河堤坝的横截面，
清
单
解 AE=BF，且 AE⊥CD，BF⊥CD，垂足分别为 E，F，AD=BC，求
读 证：∠C=∠D.
17.4 直角三角形全等的判定
考
点
清
单
解
读
返回目录
［解题思路］
突
破 过点 A 且垂直于 AC 的射线 AQ上运动，问点 P 运动到 AC
上什么位置时，△ABC 才能和△APQ 全等．
17.4 直角三角形全等的判定
返回目录

重
［答案］ 解：①当点 P 运动到 AC 中点时，AP=

难
题 AC=5=BC，∵∠C=∠QAP=90°，在 Rt△ABC 和 Rt△QPA 中
型 ∵DF=DB，DC=DE，∴Rt△CDF≌Rt△EDB（HL），∴CF=EB；
突
破
（2）设 CF=BE=x，则 AE=AB-BE=12-x，∵AD 平分∠BAC
，DE⊥AB，∠C=90°，∴CD=DE．在 Rt△ACD 和 Rt△AED
中，∵AD=AD，CD=ED，∴Rt△ACD≌Rt△AED（HL），
型
突 ， CB=AP，BA=PQ ，∴Rt△ABC≌Rt△QPA（HL），即
破
AP=BC=5 cm，此时点 P 是 AC 的中点；②当点 P 运动到
与点 C 重合时，AP=AC，在 Rt△ABC 和 Rt△PQA 中，

全等三角形判定复习-ppt公开课课件

全等三角形判定复习-ppt公开课课件

课堂小结
边角边公理 角边角公理 边边边公理 角角边公理
作业：课本P115 1~8
小结
为了规范事业单位聘用关系，建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ，保障 用人单 位和职 工的合 法权益
角角边公理（AAS）
有两角和其中一角的对边对 应相等的两个三角形全等
小结
课前热身
已知：如图，AB=DC，AD=BC. 求证： ∠A= ∠C.
例1
已知：如右图，AB、CD相交于点O， AC∥DB,OC = OD, E、F为 AB上两点，
且AE = BF. 求证：CE=DF.
A
C
E
F
D
.
例2
A
如右图， 已知：AB=AD，CB=CD.
求证：AC⊥BD.
B
O
D
C
已知：△ABC的顶点和△DBC 的顶点A和D在BC的同旁, AB =DC, AC = DB, AC和DB相交 于点O.
求证：OA =OD.
练习一
继再 续接 学再 习厉 新， 知让 识我 吧们
教学重难点
教学重点：能让学生选择适当判定方法 判定两三角形全等。
教学难点：培养学生有条理的分析、推 理能力，并写出证明过程。
前面的知识你忘记了吗？
让我们一起来 复习一下吧
我们学过几种三角形的全等判定呢？（4种）
边角边公理 角边角公理 边边边公理 角角边定理
为了规范事业单位聘用关系，建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ，保障 用人单 位和职 工的合 法权益
为了规范事业单位聘用关系，建立和 完善适 应社会 主义市 场经济法权益

2.8 直角三角形全等的判定 课件(共16张PPT)

2.8 直角三角形全等的判定 课件(共16张PPT)

DA
证明： 作射线OP ∵ PD⊥OA， PE⊥OB（已知）
P
O
1 2
∴ ∠PDO=∠PEO=Rt∠ 又∵ OP=OP（公共边），PD=PE（已知） ∴ Rt△PDO≌Rt△PEO( HL )
EB
∴ ∠1=∠2，即点P在∠AOB的平分线上
讲授新课
角平分线的性质定理的逆定理： 角的内部，到角两边距离相等的点，在这个角的平分线上。
如图所示：
（1）作出△ABC两内角的平分线，其交
点为O1；
（2）分别作出△ABC两外角平分线，其
L1 交点分别为O2，O3，O4，
L3
L2
故满足条件的修建点有四处，即O1，O2，
O3，O4．
总结归纳
1.直角三角形全等的判定定理（HL） 斜边和一条直角边对应相等的两个直角三角形全等. 2.角平分线的性质定理的逆定理： 角的内部，到角两边距离相等的点，在这个角的平分线上。
（3）一个锐角和斜边对应相等；
（ AAS ）
（4）两直角边对应相等；
（ SAS ）
（5）一条直角边和斜边对应相等．
（ HL ）
举一反三
2. 如图，点C为AD的中点，过点C的线段BE⊥AD，且AB=DE.求证: AB//ED.
证明：∵C为AD的中点， ∴ AC=DC. ∵ BE⊥AD， ∴ △ACB和△DCB都是直角三角形. 又AB=DE, ∴ Rt△ACB≌Rt△DCE(HL). ∴ ∠A=∠D. ∴ AB // ED(内错角相等,两直线平行).
如果两个直角三角形的斜边和一条直角边对应相等， 那么这两个直角三角形全等。
问题2： 证明一个命题是真命题， 有哪几个步骤呢？
1.由题意作图形，标字母或符号；

三角形全等的判定ppt课件

三角形全等的判定ppt课件

（2）取出四根硬纸条钉成一个四边形，拉动其中 两边，这个四边形的形状改变了吗？钉成 一个五 边形，又会怎么样？
（3）上面的现象说明了什 么？
三角形的框架，它的大小和形状是固定不变的， 三角形的这个性质叫做三角形的稳定性。
你能举几个应用三角形稳定性的例子吗？
练一练 1.如图，已知AB＝AC，AE＝AD，BD＝CE，试说明 △AEB △ADC．
解： BD＝CE， BD－ED＝CE－ED（等式的性质）
即BE＝CD． 在△AEB和△ADC中，
AB＝AC，(已知) AE＝AD，(已知) BE＝CD，(已证) △AEB △ADC(SSS)
2、如图，AB=CD，BF=DE，E，F是AC上两 点，且AE=CF.请你判断BF与DE的位置关系， 并说明理由.
有一个角对应相等的三角形 不一定全等
做一做 2. 给出两个条件画三角形时，有几种可能的情况？ 每种情况下作出的三角形一定全等吗？
两个条件（两个角） (2)三角形的两个角分别是：30°，50°；
30°
不一定全等
两个条件（两条边） (3)三角形的两条边分别是：4cm，6cm.
不一定全等 两个条件不能保证三角形全等.
这节课你学到了什么？
1. 三角形全等的条件： 三边对应相等的两个三角形全等 (“边边边”或“SSS”)
2. 三角形具有稳定性。
三角形全等的条件：
三边对应相等的两个三角形全等，简 写为“边边边”或“SSS”。
数学表达式： 在△ABC和△A'B'C'中
例题 已知：如图AB=CD,AD=BC.则∠A与∠C相等 吗？为什么？
动手做一做
准备几根硬纸条
（1）取出三根硬纸条钉成一个三角形，你能拉动 其中两边，使这个三角形的形状发生变化吗？

三角形全等的判定ppt课件

三角形全等的判定ppt课件
∴△ABC≌△A1B1C1（AAS）
5.HL（H.L.） 在Rt△ABC与Rt△A1B1C1中，
AB=A1B1（已知）
BC=B1C1（已证） ∴△ABC≌△A1B1C1（HL）
例题精讲
例：已知:如图，点A，C，B，D在同一条直线上，
AC=BD，AM=CN，BM=DN 求证:AM∥CN，BM∥DN.
拓展延伸
8.如图所示，AB=AC，EB=EC，AE的延长线交BC于D，且D
为BC边的中点，那么图中的全等三角形有哪几对?并选
择一对进行证明
△ABD≌△ACD
证明：∵D为BC边的中点
A
∴BD=CD
在△ABD和△ACD中
E
AB=AC
BD=CD
AD=AD
B
D
C
∴ △ABD≌△ACD（SSS)
拓展延伸
8.如图所示，AB=AC，EB=EC，AE的延长线交BC于D，且D
证明：∵AC=BD ∴AC+CB=BD+BC 即AB=CD
M
N
在△AMB和△CND中 AM=CN
BM=DN
A
C
B
D
AB=CD
∴ △AMB≌△CND（SSS)
∴∠A=∠NCD,∠MBA=∠D ∴AM∥CN，BM∥DN
例：如图，A，E，C，F在同一条直线上，AB=FD，BC=DE，
AE=FC
求证:△ABC≌△FDE.
（2）全等三角形对应角相等
PART II 全等三角形的判定 1.SSS（S.S.S.） 在△ABC与△A1B1C1中，
AB=A1B1（已知） BC=B1C1（已知） AC=A1C1（已证）
∴△ABC≌△A1B1C1（SSS）

全等三角形总复习课件

全等三角形总复习课件
解题关键
理解面积的概念和计算方法，找出全等三角形，并利用全等三角形的 性质进行计算。
常见考点
全等三角形的判定和性质、面积的计算和比较、几何图形的面积公式 等。
05
全等三角形的易错点分析
判定定理的混淆
总结词
判定定理的混淆是学生在学习全等三角形时常见的问题，主要表现在不能正确理解和区 分SSS、SAS、ASA、AAS和HL等判定定理。
03
全等三角形的解题策略
构造法
总结词
通过添加辅助线构造新的三角形，利用已知条件证明新构造的三角形与原三角形全等，从而解决问题 。
详细描述
构造法是解决全等三角形问题的一种常用策略。通过作平行线、垂线或延长线等辅助线，构造出新的 三角形，利用已知条件证明新构造的三角形与原三角形全等，从而得出所需结论。在运用构造法时， 需要充分理解题意，寻找合适的构造方式。
详细描述
计算题通常会涉及角度、边长等几何量的计算。在解题过程中，学生需要利用 全等三角形的性质和定理，找到与所求量相关的已知量，通过计算得出结果。
作图题
总结词
作图题是全等三角形应用中较为特殊的一种题型，主要考察学生的空间想象能力 和作图技能。
详细描述
作图题通常会要求学生根据已知条件，画出两个全等的三角形。在解题过程中， 学生需要理解全等三角形的性质和判定定理，并能够根据题目要求进行准确的作 图。
推论
全等三角形的周长、面积 相等。
判定定理
SSS定理
SAS定理
如果两个三角形的三边分别相等，则这两 个三角形全等。
如果两个三角形的两边及其夹角分别相等 ，则这两个三角形全等。
ASA定理
HL定理
如果两个三角形的两角及其夹边分别相等 ，则这两个三角形全等。

全等三角形的判定ppt课件完整版

全等三角形的判定ppt课件完整版

注意事项
在证明过程中，需要注意两边和所夹 的角分别相等的条件必须同时满足， 且所夹的角必须是两边的夹角，否则 不能得出全等的结论。
角边角（ASA）判定定理证明
基本思路
证明方法
注意事项
如果两个三角形有两个角和它们的夹边 分别相等，则这两个三角形全等。
可以通过构造法或者余弦定理来证明。 构造法可以构造出两个三角形，然后通 过证明它们有两个角和夹边分别相等来 得出它们全等的结论。余弦定理可以通 过三角形的边角关系来证明两个三角形 有两个角和夹边分别相等，从而得出它 们全等的结论。
注意事项
在证明过程中，需要注意两个角和其 中一个角的对边分别相等的条件必须 同时满足，否则不能得出全等的结论。 同时，AAS和ASA的区别在于所给的条 件不同，但都可以用来判定两个三角 形是否全等。
04
全等三角形的应用举例
Chapter
在几何证明中的应用
证明线段相等
通过证明两个三角形全等，可以推出它们对应的边相等，从而证 明线段相等。
全等三角形的判定ppt课件完整版
目录
• 引言 • 全等三角形的判定方法 • 全等三角形判定定理的证明 • 全等三角形的应用举例 • 实验操作与探究 • 全等三角形判定的拓展与延伸
01
引言
Chapter
三角形的定义与性质回顾
三角形的定义
由不在同一直线上的三条线段首尾顺 次相接所组成的图形。
三角形的分类
在证明过程中，需要注意两个角和夹边 分别相等的条件必须同时满足，且所夹 的边必须是两个角的夹边，否则不能得 出全等的结论。
角角边（AAS）判定定理证明
基本思路
证明方法
如果两个三角形有两个角和其中一个 角的对边分别相等，则这两个三角形 全等。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

例、如图，已知AB=AC，AD=AE，AB、DC相交
于点M，AC、BE相交于点N，∠1=∠2，试说明：
（1） △ABE ≌ △ACD （2）AM=AN A
12
D
E
M
N
B
C
创造条件！ ？
7
一、挖掘“隐含条件”判全等
AD
1.如图（1），AB=CD，AC=BD，则
△ABC≌△DCB吗?说说理由
B 图（1） C
E
D
∴ ∠CAE+∠BAE=∠BAD+∠BAE
C
A
(等量加等量，和相等) 即∠BAC=∠DAE
在△ABC和△ADE中， ∠B=∠D(已知) ∠BAC=∠DAE(已证)
AC=AE(已知)
12
∴△ABC≌ △ADE (AAS)
典型例题:
例6 :如图,已知,AB=CD, CE=DF,AE=BF, 则AE∥DF吗?为什么?
第4讲 全等三角形的判定
1
知识点
定义：能够
的两个三角形
全 等
对应元素：对应_____、对应
三 性质：全等三角形的对应边
角 形
全等三角形的
、
、对应 。
、
。
也对应相等。
判定： 、
、
、
。
全等三角形的画图:
利用直尺和圆规，根据 、 、 的
方法都可画出与已知三角形全等的三角形。
2
三角形全等的4个种判定公理：
AC=DC
A
B
∠ACB=∠DCE
BC=EC
C
△ACB≌△DCE(SAS)
E
D
AB=DE
16
典型例题:
例8 :如图在 ΔABC中, AD⊥BC于D,BE⊥AC 于E,AD交BE于F, 若BF=AC,那么∠ABC 的大小是( )
A.40° B.50° C.60° D.45°B
A
1 FE 2 DC
解: ∵AD⊥BC,BE⊥AC ∴∠ADB=∠ ADC= ∠BEC= 90°∴ ∠1=∠2 在ΔACD和ΔBDF中
为什么？
解答
C
8.“三月三，放风筝”如图（6）是小东同学自己
做的风筝，他根据AB=AD,BC=DC，不用度量，
就知道∠ABC=∠ADC。请用所学的知识给予
说明。
解答
D A
10
6.如图（4）AE=CF，∠AFD=∠CEB，DF=BE， △AFD与△ CEB全等吗？为什么？
A 解：∵AE=CF(已知)
∴AE－FE=CF－EF(等量减等量，差相等)
即AF=CE
F
在△AFD和△CEB中，
AF=CE(已证)
∠AFD=∠CEB(已知)
B
DF=BE(已知)
∴△AFD≌△CEB (SAS)
D E
C
11
7.如图（5）∠CAE=∠BAD，∠B=∠D，
AC=AE，△ABC与△ADE全等吗？为什么？
B
解：∵ ∠CAE=∠BAD(已知)
∠B=∠C
友情提示：添加条件的题目.首先要
找到已具备的条件,这些条件有些是
题目已知条件 ,有些是图中隐含条件.
9
三、熟练转化“间接条件”判全等 A
D
6如图，AE=CF，∠AFD=∠CEB，DF=BE， △AFD与△ CEB全等吗？为什么？
解答
FE
B
C
B
7.如图（5）∠CAE=∠BAD，∠B=∠D， E AC=AE，△ABC与△ADE全等吗？
SSS（边边边） SAS（边角边） ASA（角边角） AAS（角角边）
有三边对应相 等的两个三角形 全等.
有两边和它们的 夹角对应相等的 两个三角形全等.
边 三有对角两应形角相全和等等它的.们两的个夹一应形有个相全两角等等角所的.和对两及的个其边三中3角对
知识梳理:
A
A
B
C
SSA不能
A
判定全等
B
C
型例题:
例1 :如图,点B在AE上, ∠CAB=∠DAB,要使 ΔABC≌ΔABD,可补充的 一个条件是∠ACB=B=∠AEA=DC∠D.BEA
C
A
B E
D
分析：现在我们已知 A→∠CAB=∠DAB
S→ AB=AB(公共边) .
①用SAS ,需要补充条件 AB=AC, ②用ASA ,需要补充条件 ∠CBA=∠DBA, ③用AAS,需要补充条件 ∠C=∠D, ④此外,补充条件 ∠CBE=∠DBE也可以6(?)
直线平行)
13
实际运用
9. 测量如图河的宽度，某人在河的对岸找到一参照物 树木Ａ，视线 ＡＢ与河岸垂直，然后该人沿河岸 步行１０步（每步约0.75M）到O处，进行标记， 再向前步行10步到D处，最后背对河岸向前步行20 步，此时树木A，标记O，恰好在同一视线上，则
河的宽度为 15 米。
A
B
O
D
14
2.如图（2），点D在AB上，点E在AC上，CD与 B
D
BE相交于点O，且AD=AE,AB=AC.若
O
A
∠B=20°,CD=5cm，则 ∠C= 20° ,BE= 5cm .说说理由.
E C 图（2）
3.如图（3），AC与BD相交于O,若OB=OD， A
D
∠A=∠C，若AB=3cm，则CD= 3cm .
A B C D
E F
证明: AE∥DF,理由是: ∵AB=CD(已知) ∴ AB+BC=CD+BC, 即AC=BD.
在ΔACE和ΔBDF中 AC=BD(已证) CE=DF (已知) AE=BF (已知)
∴ ΔACE≌ΔBDF(SSS)
∴∠E=∠F(全等三角形的
对应角相等)
∴ AE∥DF(内错角相等,两
∠1=∠2(已证) AC= BF(已知) ∠ADC=∠ ADB (已证) ∴ ΔACD≌ΔBDF(ASA) ∴ AD=BD(全等三角形对 应边相等) ∴ ∠ABC=45 °.选DD 17
14、已知：ΔABC和ΔBDE是等边三角
形, 点D在AE的延长线上。 求证：BD + DC = AD
O
说说理由.
B 图（3）C
学习提示：公共边，公共角，
对顶角这些都是隐含的边，角相等的条件！ 8
二.添条件判全等
4、如图，已知AD平分∠BAC， 要使△ABD≌△ACD，
根据“SAS”需要添加条件 根据“ASA”需要添加条件 根据“AAS”需要添加条件
B
A
D
；
AB=AC ； C
∠BDA；=∠CDA
C
如图是用两根长度相等的拉线固定电线杆的 示意图．其中一根拉到B，另一根拉到C。那么C、 B两端点到D的距离DC和DB的大小有何关系？说明 理由。
15
如图小线明段的A设B计是方一案个：池先塘在的池长塘度旁，取一个能 直现接在到想达测A量和这B处个的池点塘C，的连长结度A，C并在延长至D 点B个水方C长，法上=度使E较测C就A，方量C等连=便不于D结地方CAC，，把便D连，B，池两结用你塘点B米有的C的尺并什长距测延么度离出长。好 测D至请E的 量E的你点长说，，明使这理 由出。来吗？想想看。