最新全等三角形复习课 公开课

享•课程介绍与目标•全等三角形基础知识回顾•全等三角形在几何证明中的应用•全等三角形在解决实际问题中的应用•拓展与提高：全等三角形的进阶知识•课程总结与反思课程介绍与目标公开课背景01初中数学全等三角形是几何学的基础内容，对于培养学生的空间想象能力和逻辑推理能力具有重要作用。

02本次公开课旨在通过复习全等三角形的相关知识，帮助学生巩固基础，提高解题能力。

掌握全等三角形的定义、性质及判定方法，能够运用全等三角形解决相关问题。

知识与技能过程与方法情感态度与价值观通过讲解、讨论、练习等多种方式，引导学生积极参与课堂活动，提高自主学习能力。

培养学生的数学兴趣，鼓励学生勇于探索、创新，形成积极的学习态度。

030201教学目标与要求教学内容与方法教学内容全等三角形的定义、性质及判定方法；全等三角形在几何证明和实际问题中的应用。

教学方法采用讲解、示范、讨论、练习等多种教学方法，注重启发式教学和探究式学习，引导学生主动思考、积极参与课堂活动。

同时，结合多媒体教学手段，使教学内容更加生动、形象。

全等三角形基础知识回顾定义：两个三角形如果三边及三角分别相等，则称这两个三角形全等。

性质全等三角形的对应边相等。

全等三角形的对应角相等。

01020304全等三角形的定义与性质HL 全等在直角三角形中，斜边和一条直角边分别相等的两个三角形全等。

全等两角和其中一个角的对边分别相等的两个三角形全等。

ASA 全等两角和它们的夹边分别相等的两个三角形全等。

SSS 全等三边分别相等的两个三角形全等。

SAS 全等两边和它们所夹的角分别相等的两个三角形全等。

全等三角形的判定方法例2已知△ABC 中，∠C = 90°，AC = BC ，AD 平分∠CAB交BC 于D ，DE⊥AB于E ，且AB = 6cm ，求△DEB 的周长。

解析根据SAS 全等的判定方法，已知两边和它们所夹的角分别相等，因此可以判定△ABC 和△DEF 全等。

2024年全等三角形复习课.课件一、教学内容本节课将复习全等三角形的相关知识，内容涉及教材第十五章第二节“全等三角形的判定与应用”。

具体包括：全等三角形的定义、判定方法（SSS、SAS、ASA、AAS）、全等三角形的性质以及在实际问题中的应用。

二、教学目标1. 熟练掌握全等三角形的定义和判定方法，能够灵活运用这些方法证明三角形全等。

2. 了解全等三角形的性质，并能运用这些性质解决实际问题。

3. 培养学生的观察能力、逻辑思维能力和空间想象力。

三、教学难点与重点重点：全等三角形的判定方法及性质。

难点：在实际问题中灵活运用全等三角形的判定方法和性质。

四、教具与学具准备1. 教具：三角板、直尺、量角器。

2. 学具：练习本、铅笔、直尺、量角器。

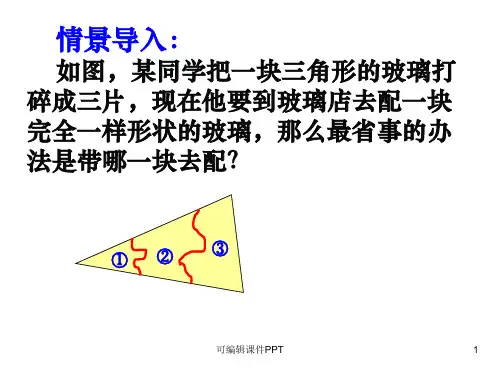
五、教学过程1. 实践情景引入（5分钟）通过展示生活中的实例，如拼接木地板、拼接三角形图案等，引出全等三角形的概念。

2. 知识回顾与讲解（15分钟）复习全等三角形的定义、判定方法和性质。

通过例题讲解，让学生掌握判定方法在实际问题中的应用。

3. 例题讲解（10分钟）选取具有代表性的例题，讲解解题思路和步骤。

例如：已知三角形的两边和夹角，求第三边的长度。

4. 随堂练习（10分钟）让学生完成教材第15页的练习题，巩固所学知识。

5. 小组讨论（10分钟）将学生分为小组，讨论全等三角形在实际问题中的应用，如建筑、工程等领域。

六、板书设计1. 全等三角形的定义、判定方法和性质。

2. 例题解题步骤和答案。

3. 练习题答案。

七、作业设计1. 作业题目：教材第16页的习题1、2、3。

2. 答案：见附件。

八、课后反思及拓展延伸1. 反思：本节课学生对全等三角形的判定方法和性质掌握情况较好，但在实际应用方面还需加强练习。

2. 拓展延伸：引导学生探索全等三角形在生活中的应用，如建筑设计、工艺品制作等，提高学生的实践能力。

重点和难点解析1. 教学难点与重点的确定2. 例题讲解的深度和广度3. 随堂练习的设计与实施4. 小组讨论的主题和引导5. 作业设计的针对性和拓展性详细补充和说明：一、教学难点与重点的确定全等三角形的判定方法是教学的难点，因为它们需要学生理解和记忆不同的情况，并能够准确地应用。

全等三角形复习课公开课一、教学内容本节课为全等三角形复习课，教材选用人教版《数学》四年级上册第六章“认识三角形”相关内容。

复习内容包括全等三角形的定义、性质、判定方法以及全等三角形的应用。

二、教学目标1. 理解并掌握全等三角形的定义、性质和判定方法；2. 能够运用全等三角形解决实际问题；3. 培养学生的空间想象能力和逻辑思维能力。

三、教学难点与重点1. 教学难点：全等三角形的判定方法及其应用；2. 教学重点：全等三角形的性质和判定方法的运用。

四、教具与学具准备1. 教具：黑板、粉笔、多媒体教学设备；2. 学具：三角板、直尺、圆规、剪刀、彩笔。

五、教学过程1. 情景引入：通过多媒体展示一个生活中的实际问题，如剪拼图形，引导学生思考全等三角形的应用。

2. 知识回顾：引导学生回顾全等三角形的定义、性质和判定方法，为学生提供相关概念的定义和性质，如“SSS”、“SAS”、“ASA”、“AAS”等。

3. 例题讲解：选取具有代表性的例题，如“已知两个三角形全等，求第三个角的大小”等问题，引导学生运用全等三角形的性质和判定方法进行解答。

4. 随堂练习：为学生提供一些有关全等三角形的练习题，如“判断两个三角形是否全等”、“已知全等三角形，求解未知边长或角度”等，巩固所学知识。

5. 小组讨论：将学生分成小组，讨论全等三角形在实际问题中的应用，如建筑设计、几何拼图等，引导学生学会将理论知识与实际问题相结合。

六、板书设计板书设计如下：全等三角形性质：1. 对应边相等2. 对应角相等3. 对应边上的高、中线、角平分线相等判定方法：1. SSS（三边相等）2. SAS（两边及夹角相等）3. ASA（两角及夹边相等）4. AAS（两角及非夹边相等）应用：1. 求解未知边长或角度2. 几何拼图3. 建筑设计七、作业设计1. 判断题：（1）全等三角形的对应边相等。

（）（2）全等三角形的对应角相等。

（）（3）全等三角形的判定方法有SSS、SAS、ASA、AAS。

全等三角形复习课件一、全等三角形的定义和性质全等三角形是指能够完全重合的两个三角形。

全等三角形的对应边相等，对应角相等。

这是全等三角形最基本也是最重要的性质。

例如，在三角形ABC 和三角形A'B'C'中，如果这两个三角形全等，那么 AB ＝ A'B'，BC ＝ B'C'，AC ＝ A'C'，∠A ＝∠A'，∠B ＝∠B'，∠C ＝∠C'。

二、全等三角形的判定方法1、 SSS（边边边）：如果两个三角形的三条边分别对应相等，那么这两个三角形全等。

例如，三角形 ABC 和三角形 A'B'C'中，AB ＝ A'B'，BC ＝ B'C'，AC ＝ A'C'，则三角形 ABC ≌三角形 A'B'C'。

2、 SAS（边角边）：如果两个三角形的两条边及其夹角分别对应相等，那么这两个三角形全等。

比如，在三角形 ABC 和三角形 A'B'C'中，AB ＝ A'B'，∠A ＝∠A'，AC ＝ A'C'，则三角形 ABC ≌三角形 A'B'C'。

3、 ASA（角边角）：如果两个三角形的两个角及其夹边分别对应相等，那么这两个三角形全等。

假设在三角形 ABC 和三角形 A'B'C'中，∠A ＝∠A'，AB ＝ A'B'，∠B ＝∠B'，那么三角形 ABC ≌三角形 A'B'C'。

4、 AAS（角角边）：如果两个三角形的两个角和其中一个角的对边分别对应相等，那么这两个三角形全等。

比如三角形 ABC 和三角形 A'B'C'中，∠A ＝∠A'，∠B ＝∠B'，BC ＝ B'C'，则三角形 ABC ≌三角形 A'B'C'。

2023全等三角形复习课件.说课课件CATALOGUE目录•课程引入•全等三角形性质与判定•三角形全等的证明方法•全等三角形在实际生活中的应用•复习巩固与提高•说课内容展示与讲解01课程引入全等三角形是指能够完全重合的两个三角形，即形状相同且大小相等的三角形。

复习全等三角形基本概念定义全等三角形的对应边相等，对应角相等，周长相等，面积相等。

性质用全等符号“≌”表示两个三角形全等。

表示方法通过本次复习，使学生进一步熟悉全等三角形的性质和判定方法，掌握全等三角形的证明方法，提高运用全等三角形解决问题的能力。

复习目标采用讲解与练习相结合的方式，通过典型例题的分析和解题方法的指导，帮助学生巩固全等三角形的知识，提高解题能力和思维水平。

复习方法引入复习目标和方法02全等三角形性质与判定1全等三角形性质回顾23定义：两个三角形全等是指能够完全重合的两个三角形。

全等三角形的性质：全等三角形的对应边相等，对应角相等。

运用全等三角形的性质可以进行简单的几何证明。

全等三角形判定方法总结•定义：两个三角形全等是指能够完全重合的两个三角形。

•常用的判定方法有：SSS、SAS、ASA、AAS、HL。

•SSS：三边对应相等的两个三角形全等。

•SAS：两边及其夹角对应相等的两个三角形全等。

•ASA：两角及其夹边对应相等的两个三角形全等。

•AAS：两角及其中一个角的对边对应相等的两个三角形全等。

•HL：斜边和一条直角边对应相等的两个直角三角形全等。

经典例题解析在△ABC和△DEF中，AB=DE，AC=DF，∠B=∠E，求证：△ABC≌△DEF。

例题1解析例题2解析此题考查的是全等三角形的判定，根据ASA可以进行证明。

在Rt△ABC和Rt△DEF中，∠A=∠D=90°，BC=EF，求证：△ABC≌△DEF。

此题考查的是全等三角形的判定，根据HL可以进行证明。

03三角形全等的证明方法直接证明方法讲解根据全等三角形的定义，直接证明两个三角形全等的方法。