向心力之绳模型杆模型专练

1、以下图，半径为r 的圆筒，绕竖直中心轴OO′转动，小物块 a 靠在圆筒的内壁上，它与圆筒的动摩擦因数为μ，现要使 a 不下滑，则圆筒转动的角速度ω起码为（）A. B. C. D.2、下边对于向心力的表达中，正确的选项是（）A.向心力的方向一直沿着半径指向圆心，所以是一个变力B.做匀速圆周运动的物体，除了遇到其余物体对它的作用外，还必定遇到一个向心力的作用C.向心力能够是重力、弹力、摩擦力中的某个力，也能够是这些力中某几个力的协力，或许是某一个力的分力D.向心力只改变物体速度的方向，不改变物体速度的大小3、对于向心力的说法，正确的选项是（）A.物体因为做圆周运动而产生了一个向心力B.向心力不改变圆周运动物体速度的大小C.做匀速圆周运动的物体其向心力即为其所受的合外力D.做匀速圆周运动的物体其向心力大小不变5、以下图，质量为 m 的木块，从半径为 r 的竖直圆轨道上的 A 点滑向 B 点，因为摩擦力的作用，木块的速率保持不变，则在这个过程中A.木块的加快度为零B.木块所受的合外力为零C.木块所受合外力大小不变，方向一直指向圆心D.木块所受合外力的大小和方向均不变6=80 kg,M=40 kg，当面拉着弹簧秤做、甲、乙两名滑冰运动员， M 甲乙圆周运动的滑冰表演，以下图，两个相距 0.9 m，弹簧秤的示数为 9.2 N，下列判断正确的选项是（）A.两人的线速度相同，约为 40 m/sB.两人的角速度相同，为 6 rad/sC.两人的运动半径相同，都是0.45 mD.两人的运动半径不一样，甲为 0.3 m,乙为 0.6 m7、以下图，在匀速转动的圆筒内壁上有一物体随圆筒一同转动而未滑动.若圆筒和物体以更大的角速度做匀速转动，以下说法正确的选项是（）A.物体所受弹力增大，摩擦力也增大B.物体所受弹力增大，摩擦力减小C.物体所受弹力减小，摩擦力也减小D.物体所受弹力增大，摩擦力不变8、用细绳拴住一球，在水平面上做匀速圆周运动，以下说法中正确的选项是（）A.当转速不变时，绳短易断B.当角速度不变时，绳短易断C.当线速度不变时，绳长易断D.当周期不变时，绳长易断9、如图,质量为 m 的木块从半径为 R 的半球形的碗口下滑到碗的最低点的过程中，假如因为摩擦力的作用使得木块的速率不变A.因为速率不变，所以木块加快度为零 C.木块下滑过程中的摩擦力大小不变B.木块下滑的过程中所受的合外力愈来愈大D.木块下滑过程中的加快度大小不变 ,方向时辰指向球心分析：木块做匀速圆周运动，所受合外力大小恒定，方向时辰指向圆心，故选项 A、B 不正确 .在木块滑动过程中，小球对碗壁的压力不一样，故摩擦力大小改变,C 错. 答案：D10、以下图，在圆滑的以角速度ω旋转的细杆上穿有质量分别为m 和 M 的两球，两球用轻微线连结 .若 M＞m，则（）A.当两球离轴距离相等时，两球相对杆不动B.当两球离轴距离之比等于质量之比时，两球相对杆都不动C.若转速为ω时，两球相对杆都不动，那么转速为 2ω时两球也不动D.若两球相对杆滑动，必定向同一方向，不会相向滑动分析：由牛顿第三定律可知 M、m 间的作使劲相等，即 F M =F m，F M=Mω2r M，F m=mω2rm，所以若 M、m 不动，则 r M∶r m=m∶M ，所以 A 、B 不对， C 对（不动的条件与ω没关）.若相向滑动，无力供给向心力， D 对. 答案：CD 11、一物体以 4m/s 的线速度做匀速圆周运动，转动周期为 2s，则物体在运动过程的任一时辰，速度变化率的大小为（）222D.4 π m/sω =2π/T=2 π/2= πv= ω *r所以r=4/πa=v ∧2/r=16/(4/π)=4 π12、在水平路面上安全转弯的汽车，向心力是（）A.重力和支持力的协力B.重力、支持力和牵引力的协力C 汽车与路面间的静摩擦力 D.汽车与路面间的滑动摩擦力二、非选择题【共3道小题】1、以下图，半径为 R 的半球形碗内，有一个拥有必定质量的物体 A，A 与碗壁间的动摩擦因数为μ，当碗绕竖直轴 OO′匀速转动时，物体 A 恰巧能紧贴在碗口邻近随碗一同匀速转动而不发生相对滑动，求碗转动的角速度 .分析：物体A 随碗一同转动而不发生相对滑动，物体做匀速圆周运动的角速度 A 做匀速圆周运动所需的向心力方向指向球心 O，故此向心力不是重力而是由碗壁对物体的弹力供给，此时物体所受的摩擦力与重力均衡 .分析：物体 A 做匀速圆周运动，向心力： Fω2Rn=m而摩擦力与重力均衡，则有μF即 F n=mg/μn=mg由以上两式可得： mω2μ即碗匀速转动的角速度为：ω=R= mg/.2、汽车沿半径为 R 的水平圆跑道行驶，路面作用于车的摩擦力的最大值是车重的1/10，要使汽车不致冲出圆跑道，车速最大不可以超出多少 ?分析：跑道对汽车的摩擦力供给向心力，1/10mg=mv2/r，所以要使汽车不致冲出圆跑道，车速最大值为 v=. 答案：车速最大不可以超出3、一质量 m=2 kg 的小球从圆滑斜面上高 h=3.5 m处由静止滑下，斜面的底端连着一个半径 R=1 m 的圆滑圆环（以下图），则小球滑至圆环极点时对环的压力为，小球起码应从多高处静止滑下才能经过圆环最高点， hmin=_________(g=10 m/s2).匀速圆周运动典型问题分析匀速圆周运动问题是学习的难点，也是高考的热门，同时它又简单和很多知识综合在一同，形成能力性很强的题目，如除力学部格外，电学中“粒子在磁场中的运动”波及的好多问题仍旧要用到匀速圆周运动的知识，对匀速圆周运动的学习可要点从两个方面掌握其特色，第一是匀速圆周运动的运动学规律，其次是其动力学规律，现就各部分波及的典型问题作点滴说明。

真题模型(二)——竖直平面的圆周运动“绳、杆”模型来源图例考向模型核心归纳2014·新课标全国卷Ⅱ第17题受力分析、圆周运动、动能定理1.常考的模型(1)物体运动满足“绳”模型特征，竖直圆轨道光滑(2)物体运动满足“绳”模型特征，竖直圆轨道粗糙(3)物体运动满足“杆”模型特征，竖直圆轨道光滑(4)物体运动满足“杆”模型特征，竖直圆轨道粗糙(5)两个物体沿竖直圆轨道做圆周运动(6)同一物体在不同的竖直圆轨道做圆周运动(7)物体受弹簧弹力、电场力或洛伦兹力共同作用下的圆周运动2.模型解法2015·新课标全国卷Ⅰ第22题圆周运动、超重、失重2016·新课标全国卷Ⅱ第16题受力分析、牛顿第二定律、圆周运动、动能定理2016·课新标全国卷Ⅱ第25题受力分析、机械能守恒定律、圆周运动、牛顿第二定律2016·新课标全国卷Ⅲ第24题受力分析、圆周运动、机械能守恒定律、牛顿第二定律2017·全国卷Ⅱ第17题平抛运动、功能关系及极值的求解方法【预测1】 (多选)如图1所示，半径为R 的内壁光滑的圆轨道竖直固定在桌面上，一个可视为质点的质量为m 的小球静止在轨道底部A 点。

现用小锤沿水平方向快速击打小球，使小球在极短的时间内获得一个水平速度后沿轨道在竖直面内运动。

当小球回到A 点时，再次用小锤沿运动方向击打小球，通过两次击打，小球才能运动到圆轨道的最高点。

已知小球在运动过程中始终未脱离轨道，在第一次击打过程中小锤对小球做功W 1，第二次击打过程中小锤对小球做功W 2。

设先后两次击打过程中小锤对小球做功全部用来增加小球的动能，则W 1W 2的值可能是( )图1A.34B.13C.23D.1解析 第一次击打后球最多到达与球心O 等高位置，根据功能关系，有W 1≤mgR ，两次击打后球可以运动到轨道最高点，根据功能关系，有W 1＋W 2－2mgR ＝12mv 2，在最高点有mg ＋N ＝m v 2R ≥mg ，由以上各式可解得W 1≤mgR ，W 2≥32mgR ，因此W 1W 2≤23，B 、C 正确。

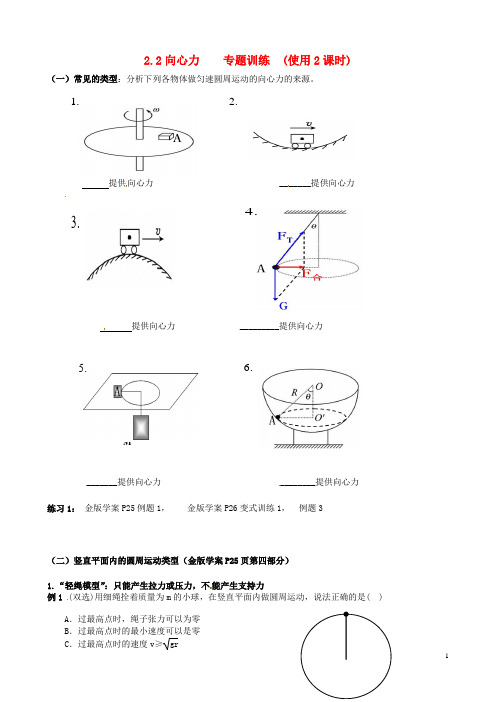
2.2向心力 专题训练 (使用2课时)（一）常见的类型：分析下列各物体做匀速圆周运动的向心力的来源。

提供向心力 _______提供向心力提供向心力 _________提供向心力_______提供向心力 ________提供向心力练习1： 金版学案P25例题1， 金版学案P26变式训练1， 例题3（二）竖直平面内的圆周运动类型（金版学案P25页第四部分）1.“轻绳模型”：只能产生拉力或压力，不能产生支持力例1 (双选)用细绳拴着质量为m 的小球，在竖直平面内做圆周运动，说法正确的是( )A ．过最高点时，绳子张力可以为零B ．过最高点时的最小速度可以是零C ．过最高点时的速度v≥gr.2.3.4M.5.6.1D ．最高点时，绳子对小球的作用力可以向上小结：在最高点时，设绳子或轨道弹力为F,则rmv mg F 2=+：①绳子伸直不拉紧，绳力为0；或者轨道无压力；上式得②物体受到向内的拉力或压力； 上式得：③特殊地，当最低点时： rmv mg F 2=-练习2：(双选)如图，半径为R 的圆周轨道固定于竖直面内，轨道内侧光滑，一质量为m 的小球在轨道内做圆周运动，经过轨道最高点时刚好不脱离轨道，正确的是( )A ．小球受到的向心力等于重力mgB ．轨道对小球的压力等于mgC ．小球的向心加速度等于g D2．“轻杆模型”：既能产生拉力，也能产生支持力例2：长度为L ＝0.50 m 的轻质细杆OA ，A 端有一质量为m ＝3.0 kg 的小球，如图所示，小球以O 点为圆心在竖直平面内做圆周运动，通过最高点时小球的速率是2.0 m/s ，g 取10 m/s 2，则此时细杆OA 受到( )A ．6.0 N 的拉力B ．6.0 N 的压力C ．24 N 的拉力D ．24 N 的压力小结：杆在最高点时，设杆力为N F①v=0时，杆为支持力 0F mg F N ==合，②r mv F F F N 2mg =-==向合③v0F mv mg F F 2====N r，向合 ④rN 2mv mg F F F =+==向合杆在最低点时，杆为拉力 rmv mg F F N 2=-=合(三)综合题型：直线运动，平抛运动，圆周运动相结合。

专题五轻绳、轻杆和轻弹簧模型一、物理学中的轻绳、轻杆和轻弹簧模型1、理想绳（轻绳）：质量不计，不可伸长，物体对它的作用力只能是拉力，它内部的弹力处处相等，总是等于其它物体拉绳子的力。

拉力的方向一定沿绳的方向，一旦外力撤去，绳中弹力立即消失，其时间不计。

2、理想杆（轻杆）：质量不计，不可伸长，不可压缩，物体对它的作用力既可以是拉力，也可以是压力，它还可以产生切向力，内部的弹力处处相等，弹力的方向不一定沿杆的方向，一旦外力撤去，弹力立即消失，其时间不计。

3、理想弹簧（轻弹簧）：质量不计，既可以伸长，也可以被压缩；物体对它的作用力既可以是压力，又可以是拉力，它内部各部分之间的作用力相等，弹力的大小为F=kx，其中k为弹簧的劲度系数，x为弹簧的伸长量或缩短量（胡克定律）；方向一定沿着弹簧轴线方向，它内部弹力变化的时间不可忽略不计，在极短时间内可认为弹簧形变量不变。

例1、如图所示，小车上有一弯折轻杆，杆下端固定一质量为m的小球。

当小车处于静止或匀速直线运动状态时，求杆对球的作用力的大小和方向。

例2、如图所示，四个完全相同的弹簧都处于水平位置，它们的右端受到大小皆为F的拉力作用，而左端的情况各不相同：①弹簧的左端固定在墙上；②弹簧的左端受大小也为F的拉力作用；③弹簧的左端拴一小物块，物块在光滑的桌面上滑动；④弹簧的左端拴一小物块，物块在有摩擦的桌面上滑动．若认为弹簧质量都为零，以L1、L2、L3、L4依次表示四个弹簧的伸长量，则有( )A．L2>L1 B．L4>L3C．L1>L3 D．L2＝L4练习1、如图所示，三角形轻支架ABC的边长AB=20cm，BC=15cm。

在A点通过细绳挂一个重30N的物体，则AB杆和AC杆所受力分别为( )A、拉力50N，压力40NB、拉力40N，压力50NC、压力50N，拉力40ND、压力40N，拉力50N练习2、如图所示，质量为m的小球置于倾角为30°的光滑斜面上，劲度系数为k的轻质弹簧一端系在小球上，另一端固定在墙上的P点，小球静止时，弹簧与竖直方向的夹角为30°，则弹簧的伸长量为( )A.B.C.D.练习3、在如图所示的支架上，有不计重力的细绳AB，细绳与竖直墙壁夹角为60°，轻杆BC（BC与墙用铰链连接）与竖直墙壁夹角为30°。

微专题 22 竖直面内的圆周运动【核心重点提示】绳、杆模型波及的临界问题绳模型杆模型常有 种类均是没有支撑的小球均是有支撑的小球过最高点 v2的临界条＝ gr由小球恰能做圆周运动得v ＝ 0由 mg ＝ m r 得 v临临 件(1)当 v ＝ 0 时， F N ＝ mg ，F N 为支持力，沿半径 (1) 过最高点时， v ≥ gr ，背叛圆心F N ＋mg ＝m v 2v 2，绳、圆轨(2)当 0<v< gr 时，－ F N ＋mg ＝m r ，F N 背叛圆 议论r道对球产生弹力 F N 心，随 v 的增大而减小剖析(2) 不可以过最高点时， (3)当 v ＝ gr 时， F N ＝ 0v< gr ，在抵达最高点前小2(4)当 v> gr 时， F N ＋mg ＝m v，F N 指向圆心并球已经离开了圆轨道r随 v 的增大而增大【核心方法点拨】在竖直平面内做圆周运动的物体，按物体运动到轨道最高点时的受力状况判断有没有支撑，运用对用的临界条件解决问题。

【微专题训练】【例题 1】如下图，半径为R 的竖直圆滑圆轨道内侧底部静止着一个圆滑小球，现给小球一个冲击使其在瞬时获得一个水平初速度v 0，若 v 0 大小不一样，则小球能够上涨到的最大高度( 距离底部 )也不一样．以下说法中正确的选项是( )RA ．假如 v 0＝gR ，则小球能够上涨的最大高度为2R B ．假如 v 0 ＝2gR ，则小球能够上涨的最大高度为23R C ．假如 v 0 ＝3gR ，则小球能够上涨的最大高度为2D ．假如 v 0＝ 5gR ，则小球能够上涨的最大高度为2R【分析】依据机械能守恒定律，当速度为v 0＝1 2 R ，A 项正确， BgR ，由 mgh ＝ mv 0解出 h ＝22项错误；当 v 0＝ 5gR ，小球正好运动到最高点， D 项正确；当 v 0＝ 3gR 时小球运动到最高 点以下，若 C 项建立，说明小球此时向心力为 0，这是不行能的．【答案】 AD【变式 1】如下图，轻绳的一端固定在O 点，另一端系一质量为 m 的小球 (可视为质点 )。

一、选择题【共12道小题】1、如图所示，半径为r的圆筒，绕竖直中心轴OO′转动，小物块a靠在圆筒的内壁上，它与圆筒的动摩擦因数为μ，现要使a不下滑，则圆筒转动的角速度ω至少为（）A. B. C. D.解析：要使a不下滑，则a受筒的最大静摩擦力作用，此力与重力平衡，筒壁给a的支持力提供向心力，则N=mrω2，而fm=mg=μN，所以mg=μmrω2，故. 所以A、B、C均错误，D正确.2、下面关于向心力的叙述中，正确的是（）A.向心力的方向始终沿着半径指向圆心，所以是一个变力B.做匀速圆周运动的物体，除了受到别的物体对它的作用外，还一定受到一个向心力的作用C.向心力可以是重力、弹力、摩擦力中的某个力，也可以是这些力中某几个力的合力，或者是某一个力的分力D.向心力只改变物体速度的方向，不改变物体速度的大小解析：向心力是按力的作用效果来命名的，它可以是物体受力的合力，也可以是某一个力的分力，因此，在进行受力分析时，不能再分析向心力.向心力时刻指向圆心与速度方向垂直，所以向心力只改变速度的方向，不改变速度的大小，即向心力不做功. 答案：ACD3、关于向心力的说法，正确的是（）A.物体由于做圆周运动而产生了一个向心力B.向心力不改变圆周运动物体速度的大小C.做匀速圆周运动的物体其向心力即为其所受的合外力D.做匀速圆周运动的物体其向心力大小不变解析：向心力并不是物体受到的一个特殊力，它是由其他力沿半径方向的合力或某一个力沿半径方向的分力提供的.因为向心力始终与速度方向垂直，所以向心力不会改变速度的大小，只改变速度的方向.当质点做匀速圆周运动时，向心力的大小保持不变. 答案：BCD4、在光滑水平面上相距20 cm的两点钉上A、B两个钉子，一根长1 m的细绳一端系小球，另一端拴在A钉上，如图所示.已知小球质量为0.4 kg，小球开始以2 m／s的速度做水平匀速圆周运动，若绳所能承受的最大拉力为4 N，则从开始运动到绳拉断历时为（）A.2.4π sB.1.4π sC.1.2π sD.0.9π s解析：当绳子拉力为4 N时，由F=可得r=0.4 m.小球每转半个周期，其半径就减小0.2 m，由分析知，小球分别以半径为1 m，0.8 m和0.6 m各转过半个圆周后绳子就被拉断了，所以时间为t==1.2π s. 答案：C5、如图所示，质量为m的木块，从半径为r的竖直圆轨道上的A点滑向B 点，由于摩擦力的作用，木块的速率保持不变，则在这个过程中A.木块的加速度为零B.木块所受的合外力为零C.木块所受合外力大小不变，方向始终指向圆心D.木块所受合外力的大小和方向均不变解析：木块做匀速圆周运动，所以木块所受合外力提供向心力. 答案：C主要考察知识点:匀速圆周运动、变速圆周运动、离心现象及其应用6、甲、乙两名溜冰运动员，M甲=80 kg,M乙=40 kg，面对面拉着弹簧秤做圆周运动的溜冰表演，如图所示，两个相距0.9 m，弹簧秤的示数为9.2 N，下列判断正确的是（）A.两人的线速度相同，约为40 m/sB.两人的角速度相同，为6 rad/sC.两人的运动半径相同，都是0.45 mD.两人的运动半径不同，甲为0.3 m,乙为0.6 m解析：甲、乙两人绕共同的圆心做圆周运动，他们间的拉力互为向心力，他们的角速度相同，半径之和为两人的距离.设甲、乙两人所需向心力为F向，角速度为ω，半径分别为r甲、r乙.则F向=M甲ω2r甲=M乙ω2r乙=9.2 N ①r甲+r乙=0.9 m ②由①②两式可解得只有D正确答案：D7、如图所示，在匀速转动的圆筒内壁上有一物体随圆筒一起转动而未滑动.若圆筒和物体以更大的角速度做匀速转动，下列说法正确的是（）A.物体所受弹力增大，摩擦力也增大B.物体所受弹力增大，摩擦力减小C.物体所受弹力减小，摩擦力也减小D.物体所受弹力增大，摩擦力不变析：物体在竖直方向上受重力G与摩擦力F，是一对平衡力，在向心力方向上受弹力F N.根据向心力公式，可知F N=mω2r，当ω增大时，F N增大，选D.8、用细绳拴住一球，在水平面上做匀速圆周运动，下列说法中正确的是（）A.当转速不变时，绳短易断B.当角速度不变时，绳短易断C.当线速度不变时，绳长易断D.当周期不变时，绳长易断析：由公式a=ω2R=知，当角速度（转速）不变时绳长易断，故A、B错误.周期不变时,绳长易断，故D正确.由,当线速度不变时绳短易断,C错9、如图,质量为m的木块从半径为R的半球形的碗口下滑到碗的最低点的过程中，如果由于摩擦力的作用使得木块的速率不变A.因为速率不变，所以木块加速度为零C.木块下滑过程中的摩擦力大小不变B.木块下滑的过程中所受的合外力越来越大D.木块下滑过程中的加速度大小不变,方向时刻指向球心解析：木块做匀速圆周运动，所受合外力大小恒定，方向时刻指向圆心，故选项A、B不正确.在木块滑动过程中，小球对碗壁的压力不同，故摩擦力大小改变,C错. 答案：D10、如图所示，在光滑的以角速度ω旋转的细杆上穿有质量分别为m和M的两球，两球用轻细线连接.若M＞m，则（）A.当两球离轴距离相等时，两球相对杆不动B.当两球离轴距离之比等于质量之比时，两球相对杆都不动C.若转速为ω时，两球相对杆都不动，那么转速为2ω时两球也不动D.若两球相对杆滑动，一定向同一方向，不会相向滑动解析：由牛顿第三定律可知M、m间的作用力相等，即F M=F m，F M=Mω2r M，F m=mω2rm，所以若M、m不动，则r M∶r m=m∶M，所以A、B不对，C对（不动的条件与ω无关）.若相向滑动，无力提供向心力，D对. 答案：CD 11、一物体以4m/s的线速度做匀速圆周运动，转动周期为2s，则物体在运动过程的任一时刻，速度变化率的大小为（）A.2m/s2B.4m/s2C.0D.4π m/s2ω=2π/T=2π/2=πv=ω*r所以r=4/πa=v∧2/r=16/(4/π)=4π12、在水平路面上安全转弯的汽车，向心力是（）A.重力和支持力的合力B.重力、支持力和牵引力的合力C 汽车与路面间的静摩擦力 D.汽车与路面间的滑动摩擦力二、非选择题【共3道小题】1、如图所示，半径为R的半球形碗内，有一个具有一定质量的物体A，A与碗壁间的动摩擦因数为μ，当碗绕竖直轴OO′匀速转动时，物体A刚好能紧贴在碗口附近随碗一起匀速转动而不发生相对滑动，求碗转动的角速度.分析：物体A随碗一起转动而不发生相对滑动，物体做匀速圆周运动的角速度ω就等于碗转动的角速度ω.物体A做匀速圆周运动所需的向心力方向指向球心O，故此向心力不是重力而是由碗壁对物体的弹力提供，此时物体所受的摩擦力与重力平衡.解析：物体A做匀速圆周运动，向心力：F n=mω2R而摩擦力与重力平衡，则有μF n=mg 即F n=mg/μ由以上两式可得：mω2R= mg/μ即碗匀速转动的角速度为：ω=.2、汽车沿半径为R的水平圆跑道行驶，路面作用于车的摩擦力的最大值是车重的1/10，要使汽车不致冲出圆跑道，车速最大不能超过多少?解析：跑道对汽车的摩擦力提供向心力，1/10mg=mv2/r，所以要使汽车不致冲出圆跑道，车速最大值为v=. 答案：车速最大不能超过3、一质量m=2 kg的小球从光滑斜面上高h=3.5 m处由静止滑下，斜面的底端连着一个半径R=1 m的光滑圆环（如图所示），则小球滑至圆环顶点时对环的压力为_____________，小球至少应从多高处静止滑下才能通过圆环最高点，hmin=_________(g=10 m/s2).解析：①设小球滑至圆环顶点时速度为v1,则mgh=mg·2R+ 1/2mv12F n+mg= mv12/R 得:F n=40 N②小球刚好通过最高点时速度为v2,则mg= mv22/R又mgh′=mg2R+1/2 mv22/R得h′=2.5R答案：40 N;2.5R匀速圆周运动典型问题剖析匀速圆周运动问题是学习的难点，也是高考的热点，同时它又容易和很多知识综合在一起，形成能力性很强的题目，如除力学部分外，电学中“粒子在磁场中的运动”涉及的很多问题仍然要用到匀速圆周运动的知识，对匀速圆周运动的学习可重点从两个方面掌握其特点，首先是匀速圆周运动的运动学规律，其次是其动力学规律，现就各部分涉及的典型问题作点滴说明。

一、选择题【共12道小题】1、如图所示，半径为r的圆筒，绕竖直中心轴OO′转动，小物块a靠在圆筒的内壁上，它与圆筒的动摩擦因数为μ，现要使a不下滑，则圆筒转动的角速度ω至少为（） A. B. C. D.解析：要使a不下滑，则a受筒的最大静摩擦力作用，此力与重力平衡，筒壁给a的支持力提供向心力，则N=mrω2，而fm=mg=μN，所以mg=μmrω2，故. 所以A、B、C均错误，D正确.2、下面关于向心力的叙述中，正确的是（）A.向心力的方向始终沿着半径指向圆心，所以是一个变力B.做匀速圆周运动的物体，除了受到别的物体对它的作用外，还一定受到一个向心力的作用C.向心力可以是重力、弹力、摩擦力中的某个力，也可以是这些力中某几个力的合力，或者是某一个力的分力D.向心力只改变物体速度的方向，不改变物体速度的大小解析：向心力是按力的作用效果来命名的，它可以是物体受力的合力，也可以是某一个力的分力，因此，在进行受力分析时，不能再分析向心力.向心力时刻指向圆心与速度方向垂直，所以向心力只改变速度的方向，不改变速度的大小，即向心力不做功. 答案：ACD3、关于向心力的说法，正确的是（）A.物体由于做圆周运动而产生了一个向心力B.向心力不改变圆周运动物体速度的大小C.做匀速圆周运动的物体其向心力即为其所受的合外力D.做匀速圆周运动的物体其向心力大小不变解析：向心力并不是物体受到的一个特殊力，它是由其他力沿半径方向的合力或某一个力沿半径方向的分力提供的.因为向心力始终与速度方向垂直，所以向心力不会改变速度的大小，只改变速度的方向.当质点做匀速圆周运动时，向心力的大小保持不变. 答案：BCD4、在光滑水平面上相距20 cm的两点钉上A、B两个钉子，一根长1 m的细绳一端系小球，另一端拴在A钉上，如图所示.已知小球质量为0.4 kg，小球开始以2 m／s的速度做水平匀速圆周运动，若绳所能承受的最大拉力为4 N，则从开始运动到绳拉断历时为（）A.2.4π s B.1.4π s C.1.2π s D.0.9π s解析：当绳子拉力为4 N时，由F=可得r=0.4 m.小球每转半个周期，其半径就减小0.2 m，由分析知，小球分别以半径为1 m，0.8 m和0.6 m各转过半个圆周后绳子就被拉断了，所以时间为t==1.2π s. 答案：C5、如图所示，质量为m的木块，从半径为r的竖直圆轨道上的A点滑向B点，由于摩擦力的作用，木块的速率保持不变，则在这个过程中A.木块的加速度为零B.木块所受的合外力为零C.木块所受合外力大小不变，方向始终指向圆心D.木块所受合外力的大小和方向均不变解析：木块做匀速圆周运动，所以木块所受合外力提供向心力. 答案：C主要考察知识点:匀速圆周运动、变速圆周运动、离心现象及其应用6、甲、乙两名溜冰运动员，M甲=80 kg,M乙=40 kg，面对面拉着弹簧秤做圆周运动的溜冰表演，如图所示，两个相距0.9 m，弹簧秤的示数为9.2 N，下列判断正确的是（）A.两人的线速度相同，约为40 m/sB.两人的角速度相同，为6 rad/sC.两人的运动半径相同，都是0.45 mD.两人的运动半径不同，甲为0.3 m,乙为0.6 m解析：甲、乙两人绕共同的圆心做圆周运动，他们间的拉力互为向心力，他们的角速度相同，半径之和为两人的距离.设甲、乙两人所需向心力为F向，角速度为ω，半径分别为r甲、r乙.则F向=M甲ω2r甲=M乙ω2r乙=9.2 N ① r甲+r乙=0.9 m ②由①②两式可解得只有D正确答案：D7、如图所示，在匀速转动的圆筒内壁上有一物体随圆筒一起转动而未滑动.若圆筒和物体以更大的角速度做匀速转动，下列说法正确的是（）A.物体所受弹力增大，摩擦力也增大B.物体所受弹力增大，摩擦力减小C.物体所受弹力减小，摩擦力也减小D.物体所受弹力增大，摩擦力不变析：物体在竖直方向上受重力G与摩擦力F，是一对平衡力，在向心力方向上受弹力F N.根据向心力公式，可知F N=mω2r，当ω增大时，F N增大，选D.8、用细绳拴住一球，在水平面上做匀速圆周运动，下列说法中正确的是（）A.当转速不变时，绳短易断B.当角速度不变时，绳短易断C.当线速度不变时，绳长易断D.当周期不变时，绳长易断析：由公式a=ω2R=知，当角速度（转速）不变时绳长易断，故A、B错误.周期不变时,绳长易断，故D正确.由,当线速度不变时绳短易断,C错9、如图,质量为m的木块从半径为R的半球形的碗口下滑到碗的最低点的过程中，如果由于摩擦力的作用使得木块的速率不变A.因为速率不变，所以木块加速度为零 C.木块下滑过程中的摩擦力大小不变B.木块下滑的过程中所受的合外力越来越大D.木块下滑过程中的加速度大小不变,方向时刻指向球心解析：木块做匀速圆周运动，所受合外力大小恒定，方向时刻指向圆心，故选项A、B不正确.在木块滑动过程中，小球对碗壁的压力不同，故摩擦力大小改变,C错. 答案：D10、如图所示，在光滑的以角速度ω旋转的细杆上穿有质量分别为m和M的两球，两球用轻细线连接.若M＞m，则（）A.当两球离轴距离相等时，两球相对杆不动B.当两球离轴距离之比等于质量之比时，两球相对杆都不动C.若转速为ω时，两球相对杆都不动，那么转速为2ω时两球也不动D.若两球相对杆滑动，一定向同一方向，不会相向滑动解析：由牛顿第三定律可知M、m间的作用力相等，即F M=F m，F M=Mω2r M，F m=mω2rm，所以若M、m不动，则r M∶r m=m∶M，所以A、B不对，C对（不动的条件与ω无关）.若相向滑动，无力提供向心力，D对. 答案：CD11、一物体以4m/s的线速度做匀速圆周运动，转动周期为2s，则物体在运动过程的任一时刻，速度变化率的大小为（）A.2m/s2B.4m/s2C.0D.4π m/s2ω=2π/T=2π/2=π v=ω*r 所以r=4/π a=v∧2/r=16/(4/π)=4π12、在水平路面上安全转弯的汽车，向心力是（）A.重力和支持力的合力B.重力、支持力和牵引力的合力C 汽车与路面间的静摩擦力 D.汽车与路面间的滑动摩擦力二、非选择题【共3道小题】1、如图所示，半径为R的半球形碗内，有一个具有一定质量的物体A，A与碗壁间的动摩擦因数为μ，当碗绕竖直轴OO′匀速转动时，物体A刚好能紧贴在碗口附近随碗一起匀速转动而不发生相对滑动，求碗转动的角速度.分析：物体A随碗一起转动而不发生相对滑动，物体做匀速圆周运动的角速度ω就等于碗转动的角速度ω.物体A做匀速圆周运动所需的向心力方向指向球心O，故此向心力不是重力而是由碗壁对物体的弹力提供，此时物体所受的摩擦力与重力平衡.解析：物体A做匀速圆周运动，向心力：F n=mω2R而摩擦力与重力平衡，则有μF n=mg 即F n=mg/μ由以上两式可得：mω2R= mg/μ即碗匀速转动的角速度为：ω=.2、汽车沿半径为R的水平圆跑道行驶，路面作用于车的摩擦力的最大值是车重的1/10，要使汽车不致冲出圆跑道，车速最大不能超过多少?解析：跑道对汽车的摩擦力提供向心力，1/10mg=mv2/r，所以要使汽车不致冲出圆跑道，车速最大值为v=. 答案：车速最大不能超过3、一质量m=2 kg的小球从光滑斜面上高h=3.5 m处由静止滑下，斜面的底端连着一个半径R=1 m的光滑圆环（如图所示），则小球滑至圆环顶点时对环的压力为_____________，小球至少应从多高处静止滑下才能通过圆环最高点，hmin=_________(g=10 m/s2).解析：①设小球滑至圆环顶点时速度为v1,则mgh=mg·2R+ 1/2mv12 F n+mg= mv12/R 得:F n=40 N②小球刚好通过最高点时速度为v2,则mg= mv22/R又mgh′=mg2R+1/2 mv22/R得h′=2.5R 答案：40 N;2.5R匀速圆周运动典型问题剖析匀速圆周运动问题是学习的难点，也是高考的热点，同时它又容易和很多知识综合在一起，形成能力性很强的题目，如除力学部分外，电学中“粒子在磁场中的运动”涉及的很多问题仍然要用到匀速圆周运动的知识，对匀速圆周运动的学习可重点从两个方面掌握其特点，首先是匀速圆周运动的运动学规律，其次是其动力学规律，现就各部分涉及的典型问题作点滴说明。