讲平面与立体表面相交
- 格式:doc
- 大小:96.00 KB
- 文档页数:4

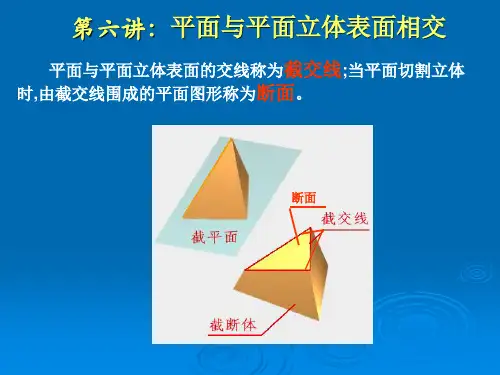
§4-2 平面与平面立体表面相交平面与立体表面的交线,称为截交线;当平面切割立体时,由截交线围成的平面图形,称为截面。
一、平面立体的截交线和断面如图4-16a所示,平面立体的截交线是截平面上的一个多边形,它的顶点是平面立体的棱线或底边与截平面的交点,它的边是截平面与平面立体表面的交线,图中截平面P与三棱锥的截交线是一个三角形ⅠⅡⅢ。
如图4-16b中的黑色图形所示,已知三棱锥SABC和正垂的截平面P,求作截交线的三面投影。
作图过程如图4-16b中的红色图形所示:(1)在棱线SA、SB、SC的正面投影s'a'、s'b'、s'c'与截平面P的有积聚性的迹线P v的相交处,作出它们的交点Ⅰ、Ⅱ、Ⅲ的正面投影1'、2'、3',与P v相重合的直线1'2'3',即为截交线△ⅠⅡⅢ的正面投影。
(2)由1'、2'、3'引投影连线,分别与sa、sb、sc和s″a″、s″b″、s″c″交出1、2、3和1″、2″、3″。
连接这些点的同面投影,就作出了截交线△ⅠⅡⅢ的水平投影△123和侧面投影△1″2″3″。
由于三个棱面的水平投影和棱面SAB、SCA的侧面投影都可见,在其上的截交线的同面投影12、23、31和1″2″、3″1″也都可见,画粗实线;棱面SBC的侧面投影不可见,在其上的截交线的侧面投影2″3″也不可见,画细虚线。
如图4-17a中的黑色图形所示,已知五棱柱的正面投影和水平投影,并用正垂面P切割掉左上方的一块,被切割掉的部分用细双点划线表示,求作截交线以及五棱柱被切割后的三面投影。
因为截交线的各边是正垂面P与五棱柱的棱面和顶面的交线,它们的正面投影都重合在P v上,因为截交线的正面投影已知,五棱柱被切割后的正面投影也已知,只要作出截交线的水平投影,就可以作出五棱柱被切割后的水平投影。
根据五棱柱的正面投影和水平投影,可以作出它的侧面投影;同理,由已作出的截交线的正面投影和水平投影,也可以作出截交线的侧面投影,从而作出五棱柱被切割后的侧面投影。

§4-2 平面与平面立体表面相交平面与立体表面的交线,称为截交线;当平面切割立体时,由截交线围成的平面图形,称为截面。
一、平面立体的截交线和断面如图4-16a所示,平面立体的截交线是截平面上的一个多边形,它的顶点是平面立体的棱线或底边与截平面的交点,它的边是截平面与平面立体表面的交线,图中截平面P与三棱锥的截交线是一个三角形ⅠⅡⅢ。
如图4-16b中的黑色图形所示,已知三棱锥SABC和正垂的截平面P,求作截交线的三面投影。
作图过程如图4-16b中的红色图形所示:(1)在棱线SA、SB、SC的正面投影s'a'、s'b'、s'c'与截平面P的有积聚性的迹线的相交处,作出它们的交点Ⅰ、Ⅱ、Ⅲ的正面投影1'、2'、3',与P v相重合的直线1'2'Pv3',即为截交线△ⅠⅡⅢ的正面投影。
(2)由1'、2'、3'引投影连线,分别与sa、sb、sc和s″a″、s″b″、s″c″交出1、2、3和1″、2″、3″。
连接这些点的同面投影,就作出了截交线△ⅠⅡⅢ的水平投影△123和侧面投影△1″2″3″。
由于三个棱面的水平投影和棱面SAB、SCA的侧面投影都可见,在其上的截交线的同面投影12、23、31和1″2″、3″1″也都可见,画粗实线;棱面SBC的侧面投影不可见,在其上的截交线的侧面投影2″3″也不可见,画细虚线。
如图4-17a中的黑色图形所示,已知五棱柱的正面投影和水平投影,并用正垂面P切割掉左上方的一块,被切割掉的部分用细双点划线表示,求作截交线以及五棱柱被切割后的三面投影。
因为截交线的各边是正垂面P与五棱柱的棱面和顶面的交线,它们的正面投影都重合在上,因为截交线的正面投影已知,五棱柱被切割后的正面投影也已知,只要作出截交线的Pv水平投影,就可以作出五棱柱被切割后的水平投影。
根据五棱柱的正面投影和水平投影,可以作出它的侧面投影;同理,由已作出的截交线的正面投影和水平投影,也可以作出截交线的侧面投影,从而作出五棱柱被切割后的侧面投影。



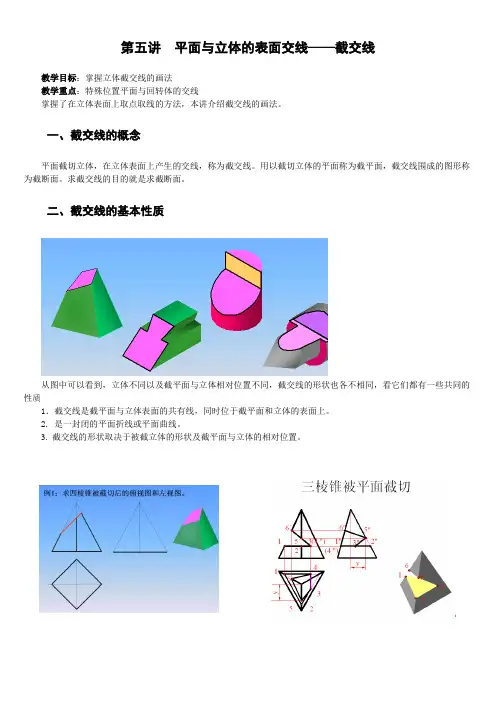
第五讲平面与立体的表面交线——截交线教学目标:掌握立体截交线的画法教学重点:特殊位置平面与回转体的交线掌握了在立体表面上取点取线的方法,本讲介绍截交线的画法。
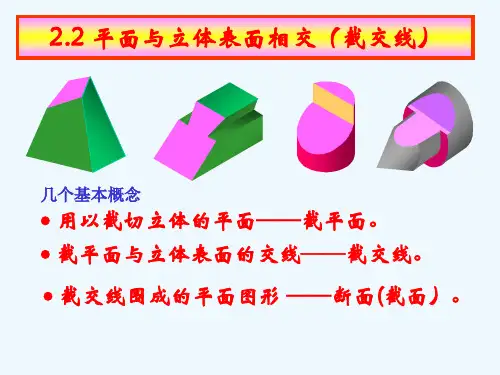
一、截交线的概念平面截切立体,在立体表面上产生的交线,称为截交线。
用以截切立体的平面称为截平面,截交线围成的图形称为截断面。
求截交线的目的就是求截断面。
二、截交线的基本性质从图中可以看到,立体不同以及截平面与立体相对位置不同,截交线的形状也各不相同,看它们都有一些共同的性质1.截交线是截平面与立体表面的共有线,同时位于截平面和立体的表面上。
2. 是一封闭的平面折线或平面曲线。
3. 截交线的形状取决于被截立体的形状及截平面与立体的相对位置。
三、平面与平面立体相交平面立体的表面都是平面,因此平面与平面立体的交线是一闭合的平面折线——多边形。
多边形的各边是截平面与立体相应棱面的交线,多边形的顶点是截平面与立体相应棱线的交点。
求截交线时,可根据具体情况求出棱线与截平面的交点,或求出棱面与截平面的交线。
实例分析:分析截平面切到哪些棱线和棱面,要分别求出与他们的交点和交线。
四、平面与回转体相交截交线是截平面与回转体表面的共有线。
截交线的形状取决于回转体表面的形状及截平面与回转体轴线的相对位置。
求截交线的方法:即求截平面与回转体表面的共有点。
求截交线的步骤:·空间及投影分析☆分析回转体的形状以及截平面与回转体轴线的相对位置,以确定截交线的形状。
☆分析截平面及回转体与投影面的相对位置,明确截交线的投影特性,如积聚性、类似性等。
找出截交线的已知投影,予见未知投影。
·画出截交线的投影当截交线的投影为非圆曲线时,其作图步骤为:☆先找特殊点,再补充中间点。
☆将各点光滑地连接起来,并判断截交线的可见性。
1.平面与圆柱相交截平面与圆柱面的交线的形状取决于截平面与圆柱轴线的相对位置。
当截平面与圆柱轴线垂直时,截交线为圆,投影如图示;当截平面与圆柱轴线平行时,截交线为平行两直线(素线),投影如图示;当截平面与圆柱轴线倾斜时,截交线为椭圆,投影如图示。

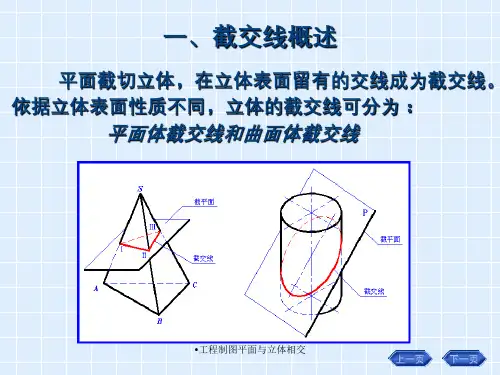
第八章 平面与立体相交•直线与立体相交¤ 8-1 平面与立体相交平面与立体相交,可看作是立体被平面所截,这个平面称为截平面...,截平面与立体表面的交线称为截交线...(图8-1)。
为了正确地画出截交线的投影,应掌握截交线的基本性质:(1)截交线是截平面和立体表面交点的集合,截交线既属于截平面,又属于立体表面,是截平面和立体表面的共有线。
(2)立体是由其表面围成的,所以截交线必然是一个或多个由直线或平面曲线围成的封闭平面图形。
图8-1 平面与立体相交求截交线的实质就是求出截平面和立体表面的共有点。
为此,可以根据立体表面的性质,在其上选取一系列适当的线(棱线、直素线或圆),求这些线与截平面的交点,然后按其可见或不可见用实线或虚线依次连成多边形或平面曲线。
一、平面与平面立体相交平面与平面立体相交,其截交线的形状是由直线围成的多边形。
多边形的顶点为平面立体上有关棱线(包括底面边线)与截平面的交点。
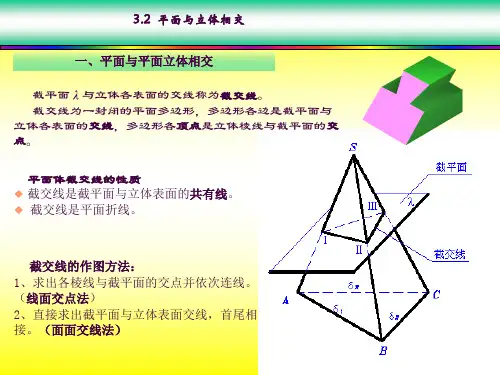
[例8-1] 三棱锥与一正垂面P相交,求截交线的投影(图8-2)。
分析:正垂面P的正面投影有积聚性,即P v,可直接求出平面P与棱线SA、SB、SC的交点Ⅰ(1,1′)、Ⅱ(2,2′)及Ⅲ(3,3′)。
顺次连接各顶点,得截交线为△ⅠⅡⅢ(△123,1′2′3′)。
103关于截交线可见性的判别,在假定截平面透明的前提下,可根据各段交线所在表面的可见与否而定。
可见表面上的交线为可见,用实线画出;不可见表面上的交线为不可见,用虚线画出。
在本例中,三棱锥的三个棱面的水平投影都为可见,故截交线的水平投影△123为可见,用实线画出;正面投影1′2′3′积聚在P V 线上,不再判别。
(a) (b)图8-2 三棱锥的截交线二、平面与曲面立体相交平面与曲面立体相交,其截交线形状一般为封闭的平面曲线。
曲线上的任何一点,都可当作是曲面上某一条线(直素线或圆)与截平面的交点。
求截交线时必须根据曲面的性质,在其 上选取一系列的直素线或圆,求出它们与截平面的交点。
第10讲 3-3 平面与立体相交
(说明:本节内容相对下一节较少,如有可能,可适当加一些下一节的内容)
教学目标:1、掌握截交线的基本特性;
2、掌握求画平面立体的截交线的一般方法、步骤;
教学重点:截交线的作图方法
教学难点:复杂平面立体的截交线的求法
教学方法:结合实例课堂讲解
教学用具:多媒体
教学过程:
工程上常遇到表面有交线的零件。
为了完整、清晰的表达出零件的形状以便正确的制造零件,应正确的画出交线。
交线通常可分为两种,一种是平面与立体表面相交形成的截.交.
线,
..如图3-1a、b中箭头所示。
另一种是两立体表面相交形成的相贯线
...,如图3-1c、d中箭头所示。
从图中可以看出,交线
..是零件上平面与立体表面或两立体表面的共有线,也是它们表面间的分界线。
由于立体由不同表面所包围,并占有一定空间范围,因此,立体表面交线通常是封闭的,如果组成该立体的所有表面,所确定立体的形状、大小和相对位置已定,则交线也就被确定。
立体的表面交线在一般的情况下是不能直接画出来的(交线为圆或直线时除外),因此,必须先设法求出属于交线上的若干点,然后把这些点连接起来。
本节着重介绍平面与立体相交表面交线(截交线)的画法。
一、概述
平面与立体相交,即立体被平面截切所产生的表面交线称为截交线,该平面称为截平面。
....(一)截交线的性质
由于立体表面的形状不同和截平面所截切的位置不同,截交线也表面为不同的形状,但任何截交线都具有下列基本性质:
1.共有性
截交线既属于截平面,又属于立体表面,故截交线是截平面与立体表面的共有线,截交线上的每一点均为截平面与立体表面的共有线。
2.封闭性
由于任何立体都占有一定的封闭空间,而截交线又为平面截切立体所得,故截交线所围成的图形一般是封闭的平面图形。
3.截交线的形状
截交线的形状取决于立体的几何性质极其与截平面的相对位置,通常为平面折线、平面曲线或平面直线组成。
当平面与片面立体相交时,其截交线为封闭的平面折线(图3-2)。
当平面与回转提相交时,其截交线一般为封闭的片面曲线(图3-3a)或平面曲线和直线围成的封闭的平面图形(图3-3b)或平面多边形(图3-3c)。
(二)求画截交线的一般方法、步骤
求画截交线就是求画截平面与立体表面的一系列共有点。
求共有点的方法通常有:具体作图步骤为:
(1)找(求)出属于截交线上一系列的特殊点;
(2)求出若干一般点;
(3)判别可见性;
(4)顺次连接各点(成折线或曲线)。
1.面上取点法
平面与立体相交,截片面处于特殊位置,截交线有一个投影或两个投影有积聚性,利
用积聚性采用面上取点法,求出截交线上共有点的另外一个或两个投影,此方法称为面上
..
取点法。
....图3-2b所示唯一正放的正六棱柱被正垂面P截切,由于截平面P是正垂面,截交线的正面投影可直接确定(即积聚在截平面的有积聚性的同面投影上),截交线的水平投影积聚在正六棱柱各侧棱面水平投影上,故由截交线的正面投影和水平投影可求出其侧面投影。
2.线面交点法
平面与立体相交,截平面处于特殊位置,截交线有一个投影或两个投影有积聚性,求立体表面上的棱线或素线与截平面的交点,该交点即为截交线上的点(共有点),此方法称为线.
面交点法
....,如图3-4所示。
二、平面与平面立体相交
平面与平面立体相交,其截交线是一封闭的平面折线。
求平面与平面立体的截交线,只要求出平面立体有关的棱线与截平面的交点,经判别可见性,然后依次连接各交点,即得所求的截交线。
也可直接求出截平面与立体有关表面的交线,由各交线构成的封闭折线即为所求的截交线。
当截平面为特殊位置时,它所垂直的投影面上的投影有积聚性。
对于正放的棱柱,因各表面都处于特殊位置,故可利用面上取点法求画其截交线(图3-2)。
对于棱锥,因含有一般位置平面,故可采用线面交点法求画截交线。
[例3-1] 求正垂面P与正四棱锥的截交线(图3-4)
分析截平面P为正垂面,它与正四棱锥的四个侧棱面都相交,故截交线围成一个四边形。
由于截平面P的正面投影有积聚性,所以四棱锥各侧棱线的正面投影s′a′、s′b′、s′c′、s′(d′)与Pv的交点1′、2′、3′、(4′)即为四边形四个顶点的正面投影,它们都在Pv上,故本题主要是求截交线的水平投影和侧面投影。
作图方法如下:根据点的投影规律,在相应的棱线上求出属于截交线的交点,经判别可见性,然后依次连接各点的同面投影,使得正四棱锥被正垂面P截切后的投影。
作业:P43-P44。