必修五周测试题(一)

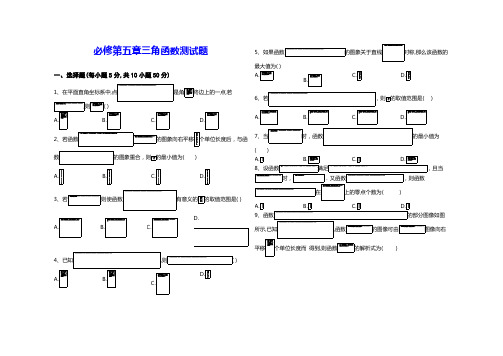
必修第五章三角函数测试题一、选择题(每小题5分,共10小题50分)1、在平面直角坐标系中,点是角终边上的一点,若,则( ) B.C.D.2、若函数的图象向右平移个单位长度后，与函数的图象重合，则的最小值为( ) A.B.C.D.3、若,则使函数有意义的的取值范围是( )A. B. C.D.4、已知,则( )A.B.C.D.5、如果函数的图象关于直线对称,那么该函数的( ) A.B.C. D.6、若，则的取值范围是( ) A.B.C.D.7、当时，函数的最小值为( )A. B. C. D.8、设函数满足，且当时，．又函数，则函数在上的零点个数为( ) A. B.C.D.9、函数的部分图像如图所示,已知,函数的图像可由图像向右平移个单位长度而 得到,则函数的解析式为( )10、设函数则下列结论错误的是( )A.的一个周期为B.的图像关于对称C.一个零点为D.在减二、填空题(每小题5分,共7小题35分)11、已知：①，②，③，④，其中是第一象限角的为__________(填序号)． 12、已知函数的部分图像如图所示,若图中在点,处取得极大值,在点,处取得极小值,且四边形的面积为,则的值是__________.13、关于函数，下列命题： ①若存在，有时，成立；②在区间上是单调递增；③函数的图像关于点成中心对称图像； ④将函数的图像向右平移个单位后将与的图像重合．其中正确的命题序号__________（注：把你认为正确的序号都填上） 14、确定下列三角函数值的符号：__________;__________;____________________;__________;__________15、函数__________,最小值为__________. 16、已知角终边上一点的坐标为,则是第__________象限角,__________.17、若函数的周期,则__________,且函数的单调递减区间为__________.(是自然对数的底数)三、解答题(每小题12分,共5小题60分)18、设，求的取值范围．19、已知角的终边经过点,求下列各式的值.(1);(2).20、设函数，图象的一条对称轴是直线.(1)求；(2)求函数的单调增区间．21、将函数的图象上所有点的横坐标缩短到原来的倍(纵坐标不变),再将所得的图象向左平移个单位长度后得到函数的图象. (1)写出函数的解析式;(2)若, ,求的最小值.22、若函数对任意都有．(1)求的值；(2)求的最小正值；(3)当取最小正值时，若，求的最大值和最小值．必修第五章三角函数测试题答案解析第1题答案 B第1题解析 因为,,所以角的终边落在第一象限,并且根据角的三角函数值的定义,,结合,得出.第2题答案 D第2题解析向右平移个单位长度后得到函数解析式，即，显然当时两图象重合，此时，∵，∴时，取最小值．第3题答案 C第3题解析 ∵要使函数有意义,则,.又,∴.第4题答案 A第4题解析 α化简得,则=故选:A第5题答案 C第5题解析(令,则),则则函数的最大值为,∵函数的图象关于直线对称,∴,即,,则,平方得. 得,即,则,则函数的最大值为.第6题答案 C第6题解析 ∵，∴当时，此式的取值范围是，而在上小于，故排除；在上,∴不可能相等，所以排除，故选．第7题答案 C第7题解析 ∵，∴,利用的单调性可得，当时，，故选C ．第8题答案 B第8题解析 ∵，∴函数为偶函数．又∵，∴，故函数的周期为．∵，∴为偶函数．∵当时，． 所以当时，，即．当时，；当时，．又．综合以上两函数的特点，可作出函数的大致图象(如图)，函数除了0、1这两个零点之外，分别在区间上各有一个零点，共有个零点，故选B ．第9题答案第9题解析由图象可知最小正周期:,∴,又∵ 在时取最小值,∴,∴.又∵,∴ ,∴.又∵ 图象过点,∴ ,∴ .,把图象向右平移个单位后得到函数, ∴. 第10题答案D第10题解析由题意,函数,可知最小正周期为,则也是函数的一个周期,所以A是正确的;令,可得(最大值),所以是函数的其中一条对称轴,所以B是正确的;令,则,所以是函数一个零点,所以C是正确的;当,则,函数在单调递增,所以D不正确, 故选D.第11题答案②③④第11题解析， ，．第12题答案第12题解析 根据题意可得四边形为平行四边形,∵四边形的面积为,∴ ,即,∴函数的最小正周期为,∴,即.第13题答案 ①③④ 第13题解析，显然函数周期为，若存在，有时，成立，故①正确；当时，故图形图像关于点成中心对称；故③正确；将函数的图像向右平移个单位后，得到函数第14题答案 +- 0 - + +第14题解析 角的终边在第二象限，∴；；；；角的终边在第二象限，∴；。

2014年上学期高一理科数学第九周周测试卷一、选择题（每小题5分，共25分）1．已知数列{}n a 中，13a =，26a =，且21n n n a a a ++=-，则数列的第五项为（ ）A . 6B . 3-C . 12-D . 6-2．某种商品投产后,计划两年后使成本降低36％,那么平均每年应降低成本（ ）A ． 18％ B.20％ C.24％ D.30％3．设n S 为等比数列{}n a 的前n 项和，3432S a =-，2332S a =-，则公比q =( )A.2B.4C.5D.64．已知等比数列{}n a ，公比21=q 且3049531=++++a a a a ，则++21a a 503a a ++ 等于( ) A ．35 B ．40 C ．45 D ．505．等差数列{}n a 的前n 项和为n S ，若0211=-++-m m m a a a ，3812=-m S ，则m =( ) A ．8B ．9C ．10D ．11二、填空题（每小题5分，共25分）6．设等比数列{}n a 的公比12q =，前n 项和为n S ，则44S a = ． 7．已知等比数列{}n a 的前n 项和为n S ，3231510=S S ，则此数列的公比为 ． 8．三个数的比值为3:5:11，各减去2后所得的三数成等比数列，则原来三个数的和为______9．在等比数列{}n a 中，675=⋅a a ，2105a a +=，则1810a a = 10．在等比数列{}n a 中，公比2=q ，25log log log 1022212=+++a a a ，则=+++1021a a a ．2014年上学期高一理科数学第九周周测答题卷班级： 姓名： 座号： 得分-卷面分：题号 1 2 3 4 5答案6. 7. 8. 9. 10.三、解答题(11题12分，12题13分，共25分)11．已知数列{}n a 的通项公式n a 与前n 项和n S 公式之间满足23n n S a =-关系.求：（1）1a 的值；（2）数列{}n a 的通项公式；（3）数列{}n a 的前n 项和n S .已知n 是首项为19，公差为-2的等差数列，n 为n 的前项和.（Ⅰ）求通项n a 及n S ；（Ⅱ）设{}n n b a -是首项为1，公比为3的等比数列，求数列{}n b 的通项公式及其前n 项和n T .。

五年级数学上册：三角形的周长测试题(含答案)五年级数学上册：三角形的周长测试题（含答案）题目一求下列三角形的周长：1. 已知三角形的三条边分别为12cm、15cm和8cm，求三角形的周长。

2. 三角形的周长为36cm，其中两条边分别为10cm和14cm，求第三条边的长。

3. 若三角形的周长为24.5cm，且两条边的长度分别为6cm和8cm，求第三条边的长。

答案一1. 三角形的周长为 12cm + 15cm + 8cm = 35cm。

2. 设第三条边长为 x，则根据三角形周长的定义，有 10cm + 14cm + x = 36cm。

解方程得 x = 12cm。

3. 设第三条边长为 x，则根据三角形周长的定义，有 6cm +8cm + x = 24.5cm。

解方程得 x = 10.5cm。

题目二根据已知条件，判断下列三角形的周长是否可以确定，若可以确定，请计算周长：1. 三角形的两条边长分别为5cm和7cm，且夹角为60度。

2. 三角形的两条边长分别为8cm和12cm，且夹角为90度。

3. 三角形的两条边长分别为3cm和4cm，且夹角为30度。

答案二1. 可以确定三角形的周长。

根据余弦定理，已知两边和夹角可以计算第三边，再加上已知两边的长度，即可计算周长。

假设第三边长为 x，则根据余弦定理，有 x² = 5² + 7² - 2 × 5 × 7 × cos60°。

解以上方程得 x = 5.60cm。

所以三角形的周长为 5cm + 7cm + 5.60cm = 17.60cm。

2. 可以确定三角形的周长。

根据勾股定理，已知两边可以计算第三边，再加上已知两边的长度，即可计算周长。

假设第三边长为 x，则根据勾股定理，有 x² = 8² + 12²。

解以上方程得 x = 14.42cm。

所以三角形的周长为 8cm + 12cm + 14.42cm = 34.42cm。

2024年【每周一测】第五周数学五年级下册基础练习题（含答案）试题部分一、选择题：1. 一个三位数的十位和百位数字相同，且都不为零，个位数字比十位数字大2，这个三位数是（）。

A. 255B. 336C. 447D. 5582. 下列各数中，与2.3最接近的整数是（）。

A. 2B. 3C. 4D. 53. 一个三角形的最长边长是10厘米，那么它的面积不可能是（）平方厘米。

A. 20B. 25C. 30D. 404. 下列各数中，能被2和3整除的是（）。

A. 36B. 48C. 56D. 635. 0.25×4×0.25的结果是（）。

A. 0.25B. 0.5C. 1D. 46. 下列各数中，与4.8相乘后积为一位数的是（）。

A. 2.1B. 3.2C. 4.5D. 5.67. 一个平行四边形的底是8厘米，高是3厘米，它的面积是（）平方厘米。

A. 24B. 26C. 28D. 308. 下列各数中，与8相加后和为整百数的是（）。

A. 92B. 93C. 94D. 959. 一个数乘以9后，再除以3，结果是27，这个数是（）。

A. 3B. 6C. 9D. 1210. 下列各数中，与0.8相乘后积为1.6的是（）。

A. 2B. 1.2C. 0.8D. 0.5二、判断题：1. 一个数既是3的倍数，又是4的倍数，那么这个数一定是12的倍数。

（）2. 1千克等于1000克，所以1克等于1000千克。

（）3. 两个锐角相加的和一定是钝角。

（）4. 一个三位数的最高位是百位。

（）5. 0.4的计数单位是0.1。

（）三、计算题：1. 456 + 789 =2. 1000 543 =3. 72 × 35 =4. 504 ÷ 6 =5. ÷ 4 =6. 7 × (45 + 23) =7. (987 432) × 5 =8. 63 ÷ 7 + 25 × 2 =9. 450 ÷ 90 16 +10. 8 × (7 + 6 ÷ 3) =11. 64 ÷ 8 × 12 ÷ 3 =12. 100 25 × 2 +13. 9 × 9 10 ÷ 5 =14. 81 ÷ (3 + 1) =15. 120 ÷ (6 2) =16. 75 ÷ 15 + 8 × 3 =17. 5 × (4 + 3 × 2) =18. (9 + 6) ÷ 3 × 7 =19. 56 ÷ 7 3 × 4 +20. 6 × (8 5) ÷ 2 =四、应用题：1. 小明有3个苹果，小华比小明多2个苹果，小华有多少个苹果？2. 一个长方形的长是10厘米，宽是5厘米，求这个长方形的面积。

高一地理必修一第一章测试题一、选择题（每题2分，共20分）1. 地球自转一周的时间是：A. 12小时B. 24小时C. 48小时D. 72小时2. 地球公转的周期是：A. 1个月B. 1季度C. 1年D. 10年3. 地理坐标中，纬度的起始线是：A. 赤道B. 本初子午线C. 国际日期变更线D. 南北极点4. 地球上的五带分别是：A. 热带、亚热带、温带、寒带、极地B. 热带、温带、寒带、极地、亚热带C. 热带、温带、亚热带、寒带、极地D. 寒带、温带、热带、亚热带、极地5. 以下哪个不是地球自转产生的地理现象：A. 日夜交替B. 季节变化C. 地方时差D. 地转偏向力6. 地球的赤道周长大约是：A. 20000公里B. 40000公里C. 60000公里D. 80000公里7. 地球上的经度起始线是：A. 赤道B. 本初子午线C. 180度经线D. 南北极点8. 以下哪个现象与地球公转有关：A. 潮汐现象B. 季节变化C. 地球形状D. 地壳运动9. 地球的自转速度在赤道处是：A. 最快B. 最慢C. 无变化D. 无法确定10. 地球上的经度和纬度是：A. 相对的B. 独立的C. 互补的D. 相互影响的二、填空题（每空1分，共10分）11. 地球的自转方向是________。

12. 地球的公转轨道呈________形状。

13. 地球上的经度范围是________。

14. 地球上的纬度范围是________。

15. 地球上的赤道是________度纬线。

16. 地球上的极圈是________度纬线。

17. 地球上的回归线是________度纬线。

18. 地球上的极点是________和________。

19. 地球上的五带中，没有阳光直射的地带是________。

20. 地球上的五带中，有极昼极夜现象的地带是________。

三、简答题（每题5分，共10分）21. 简述地球自转和公转的区别。

22. 解释什么是地理坐标系统，并说明它在日常生活中的应用。

五年级数学第一学期周测试题五年级数学第一学期周测试题班级姓名得分一、直接写出得数：2.6－( )＝1.643.5 8 10＝ 0._＋( )＝0.21 5 2＝ ( )－0._＝9.99 0.6 10 0.1＝8._ ( )＝8_ 6.2＋5.9＋5.9－6.2＝ 0.72 2.4＝二、解方程：：3 1.8－0.6_＝5.1 0.5(3+_)＝6.2 _ 0.5－10+2=04(0.9＋_)＝2.2_ (9_＋59－5_) 3=29 6.4―2(_+1.2)＝0.4三、递等式计算：（能简便的要简便）(1) 3.75－2.76＋1.25－1._ (2) (6.74＋6.74 6.74－6.74) 6.74(3) [1.8－1.8 (1.8－1.8)] 0.36 (4) (30－_.4 _) 0.2－1.5(5) 4.8 2.5 1.25 (6) 2.34 98＋4.68四、文字题：1、一个数的5倍比这个数的2.5倍多2、一个数的4倍是4_,这个数比另一4.6，这个数是多少？个数少_.另一个数是几?五、应用题：1、2支钢笔比5支活动铅笔贵2元,每支钢笔_元.每支活动铅笔多少元?2、一列火车从A地到相距_00千米的B地去，前3小时每小时行80千米，剩下的路程要求在_小时行完，那么每小时应行多少千米？3、果园里有梨树_0棵，桔树比梨树多20棵，比苹果树的3倍少30棵。

苹果树有多少棵？4、一组同学计划种树苗65棵,实际平均每人种了7棵,比计划多种5棵.这组同学有几人?:5、水杯里的水的容量乘7，再加上40毫升，就和水瓶里的水的容量一样多，水瓶里的水有2._升，水杯里有多少升水？6、李师傅6小时加工84个零件。

照这样计算，他8小时能加工多少个零件？7、装订小组装一批图书，原计划每天装订240册，_天完成；实际每天多装订60册，实际几天完成任务？8、一筐苹果和一筐桔子共重90千克，一筐苹果重量是桔子的3.5倍。

周周清测试卷（10）5.9(时间:90分钟分数: )一、填空题。

(22分)1.3.05平方米=( )平方分米4800平方厘米=( )平方分米6050平方米=( )公顷3平方米4平方分米=( )平方米2.小明考了98分,比李伟多a分,则李伟考了()分。

3.一本书260页,每天看x页,看了5天。

还剩下()页没看。

如果x=35,还剩下()页没看。

4.一个平行四边形的底是2米,高是8分米,它的面积是( )平方分米。

5.一个平行四边形的面积是20平方厘米,底是5厘米,它的高是( )厘米。

6.一个三角形的底是6厘米,高是3厘米,面积是( )平方厘米,与它等底等高的平行四边形面积是( )平方厘米。

7.三个连续的偶数和是30,则这三个数分别是( )、( )、( )。

8.一个梯形的上底是3厘米,下底是5厘米,高比下底少1厘米,面积是( )平方厘米。

另一个梯形的上底是2厘米,下底是上底的3倍,高是上底的一半,面积是( )平方厘米。

9.右图中平行四边形的面积是15cm2,阴影部分的面积是( )。

10.20的所有因数有( ),其中( )是5的倍数。

11.□45□是3的倍数,这个四位数最小是( ),把135分解质因数为( )。

12.一个三位数,它的个位上是最小的质数,十位上是最小的合数,百位上是最小的奇数,这个三位数是( )。

二、判断题。

(对的画“√”,错的画“✕”)(8分)1.等式都是方程,方程都是等式。

( )2.如果两个三角形面积相等,那么它们一定等底等高。

( )3.两个面积相等的三角形可以拼成一个平行四边形。

( )4.梯形面积是平行四边形面积的一半。

( )5.梯形的高不变,如果上底增加2厘米,下底减少2厘米,面积不变。

( )6.两个等底等高的平行四边形,形状不一定完全相同。

( )7.只要是6的倍数,就一定是3的倍数。

( )8.一个数的因数的个数是有限的,倍数的个数是无限的。

( )三、选择题。

(把正确答案的序号填在括号里)(6分)1.下面是方程的是( )。

一、选择题1．在ABC 中，内角A ､B ､C 所对的边分别是a ､b ､c ，已知14b c a -=，2sin 3sin B C =，ABC 的面积为3154，则a =（ ） A ．2B ．3C ．4D ．52．在ABC ∆中，若sin (sin cos )sin 0A B B C +-=，sin cos 20B C +=，4a =，则ABC ∆的面积为（ ）A ．243+B ．43+C ．623+D ．843+3．如图，四边形ABCD 中，CE 平分ACD ∠，23AE CE ==，3DE =，若ABC ACD ∠=∠，则四边形ABCD 周长的最大值（ ）A ．24B ．1233+C ．183D ．(3534．2020年5月1日起，新版《北京市生活垃圾管理条例》实施，根据该条例：小区内需设置可回收垃圾桶和有害垃圾桶.已知李华要去投放这两类垃圾，他从自家楼下出发，向正北方向走了80米，到达有害垃圾桶，随后向南偏东60°方向走了30米，到达可回收物垃圾桶，则他回到自家楼下至少还需走（ ） A ．50米B ．57米C ．64米D ．70米5．设,,a b c 分别是ABC 中,,A B C ∠∠∠所对边的边长，则直线sin 0x A a y c ⋅+⋅+=与sin sin 0b x y B C ⋅-⋅+=位置关系是（ ） A ．平行B ．重合C ．垂直D ．相交但不垂直6．已知,,a b c 分别是ABC ∆的三个内角,,A B C 所对的边，若1,3a b ==B 是,A C 的等差中项，则角C =（ ） A ．30B ．45︒C ．60︒D ．90︒7．ABC 的内角,,A B C 的对边分别为,,a b c ，若222sin sin sin 3sin sin A C B A C +-=，1b =，则223a c -的最小值为（ ）A ．4-B ．23-C ．2-D ．3-8．已知锐角ABC 的内角,,A B C 的对边分别为,,a b c .若()2c a a b =+，则2cos cos()AC A -的取值范围是（ ）A ．2,1⎛⎫⎪⎪⎝⎭B ．13,2⎛⎫⎪⎪⎝⎭ C ．23,⎛⎫⎪⎪⎝⎭D ．1,12⎛⎫ ⎪⎝⎭9．在△ABC 中，a 2tanB =b 2tanA ，则△ABC 是（ ） A ．等腰三角形 B ．直角三角形 C ．等腰直角三角形D ．等腰或直角三角形10．如图，测量河对岸的塔高AB 时，选与塔底B 在同一水平面内的两个测点C 与D .现测得15BCD ∠=︒，45BDC ∠=︒，302CD m =，并在点C 测得塔顶A 的仰角为30，则塔高AB 为( )A ．302mB ．203mC ．60mD ．20m11．已知在ABC 中，内角A 、B 、C 所对的边分别为a 、b 、c ，若ABC 的面积为S ，且222()S a b c =+-，则tan C =（ ）A ．43-B ．34-C ．34D ．4312．在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，若角A ，B ，C 成等差数列，且直线ax +cy ﹣12＝0平分圆x 2+y 2﹣4x ﹣6y ＝0的周长，则△ABC 的面积的最大值为（ ） A ．33B ．332C ．32D 3二、填空题13．已知60A =︒，ABC 的三个内角A ，B ，C 的对边分别为a ，b ，c ，其中7a =，133sin sin 14B C +=，则bc 的值为______. 14．如图，点A 是半径为1的半圆O 的直径延长线上的一点，3OA =B 为半圆上任意一点，以AB 为一边作等边ABC ，则四边形OACB 的面积的最大值为___________.15．在ABC ∆中，角A ，B ，C 的对边分别为a ，b ，c ，则满足10a =，18b =，30A =︒的三角形解的个数是______.16．在ABC 中，2AB =，30C ︒=，则AB BC 的取值范围是________. 17．在锐角ABC ∆中，2AC =，22AB =D 在BC 边上，并且2BD DC =，6π∠=CAD ，则ABC ∆的面积为__________．18．在ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，面积为S ，且满足22()a b c S --=，b ＋c ＝2，则S 的最大值是________19．在ABC 中，2AB =，4AC =．BC 边上的中线2AD =，则=ABC S △_____． 20．在△ABC 中，内角A ，B ，C 的对边分别是a ，b ，c ，若2b =，2a c =，则当角C 取最大值时，△ABC 的面积为__________．三、解答题21．已知ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，若1||2AB AC AC ⋅=，且1c =. 在①cos cos 2a C c A +=；② sin 3cos b C c B c =；③ sin 2sin a B c A =这三个条件中任选一个，补充在下面问题中，并解答问题. （1）求角A ；（2）若___________，角B 的平分线交AC 于点D ，求BD 的长. (注：如果选择多个条件分别解答，按第一个解答计分)22．ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知A 为锐角，22sin cos 2c a B C ab--=. （1）求A ；（2）若34b c =，且BC 边上的高为23ABC 的面积. 23．ABC 的内角,,A B C 的对边分别为,,a b c ．已知222sin sin sin sin sin B A C A C --=．（1）求B ；（2）若3b =，当ABC 的周长最大时，求它的面积． 24．已知ABC 的内角,,A B C 的对边分别为,,a b c ，2cos cos cos aA b C c B=+.（1）求角A 的大小；（2）若a =11b c+的取值范围. 25．在ABC 中，角,,A B C 所对的边分别为,,,a b c 已知1b =，面积28sin aS A=，再从以下两个条件中选择其中一个作为已知，求三角形的周长.（1）6B π=;（2）B C =.注:如果选择多个条件分别解答，按第一个解答计分.26．在ABC 中，a ，b ，c 分别为角A ，B ，C 的对边，222sin sin sin sin sin A C B A C +=+.（1）求角B 的大小；（2）若ABC 为锐角三角形，b =2a c -的取值范围.【参考答案】***试卷处理标记，请不要删除一、选择题 1．C 解析：C 【分析】首先利用正弦定理表示为23b c =，再结合余弦定理求cos A 和sin A ，并利用1sin 2ABCS bc A ==求a的值. 【详解】2sin 3sin B C =，由正弦定理可知23b c =， 14b c a -=，可得13,24c a b a ==，∴2221cos 24b c a A bc +-==-，sin A ==，1131sin 2242ABCSbc A a a ==⨯⨯=，解得：4a =. 故选：C 2．C解析：C 【分析】在ABC ∆中，()sin sin B A C +=，化简sin (sin cos )sin 0A B B C +-=可得4A π=，又sin cos 20B C +=和34B C π+=，解得3B π=，512C π=，最后通过正弦定理求出1)c =，再根据三角形面积公式得到面积.【详解】由sin (sin cos )sin 0A B B C +-=得：sin sin sin cos sin cos cos sin sin sin cos sin 0A B A B A B A B A B A B ⋅+⋅-⋅-⋅=⋅-⋅=，∴sin cos A A =，又0()A π∈，，则4A π=，则34B C π+=， 又3sin cos 2sin 22B C C π⎛⎫=-=-⎪⎝⎭，则3222B C k ππ=-+或222B C k ππ=-+，(0)B C π∈、，，则322B C π+=或22C B π-=，又34B C π+=，则取22C B π-=，得3B π=，512C π=，又4a =，根据正弦定理，sin 1)sin a Cc A ⋅==，∴1sin 62ABC S ac B ∆=⋅=+ 故选C. 【点睛】思路点睛：在三角形中，由于A B C π++=,根据诱导公式，()sin sin A B C +=，()sin sin A C B +=,()sin sin C B A +=，()cos cos A B C +=-,()cos cos A C B +=-,()cos cos C B A +=-等，以上常见结论需要非常熟练. 3．D解析：D 【分析】ACD △和CDE △中，结合正弦定理可求得6ACE DCE π∠=∠=，这样可得,DC AC ，在ABC 中，由余弦定理得2222cos3AC AB BC AB BC π=+-⋅，应用基本不等式可得AB BC +的最大值，从而可得四边形ABCD 周长的最大值． 【详解】设ABC ACD ∠=∠2θ=，(0,)2πθ∈，∵CE 平分ACD ∠，∴DCE ACE θ∠=∠=， 又AE CE =，∴EAC ACE θ∠=∠=，AE CE ==DE =AD =ACD △中，由正弦定理得sin sin CD AD DAC ACD =∠∠，则CD ==， CDE △中，2DEC EAC ECA θ∠=∠+∠=，由正弦定理得sin sin CD DE CED DCE =∠∠，则CD θ==，∴θ=，解得cos θ=，6πθ=，∴3CD ==，ACD △中，由角平分线定理得AC AE CD DE ==236AC =⨯=． ABC 中，23ABC πθ∠==，由余弦定理得2222cos 3AC AB BC AB BC π=+-⋅，即2222223136()3()()()44AB BC AB BC AB BC AB BC AB BC AB BC AB BC =+-⋅=+-⋅≥+-+=+，当且仅当AB BC =时等号成立，12AB BC +≤，此时ABC 为等边三角形．∴AB BC CD DA +++的最大值为12315++=+ 故选：D ． 【点睛】本题主要考查正弦定理、余弦定理的应用，考查基本不等式求最值，在平面图形中充分利用平面几何的知识可减少计算量．本题解题关键是求出6ACE π∠=．4．D解析：D 【分析】画出图形，在ABC 中，利用余弦定理，即可求解AC 的长，得到答案. 【详解】由题意，设李华家为A ，有害垃圾点为B ，可回收垃圾点为C ， 则李华的行走路线，如图所示，在ABC 中，因为80,30,60AB BC B ===， 由余弦定理可得：70AC ===米， 即李华回到自家楼下至少还需走70米. 故选：D .【点睛】本题主要考查了解三角形的实际应用，以及余弦定理的应用，其中解答中作出示意图，结合余弦定理求解是解答的关键，着重考查推理与运算能力.5．C解析：C 【解析】,,a b c 分别是ABC 中,,A B C ∠∠∠所对边的边长，则直线sin 0x A a y c ⋅+⋅+=斜率为：sin Aa-， sin sin 0b x y B C ⋅-⋅+=的斜率为：sin bB， ∵sin sin A ba B-=﹣1，∴两条直线垂直．故选C ．6．A解析：A 【详解】由题设可得060B =311sin sin 2A A =⇒=，则030A =或0150A =，但a b AB <⇔<，应选答案A ．7．A解析：A 【分析】由222sin sin sin 3sin sin A C B A C +-=，利用正弦定理和余弦定理，可得6B π=，再根据正弦定理、三角形内角和及两角和的余弦公式，得到223a c -4cos 3C π⎛⎫=+ ⎪⎝⎭，借助角C 的范围，即可求得结果. 【详解】222sin sin sin 3sin sin A C B A C +-=，∴2223a c b ac +-=，∴2222a c b ac +-=∴cos 2B =，又0B π<<，∴6B π=，12sin sin sin sin 6b A C B ac π====， ∴2sin a A =，2sin c C =，∴24sin a A C -=-4sin()B C C =+-4sin()6C C π=+-14cos 22C C C ⎛⎫=+- ⎪ ⎪⎝⎭2cos C C =-14cos 2C C ⎛⎫=- ⎪ ⎪⎝⎭4cos 3C π⎛⎫=+ ⎪⎝⎭因为506C π<<，所以7336C πππ<+<， 所以当3C ππ+=时，2a -取得最小值，且最小值为4-. 故选：A. 【点睛】本题考查了正弦定理和余弦定理的应用、三角形内角和的应用、两角和的余弦公式及余弦型函数的最值问题，考查学生对这些知识的掌握能力，属于中档题.在解有关三角形的题目时，要有意识地考虑用哪个定理更合适，一 般地，如果式子中含有角的余弦或边的二次式时，要考虑用余弦定理；如果式子中含有角的正弦或边的一次式时，则考虑用正弦定理.8．C解析：C 【分析】由余弦定理和正弦定理进行边化角，结合诱导公式和两角和与差的正弦公式可得2C A =，由锐角三角形得出A 角范围，再代入化简求值式，利用余弦函数性质可得结论． 【详解】∵2()c a a b =+，∴22222cos c a ab a b ab C =+=+-，∴(12cos )b a C =+，由正弦定理得sin sin (12cos )B A C =+，∴sin()sin (12cos )sin cos cos sin A C A C A C A C +=+=+，整理得sin sin cos cos sin sin()A C A C A C A =-=-，∵,A C 是三角形的内角，∴A C A =-，即2C A =，又三角形是锐角三角形，∴2222A A A πππ⎧<⎪⎪⎨⎪--<⎪⎩，解得64A ππ<<，由2C A =得22cos cos cos cos()cos A A A C A A ==∈-⎝⎭． 故选：C ． 【点睛】本题考查正弦定理和余弦定理的边角转换，考查两角与差的正弦公式，余弦函数的性质，考查学生分析问题解决问题的能力，属于中档题．9．D解析：D 【分析】根据正弦定理22tan ta in n s sin B B A A =⋅⋅，化简得到sin 2sin 2A B =，得到答案. 【详解】22tan tan a B b A =，故22tan ta in n s sin B B A A =⋅⋅，即sin 2sin 2A B =.故22A B =或22A B π+=，即A B =或2A B π+=.故选：D . 【点睛】本题考查了正弦定理判断三角形形状，意在考查学生的计算能力.10．D解析：D 【分析】由正弦定理确定BC 的长，再tan30AB BC 求出AB ．【详解】15BCD ∠=︒，45BDC ∠=︒120CBDsin 45BC302sin 45203BC3tan 3020320AB BC故选D 【点睛】本题是正弦定理的实际应用，关键是利用正弦定理求出BC ，属于基础题．11．A解析：A 【分析】由三角形面积公式和余弦定理可得C 的等式，利用二倍角公式求得tan2C，从而求得tan C ．【详解】∵222222()2S a b c a b ab c =+-=++-，即22212sin 22ab C a b ab c ⨯⋅=++-， ∴222sin 2ab C ab a b c ⋅-=+-，又222sin 2sin cos 1222a b c ab C ab CC ab ab +-⋅-===-，∴sin cos 12C C +=， 即22cos sin cos 222C C C =，则tan 22C =，∴222tan2242tan 1231tan2CC C ⨯===---， 故选：A ． 【点睛】本题考查三角形面积公式，余弦定理，考查二倍角公式，同角间的三角函数关系，掌握相应的公式即可求解．属于中档题，考查了学生的运算求解能力．12．B解析：B 【分析】由三角形内角和公式以及等差数列的性质可得3B π=，根据直线过圆心可得2312a c +=，根据基本不等式可得6ac ≤，最后由三角形面积公式得结果.【详解】在△ABC 中，A +B +C ＝π，∵角A ，B ，C 成等差数列，∴2B ＝A +C ， ∴2B ＝π﹣B ，∴B 3π=．∵直线ax +cy ﹣12＝0平分圆x 2+y 2﹣4x ﹣6y ＝0的周长， ∴圆心（2，3）在直线ax +cy ＝12上，则2a +3c ＝12， ∵a ＞0，c ＞0，∴12＝2a +3c ≥ac ≤6．当且仅当2a ＝3c ，即a ＝3，c ＝2时取等号．∴11sin 62222ABCSac B =≤⨯⨯=， ∴△ABC故选：B. 【点睛】本题主要考查了直线与圆的位置关系，基本不等式以及三角形面积公式的应用，属于中档题.二、填空题13．40【分析】首先根据正弦定理求并表示最后根据余弦定理求的值【详解】根据正弦定理可知根据余弦定理可知得解得：故答案为：40【点睛】方法点睛：(1)在解有关三角形的题目时要有意识地考虑用哪个定理更适合或解析：40 【分析】首先根据正弦定理求2R ，并表示sin sin 22b c B C R R+=+，最后根据余弦定理求bc 的值. 【详解】22sin a R R A =⇒==，根据正弦定理可知1322b c b c R R +=⇒+=， 根据余弦定理可知()2222222cos 3a b c bc A b c bc b c bc =+-=+-=+-，得249133bc =-，解得：40bc =. 故答案为：40 【点睛】方法点睛：(1)在解有关三角形的题目时，要有意识地考虑用哪个定理更适合，或是两个定理都要用，要抓住能够利用某个定理的信息，一般地，如果式子中含有角的余弦或边的二次式，要考虑用余弦定理；如果遇到的式子中含有角的正弦或边的一次式时，则考虑用正弦定理；以上特征都不明显时，则要考虑两个定理都有可能用到；(2)解题中注意三角形内角和定理的应用及角的范围限制．14．【分析】设表示出的面积及的面积进而表示出四边形的面积并化简所得面积的解析式为正弦函数形式再根据三角函数的有界性进行求解【详解】四边形的面积的面积的面积设则的面积的面积四边形的面积故当即时四边形的面积解析：【分析】设AOB θ∠=，表示出ABC 的面积及OAB 的面积，进而表示出四边形OACB 的面积，并化简所得面积的解析式为正弦函数形式，再根据三角函数的有界性进行求解． 【详解】四边形OACB 的面积OAB =△的面积ABC +△的面积，设AOB θ∠=，2222cos 31214AB OA OB OA OB θθθ∴=+-⋅⋅=+-⨯=-则ABC 的面积213sin 60cos 22AB AC AB θ=⋅⋅︒==OAB 的面积11sin 122OA OB θθθ=⋅⋅=⨯=，四边形OACB 的面积3cos 2θθ=+13(sin )60)2θθθ==-︒，故当6090θ-︒=︒，即150θ=︒时，四边形OACB =故答案为： 【点睛】方法点睛：应用余弦定理一定要熟记两种形式：（1）2222cos a b c bc A =+-；（2）222cos 2b c a A bc+-=，同时还要熟练掌握运用两种形式的条件.另外，在解与三角形、三角函数有关的问题时，还需要记住30,45,60︒︒︒等特殊角的三角函数值，以便在解题中直接应用.15．2【分析】直接利用正弦定理得到答案【详解】根据正弦定理得到：故故满足条件的三角形共有个故答案为：【点睛】本题考查了利用正弦定理判断三角形的个数问题意在考查学生的应用能力解析：2 【分析】直接利用正弦定理得到答案. 【详解】根据正弦定理得到：sin sin a b A B=，故9sin 10B =，91sin sin 10B A >=>. 故满足条件的三角形共有2个. 故答案为：2. 【点睛】本题考查了利用正弦定理判断三角形的个数问题，意在考查学生的应用能力.16．【分析】首先根据正弦定理得化简得到再求其范围即可【详解】由正弦定理得：所以所以因为所以即故的取值范围是故答案为：【点睛】本题主要考查正弦定理的应用同时考查三角函数的值域问题属于中档题 解析：[6,2]-【分析】首先根据正弦定理得4sin =BC A ，化简得到()4sin 2302⋅=+-AB BC A ，再求其范围即可. 【详解】 由正弦定理得：4sin sin ==AB BCC A，所以4sin =BC A . 所以()cos 1808sin cos ⋅=⋅-=-AB BC AB BC B A B()()8sin cos 180308sin cos 30⎡⎤=--+=+⎣⎦AA A A 218sin sin cos 4sin 22⎛⎫=-=- ⎪⎪⎝⎭A A A A A A ()()221cos 24sin 2302=--=+-A A A因为0150<<A ，所以3030330<2+<A ， 即()1sin 2301-≤+≤A ，()64sin 23022-≤+-≤A .故AB BC 的取值范围是[6,2]-. 故答案为：[6,2]- 【点睛】本题主要考查正弦定理的应用，同时考查三角函数的值域问题，属于中档题.17．【分析】在中由正弦定理可得到在中由正弦定理可得到由是锐角可知结合三角形的面积公式可得到答案【详解】在中由正弦定理得：则在中由正弦定理得：则因为所以由于三角形是锐角三角形故则故的面积为【点睛】本题考查 1【分析】在ADC ∆中，由正弦定理sin sin DC AC CAD ADC =∠∠，可得到1sin ADC DC∠=，在ADB ∆中，由正弦定理sin sin DB ABBAD ADB=∠∠，可得到12sin sin 2DCDB ADBDC BAD AB ∠∠===，由BAD ∠是锐角，可知4BAD π∠=，46BAC ππ∠=+，结合三角形的面积公式可得到答案．【详解】在ADC ∆中，由正弦定理得：sin sin DC ACCAD ADC=∠∠，则11sin 2sin6ADC DC DCπ∠=⨯⨯=， 在ADB ∆中，由正弦定理得：sin sin DB AB BAD ADB =∠∠，则sin sin DB ADBBAD AB ∠∠=，因为1sin sin ADB ADC DC∠=∠=，2BD DC =，所以122sin 22DCDC BAD ∠==，由于三角形是锐角三角形，故4BAD π∠=，则26sin sin 46BAC ππ+⎛⎫∠=+=⎪⎝⎭，故ABC ∆的面积为126222312+⨯⨯⨯=+.【点睛】本题考查了正弦定理在解三角形中的应用，考查了三角形的面积公式，属于中档题．18．【分析】结合余弦定理同角三角函数的基本关系式和基本不等式先求得然后求得的最大值【详解】由余弦定理得依题意所以由于是三角形的内角所以所以由解得所以当且仅当时等号成立所以的最大值为故答案为：【点睛】本小 解析：417【分析】结合余弦定理、同角三角函数的基本关系式和基本不等式，先求得sin A ，然后求得S 的最大值. 【详解】由余弦定理得2222cos a b c bc A =+-， 依题意221()sin 2a b c S bc A --==，2b c +=， ()()222212cos 221cos sin sin 41cos 2b c bc A b c bc bc A bc A A A +---+=-=⇒=-，所以1cos 1sin 4A A =-，221sin 1sin 14A A ⎛⎫+-= ⎪⎝⎭,2171sin sin 0162A A -=，由于A 是三角形ABC 的内角，所以sin 0A >，所以由2171sin sin 0162A A -=解得8sin 17A =.所以21444sin 21717217b c S bc A bc +⎛⎫==≤⨯= ⎪⎝⎭，当且仅当1b c ==时等号成立，所以S 的最大值为417. 故答案为：417【点睛】本小题主要考查余弦定理解三角形，考查三角形的面积公式，考查基本不等式求最值，属于中档题.19．【分析】中分别用余弦定理表示再利用解边长再根据余弦定理求角最后根据三角形面积公式求解【详解】设中中解得：中故答案为：【点睛】本题考查解三角形重点考查数形结合分析问题计算能力属于基础题型 解析：15【分析】ABD △，ADC 中，分别用余弦定理表示cos ADB ∠，cos ADC ∠，再利用cos cos 0ADB ADC ∠+∠=解边长BC ，再根据余弦定理求角BAC ∠，最后根据三角形面积公式求解. 【详解】 设BD DC x ==，ABD △中，22222cos 224x xADB x +-∠==⋅⋅，ADC 中，22222412cos 224x x ADC x x+--∠==⋅⋅ 180ADB ADC ∠+∠=，cos cos 0ADB ADC ∴∠+∠=,212044x x x -∴+=，解得：6x =26BC ∴=， ABC 中，(22224261cos 2244BAC +-∠==-⨯⨯,sin BAC ∴∠==1242ABCS∴=⨯⨯=【点睛】本题考查解三角形，重点考查数形结合分析问题，计算能力，属于基础题型.20．【分析】由余弦定理可得再利用基本不等式的性质可得的最大值再利用三角形面积计算公式即可得出【详解】解：在中由余弦定理可得：时取等号此时当取最大值时的面积故答案为：【点睛】本题考查了余弦定理基本不等式的【分析】由余弦定理可得cos C ，再利用基本不等式的性质可得C 的最大值，再利用三角形面积计算公式即可得出． 【详解】解：2b =，2a c =，∴在ABC ∆中，由余弦定理可得：22222441311cos ()22222242a b c c c c C ab c c +-+-===+⨯⨯⨯，(0,)C π∈，3c =时取等号．此时，3a =， 06Cπ∴<，∴当C 取最大值6π时，ABC 的面积11222S =⨯=．【点睛】本题考查了余弦定理、基本不等式的性质、三角形面积计算公式，考查了推理能力与计算能力，属于中档题．三、解答题21．（1）3A π=； （2 【分析】（1）由1||2AB AC AC ⋅=，得到1cos 2AB A =，进而求得1cos 2A =，即可求解；（2）分别选①②③，结合正弦定理和余弦定理，求得2B π=，得到4ABD π∠=，进而得到sin ADB ∠的值，在ABD △中结合正弦定理，即可求解. 【详解】 （1）由1||2AB AC AC ⋅=，可得1cos ||2AB AC A AC ⋅=，所以1cos 2AB A =，又由1c =，所以1cos 2A =， 因为(0,)A π∈，所以3A π=. （2）若选①：因为cos cos 2a C c A +=，由余弦定理可得222222222a b c b c a a c ab bc+-+-⋅+⋅=，整理得220b b，解得2b =，又由余弦定理可得2222212cos 2122132a b c bc A =+-=+-⨯⨯⨯=，即a = 因为222a c b +=，所以2B π=，又因为角B 的平分线交AC 于点D ，可得4ABD π∠=，所以5()3412ADB ππππ∠=-+=，则sin sin[()]sin cos cos sin 343434ADB πππππππ∠=-+=+=， 在ABD △中，由正弦定理可得sin sin ABBD A ADB=⋅==∠. 若选②：由sin cos bC B c =，根据正弦定理可得sin sin cos sin B C C B C =， 因为(0,)Cπ∈，可得sin 0C >，所以sin1B B =， 可得sin 2sin()13B B B π-=-=，即1sin()32B π-=，因为2333B πππ-<-<，所以36B ππ-=，可得2B π=又因为角B 的平分线交AC 于点D ，可得4ABD π∠=，所以5()3412ADB ππππ∠=-+=，则sin sin[()]sin cos cos sin 343434ADB πππππππ∠=-+=+=， 在ABD △中，由正弦定理可得sin sin ABBD A ADB=⋅==∠. 若选③：由sin 2sin a B c A =，根据正弦定理可得sin sin 2sin sin A B C A =， 因为(0,)C π∈，可得sin 0C >，可得sin 2sin B C =， 又由()()3C A B B πππ=-+=-+，可得sin 2sin 2sin()sin 3B C B B B π==+=+，所以cos 0B =，因为(0,)B π∈，所以2B π=.又因为角B 的平分线交AC 于点D ，可得4ABD π∠=，所以5()3412ADB ππππ∠=-+=，则sin sin[()]sin cos cos sin 343434ADB πππππππ∠=-+=+=， 在ABD △中，由正弦定理可得sin sin ABBD A ADB=⋅==∠. 【点睛】方法点睛：对于解三角形问题的常见解题策略：对于解三角形问题，通常利用正弦定理进行“边转角”寻求角的关系，利用“角转边”寻求边的关系，利用正、余弦定理解三角形问题是高考高频考点，同时注意三角形内角和定理，三角形面积公式在解题中的应用. 22．（1）6π；（2） 【分析】（1）先用余弦定理化余弦为边，再用正弦定理化边为角从而求得A ；（2）由余弦定理用c 表示a ，然后把三角形的面积用两种方法表示求得c ，从而可计算出面积． 【详解】（1）由22sin cos 2c a B C ab--=得222sin 2cos ab B ab C c a -=-，由余弦定理得222222sin ab B c a b c a +--=-，所以2sin a B b =， 由正弦定理得2sin sin sin A B B =，B 是三角形内角，sin 0B ≠， 所以1sin 2A =，又A 为锐角，所以6A π=．（2）由（1）2222232cos 2cos 166a b c bc A c c c π=+-=+-⋅⋅2716c =，4a =，所以11sin 22ABC S bc A a ==⨯△2111222⨯=⨯c =b == 111sin 222ABC S bc A ===△【点睛】思路点睛：本题考查正弦定理、余弦定理、三角形面积公式．利用正弦定理和余弦定理进行边角互化是解题关键．三角形的面积采取了二次计算，通过不同的计算方法得出等式，从而求解．这是一种解题技巧．23．（1）23B π=；（2）ABC S =△. 【分析】（1）利用正弦定理角化边，整理求得cos B ，由B 的范围可得结果；（2）利用余弦定理和基本不等式可求得当3a c ==时周长最大，由三角形面积公式可求得结果. 【详解】（1）由正弦定理得：222b ac ac --=，2221cos 22a cb B ac +-∴==-，()0,B π∈，23B π∴=； （2）由余弦定理得：()()222222cos 29b a c ac B a c ac ac a c ac =+-=+-+=+-=，()2292a c ac a c +⎛⎫∴=+-≤ ⎪⎝⎭（当且仅当a c =时取等号），6a c ∴+≤，∴当3a c ==时，ABC 取得最大值，此时19sin 22ABCSac B ===. 【点睛】方法点睛：求解与边长相关的最值或取值范围类问题通常有两种方法：①利用正弦定理边化角，将所求式子转化为与三角函数值域有关的问题的求解，利用三角恒等变换和三角函数的知识来进行求解；②利用余弦定理构造方程，结合基本不等式求得基本范围；应用此方法时，需注意基本不等式等号成立的条件. 24．（1）3A π=；（2）⎫+∞⎪⎪⎣⎭. 【分析】（1）利用正弦定理边化角可化简已知关系式求得cos A ，结合A 的范围可求得结果；（2）解法一：利用正弦定理边化角可整理得到1161sin 262B b c B ππ⎛⎫+ ⎪⎝⎭+=⎛⎫-+⎪⎝⎭，利用B 的范围可求得sin 6B π⎛⎫+⎪⎝⎭的范围，代入整理可求得结果； 解法二：利用余弦定理和基本不等式可求得3bc ≤，整理得到11b c +=合二次函数的性质可求得所求的范围. 【详解】（1）由正弦定理得：()sin sin 2cos sin cos sin cos sin A AA B C C B B C ==++. B C A π+=-，()sin sin B C A ∴+=，2cos 1A ∴=，即1cos 2A =， ()0,A π∈，3A π∴=.（2）解法一：由正弦定理知，2sin sin sin sin 3a b c A B C ====，sin sin 1111sin sin 3612sin 2sin 2sin sin 2sin sin sin 2362B B B B C b c B C B C B B B ππππ⎛⎫⎛⎫+++ ⎪ ⎪+⎝⎭⎝⎭∴+=+===⎛⎫⎛⎫+-+⎪ ⎪⎝⎭⎝⎭.3A π=，20,3B π⎛⎫∴∈ ⎪⎝⎭. 令6B πθ=+，则5,66ππθ⎛⎫∈ ⎪⎝⎭，则1sin ,12θ⎛⎤∈ ⎥⎝⎦.则11cos 24sin sin 22sin 22b cθθθθ⎫+====+∞⎪⎪⎣⎭-+--+⎪⎝⎭.解法二：3a =，3A π=，∴由余弦定理知：2232b c bc bc bc +-=≥-（当且仅当b c =时取等号）， 3bc ∴≤，()233b c bc +=+，则113bc ≥，11b c b c bc +∴+===.11b c ∴+的取值范围为⎫+∞⎪⎪⎣⎭. 【点睛】方法点睛：求解与边长相关的取值范围类问题通常有两种方法：①利用正弦定理边化角，将所求式子转化为与三角函数值域有关的问题的求解，利用三角恒等变换和三角函数的知识来进行求解；②利用余弦定理构造方程，结合基本不等式求得基本范围；将所求式子化为符合基本不等式的形式或配凑成函数的形式来进行求解；应用此方法时，需注意基本不等式等号成立的条件.25．2+ 【分析】利用三角形的面积公式，结合已知面积变形可得1sin sin 4B C =，再利用所选条件结合正弦定理求出另外两边，可得三角形的周长. 【详解】由三角形的面积公式可知，1sin 2S ab C =， 21sin 28sin a ab C A∴=， 整理得4sin sin ,b A C a =由正弦定理得:4sin sin sin sin ,B A C A =因为sin 0A ≠，4sin sin 1,B C ∴=1sin sin 4B C ∴=， 若选择条件（1）由6B π=：得1sin 2B =，则1sin 2C =， 又,,A B C 为三角形的内角，6B C π∴==，2,3A π∴= 由正弦定理得sin sin sin a b c A B C ==代入1,b c ==解得a =∴三角形的周长为2若选择条件（2）B C =，则由B C =，得sin sin ,B C = 又1sin sin 4B C =，1sin sin 2B C ∴== 又,,A B C 为三角形的内角，,6B C π∴==23A π∴=. 由正弦定理得:sin sin sin a b c A B C ==，代入1,b c ==解得a =∴三角形的周长为2【点睛】关键点点睛：利用三角形的面积公式和正弦定理求出三角形的另外两边是解题关键. 26．（1）3B π=；（2）()0,3.【分析】（1）利用正弦定理边角互化，再利用余弦定理求出角B 的大小；（2）利用正弦定理结合三角恒等变换化简2a c -，再由锐角三角形得出C 的范围，进而得出答案．【详解】（1）由已知222sin sin sin sin sin A C B A C +=+，结合正弦定理，得222a c b ac +=+. 再由余弦定理，得2221cos 222a cb ac B ac ac +-===，又()0,B π∈，则3B π=.（2）由3B π=，b = 224sin 2sin 4sin 2sin 3a c AC C C π⎛⎫-=-=-- ⎪⎝⎭224sin cos cos sin 2sin 33C C C C ππ⎛⎫=--= ⎪⎝⎭因为ABC 为锐角三角形，则62C ππ<<，则0cos C << 所以2a c -的取值范围为()0,3.。

人教版高一数学必修一第五单元《三角函数》单元练习题(含答案)人教版高一数学必修一第五单元《三角函数》单元练题（含答案）一、单选题1.已知函数$f(x)=\cos 2x+3\sin 2x+1$，则下列判断错误的是（）A。

$f(x)$的最小正周期为$\pi$B。

$f(x)$的值域为$[-1,3]$C。

$f(x)$的图象关于直线$x=\dfrac{\pi}{6}$对称D。

$f(x)$的图象关于点$\left(-\dfrac{\pi}{4},0\right)$对称2.已知函数$y=\sin(\omega x+\dfrac{\pi}{2})$在区间$\left[0,\dfrac{\pi}{3}\right]$上单调递增，则$\omega$的取值范围是A。

$\left[0,\dfrac{1}{2}\right]$B。

$\left[\dfrac{1}{2},1\right]$C。

$\left[\dfrac{1}{3},2\right]$D。

$\left[\dfrac{2}{3},3\right]$3.若角$\alpha$的终边过点$P(2,2)$，则$\sin\alpha=$（）A。

1B。

-1C。

$\dfrac{1}{\sqrt{10}}$D。

$-\dfrac{1}{\sqrt{10}}$4.若$x$是三角形的最小内角，则函数$y=\sin x+\cos x+\sin x\cos x$的值域是（）A。

$[-1,+\infty)$B。

$[1,2]$C。

$[0,2]$D。

$\left[1,\dfrac{2+\sqrt{2}}{2}\right]$5.下列说法正确的个数是（）①大于等于，小于等于90的角是锐角；②钝角一定大于第一象限的角；③第二象限的角一定大于第一象限的角；④始边与终边重合的角的度数为$360^\circ$。

A。

1B。

2C。

3D。

46.角$\alpha$的终边经过点$(2,-1)$，则$2\sin\alpha+3\cos\alpha$的值为（）A。