有理数的乘除法过关训练试题和答案

1. 先乘方，再乘除，最后加减；2. 同级运算，从左到右进行；3. 如有括号，先做括号内的运算，按小括号、中括号、大括号依次进行。

1、12411 ()()()23523+-++-+-2、4(81)( 2.25)()169-÷-⨯-÷3、11(22)3(11)+--⨯-4、31(12)()15(1)45+⨯--⨯-5、2232[3()2]23-⨯-⨯--6、 33102(4)8-÷--7、)]21)21[(122--÷ 8、121)]3()2[(2⨯-⨯-9、)6(]32)5.0[(22-⨯-- 10、23533||()14714-⨯-÷11、—22—(—2)2—23+(—2)3 12、2223116(1)(3)(1)(3)22-⨯---÷-⨯-13、199711(1)(10.5)()312----⨯÷- 14、33514(1)(8)(3)[(2)5]217---⨯+-÷-+15、－10 + 8÷(－2 )2 －(－4 )×(－3 ) 16、－49 + 2×(－3 )2 + (－6 )÷(－91)17、－14 + ( 1－0.5 )×31×[2×(－3)2] 18、(－2)2－2×[(－21)2－3×43]÷51．19、)8()4()6(52-÷---⨯ 20、0)132()43(2⨯+-+-21、6)12()4365127(÷-⨯+- 22、22)4()5(25.0)4()85(-⨯-⨯--⨯-23、)23232(21)21(2--⨯+- 24、[][]332)2(3)5(6)7(4-÷--+÷-⨯-25、6－（－12）÷2)2(- 26、（-48）÷ 8 －（-5）÷2)21(-27、42×)43()32(-+-÷ 0.25 28、()23)9181(-÷-29、()()333232÷---⨯- 30、(－5)×6＋(－125) ÷(－5)3 31、)251(4)5(25.0-⨯⨯-⨯-- 32、22)3(61)2132(1-+÷-+- 1、【基础题】计算：（1）618－÷）（－）（－312⨯； （2））（－＋51232⨯； （3））（－）（－49⨯＋）（－60÷12； （4）23）（－×[ ）＋（－－9532 ]. （1））（－）＋（－2382⨯； （2）100÷22）（－－）（－2÷）（－32；（3））（－4÷）（－）（－343⨯； （4））（－31÷231）（－－3214）（－⨯. （1）36×23121）－（； （2）12.7÷）（－1980⨯； （3）6342＋）（－⨯； （4））（－43×）－＋（－31328； （5）1323－）（－÷）（－21； （6）320－÷34）（－81－；（7）236.15.02）－（－）（－⨯÷22）（－； （8））（－23×[ 2322－）（－ ]；（9）[ 2253）－（－）（－ ]÷）（－2； （10）16÷）（－）－（－）（－48123⨯. （1）11＋（－22）－3×（－11）； （2）0313243⨯⨯）－（－）（－；（3）2332－）（－； （4）23÷[ ）－（－）（－423]； （5））－（8743÷）（－87； （6））＋（）（－654360⨯； （7）－27+2×()23-+（－6）÷()231-； （8））（－）－＋－（－4151275420361⨯⨯. （1））－（－258÷）（－5； （2）－33121）（－－⨯； （3）223232）－（－）（－⨯⨯； （4）0132432⨯⨯）＋（－）（－；（5））（－＋51262⨯； （6）－10＋8÷()22-－4×3； （7）－51－()()[]55.24.0-⨯-； （8）()251-－（1－0.5）×31；（1）（－8）×5－40； （2）（-1.2）÷（-13）-（-2）；（3）-20÷5×14+5×（-3）÷15； （4）-3[-5+（1-0.2÷35）÷（-2）]；（5）－23÷153×（-131）2÷（132）2； （6）－52＋(1276185+-)×(－2.4)参考答案1、-1/52、-13、224、95、96、 07、-488、-19、-15 10、-15/34311、-24 12、-89 13、3 14、2 15、-20 16、23 17、2 18、24 19、-28 20、9/16 21、1 22、10 23、-1/12 24、104/3 25、9 26、14 27、-31 28、-81又1/81 29、-9 30、-29 31、-1/5 32、91、【答案】 （1）17； （2）511； （3）31； （4）－112、【答案】 （1）－10； （2）22； （3）－16； （4）－253、【答案】 （1）1； （2）0； （3）42； （4）23； （5）18； （6）0； （7）－4.64；（8）37； （9）8； （10）－25. 4、【答案】 （1）22； （2）0； （3）－17； （4）－423； （5）71； （6）－95； （7）－85；（8）6 .5、【答案】 （1）3； （2）1； （3）－54； （4）0； （5）526； （6）－20； （7）－2； （8）－67. 6、【答案】（1）－80； （2）5.6； （3）－2； （4）16； （5）－516； （6）－2.9复习 有理数的乘除、乘方运算测试题一、填空题（每小题3分，共30分） 1．3×（－2）=________，（－6）×（－31）=________． 2．（－3）2的底数是________，结果是________；－32的底数是________，结果是________．3．（－61）÷（+23）=________；－493÷（－176）=________；（+8）÷（－41）=________． 4．23×（－41）3=________；（－91）÷（+34）2=________．5．（－32）×________=1；（－32）×________=－16．－65×（－2．4）×（－53）=________．7．－32×（－5）2÷（－21）3=________．8．我国台湾省的面积约为3600平方公里，用科学记数法表示为________． 9．+121的倒数是________；________的倒数是－54． 10．用“＞”“＜”填空： ①23________22②（21）2________（21）3③32________22④（－2）3________（－2）2二、判断题（每小题1分，共5分） 11．零除以任何数都得零（ ）12．互为相反数的两个数的积为负数（ ） 13．如果ab ＞0，则a ＞0且b ＞0（ ）14．1除以一个非零数的商叫做这个数的倒数（ ）15．（－3）5表示5个－3相乘（ ） 三、选择题（每小题3分，共21分） 16．下列说法，其中错误的有①一个数与1相乘得原数；②一个数乘以－1得原数的相反数；③0乘以任何数得0；④同号两数相乘，符号不变．A ．1个B ．2个C ．3个D ．4个17．下列各对数：①1与1；②－1与1；③a －b 与b －a ；④－1与－1；⑤－5与|6|，其中互为倒数的是A ．①②③B ．①③⑤C ．①③④D ．①④ 18．下列各题中两个式子的值相等的是A ．－23与（－2）3B ．32与23C ．（－2）2与 －22D ．|－2|与－|－2| 19．下列结论中，其中正确的个数为①0的倒数是0；②一个不等于0的数的倒数的相反数与这个数的相反数的倒数相等；③其倒数等于自身的数是±1；④若a ，b 互为倒数，则－ab=－1．A ．4B ．3C ．2D ．1 20．下列各式中结果大于0的是A ．1－910×3B ．（1－910）×3C ．1－（9×3）10D ．（1－9）10×3 21．下列说法中正确的是 A ．一个数的平方必为正数B ．一个数的平方必小于这个数的绝对值C ．一个数的平方必大于这个数D ．一个数的平方不可能为负数22．用科学记数法表示的数2．89×104，原来是A ．2890B ．2890000C ．28900D ．289000 四、计算题（共35分）23．（3分）（－3）×（－5）×（+12）×（－21） 24．（3分）－6÷（+3）÷（－4）×（+2） 25．（3分）－5－6÷（－3）26．（3分）（－81）÷241×91÷（－16） 27．（3分）－22×（－3）÷5428．（3分）（－1）2000×（－1）2001×（－1）2002÷（－1）200329．（3分）（－2）×（－2001）×［－21－（－21）］×1－2002 30．（3分）－)45()45(5222-÷-⨯⨯ 31．（3分）（－5）2÷5×632．（3分）（－2.5）÷（－310）×（－3） 33．（5分）30×（21－31+53－109）五、解答题（9分） 34．已知A=a+a 2+a 3+……+a 2000（1）若a =1，求A 的值． （2）若a =－1，求A 的值．参考答案一、1．－6 2 2．－3 9 3 －9 3．－91 913 －32 4．－81 －161 5．－23 23 6．－1.2 7．1800 8．3.6×103平方公里9．32 －14110．＞ ＞ ＞ ＜ 二、11．× 12．× 13．× 14．√ 15．√三、16．A 17．D 18．A 19．B 20．D 21．D 22．C 四、23．－90 24．1 25．－3 26．4127．15 28．1 29．－2002 30．1 31．30 32．－4933．－4 五、34．（1）2000 （2）0。

七年级有理数乘除混合运算练习题一、计算题1.计算(1)()1124⎛⎫-÷- ⎪⎝⎭. (2)()0.750.25-÷.(3)()00.12÷-.(4)()11.254-÷. 2.计算.(1)()()50.750.34-÷÷-. (2)()349731221⎛⎫⎛⎫⨯⨯- ⎪ ⎪⎝⎭⎝-÷⎭- . (3)()11150.6 1.75232⎛⎫-⨯-⨯÷- ⎪⎝⎭. (4)3777148128⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+--+-÷- ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦. 3.计算 (1)4512117621⎛⎫⎛⎫⎛⎫÷÷ ⎪ ⎪ ⎪⎝⎭⎝-⎭⎝-⎭-. (2)()14812649⎛⎫-÷⨯-÷ ⎪⎝⎭. (3)11111345660⎛⎫⎛⎫-+-÷- ⎪ ⎪⎝⎭⎝⎭. 4.计算(1)()()755-÷-. (2)80.1253-÷. (3)512557-÷. (4)()()1.250.52÷-÷-5.用简便方法计算(1)()()()11.2548220⎛⎫+⨯-⨯- ⎪⎭⨯-⎝. (2)()532.465⎛⎫⎛⎫-⨯-⨯+ ⎪ ⎪⎝⎭⎝⎭.(3)()312461014313⎛⎫⎛⎫⎛⎫⨯+⨯-⨯- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭-. (4)()()()()181201250.0012-⎛⎫⨯⨯⨯⨯ ⎪--⎭-⎝ . (5)513160522++-+⎡⎤⎛⎫⎛⎫⎛⎫-⨯ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦. (6)341000.70.03105⎛⎫-⨯--+ ⎪⎝⎭. (7)1314414⎛⎫-⨯ ⎪⎝⎭. 6.计算 (1)8394⎛⎫⎛⎫⨯ ⎪ ⎪⎝⎭⎝-⎭-. (2)211135⎛⎫+⨯⎛⎫ ⎪⎝⎭- ⎪⎝⎭. (3)()54123116547⎛⎫⎛⎫⎛⎫⎛⎫-⨯+⨯-⨯-⨯+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭. 7.若规定两数,a b 通过“※”运算得到4ab ，即4a b ab =※，如2642648=⨯⨯=※，请你求出35※的值.8.计算(1)()1481341()1139⎛⎫⎛⎫⨯÷- -÷+⎝-⎪ ⎪⎭⎝⎭. (2)()453251⎡⎤⎛⎫⎛⎫÷÷- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣-⎦-. (3)157136918⎛⎫⎛⎫-+÷- ⎪ ⎪⎝⎭⎝⎭. 9.计算4312773⎛⎫+⨯- ⎪⎝⎭. 10.计算:()497-÷-= ，1121635⎛⎫-÷= ⎪⎝⎭ ，()()()110441÷-+÷---⨯= ，()()270.5-÷-= .11.计算下列各题(1)()()4812-÷-. (2)112136⎛⎫÷- ⎪⎝⎭.(3)()21354⎛⎫⎛⎫-÷-÷- ⎪ ⎪⎝⎭⎝⎭. (4)733.584⎛⎫-÷⨯- ⎪⎝⎭. 12.用简便方法计算201520142014201420152015⨯-⨯.13.计算 (1)5129165⎛⎫⎛⎫-⨯⨯- ⎪ ⎪⎝⎭⎝⎭. (2)()11112362⎛⎫-+-⨯- ⎪⎝⎭(3)()127813⨯-. (4) ()2215130.34130.343737-⨯-⨯+-⨯-⨯. 14.计算18361129⎛⎫-⨯-- ⎪⎝⎭. 15.计算1111111...12015201420131000⎛⎫⎛⎫⎛⎫⎛⎫-⨯-⨯-⨯⨯- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭. 16.计算 (1)1123⎛⎫-⨯- ⎪⎝⎭(2)113135⎛⎫⨯- ⎪⎝⎭(3)()()345-⨯-(4)()()()355302005-⨯-⨯-17.计算：（1）20(14)(18)13-+----；（2）41(0.125)()()778-⨯-÷-⨯；（3）7211()(4)9353-÷--⨯-； （4）5752()3(2)81283--÷--. 18.计算： （1）6133()(1)()15245-÷---⨯；（2）11 5322()22-÷⨯--÷-；（3）11 2(3)12()64⨯-+⨯+.19.计算：（1）11711()()8283-÷-⨯-；（2）121 (13)51513335 -÷-÷+⨯；（3）1121 ()() 36530+-÷-；（4）1111[(2)]223-÷+⨯-.20.计算下列各题：（1）11 (3)(10)(2)32-÷-⨯-；（2）115 0.25()6817÷⨯-；（3）14(27)2(24)49-÷⨯÷-.21.计算：（1）3()54-÷；（2）4 18(1)5 -÷-;（3）22(8)7÷-；（4）21 (3)(5)32 -÷.22.化简：（1）3612--；（2）255---；（3）60.3--；（4）123-.23.用简便方法计算：（1）523()(12) 1234+-⨯-；（2）113(19)19(19)424-⨯--⨯-⨯-. 24.若定义一种新的运算*“”，规定有理数4a b ab *=,如2342324*=⨯⨯=. (1)求()34*-的值；(2)求()()263-**的值.25.用简便方法计算：（1）1117()(60)34515--+-⨯-； （2）1882173()()772222⨯-⨯⨯-； （3）2215130.34(13)0.343737-⨯-⨯+⨯--⨯. 26.计算下列各题： （1）7(0.25)()4(18)9-⨯-⨯⨯-；（2）29155⨯；（3）7537()3696418-+-⨯； （4）666(5)(3)(7)(3)12(3)777-⨯-+-⨯-+⨯-.27.计算：（1）1(2)()(3)2-⨯-⨯-；（2）(0.1)1000(0.01)-⨯⨯-；（3）1239()()()2348-⨯-⨯⨯-；（4）8211(2)(1)(2)(4)317152+⨯-⨯+⨯-. 28.计算：（1）( 1.2)(3)-⨯-；（2）7(1)08-⨯；（3）11(1)(4)32-⨯-；（4）1 ( 2.5)23 -⨯.29.计算:(1)71131262142⎛⎫⎛⎫⎛⎫-⨯-⨯÷-⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(2)11131 21 532114⎛⎫⨯-⨯÷-⎪⎝⎭参考答案1.答案：(1)48.(2)3-.(3)0.(4)5-.解析：2.答案：(1)2.(2)3-.(3)1135，(4)123-. 解析：3.答案：(1)162121-；(2)83；(3)7-. 解析：4.答案：(1)15；(2)364-；(3)1257-； (4)54. 解析：5.答案：(1)81-.(2)1.2.(3)6-.(4)0.004-.(5)19-.(6)37.(7)5597-. 解析：6.答案：(1)23；(2) 2-；(3)8156-. 解析：7.答案：60.解析：8.答案：（1）()14131418931⎛⎫⎛⎫⎛⎫÷+⨯-÷-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 44138113914=-⨯⨯⨯ 7221077=-=-. (2)()124535⎡⎤⎛⎫⎛⎫-÷-÷- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦ 124525=-÷⨯ 2453545=-⨯⨯=-. (3)157136918⎛⎫⎛⎫-+÷- ⎪ ⎪⎝⎭⎝⎭ ()15718369⎛⎫=-+⨯- ⎪⎝⎭ ()()()157181818368=⨯--⨯-+⨯-615145=-+-=-.解析：9.答案：原式43743177377⎛⎫=+⨯-=-=- ⎪⎝⎭. 解析：10.答案：7-，2-，5-，54.解析：11.答案：(1)()()(4812)48124-÷-=+÷=. (2)117776212363637⎛⎫⎛⎫⎛⎫÷-=-÷=-⨯=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭. (3)()()()21533430542⎛⎫⎛⎫⎛⎫-÷-÷-=-⨯-⨯-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭. (4)733.584⎛⎫-÷⨯- ⎪⎝⎭833.574⎛⎫=-⨯⨯- ⎪⎝⎭7833274=⨯⨯=. 解析：12.答案：原式()()201520140000201420142015000020150=⨯+-⨯+=.解析：13.答案：(1)515529129296566⎛⎫⎛⎫⎛⎫⎛⎫-⨯⨯-=-⨯-⨯= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭. (2)()11112362⎛⎫+-⨯- ⎪⎝⎭()()()111121212362⎛⎫=-⨯-+⨯--⨯- ⎪⎝⎭4268=-+=. (3)()121278781313⨯-=-⨯⨯18813⎡⎤⎛⎫=--⨯ ⎪⎢⎥⎝⎭⎣⎦188813⎛⎫=-⨯-⨯ ⎪⎝⎭8564631313⎛⎫=--=- ⎪⎝⎭. (4)()15.342722130.341337-⨯-⨯+⨯-⨯-2125130.343377⎛⎫⎛⎫=-⨯+-⨯+ ⎪ ⎪⎝⎭⎝⎭. 解析：14.答案：原式183636361129=-⨯+-⨯-⨯3323671=---=. 解析：15.答案：原式201420132012999999...20152014201310002015⎛⎫⎛⎫⎛⎫⎛⎫=-⨯-⨯-⨯⨯-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭. 解析：16.答案：(1)1111123226⎛⎫-⨯-=⨯= ⎪⎝⎭. (2)111063143535⎛⎫⎛⎫⨯-=-⨯=- ⎪ ⎪⎝⎭⎝⎭.(3)()()34534560⨯⨯--=⨯⨯=.(4)()()()3553020050-⨯-⨯⨯-=.解析：17.答案：（1）解：原式2014181329=--+-=-.（2）解：原式14()(8)7487=-⨯-⨯-⨯=-. （3）解：原式774543915333=÷+=+=. （4）解：原式292981872483333=-÷+=-+=. 解析：18.答案：（1）解：原式623846()2534555=-⨯-+⨯=+= （2）解：原式313152(2)5482244=-⨯-⨯-=-+=. （3）解：原式1161212623164=-+⨯+⨯=-++=-. 解析：19.答案：（1）解：原式1311811()()1()()883833=-÷-⨯-=-⨯-⨯- 11181()()13399=--⨯-=-= （2）解：原式4051(13)335=--+⨯1(1513)5=-+⨯12(2)55=-⨯=- （3）解：原式112()(30)365=+-⨯- 112(30)(30)(30)365=⨯-+⨯--⨯- (10)(5)(12)105123=-+---=--+=-（4）解：原式312313()()69223262=-÷-=-÷-=⨯= 解析：20.答案：（1）解：原式10155()31026=-⨯⨯=-（2）解：原式1515150.2568()0.25417()(0.254)[17()]1(15)15171717=⨯⨯-=⨯⨯⨯-=⨯⨯⨯-=⨯-=-（3）解：原式4412 (27)()99249 =-⨯⨯⨯-=.解析：21.答案：（1）解：原式313 ()4520 =-⨯=-（2）解：原式5 18109=⨯=（3）解：原式1612()787 =⨯-=-（4）解：原式11223113 =-⨯=-解析：22.答案：（1）解：36(36)(12)36123 12-=-÷-=÷= -（2）解：25(25)(5)(255)55--=--÷-=-÷=--（3）解：66(0.3)(60.3)200.3-=-÷-=+÷=-（4）解：11111 2332236 -=-÷=-⨯=-解析：23.答案：（1）解：原式523(12)(12)()(12)5894 1234=⨯-+⨯-+-⨯-=--+=-（2）解：原式113119 (19)()19()42422 =-⨯-+-=-⨯-=.解析：24.答案：（1）解：3*(4)43(4)48-=⨯⨯-=-（2）(2)*(6*3)(2)*(463)(2)*724(2)72576 -=-⨯⨯=-=⨯-⨯=-解析：25.答案：（1）解：原式1117()(60)(60)(60)(60) 34515=-⨯--⨯-+⨯--⨯-2015122851 =+-+=（2）解：原式2278821[()][()]722722=⨯-⨯-⨯1(12)12=-⨯-=（3）解：原式2152 13130.340.343377 =-⨯-⨯-⨯-⨯215213()()0.343377=-⨯++--⨯13110.34130.3413.34 =-⨯-⨯=--=-解析：26.答案：（1）解：原式1717418(4)(18)11414 4949=-⨯⨯⨯=-⨯⨯⨯=-⨯=-（2）解：方法1：原式4715141 5=⨯=方法2：原式22(9)159151514155=+⨯=⨯+⨯=（3）解：原式7537363636362830271411 96418=⨯-⨯+⨯-⨯=-+-=（4）解：原式66 (5712)(3)0(3)077=--+⨯-=⨯-=.解析：27.答案：（1）解：原式1(23)32=-⨯⨯=-（2）解：原式0.110000.011=⨯⨯=（3）解：原式12399()234832 =-⨯⨯⨯=-（4）解：原式70931927 317152=⨯⨯⨯=.解析：28.答案：（1）解：原式(1.23) 3.6=+⨯=（2）解：原式0=（3）解：原式4949 ()()6 3232=-⨯-=⨯=（4）解：原式5735236 =-⨯=-.解析：29.答案：(1)12-(2)225-解析：(1)原式()7131223142⎛⎫⎛⎫=-⨯-⨯⨯-=- ⎪ ⎪⎝⎭⎝⎭ (2)原式1113425611525⎛⎫=⨯-⨯⨯-=- ⎪⎝⎭。

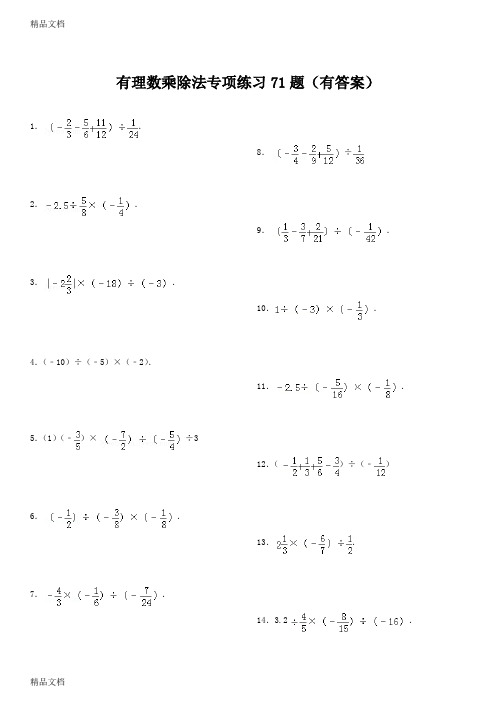
人教版初中数学七年级上册1.4有理数的乘除法同步训练题一、选择题1．两个非零有理数的和为零，则它们的商是（ ）A ．0B ．1-C ．+1D ．不能确定2.下列说法错误的是（ ）A. 一个数同0相乘仍得0B. 一个数同1相乘仍得原数C. 一个数同-1相乘仍得原数的相反数D.互为相反数的两数积是13.若0ab >，则（ ）A.0,0a b >>B.0,0a b <<C. ,a b 同号D.不确定4.如果00ab a b >+>且，那么a b 、（ ）A.同为正B.同为负C.异号D.不能确定5.如果四个有理数相乘，积为负数，那么负因数个数为（ ）A.1个B.3个C.1个和3个D.1个或3个6.为比较两个有理数的大小，提出四种方法（1）倒数大的反而小。

（2）绝对值大的反而小。

（3）平方后大的数较大。

（4）求两数的商，若商大于1，则被除数较大；若商等于1，则两数相等；若商小于1，则除数较大。

则这四种方法（ ）A.都正确B.都不正确C.只有一个正确D.只有一个不正确7.若0,0,x y xy x y +<<>则有( )A ．x ＞0，y ＜0，x 绝对值较大B ．x ＞0，y ＜0，y 绝对值较大C ．x ＜0，y ＞0，x 绝对值较大D ．x ＜0，y ＞0，y 绝对值较大8.若19980a b +=则ab 是（ ）A.正数B.非正数C.负数D.非负数9.已知式子2x y +的值是3, 则代数式241x y ++的值是( )A.1B.4C.7D.不能确定10.若1-=a a，则a 为（ ）A. 0a >B. 0a <C. 01a <<D. 10a -<<二、填空题11.如果00ab a b >+<且，那么,a b 应满足_____________。

12.如果00ab a b =+=且那么,a b _____________。

七年级上册数学《第2章有理数及其运算》专题 有理数的乘除法计算题题型一 两个数有理数相乘1．计算：（1）﹣0.5×（﹣6）；（2）23×（−56）； （3）2021×（﹣1）；（4）（﹣2020）×0．（1）（﹣5）×4；（2）1×（﹣7）；（3）(−25)×(−14)；（4）312×(−213)．3．计算：（1）（﹣3.75）×（﹣135）； （2）（﹣10.8）×527．4．计算：（1）12×（−14）； （2）（﹣2）×（﹣6）； （3）（−12023）×0；（4）（﹣2.5）×213； （5）123×（﹣115）．（1）0×（﹣112）； （2）（﹣0.25）×（−45）；（3）85×（−154）； （4）（﹣416）×0.2．6．计算：（1）14×（﹣8）； （2）−12×（−13）；（3）﹣4×112； （4）（﹣0.6）×（﹣113）．题型二 多个有理数相乘7．计算：（1）（﹣2）×（−12）×（﹣3）；（2）（﹣0.1）×1000×（﹣0.01）．8．计算：（1）8×（﹣134）×（﹣4）×（﹣2）； （2）（﹣3）×56×（−45）×（−14）；（3）（﹣2）×5×（﹣5）×（﹣2）×（﹣7）．9．计算：（1）3×（﹣1）×（−13）．（2）﹣1.2×5×（﹣3）×（﹣4）． （3）（−512）×415×（−32）×（﹣6）． （4）54×（﹣1.2）×（−19）．10．计算下列各式：（1）（﹣8）×9×（﹣1.25）×（−19）；（2）（﹣5）×6×（−45）×14；（3）（﹣0.25）×（−79）×4×（﹣18）； （4）﹣3×56×（−95）×（−14）；（5）37×（−45）×712×58； （6）（﹣8）×（−43）×（﹣1.25）×（54）．11．计算：（1）（﹣18）×（﹣49）×0×（﹣13）×（﹣49）；（2）﹣5×（﹣8）×（﹣7）×（﹣0.125）； （3）（−14）×（﹣123）×（﹣4）×35； （4）−35×（−56）×（﹣6）．12．计算：（1）（﹣8）×（﹣12）×（﹣0.125）×（−13）×（﹣0.001）； （2）（﹣127）×57÷（−34）×213÷（−57）+（﹣2.5）÷（﹣0.25）×25．题型三 利用乘法运算律简便计算13．（2023秋•泰州月考）用简便方法计算：（1）191516×(−8)；（2）（﹣99）×999．14．用简便方法计算：（1）（﹣2）×（﹣7）×（+5）×（−1 7）；（2）﹣0.125×7×（﹣5）×8．15．用简便方法计算：（1）（﹣7.5）×（+25）×（﹣0.04）；（2）（﹣4120）×1.25×（﹣8）．16．（2024春•南岗区校级期中）用简便方法计算：（1）24×(34−156+78)；（2）4.27×(−611)−8.73×611−2×(−611)．17．（2024春•南岗区校级月考）用简便方法计算：（1）(−65)×(−23)+(−65)×173； （2）−361229×112．18．用乘法运算律，将下列各式进行简便计算： （1）（﹣112）×（﹣7）×23； （2）)25.1()541(8)5(-⨯-⨯⨯- （3）（﹣48）×（−34+56−712）； （4）0.7×311−6.6×37−1.1×37+0.7×811． （5）﹣392324×（﹣12） （6）4.61×37−5.39×（−37）+3×（−37）．题型四 两个有理数的除法19．计算：（1）（﹣6.5）÷（﹣0.5）；（2）4÷（﹣2）；（3）0÷（﹣1 000）；（4）（﹣2.5）÷58．20．计算：（1）0÷（﹣2022）；（2）（﹣27）÷9； （3）（−43）÷43；（4）−32÷1.521．计算：（1）（﹣68）÷（﹣17）；（2）（﹣0.75）÷0.25； （3）（−78）÷（﹣1.75）；（4）312÷（﹣7）22．用简便方法计算：99989÷（﹣119）．题型五 多个有理数的除法23．计算：（1）﹣5÷（﹣123）；（2）（−34）÷（−37）÷（﹣116）．24．计算：（1）﹣36÷（﹣113）÷（−32）； （2）15÷（﹣123）÷（−910）．25．计算： （1）（−47）÷（−314）÷（−23）；（2）（﹣0.65）÷（−57）÷（﹣213）÷（+310）．26．计算：（1）﹣3÷（−34）÷（−34）；（2）（﹣12）÷（﹣4）÷（﹣115）； （3）（−23）÷（−87）÷0.25； （4）（﹣212）÷（﹣5）÷（﹣310）．27．计算： （1）（−23）÷（−85）÷（﹣0.25）；（2）（﹣81）÷94÷94÷（﹣16）；（3）（﹣6.5）÷（−12）÷（−25）÷（﹣5）．题型六 有理数乘除混合运算28．（2023秋•大兴区期中）计算：（﹣6）×（﹣4）÷（﹣3）×2．29．(−64)÷223×(−38)÷9．30．（2024春•松江区期末）计算：25÷(−212)×334．31．（2024春•杨浦区校级期中）计算：178÷（﹣412+34）×（−34）32．计算：619÷（﹣112）×1924．33．（2023秋•九江期末）计算：15×(−34)+(−15)×32+15÷4．34．（2023秋•榆树市期中）计算：（﹣54）÷34×43÷（﹣32）．35．（2024春•黄浦区期中）计算：(−412)÷725×(−43)×(−125)．36．计算：（1）（﹣32）÷4×（−1 16）；（2）（−23）×（−85）÷（﹣178）．37．（2024•香坊区校级开学）计算．（1）813÷6+16×413． （2）78÷(1−15÷415)．38．计算： （1）1.25÷（﹣0.5）÷（﹣212）×1 （2）（﹣81）÷（+314）×（−49）÷（﹣1113）39．（2023秋•秀峰区校级月考）计算： （1）(−81)÷94×49÷(−16)．（2）−5÷(−127)×45×(−214)÷7．题型七 有理数加减乘除混合运算40．（2023秋•昌邑区校级期末）（−112+13−12）÷（−118）．41．计算：24÷（12−13+14−16）42．（2023春•浦东新区校级期中）−142÷（16−27+23−314）43．（2024春•呼兰区校级月考）用简便方法计算：（1）(−178)−(−214)+(−414)−(+318)；（2）−24×(−12+34−13)−|−312|．44．计算：（1）75×(13−12)×37÷54； （2）(56−37+13−914)÷(−142)．45．计算．（1）（﹣1155）÷[（﹣11）×（+3）×（﹣5）]；（2）375÷(−23)÷(−32)（3）(−1313)÷(−5)+(−623)÷(−5)．46．计算：（1）（+1.25）÷（﹣0.5）×（−85）；（2）﹣2.5÷（−516）×（−18）÷（−14）． （3）（﹣45）÷（﹣9）＋4×（﹣34） （4）2111()()32305⎡⎤-÷⨯-⎢⎥⎣⎦47．（2023春•松北区校级月考）计算：（1）8+（−14）﹣5﹣（﹣0.25）；（2）﹣36×（−23+56−712−89）；（3）﹣2+2÷(−12)×2；（4）﹣3.5×(16−0.5)×37÷12． 题型八 利用“倒数法”解决问题48．阅读下列材料：计算：112÷（13−14+112） 解：原式的倒数为 （13−14+112）÷112 ＝（13−14+112）×12 =13×12−14×12+112×12 ＝2故原式=12请仿照上述方法计算：（−142）÷（16−314+23−27）49．阅读材料，回答问题．计算：（−115）÷（15−13）． 解：方法一：原式＝（−115）÷（315−515）＝（−115）÷（−215）=12． 方法二：原式的倒数为：（15−13）÷（−115）＝（15−13）×（﹣15）=15×（﹣15）−13×（﹣15）＝﹣3+5＝2故原式=12．用适当的方法计算：（−130）÷（23−110+16−25）．50．（2023秋•望花区期末）我们知道乘法有分配律，遇到比较复杂的混合运算时．有的时候可以运用乘法分配律很容易去解决．（1）计算：(13−16+14)×12； （2）由于除法没有分配律，在遇到除法的类似混合运算时，我们计算会很困难，在学完倒数时，小明对这种除法的混合运算有了自己的想法：先算这个式子的倒数，再利用倒数的意义得出原结果下面是小明的计算过程120÷(14−15+12) 解：原式的倒数为：(14−15+12)÷120 =(14−15+12)×20=14×20−15×20+12×20＝5﹣4+10＝11．故原式=111 请你根据对小明的方法的理解，计算(−124)÷(14−512+38)．。

有理数的乘除法测试时间：60分钟总分：100一、选择题（本大题共10小题，共30.0分）1.若，则下列各式正确的是A. B. C. D. 无法确定2.正整数x、y满足，则等于A. 18或10B. 18C. 10D. 263.若，，且，则等于A. 1或B. 5或C. 1或5D. 或4.算式之值为何？A. B. C. D.5.计算的值是A. 6B. 27C.D.6.若，，且，则的值为A. B. C. 5 D.7.两个不为零的有理数相除，如果交换被除数与除数的位置而商不变，那么这两个数一定是A. 相等B. 互为相反数C. 互为倒数D. 相等或互为相反数8.的倒数与4的相反数的商是A. B. 5 C. D.9.计算等于A. 1B.C.D.10.计算：的结果是A. 1B.C.D.二、填空题（本大题共10小题，共30.0分）11.若，，则ab______ 0；若，，则ab______12.已知，，且，则的值等于______ ．13.比大的数是______ ；比小______ ；数______ 与的积为14．14.若“”是一种数学运算符号，并且，，，，则的值为______ ．15.计算的结果是______ ．16.四个互不相等的整数a、b、c、d，使，则______ ．17.______ ．18.计算：______．19.化简：______ ．20.已知，，且，则的值为______ ．三、计算题（本大题共4小题，共24.0分）21.22.运算：23.．24.．四、解答题（本大题共2小题，共16.0分）25.数学老师布置了一道思考题“计算：”，小明仔细思考了一番，用了一种不同的方法解决了这个问题．小明的解法：原式的倒数为，所以．请你判断小明的解答是否正确，并说明理由．请你运用小明的解法解答下面的问题．计算：．26.利用适当的方法计算：．答案和解析【答案】1. C2. A3. B4. D5. D6. B7. D8. C9. B10. C11. ；12. 8或13. ；；14. 10015. 316. 1217.18.19. 320. 或21. 解：原式，．22. 解：原式．23. 解：原式．24. 解：原式，．25. 解：正确，理由为：一个数的倒数的倒数等于原数；原式的倒数为，则．26. 解：原式．【解析】1. 解：，同号两数相乘得正，不等式两边乘以同一个正数，不等号的方向不变．故选C．根据有理数乘法法则：两数相乘，同号得正可得再根据不等式是性质：不等式两边乘或除以同一个负数，不等号的方向改变，解答此题．主要考查了不等式的基本性质：不等式两边加或减同一个数或式子，不等号的方向不变不等式两边乘或除以同一个正数，不等号的方向不变不等式两边乘或除以同一个负数，不等号的方向改变．2. 解：，y是正整数，、均为整数，，或，存在两种情况：，，解得：，，；，解得：；或10，故选A．易得、均为整数，分类讨论即可求得x、y的值即可解题．本题考查了整数的乘法，本题中根据或分类讨论是解题的关键．3. 解：因为，，所以，，因为，所以，，所以；所以，，所以；故选B先由绝对值和平方根的定义求得x、y的值，然后根据分类计算即可．本题主要考查的平方根的定义、绝对值、有理数的加法，求得当时，，当时，是解题的关键．4. 解：原式．故选：D．根据有理数的乘法法则，先确定符号，然后把绝对值相乘即可．本题考查的是有理数的乘法，掌握乘法法则是解题的关键，计算时，先确定符号，然后把绝对值相乘．5. 解：原式，故选：D．利用有理数的乘法法则进行计算，解题时先确定本题的符号．本题考查了有理数的乘法，解题的关键是确定运算的符号．6. 解：，，，，，当，，即当，，；当，，即，，．故选B．首先用直接开平方法分别求出a、b的值，再由可确定a、b同号，然后即可确定a、b的值，然后就可以求出的值．本题考查了平方根的定义注意一个正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根．7. 解：根据题意得，由比例的性质得：．．．或．故选：D．设这两个数分别为a、b，根据题意得到，从而可得到，从而可判断出a、b之间的关系．本题主要考查的是有理数的除法、平方差公式的应用，得到是解题的关键．8. 解：的倒数是，4的相反数是，．故选C．依据相反数、倒数的概念先求得的倒数与4的相反数，然后根据有理数的除法法则求出它们的商．主要考查相反数、倒数的概念及有理数的除法法则．9. 解：，故选：B．根据有理数的除法法则：除以一个数等于乘以这个数的倒数，可得答案．本题考查了有理数的除法，解题关键是把有理数的除法转化成有理数的乘法．10. 解：，故选：C．根据有理数的除法，即可解答．本题考查了有理数的除法，解决本题的关键是熟记有理数的除法．11. 解：若，，则；若，，则．故答案为：；．利用有理数乘法法则判断即可得到结果．此题考查了有理数的乘法，熟练掌握乘法法则是解本题的关键．12. 解：，，且，，或，，则或．故答案为：8或根据题意利用有理数的乘法法则判断x与y异号，再利用绝对值的代数意义求出x与y的值，即可求出的值．此题考查了有理数的乘法与减法，以及绝对值，熟练掌握运算法则是解本题的关键．13. 解：比大的数是：；比小；；故答案为：，，．比大的数是，根据有理数的加法法则即可求解；根据题意列式，列出算式，再进行计算即可；根据除法法则进行计算即可．本题考查了有理数的除法和加减法运算，熟练掌握运算法则是解题的关键；注意题中“大”、“小”的意思．14. 解：．故答案为：100．根据“”的运算方法列出算式，再根据有理数的乘法和有理数的除法运算法则进行计算即可得解．本题考查了有理数的乘法，有理数的除法，读懂题目信息，理解新定义的运算方法是解题的关键．15. 解：原式，故答案为：3．根据有理数的除法和乘法，即可解答．本题考查了有理数的乘法和除法，解决本题的关键是把除法转化为乘法计算．16. 解：四个互不相等的整数，，，的积为25，这四个数只能是1，，5，，，，，，则．故答案为：12．找出25的四个互不相等的因数，即1，，5，．本题主要考查了有理数的乘法及加法，解题的关键是要理解25分成四个互不相等的因数只能是1，，5，．17. 解：原式，故答案为：原式利用除法法则变形，约分即可得到结果．此题考查了有理数的除法，熟练掌握运算法则是解本题的关键．18. 解：原式，故答案为：．根据有理数的除法，可得有理数的乘法，根据有理数的乘法，可得答案．本题考查了有理数的除法，利用有理数的除法是解题关键．19. 解：，故答案为：3．根据分数的分子分母同号得正，能约分的要约分，可得答案．本题考查了有理数的除法，分子分母同号得正异号得负，并把绝对值相除．20. 解：，，，，，当时，，，当时，，，故答案为：或．根据绝对值的性质求出a，b，再根据有理数的加法判断出b的值，有理数的除法进行计算即可得解．本题考查了有理数的除法，绝对值的性质，有理数的加法，熟练掌握运算法则是解题的关键．21. 根据有理数的除法法则，先把除法化成乘法，再根据有理数的乘法进行计算即可．本题主要考查对有理数的乘法、除法等知识点的理解和掌握，能熟练地运用法则进行计算是解此题的关键．22. 原式先计算括号中的加减运算，再计算除法运算即可得到结果．此题考查了有理数的除法，熟练掌握除法法则是解本题的关键．23. 原式利用乘法分配律计算即可得到结果．此题考查了有理数的乘法，熟练掌握运算法则是解本题的关键．24. 根据乘法算式的特点，可以用括号内的每一项与相乘，计算出结果．在进行有理数的乘法运算时，要灵活运用运算律进行计算．25. 正确，利用倒数的定义判断即可；求出原式的倒数，即可确定出原式的值．此题考查了有理数的除法，熟练掌握运算法则是解本题的关键．26. 逆用乘法的分配律，将提到括号外，然后先计算括号内的部分，最后再算乘法即可．本题主要考查的是有理数的乘法，逆用乘法分配律进行简便计算是解题的关键．。

有理数乘除练习题有理数是我们数学中的一个重要概念，它包括整数、分数和小数。

在日常生活中，我们经常会遇到有理数的乘除运算。

下面，我将为大家提供一些有理数乘除的练习题，帮助大家巩固和提高自己的数学能力。

1. 乘法练习题(1) 计算：(-3) × 4 = ?解答：根据乘法的性质，负数与正数相乘的结果是负数。

所以，(-3) × 4 = -12。

(2) 计算：(-2) × (-5) = ?解答：根据乘法的性质，两个负数相乘的结果是正数。

所以，(-2) × (-5) = 10。

(3) 计算：2/3 × (-9/4) = ?解答：将分数转化为小数，得到2/3 × (-9/4) = 2/3 × (-2.25)。

然后，进行小数的乘法运算，得到-1.5。

2. 除法练习题(1) 计算：(-12) ÷ 3 = ?解答：根据除法的性质，负数除以正数的结果是负数。

所以，(-12) ÷ 3 = -4。

(2) 计算：(-15) ÷ (-5) = ?解答：根据除法的性质，两个负数相除的结果是正数。

所以，(-15) ÷ (-5) = 3。

(3) 计算：6 ÷ (-2/3) = ?解答：将除数转化为倒数，得到6 ÷ (-2/3) = 6 × (-3/2)。

然后，进行分数的乘法运算，得到-9。

通过以上练习题，我们可以看到有理数的乘除运算规律。

对于乘法而言，符号的正负与乘数和被乘数的正负有关，同号得正，异号得负。

对于除法而言，符号的正负与被除数和除数的正负有关，同号得正，异号得负。

当然，对于分数的乘除运算，我们需要将其转化为小数进行计算，然后再将结果转化为分数形式。

除了以上的练习题，我们还可以通过一些实际问题来练习有理数的乘除运算。

比如：小明每天早上骑自行车上学，上学的路程是6.5公里，他共骑行了5天。

有理数的加减乘除混合运算练习题一、能力提升1.下列等式成立的是()A.(-5)÷(1-2)=(-5)÷(-1)B.1÷(-2 021)=(-2 021)÷1C.(-5)×6÷=(-5)×÷6D.(-7)÷=(-7)÷-7÷(-1)2.在算式4-|-3□5|中的□所在位置,为使计算出的值最小,应填入的运算符号是()A.+B.-C.×D.÷3.一个容器装有1 L水,按照如下要求把水倒出:第1次倒出 L水,第2次倒出的水量是 L的,第3次倒出的水量是 L的,第4次倒出的水量是 L的,……按照这种倒水的方法,倒了10次后容器内剩余的水量是()A. LB. LC. LD. L4.用计算器计算:(-2.3)÷0.8×(-3)=.5.已知a=-1,b=,c=-20,则(a-b)÷c的值是.6.现有四个有理数-1,-3,4,4,将这四个数(每个数用且只用一次)进行加减乘除四则运算,使其结果为24,请写出这样的一个算式: .7.已知=3,=10,=15,……观察上面的计算过程,寻找规律并计算=.8.计算:(1);(2)×18-1.45×6+3.95×6.9.市场销售人员把某一天两种冰箱的销售情况制成表格如下:种类售价/元盈利/%甲种冰箱1500 25乙种冰箱1500 -25已知这两种冰箱各售出一台,根据以上信息,请你判断商家是盈利还是亏本.若盈利,盈利了多少?若亏本,亏本了多少?10.下面是小明计算-20÷的解题过程,他的计算正确吗?如果不正确,请改正.-20÷=-20÷=-20÷1=-2011.前进的道路:从起点——数字1出发,顺次经过每一个分岔口,选择+、-、×、÷四种运算之一进行运算,到达目的地时结果要恰好是10.你能找到前进的道路吗?道路不止一条,请你至少找出3条,并列出你的算式.12.已知有理数a,b,c满足=1,求的值.二、创新应用13.阅读下题解答:计算:分析:利用倒数的意义,先求出原式的倒数,再得原式的值.解:×(-24)=-16+18-21=-19.所以原式=-.根据阅读材料提供的方法,完成下面的计算:.答案:一、能力提升1.A2.C根据算式的特点,要使计算出的值最小,需使|-3□5|的值最大,故应填入“×”号.3.D4.8.6255.当a=-1,b=,c=-20时,(a-b)÷c=÷(-20)=÷(-20)=.6.答案不唯一,如:(4+4)×(-3)÷(-1)=247.210由题意可知,=210.8.解:(1)===-2+3-=1-.(2)×18-1.45×6+3.95×6=14-15+7-=6+=21.9.解:1500÷(1+25%)=1200(元),1500÷(1-25%)=2000(元).1200+2 000=3 200(元),1500×2=3000(元).3000-3200=-200(元).因此亏本了,亏本了200元.10.解:小明的计算不正确.原式=-20×5×5=-500.11.解:答案不唯一,如(1)[1-(-2)]×3+(-4)+5=10;(2)[1-(-2)]÷3-(-4)+5=10;(3)[1-(-2)+3+(-4)]×5=10;(4)1×(-2)+3-(-4)+5=10.12.解:由=1,得a,b,c必为一负二正,所以=-1.二、创新应用13.解:=×(-42)=-21+14-30+112=75.故原式=.。

有理数的乘除法练习题一、选择1.如果两个有理数在数轴上的对应点在原点的同侧,那么这两个有理数的积一定为正。

(A)2.若干个不等于的有理数相乘,积的符号由负因数和正因数个数的差为决定。

(D)3.下列运算结果为负值的是(-7)×(-6)。

(A)4.下列运算错误的是1(6) 3.(B)5.若两个有理数的和与它们的积都是正数,则这两个数是符号相同的非零数。

(B)6.下列说法正确的是任何有理数都有倒数。

(C)7.关于0,下列说法不正确的是0有倒数。

(C)8.下列运算结果不一定为负数的是异号两数相加。

(C)9.下列运算有错误的是1÷(-3)=3×(-3)。

(A)10.下列运算正确的是3=3 1.(A)二、填空1.如果两个有理数的积是正的,那么这两个因数的符号一定相同。

2.如果两个有理数的积是负的,那么这两个因数的符号一定相反。

3.奇数个负数相乘,结果的符号是负数。

4.偶数个负数相乘,结果的符号是正数。

5.如果(1/4)×(1/3)×(4/2)>0,那么a/b>0.6.如果5a>0,0.3b0.7.-0.125的相反数的倒数是8.三、解答1.计算：1) -a答案：-a2) a+(-a)答案：02.计算：1) 8×(-a)答案：-XXX3.计算：1) (-1)×(-1)×(-1)×(-1)-(-1)×(-1) 答案：02) 1-(-a)答案：1+a4.计算：1) (+48)÷(+6)答案：82) (-3)÷5答案：-3/53) 4÷(-2)答案：-24) 0÷(-1000)答案：0若a>0，则：aa = a×a若a<0，则：aa = (-a)×(-a)1.对于表达式(1) -a，其结果为-a。

2.对于表达式(1) 8×(-a)，其结果为-8a。

有理数乘除混合运算过关测试（三）（通用版）试卷简介:主要考查有理数的乘法法则和除法法则，灵活地利用有理数乘法交换律和结合律简化运算一、单选题(共25道，每道4分)1.计算的结果是( )A.-150B.-170C.150D.170答案：D试题难度：三颗星知识点：有理数乘除混合运算2.计算的结果是( )A.-700B.-580C.-680D.700答案：A试题难度：三颗星知识点：有理数乘除混合运算3.计算的结果是( )A.0.9B.-9C.9D.90答案：B试题难度：三颗星知识点：有理数乘除混合运算4.计算的结果是( )A.7B.0.7C.-7D.-0.7答案：A试题难度：三颗星知识点：有理数乘除混合运算5.计算的结果是( )A.144B.-144C.9D.-9答案：C试题难度：三颗星知识点：有理数乘除混合运算6.计算的结果是( )A.-290B.290C.145D.-145答案：A试题难度：三颗星知识点：有理数乘除混合运算7.计算的结果是( )A.23B.-18.4C.-23D.27.6答案：C试题难度：三颗星知识点：有理数乘除混合运算8.计算的结果是( )A.-10B.10C. D.答案：B试题难度：三颗星知识点：有理数乘除混合运算9.计算的结果是( )A.-50B.-5C.5D.50答案：B试题难度：三颗星知识点：有理数乘除混合运算10.计算的结果是( )A.6B.2C.-3D.-6答案：D试题难度：三颗星知识点：有理数乘除混合运算11.计算的结果是( )A.15B.-15C.-150D.1.5答案：A试题难度：三颗星知识点：有理数乘除混合运算12.计算的结果是( )A.-4B.4C. D.答案：B试题难度：三颗星知识点：有理数乘除混合运算13.计算的结果是( )A. B.C.3D.-3答案：D试题难度：三颗星知识点：有理数乘除混合运算14.计算的结果是( )A. B.C. D.答案：C试题难度：三颗星知识点：有理数乘除混合运算15.计算的结果是( )A.5B.-5C. D.答案：A试题难度：三颗星知识点：有理数乘除混合运算16.计算的结果是( )A.-170B.170C. D.答案：B试题难度：三颗星知识点：有理数乘除混合运算17.计算的结果是( )A.2B.-2C.-18D.18答案：D试题难度：三颗星知识点：有理数乘除混合运算18.计算的结果是( )A.-30.5B.30.5C.61D.-61答案：C试题难度：三颗星知识点：有理数乘除混合运算19.计算的结果是( )A. B.C. D.答案：B试题难度：三颗星知识点：有理数乘除混合运算20.计算的结果是( )A.-15B.15C.30D.-30答案：C试题难度：三颗星知识点：有理数乘除混合运算21.计算的结果是( )A.60B.-60C. D.答案：A试题难度：三颗星知识点：有理数乘除混合运算22.计算的结果是( )A. B.C.40D.-40答案：C试题难度：三颗星知识点：有理数乘除混合运算23.计算的结果是( )A.-0.3B.0.3C.-3D.3答案：C试题难度：三颗星知识点：有理数乘除混合运算24.计算的结果是( )A.35B.-35C.2240D.-2240答案：B试题难度：三颗星知识点：有理数乘除混合运算25.计算的结果是( )A.-100B.10C.100D.-10答案：C试题难度：三颗星知识点：有理数乘除混合运算。