获得往复运动的机构优秀课件

技术创新推动发展 随着科技的不断进步和创新，往复式压缩机的技术水平将 不断提高，推动行业向更高层次发展。
国际化竞争加剧 随着全球化的深入发展，往复式压缩机行业将面临更加激 烈的国际化竞争，企业需要加强技术创新和品牌建设以提 高竞争力。
THANKS
感谢观看
降低压缩后气体的温度。
缓冲罐
减小气流脉动和噪音。
油分离器
分离压缩空气中的油分。
储气罐
储存压缩空气，稳定气流和压力。
控制系统
电动机
提供动力，驱动曲轴旋转。
传感器
监测压缩机的各项运行参数，如压力、温度、 流量等。
控制面板
设定和控制压缩机的运行参数。
电磁阀
控制气路通断，实现压缩机的加载和卸载。
安全保护装置
03
空气压缩机、氧气压缩机、氮气压缩机等。
往复式压缩机应用领域
石油化工
用于气体压缩、输送和 储存，如天然气、石油
气等。
制冷空调
动力工程
其他领域
用于制冷剂的压缩和循 环，实现制冷和空调功
能。
用于气体动力设备的驱 动和控制，如燃气轮机、
内燃机等。
如冶金、矿山、纺织、 医药等行业中的气体压
缩和输送。
02
考虑运行环境 根据安装地点的环境条件，选择适合的压缩机材 质和防护措施。
3
了解制造商的信誉和售后服务 选择有良好信誉和售后服务的制造商。
设计流程与方法
确定设计参数
包括气体性质、流量、压力等。
选择压缩机类型
根据设计参数和工艺要求，选择合适的压缩机类型。
设计流程与方法
进行热力计算
确定压缩机的功率、冷却方式等。
01
连接压缩机进出口管道，确保管道连接牢 固、密封良好。

详细描述
在曲柄连杆机构中，活塞在气缸内进行往复运动，由于连杆的摆动，使得活塞的直线运 动转变为曲轴的旋转运动。在这个过程中，曲轴的旋转运动将能量输出，驱动车辆或其 他机械运动。曲柄连杆机构的特点在于其能够将活塞的往复运动转变为旋转运动，从而
实现能量的高效转换。
分类与应用
总结词
曲柄连杆机构有多种分类方式，如按照曲轴 的形状可分为直列式和V型式，广泛应用于 汽车、摩托车等动力机械中。
缸体的材料选择也很重要，通常采用高强度合金钢或不锈钢制造，以提高其使用寿 命。
03
曲柄连杆机构的工作特性
运动特性
曲柄连杆机构是发动机中的重要 机构，它将活塞的直线运动转化 为曲轴的旋转运动，实现发动机
的做功过程。
曲柄连杆机构的运动特性包括曲 轴的旋转运动、活塞的往复直线
运动以及连杆的摆动运动等。
优化方法
采用数学建模、数值分析和计算机仿 真等方法进行优化设计。
优化流程
建立曲柄连杆机构的数学模型→确定 优化变量和约束条件→选择合适的优 化算法→进行优化计算→分析优化结 果→改进设计。
优化实例与结果分析
优化实例
以某实际应用的曲柄连杆机构为例，进行优化设计。
结果分析
通过对比优化前后的性能指标，分析优化效果。例如，运动性能提升、能耗降 低、振动减小等。同时，对优化后的曲柄连杆机构进行实验验证，确保优化结 果的可靠性和实用性。
05
曲柄连杆机构的常见问题与维护
常见问题与原因分析
01
02
03
04
曲柄连杆机构异响
由于润滑不良、装配间隙不当 或零件疲劳损坏等原因，可能 导致或曲轴轴瓦材料疲劳 极限较低可能导致曲轴轴瓦烧 蚀，影响曲柄连杆机构的正常 运转。

课件提纲
工作原理
性能参数
结构
操作运行
1
2
3
4
*
往复压缩机
前言
压缩机是输送气体并提高气体压力能的机器 在石油化工厂中;压缩机主要压缩原料气 空气或中间过程的介质气体;以满足石油化工生产工艺的需要 压缩机按其工作原理可分为速度型和容积型两种 速度型压缩机靠气体在高速旋转的叶轮的作用下;得到巨大的动能;随后在扩压器中急剧降低;使气体的动能转变为势能;也就是压力能 容积型压缩机靠在气缸内作往复或回转运动的活塞;使容积缩小而提高气体压力
*
往复压缩机
3 3 气阀
目前;活塞式压缩机所应用的气阀;都是随着气缸内气体压力的变化而自行开闭的自动阀;由阀座 运动密封元件阀片或阀芯 弹簧 升程限制器等组成
*
往复压缩机
3 3 气阀
自动阀的阀片在两边压差的作用下开启;在弹簧作用力下关闭 阀片与阀座或升程限制器之间的粘附力 阀片与导向块之间的摩擦力等;也影响阀片的开启与关闭
*
往复压缩机
2 6 多级压缩
所谓多级压缩是将气体的压缩过程分在若干级中进行;并在每级压缩后将气体导入中间冷却器进行冷却 如图所示
1st stage
2nd stage
3 bar 8 bar 1 bar 3 bar
Q
*
往复压缩机
2 6 多级压缩的理由/优势
可以节省压缩气体的指示功; 下图为两级压缩与单级压缩所耗功之比 当第一级压缩达到压力P2后;将气体引入中间冷却器中冷却;使气体冷却到原始温度T1 因此使排出的气体容积由V2减至V2’;然后进入第二级压缩到最终压力 这样;从图中可以看出;实行两级压缩后;与一级压缩相比节省了图中绿色区域的功 采用多级压缩可以节省功的主要原因是进行中间冷却 如果没有中间冷却;第一级排出的气体容积不是因冷却而由V2减至V2’;而仍然以V2的容积进行二级压缩;则所消耗的功与单级压缩相同

填料函
填料函防止气体泄漏，同时润滑活塞杆。
气阀
进排气阀控制气体的流入和排出。
曲轴
曲轴将旋转运动转化为活塞的往复运动。
润滑系统
润滑系统为压缩机提供润滑油，保证正常运行。
往复式压缩机的工作原理图解
吸气过程
压缩过程
活塞向下运动，进气阀打开，气体进入气缸 。
活塞向上运动，气体被压缩。
排气过程
循环过程
活塞到达上止点，排气阀打开，压缩气体排 出。
往复式压缩机的日常维护
保持压缩机的清洁，防止灰尘和 杂物进入内部。
检查冷却系统，确保冷却效果良 好。
定期检查压缩机的各个部件，包 括轴承、活塞环、气缸、曲轴等 ，确保其正常运转。
定期更换润滑油，保证润滑效果 。
对电气控制系统进行定期检查， 确保其安全可靠。
往复式压缩机的常见故障及排除方法
压缩机无法启动
往复式压缩机培训课件优秀课件
xx年xx月xx日
contents
目录
• 往复式压缩机概述 • 往复式压缩机工作原理 • 往复式压缩机的操作与维护 • 往复式压缩机的优化与改进 • 往复式压缩机的发展趋势与展望 • 往复式压缩机培训课件总结与展望
01
往复式压缩机概述
往复式压缩机的定义
往复式压缩机是一种通过活塞在气缸内往复运动来压缩气体 的机械设备。
检查电源连接是否正常，检查控制电路是否正常 ，检查电机是否故障。
压缩机压力不足
检查压缩机的气缸和活塞环是否磨损或损坏，检 查压缩机的密封件是否漏气，检查压缩机的控制 阀是否正常。
压缩机运行异常
检查压缩机的各个部件是否正常，检查润滑系统 是否正常，检查冷却系统是否正常。
压缩机噪音过大

*
往复压缩机
前言
压缩机
速度型
容积型
轴流式
离心式
混流式
回转式
往复式
滑片式
螺杆式
转子式
膜式
活塞式
压缩机按结构型式不同;分类如下：
*
往复压缩机
1 工作原理
往复式压缩机通过曲轴连杆机构将曲轴旋转运动转化为活塞往复运动; 当曲轴旋转时;通过连杆的传动;驱动活塞便做往复运动;由气缸内壁 气缸盖和活塞顶面所构成的工作容积则会发生周期性变化; 曲轴旋转一周;活塞往复一次;气缸内相继实现进气 压缩 排气的过程;即完成一个工作循环;
*
往复压缩机
2 5 多级压缩
p
1级压缩曲线
1级
volume
pressure
V
2nd stage
2级压缩曲线
单级压缩——压比很大
通过中间冷却节省的压缩功 减去 级间冷却器产生的损耗
2级
1、2级级间冷却
*
往复压缩机
2 6 多级压缩的理由/优势
2 可以降低排气温度 通过多级压缩中间冷却后降低了气体的进气温度;压缩过程接近等温压缩;可以显著降低排气温度; 排气温度过高;会使润滑油粘度降低;性能恶化或形成积炭现象；使气阀的工作寿命下降; 对某些特种气体压缩机;排气温度过高还会引发腐蚀或爆炸;
课件提纲
工作原理
性能参数
结构
操作运行
1
2
3
4
*
往复压缩机
前言
压缩机是输送气体并提高气体压力能的机器; 在石油化工厂中;压缩机主要压缩原料气 空气或中间过程的介质气体;以满足石油化工生产工艺的需要; 压缩机按其工作原理可分为速度型和容积型两种; 速度型压缩机靠气体在高速旋转的叶轮的作用下;得到巨大的动能;随后在扩压器中急剧降低;使气体的动能转变为势能;也就是压力能; 容积型压缩机靠在气缸内作往复或回转运动的活塞;使容积缩小而提高气体压力;

篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的，因 此，篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
第二章 往复泵
知识目标
1．掌握往复泵的基本结构和工作原理。 2．了解泵阀、空气室的结构和工作原理。 3．掌握柱塞泵的基本结构和工作原理。 4．了解柱塞泵的变量方式、原理及控制方法。 5．熟悉往复泵和柱塞泵典型实例。
图2-2 往复泵工作原理图
1-吸入滤器；2-吸入管；3-吸入阀； 4-泵缸；5-活塞；6-活塞杆；7-阀箱；
8-排出阀；9-排出管
7
篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的，因 此，篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
第一节 概述
活塞式往复泵工作演示
能力目标
1．能进行往复泵拆装、检查及维护。 2．能进行柱塞泵拆装、检查及维护。 3．能对泵的常见故障进行分析、诊断和排除。
1
篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的，因 此，篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
第一节 概述
一、分类
往复泵是一种容积式泵，它是靠活塞或柱塞的往复运动， 使工作容积发生变化而实现吸排液体的泵。
第一节 概述
4
篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的，因 此，篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
第一节 概述
柱塞式往复泵
柱塞式往复泵（简称柱塞泵）是液压系统的一个重要装 置，柱塞泵具有额定压力高、结构紧凑、效率高和流量调节 方便等优点，被广泛应用于高压和流量需要调节的场合。
流量不均匀，存在惯性影响。
转速不宜太快。

当曲轴旋转时，通过连杆的传动，驱动活塞便 做往复运动，由气缸内壁、气缸盖和活塞顶面 所构成的工作容积则会发生周期性变化。曲轴 旋转一周，活塞往复一次，气缸内相继实现进 气、压缩、排气的过程，即完成一个工作循环。
2023/2/28
3
往复压缩机
1.1 理论工作循环
为了更好地理解活塞压缩机的工作原理，这里重点 介绍理论工作循环。假定压缩机没有余隙容积，没 有吸、排气阻力，没有热量交换，则压缩机工作时， 汽缸内的压力和容积的关系如下图所示。压缩机的 理论工作过程可以简化成下图示的三个热力过程。
8
往复压缩机
1.2 实际工作循环
压缩机工作过程中活塞环、填料、气阀不 可避免存在泄露，每个循环的排气量总小 于实际吸气量。压缩机的进气阻力过大， 会造成压缩机排气量减少。余隙容积过大 会降低排气量，使指示功图面积变小。
2023/2/28
9
往复压缩机
1.2.1 实际过程与理论过程的区别
由于余隙容积的存在，实际工作循环由膨胀、吸气、 压缩、排气四个过程组成，而理论循环无膨胀过程。
2023/2/28
22
往复压缩机
Quantity
2.7 气量调节方式
• 卸荷器调节
Compressor delivery pressure
• 旁通调节
• 余隙腔调节
• 变转速调节 M
2023/2/28
23
3.6.4
往复压缩机
3 结构
压缩机主要由机体、曲轴、连杆、活塞组、 阀门、轴封、油泵、能量调节装置、润滑 油系统、进出口缓冲罐/气液分离器等部件 组成。
胀所占的容积增加，气缸实际吸气量减少。 采用多级压缩，压力比下降，因而容积系 数增加。

04
连杆机构的力分析
平面连杆机构的力分析
平面连杆机构力分析的基本方法
通过解析法和图解法对平面连杆机构进行力分析，解析法基于牛顿第二定律和动力学方程 ，图解法则通过作图和量测来求解。
平面连杆机构力分析的应用
在机械设计、机械动力学、机器人学等领域中，平面连杆机构的力分析是研究和优化机构 性能的重要手段。
总结词
装配与调试是连杆机构制作过程中的关 键步骤，涉及到机构的整体协调性和工 作性能。
VS
详细描述
在装配过程中，应按照设计图纸和技术要 求，正确安装每个零件，确保机构运动副 的配合精度和稳定性。调试则是在装配完 成后，对机构进行运动测试和调整，以检 查机构的工作状态和性能指标是否达到设 计要求，并根据需要进行调整优化。
导杆机构
导杆机构由导杆、连杆和滑块组 成，其中导杆为主动件，滑块为
从动件。
导杆机构可以实现滑块的往复运 动或复杂的轨迹运动，常用于实
现机械的自动化和精密控制。
导杆机构在机床、纺织机械、包 装机械等领域有广泛应用。
摇块机构和定块机构
01
02
03
04
摇块机构和定块机构是两种特 殊的连杆机构，分别由摇块和
平面连杆机构力分析的局限性
对于复杂机构，解析法可能难以求解，图解法则需要大量实验和经验，且精度难以保证。
空间连杆机构的力分析
1 2 3
空间连杆机构力分析的基本方法
基于牛顿第三定律和达朗贝尔原理，通过建立空 间连杆机构的平衡方程进行求解。
空间连杆机构力分析的应用
在航天器、机器人、精密仪器等领域中，空间连 杆机构的力分析对于提高机构的稳定性和精度具 有重要意义。
详细描述
在古代，人们已经使用简单的机械工具，如杠杆、滑 轮等来实现各种工作。随着科技的发展，人们开始将 多个简单机械组合在一起，形成了复杂的连杆机构。 18世纪末的工业革命时期，连杆机构逐渐得到广泛应 用，并成为实现各种复杂运动的理想选择。随着计算 机技术和优化算法的发展，现代的连杆机构设计更加 精确和高效，能够满足各种复杂的工作需求。

往复式压缩机主要零部件
连杆
连杆体材料: 45#锻件; 合金钢锻件; 球铁 连杆螺栓材料: 优质合金钢40Cr, 35CrMoA 小头瓦材料: 铜合金;钢浇巴氏合金 大头瓦: 与主轴承相同
往复式压缩机主要零部件
十字头是连接作摇摆运动的连杆与作往复运动的活塞杆的构件，具 有导向作用。连杆力，活塞力、侧向力在此交汇。
1
2
v
往复式压的压力范围十分有限，当需 要更高压力的场合时，显然，这样高的压力不可能 用单级实现，必须采用多级压缩。 多级压缩：将气体分在若干级中进行逐级压缩， 并在级与级之间将气体进行冷却。
往复式压缩机原理
多级压缩的理由/优势
1. 可以节省压缩气体的指示功。 下图为两级压缩与单级压缩所耗功之比。当第一级压缩达到压力P2 后，将气体引入中间冷却器中冷却，使气体冷却到原始温度T1.因此使 排出的气体容积由V2减至V2’，然后进入第二级压缩到最终压力。这样， 从图中可以看出，实行两级压缩后，与一级压缩相比节省了图中绿色区 域的功。 采用多级压缩可以节省功的主要原因是进行中间冷却。如果没有中 间冷却，第一级排出的气体容积不是因冷却而由V2减至V2’，而仍然以 V2的容积进行二级压缩，则所消耗的功与单级压缩相同。
入口缓冲罐 入口过滤器
出口缓冲罐
冷却器
分 离 罐
往复式压缩机主要零部件
活塞压缩机中，在零件相互滑动的部件，如活塞环与气缸、填料与 活塞杆、主轴承、连杆大头瓦、连接小头衬套以及十字头滑道等处，要 注入润滑剂进行润滑，以达到如下目的： 减小摩擦功率，降低压缩机功率消耗； 减少滑动部位的磨损，延长零件寿命； 润滑剂有冷却作用，可导致摩擦热，使零件工作温度过高，从而保 证滑动部位必要的运转间隙，防止滑动部位咬死或烧伤； 用油作润滑剂时，还有防止零件生锈的作用。

l 3r 300(mm) 240(转/ min)
3
数学模型
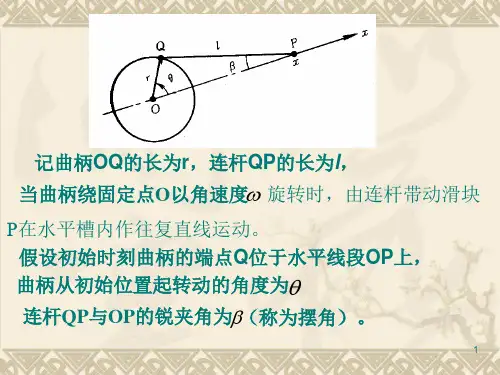
取O点为坐标原点，OP方向为x轴正方向，P在x 轴上的坐标为x，那么可用x表示滑块的位移。
利用三角关系，立即得到
x r cos l2 r2 sin2
(1.1)
t dx dx d dx
(1.2)
dt d dt d
4
x r cos l2 r2 sin2
(1.1)
dx r sin r2 sin cos (1.3)
d
l2 r2 sin2
于是滑块的速度
v dx dx d dx dt d dt d
r sin 1
r cos
(1.4)
l2 r2 sin2
进而，可以得到滑块的加速度为
（1.4）进行近似。
v
r sin 1
r cos
l2
r2
sin2
(1.4)
仍利用公式（1.12）
(1 )a 1 a , 1 (1.12)
1
l 2 r 2 sin 2
1 l
1
r2 l2
sin 2
1
2
1 l
1
r2 2l 2
sin 2
把上式代入（1.4），就得到滑块速度的近似模型
2
12
、5
12
之间。
运用方程求根的数值方法，例如Newton法，对于加
速度的三种表达式，分别可以得出
1.2772 0.407时 , a 0
1.2773 0.407时 , a2 0 1.2862 0.409时 , a1 0
因此在求加速度（绝对值）的最值时，近似模型
也是十分有效的。
利用滑块位移的解析式（8.1）和近似式（8.13），

摄影三脚架中的平面四杆机 构通常由三根支撑杆和若干 个连接杆组成。
三根支撑杆通常具有较好的 弹性和韧性，可以适应不同 地形和环境，提供稳定的支 撑效果。连接杆则将三根支 撑杆连接在一起，形成稳定 的三角形结构。
挖掘机机构
挖掘机是一种广泛应用于建筑、道路 、矿山等领域的工程机械设备。它的 主要功能是通过挖掘斗的升降、旋转 和移动来实现挖掘作业。
作用
03
连杆在机构中起到传递运动和动力的作用，还可以改变运动的
方向。
转动副
定义
转动副是平面四杆机构的基本组成之一，是一种 连接两个构件的相对转动的运动副。
特点
转动副由两个构件组成，一个构件作为固定轴， 另一个构件围绕固定轴旋转。
作用
转动副在机构中起到传递运动和动力的作用，同 时也可以改变运动的方向。
双摇杆机构
由两个摇杆和两个连架杆组成的平面四杆机构。双摇杆机构中，两个摇 杆长度相等且平行，连架杆相对摇杆做往复摆动，可以实现将摇杆的往 复摆动转换为连架杆的往复摆动。
平面四杆机构的应用
实例1
缝纫机踏板机构。当脚踏板低速转动时，通过一个曲柄摇杆 机构将脚踏板的往复摆动转换为缝针的上下摆动；当脚踏板 快速转动时，通过一个双曲柄机构将脚踏板的往复摆动转换 为缝针的上下摆动。
利用计算机辅助设计软件进行 数值仿真，通过对机构参数的
调整，实现最优设计。
基于实验设计的优化
通过实验测试机构的性能，利 用实验设计方法对机构进行优 化。
基于人工智能的优化
利用人工智能算法，如神经网 络、遗传算法等，对机构的参 数进行优化。
多学科优化方法
综合考虑机构的多学科因素， 如结构、运动、动力学等，实
转向机构是汽车底盘的一个重要组成部分，它的 主要功能是控制汽车的行驶方向，使车辆能够按 照驾驶员的意愿进行转弯或者改变行驶方向。

往复压缩机的环保要求和排放标准
• 废弃物处理：对废弃的压缩机和配件进行环保处理，避免 对环境造成污染。
往复压缩机的环保要求和排放标准
排放标准
废气排放：符合国家和地方的废气排放标准，如SO2、NOx等污染物的 限量排放。
噪声排放：遵守工业噪声排放标准，确保压缩机噪声在规定范围内。
往复压缩机的节能技术和应用前景
节能技术
采用高效电机：提高电机效率，降低能耗。
余热回收：利用压缩机产生的余热进行供暖或发 电。
往复压缩机的节能技术和应用前景
• 变频调速技术：根据实际需求调整压缩机运行频率，节省能源 。
往复压缩机的节能技术和应用前景
应用前景
新能源领域：往复压缩机可用于储能、氢能等领域，推 动新能源技术的发展。
工业领域：随着工业领域对气体压缩需求的增加，往复 压缩机将继续发挥重要作用。
01
安全防护措施
02
03
04
安装防护罩：对运动部件进行 防护，防止人员接触。
配备耳塞和防振手套：降低噪 声和振动对人员的影响。
安全阀和压力表：监测压缩机 内压力，确保在安全范围内运
行。
往复压缩机的环保要求和排放标准
环保要求 减少废气排放：采用低污染、低能耗的压缩机技术和燃料。
降低噪声污染：控制压缩机噪声在环保标准以内。
往复压缩机培训课 件
汇报人： 日期:
பைடு நூலகம்录
• 往复压缩机概述 • 往复压缩机的结构和组成部分 • 往复压缩机的操作和维护 • 往复压缩机的安全和环保
01
往复压缩机概述
往复压缩机的定义和工作原理
定义
往复压缩机是一种通过活塞在气缸内做往复运动，从而实现气体压缩的机械设 备。