江苏省姜淮高考复读学校高三数学寒假作业(1)

淮安市范集中学高三年级数学寒假作业班级 姓名 编号 08 得分 家长签字 课题 复数、概率日期 1.30 主备 人 卢盼 审核 人 书写 评价1．复数i 1＋2i(i 是虚数单位)的实部是________．2. 复数53＋4i的共轭复数是________．3．(2010年南京第一次调研)复数z ＝(1＋i)21－i对应的点在第________象限．4．有3张奖券，其中2张可中奖，现3个人按顺序依次从中抽一张，小明最后抽，则他抽到中奖券的概率是__________.5．有3个两两互斥的事件A 、B 、C ，已知事件A+B+C 是必然事件，事件A 的概率是事件B 的概率的2倍，事件C 的概率比事件B 的概率大0.2，则事件A 的概率为___________．6．(2010年福建质检)如图，正方形ABCD 的边长为2，△EBC 为正三角形．若向正方形ABCD 内随机投掷一个质点，则它落在△EBC 内的概率为________．7．设A 为圆周上一定点，在圆周上等可能地任取一点与A 连结，则弦长超过半径的概率为________．8．从1、2、3、4中任取两个不同的数字构成一个两位数，则这个两位数大于20的概率为________．9.一个骰子连续投2 次，点数和为4 的概率 ．10．在平面直角坐标系xoy 中，设D 是横坐标与纵坐标的绝对值均不大于2的点构成的区域， E 是到原点的距离不大于 1 的点构成的区域，向 D 中随机投一点，则落入 E 中的概率 ．11.(2008年高考山东卷)现有8名奥运会志愿者，其中志愿者A 1、A 2、A 3通晓日语，B 1、B 2、B 3通晓俄语，C 1、C 2通晓韩语．从中选出通晓日语、俄语和韩语的志愿者各1名，组成一个小组．(1)求A 1被选中的概率；(2)求B 1和C 1不全被选中的概率．12. 抛掷一枚均匀的正方体骰子，骰子的每个面上分别标有数字1、2、3、4、5、6，连续抛掷两次，将骰子朝上的点数作为直角坐标系中点P 的坐标(第一次为横坐标，第二次为纵坐标)，四边形ABCD 为不等式组⎩⎪⎨⎪⎧ x －y ＋2≥00≤x ≤4y ≥0表示的平面区域．(1)求点P 落在四边形区域ABCD 内(含边界)的概率；(2)是否存在一种平移，使得区域ABCD 平移若干个单位后，点P 落在区域ABCD 内的概率为14，若存在，指出其中一种平移方式，若不存在，请说明理由．。

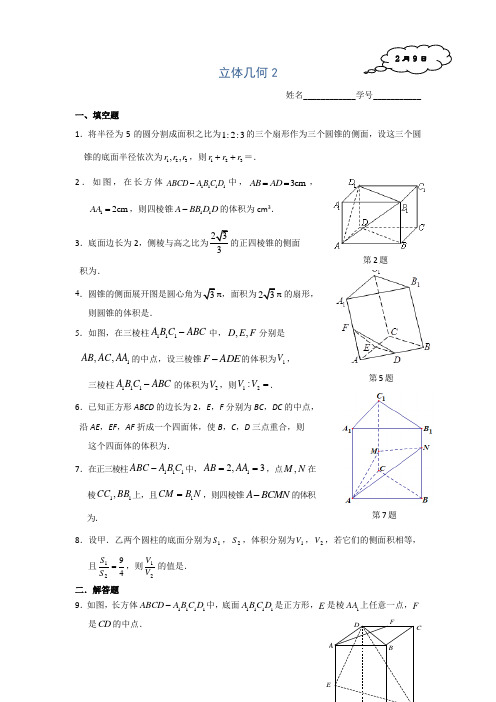
FEDCBA立体几何2姓名____________学号___________一、填空题1．将半径为5的圆分割成面积之比为1:2:3的三个扇形作为三个圆锥的侧面，设这三个圆锥的底面半径依次为123,,r r r ，则123r r r ++＝．2．如图，在长方体1111ABCD A B C D -中，3cm AB AD ==，12cm AA =，则四棱锥11A BB D D -的体积为cm 3．3．底面边长为2，侧棱与高之比为3的正四棱锥的侧面 积为．4，面积为的扇形，则圆锥的体积是．5．如图，在三棱柱ABC C B A -111中，F E D ,,分别是1,,AA AC AB 的中点，设三棱锥ADE F -的体积为1V ，三棱柱ABC C B A -111的体积为2V ，则=21:V V ．6．已知正方形ABCD 的边长为2，E ，F 分别为BC ，DC 的中点， 沿AE ，EF ，AF 折成一个四面体，使B ，C ，D 三点重合，则 这个四面体的体积为．7．在正三棱柱111ABC A B C -中，12,3AB AA ==，点,M N 在 棱11,CC BB 上，且1CM B N =，则四棱锥A BCMN -的体积 为．8．设甲．乙两个圆柱的底面分别为1S ，2S ，体积分别为1V ，2V ，若它们的侧面积相等，且4921=S S ，则21V V 的值是．二．解答题9．如图，长方体1111ABCD A B C D -中，底面1111A B C D 是正方形，E 是棱1AA 上任意一点，F 是CD 的中点．(1) 证明：BD 1EC ⊥； (2) 若AF ∥平面C 1DE ，求1AEA A的值．10．如图，在直三棱柱111A B C ABC -中，AB ⊥BC ，E ，F 分别是1A B ，1AC 的中点． (1) 求证：EF ∥平面ABC ；(2) 求证：平面AEF ⊥平面11AA B B ．立体几何21．解：52．解：∵长方体底面ABCD 是正方形，∴△ABD中BD ，BDcm （它也是11A BB D D -中11BB D D 上的高）．∴四棱锥11A BB D D -的体积为123⨯． FBCE A1A 1B 1COG D 1C 1B 1A 1FEDCB A3，侧面积为1422⨯⨯=4．解：设圆锥的底面半径为r ，母线长为l ，解得l =2，r，∴圆锥高h =1，则体积V =π． 5．解：112211111334224ADE ABC V S h S h V ==⨯⨯=，121:24V V = 6．解：以AE ，EF ，AF 为折痕，使得D C B ,,三点合于点P ，在折叠过程中，始终有DF AD BE AB ⊥⊥,，即PE AP ⊥，PF AP ⊥，∴PEF AP 面⊥，∴这个四面体的体积为31211213131=⨯⨯⨯⨯=⋅=∆-AP S V PEF PEF A ． 7．解:1CM B N =,111112BCMN MC B N BCC B S S S ∴==111111113233A BCMN A BCCB A BCB B ABC ABC V V V V S BB ----∆∴====⋅==．8．解：设甲．乙两个圆柱的底面和高分别为1r ．1h ，2r ．2h ，则112222r h r h ππ=，1221h r h r =，又21122294S r S r ππ==，∴1232r r =，则222111111212222222221232V r h r h r r r V r h r h r r r ππ==⋅=⋅==．9．证明：(1) 连接AC ，11//,,,AE CC E A C C ⇒共面． 长方体1111ABCD A B C D -中，底面1111A B C D 是正方形， ∴,,AC BD EA BD ACEA A ⊥⊥=．∴BD ⊥面1EACC ，∴1BD EC ⊥．(2) 取11C D 的中点G ，连接FG 交1C D 于点O ， 易知FG ∥DD 1，FG = DD 1，且点O 为FG 的中点， ∴1,,,A A G F 四点共面， ∴平面11C DEAAGF OE =平面． ∵AF ∥平面C 1DE ，AF ∥OE ． 又点O 为FG 的中点，∴1AE A A =12． 10．证明：(1) 连结1A C ．∵直三棱柱111A B C ABC -中，11AA C C 是矩形，FBCE A1A 1B 1C∴点F 在1A C 上，且为1A C 的中点．在△1A BC 中，E ，F 分别是1A B ，1A C 的中点， ∴EF ∥BC ．又∵BC ⊂平面ABC ， EF ⊄平面ABC ， ∴EF ∥平面ABC ．(2) ∵直三棱柱111A B C ABC -中，1B B ⊥平面ABC ， ∴1B B ⊥BC ． ∵EF ∥BC ，AB ⊥BC ， ∴AB ⊥EF ，1B B ⊥ EF ． ∵1B BAB B =，∴EF ⊥平面11ABB A ． ∵EF ⊂平面AEF ， ∴平面AEF ⊥平面11ABB A ．。

2024—2025学年第一学期高三12月质量测试数学注意事项：本卷考试时间为120分钟，满分为150分。

一、选择题：本题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知集合，则A．B．C．D．2．已知复数满足，则A．B．C．D．3．已知平面向量，，满足，，，，则的最小值为A．1B．C．3D．44．在锐角三角形ABC中，，则的范围是A．B．C．D．5．已知三棱锥满足，，，且其表面积为24，若点（正投影在内部）到，，的距离相等，则三棱锥的体积为A．B．C．D．6．对于函数，若存在，使，则称点与点是函数的一对“隐对称点”.若函数的图象存在三对“隐对称点”，则实数的取值可以是A．B．C．D．7．已知函数，则函数的零点个数为A．9B．10C．11D．128．已知定义在上的函数满足，且当时，，则A．B．C．D．二、选择题：本题共3小题，每小题6分，共18分。

在每小题给出的选项中，有多项符合题目要求。

全部选对的得6分，部分选对的得部分分，有选错的得0分。

9．判断下列命题中正确的有A．对于回归分析，相关系数的绝对值越大，说明拟合效果越好B．将一组数据中的每个数据都加上同一个常数后，方差恒不变C．已知随机变量X服从二项分布，若，，则D．设随机变量ξ服从正态分布，若，则10．已知函数，的定义域均为，若存在函数，使得函数，在上有，，，恒成立，则称，为一组“双向奔赴”函数.下列各组函数中，符合“双向奔赴”函数的有A．，，B．，，C．，，D．，，11．已知曲线．点，，则以下说法正确的是A．曲线C不存在点P，使得B．曲线C关于原点对称C．直线与曲线C没有交点D．点Q是曲线C上在第三象限内的一点，过点Q向作垂线，垂足分别为A，B，则三、填空题：本题共3小题，每小题5分，共15分。

12．已知双曲线的左、右焦点分别为、，若双曲线的左支上一点满足，以为圆心的圆与的延长线相切于点，且，则双曲线的离心率为.13．已知函数（为常数，e为自然对数的底数）的图象在点A（e,1）处的切线与该函数的图象恰好有三个公共点，则实数的取值范围是_____.14．某校高三1班10名同学、高三2班20名同学、高三3班10名同学参加“强国有我”演讲比赛，采用随机抽签的方式确定出场顺序，每位同学依次出场．记“高三1班全部学生完成比赛后，高三2班和高三3班都有学生尚未完成比赛”为事件A，则事件A发生的概率为．四、解答题：本题共5小题，共77分。

一．基础题组1. 【高考模拟试卷南通市数学学科基地命题(6)】若对任意的x ∈D ，均有f1(x)≤f(x)≤f2(x)成立，则称函数f(x)为函数f1(x)到函数f2(x)在区间D 上的“折中函数”．已知函数f(x)＝(k －1)x －1，g(x)＝0，h(x)＝(x ＋1)ln x ，且f(x)是g(x)到h(x)在区间[1,2e]上的“折中函数”，则实数k 的取值集合为________． 【答案】{2}考点：新定义，不等式恒成立，导数与单调性. 2. 【】用火柴棒摆“金鱼”，如图所示：按照上面的规律，第○n 个“金鱼”图需要火柴棒的根数是． 【答案】62n + 【解析】试题分析：由题意得：“金鱼”图需要火柴棒的根数依次构成一个等差数列，首项为8，公差为6，因此第n 项为62n + 考点：等差数列3. 【淮安市－度第二学期高二调查测试】对于数列{n a }，定义数列{n n a a -+1}为数列{n a }的“差数列”，若21=a ，{n a }的“差数列”的通项为n2，则数列{n a }的前n 项和n S =.【答案】122n +- 【解析】试题分析：由题意得：12n n n a a +-=，所以1122(12)22222212n n n n n a ----=++++=+=-，所以n S 122n +=-考点：等比数列求和，累加法求通项4. 【淮安市－度第二学期高二调查测试】已知函数()2log 1f x a x =+（0a ≠），定义函数()()(),0,0f x x F x f x x ⎧>⎪=⎨-<⎪⎩，给出下列命题：①()()F x f x =；②函数()F x 是偶函数；③当0a <时，若01m n <<<，则有()()0F m F n -<成立；④当0a >时，函数()2y F x =-有4个零点．其中正确命题的个数为． 【答案】3考点：函数性质5. 【高考模拟试卷南通市数学学科基地命题(5)】一个非空集合中的各个元素之和是3的倍数，则称该集合为“好集”．记集合 {1，2，3，…，3n}的子集中所有“好集”的个数为f(n)． （1）求f(1)，f(2)的值； （2）求f(n)的表达式．【答案】（1）f(1)=3，f(2)＝23；（2）f(n)＝2n(4n －1)3+2n －1．试题解析：(1)易得f(1)=3；当n=2时，集合{1，2，3，4，5，6}的子集中是“好集”的有：单元集：{3}，{6}共2个，双元集{1,2}，{1,5}，{2,4}，{4,5}，{3,6}共5个，三元集有：{1,2,3}，{1,2,6}，{1,3,5}，{1,5,6}，{4,2,3}，{4,2,6}，{4,3,5}，{4,5,6}共8个，四元集有{3,4,5,6}，{2,3,4,6}，{1,3,5,6}，{1,2,3,6}，{1,2,4 ,5}共五个，五元集{1,2,4,5,6}，{1,2,3,4,5}共2个，还有一个全集．故f(2)＝1+(2+5)×2+8＝23．(2)首先考虑f(n+1)与f(n)的关系．集合{1，2，3，…，3n，3n+1，3n+2，3n+3}在集合{1，2，3，…，3n}中加入3个元素3n+1，3n+2，3n+3．故f(n+1)的组成有以下几部分：①原有的f(n)个集合；②含有元素3n+1的“好集”是{1，2，3，…，3n}中各元素之和被3除余2的集合，含有元素是3n+2的“好集”是{1，2，3，…，3n}中各元素之和被3除余1的集合，含有元素是3n+,3的“好集”是{1，2，3，…，3n}中各元素之和被3除余0的集合，合计是23n；③含有元素是3n+1与3n+2的“好集”是{1，2，3，…，3n}中各元素之和被3除余0的集合，含有元素是3n+2与3n+3的“好集”是{1，2，3，…，3n}中各元素之和被3除余1的集合，含有元素是3n+1与3n+3的“好集”是{1，2，3，…，3n}中各元素之和被3除余2的集合，合计是23n ；④含有元素是3n+1，3n+2，3n+3的“好集”是{1，2，3，…，3n}中“好集”与它的并，再加上{3n+1，3n+2，3n+3}． 所以，f(n+1)＝2 f(n)+2×23n+1． 两边同除以2n+1，得f(n+1)2n+1－f(n)2n ＝4n+12n+1，所以f(n)2n ＝4n1+4n2+…+4+12n +12n1+…+122+32＝4n －13+1－12n ，即f(n)＝2n(4n －1)3+2n －1．考点：新定义，子集，归纳推理.6. 【高考模拟试卷南通市数学学科基地命题(2)】汽车从刹车开始到完全静止所用的时间叫做刹车时间；所经过的距离叫做刹车距离.某型汽车的刹车距离s(单位米)与时间t(单位秒)的关系为32510s t k t t =-⋅++，其中k 是一个与汽车的速度以及路面状况等情况有关的量．（1）当k=8时，且刹车时间少于1秒，求汽车刹车距离；（2）要使汽车的刹车时间不小于1秒钟，且不超过2秒钟，求k 的取值范围． 【答案】（1）6752210米；（2）⎥⎦⎤⎢⎣⎡∈461,8k .（2）汽车的瞬时速度为'v s =，所以21521v t kt =-+ 汽车静止时0v =，故问题转化为215210t kt -+=在[]1,2内有解又21511215t k t t t+==+，115215t t +≥，当且仅当1115,15t t t ==时取等号， []11,215t =∉，∴记1()15f tt t=+， '21()15f t t =-，[1,2]t ∈，'21()150f t t ∴=->，()f t ∴单调递增， ⎥⎦⎤⎢⎣⎡∈∴261,16)(t f ，⎥⎦⎤⎢⎣⎡∈261,162k ，即⎥⎦⎤⎢⎣⎡∈461,8k ，故k 的取值范围为⎥⎦⎤⎢⎣⎡∈461,8k . 考点：导数的物理意义，方程有解问题.7. 【高考模拟试卷南通市数学学科基地命题(3)】若数列{}n C 满足①21n n n c c c ++≤，②存在常数(M M 与n无关），使n c M ≤.则称数列{}n c 是“和谐数列”.（1）设n S 为等比数列{}n a 的前n 项和，且442,30a S ==，求证：数列{}n S 是“和谐数列”；（2）设{}n a 是各项为正数，公比为q 的等比数列，n S 是{}n a 的前n 项和，求证：数列{}n S 是“和谐数列”的充要条件为01q <<.【答案】（1）详见解析（2）详见解析试题解析：（1）设公比为q ，则3411414161(1)21a a q a a q q s q ⎧==⎧⎪⎪⇒⎨⎨-==⎪⎪⎩-⎩, 所以51322n n s -=-.25311(32)(32)22n n n n s s +--=--253281113232()222n n n ----++2428113223222n n ---+=214411(32)3222n n n S +---=-=.且513232.2n n S -=-<即存在常数32,所以，数列{}n S 是“和谐数列” .（1）当1,q =则1,n S na =因为10,a >所以，不存在M ，使1na M <对1n N -∈恒成立; 当1q >，则111(1)111n n n a q a aS q q q q -==---- 所以，对于给定的正数M ，若11,11n a aq M q q ->-- 因为，1q >，所以，11log (1).q q n M a ->+ 即当11log (1)q q n M a ->+时，有n S M >. 所以，不存在常数M ，使.n S M ≤ 所以，0 1.q <<综上,数列{}n S 是“和谐数列”的充要条件为其公比为01q <<.考点：充要关系，新定义8．【南京一中等五校高三联考（四模）数学】已知两个无穷数列{}{},n n a b 分别满足12n n a a +-=，2214n nb b +=，且111,1a b ==-．（1）若数列{}{},n n a b 都为递增数列，求数列{}{},n n a b 的通项公式；（2）若数列{}n c 满足：存在唯一的正整数()r r N *∈，使得1r r c c +<，称数列{}n c 为“梦r 数列”；设数列{}{},n n a b 的前n 项和分别为,n n S T ，① 若数列{}n a 为“梦5数列”，求n S ；② 若{}n a 为“梦1r 数列”，{}n b 为“梦2r 数列”，是否存在正整数m ，使得1m m S T +=，若存在，求m 的最大值；若不存在，请说明理由．【答案】（1）21n a n =-，11,12,2n n n b n --=⎧=⎨≥⎩（2）①22,5420,6n n n S n n n ⎧≤⎪=⎨-+≥⎪⎩②max 6m =试题解析：（1）数列{}{},n n a b 都为递增数列，∴12n n a a +-=，21212,2,n n b b b b n N *++=-=∈，∴21n a n =-，11,12,2n n n b n --=⎧=⎨≥⎩； ………4分（2）①∵数列{}n a 满足：存在唯一的正整数=5r ，使得1r r a a +<，且12n n a a +-=，∴数列{}n a 必为1,3,5,7,9,7,9,11,⋅⋅⋅，即前5项为首项为1，公差为2的等差数列，从第6项开始为首项7，公差为2的等差数列，故22,5420,6n n n S n n n ⎧≤⎪=⎨-+≥⎪⎩； ………8分②∵2214n n b b +=即12n n b b +=±，1||2n n b -∴=………9分而数列{}n b 为“梦数列”且11b =-，∴数列{}n b 中有且只有两个负项．假设存在正整数m ，使得+1m m S T =，显然1m ≠，且m T 为奇数，而{}n a 中各项均为奇数，∴m 必为偶数． ………10分首先证明：6m ≤． 若7m >，数列{}n a 中()()21max 1321(1)m S m m +=++⋅⋅⋅++=+，而数列{}n b 中，m b 必然为正，否则()()1121212122230m m m m T b ---=-++⋅⋅⋅+-≤-++⋅⋅⋅++-=-<，显然矛盾；（※）∴()()()13211min 12+22223m m m m m T ----=-++⋅⋅⋅++-+=-，设122(1)3m m c m -=-+-，易得11223,m m m m d c c m -+=-=--而11220m m m d d -+-=->，()7m >，∴{}m d ()7m >为增数列，且70d >进而{}m c ()7m >为增数列，而80c >，∴()()min max m m T S >，即6m ≤． ………14分当6m =时，构造：{}n a 为1,3,1,3,5,7,9,⋅⋅⋅，{}n b 为1,2,4,8,16,32,64,--⋅⋅⋅ 此时12r =，24r =所以max 6m =，对应的12r =，24r =………16分 考点：1.等差数列；2等比数列；3.新定义；4.递增数列； 9. 【扬州中学高三4月双周测数学试题】（本小题满分16分）设数列{}n a 的通项公式为n a pn q =+(,0)n N p *∈>，数列{}n b 定义如下：对于正整数m ，m b 是使得不等式n a m ≥成立的所有n 中的最小值. （1）若11,23p q ==-，求3b ; （2）若2,1p q ==-，求数列{}m b 的前2m 项和公式;（3）是否存在p 和q ，使得32m b m =+()m N *∈？如果存在，求p 和q 的取值范围？如果不存在，请说明理由.【答案】（1）37b =；（2）22m m +；（3）121,[,]333p q =∈--. 【解析】试题分析：(1)已知说明1123n a n =-，要求3b ，只要求得不等式11323n -≥的最小整数解即可；（2）同样21n a n =-，为了求m b ，我们要解不等式21n m -≥，即12m n +≥，因此按m 的奇偶分类讨论：当21m k =-时，()m b k k N *=∈，当2m k =时，1()m b k k N *=+∈，这样在求数列{}m b 的前2m 项和2m S 时也要分组求和，奇数项一起，偶数项一起分别求和；（3）存在性命题，都是假设存在，然后计算，本题假设存在的意思就是说不等式pn q m +≥的最小整数解为32m +，由于0p >，因此m q n p ->，则3132m qm m p-+<≤+，即2(31)p q p m p q --≤-<--对任意的正整数m 都成立.于是有310p -=，13p =，代入上式又得2133q -≤<-.故结论为存在.考点：不等式的整数解，分类讨论，分组求和，存在性命题. 二．能力题组1. 【高考模拟(南通市数学学科基地命题)(2)】（本小题满分10分）一个非空集合中的各个元素之和是3的倍数，则称该集合为“好集”．记集合 {1，2，3，…，3n}的子集中所有“好集”的个数为f(n)． （1）求f(1)，f(2)的值； （2）求f(n)的表达式．【答案】（1）f(1)=3，f(2)＝23；（2）f(n)＝2n(4n －1)3+2n －1．试题解析：(1)易得f(1)=3；当n=2时，集合{1，2，3，4，5，6}的子集中是“好集”的有：单元集：{3}，{6}共2个，双元集{1,2}，{1,5}，{2,4}，{4,5}，{3,6}共5个，三元集有：{1,2,3}，{1,2,6}，{1,3,5}，{1,5,6}，{4,2,3}，{4,2,6}，{4,3,5}，{4,5,6}共8个，四元集有{3,4,5,6}，{2,3,4,6}，{1,3,5,6}，{1,2,3,6}，{1,2,4 ,5}共五个，五元集{1,2,4,5,6}，{1,2,3,4,5}共2个，还有一个全集．故f(2)＝1+(2+5)×2+8＝23．(2)首先考虑f(n+1)与f(n)的关系．集合{1，2，3，…，3n，3n+1，3n+2，3n+3}在集合{1，2，3，…，3n}中加入3个元素3n+1，3n+2，3n+3．故f(n+1)的组成有以下几部分：①原有的f(n)个集合；②含有元素3n+1的“好集”是{1，2，3，…，3n}中各元素之和被3除余2的集合，含有元素是3n+2的“好集”是{1，2，3，…，3n}中各元素之和被3除余1的集合，含有元素是3n+,3的“好集”是{1，2，3，…，3n}中各元素之和被3除余0的集合，合计是23n；③含有元素是3n+1与3n+2的“好集”是{1，2，3，…，3n}中各元素之和被3除余0的集合，含有元素是3n+2与3n+3的“好集”是{1，2，3，…，3n}中各元素之和被3除余1的集合，含有元素是3n+1与3n+3的“好集”是{1，2，3，…，3n}中各元素之和被3除余2的集合，合计是23n ；④含有元素是3n+1，3n+2，3n+3的“好集”是{1，2，3，…，3n}中“好集”与它的并，再加上{3n+1，3n+2，3n+3}． 所以，f(n+1)＝2 f(n)+2×23n+1． 两边同除以2n+1，得f(n+1)2n+1－f(n)2n ＝4n+12n+1，所以f(n)2n ＝4n1+4n2+…+4+12n +12n1+…+122+32＝4n －13+1－12n ，即f(n)＝2n(4n －1)3+2n －1．考点：新定义，子集，归纳推理.2. 【扬州市—度第四次调研测试试题高三数学】设集合{1,0,1}M =-,集合123{(,,)|,1,2,,}n n i A x x x x x M i n =∈=，，,集合n A 中满足条件“121||||||n x x x m ≤+++≤”的元素个数记为nm S ．⑴求22S 和42S 的值；⑵当m n <时,求证：nm S 111322n m n +++<+-．【答案】⑴228S =,4232S =；⑵见试题解析.试题解析：⑴228S =,4232S =；因为当0k n ≤≤时,1kn C ≥,故10k n C -≥ 所以1122222n m mm n n n S C C C =+++001122112(222)(1)2(1)2m m m m nn n n n n n n C C C C C C ++<+++++-++-0011221112(222222)(222)m m m m n nm m n n n n n n n C C C C C C ++++=+++++++-++11(12)(22)n n m ++=+--11322n n m ++=-+．考点：1.集合；2.排列组合；3.推理证明.一、选择题（共8小题，每小题5分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项）1.5分）下列函数中，在区间（0，+∞）上为增函数的是（）A.y=B.y=（x﹣1）2C.y=2﹣xD.y=log0.5（x+1）2.（（5分）已知集合A={x|x2﹣2x=0}，B={0，1，2}，则A∩B=（）A.{0}B.{0，1}C.{0，2}D.{0，1，2}3.（5分）曲线（θ为参数）的对称中心（）A.在直线y=2x上B.在直线y=﹣2x上C.在直线y=x﹣1上D.在直线y=x+1上4.（5分）当m=7，n=3时，执行如图所示的程序框图，输出的S的值为（）A.7B.42C.210D.8405.（5分）设{an}是公比为q的等比数列，则“q＞1”是“{an}为递增数列”的（）A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件6.（5分）若x，y满足，且z=y﹣x的最小值为﹣4，则k的值为（）A.2B.﹣2C.D.﹣7.（5分）在空间直角坐标系Oxyz中，已知A（2，0，0），B（2，2，0），C（0，2，0），D（1，1，），若S1，S2，S3分别表示三棱锥D﹣ABC在xOy，yOz，zOx坐标平面上的正投影图形的面积，则（）A.S1=S2=S3B.S2=S1且S2≠S3C.S3=S1且S3≠S2D.S3=S2且S3≠S18.（5分）学生的语文、数学成绩均被评定为三个等级，依次为“优秀”“合格”“不合格”.若学生甲的语文、数学成绩都不低于学生乙，且其中至少有一门成绩高于乙，则称“学生甲比学生乙成绩好”.如果一组学生中没有哪位学生比另一位学生成绩好，并且不存在语文成绩相同、数学成绩也相同的两位学生，则这一组学生最多有（）A.2人B.3人C.4人D.5人二、填空题（共6小题，每小题5分，共30分）9.（5分）复数（）2=.10.（5分）已知向量，满足||=1，=（2，1），且+=（λ∈R），则|λ|=.11.（5分）设双曲线C经过点（2，2），且与﹣x2=1具有相同渐近线，则C的方程为；渐近线方程为.12.（5分）若等差数列{an}满足a7+a8+a9＞0，a7+a10＜0，则当n=时，{an}的前n项和最大.13.（5分）把5件不同产品摆成一排，若产品A与产品B相邻，且产品A与产品C不相邻，则不同的摆法有种.14.（5分）设函数f（x）=Asin（ωx+φ）（A，ω，φ是常数，A＞0，ω＞0）若f（x）在区间[，]上具有单调性，且f（）=f（）=﹣f（），则f（x）的最小正周期为.三、解答题（共6小题，共80分，解答应写出文字说明、演算步骤或证明过程）15.（13分）如图，在△ABC中，∠B=，AB=8，点D在边BC上，且CD=2，cos∠ADC=.（1）求sin∠BAD；（2）求BD，AC的长.16.（13分）李明在10场篮球比赛中的投篮情况统计如下（假设各场比赛相互独立）；场次投篮次数命中次数场次投篮次数命中次数主场1 22 12 客场1 18 8 主场2 15 12 客场2 13 12 主场3 12 8 客场3 21 7 主场4 23 8 客场4 18 15 主场5 24 20 客场5 25 12 （1）从上述比赛中随机选择一场，求李明在该场比赛中投篮命中率超过0.6的概率；（2）从上述比赛中随机选择一个主场和一个客场，求李明的投篮命中率一场超过0.6，一场不超过0.6的概率；（3）记是表中10个命中次数的平均数，从上述比赛中随机选择一场，记X为李明在这场比赛中的命中次数，比较EX与的大小（只需写出结论）.17.（14分）如图，正方形AMDE的边长为2，B，C分别为AM，MD的中点，在五棱锥P ﹣ABCDE中，F为棱PE的中点，平面ABF与棱PD，PC分别交于点G，H.（1）求证：AB∥FG；（2）若PA⊥底面ABCDE，且PA=AE，求直线BC与平面ABF所成角的大小，并求线段PH 的长.18.（13分）已知函数f（x）=xcosx﹣sinx，x∈[0，]（1）求证：f（x）≤0；（2）若a＜＜b对x∈（0，）上恒成立，求a的最大值与b的最小值.19.（14分）已知椭圆C：x2+2y2=4，（1）求椭圆C的离心率（2）设O为原点，若点A在椭圆C上，点B在直线y=2上，且OA⊥OB，求直线AB与圆x2+y2=2的位置关系，并证明你的结论.20.（13分）对于数对序列P：（a1，b1），（a2，b2），…，（an，bn），记T1（P）=a1+b1，Tk（P）=bk+max{Tk﹣1（P），a1+a2+…+ak}（2≤k≤n），其中max{Tk﹣1（P），a1+a2+…+ak}表示Tk﹣1（P）和a1+a2+…+ak两个数中最大的数，（Ⅰ）对于数对序列P：（2，5），（4，1），求T1（P），T2（P）的值；（Ⅱ）记m为a，b，c，d四个数中最小的数，对于由两个数对（a，b），（c，d）组成的数对序列P：（a，b），（c，d）和P′：（c，d），（a，b），试分别对m=a和m=d两种情况比较T2（P）和T2（P′）的大小；（Ⅲ）在由五个数对（11，8），（5，2），（16，11），（11，11），（4，6）组成的所有数对序列中，写出一个数对序列P使T5（P）最小，并写出T5（P）的值（只需写出结论）.高考模拟题复习试卷习题资料高考数学试卷（理科）（附详细答案）参考答案与试题解析（5分）下列函数中，在区间（0，+∞）上为增函数的是（）A.y=B.y=（x﹣1）2C.y=2﹣xD.y=log0.5（x+1）【分析】根据基本初等函数的单调性，判断各个选项中函数的单调性，从而得出结论. 【解答】解：由于函数y=在（﹣1，+∞）上是增函数，故满足条件，由于函数y=（x﹣1）2在（0，1）上是减函数，故不满足条件，由于函数y=2﹣x在（0，+∞）上是减函数，故不满足条件，由于函数y=log0.5（x+1）在（﹣1，+∞）上是减函数，故不满足条件，故选：A.【点评】本题主要考查函数的单调性的定义和判断，基本初等函数的单调性，属于基础题.一、选择题（共8小题，每小题5分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项）2.（5分）已知集合A={x|x2﹣2x=0}，B={0，1，2}，则A∩B=（）A.{0}B.{0，1}C.{0，2}D.{0，1，2}【分析】解出集合A，再由交的定义求出两集合的交集.【解答】解：∵A={x|x2﹣2x=0}={0，2}，B={0，1，2}，∴A∩B={0，2}故选：C.【点评】本题考查交的运算，理解好交的定义是解答的关键.3.（5分）曲线（θ为参数）的对称中心（）A.在直线y=2x上B.在直线y=﹣2x上C.在直线y=x﹣1上D.在直线y=x+1上【分析】曲线（θ为参数）表示圆，对称中心为圆心，可得结论.【解答】解：曲线（θ为参数）表示圆，圆心为（﹣1，2），在直线y=﹣2x 上，故选：B.【点评】本题考查圆的参数方程，考查圆的对称性，属于基础题.4.（5分）当m=7，n=3时，执行如图所示的程序框图，输出的S的值为（）A.7B.42C.210D.840【分析】算法的功能是求S=7×6×…×k的值，根据条件确定跳出循环的k值，计算输出S的【解答】解：由程序框图知：算法的功能是求S=7×6×…×k的值，当m=7，n=3时，m﹣n+1=7﹣3+1=5，∴跳出循环的k值为4，∴输出S=7×6×5=210.故选：C.【点评】本题考查了循环结构的程序框图，根据框图的流程判断算法的功能是解答本题的关键.5.（5分）设{an}是公比为q的等比数列，则“q＞1”是“{an}为递增数列”的（）A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件【分析】根据等比数列的性质，结合充分条件和必要条件的定义进行判断即可得到结论. 【解答】解：等比数列﹣1，﹣2，﹣4，…，满足公比q=2＞1，但{an}不是递增数列，充分性不成立.若an=﹣1为递增数列，但q=＞1不成立，即必要性不成立，故“q＞1”是“{an}为递增数列”的既不充分也不必要条件，故选：D.【点评】本题主要考查充分条件和必要条件的判断，利用等比数列的性质，利用特殊值法是解决本题的关键.6.（5分）若x，y满足，且z=y﹣x的最小值为﹣4，则k的值为（）A.2B.﹣2C.D.﹣【分析】对不等式组中的kx﹣y+2≥0讨论，当k≥0时，可行域内没有使目标函数z=y﹣x取得最小值的最优解，k＜0时，若直线kx﹣y+2=0与x轴的交点在x+y﹣2=0与x轴的交点的左边，z=y﹣x的最小值为﹣2，不合题意，由此结合约束条件作出可行域，化目标函数为直线方程的斜截式，由图得到最优解，联立方程组求出最优解的坐标，代入目标函数得答案. 【解答】解：对不等式组中的kx﹣y+2≥0讨论，可知直线kx﹣y+2=0与x轴的交点在x+y﹣2=0与x轴的交点的右边，故由约束条件作出可行域如图，当y=0，由kx﹣y+2=0，得x=，∴B（﹣）.由z=y﹣x得y=x+z.由图可知，当直线y=x+z过B（﹣）时直线在y轴上的截距最小，即z最小.此时，解得：k=﹣.故选：D.【点评】本题考查简单的线性规划，考查了数形结合的解题思想方法，是中档题.7.（5分）在空间直角坐标系Oxyz中，已知A（2，0，0），B（2，2，0），C（0，2，0），D（1，1，），若S1，S2，S3分别表示三棱锥D﹣ABC在xOy，yOz，zOx坐标平面上的正投影图形的面积，则（）A.S1=S2=S3B.S2=S1且S2≠S3C.S3=S1且S3≠S2D.S3=S2且S3≠S1【分析】分别求出三棱锥在各个面上的投影坐标即可得到结论.【解答】解：设A（2，0，0），B（2，2，0），C（0，2，0），D（1，1，），则各个面上的射影分别为A'，B'，C'，D'，在xOy坐标平面上的正投影A'（2，0，0），B'（2，2，0），C'（0，2，0），D'（1，1，0），S1=.在yOz坐标平面上的正投影A'（0，0，0），B'（0，2，0），C'（0，2，0），D'（0，1，），S2=.在zOx坐标平面上的正投影A'（2，0，0），B'（2，0，0），C'（0，0，0），D'（0，1，），S3=，则S3=S2且S3≠S1，故选：D.【点评】本题主要考查空间坐标系的应用，求出点对于的投影坐标是解决本题的关键.8.（5分）学生的语文、数学成绩均被评定为三个等级，依次为“优秀”“合格”“不合格”.若学生甲的语文、数学成绩都不低于学生乙，且其中至少有一门成绩高于乙，则称“学生甲比学生乙成绩好”.如果一组学生中没有哪位学生比另一位学生成绩好，并且不存在语文成绩相同、数学成绩也相同的两位学生，则这一组学生最多有（）A.2人B.3人C.4人D.5人【分析】分别用ABC分别表示优秀、及格和不及格，根据题干中的内容推出文成绩得A，B，C的学生各最多只有1个，继而推得学生的人数.【解答】解：用ABC分别表示优秀、及格和不及格，显然语文成绩得A的学生最多只有1个，语文成绩得B得也最多只有一个，得C最多只有一个，因此学生最多只有3人，显然（AC）（BB）（CA）满足条件，故学生最多有3个.故选：B.【点评】本题主要考查了合情推理，关键是找到语句中的关键词，培养了推理论证的能力.二、填空题（共6小题，每小题5分，共30分）9.（5分）复数（）2= ﹣1 .【分析】由复数代数形式的除法运算化简括号内部，然后由虚数单位i的运算性质得答案. 【解答】解：（）2=.故答案为：﹣1.【点评】本题考查了复数代数形式的除法运算，考查了虚数单位i的运算性质，是基础题.10.（5分）已知向量，满足||=1，=（2，1），且+=（λ∈R），则|λ|=. 【分析】设=（x，y）.由于向量，满足||=1，=（2，1），且+=（λ∈R），可得，解出即可.【解答】解：设=（x，y）.∵向量，满足||=1，=（2，1），且+=（λ∈R），∴=λ（x，y）+（2，1）=（λx+2，λy+1），∴，化为λ2=5.解得.故答案为：.【点评】本题考查了向量的坐标运算、向量的模的计算公式、零向量等基础知识与基本技能方法，属于基础题.11.（5分）设双曲线C经过点（2，2），且与﹣x2=1具有相同渐近线，则C的方程为；渐近线方程为 y=±2x .【分析】利用双曲线渐近线之间的关系，利用待定系数法即可得到结论.【解答】解：与﹣x2=1具有相同渐近线的双曲线方程可设为﹣x2=m，（m≠0），∵双曲线C经过点（2，2），∴m=，即双曲线方程为﹣x2=﹣3，即，对应的渐近线方程为y=±2x，故答案为：，y=±2x.【点评】本题主要考查双曲线的性质，利用渐近线之间的关系，利用待定系数法是解决本题的关键，比较基础.12.（5分）若等差数列{an}满足a7+a8+a9＞0，a7+a10＜0，则当n= 8 时，{an}的前n项和最大.【分析】可得等差数列{an}的前8项为正数，从第9项开始为负数，进而可得结论.【解答】解：由等差数列的性质可得a7+a8+a9=3a8＞0，∴a8＞0，又a7+a10=a8+a9＜0，∴a9＜0，∴等差数列{an}的前8项为正数，从第9项开始为负数，∴等差数列{an}的前8项和最大，故答案为：8.【点评】本题考查等差数列的性质和单调性，属中档题.13.（5分）把5件不同产品摆成一排，若产品A与产品B相邻，且产品A与产品C不相邻，则不同的摆法有 36 种.【分析】分3步进行分析：①用捆绑法分析A、B，②计算其中A、B相邻又满足B、C相邻的情况，即将ABC看成一个元素，与其他产品全排列，③在全部数目中将A、B相邻又满足A、C相邻的情况排除即可得答案.【解答】解：先考虑产品A与B相邻，把A、B作为一个元素有种方法，而A、B可交换位置，所以有2=48种摆法，又当A、B相邻又满足A、C相邻，有2=12种摆法，故满足条件的摆法有48﹣12=36种.故答案为：36.【点评】本题考查分步计数原理的应用，要优先分析受到限制的元素，如本题的A、B、C.14.（5分）设函数f（x）=Asin（ωx+φ）（A，ω，φ是常数，A＞0，ω＞0）若f（x）在区间[，]上具有单调性，且f（）=f（）=﹣f（），则f（x）的最小正周期为π .【分析】由f（）=f（）求出函数的一条对称轴，结合f（x）在区间[，]上具有单调性，且f（）=﹣f（）可得函数的半周期，则周期可求.【解答】解：由f（）=f（），可知函数f（x）的一条对称轴为x=，则x=离最近对称轴距离为.又f（）=﹣f（），则f（x）有对称中心（，0），由于f（x）在区间[，]上具有单调性，则≤T⇒T≥，从而=⇒T=π.故答案为：π.【点评】本题考查f（x）=Asin（ωx+φ）型图象的形状，考查了学生灵活处理问题和解决问题的能力，是中档题.三、解答题（共6小题，共80分，解答应写出文字说明、演算步骤或证明过程）15.（13分）如图，在△ABC中，∠B=，AB=8，点D在边BC上，且CD=2，cos∠ADC=.（1）求sin∠BAD；（2）求BD，AC的长.【分析】根据三角形边角之间的关系，结合正弦定理和余弦定理即可得到结论.【解答】解：（1）在△ABC中，∵cos∠ADC=，∴sin∠ADC====，则sin∠BAD=sin（∠ADC﹣∠B）=sin∠ADC•cosB﹣cos∠ADC•sinB=×﹣=.（2）在△ABD中，由正弦定理得BD==，在△ABC中，由余弦定理得AC2=AB2+CB2﹣2AB•BCcosB=82+52﹣2×8×=49，即AC=7.【点评】本题主要考查解三角形的应用，根据正弦定理和余弦定理是解决本题本题的关键，难度不大.16.（13分）李明在10场篮球比赛中的投篮情况统计如下（假设各场比赛相互独立）；场次投篮次数命中次数场次投篮次数命中次数主场1 22 12 客场1 18 8 主场2 15 12 客场2 13 12 主场3 12 8 客场3 21 7 主场4 23 8 客场4 18 15 主场5 24 20 客场5 25 12 （1）从上述比赛中随机选择一场，求李明在该场比赛中投篮命中率超过0.6的概率；（2）从上述比赛中随机选择一个主场和一个客场，求李明的投篮命中率一场超过0.6，一场不超过0.6的概率；（3）记是表中10个命中次数的平均数，从上述比赛中随机选择一场，记X为李明在这场比赛中的命中次数，比较EX与的大小（只需写出结论）.【分析】（1）根据概率公式，找到李明在该场比赛中超过0.6的场次，计算即可，（2）根据互斥事件的概率公式，计算即可.（3）求出平均数和EX，比较即可.【解答】解：（1）设李明在该场比赛中投篮命中率超过0.6为事件A，由题意知，李明在该场比赛中超过0.6的场次有：主场2，主场3，主场5，客场2，客场4，共计5场所以李明在该场比赛中投篮命中率超过0.6的概率P（A）=，（2）设李明的投篮命中率一场超过0.6，一场不超过0.6的概率为事件B，同理可知，李明主场命中率超过0.6的概率，客场命中率超过0.6的概率，故P（B）=P1×（1﹣P2）+P2×（1﹣P1）=；（3）=（12+8+12+12+8+7+8+15+20+12）=11.4EX=【点评】本题主要考查了概率的计算、数学期望，平均数，互斥事件的概率，属于中档题.17.（14分）如图，正方形AMDE的边长为2，B，C分别为AM，MD的中点，在五棱锥P﹣ABCDE中，F为棱PE的中点，平面ABF与棱PD，PC分别交于点G，H.（1）求证：AB∥FG；（2）若PA⊥底面ABCDE，且PA=AE，求直线BC与平面ABF所成角的大小，并求线段PH 的长.【分析】（1）运用线面平行的判定定理和性质定理即可证得；（2）由于PA⊥底面ABCDE，底面AMDE为正方形，建立如图的空间直角坐标系Axyz，分别求出A，B，C，E，P，F，及向量BC的坐标，设平面ABF的法向量为n=（x，y，z），求出一个值，设直线BC与平面ABF所成的角为α，运用sinα=|cos|，求出角α；设H（u，v，w），再设，用λ表示H的坐标，再由n=0，求出λ和H的坐标，再运用空间两点的距离公式求出PH的长.【解答】（1）证明：在正方形AMDE中，∵B是AM的中点，∴AB∥DE，又∵AB⊄平面PDE，∴AB∥平面PDE，∵AB⊂平面ABF，且平面ABF∩平面PDE=FG，∴AB∥FG；（2）解：∵PA⊥底面ABCDE，∴PA⊥AB，PA⊥AE，如图建立空间直角坐标系Axyz，则A（0，0，0），B（1，0，0），C（2，1，0），P（0，0，2），E（0，2，0），F（0，1，1），，设平面ABF的法向量为=（x，y，z），则即，令z=1，则y=﹣1，∴=（0，﹣1，1），设直线BC与平面ABF所成的角为α，则sinα=|cos＜，＞|=||=，∴直线BC与平面ABF所成的角为，设H（u，v，w），∵H在棱PC上，∴可设，即（u，v，w﹣2）=λ（2，1，﹣2），∴u=2λ，v=λ，w=2﹣2λ，∵是平面ABF的法向量，∴=0，即（0，﹣1，1）•（2λ，λ，2﹣2λ）=0，解得λ=，∴H（），∴PH==2.【点评】本题主要考查空间直线与平面的位置关系，考查直线与平面平行、垂直的判定和性质，同时考查直线与平面所成的角的求法，考查运用空间直角坐标系求角和距离，是一道综合题.18.（13分）已知函数f（x）=xcosx﹣sinx，x∈[0，]（1）求证：f（x）≤0；（2）若a＜＜b对x∈（0，）上恒成立，求a的最大值与b的最小值.【分析】（1）求出f′（x）=cosx﹣xsinx﹣cosx=﹣xsinx，判定出在区间∈（0，）上f′（x）=﹣xsinx＜0，得f（x）在区间∈[0，]上单调递减，从而f（x）≤f（0）=0.（2）当x＞0时，“＞a”等价于“sinx﹣ax＞0”，“＜b”等价于“sinx﹣bx＜0”构造函数g（x）=sinx﹣cx，通过求函数的导数讨论参数c求出函数的最值，进一步求出a，b的最值.【解答】解：（1）由f（x）=xcosx﹣sinx得f′（x）=cosx﹣xsinx﹣cosx=﹣xsinx，此在区间∈（0，）上f′（x）=﹣xsinx＜0，所以f（x）在区间∈[0，]上单调递减，从而f（x）≤f（0）=0.（2）当x＞0时，“＞a”等价于“sinx﹣ax＞0”，“＜b”等价于“sinx﹣bx＜0”令g（x）=sinx﹣cx，则g′（x）=cosx﹣c，当c≤0时，g（x）＞0对x∈（0，）上恒成立，当c≥1时，因为对任意x∈（0，），g′（x）=cosx﹣c＜0，所以g（x）在区间[0，]上单调递减，从而，g（x）＜g（0）=0对任意x∈（0，）恒成立，当0＜c＜1时，存在唯一的x0∈（0，）使得g′（x0）=cosx0﹣c=0，g（x）与g′（x）在区间（0，）上的情况如下：x （0，x0） x0 （x0，）g′（x）+ ﹣g（x）↑↓因为g（x）在区间（0，x0）上是增函数，所以g（x0）＞g（0）=0进一步g（x）＞0对任意x∈（0，）恒成立，当且仅当综上所述当且仅当时，g（x）＞0对任意x∈（0，）恒成立，当且仅当c≥1时，g（x）＜0对任意x∈（0，）恒成立，所以若a＜＜b对x∈（0，）上恒成立，则a的最大值为，b的最小值为1 【点评】本题考查利用导数求函数的单调区间；利用导数求函数的最值；考查解决不等式问题常通过构造函数解决函数的最值问题，属于一道综合题.20.（13分）对于数对序列P：（a1，b1），（a2，b2），…，（an，bn），记T1（P）=a1+b1，Tk（P）=bk+max{Tk﹣1（P），a1+a2+…+ak}（2≤k≤n），其中max{Tk﹣1（P），a1+a2+…+ak}表示Tk﹣1（P）和a1+a2+…+ak两个数中最大的数，（Ⅰ）对于数对序列P：（2，5），（4，1），求T1（P），T2（P）的值；（Ⅱ）记m为a，b，c，d四个数中最小的数，对于由两个数对（a，b），（c，d）组成的数对序列P：（a，b），（c，d）和P′：（c，d），（a，b），试分别对m=a和m=d两种情况比较T2（P）和T2（P′）的大小；（Ⅲ）在由五个数对（11，8），（5，2），（16，11），（11，11），（4，6）组成的所有数对序列中，写出一个数对序列P使T5（P）最小，并写出T5（P）的值（只需写出结论）.【分析】（Ⅰ）利用T1（P）=a1+b1，Tk（P）=bk+max{Tk﹣1（P），a1+a2+…+ak}（2≤k≤n），可求T1（P），T2（P）的值；（Ⅱ）T2（P）=max{a+b+d，a+c+d}，T2（P′）=max{c+d+b，c+a+b}，分类讨论，利用新定义，可比较T2（P）和T2（P′）的大小；（Ⅲ）根据新定义，可得结论.【解答】解：（Ⅰ）T1（P）=2+5=7，T2（P）=1+max{T1（P），2+4}=1+max{7，6}=8；（Ⅱ）T2（P）=max{a+b+d，a+c+d}，T2（P′）=max{c+d+b，c+a+b}.当m=a时，T2（P′）=max{c+d+b，c+a+b}=c+d+b，∵a+b+d≤c+d+b，且a+c+d≤c+b+d，∴T2（P）≤T2（P′）；当m=d时，T2（P′）=max{c+d+b，c+a+b}=c+a+b，∵a+b+d≤c+a+b，且a+c+d≤c+a+d，∴T2（P）≤T2（P′）；∴无论m=a和m=d，T2（P）≤T2（P′）；（Ⅲ）数对（4，6），（11，11），（16，11），（11，8），（5，2），T5（P）最小；T1（P）=10，T2（P）=26；T3（P）42，T4（P）=50，T5（P）=52.【点评】本题考查新定义，考查学生分析解决问题的能力，正确理解与运用新定义是解题的关键.19.（14分）已知椭圆C：x2+2y2=4，（1）求椭圆C的离心率（2）设O为原点，若点A在椭圆C上，点B在直线y=2上，且OA⊥OB，求直线AB与圆x2+y2=2的位置关系，并证明你的结论.【分析】（1）化椭圆方程为标准式，求出半长轴和短半轴，结合隐含条件求出半焦距，则椭圆的离心率可求；（2）设出点A，B的坐标分别为（x0，y0），（t，2），其中x0≠0，由OA⊥OB得到，用坐标表示后把t用含有A点的坐标表示，然后分A，B的横坐标相等和不相等写出直线AB的方程，然后由圆x2+y2=2的圆心到AB的距离和圆的半径相等说明直线AB 与圆x2+y2=2相切.【解答】解：（1）由x2+2y2=4，得椭圆C的标准方程为.∴a2=4，b2=2，从而c2=a2﹣b2=2.因此a=2，c=.故椭圆C的离心率e=；（2）直线AB与圆x2+y2=2相切.证明如下：设点A，B的坐标分别为（x0，y0），（t，2），其中x0≠0.∵OA⊥OB，∴，即tx0+2y0=0，解得.当x0=t时，，代入椭圆C的方程，得.故直线AB的方程为x=，圆心O到直线AB的距离d=.此时直线AB与圆x2+y2=2相切.当x0≠t时，直线AB的方程为，即（y0﹣2）x﹣（x0﹣t）y+2x0﹣ty0=0.圆心O到直线AB的距离d=.又，t=.故=.此时直线AB与圆x2+y2=2相切.【点评】本题考查椭圆的简单几何性质，考查了圆与圆锥曲线的综合，训练了由圆心到直线的距离判断直线和圆的位置关系，体现了分类讨论的数学思想方法，考查了计算能力和逻辑思维能力，是压轴题.。

淮安市2024-2025学年度第一学期高三年级第一次调研测试数学试题（答案在最后）2024.11注意事项考生在答题前请认真阅读本注意事项及各题答题要求1.答卷前，考生务必将自己的姓名、准考证号填写在答题卡上.2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案标号.回答非选择题时，将答案写在答题卡上.写在本试卷上无效.3.考试结束后，只要将答题卡交回.一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合{}11M x x =-<<∣，{}220N x x x =->∣，则M N ⋃=（）A.()0,1 B.()1,0-C.()(),12,-∞+∞ D.()(),12,-∞-+∞ 2.若复数z 满足12i2iz -=-（i 为虚数单位），则z 的模z =（）A.1B.5C.D.533.已知等差数列{}n a 的公差为2，且2a ，3a ，6a 成等比数列，则452a a -=（）A.1- B.1C.2D.34.已知幂函数()()2231t f x t t x-=--的图象与y 轴无交点，则t 的值为（）A .2- B.1- C.1D.25.已知函数()()sin 2,f x x x ϕ=+∈R ，则“()00f =”是“函数()f x 为奇函数”的（）A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分又不必要条件6.已知e 是单位向量，a 满足3a e a e +=- ，则a 在e方向上的投影为（）A.12-B.13C.12D.17.在外接圆半径为4的ABC V 中，30ABC ∠=o ，若符合上述条件的三角形有两个，则边AB 的长可能为（）A.2B.3C.4D.58.已知函数()221x f x x =+，正数a ，b 满足()()1f a f b +=，则()22229481a b a b-+的最大值为（）A.124B.112C.16D.14二、选择题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.9.已知,,a b c ∈R ，则下列说法正确的是（）A.若a bc c>，0c <，则a b <B.若0a >，0b >，则a b +≤C.若a b >，0ab >，则11a b>D.若0a >，0b >，0m >，则b m ba m a+>+10.在数列{}n a 和{}n b 中，111a b ==，11n n a a n +-=+*1,n =∈N ，下列说法正确的有（）A.2n b n= B.()()122n n n a ++=C.36是{}n a 与{}n b 的公共项D.11112ni i i b a =++<-∑11.已知函数()2221xx f x x=++，（）A.函数()f x 为单调减函数B.函数()f x 的对称中心为()0,1C.若对0x ∀>，()()f x f x a >-+恒成立，则2a ≤D.函数()π2sin 12g x x ⎛⎫=+⎪⎝⎭，[)(]19,00,19x ∈- 与函数()y f x =的图象所有交点纵坐标之和为20三、填空题：本题共3小题，每小题5分，共15分.12.4log 94214log 3log 223+-=______.13.已知sin cos 5αα+=，则tan2πtan 4αα=⎛⎫+ ⎪⎝⎭______.14.已知函数()cos f x x =，将函数()y f x =图象上各点的横坐标缩短为原来的12，纵坐标不变，再将所得图象上各点向左平移π4个单位长度，得到()y g x =的图象.设函数()()()2h x g x f x =-，若存在x ∈R使()280x m m -+≥成立，则实数m 的取值范围为______.四、解答题：本题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤.15.设A ，B ，C ，D 为平面内的四点，已知()3,1A ，()2,2B -，()1,4C -.（1）若四边形ABCD 为平行四边形，求D 点的坐标；（2）若A ，C ，D 三点共线，18BD AC ⋅=-，求D 点的坐标.16.设()f x 是奇函数，()g x 是偶函数，且()()π4f x g x x ⎛⎫+=+ ⎪⎝⎭.（1）求函数()f x ，()g x 的解析式；（2）设()()π3h x f x g x ⎛⎫=+⋅ ⎪⎝⎭，π0,2x ⎡⎤∈⎢⎥⎣⎦.当()2h x =时，求x 的值.17.在ABC V 中，角A ，B ，C 对应的边分别为a ，b ，c ，且22cos 0c b a C -+=.（1）求A ；（2）如图，过ABC V 外一点P 作PB AB ⊥，PC AC ⊥，PB =，4AC =，求四边形ABPC 的面积.18.已知数列{}n a 的前n 项和为n S ，11a =，24a =，37a =，且()1n n AS n a B +=+.（1）求数列{}n a 的通项公式；（2）若*N k ∈，当k n a =时，n b k =；当1k k a n a +<<时，12k nn b b -=.①求数列{}3k b 的前k 项和k T ；②当1k n a +=时，求证：2212520n k b ka -+-≥.19.已知函数()32f x x ax =-.（1）讨论函数()f x 的单调性；（2）若()ln f x x ≥恒成立.①求实数a 的取值范围；②当a 取最大值时，若12341x x x x +++=（1x ，2x ，3x ，4x 为非负实数），求()()()()12233441x f x x f x x f x x f x +++的最小值.淮安市2024-2025学年度第一学期高三年级第一次调研测试数学试题2024.11注意事项考生在答题前请认真阅读本注意事项及各题答题要求1.答卷前，考生务必将自己的姓名、准考证号填写在答题卡上.2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案标号.回答非选择题时，将答案写在答题卡上.写在本试卷上无效.3.考试结束后，只要将答题卡交回.一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合{}11M x x =-<<∣，{}220N x x x =->∣，则M N ⋃=（）A.()0,1 B.()1,0-C.()(),12,-∞+∞ D.()(),12,-∞-+∞ 【答案】C 【解析】【分析】解不等式可得集合()(),02,N ∞∞=-⋃+，再由并集运算可得结果.【详解】解不等式220x x ->可得()(),02,N ∞∞=-⋃+，又{}()111,1M xx =-<<=-∣，可得()(),12,M N ∞∞⋃=-⋃+.故选：C2.若复数z 满足12i2iz -=-（i 为虚数单位），则z 的模z =（）A.1B.55C.D.53【答案】A 【解析】【分析】根据模长的运算公式以及性质求解即可.【详解】由题意可知：12i 12iz -===-，故选：A.3.已知等差数列{}n a 的公差为2，且2a ，3a ，6a 成等比数列，则452a a -=（）A.1-B.1C.2D.3【答案】D 【解析】【分析】根据等比数列性质利用等差数列通项公式计算可得11a =-，代入计算可得结果.【详解】由2a ，3a ，6a 成等比数列可得2326a a a =，即()()()21114210a a a +=++，解得11a =-，所以可得()()4511122342143a a a d a d a d -=+-+=+=-+=，故选：D.4.已知幂函数()()2231t f x t t x-=--的图象与y 轴无交点，则t 的值为（）A.2- B.1- C.1D.2【答案】B 【解析】【分析】根据幂函数的定义和图象特点可得出关于实数t 的等式与不等式，即可解出t 的值.【详解】因为幂函数()()2231t f x t t x-=--的图象与y 轴无交点，则211230t t t ⎧--=⎨-≤⎩，解得1t =-.故选：B.5.已知函数()()sin 2,f x x x ϕ=+∈R ，则“()00f =”是“函数()f x 为奇函数”的（）A .充要条件B.充分不必要条件C.必要不充分条件D.既不充分又不必要条件【答案】A 【解析】【分析】结合正弦函数的奇偶性以及充要条件的定义判断即可.【详解】若()00f =，则sin 0ϕ=，则πk ϕ=，Z k ∈，所以()()sin 2πsin2f x x k x =+=±，则()f x 为奇函数.若()f x 为奇函数，则一定有()00f =.则“()00f =”是“函数()f x 为奇函数”的充要条件.故选：A.6.已知e 是单位向量，a 满足3a e a e +=- ，则a 在e方向上的投影为（）A.12-B.13C.12D.1【答案】D 【解析】【分析】根据向量数量积运算公式，求得a 在e方向上的投影，进而可得投影.【详解】3a e a e +=- ，2222269a a e e a a e e ∴+⋅+=-⋅+，88a e ∴⋅=，即1a e ⋅= ，a 在e 上投影向量2||a e e e e ⋅=，所以a 在e 方向上的投影为1.故选：D.7.在外接圆半径为4的ABC V 中，30ABC ∠=o ，若符合上述条件的三角形有两个，则边AB 的长可能为（）A.2B.3C.4D.5【答案】D 【解析】【分析】根据给定条件，由三角形有两解的条件，结合正弦定理求出边AB 的范围.【详解】在ABC V 中，30ABC ∠=o ，由ABC V 有两解，得30150C << ，且90C ≠ ，则1sin 12C <<，由ABC V 外接圆半径为4及正弦定理，得8sin (4,8)AB C =∈，所以边AB 的长可能为5.故选：D8.已知函数()221x f x x =+，正数a ，b 满足()()1f a f b +=，则()22229481a b a b-+的最大值为（）A.124B.112C.16D.14【答案】B 【解析】【分析】方法一：根据()()1f a f b +=可得1ab =，再由基本不等式计算可得结果；方法二：由函数解析式可得()11f a f a ⎛⎫+= ⎪⎝⎭，再由单调性可得1ab =，利用基本不等式计算可得结果.【详解】方法一：由()()1f a f b +=可得222222211111111a b b a b b b=-==++++，易知()2111f x x=-+在()0,∞+上单调递增，因此可得1a b =，即1ab =；又()222222292929136481481(29)362929aba b a b a b a b a b a b a b---===++-+-+-要求()22229481a ba b-+的最大值，只需考虑290a b ->即可，因此1136122929a b a b≤=-+-，当且仅当)311,23a b +-==时，等号成立；故选：B.方法二：()()1f a f b +=，而()11f a f a ⎛⎫+= ⎪⎝⎭，所以()1f b f a ⎛⎫= ⎪⎝⎭；而()2111f x x =-+在()0,∞+上单调递增，所以1b a=，即1ab =，因此原式2222929481(29)36a b a ba b a b --==+-+，要求其最大值，只需考察290a b ->可得原式1136122929a b a b=≤=-+-，当且仅当2961a b ab -=⎧⎨=⎩时，即)311,23a b ==时等号成立；故选：B.二、选择题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.9.已知,,a b c ∈R ，则下列说法正确的是（）A.若a bc c>，0c <，则a b <B.若0a >，0b >，则a b +≤C.若a b >，0ab >，则11a b>D.若0a >，0b >，0m >，则b m ba m a+>+【答案】AB 【解析】【分析】利用作差法可判断A ，利用不等式222ab a b ≤+可判断B ，利用特殊值法可判断C 、D.【详解】由a b c c >，得0a b c c->，即0a bc ->，又0c <，则0a b -<，即a b <，故A 正确；因为222ab a b ≤+，所以()222222ab a b a b ++≤+，即()()2222a b a b +≤+，又因为0a >，0b >，所以a b +≤B 正确；假设1a =-，2b =-，满足0ab >，a b >，此时11a =-，112b =-，11a b >不成立，故C 错误；假设1a =，1b =，1m =，满足0a >，0b >，0m >，此时1b m a m +=+，1b a =，b m ba m a+>+不成立，故D 错误；故选：AB.10.在数列{}n a 和{}n b 中，111a b ==，11n n a a n +-=+*1,n =∈N ，下列说法正确的有（）A .2n b n= B.()()122n n n a ++=C.36是{}n a 与{}n b 的公共项D.11112ni i i b a =++<-∑【答案】ACD 【解析】【分析】A：根据等差数列定义求的通项公式，则n b 可求；B ：累加法求{}na 的通项公式；C ：根据通项公式计算并判断；D ：采用裂项相消法求和并证明.【详解】对于A：因为*1,n =∈N，所以是以1为首项，1为公差的等差数列，()111n n =+-⨯=，所以2n b n =，故正确；对于B ：因为()*213212,3,,2,n n a a a a a a n n n --=-=⋅⋅⋅-=≥∈N ，所以123n a n a =+-++ ，所以()()112322n n n a n n +=+++⋅⋅⋅+=≥，当1n =时，11a =符合条件，所以()12n n n a +=，故错误；对于C ：令()1362n n +=，解得8n =(负值舍去)，所以836a =，令236n =，解得6n =(负值舍去)，所以66b =，所以86a b =，即36是{}n a 与{}n b 的公共项，故正确；对于D ：因为()()()2111111212112n n n n b a n n n ++⎛⎫==- ⎪++-+⎝⎭+-，所以11111111112121222311ni i i b a n n n =++⎛⎫⎛⎫=-+-+⋅⋅⋅+-=-< ⎪ ⎪-++⎝⎭⎝⎭∑，故正确；故选：ACD.11.已知函数()2221xx f x x=++，（）A.函数()f x 为单调减函数B.函数()f x 的对称中心为()0,1C.若对0x ∀>，()()f x f x a >-+恒成立，则2a ≤D.函数()π2sin 12g x x ⎛⎫=+ ⎪⎝⎭，[)(]19,00,19x ∈- 与函数()y f x =的图象所有交点纵坐标之和为20【答案】BCD 【解析】【分析】去绝对值分类讨论可得函数解析式，易知()f x 在0,+∞以及(),0∞-上是分别单调递减的，即A 错误，易知()f x 满足()()2f x f x -+=，可知B 正确，再利用函数单调性以及不等式恒成立计算可得C 正确，画出两函数在同一坐标系下的图象根据周期性计算可得D 正确.【详解】对于A ，易知当0x >时，()2221x f x =++，0x <时()2221x f x =-+，因此可得()f x 在0,+∞以及(),0∞-上分别为单调递减函数，即A 错误；对于B ，易知函数()f x 满足()()2222121x xf x f x --+=+=++，因此可得()f x 关于0,1对称，即B 正确；对于C ，由()()f x f x a >-+，即()22f x a >+，即()12a f x >+在0x >时恒成立，易知()22221xf x =+>+在0,+∞上恒成立，所以可得212a≥+，解得2a ≤，即C 正确；对于D,画出函数()f x 以及π2sin 12y x ⎛⎫=+⎪⎝⎭的图象如下图所示：易知()π2sin 12g x x ⎛⎫=+⎪⎝⎭也关于0,1对称，()g x 的周期为4，一个周期与()f x 有两个交点，5个周期有10个交点，()f x 与()g x 在[)(]19,00,19-⋃共20个交点，即20110220ii y==⨯=∑，故D 正确，故选：BCD.【点睛】关键点点睛：本题关键在于根据函数()f x 以及()π2sin 12g x x ⎛⎫=+ ⎪⎝⎭都关于0,1成中心对称，再由函数周期性计算可得结果.三、填空题：本题共3小题，每小题5分，共15分.12.4log 94214log 3log 223+-=______.【答案】2-【解析】【分析】应用对数运算律化简求值即可.【详解】2log 342444144log 3log 2log 3log 3log 43132233+-=+-=-=-=-.故答案为：−213.已知sin cos 5αα+=，则tan2πtan 4αα=⎛⎫+ ⎪⎝⎭______.【答案】4-【解析】【分析】利用恒等变换公式以及商数关系进行化简并计算.【详解】因为()()cos sin sin2sin2sin21tan tan2cos cos21tan πcos sin cos21tan tan cos21tan 4cos αααααααααααααααααα-⎛⎫ ⎪-⎝⎭===+++⎛⎫⎛⎫+ ⎪⎪-⎝⎭⎝⎭()()()()222sin2cos sin sin2sin25sin21cos sin cos sin cos sin 5αααααααααααα-====-++，而()21sin cos 1sin25ααα+=+=，所以4sin25α=-，5sin24α=-，故答案为：4-.14.已知函数()cos f x x =，将函数()y f x =图象上各点的横坐标缩短为原来的12，纵坐标不变，再将所得图象上各点向左平移π4个单位长度，得到()y g x =的图象.设函数()()()2h x g x f x =-，若存在x ∈R使()280x m m -+≥成立，则实数m 的取值范围为______.【答案】[]1,9-【解析】【分析】求得函数()g x 的解析式，进而求得ℎ的解析式，利用导数求得ℎ的最大值.【详解】将函数=图象上各点的横坐标缩短为原来的12得到函数()2cos2f x x =的图象，再将所得图象上各点向左平移π4个单位长度，得到ππ2cos244f x x ⎡⎤⎛⎫⎛⎫+=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，所以()πcos2sin24g x x x ⎛⎫=+=- ⎪⎝⎭，()sin22cos h x x x =--，可得ℎ周期为2π，()2cos22sin 0h x x x =-+='，所以22(12sin )2sin 0x x --+=，所以1sin 2x =或sin 1x =-，解得π6x =或5π6或3π2，当π0,6x ⎛⎫∈ ⎪⎝⎭，ℎ′<0，所以ℎ在π0,6⎛⎫ ⎪⎝⎭单调递减，当π5,π66x ⎛⎫∈⎪⎝⎭，ℎ′>0，所以ℎ在π5,π66⎛⎫⎪⎝⎭单调递增，当53π,π62x ⎛⎫∈⎪⎝⎭，ℎ′<0，所以ℎ在53π,π62⎛⎫⎪⎝⎭单调递减，当3π,2π2x ⎛⎫∈⎪⎝⎭，ℎ′，所以ℎ在3π,2π2⎛⎫⎪⎝⎭单调递增，()02h =-，5π62h ⎛⎫= ⎪⎝⎭，()2π2h =-，max()2h x =，因为存在∈使()280x m m -+≥成立，所以2980m m -+≥所以19m -≤≤，所以实数m 的取值范围为[1,9]-.故答案为：[1,9]-.四、解答题：本题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤.15.设A ，B ，C ，D 为平面内的四点，已知()3,1A ，()2,2B -，()1,4C -.（1）若四边形ABCD 为平行四边形，求D 点的坐标；（2）若A ，C ，D 三点共线，18BD AC ⋅=-，求D 点的坐标.【答案】（1）()4,3D（2）118,55D ⎛⎫⎪⎝⎭【解析】【分析】（1）设(),D x y ，利用BC AD =，可求D 点的坐标；（2）利用三点共线，可得AD AC λ=，可得()34,13D λλ-+，利用数量积可求D 点的坐标.【小问1详解】因为()3,1A ，()2,2B -，()1,4C -，所以()1,2BC =，因为四边形ABCD 为平行四边形，所以BC AD =，设(),D x y ，所以()3,1AD x y =--，所以314123x x y y ⎧-==⎧⇒⎨⎨-==⎩⎩，所以()4,3D 【小问2详解】因为A ，C ，D 三点共线，()4,3AC =-，所以设()()4,34,3AD AC λλλλ==-=-，又()3,1A ，所以()34,13D λλ-+，所以()54,31BD λλ=--，又()()1454331185BD AC λλλ⋅=--+-=-⇒=所以118,55D ⎛⎫⎪⎝⎭.16.设()f x 是奇函数，()g x 是偶函数，且()()π4f x g x x ⎛⎫+=+ ⎪⎝⎭.（1）求函数()f x ，()g x 的解析式；（2）设()()π3h x f x g x ⎛⎫=+⋅ ⎪⎝⎭，π0,2x ⎡⎤∈⎢⎥⎣⎦.当()2h x =时，求x 的值.【答案】（1）()()sin ,cos f x x g x x ==（2）0x =或π6x =【解析】【分析】（1）根据条件，利用正、余弦函数的奇偶性，得到()()sin cos f x g x x x +=+，()()sin cos f x g x x x -+=-+，联立即可求解；（2）利用正弦的和角公式、倍角公式及辅助角公式，得到1π()sin 2234h x x ⎛⎫=++⎪⎝⎭，结合条件得到πsin 232x ⎛⎫+=⎪⎝⎭，再利用特殊角的三角函数值，即可求解.【小问1详解】因为()()π)sin cos 4f xg x x x x +=+=+①，()f x 为奇函数，()g x 为偶函数，()()()()sin cos f x g x x x ∴-+-=-+-，即()()sin cos f x g x x x -+=-+②，联立①②，解得()sin f x x =，()cos g x x =.【小问2详解】因为()2π1sin cos sin cos cos 322h x x x x x x ⎛⎫=+⋅=+ ⎪⎝⎭()11πsin21cos2sin 244234x x x ⎛⎫=++=++ ⎪⎝⎭，当()2h x =时，1ππsin 2sin 2234232x x ⎛⎫⎛⎫++=⇒+=⎪ ⎪⎝⎭⎝⎭02x π≤≤，ππ4π2333x ∴≤+≤，ππ233x ∴+=或2π3，0x ∴=或π6x =.17.在ABC V 中，角A ，B ，C 对应的边分别为a ，b ，c ，且22cos 0c b a C -+=.（1）求A ；（2）如图，过ABC V 外一点P 作PB AB ⊥，PC AC ⊥，PB =4AC =，求四边形ABPC 的面积.【答案】（1）π3（2）1332【解析】【分析】（1）根据正弦定理及两角和的正弦公式求解；（2）解法一：连接AP ，设θ∠=CAP ，由条件求得即tan θ，求出CP ，AP ，AB ，由ABPC ABP ACP S S S =+△△计算即可；解法二：延长CP ，AB 交于点Q ，则π6Q ∠=，求出BQ ，CQ ，由ABPC ACQ PBQ S S S =-△△计算即可.【小问1详解】∵22cos 0c b a C -+=，∴根据正弦定理得sin 2sin 2sin cos 0C B A C -+=，∴()sin 2sin 2sin cos 0C A C A C -++=，∴sin 2sin cos 2cos sin 2sin cos 0C A C A C A C --+=，sin 2cos sin C A C ∴=，sin 0C > ，1cos 2A ∴=，0πA << ，π3A ∴=.【小问2详解】解法一：连接AP ，设θ∠=CAP ，在Rt ACP 和Rt ABP 中，cos sin π3BP AP ACθθ==⎛⎫- ⎪⎝⎭，即43433tan cos cos 231sin cos sin 322πθθθθθθ=⇒==⎛⎫-- ⎪⎝⎭，3432CP ∴=⨯=，27AP =，5AB ∴=，∴四边形ABPC 的面积1135343222ABPC ABP ACP S S S =+=⨯⨯⨯△△.解法二：延长CP ，AB 交于点Q，π3A =Q ，PC AC ⊥，6πQ ∴∠=，3= PB ，33πtan 6BQ ∴==，4AC = ，43πtan 6CQ ∴==，∴四边形ABPC 的面积1134333222ABPC ACQ PBQ S S S =-=⨯⨯⨯⨯△△.18.已知数列{}n a 的前n 项和为n S ，11a =，24a =，37a =，且()1n n AS n a B +=+.（1）求数列{}n a 的通项公式；（2）若*N k ∈，当k n a =时，n b k =；当1k k a n a +<<时，12k nn b b -=.①求数列{}3k b 的前k 项和k T ；②当1k n a +=时，求证：2212520n k b ka -+-≥.【答案】（1）32n a n =-（2）①()131449k k k T +-⋅+=②证明见解析【解析】【分析】（1）根据已知条件赋值法列方程组计算求出,A B ,再应用1n n n a S S -=-，化简得出23n a n+=进而得出n a 即可；（2）①由12k nn b b -=得出34k k b k =⋅再应用错位相减法即可求解；②构造数列22522(31)n n c n =⋅-⋅+再根据数列单调性即可证明不等式.【小问1详解】在()1n n AS n a B +=+中，分别令()421,25272A B A n A B B =+⎧=⎧=⇒⇒⎨⎨=+=-⎩⎩()122n n S n a +∴=-，当2n ≥时，()()1212n n S n a -=--，两式相减得出()1212n n n a na n a +=---，()()1122n n na n a n +∴-+=≥，1n =也满足上式()*111112,211n n n n a a na n a n n n n n ++⎛⎫∴-+=∈⇒-=- ⎪++⎝⎭N *122,1n n a a n n n+++⇒=∈+N 2n a n +⎧⎫∴⎨⎬⎩⎭为常数列，2332n n a a n n +=⇒=-【小问2详解】①当32n k =-时，n b k =，当3231k n k -<<+时，12k nn b b -=32n k ∴=-时，23n n b +=，31332312k k k k k b b b b ---==312k k b k -∴=⋅，34kk b k =⋅()1213631424144k k k k T b b b k k -∴=+++=⋅+⋅++-⋅+⋅ ，()()23114142424144k k k k T k k k -+∴=⋅+⋅++-⋅+-⋅+⋅ ，两式相减得出()()1231141413443444444143k k k k k k k T k k +++--⋅--=++++-⋅=-⋅=- ()131449k kk T +-⋅+∴=②131k n a k +==+，2312kn k b b k --==⋅222212522522(31)2522(31)k k n k b ka k k k k k -+⎡⎤∴-=⋅-⋅+=⋅-⋅+⎣⎦令22522(31)n n c n =⋅-⋅+，12212522(34)2522(31)n n n n c c n n ++-=⋅-⋅+-⋅+⋅+()252665n nn d =⋅-+=()()112526611252665252360n n n n n d d n n ++-=⋅-+-⋅++=⋅->{}n d ∴在*N n ∈上单调递增，注意到12n ≤≤时，10n n n d c c +=-<，当3n ≥时，10n n n d c c +=->，123c c c ∴>>且345c c c <<<30n c c ∴≥=，22522(31)0k k c k ∴=⋅-⋅+≥2212520n k b ka -+∴-≥.【点睛】关键点点睛：解题的关键点是构造数列结合数列的单调性得出22522(31)0k k c k =⋅-⋅+≥即可得证.19.已知函数()32f x x ax =-.（1）讨论函数()f x 的单调性；（2）若()ln f x x ≥恒成立.①求实数a 的取值范围；②当a 取最大值时，若12341x x x x +++=（1x ，2x ，3x ，4x 为非负实数），求()()()()12233441x f x x f x x f x x f x +++的最小值.【答案】（1）答案见解析（2）①(],1-∞②116-【解析】【分析】（1）分0,0,0a a a =><三种情况讨论再应用导函数正负判断函数单调性；（2）①把恒成立问题转化为最值问题，应用导数求出函数min ()1g x =得解；②先构造函数()()321144F x f x x x x x =+=-+根据函数单调性得出()()()()()122334411223341414x f x x f x x f x x f x x x x x x x x x +++≥-+++再结合基本不等式求解.【小问1详解】()()23232f x x ax x a x-='=-当0a =时，()230f x x '=≥，()f x \在R 上单调递增当0a <时，()f x 的单调增区间为2,3a ⎛⎫-∞ ⎪⎝⎭，()0,∞+，()f x 的单调减区间为2a,03⎛⎫ ⎪⎝⎭当0a >时，()f x 的单调增区间为(),0-∞，2,3a ⎛⎫+∞ ⎪⎝⎭；单调减区间为20,3a ⎛⎫ ⎪⎝⎭【小问2详解】①由32ln x ax x -≥恒成立322min minln ln x x x a x x x ⎛⎫-⎛⎫⇒≤=- ⎪ ⎪⎝⎭⎝⎭令()2ln x g x x x =-，()3432ln 2ln 11x x x x x g x x x +='--=-令()32ln 1x x x ϕ=+-，()x ϕ在()0,∞+上单调递增注意到()10ϕ=，∴当01x <<时，()0x ϕ<，()0g x '<，()g x 单调递减；当1x >时，()0x ϕ>，()0g x '>，()g x 单调递增，()min ()11g x g ∴==，1a ∴≤，实数a 的取值范围为(],1-∞.②当a 取最大值时，1a =，12340,,,1x x x x ≤≤()32f x x x =-，()232f x x x '=-，()f x 在11,28⎛⎫- ⎪⎝⎭处的切线，1311244k f ⎛⎫==-=- ⎪⎝⎭'，构造()()321144F x f x x x x x =+=-+，()()()2221611128132444x x x x F x x x '---+=-+==()f x 在10,6⎛⎫ ⎪⎝⎭上单调递增；11,62⎛⎫ ⎪⎝⎭上单调递减；1,12⎛⎫ ⎪⎝⎭上单调递增注意到()00F =，102F ⎛⎫= ⎪⎝⎭，()0F x ∴≥对[]0,1x ∀∈恒成立()()()()()()()()1112122223233334344441141144114411441144fx x x f x x x f x x x f x x x f x x x f x x x f x x x f x x x ⎧⎧≥-≥-⎪⎪⎪⎪⎪⎪≥-≥-⎪⎪∴⇒⎨⎨⎪⎪≥-≥-⎪⎪⎪⎪⎪⎪≥-≥-⎩⎩()()()()()122334411223341414x f x x f x x f x x f x x x x x x x x x ∴+++≥-+++()()132414x x x x =-++而()()212341324124x x x x x x x x +++⎛⎫++≤= ⎪⎝⎭当且仅当1324x x x x +=+时取“=”，()()()()122334*********x f x x f x x f x x f x ∴+++≥-⨯=-当1234121200x x x x ⎧=⎪⎪⎪=⎨⎪=⎪⎪=⎩时可取“=”，综上：()()()()12233441min 116x f x x f x x f x x f x ⎡⎤+++=-⎣⎦.【点睛】关键点点睛：解题的关键点是构造函数()()321144F x f x x x x x =+=-+根据函数的单调性结合基本不等式即可求解.。

2023~2024学年度第一学期高三年级期末调研测试数学试卷 2024.1总分：150分 时间：120分钟注意事项：1．答卷前，考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

3．考试结束后，将答题卡交回。

一、选择题：本题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知(1+i)i z =，则复数z 的虚部为 A ．12B ．12−C ．1i 2D ．1i 2−2．已知集合1{|,}2S x x k k ==−∈Z ，1{|2,}2T x x k k ==+∈Z ，则ST =A ．SB ．TC ．ZD ．∅3．随机变量X ~2(2,)N σ，若()1.5P X m =≤，()2 2.513P X m =−≤≤，则()2.5P X =≤ A ．0.25B ．0.5C ．0.75D ．0.854．图1是蜂房正对着蜜蜂巢穴开口的截面图，它是由许多个正六边形互相紧挨在一起构成．可以看出蜂房的底部是由三个大小相同的菱形组成，且这三个菱形不在一个平面上．研究表明蜂房底部的菱形相似于菱形十二面体的表面菱形，图2是一个菱形十二面体，它是由十二个相同的菱形围成的几何体，也可以看作正方体的各个正方形面上扣上一个正四棱锥（如图3），且平面ABCD 与平面ATBS 的夹角为45︒，则cos ASB ∠=图1 图2 图3A ．22B ．32 C ．13D ．223S ABC DT5．某学校广播站有6个节目准备分2天播出，每天播出3个，其中学习经验介绍和新闻报道两个节目必须在第一天播出，谈话节目必须在第二天播出，则不同的播出方案共有 上的中线，则AD BE ⋅的值为．2−26(2ln 2)e c −=．b c a << 要求。

江苏省淮阴中学、姜堰中学等三校2024届高三上学期12月数学试题一、单项选择题（本大题共8小题，每小题5分，共40分.）1.设集合{}2log 1M x x =>，303x N x x +⎧⎫=<⎨⎬-⎩⎭，则M N ⋂=（）A.[)2,3 B.()2,3 C.()2,+∞ D.()1,+∞2.设m ∈R ，则“2m =”是“直线1:210l mx y +-=与直线()2:3110l x m y +++=”平行的（）条件A.充分不必要B.必要不充分C.充要D.既不充分又不必要3.(sin 40tan10=（）A.2B.－2C.1D.－14.已知{}n a 为等比数列，n S 为数列{}n a 的前n 项和，122n n a S +=+，则5a 的值为（）A.18B.54C.162D.4865.在ABC 中，点D 为BC 边中点，点E 在线段AC 上，且2AE EC =，若AD a = ，BE b = ，则AB为（）A.1324a b - B.1223a b+C.1324a b+D.1223a b -6.设1F ，2F 分别是椭圆()2222:10x y C a b a b+=>>的左、右焦点，过2F 作x 轴的垂线与椭圆C 交于A ，B 两点，若1ABF 为钝角三角形，则离心率的取值范围为（）A.01e <<-B.11e -<< C.112e << D.102e <<7.魏晋时期刘徽撰写的《海岛算经》是关于测量的数学著作，其中第一题是测量海岛的高.如图1，点E ，H ，G 在水平线AC 上，DE 和FG 是两个垂直于水平面且等高的测量标杆的高度，称为“表高”，EG 称为“表距”，GC 和EH 都称为“表目距”，GC 与EH 的差称为“表目距的差”，则海岛的高AB ⨯=+表高表距表高表目距的差，某同学受此法的启发设计了另一种测量此山高度的方案（如图2）；他站在水平线AC 上，同时在水平线AC 上放一个小镜子（视为点P ），他在距离镜子a 米点Q 时，通过镜子看到了山顶，然后沿水平线AC 向靠近山的方向走了m 米，到达M 点，再将镜子放在距离自己b 米的前方点N 处，此时又看到了山顶，若此人的眼睛到水平线AC 的距离为h 米，则此山的高度约为（）米A.mhh a b+- B.mhh a b-- C.hmh a b-- D.hmh a b+-8.设tan 0.21a =，ln1.21b =，21121c =，则下列大小关系正确的是（）A.a b c<< B.a c b<< C.c b a<< D.c<a<b二、多项选择题（本大题共4小题，每小题5分，共20分.）9.已知0a >，0b >，且1a b +=，下列说法正确的是（）A.114a b+≤ B.2212a b +≥C.122a b -<D.+≤10.已知复数1z ，2z ，则下列命题成立的有（）A.若1212z z z z +=-，则120z z = B.11,Z nnz z n =∈C.若22120z z +=，则12=z z D.1212z z z z ⋅=⋅11.已知函数()()πsin 06f x x ωω⎛⎫=+> ⎪⎝⎭在[]0,2π有且仅有4个零点，则下列各选项正确的是（）A.()f x 在区间π0,6⎛⎫⎪⎝⎭单调递增 B.ω的取值范围是2329,1212⎡⎫⎪⎢⎣⎭C.()f x 在区间()0,2π有2个极小值点D.()f x 在区间()0,2π有3个极大值点12.已知函数()f x ，()g x 的定义域均为R ，()g x '为()g x 的导函数，且()()1f x g x +'=，()()43f x g x -'-=，若()g x 为奇函数，则（）A.()22f = B.()()042g g ''+=- C.()()13f f -=- D.()()44g g ''-=三、填空题（本大题共4小题，每小题5分，共20分）13.已知()1,a x = ，()1,b x =- ，若2a b - 与a 垂直，则实数x =____________.14.已知直线l 满足：原点到它的距离为2，点()3,0到它的距离为，请写出满足条件的直线l 的一个方程：______________.15.当实数0a ≠时，函数()()1e xf x x a x =--有且只有一个可导极值点，则实数a 的取值范围为________.16.已知[]x 为不超过x 的最大整数，例如[]0.20=，[]1.21=，[]0.51-=-，设等差数列{}n a 的前n 项和为()12n n nS a =+且515S =，记[]2log n n b a =，则数列{}n b 的前100项和为__________.四、解答题（本大题共6小题，共70分.解答时应写出文字说明、证明过程或演算步骤）17.已知π(sin(),1)4a x =+ ，2)b x = .（1）当π[0,]4x ∈，5a =时，求7πsin()12x +；（2）若()f x a b =⋅，求()f x 的值域.18.已知圆T 经过()4,0A ，()2,4B ，()5,3C .（1）求圆T 的方程；（2）过点71,3P ⎛⎫⎪⎝⎭的直线l 交圆T 于M 、N 两点，且2MP PN = ，求直线l 的方程.19.在ABC 中，内角A ，B ，C 的对边分别是a ，b ，c ，已知2c =，且12cos 2a Bb =+.（1）求ABC 周长的最大值；（2）若()sin sin 2sin 2C B A A +-=，且a b <，求角A.20.已知数列{}n a 满足13a =，当()*2N n n ≥∈时，()111nn na n a-=++.（1）求{}n a 的通项公式；（2）求数列πsin2n n a ⎧⎫⎨⎬⎩⎭的前n 项和n T .21.已知函数()()e0xf x ax a =≠，()2g x x =-.（1）求()f x 的单调区间；（2）当0x >时，()f x 与()g x 有公切线，求实数a 的取值范围.22.已知椭圆()2222:10x y C a b a b+=>>的一条准线方程为4x =，长轴长为4，过点()2,1P -作直线l 交椭圆C 于点M 、N .（1）求椭圆C 的方程；（2）在x 轴上是否存在一定点Q ，使得直线QM ，QN 的斜率1k ，2k 满足1211k k +为常数？若存在，求出Q 点坐标；若不存在，说明理由.2023~2024学年度第一学期阶段性测试高三数学试题一、单项选择题（本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的）1.设集合{}2log 1M x x =>，303x N x x +⎧⎫=<⎨⎬-⎩⎭，则M N ⋂=（）A.[)2,3 B.()2,3 C.()2,+∞ D.()1,+∞【答案】B 【解析】【分析】解不等式化简集合A ，B ，再利用交集的定义求解即得.【详解】依题意，22{|log log 2}{|2}Mx x x x =>=>，{|(3)(3)0}{|33}N x x x x x =+-<=-<<，解得(2,3)M N = .故选：B2.设m ∈R ，则“2m =”是“直线1:210l mx y +-=与直线()2:3110l x m y +++=”平行的（）条件A.充分不必要B.必要不充分C.充要D.既不充分又不必要【答案】C 【解析】【分析】根据充分条件和必要条件的定义，结合两直线平行的条件分析判断.【详解】当2m=时，直线1:2210l x y +-=，直线2:3310l x y ++=，此时221331-=≠，所以直线1l ‖2l ，当1l ‖2l 时，21(10)311m m m -=≠+≠+，得(1)61210m m m m +=⎧⎪+≠-⎨⎪+≠⎩，解得2m =，所以“2m=”是“直线1:210l mx y +-=与直线()2:3110l x m y +++=”平行的充要条件，故选：C3.(sin 40tan10= （）A.2B.－2C.1D.－1【答案】D 【解析】【分析】利用切化弦，三角恒等变换，逆用两角差的正弦公式，二倍角公式，诱导公式化简求值.【详解】(sin 40tan10sin10=sin40(cos10sin 4012(sin10)22sin 40cos102(cos 60sin10sin 60cos10)sin 40cos102sin(1060)sin 40cos102sin 50sin 40cos102sin ︒︒⋅︒=︒︒=︒⋅︒︒⋅︒-︒⋅︒=︒⋅︒︒-︒=︒⋅︒-︒=︒⋅︒-=⋅ 40cos 40cos10sin 80cos101︒⋅︒︒-︒=︒=-故选:D4.已知{}n a 为等比数列，n S 为数列{}n a 的前n 项和，122n n a S +=+，则5a 的值为（）A.18B.54C.162D.486【答案】C 【解析】【分析】由题意对所给的递推关系式进行赋值，得到关于1,a q 的方程组，从而利用等比数列的通项公式即可得解.【详解】因为122n n a S +=+，{}n a 为等比数列，设其公比为q ，当1n=时，2122a a =+，即1122a q a =+，当2n =时，()31222a a a =++，即()211122a q a a q =++，联立()1121112222a q a a q a a q =+⎧⎨=++⎩，解得12,3a q ==（0q =舍去），则445123162a a q ==⨯=.故选：C.5.在ABC 中，点D 为BC 边中点，点E 在线段AC 上，且2AE EC =，若AD a = ，BEb = ，则AB为（）A.1324a b -B.1223a b +C.1324a b +D.1223a b -【答案】A 【解析】【分析】先以,AB AC 为基底表示出AD 和BE，然后消去AC 可得.【详解】因为点D 为BC 边中点，2AE EC =，所以()1213AD AB AC BE AE AB AC AB ⎧=+⎪⎪⎨⎪=-=-⎪⎩，消去AC 得234AD BE AB -= ，即13132424AB AD BE a b =-=-.故选：A.6.设1F ，2F 分别是椭圆()2222:10x y C a b a b+=>>的左、右焦点，过2F 作x 轴的垂线与椭圆C 交于A ，B 两点，若1ABF 为钝角三角形，则离心率e 的取值范围为（）A.01e <<B.11e -<< C.112e << D.102e <<【答案】A 【解析】【分析】根据题意，得到212b F F a<，得到2220c ac a +-<，转化为2210e e +-<，进而求得椭圆C 的离心率的取值范围.【详解】由1F ，2F 分别是椭圆2222:1x y C a b+=的左、右焦点，过2F 作x 轴的垂线与椭圆C 交于,A B 两点，可得22b AB a=，即22b AF a=，因为1ABF 为钝角三角形，则1245AF F ∠>︒，可得212b F F a <，即22b c a<，即22b ac >，又因为222b a c =-，可得222a c ac ->，即2220c ac a +-<，即2210e e +-<，且01e <<，解得01e <<-，即椭圆C 的离心率的取值范围为1)-.故选：A.7.魏晋时期刘徽撰写的《海岛算经》是关于测量的数学著作，其中第一题是测量海岛的高.如图1，点E ，H ，G 在水平线AC 上，DE 和FG 是两个垂直于水平面且等高的测量标杆的高度，称为“表高”，EG 称为“表距”，GC 和EH 都称为“表目距”，GC 与EH 的差称为“表目距的差”，则海岛的高AB ⨯=+表高表距表高表目距的差，某同学受此法的启发设计了另一种测量此山高度的方案（如图2）；他站在水平线AC 上，同时在水平线AC 上放一个小镜子（视为点P ），他在距离镜子a 米点Q 时，通过镜子看到了山顶，然后沿水平线AC 向靠近山的方向走了m 米，到达M 点，再将镜子放在距离自己b 米的前方点N 处，此时又看到了山顶，若此人的眼睛到水平线AC 的距离为h 米，则此山的高度约为（）米A.mhh a b+- B.mhh a b-- C.hmh a b-- D.hmh a b+-【答案】B 【解析】【分析】利用三角形相似得到线段比，从而转化得解.【详解】记此人的眼睛在,M Q 处的位置分别为,D E ，如图，由题意可知ABN MDN ∽，ABP QEP ∽，所以AB ANMD MN=，AB APQE PQ=，又DM EQ h ==，MQ m =，,PQ a MN b ==，所以AB ANh b=，AB AP h a =，则b AB AN h ⋅=，a ABAP h⋅=，因为AP AN PN MP MN m a b -==+=-+，所以a AB b AB m a b h h ⋅⋅-=-+，解得mhAB ha b=--.故选：B.8.设tan 0.21a=，ln1.21b =，21121c =，则下列大小关系正确的是（）A.a b c<< B.a c b<< C.c b a<< D.c<a<b 【答案】C 【解析】【分析】首先通过构造函数得到当π02x <<时，tan x x >，再通过构造函数()()πln 1,02f x x x x =-+<<进一步得到()ln 1x x >+，π0,2x ⎡⎤∈⎢⎥⎣⎦，由此即可比较,a b ，通过构造函数()()ln 1,01x g x x x x=+->+即可比较,c b ，由此即可得解.【详解】设()πtan ,02h x x x x =-<<，则()()22cos cos sin sin 1π110,0cos cos 2x x x x h x x x x ⋅--'=-=-><<，所以()tan hx x x =-在π0,2⎛⎫⎪⎝⎭上单调递增，所以()()tan 00hx x x g =->=，即πtan ,02x x x ><<，令()()πln 1,02f x x x x =-+<<，则()11011x f x x x'=-=>++，所以()()ln 1f x x x =-+在π0,2⎛⎫⎪⎝⎭上单调递增，从而()()()ln 100f x x x f =-+>=，即()ln 1x x >+，π0,2x ⎛⎫∈ ⎪⎝⎭，所以()tanln 1x x x >>+，π0,2x ⎛⎫∈ ⎪⎝⎭，从而当0.21x =时，tan 0.21ln1.21a b =>=，令()()ln 1,01x g x x x x =+->+，则()()()()22110111x x x g x x x x +-'=-=>+++，所以()()ln 11xg x x x =+-+在()0,∞+上单调递增，所以()()210.21ln1.2100121g g =->=，即21ln1.21121b c =>=，综上所述：21tan 0.21ln1.21121a b c =>=>=.故选：C.【点睛】关键点睛：本题的关键是在比较,a b 的大小关系时，可以通过先放缩再构造函数求导，而在比较,c b 大小关系时，关键是通过构造适当的函数，通过导数研究函数单调性，从而来比较大小.二、多项选择题（本大题共4小题，每小题5分，共20分.在每小题给出的四个选项中，有多项符合题目要求的.全部选对的得5分，部分选对的得2分，有选错的得0分）9.已知0a >，0b >，且1a b +=，下列说法正确的是（）A.114a b+≤ B.2212a b +≥C.122a b -< D.≤【答案】BD 【解析】【分析】根据题意结合基本不等式和三角函数的性质，逐项判定，即可求解.【详解】因为0a >，0b >，且1a b +=，对于A 中，由1111()()224b a a b a b a b a b +=++=++≥+=，当且仅当b a a b=时，即12ab ==时，等号成立，所以A 不正确；对于B 中，由22221()21212(22a b a b a b ab ab ++=+-=-≥-⋅=，当且仅当12ab ==时，等号成立，所以B 正确；对于C 中，因为0a >，0b >，且1a b +=，可得10b a -=-<，又因为函数2x y =为单调递增函数，可得22a a ->，所以122a b ->，所以C 不正确；对于D 中，因为0a >，0b >，且1a b +=，设22πsin ,cos ,(02a b θθθ==<<，sin 2cos )θθθϕ+=+=+≤，其中tan 2ϕ=，所以D 正确.故选；BD.10.已知复数1z ，2z ，则下列命题成立的有（）A.若1212z z z z +=-，则12z z = B.11,Znn z z n =∈C.若22120z z +=，则12=z z D.1212z z z z ⋅=⋅【答案】BCD 【解析】【分析】举例说明判断A ；利用复数的三角形式计算判断B ；利用复数的代数形式，结合模及共轭复数的意义计算判断CD.【详解】对于A ，当121i,1i =+=-z z 时，12122z z z z +==-，而1220z z =≠，A 错误；对于B ，令1(cos isin ),0,R z r r θθθ=+≥∈，则1(cos isin )n n z r n n θθ=+，于是1|||cos isin |n n n z r n n r θθ=+=，而1||z r =，即有1||n n z r =，因此11nn z z =成立，B 正确；设复数1i(,R)z a b a b =+∈，2i(,)z c d c d =+∈R ，对于C ，由22120z z +=，得2222()(22)i 0a b c d ab cd -+-++=，则22220220a b c d ab cd ⎧-+-=⎨+=⎩，2222120z z -=-=，因此12=z z ，C 正确；对于D ，21(i)(i)()()i z a b c d ac bd c z ad b ⋅=++=-++，则21()()i z ac bd a b z d c ⋅=--+，12(i)(i)()()i z z a b c d ac bd ad bc ⋅=--=--+，因此1212z z z z ⋅=⋅，D 正确.故选：BCD11.已知函数()()πsin 06f x x ωω⎛⎫=+> ⎪⎝⎭在[]0,2π有且仅有4个零点，则下列各选项正确的是（）A.()f x 在区间π0,6⎛⎫⎪⎝⎭单调递增B.ω的取值范围是2329,1212⎡⎫⎪⎢⎣⎭C.()f x 在区间()0,2π有2个极小值点D.()f x 在区间()0,2π有3个极大值点【答案】BC 【解析】【分析】由题意得到当且仅当ω满足π2π4π6π2π5π6ωω⎧+≥⎪⎪⎨⎪+<⎪⎩，即2329,1212ω⎡⎫∈⎪⎢⎣⎭由此判断B ；进一步结合复合函数单调性、三角函数单调性以及B 选项分析即可进一步判断ACD.【详解】对于B ，由题意当[]0,2πx ∈时，πππ,2π666x ωω⎡⎤+∈+⎢⎥⎣⎦，由题意函数()()πsin 06f x x ωω⎛⎫=+> ⎪⎝⎭在[]0,2π有且仅有4个零点，所以当且仅当π2π4π6π2π5π6ωω⎧+≥⎪⎪⎨⎪+<⎪⎩，解得23291212ω≤<，即ω的取值范围是2329,1212⎡⎫⎪⎢⎣⎭，故B 正确；对于C ，()0,2πx ∈时，πππ,2π666x ωω⎛⎫+∈+ ⎪⎝⎭，由B 选项分析可知π4π2π5π6t ω≤=+<，而sin y t =在ππ,2π66ω⎛⎫+ ⎪⎝⎭确定的极小值点有且仅有两个：3π7π,22，故C 选项正确；对于D ，()0,2πx ∈时，πππ,2π666x ωω⎛⎫+∈+ ⎪⎝⎭，由B 选项分析可知π4π2π5π6t ω≤=+<，而sin y t =在ππ,2π66ω⎛⎫+ ⎪⎝⎭确定的极大值点有两个：π5π,22，但当π9π4π2π62t ω≤=+≤时，()f x 在区间()0,2π有且仅有2个极大值点，故D 选项错误；对于A ，由B 选项分析可知2329,1212ω⎡⎫∈⎪⎢⎣⎭，不妨取2329,11252212ω∈=⎡⎫⎪⎢⎣⎭，此时ππ37π,6672t x ω⎛⎫=+∈ ⎪⎝⎭，而sin y t =在ππ,62⎛⎫ ⎪⎝⎭单调递增，在π37π,272⎛⎫⎪⎝⎭上单调递减，故A 选项错误.故选：BC.12.已知函数()f x ，()g x 的定义域均为R ，()g x '为()g x 的导函数，且()()1f x g x +'=，()()43f x g x -'-=，若()g x 为奇函数，则（）A.()22f = B.()()042g g ''+=- C.()()13f f -=- D.()()44g g ''-=【答案】ABD 【解析】【分析】根据题意分析可知()g x '为偶函数，()()42'+-=-'g x g x ，且()g x '的周期为8，利用赋值法结合题意逐项分析判断.【详解】已知函数()f x ，()g x 的定义域均为R ，因为()()1f x g x +'=，()()43f x g x -'-=，可得()()42'+-=-'g x g x ，又因为()g x 为奇函数，则()()g x g x =--，可得()()g x g x ''=-，即()g x '为偶函数，则()()42+=''--g x g x ，即()()42''++=-g x g x ，可得()()842''+++=-g x g x ，所以()()8x g x g ''+=，可知()g x '的周期为8.对于选项A ：因为()()42'+-=-'g x g x ，()()1f xg x +'=令2x =，则()()222''+=-g g ，()()221+='f g ，可得()21g '=-，()22f =，故A 正确；对于选项B ：因为()()42'+-=-'g x g x ，令0x =，可得()()042g g ''+=-，故B 正确；对于选项C ：因为()()42'+-=-'g x g x ，且()g x '为偶函数，则()()42''-++=-g x g x ，令=1x -，可得()()132''+=-g g ，又因为()()1f x g x +'=，令1,3x =-，则()()111'-+-=f g ，()()331+='f g ，可得()()()()13132'-++-+='f f g g ，可得()()134f f -+=，但由题设条件无法推出()()13f f -=-，故C 错误；对于选项D ：因为()g x '的周期为8，故()()44g g ''-=，故D 正确；故选：ABD.【点睛】方法点睛：函数的性质主要是函数的奇偶性、单调性和周期性以及函数图象的对称性，在解题中根据问题的条件通过变换函数的解析式或者已知的函数关系，推证函数的性质，根据函数的性质解决问题．三、填空题（本大题共4小题，每小题5分，共20分）13.已知()1,a x = ，()1,b x =- ，若2a b - 与a垂直，则实数x =____________.【答案】【解析】【分析】根据给定条件，利用垂直关系的向量表示及数量积的坐标表示，列出方程求解即得.【详解】由()1,a x =，()1,b x =- ，得2221,1a x a b x =+⋅=-+ ，由2a b - 与a 垂直，得2(2)20a b a a a b -⋅=-⋅= ，即有22(1)2(1)0x x +--+=，解得x =所以实数x =.故答案为：14.已知直线l满足：原点到它的距离为2，点()3,0到它的距离为，请写出满足条件的直线l 的一个方程：______________.【答案】10x y -+=（答案不唯一，10x y ++=）【解析】【分析】设出直线l 的方程，利用点到直线的距离公式，列式不解即得.【详解】当直线l 的斜率不存在时，设l 的方程为x a =，于是||2a =，且|3|a -=，显然无解，当直线l 的斜率存在时，设l 的方程为y kx b =+，即0kx y b -+=，于是2==，整理得22222168k b k kb b ⎧-=-⎨++=⎩，消去常数项得()(35)0k b k b -+=，即有0k b -=或350k b +=，由22210k b k b ⎧-=-⎨-=⎩解得1k b ==或1k b ==-，而方程组2221350k b k b ⎧-=-⎨+=⎩无解，因此1k b ==或1k b ==-，所以直线l 的方程为10x y -+=或10x y ++=.故答案为：10x y -+=15.当实数0a ≠时，函数()()1e xf x x a x=--有且只有一个可导极值点，则实数a 的取值范围为________.【答案】1[e,)-+∞【解析】【分析】根据题意，转化为()e x g x x =与y a =±的图象交点个数问题，分类讨论，利用导数求得函数()g x 的单调性与极小值，结合图象，即可求解.【详解】由函数()()()()1e ,01e 1e ,0xxxx ax x f x x a x x ax x ⎧--≥⎪=--=⎨-+<⎪⎩，当0x ≥时，可得()e xf x x a '=-；当0x <时，可得()e x f x x a '=+，令()e x g x x =，可得()(1)e x g x x '=+，当1x <-时，()0g x '<，()g x 单调递减；当1x >-时，()0g x '>，()g x 单调递增，所以，当=1x -时，函数取得极小值，极小值为()11eg --=-，且0x <时，()0g x <，()00g =，其函数()g x 的图象，如图所示，因为函数()f x 有且只有一个可导极值点，显然当0a <时，y a =与()e x g x x =在[)0,∞+上无交点，y a =-与()e xg x x =在(),0∞-上无交点，故不合题意，舍去，且由题目条件所知0a ≠，则0a >，①当函数()e x g x x =在[)0,∞+上与y a =，在(),0∞-上与y a =-上总共有一个交点时，当0a >时，设函数()f x 的唯一可导极值点为0x ，由图知00x >，若()e 0x f x x a ='-=在[0,)+∞有一个实数根，且()e 0x f x x a '=+=在(,0)-∞上没有实数根，则1ea a ->⎧⎨>⎩，可得1e a ->，此时0x 即为直线y a =与()()e 0x g x x x =≥的交点横坐标，符合题意；②若()e 0x f x x a ='-=在[0,)+∞有一个实数根，且在()e 0x f x x a '=+=在(,0)-∞上有且仅有一个实数根，且此零点的左右两侧导函数值不变号，则10ea a ->⎧⎨-=-⎩，可得1e a -=，此时满足题意，综上可得，实数a 的取值范围为1[e ,)-+∞.故答案为：1[e,)-+∞.16.已知[]x 为不超过x 的最大整数，例如[]0.20=，[]1.21=，[]0.51-=-，设等差数列{}n a 的前n 项和为()12n n n S a =+且515S =，记[]2log nn b a =，则数列{}n b 的前100项和为__________.【答案】480【解析】【分析】求出na n =，则得到[]2log nb n =，再利用[]x 的定义即可求出答案.【详解】由题意得()()1122nn n n nS a a a =+=+，所以11a =，()515355152S a a a =+==，所以33a =，所以公差3112d -==，所以n a n =，[][]22log log n n b a n ==，当1n=时，10b =，当23n ≤≤时，1n b =，当47n ≤≤时，2n b =，当815n ≤≤时，3n b =，当1631n ≤≤时，4n b =，当3263n ≤≤时，5n b =，当64100n ≤≤时，6n b =，所以数列{}n b 的前100项和为0122438416532637480+⨯+⨯+⨯+⨯+⨯+⨯=.故答案为：480.【点睛】关键点睛：本题的关键是求出na n =，再利用取整函数的定义对nb 分类讨论，最后计算出答案.四、解答题（本大题共6小题，共70分.解答时应写出文字说明、证明过程或演算步骤）17.已知π(sin(),1)4a x =+ ，2)b x = .（1）当π[0,4x ∈，5a = 时，求7πsin()12x +；（2）若()f x a b =⋅ ，求()f x 的值域.【答案】（1）410+；（2）5[,14-.【解析】【分析】（1）利用给定的模求出π4x +的正余弦，再利用和角的正弦公式求解即得.（2）利用数量积的坐标表示求出()f x ，再利用换元法，结合二次函数求出函数值域.【小问1详解】由π(sin(),1)4a x =+ ，5a = ，得2π41sin ()1425x ++=，即2π16sin (425x +=，由π[0,]4x ∈，得πππ[,442x +∈，解得π4π3sin(),cos()4545x x +=+=，所以7πππππππ4134sin()sin[()]sin()cos cos()sin 12434343525210x x x x ++=++=+++=⨯+⨯=.【小问2详解】依题意，π())sin 2sin cos 2sin cos 4f x a b x x x x x x=⋅=++=++2sin cos (sin cos )1x x x x =+++-，令πsin cos )[4t x x x +=∈=+，则22151()24y t t t =+-=+-，当12t =-时，min 54=-y ，当t =时，max 1y =+所以()f x 的值域是5[,14-+.18.已知圆T 经过()4,0A ，()2,4B ，()5,3C .（1）求圆T 的方程；（2）过点71,3P ⎛⎫⎪⎝⎭的直线l 交圆T 于M 、N 两点，且2MP PN =，求直线l 的方程.【答案】（1）226480x y x y +--+=（2）1x =，或351270--=x y 【解析】【分析】（1）设圆T 的方程为()2222040x y Dx Ey F D E F ++++=+->，代入A 、B 、C 三点坐标可得答案；（2）当直线l 的斜率不存在时，方程为1x =，求出M 、N 点坐标满足题意；当直线l 的斜率存在时，设方程为()713-=-y k x ，与圆T 的方程联立，设()()1122,,,Mx y N x y ，利用2MP PN =可得2123+=x x ，再由韦达定理求出1x 、2x ，再根据12x x 可得答案.【小问1详解】设圆T 的方程为()2222040x y Dx Ey F D E F ++++=+->，因为圆T 经过()4,0A ，()2,4B ，()5,3C ，所以16040416240259530D F D E F D E F +++=⎧⎪++++=⎨⎪++++=⎩，解得648D E F =-⎧⎪=-⎨⎪=⎩，满足224361632200+-=+-=>D E F ，所以圆T 的方程226480x y x y +--+=；【小问2详解】由（1）圆T 的方程为226480x y x y +--+=，因为2277816480339⎛⎫+--⨯+=-< ⎪⎝⎭，所以点P 在圆T 内，当直线l 的斜率不存在时，方程为1x =，与圆T 的方程联立即2216480x x y x y =⎧⎨+--+=⎩，解得11x y =⎧⎨=⎩或13x y =⎧⎨=⎩，当()1,1M 时，则()1,3N ，所以8220,0,33⎛⎫⎛⎫=≠= ⎪ ⎝⎭⎝⎭ MP PN ，不满足题意，当()1,1N 时，则()1,3M ，所以4420,,0,33⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭ MP PN ，满足题意，当直线l 的斜率存在时，设方程为()713-=-y k x ，与圆T 的方程联立即()227136480y k x x y x y ⎧-=-⎪⎨⎪+--+=⎩，整理得()222222371260339⎛⎫++-+-+-+= ⎪⎝⎭k x k k x k k ，设()()1122,,,Mx y N x y ，可得212222631-+=++x x k k k ，2122237391-++=x k k kx ，1122771,,1,33⎛⎫⎛⎫=--=-- ⎪ ⎪⎝⎭⎝⎭ MP x y PN x y ，由2MP PN =得12221x x -=-，可得2123+=x x ，221211122263231-++=++=+=+k k x x x x x x k ，可得2122331+-=+k k x k ，2224931-+=+k k x k ，所以2222221223724393933111-+++=+=-++⨯-x k k k k k k x k k k ，解得3512k =，所以直线l 的方程为()7351312-=-y x ，即351270--=x y ，综上所述，直线l 的方程为1x =，或351270--=x y.19.在ABC 中，内角A ，B ，C 的对边分别是a ，b ，c ，已知2c =，且12cos 2a Bb =+.（1）求ABC 周长的最大值；（2）若()sin sin 2sin 2C B A A +-=，且a b <，求角A .【答案】（1）6；（2）π6.【解析】【分析】（1）根据给定等式，借助正弦定理边化角，再利用和角的正弦公式化简并求出C ，然后利用余弦定理求解即得.（2）利用和差角的正弦公式、二倍角的正弦公式求解即得.【小问1详解】在ABC 中，由正弦定理及12cos 2a Bb =+，2c =，得1sin sin cos sin 2A C B B =+，则有1sin()sin cos sin 2B C C B B +=+，即1sin cos cos sin sin cos sin 2B C B C C B B +=+，即有1sincos sin 2B C B =，而0πB <<，即sin 0B >，因此1cos 2C =，又0πC <<，则π3C =，由余弦定理得2222222π142cos()3()3()()324a b c a b ab a b ab a b a b +==+-=+-≥+-⋅=+，当且仅当a b =时取等号，此时max ()4a b +=，所以当2ab c ===时，ABC 的周长取得最大值6.【小问2详解】在ABC 中，由sin sin()2sin 2C B A A +-=，得sin()sin()2sin 2B A B A A ++-=，化简得2sin cos 4sin cos B A A A =，由a b <，知A 是锐角，即cos 0A >，因此sin 2sin B A =，由（1）得，πsin()2sin 3A A +=，即1cos sin 2sin 22A A A +=，整理得tan 3A =，所以π6A =.20.已知数列{}n a 满足13a =，当()*2N n n ≥∈时，()111n n na n a -=++.（1）求{}n a 的通项公式；（2）求数列πsin 2n n a ⎧⎫⎨⎬⎩⎭的前n 项和n T .【答案】（1）21,N na n n *=+∈（2）2,431,42,N 1,41,4n n n k n n k T k n n k n n k*+=-⎧⎪+=-⎪=∈⎨--=-⎪⎪-=⎩【解析】【分析】（1）根据题意构造新数列1nna b n =+，利用累加法求得{}n b 的通项公式，进而求得{}n a 的通项公式.（2）根据（1）中所求知21,430,42πsin 21,4120,4n n n n k n k n c a n n k n k+=-⎧⎪=-⎪==⎨--=-⎪⎪=⎩，分四种情况依次求数列πsin 2n n a ⎧⎫⎨⎬⎩⎭的前n 项和n T 即可.【小问1详解】由题13a =且当()*2N n n ≥∈时，()111nn na n a -=++，则11,21(1)n n a a n n n n n -=+≥++，令113,1112n n a a b b n ===++，即11111,2(1)1nn n n b b b b n n n n n --=+⇒-=-≥++，则211123bb -=-，323411b b -=-，L ，1111n n b b n n --=-+，累加得1111,22,2211n nb b n b n n n -=-≥⇒=-≥++，132b =也符合，所以12,N 1n b n n *=-∈+，1221,N 11n n n a b a n n n n *=-=⇒=+∈++.【小问2详解】由（1）得21na n =+，令πsin2n n n c a =，则21,430,42πsin 21,4120,4n n n n k n k n c a n n k n k+=-⎧⎪=-⎪==⎨--=-⎪⎪=⎩，其中N k *∈，即12343,0,7,0c c c c ===-=，L，434241485,0,81,0,N k k k k c k c c k c k *---=-==-+=∈，因为43424144,N k k k k cc c c k *---+++=-∈所以当4n k =时，1244n n nT c c c n =+++=-⨯=- ，当41n k =-时，1114014n n n n T T c n +++=-=-⨯-=--，当42n k =-时，()()2212421114n n n n n T T c c n n ++++=--=-⨯--+-=+，当43n k =-时，111102n n n T T c n n ++=-=++-=+，则数列πsin 2n n a ⎧⎫⎨⎬⎩⎭的前n 项和122,431,42,N 1,41,4n n n n k n n k T c c c k n n k n n k*+=-⎧⎪+=-⎪=+++=∈⎨--=-⎪⎪-=⎩ .21.已知函数()()e 0x f x ax a =≠，()2g x x =-.（1）求()f x 的单调区间；（2）当0x >时，()f x 与()g x 有公切线，求实数a 的取值范围.【答案】21.答案见解析22.1,0e ⎡⎫-⎪⎢⎣⎭【解析】【分析】（1）根据题意，求得()(1)e x f x a x '=+，分类讨论，即可求得函数的单调区间；（2）设公切线与()y f x =和()y g x =的切点分别为121(,))e ,(,x x b t b a -，根据导数的几何意义求得切线方程，转化为()1211214,(0)1ex x a x x -=>+，设()()2241exx h x x =+，利用导数求得函数()hx 的单调性与极值，得出函数()h x 的值域，即可求解.【小问1详解】解：由函数()()0x f x axe a =≠，可得()(1)e x f x a x '=+，当0a >时，可得(,1)x ∈-∞-时，()0f x '<，()f x 单调递减，(1,)∈-+∞x 时，()0f x ¢>，()f x 单调递增；当0a <时，可得(,1)x ∈-∞-时，()0f x ¢>，()f x 单调递增，(1,)∈-+∞x 时，()0f x '<，()f x 单调递减.【小问2详解】解：设公切线与()y f x =和()y g x =的切点分别为121(,))e ,(,x x b t b a -，可得()111(1)e x kf x a x '==+，可得切线方程为1111(1)e ()x x y ate a x x x -=+-，即112111(1)e ()e x x t y a x x ate a x t =++-+，即()112111e e x x y a x x ax =+-由()2g x x =-，可得()2g x x '=-，则2k b =，所以切线方程为22y bx b =-+所以1112212(1)e x x b a x b ax e⎧-=+⎨=-⎩，可得1211214,(0)(1)ex x a x x -=>+，设()2124,(0)(1)e xx h x x x =>+，可得()34(2)(1)(1)e x x x x h x x -+-'=+，当01x <<时，()0h x '>，()h x 单调递增；当1x >时，()0h x '<，()h x 单调递减，所以，当1x =时，函数()h x 取得极大值，极大值为()11eh =，又由当0x →时，()0h x →；当x →+∞时，()0h x →，所以()10e h x <≤，所以10e a <-≤时，即实数a 的取值范围为1,0e ⎡⎫-⎪⎢⎣⎭.【点睛】方法策略：利用导数研究参数问题的求解策略：1、分离参数法：根据不等式的基本性质将参数分离出来，得到一端是参数，一端是变量的表达式的不等式，转化为求解含有变量的表达式对应的函数的最值问题，进而求得参数的范围；2、构造函数法：根据不等式的恒成立，构造新函数，利用导数求得新函数的单调性，求出函数的最值（值域），进而得出相应的含参数的不等式，从而求解参数的取值范围；3、图象法：画出不等式对应的函数的图象，结合函数图象的走势规律，确定函数的极值点或最值点的位置，进而求得参数的取值范围.22.已知椭圆()2222:10x y C a b a b+=>>的一条准线方程为4x =，长轴长为4，过点()2,1P -作直线l 交椭圆C 于点M 、N .（1）求椭圆C 的方程；（2）在x 轴上是否存在一定点Q ，使得直线QM，QN 的斜率1k ，2k 满足1211k k +为常数？若存在，求出Q 点坐标；若不存在，说明理由.【答案】（1）22143x y +=（2）()2,0【解析】【分析】（1）由题意根据准线方程、长轴长、平方关系列出方程组，即可得解.21（2）不妨设直线:(2)1l y k x =++，0(,0)Q x ，1122(,),(,)M x y N x y ，将直线方程与椭圆方程联立根据韦达定理，可将1211k k +表示成含0,x k 的代数式，根据1211k k +定值的条件判断0x 是否存在即可.【小问1详解】由题意椭圆()2222:10x y C a b a b +=>>的一条准线方程为4x =，长轴长为4，即24,24a a c==，又因为222a b c =+，所以2,1,a c b ===C 的方程为22143x y +=.【小问2详解】由题意可知，直线l 的斜率的存在，所以可设:(2)1l y k x =++，联立22143x y +=可得222(34)8(21)4(21)120k x k k x k +++++-=，设1122(,),(,)M x y N x y ，()()()()22221642144342112961202k k k k k k ⎡⎤∴∆=+-++-=->⇒<⎣⎦，21212228(21)4(21)12+=,=3+43+4k k k x x x x k k ++--，若存在满足条件的0(,0)Q x ，10201020121212112121x x x x x x x x k k y y kx k kx k ----∴+=+=+++++10220112()(21)()(21)(21)(21)x x kx k x x kx k kx k kx k -+++-++=++++1201202212122(21)()2(21)(21)()(21)kx x k kx x x x k k x x k k x x k ++-+-+=+++++00(2412)6123x k x k -+-=+当00(2412)6=123x x -+-时，0=2x ，这时12114k k +=-，即满足条件的(2,0)Q .。

（指、对、幂（2））班级： 姓名： 成绩：一.填空题:(本题每小题5分共50分)1.已知函数x y a log =)10(≠>a a 且在]4,2[∈x 上的最大值比最小值大1，则a ＝______.2.函数271312-=-x y 的定义域为 . 3.函数x y -=)41(的值域是 .4.若132log )3(<+a ，则a 的取值范围是________. 5.函数1241++=+x x y 的值域为 . 6.函数122-+=ax xy 在区间（－∞，3）上单调递减，则实数a 的取值范围是 . 7.若2121)23(1---<+a a ）（，则实数a 的范围是 .8.函数)(x f 是定义在),0(+∞上的增函数，对正数y x ,都有)()()(y f x f xy f +=成立，则不等式0)(log 2<x f 的解集为 .9.已知函数)0(,)0(,)2()1()1(log )(2>≤⎩⎨⎧----=x x x f x f x x f 则)2009(f = . 10.定义：区间的长度等于12x x -，函数)1(|log |>=a x y a 的定义域为)](,[n m n m <，值域为[0,1]，若区间],[n m 的长度的最小值为43，则实数a 的值为 . 二.解答题:（本题共5小题,每题10分共50分）11.已知2222)1()(----=m m xm m x f 是幂函数，且当∈x ),0(+∞时是减函数，求实数m 及相应的幂函数. 12.若21log 321-≤≤-x ，求)4)(log 2(log 22x x y =的最大值以及取得最大值时的相应的x 值. 13. 2009年人才招聘会上，有甲、乙两公司分别开出它们的工资标准，甲公司允诺第一年月工资为1500元，以后每年月工资比上一年月工资增加230元；乙公司允诺第一年月工资数为2000元，以后每年月工资在上一年的月工资基础上递增5%，若某大学生年初被甲、乙两家公司同时录取，试问：⑴若该大学生分别在甲公司或乙公司连续工作n 年，则他在第n 年的月工资收入分别是多少？⑵该人打算连续在一家公司工作3年，仅从工资收入总量较多作为应聘标准（不记其他因素），该人应选择哪家公司，为什么？14.已知函数y=log 311-+x x . (1)求函数f （x ）的定义域、值域;(2)判断函数的奇偶性并证明;(3)判断函数在（1，+∞）上的单调性，并用函数单调性定义证明.15.已知函数)(122)(R m m x f x ∈-+=为奇函数. ⑴求m 的值； ⑵求函数)(x f y =的单调区间，并证明； ⑶记222)(log )1()(kx x f x x g +-=，若函数)(x g y =在区间（0,1）上单调递增，求实数k 的取值范围.。

15高三数学寒假作业十五(含答案)一、填空题1.A={x|x≤2}，B={-1,1,2}，则A∩B={-1,1,2}。

2.z=1+i。

3.输出结果为12.4.y=3x²/31.5.m=1/2.6.概率为2/5.7.最大值为5.8.g(x)=2cos(2(x+π))/π。

9.1/3.10.a1=3，q=2/3.11.b-a=π/6.12.m≤-3或m≥-1.13.x-y=3.14.最大值为5.二、解答题15.证明：设a,b,c,d为正整数，且a<b<c<d，且a+d=b+c，则d-a=b-c。

因为a+d=b+c，所以a+c=b+d。

又因为a<b<c<d，所以a+c<b+c<d+c，即a+c<d+c。

所以d-a<b-c，即d-a≤b-c-1.因为d-a和b-c都是正整数，所以d-a≤b-c-2.所以d-a≤(b-a)-(c-b)≤2.因为a<b<c<d，所以d-a≥3.所以d-a=3，b-c=2，即d=b+2，c=b+1，a=b-1.所以a=11，b=12，c=13，d=14.因此，满足条件的四个正整数为11，12，13，14.1) 数列 $\{a_n\}$ 的通项公式为 $a_n =n(1+\frac{1}{n+1})$。

2) 数列 $\{b_n\}$ 的通项公式为 $b_n =\sqrt{\frac{a_{n+1}}{n}}$。

3) 数列 $\{c_n\}$ 中不存在不同两项 $c_i。

c_j$ （$1\leq i<j。

i,j\in \mathbb{N}$），使得 $c_i+c_j$ 是数列 $\{c_n\}$ 的项。

解析：1) 首先对 $a_{n+1}$ 进行变形，得到 $a_{n+1} =(n+1)(1+\frac{1}{n+2})$。

然后将 $a_{n+1}$ 带入 $a_n$ 的式子中，得到 $a_n =n(1+\frac{1}{n+1})$。