2023年高三数学寒假作业16(Word含答案解析)
- 格式:docx
- 大小:1.22 MB
- 文档页数:21

高二数学寒假作业(四)一、选择题,每小题只有一项是正确的。
1.公比为2的等比数列{an)的各项都是正数,且=16,则a6等于A .1B .2C .4D .82.等比数列{a n }的前n 项和为S n ,已知S 3=a 2+10a 1,a 5=9,则a 1=( )3.一个有11项的等差数列,奇数项之和为30,则它的中间项为( ) A .8 B .7 C .6D .54.在ABC △中,已知4,6a b ==,60B =,则sin A 的值为A.26 B. 23 C. 36D. 335.在060,20,40===∆C c b ABC 中,已知,则此三角形的解为( ) A.有一解 B.有两解 C.无解 D.有解但解的个数不确定6.若n =(1,-2,2)是平面α的一个法向量,则下列向量能作为平面α法向量的是 A .(1,-2,0) B .(0,-2,2) C .(2,-4,4) D .(2,4, 4)7.已知点(3,1,4)A --,(3,5,10)B -则线段AB 的中点M 的坐标为 ( ) A. ()0,4,6-B. ()0,2,3-C. ()0,2,3D. ()0,2,6-8.已知椭圆12222=+b x a y ( a > b > 0) 的离心率为1e ,准线为1l 、2l ;双曲线132222=-b y a x 离心率为2e ,准线为3l 、4l ;;若1l 、2l 、3l 、4l 正好围成一个正方形,则21e e 等于( )A.33 B .36 C.22D. 2 9.下列命题是真命题的为 ( ) A .若11x y=,则x y = B .若21x =,则1x =C .若x y =,D .若x y <,则 22x y <二、填空题10.已知条件p :1≤x ,条件q :11<x,则p ⌝是q 的_____________________条件. 11.已知x 、y 满足约束条件⎪⎩⎪⎨⎧≤≥+≥+-3005x y x y x ,则y x z 42+=的最小值为 .12.设椭圆22162x y +=和双曲线2213x y -=的公共焦点为1F ,2F ,P 是两曲线的一个交点,12cos PF F ∠的值是 。

高三数学寒假作业满分150分,考试时间120分钟姓名____________ 班级_________学号__________一、填空题(每题4分,共56分): 1、已知i 2321+-=ω,则行列式=111222ωωωωωω2、函数2()43(3)f x x x x =-++≥的反函数是1()f x -,则1(9)f --的值是_______3、已知等差数列{}n a 的前n 项和为n S ,且111634a a a +=-,则11S = 。
4、已知向量a,b 夹角为60,2,1a b ==,则b a -=_________. 5、若集合|,3A x k x k k Z ππππ⎧⎫=+≤≤+∈⎨⎬⎩⎭,{}|22B x x =-≤≤,则B A =________ 6、如图是函数()sin(),(0,0,||)2f x A x A πωϕωϕ=+>><的图象,则其解析式是___.7、在集合{|,1,2,,10}6n M x x n π=== 中任取一个元素,所取元素恰好满足方程1cos 2x = 的概率是_________8、若行列式,021421=-x 则=x ▲. 9、阅读右面的程序框图,则输出的S = .10、设AB 是椭圆Γ的长轴,点C 在Γ上,且4CBA π∠=,若AB=4,BC =,则Γ的两个焦点之间的距离为________11、已知关于x 的不等式x 2-ax +2a >0在R 上恒成立,则实数a 的取值范围是_________. 12、设函数()f x 在(0,)+∞内可导,且()x x f e x e =+,则(1)x f =______________ 13、在xOy 平面上,将两个半圆弧22(1)1(1)x y x -+=≥和22(3)1(3)x y x -+=≥、两条直线1y =和1y =-围成的封闭图形记为D ,如图中阴影部分.记D 绕y 轴旋转一周而成的几何体为Ω,过(0,)(||1)y y ≤作Ω的水平截面,所得截面面积为48π,试利用祖暅原理、一个平放的圆柱和一个长方体,得出Ω的体积值为__________ 14、关于函数()(sin cos )cos f x x x x =+⋅,给出下列命题: ①()f x 的最小正周期为2π; ②()f x 在区间(0,)8π上为增函数;③直线38x π=-是函数()f x 图像的一条对称轴; ④对任意x R ∈,恒有()()14f x f x π-+-=。

新课标高三数学寒假作业10一、选择题.1.已知命题p :?x ∈R ,sinx ≤1,则¬p 为() A .?x ∈R ,sinx ≥1B .?x ∈R ,sinx ≥1C .?x ∈R ,sinx >1D .?x ∈R ,sinx >1 2.已知函数)(x f 是R 上的增函数,(0,2)A ,(3,2)B 是其图象上的两点,那么2|)1(|x f 的解集是()A .(1,4)B .(-1,2)C .),4[)1,(D .),2[)1,(3.若{a n }为等差数列,S n 是其前n 项和,且,则tana 6的值为() A .B .C .D .4.log 2sin +log 2sin +log 2sin π=( )A .﹣3B .﹣1C .1D .35.已知向量=(2,2),=(4,1),点P 在x 轴上,则?取最小值时P 点坐标是( )A .(﹣3,0)B .(1,0)C .(2,0)D .(3,0)6.若实数经,x ,y 满足,则z=y ﹣x 的最小值为()A . 0B . 1C . 2D . 37.某几何体的三视图如图,则该几何体的表面积为( )A .3+3B .8+3C .6+6D .8+68.(5分)执行如图所示的程序框图,则输出S 的值等于()A .B .C .D .9.(5分)已知O 为坐标原点,A 、B 为曲线y=上的两个不同点,若?=6,则直线AB 与圆x 2+y 2=的位置关系是() A .相交 B .相离 C .相交或相切 D .相切或相离10.双曲线221x ym 的离心率3e ,则以双曲线的两条渐近线与抛物线2y mx 的交点为顶点的三角形的面积为A .42B .122C .82D .162二.填空题.11.在数列n a 中,已知111,(1)cos(1)n n n a a a n ,记n S 为数列n a 的前n 项和,则2015S . 12.已知ABC 中,设三个内角C B A ,,所对的边长分别为c b a ,,,且6,3,1A b a , 则c =.13.点M(x ,y)是不等式组表示的平面区域Ω内的一动点,使z =y -2x 的值取得最小的点为A(x 0,y 0),则(O 为坐标原点)的取值范围是________.14.(5分)设变量x,y满足,则z=|x﹣3y|的最大值为.三、解答题.15.(13分)函数.(1)若f(x)在点(1,f(1))处的切线斜率为,求实数a的值;(2)若f(x)在x=1取得极值,求函数f(x)的单调区间.16.已知椭圆C:+=1(a>b>0)的左,右焦点分别为F1,F2,上顶点为B.Q为抛物线y2=12x 的焦点,且?=0,2+=0.(Ⅰ)求椭圆C的标准方程;(Ⅱ)过定点P(0,2)的直线l与椭圆C交于M,N两点(M在P,N之间),设直线l的斜率为k (k>0),在x轴上是否存在点A(m,0),使得以AM,AN为邻边的平行四边形为菱形?若存在,求出实数m的取值范围;若不存在,请说明理由.17.(14分)(2007?天津)设函数f(x)=﹣x(x﹣a)2(x∈R),其中a∈R.(Ⅰ)当a=1时,求曲线y=f(x)在点(2,f(2))处的切线方程;(Ⅱ)当a≠0时,求函数f(x)的极大值和极小值;(Ⅲ)当a>3时,证明存在k∈,使得不等式f(k﹣cosx)≥f(k2﹣cos2x)对任意的x∈R恒成立.。

高三数学寒假作业十五一、填空题(本大题共14小题,每小题5分,共计70分.不需要写出解答过程) 1.已知集合A ={}220x x x -≤,B ={﹣1,1,2},则AB = .2.设复数21iz =+(其中i 为虚数单位),则z = . 3.右图是一个算法的伪代码,则输出的结果是 .4.顶点在原点且以双曲线221124x y -=的右焦点为焦点的抛物 线方程是 . 第3题 5.已知在平面直角坐标系xOy 中,直线l 1:20x my m -+-=,l 2:(2)10mx m y +--=,若直线l 1∥l 2,则m = .6.从“1,2,3,4,5”这组数据中随机去掉两个不同的数,则剩余三个数能构成等差数列的概率是 .7.若实数x ,y 满足条件1010330x y x y x y +-≥⎧⎪--≤⎨⎪-+≥⎩,则32z x y =+的最大值为 .8.将函数()cos 2f x x =的图象向左平移6π个单位长度后,再将图象上各点的纵坐标变为原来的2倍,得到函数()y g x =的图象,则()4g π= .9.已知正方体ABCD —A 1B 1C 1D 1棱长为1,点E 是棱AD 上的任意一点,点F 是棱B 1C 1上的任意一点,则三棱锥B —ECF 的体积为 .10.等比数列{}n a 的前三项和342S =,若1a ,23a +,3a 成等差数列,则公比q = .11.记集合A =[a ,b ],当θ∈[6π-,4π]时,函数2()23sin cos 2cos f θθθθ=+的值域为B ,若“A x ∈”是“B x ∈”的必要条件,则b ﹣a 的最小值是 .12.已知函数331()0()220x x x x f x x x ⎧-+<⎪=⎨⎪--≥⎩,,,若对任意的x ∈[m ,m +1],不等式(1)f x -≤()f x m +恒成立,则实数m 的取值范围是 .13.过直线l :2y x =-上任意一点P 作圆C :221x y +=的一条切线,切点为A ,若存在定点B(0x ,0y ),使得PA =PB 恒成立,则0x ﹣0y = .14.在平面直角坐标系xOy 中,已知三个点A(2,1),B(1,﹣2),C(3,﹣1),点P(x ,y )满足(OP OA)(OP OB)1⋅⨯⋅=-,则2OP OC OP⋅的最大值为 .二、解答题(本大题共6小题,共计90分.解答应写出文字说明,证明过程或演算步骤.) 15.(本题满分14分)在四棱锥P —ABCD 中,底面ABCD 是平行四边形,E 是AP 的中点,AB ⊥BD, PB ⊥PD ,平面PBD ⊥底面ABCD .(1)求证:PC ∥平面BDE ; (2)求证:PD ⊥平面PAB .16.(本题满分14分)如图,在△ABC 中,点D 是边BC 上一点,AB =14,BD =6,BA BD 66⋅=.(1)若C >B ,且cos(C ﹣B)=1314,求角C ; (2)若△ACD 的面积为S ,且1CA CD 2S =⋅,求AC 的长度.17.(本题满分14分)在平面直角坐标系xOy中,椭圆E:22221x ya b+=(a>b>0)的长轴长为4,左准线l的方程为x=﹣4.(1)求椭圆的标准方程;(2)直线l1过椭圆E的左焦点F1,且与椭圆E交于A,B两点.①若AB=247,求直线l1的方程;②过A作左准线l的垂线,垂足为A1,点G(52-,0),求证:A1,B,G三点共线.18.(本题满分16分)某游乐场过山车轨道在同一竖直钢架平面内,如图所示,矩形PQRS的长PS为130米,宽RS为120米,圆弧形轨道所在圆的圆心为O,圆O与PS,SR,QR分别相切于点A,D,C,T为PQ的中点.现欲设计过山车轨道,轨道由五段连接而成.出发点N在线段PT 上(不含端点,游客从点Q处乘升降电梯至点N),轨道第一段NM与圆O相切于点M,再沿着圆弧轨道MA到达最高点A,然后在点A处沿垂直轨道急速下降至点O处,接着沿直线轨道OG滑行至地面点G处(设计要求M,O,G三点共线),最后通过制动装置减速沿水平轨道GR滑行到达终点R.记∠MOT为α,轨道总长度为l米.lα,并写出α的取值范围;(1)试将l表示为α的函数()(2)求l最小时cosα的值.19.(本题满分16分)已知函数2()ln ()f x x a x x =+-(a ∈R). (1)当a =0,证明:()1f x x <-;(2)如果函数()f x 有两个极值点1x ,2x (1x <2x ),且12()()f x f x k +<恒成立,求实数k 的取值范围;(3)当a <0时,求函数()f x 的零点个数.20.(本题满分16分)已知N n *∈,数列{}n a 的前n 项和为n S ,且11n n S a a +=-;数列{}n b 的前n 项和为n T ,且满足1(1)2n n n T b n n b +=++,且12a b =.(1)求数列{}n a 的通项公式; (2)求数列{}n b 的通项公式; (3)设n n na cb =,问:数列{}n c 中是否存在不同两项i c ,j c (1≤i <j ,i ,j N *∈),使i c +j c 仍是数列{}n c 中的项?,j ;若不存在,请说明理由.高三数学寒假作业十五参考答案11.3 12.13.14.15.16.17.18.19.20.高三数学寒假作业十五(含答案)11。
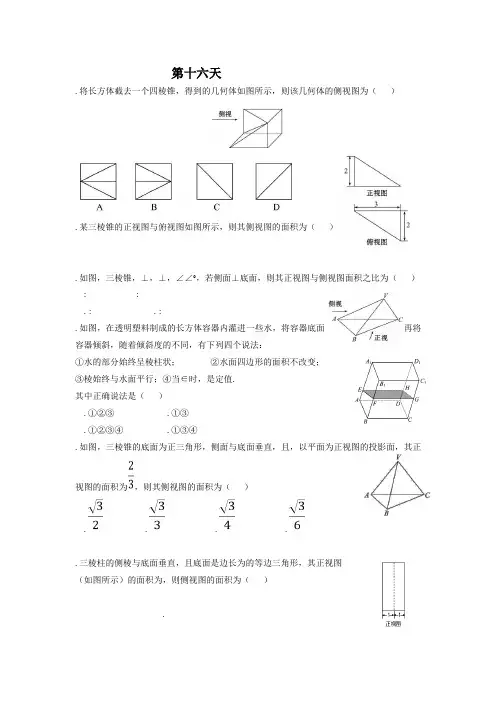
第十六天.将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的侧视图为().某三棱锥的正视图与俯视图如图所示,则其侧视图的面积为().如图,三棱锥,⊥,⊥,∠∠°,若侧面⊥底面,则其正视图与侧视图面积之比为()::.: .:.如图,在透明塑料制成的长方体容器内灌进一些水,将容器底面一边固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:①水的部分始终呈棱柱状;②水面四边形的面积不改变;③棱始终与水面平行;④当∈时,是定值.其中正确说法是().①②③ .①③.①②③④ .①③④.如图,三棱锥的底面为正三角形,侧面与底面垂直,且,以平面为正视图的投影面,其正视图的面积为,则其侧视图的面积为().....三棱柱的侧棱与底面垂直,且底面是边长为的等边三角形,其正视图(如图所示)的面积为,则侧视图的面积为()..多面体的底面为矩形,其正(主)视图和侧(左)视图如图,其中正(主)视图为等腰梯形,侧(左)视图为等腰三角形,则的长为(). . ..一个几何体的三视图如图所示,其中正视图和侧视图是腰长为的两个全等的等腰直角三角形. 用多少个这样的几何体可以拼成一个棱长为的正方体()个个个.个.如图,网格纸上正方形小格的边长为(表示),图中粗线画出的是某零件的三视图,该零件由一个底面半径为,高为的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为().....某空间几何体的三视图如图所示,则这个空间几何体的表面积是()ππππ.一个几何体的正视图为一个三角形,则这个几何体可能是下列几何体中的(填入所有可能的几何体的编号).①三棱锥;②四棱锥;③三棱柱;④四棱柱;⑤圆锥;⑥圆柱.。

高三数学寒假作业满分150分,考试时间120分钟姓名____________ 班级_________学号__________一、填空题(每题4分,共56分): 1、若0)231(=-∞→nn x lin ,则实数x 的取值范围是____________; 2、函数)1(log )(2-=x x f )21(≤<x 的反函数=-)(1x f.3、数列{}n a 是公差不为0的等差数列,且862a a a =+,则=55a S . 4、已知向量2)(,6||,1||=-⋅==,则向量与向量的夹角是__________. 5、已知集合A ={x ||x -1|<2},B ={x | 02x bx -<+},若A ∩B ≠φ,则实数b 的取值范围是________.6、在ABC ∆中,内角,,A B C 的对边分别为,,c a b ,若22,sin a b C B -==,则A =__________.7、如右图,该程序运行后输出的结果为 .8、设非零常数d 是等差数列12319,,,,x x x x 的公差,随机变量ξ等可能地取值12319,,,,x x x x ,则方差_______D ξ=9、已知直线1)13()2(--=-x a y a ,为使这条直线不经过第二象限,则实数a 的范围是 10、已知实数x 、y 满足方程()()22111x a y -++-=,当0y b ≤≤(b R ∈)时,由此方程可以确定一个偶函数()y f x =,则抛物线212y x =-的焦点F 到点(,)a b 的轨迹上点的距离最大值为____________.11、四棱锥P —ABCD ABCD 是边长为2的正方形,则CD 与PA 所成角的余弦值为 .12、设α为锐角,若4cos 65απ⎛⎫+= ⎪⎝⎭,则)122sin(π+a 的值为 ▲ .13、函数()2ln f x x =的图像与函数()245g x x x =-+的图像的交点个数为__________.14、下列五个命题中,正确的命题的序号是_____________. ①函数2tanxy =的图象的对称中心是Z k k ∈),0,(π; ②)(x f 在()b a ,上连续,()()0)()(0,,00<=∈b f a f x f b a x 则且; ③函数)32sin(3π+=x y 的图象可由函数x y 2sin 3=的图象向右平移3π个单位得到; ④)(x f 在R 上的导数)1(2)2(,0)()(),(f f x f x f x x f <<-''则且; ⑤函数)2cos 21ln(x y +=的递减区间是⎪⎭⎫⎢⎣⎡+4,πππk k ()Z k ∈. 二、选择题(每题5分,共20分): 15、已知函数1()ln 2(0),f x x x x=-+>则函数)(x f 的零点个数是( ) A.0 B.1 C.2 D.316、连掷两次骰子得到的点数分别为m 和n ,若记向量()m n,a =与向量(12)=- ,b 的夹角为θ,则θ为锐角的概率是 .17、已知1l 、2l 、3l 是空间三条不同的直线,下列命题中正确的是( ).A 如果21l l ⊥ ,32//l l .则31l l ⊥. .B 如果21//l l ,32//l l .则1l 、2l 、3l 共面. .C 如果21l l ⊥ ,32l l ⊥.则31l l ⊥. .D 如果1l 、2l 、3l 共点.则1l 、2l 、3l 共面.18、已知点F 1、F 2分别是椭圆22221x y a b+=的左、右焦点,过F 1且垂直于x 轴的直线与椭圆交于A 、B 两点,若△ABF 2为正三角形,则该椭圆的离心率e 为 ( )(A )12 (B )(C )13(D三、解答题(本大题满分74分):19、(本题满分12分)已知真命题:“函数()y f x =的图像关于点( )P a b 、成中心对称图形”的充要条件为“函数()y f x a b =+- 是奇函数”.(1)将函数32()3g x x x =-的图像向左平移1个单位,再向上平移2个单位,求此时图像对应的函数解析式,并利用题设中的真命题求函数()g x 图像对称中心的坐标; (2)求函数22()log 4xh x x=- 图像对称中心的坐标; (3)已知命题:“函数 ()y f x =的图像关于某直线成轴对称图像”的充要条件为“存在实数a 和b,使得函数()y f x a b =+- 是偶函数”.判断该命题的真假.如果是真命题,请给予证明;如果是假命题,请说明理由,并类比题设的真命题对它进行修改,使之成为真命题(不必证明).20、(本题满分14分)已知数列{}n a 的首项14a =,前n 项和为n S , 且+n+1n -3S -2n-4=0(n N )S ∈ (1)求数列{}n a 的通项公式;(2)设函数23121()n n n n f x a x a x a x a x --=++++ ,/()f x 是函数()f x 的导函数,令/(1)n b f =,求数列{}n b 的通项公式,并研究其单调性。

高三数学寒假作业满分150分,考试时间120分钟姓名____________ 班级_________学号__________一、填空题(每题4分,共56分):1、复数5i2i =+ . 2、已知,a b 均为单位向量,且它们的夹角为60°,当||()a b R λλ-∈取最小值时,λ=___________.3、已知集合⎭⎬⎫⎩⎨⎧∈==R x y y A x ,21|,{}R x x y y B ∈-==),1(log |2,则=⋂B A ▲ .4、求值:002cos10sin 20cos 20-= .5、在锐角ABC ∆中,1,2,BC B A ==则AC 的取值范围为 ______6、盒子中装有编号为1,2,3,4,5,6,7的七个球,从中任意取出两个,则这两个球的编号之积为偶数的概率是 (结果用最简分数表示).7、执行右面的程序框图,若输出的3132S =,则输入的整数p 的值为__________.8、设m 为常数,若点(0,5)F 是双曲线2219y x m -=的一个焦点,则m = 。
9、不等式的解集是___________。
10、曲线y =x (3ln x +1)在点)1,1(处的切线方程为________11、给定区域D :4440x y x y x +≥⎧⎪+≤⎨⎪≥⎩,令点集()()000000{,|,,,T x y D x y Z x y =∈∈,是z x y =+在D 上取得最大值或最小值的点},则T 中的点共确定______条不同的直线.12、若22221231111,,,x S x dx S dx S e dx x ===⎰⎰⎰则123S S S 的大小关系为________________.13、已知函数()y f x =的图像是折线段ABC ,其中(0,0)A 、1(,1)2B 、(1,0)C ,函数()y xf x =(01x ≤≤)的图像与x 轴围成的图形的面积为14、已知数列,圆,圆,若圆C 2平分圆C 1的周长,则的所有项的和为 .二、选择题(每题5分,共20分):15、当210≤<x 时x a x log 4<,则a 的取值范围是( )A )22,0( B )1,22( C )2,1( D )2,2( 16、下列判断正确的是( )A .棱柱中只能有两个面可以互相平行B .底面是正方形的直四棱柱是正四棱柱C .底面是正六边形的棱台是正六棱台D .底面是正方形的四棱锥是正四棱锥17、双曲线22221124x y m m-=+-的焦距为( ) A.4B. C.8 D.与m 无关18、棱长为1的正三棱柱111C B A ABC -中,异面直线1AB 与BC 所成角的大小为 三、解答题(本大题满分74分): 19、(本题满分12分)在△ABC 中,内角,,A B C 所对的边分别为,,a b c ,已知s i n (t a n t a n )t a n t aB AC A C +=. (Ⅰ)求证:,,a b c 成等比数列; (Ⅱ)若1,2a c ==,求△ABC 的面积S .20、(本题满分14分)设函数22()(1)f x ax a x =-+,其中0a >,区间|()>0I x f x =(Ⅰ)求的长度(注:区间(,)αβ的长度定义为βα-); (Ⅱ)给定常数(0,1)k ∈,当时,求l 长度的最小值.21、(本题满分14分)如图,在三棱锥ABC S -中,平面⊥S A B 平面S B C ,BC AB ⊥,AB AS =,过A 作SB AF ⊥,垂足为F ,点G E ,分别是棱SC SA ,的中点.求证:(1)平面//EFG 平面ABC ; (2)SA BC ⊥.22、(本题满分16分)正项数列{}n a 的前n 项和n S 满足:222(1)()0n n S n n S n n -+--+=. (1)求数列{}n a 的通项公式n a ; (2)令221(2)n nn b n a +=+,数列{}n b 的前n 项和为n T ,证明:对于任意的*n N ∈,都有564n T <. 23、(本题满分18分)已知函数a ax x a x x f ---+=232131)(,x 其中a>0.(I )求函数)(x f 的单调区间;(II )若函数)(x f 在区间(-2,0)内恰有两个零点,求a 的取值范围;(III )当a=1时,设函数)(x f 在区间]3,[+t t 上的最大值为M (t ),最小值为m (t ),记g(t)=M(t)-m(t),求函数g(t)在区间]1,3[--上的最小值。

高三数学寒假作业满分150分,考试时间120分钟姓名____________ 班级_________学号__________一、填空题(每题4分,共56分):1、若2()(1)1f x x a x =+-+是定义在R 上的偶函数,则实数a=________. 2、设1111()1232f n n n n n=+++++++ ,则 2lim [(1)()]n n f n f n →∞+-=___________.3、设O 是ABC ∆的三边中垂线的交点,,,a b c 分别为角,,A B C对应的边,已知4、满足条件{0,1}∪A={0,1}的所有集合A 的个数是 个5、已知函数f(x)=R x x x ∈--+,12cos 3)4(sin 22π,若函数)()(a x f x h +=的图象关于点)0,3(π-对称,且),,0(π∈a 则a 的值为________.6、把4个不同的球任意投入4个不同的盒子内(每盒装球数不限),则无空盒的概率为________.7x b =+有实根,则实数b 的取值范围是 .8、如图,过抛物线22(0)y px p =>的焦点F 的直线l 依次交抛物线及其准线于点A 、B 、C ,若|BC|=2|BF|,且|AF|=3,则抛物线的方程是 。
9、在△ABC 中,若222sin sin sin A B C +<,则△ABC 的形状是__________________.10、设y kx z +=,其中实数y x ,满足⎪⎩⎪⎨⎧≤--≥+-≥-+04204202y x y x y x ,若z 的最大值为12,则实数=k ________.11、直线l 过抛物线C : x 2=4y 的焦点且与y 轴垂直,则l 与C 所围成的图形的面积等于__________. 12、设()g x 是定义在R 上,以1为周期的函数,若函数()()f x x g x =+在区间[0,1]上的值域为[2,5]-,则()f x 在区间[0,3]上的值域为____________________. 13、已知函数()y =f x 满足(+1)=(-1)f x f x ,且[1,1]x ∈-时,2()=f x x ,则函数()y =f x 与3log y =|x |的图象的交点的个数是 .14、函数()f x 的定义域为A ,若12,x x A ∈且12()()f x f x =时总有12x x =,则称()f x 为单函数.例如,函数()f x =2x+1(x ∈R )是单函数.下列命题:①函数2()f x x =(x ∈R )是单函数;②若()f x 为单函数,12,x x A ∈且12x x ≠,则12()()f x f x ≠; ③若f :A→B 为单函数,则对于任意b B ∈,它至多有一个原象; ④函数()f x 在某区间上具有单调性,则()f x 一定是单函数. 其中的真命题是_________.(写出所有真命题的编号)二、选择题(每题5分,共20分):15、用数学归纳法证明4221232n n n ++++⋅⋅⋅+=,则当1n k =+时左端应在n=k 的基础上加上 A.21k + B.()21k +C.()()42112k k +++D.()()()()22221231k k k k ++++++⋅⋅⋅++16、设0a >且1a ≠,则“函数()x f x a =”在R 上是增函数”是“函数()ag x x =”“在(0,)+∞上是增函数”的(A)充分不必要条件 (B)必要不充分条件 (C)充要条件 (D)既不充分也不必要条件 17、已知m ,n 是两条不同的直线,α为平面,则下列命题正确的是 (A) //,////m n m n αα若则 (B),,m n m n αα⊥⊥⊥若则 (C),//,m n m n αα⊥⊥若则(D)若m 与α相交,n 与α相交,则m,n 一定不相交18、已知圆()()221:231C x y -+-=,圆()()222:349C x y -+-=,,M N 分别是圆12,C C 上的动点,P 为x 轴上的动点,则PM PN +的最小值为( )A.4B1C.6-D三、解答题(本大题满分74分):19、(本题满分12分)()sin()f x A x ωϕ=+(其中0,0,A ωπϕπ>>-<< )在6x π=处取得最大值2,其图象与轴的相邻两个交点的距离为2π(I )求()f x 的解析式; (II )求函数426cos sin 1()()6x x g x f x π--=+的值域。

2023年高二寒假作业检测试卷数学(答案在最后)本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分,共8页.时量120分钟.满分150分.第I 卷一、选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知数列{}n a 为等比数列,则“5a ,7a 是方程2202210x x ++=的两实根”是”61a =,或61a=-”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】A 【解析】【分析】根据等比数列的性质,利用充分条件和必要条件的定义进行判断即可.【详解】解:在等比数列中,若5a ,7a 是方程2202210x x ++=的两实根,571a a ∴=,5720220a a +=-<,则50a <,70a <,则57661a a a a ==,则61a =或61a =-,即充分性成立,当61a =,或61a =-时,能推出57661a a a a ==,但无法推出572022a a +=-,即必要性不成立,即“5a ,7a 是方程2202210x x ++=的两实根”是“61a =,或61a =-”的充分不必要条件,故选:A .2.某中学高三(1)班有50名学生,在一次高三模拟考试中,经统计得:数学成绩(110,100)X N ~,则估计该班数学得分大于120分的学生人数为()(参考数据:()0.68,(2)0.95P X P X μσμσ-<≈-<≈)A.16B.10C.8D.2【答案】C 【解析】【分析】根据正态分布的性质,结合题中所给的公式进行求解即可.【详解】因为数学成绩(110,100)X N ~,所以110,10μσ==,因此由1(11010)0.68(100120)0.68(110120)0.680.34,2P X P X P X -<≈⇒<<≈⇒<<≈⨯=所以有11(120)(110120)]0.340.1622P X P X ≥=-<<=-=,估计该班数学得分大于120分的学生人数为0.16508⨯=,故选:C 3.若21π2cos cos 23αα⎛⎫-=+ ⎪⎝⎭,则tan 2α的值为()A.3-B.3C. D.【答案】D 【解析】【分析】利用两角差的余弦公式和二倍角的正弦公式化简题给条件,得到三角函数齐次式,进而求得tan 2α的值【详解】2221112cos 2cos sin sin 21cos 2sin 23222π222ααααααα⎛⎫⎛⎫-=+=++=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭由11cos 2sin 21cos 222ααα-=+,可得32cos 222αα=又cos 20α≠,则tan 2α=故选:D4.按从小到大顺序排列的9个数据:10,16,25,33,39,43,m ,65,70,若这组数据的第一四分位数与第三四分位数的和是73,则m 等于()A.40B.48C.50D.57【答案】B 【解析】【分析】利用百分位数的求法,分别求出第一四分位数与第三四分位数,进而求出m 的值.【详解】对于已知9个数据:1016253339,43,,6570m ,,,,,, 925% 2.25⨯=,∴第一四分位数为25,975% 6.75⨯= ,∴第三四分位数为m ,2573m ∴+=,解得48m =.故选:B.5.若函数()sin 6f x x πω⎛⎫=+ ⎪⎝⎭(0ω>)在,44ππ⎛⎫- ⎪⎝⎭有最大值无最小值,则ω的取值范围是()A.48,33⎛⎫⎪⎝⎭B.48,33⎛⎤⎥⎝⎦C.416,33⎛⎫⎪⎝⎭D.416,33⎛⎤⎥⎝⎦【答案】B 【解析】【分析】求出,64646x ππωππωπω⎛⎫+∈-++ ⎪⎝⎭,根据题意结合正弦函数图象可得答案.【详解】∵,44x ππ⎛⎫∈-⎪⎝⎭,∴,64646x ππωππωπω⎛⎫+∈-++ ⎪⎝⎭,根据题意结合正弦函数图象可得46232462πωππππωππ⎧-+≥-⎪⎪⎨⎪<+≤⎪⎩,解得4833ω<≤.故选:B.6.椭圆C :()222210y x a b a b+=>>的上顶点为A ,点P ,Q 均在C 上,且关于x 轴对称,若直线AP ,AQ的斜率之积为43,则C 的离心率为()A.2B.2C.12D.13【答案】C 【解析】【分析】设P 点坐标,Q 点与P 点关于x 轴对称,坐标可用P 点坐标表示,代入斜率之积的关系式,再结合椭圆方程,化简可得a 与b 的关系,即可求出离心率.【详解】()0,A a ,设()11,P x y ,则()11,Q x y -,则11AP y a k x -=,11AQ y ak x --=,22111211143AP AQy a y a a y k k x x x ----⋅=⋅==,又2211221y x a b +=,则()2221212b a y x a -=,所以()222122221243a y a b b a y a -==-,即2234b a =,所以椭圆C的离心率12c e a ===,故选:C.7.在平面内,定点A ,B ,C ,D 满足DA =DB =DC ,DA ⋅ DB =DB ⋅ DC =DC ⋅ DA=–2,动点P ,M满足AP =1,PM =MC,则2BM 的最大值是A.434B.494C.37634+ D.372334+【答案】B 【解析】【详解】试题分析:由已知易得120,2ADC ADB BDC DA DB DC ∠=∠=∠=︒===.以D 为原点,直线DA 为x 轴建立平面直角坐标系,如图所示,则()((2,0,1,,.A B C ---设(),,P x y 由已知1AP = ,得()2221x y -+=,又13133,,,,,2222x y x y PM MC M BM ⎛⎫⎛⎫-+++=∴∴= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭ ()(222+14x y BM ++∴=,它表示圆()2221x y -+=上的点()x y ,与点(1,--的距离的平方的14,()22max149144BM⎫∴==⎪⎭,故选B.【考点】平面向量的数量积运算,向量的夹角,解析几何中与圆有关的最值问题【名师点睛】本题考查平面向量的夹角与向量的模,由于结论是要求向量模的平方的最大值,因此我们要把它用一个参数表示出来,解题时首先对条件进行化简变形,本题中得出120ADC ADB BDC ∠=∠=∠=︒,且2DA DB DC ===,因此我们采用解析法,即建立直角坐标系,写出点,,,A B C D 的坐标,同时动点P 的轨迹是圆,则()(22214x y BM +++=,因此可用圆的性质得出最值.因此本题又考查了数形结合的数学思想.8.甲罐中有5个红球,2个白球和3个黑球,乙罐中有4个红球,3个白球和3个黑球(球除颜色外,大小质地均相同).先从甲罐中随机取出一球放入乙罐,分别以1A ,2A 和3A 表示由甲罐中取出的球是红球,白球和黑球的事件;再从乙罐中随机取出一球,以B 表示由乙罐中取出的球是红球的事件.下列结论正确的个数是()①事件1A 与2A 相互独立②24()11P B A =∣③9()22P B =④14()9P A B =∣A.4 B.3C.2D.1【答案】C 【解析】【分析】根据独立事件的概念判断①,计算条件概率判断②,根据全概率公式求解判断②④,即可回答.【详解】显然,1A ,2A ,3A 是两两互斥的事件,且()1515232P A ==++,()2215235P A ==++,而1212(())0()P A A P A P A =≠⋅,①错误;()2215235P A ==++,()214451155P A B =⨯=,所以()2411P B A =,②正确;()()()()()()1122331541349()211115101122P B P B A P A P B A P A P B A P A =⋅+⋅+⋅=⨯+⨯+⨯=,③正确;()()111552119()922P A B P A B P B ⨯===,④错误,综上:结论正确的个数为2.故选:C.二、选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得2分)9.关于x ,y 的方程2222124x y m m+=+-(其中24m ≠)表示的曲线可能是()A.焦点在y 轴上的双曲线B.圆心为坐标原点的圆C.焦点在x 轴上的双曲线D.长轴长为的椭圆【答案】BC 【解析】【分析】根据各曲线的定义逐项验证参数的取值即可得出答案.【详解】解:对于A :若曲线表示焦点在y 轴上的双曲线,则220m +<,无解,选项A 错误;对于B :若曲线表示圆心为坐标原点的圆,则2224m m +=-,解得1m =±,选项B 正确;对于C :若曲线表示焦点在x 轴上的双曲线,则240m -<,所以m>2或2m <-,选项C 正确;对于D:若曲线表示长轴长为的椭圆,则2a =a =,则22240242m m m a ⎧->⎪+>-⎨⎪=⎩或22240242m m m a⎧->⎪+<-⎨⎪=⎩,无解,选项D 错误.故选:BC.10.早在西元前6世纪,毕达哥拉斯学派已经知道算术中项,几何中项以及调和中项,毕达哥拉斯哲学家阿契塔在《论音乐》中定义了上述三类中项,其中,算术中项,几何中项的定义与今天大致相同,而今我们称2a b+为正数a ,ba ,b的几何平均数,并把这两者结合的不等式()0,02a b a b +≤>>叫做基本不等式,下列与基本不等式有关的命题中正确的是()A.若0a >,0b >,21a b +=,则1142a b+≥B.若0a >,0b >,11133a b a b+=++,则+a b 的最小值为1C.若0a >,0b >,2210b ab +-=,则+2a b 的最小值为3+12D.0a >,0b >,4a b +=,则2222a b a b +++的最小值为2【答案】ABD 【解析】【分析】根据给定条件,利用均值不等式逐项计算判断作答.【详解】对于A ,0a >,0b >,21a b +=,则11112(2)()224222b a a b a b a b a b +=++=++≥+,当且仅当22b a a b=,即122a b ==时取等号,A 正确;对于B ,0a >,0b >,11133a b a b+=++,则1[(3)(311)]43(3a b a b a b a b a b +=++++++11(2)1433433a b a b a b a b ++=++≥+=++,当且仅当3333a b a b a b a b =++++,即12a b ==时取等号,B 正确;对于C ,0a >,0b >,2210b ab +-=,则有122b a b =-,13+222b a b b =+≥,当且仅当1322b b =,即3b =时取等号,由122b a b =-及3b =得:3a b ==,所以当3a b ==时,+2a bC 不正确;对于D ,0a >,0b >,4a b +=,则8(2)(2)a b =+++≥,当且仅当2a b ==时取等号,因此,当2a b ==时,(2)(2)a b ++取得最大值16,222222222224222()32222(2)(2)(2)(2)(2)(2)(2)(2)a b a b ab a b ab a b a b a b a b a b a b a b +++++++====≥++++++++++,所以当2a b ==时,2222a b a b +++的最小值为2,D 正确.故选:ABD11.(多选),,a b c 分别为ABC 内角,,A B C 的对边,已知sin (3)sin b A b c B =-,且1cos 3A =,则()A.3a c b +=B.tan A =C.ABC 的周长为4cD.ABC 的面积为29c 【答案】ABD【解析】【分析】由正弦定理得()3ba b c b =-,即可判断A 选项;由平方关系及商数关系即可判断B 选项;先由余弦定理得32b c =,再求出周长即可判断C 选项;先求得2,3a cb a ==,再求面积即可判断D 选项.【详解】由正弦定理得()3ba b c b =-,整理得3a b c =-,即3a c b +=,A 正确;由1cos 3A =可得22sin 3A ==,则sin tan cos A A A ==B 正确;由余弦定理得2222cos a b c bc A =+-,又3a b c =-,可得()2221323b c b c bc -=+-⋅,整理得32b c =,ABC 的周长为843a b c b c ++==,C 错误;由上知:3a b c =-,32b c =,可得2,3a cb a ==,则ABC 的面积为22112sin 223399bc A a a a c =⋅⋅⋅==,D 正确.故选:ABD .12.如图,正方体1111ABCD A B C D -的棱长为1,E 、F 是线段11B D 上的两个动点,且12EF =,则下列结论中正确的是()A.AC BE⊥B.//EF 平面ABCDC.AEF △的面积与BEF △的面积相等D.三棱锥E ABF -的体积为定值【答案】ABD 【解析】【分析】证明出AC ⊥平面11DD B B ,利用线面垂直的性质可判断A 选项;利用面面平行的性质可判断B 选项;利用三角形的面积公式可判断C 选项;利用锥体的体积公式可判断D 选项.【详解】对于A ,由正方体的结构特征可知,1DD ⊥平面ABCD ,而AC ⊂平面ABCD ,则1D D AC ⊥,连接BD ,又因为四边形ABCD 为正方形,所以,AC BD ⊥,因为1DD BD D =I ,且1D D 、BD ⊂平面11DD B B ,所以,AC ⊥平面11DD B B ,因为BE ⊂平面11DD B B ,所以,AC BE ⊥,故A 正确;对于B 选项,因为平面1111//A B C D 平面ABCD ,EF ⊂平面1111D C B A ,则//EF 平面ABCD ,B 对;对于C 选项,设AC BD O = ,取11B D 的中点M ,连接OM 、AM ,由A 选项可知AC ⊥平面11BB D D ,即AO ⊥平面11BB D D ,又11B D ⊂平面11BB D D ,所以,11AO B D ⊥,又11//BB DD 且11BB DD =,所以,四边形11BB D D 为平行四边形,所以,11//BD B D 且11BD B D =,因为M 、O 分别为11B D 、BD 的中点,所以,1//DO D M 且1DO D M =,所以,四边形1DD MO 为平行四边形,则1OM DD =,因为1DD ⊥平面ABCD ,DO ⊂平面ABCD ,所以,1DD DO ⊥,所以,四边形1DD MO 为矩形,则11OM B D ⊥,又AO OM O = ,AO 、OM ⊂平面AOM ,所以,11B D ⊥平面AOM ,又AM ⊂平面AOM ,所以,11AM B D ⊥,因为11AM DD BB =>=,所以,11122AEF BEF S EF AM EF BB S =⋅>⋅=△△,C 错;对于D ,因为BEF △的面积为1111112224BEF S EF BB =⋅=⨯⨯=△,又点A 到平面BEF 的距离为定值,故三棱锥A BEF -的体积为定值,D 对.故选:ABD.第II 卷三、填空题(本题共4小题,每小题5分,共20分)13.数列{}n a 中,若11a =,12n n na a n +=+,则191k k a ==∑___________.【答案】1910##1.9【解析】【分析】依题意可得12n n a na n +=+,再利用累乘法求出数列的通项公式,最后利用裂项相消法求和即可;【详解】解:因为12n n na a n +=+,所以12n n a n a n +=+,所以111n n a n a n --=+,122n n a n a n ---=,L ,3224a a =,2113a a =,累乘可得132********143n n n n a a a a n n a a a a n n -----⨯⨯⨯⨯=⨯⨯⨯⨯+ 即()121n a a n n =+,因为11a =,所以()211211n a n n n n ⎛⎫==- ⎪++⎝⎭,所以191111111111111921222121223192022319202010k k a =⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-+-++-=-+-++-=-=⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭∑ 故答案为:191014.在622(1)x x x ⎛⎫++ ⎪⎝⎭的展开式中,x 的系数是___________(用数字作答).【答案】240【解析】【分析】只要求出622x x ⎛⎫+ ⎪⎝⎭的展开式含x 的系数,即可得到答案;【详解】622x x ⎛⎫+ ⎪⎝⎭的展开式的通项为:()6212316622,0,1,,6rr rr r r r T C x C x r x --+⎛⎫=⋅⋅=⋅= ⎪⎝⎭,当1230r -=,即4r =时,622(1)x x x ⎛⎫++ ⎪⎝⎭展开式x 的系数为:446C 2240⋅=.当1231r -=显然不成立;故答案为:24015.已知函数()2ln f x x x ax =+存在减区间,则实数a 的取值范围为______.【答案】322ea -<【解析】【分析】函数()2ln f x x x ax =+存在减区间,则()0f x '<有解可求解.【详解】由题可知()2ln f x x x x a '=++,因为函数2()ln f x x x ax =+存在减区间,则()0f x '<在()0+∞,上有解,即2ln 0x x x a ++<有解,令()2ln g x x x x a =++,()2ln 3g x x '=+,令()0g x '>,解得32ex ->;令()0g x '<,解得320e x -<<,所以()g x 在32(0,e )-单调递减,32(e ,)-+∞单调递增,所以33332222min()(e )3ee2eg x g a a ----==-++=-+,因为2ln 0x x x a ++<有解,所以322e0a --+<,解得322e a -<.故答案为:322ea -<16.给图中A ,B ,C ,D ,E ,F 六个区域进行染色,每个区域只染一种颜色,且相邻的区域不同色.若有5种颜色可供选择,则共有_______种不同的染色方案.【答案】780【解析】【分析】首先根据使用的颜色种类分为三类,再对每种情况进行分类讨论,使用分步乘法以及分类加法即可求解.【详解】由题意可知,若满足相邻区域不同色,最少需要三种颜色,最多需要五种颜色.当有3种颜色时,则BD 同色,EC 同色,AF 同色,此时的涂色种类为111543C C C 60=种.当有4种颜色时,则有三种情况:①BD 不同色,EC 同色,AF 同色,此时涂色种类为2115322C C C 120⨯=种;②BD 同色,EC 不同色,AF 同色,此时涂色种类为2115322C C C 120⨯=种;③BD 同色,EC 同色,AF 不同色,此时涂色种类为2115322C C C 120⨯=种;即当有4种颜色时,总的涂色种类为120120120360++=种.当有5种颜色时,则有三种情况:①BD 不同色,EC 不同色,AF 同色,此时涂色种类为2215314C C C 120⨯=种;②BD 同色,EC 不同色,AF 不同色,此时涂色种类为2215314C C C 120⨯=种;③BD 不同色,EC 同色,AF 不同色,此时涂色种类为2215314C C C 120⨯=种;即当有5种颜色时,总的涂色种类为120120120360++=种.综上,总的共有60360360780++=种不同的方案.故答案为:780四、解答题(本题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤)17.已知直线l :()210ax a y +-+=.(1)若直线l 在x 轴上截距和在y 轴上截距相等,求a 的值;(2)若直线l 与圆22111225x y ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭相切,求a 的值.【答案】(1)1;(2)4或2-.【解析】【分析】(1)分别令0x =,0y =,得到截距,解方程即可;(2)根据圆心到直线的距离等于半径列出方程求解.【详解】(1)易知直线l 的截距不能为0,令0x =,12y a=--,令0y =,1x a =-;则1112a a a-=-⇒=-故a 的值为1(2)圆心11,22⎛⎫⎪⎝⎭到直线l 的距离d ==2412445a a =⇒-+22804a a a --=⇒=或2a =-故a 的值为4或2-.18.已知数列{}n a 满足11a =,且2112)2(n n na n a n n +-+=+.(1)求23,a a ;(2)证明数列n a n ⎧⎫⎨⎬⎩⎭是等差数列,并求{}n a 的通项公式.【答案】(1)23615a a =,=(2)证明见解析,22n a n n =-【解析】【分析】(1)由递推公式直接求出23,a a ;(2)利用构造法得到121n n a a n n +-=+,即可证明n a n ⎧⎫⎨⎬⎩⎭是等差数列,并写出{}n a 的通项公式.【小问1详解】由题意可得2124a a -=,则2124a a =+,又11a =,所以26a =.由322312a a -=,得322123a a =+,所以315a =.【小问2详解】由已知得1(1)2(1)n nna n a n n +-+=+,即121n na a n n+-=+,所以数列n a n ⎧⎫⎨⎬⎩⎭是首项为111a =,公差为2d =的等差数列,则12(1)21na n n n=+-=-,所以22n a n n =-.19.某高校的大一学生在军训结束前,需要进行各项过关测试,其中射击过关测试规定:每位测试的大学生最多有两次射击机会,第一次射击击中靶标,立即停止射击,射击测试过关,得5分;第一次未击中靶标,继续进行第二次射击,若击中靶标,立即停止射击,射击测试过关,得4分;若未击中靶标,射击测试未能过关,得2分.现有一个班组的12位大学生进行射击过关测试,假设每位大学生两次射击击中靶标的概率分别为m ,0.5,每位大学生射击测试过关的概率为p .(1)设该班组中恰有9人通过射击过关测试的概率为()f p ,求()f p 取最大值时p 和m 的值;(2)在(1)的结果下,求该班组通过射击过关测试所得总分的平均数.【答案】(1)p ,m 的值分别为0.75,0.5.(2)48【解析】【分析】(1)根据已知条件列出99312()C (1)f p p p =-()01p <<,求导得9839212'()C 9(1)3(1)f p p p p p ⎡⎤=---⎣⎦()01p <<,利用导数判断函数的单调性,求出()f p 取最大值时p 的值,再根据0.50.50.75m +=,解得0.5m =即可.(2)根据题意设一位大学生通过测试所得分数的平均值,求出X 的所有可能取值,并求出每个取值所对应的概率,求得一位大学生射击过关测试所得分数的平均数()E X ,最后确定该班组通过射击过关测试所得总分的平均数即可.【小问1详解】99312()C (1)f p p p =-,01p <<,∴9839212'()C 9(1)3(1)f p p p p p ⎡⎤=---⎣⎦982123C (1)(34)p p p =--,01p <<,由'()0f p =,得0.75p =,由'()0f p >,得00.75p <<,由'()0f p <,得0.751p <<,∴()f p 在(0,0.75)上是增函数,在(0.75,1)上是减函数,∴0.75p =是()f p 的极大值点,也是()f p 的最大值点,因为()()1110.50.50.5p mm =---=+,此时,由0.50.50.75m +=,解得0.5m =.∴()f p 取得最大值时,p ,m 的值分别为0.75,0.5.【小问2详解】设一位大学生射击过关测试所得分数为随机变量X ,则X 的可能取值分别为5,4,2,则(5)0.5P X ==,(4)(10.5)0.50.25P X ==-⨯=,(2)(10.5)(10.5)0.25P X ==--=,∴一位大学生射击过关测试所得分数的平均数:()50.540.2520.254E X =⨯+⨯+⨯=.∴该班组通过射击过关测试所得总分的平均数为:12448⨯=.20.如图,在四棱锥S ABCD -中,四边形ABCD 是矩形,SAD 是正三角形,且平面SAD ⊥平面ABCD ,1AB =,P 为棱AD 的中点,四棱锥S ABCD -的体积为3.(1)若E 为棱SB 的中点,求证://PE 平面SCD ;(2)在棱SA 上是否存在点M ,使得平面PMB 与平面SAD 所成锐二面角的余弦值为235?若存在,指出点M 的位置并给以证明;若不存在,请说明理由.【答案】(1)证明见解析;(2)存在点M ,位于AS 靠近点S 的三等分点处满足题意.【解析】【分析】(1)取SC 中点F ,连接,EF FD ,得到//PE FD ,然后利用线面平行的判定定理得到//PE 平面SCD ;(2)假设在棱SA 上存在点M 满足题意,建立空间直角坐标系,设()01AM AS λλ=≤≤,根据平面PMB 与平面SAD 的夹角的余弦值为5,则两平面法向量所成角的余弦值的绝对值等于5,求出λ,即可得出结论.【小问1详解】取SC 中点F ,连接,EF FD ,,E F 分别为,SB SC 的中点,//EF BC ∴,12EF BC =底面四边形ABCD 是矩形,P 为棱AD 的中点,//PD BC ∴,12PD BC =.//EF PD ∴,EF PD =,故四边形PEFD 是平行四边形,//PE FD \.又FD ⊂ 平面SCD ,PE ⊄平面SCD ,//PE ∴平面SCD .【小问2详解】假设在棱SA 上存在点M 满足题意,在等边SAD 中,P 为AD 的中点,所以SP AD ⊥,又平面SAD ⊥平面ABCD ,平面SAD ⋂平面ABCD AD =,SP ⊂平面SAD ,SP ∴⊥平面ABCD ,则SP 是四棱锥S ABCD -的高.设()0AD m m =>,则2SP m =,ABCD S m =矩形,113323ABCD S ABCD V S SP m m 矩形四棱锥-∴=⋅=⨯=,所以2m =.以点P 为原点,PA ,PS的方向分别为,x z 轴的正方向,建立如图所示的空间直角坐标系,则()0,0,0P ,()1,0,0A ,()1,1,0B ,(3S ,故()1,0,0PA = ,()1,1,0PB =uu r,(3AS =- .设()()301AM AS λλλλ==-≤≤,()13PM PA AM λλ∴=+=-.设平面PMB 的一个法向量为()1,,n x y z =,则11(1)300n PM x z n PB x y λλ⎧⋅=-+=⎪⎨⋅=+=⎪⎩ 取)13,3,1n λλλ=-.易知平面SAD 的一个法向量为()20,1,0n =u u r,1212212323cos ,7215n n n n n n -l ×\===l -l +u v u u v u v u u v u v u u v ,01λ≤≤ ,∴23λ=故存在点M ,位于AS 靠近点S 的三等分点处满足题意.21.已知双曲线()2222:10,0x y C a b a b-=>>的左,右焦点分别为()16,0F -,)26,0F .且该双曲线过点(22,2P .(1)求C 的方程;(2)如图.过双曲线左支内一点(),0T t 作两条互相垂直的直线分别与双曲线相交于点A ,B 和点C ,D .当直线AB ,CD 均不平行于坐标轴时,直线AC ,BD 分别与直线x t =相交于P .Q 两点,证明:P ,Q 两点关于x 轴对称.【答案】(1)22142x y -=(2)证明见解析【解析】【分析】(1)根据已知条件,建立关于,a b 的方程组,求解方程组即可得答案;(2)由题意,设直线AB 的方程为x my t =+,直线CD 的方程为1x y t m=-+,点()()()()11223344,,,,,,,A x y B x y C x y D x y ,联立22142x y x my t ⎧-=⎪⎨⎪=+⎩,由韦达定理可得212122224,22mt t y y y y m m --+==--,同理可得()2234342242,1212t m mt y y y y m m -+==--,由直线AC 的方程()133111y y y y x x x x --=--可得()2132131,m y y P t m y y ⎛⎫+ ⎪ ⎪+⎝⎭,同理可得()2242241,m y y Q t m y y ⎛⎫+ ⎪ ⎪+⎝⎭,然后计算0P Q y y +=即可得证.【小问1详解】解:由已知可得22226821a b a b⎧+=⎪⎨-=⎪⎩,解得224,2a b ==,所以双曲线C 的方程为22142x y -=;【小问2详解】证明:由题意,设直线AB 的方程为x my t =+,直线CD 的方程为1x y t m=-+,点()()()()11223344,,,,,,,A x y B x y C x y D x y ,由22142x y x my t ⎧-=⎪⎨⎪=+⎩,得()2222240m y mty t -++-=,则()()22222(2)424168320mt m tm t ∆=---=+->,得2224m t +>,所以212122224,22mt t y y y y m m --+==--,同理可得()2234342242,1212t m mt y y y y m m-+==--,其中,m t 满足2224t m +>,直线AC 的方程为()133111y y y y x x x x --=--,令x t =,得()131113y yy t x y x x -=-+-,又11331,x my t x y t m =+=-+,所以()2121331m y y y m y y +=+,即()2132131,m y y P t m y y ⎛⎫+ ⎪ ⎪+⎝⎭,同理可得()2242241,m y y Q t m y y ⎛⎫+ ⎪ ⎪+⎝⎭,因为()()()()()()()2222123412341324222213241324111m m y y y y y y y y my y m y y m y y m y y my y m y y ⎡⎤++++++⎣⎦+=++++()()()()()222222222221324442212122120m t t m mt mt m m m m m m y y m y y ⎡⎤---+⋅+⋅⎢⎥----⎢⎥⎣⎦==++,所以,P Q 两点关于x 轴对称.22.已知函数()()ln 2f x a x x =+-.(1)当1a =时,求()f x 的最大值;(2)设点()()11,A x f x 和()()22,B x f x 是曲线()y f x =上不同的两点,且()()12f x f x =,若12ak x x <+恒成立,求实数k 的取值范围.【答案】(1)1;(2)(],2∞-.【解析】【分析】(1)当1a =时,()ln 2f x x x =+-,求导判断函数得单调性,进而可以求出最值;(2)不妨设120x x >>,进而由题意可得1211221ln 0,1x x xk x x x -⋅-<+设12(1)x t t x =>,构造函数1()ln (1)1t g t k t t t -=⋅->+,利用导数研究函数()g t 在()1,+∞的最小值即可求出结果.【详解】(1)当1a =时,()ln 2f x x x =+-,()f x 的定义域为()0,+∞,11()1xf x x x -='-=当01x <<时,()0f x '>;当1x >时,()0f x '<,所以()f x 在()0,1上为增函数,在()1,+∞上为减函数,所以1x =是()f x 的极大值点,也是()f x 的最大值点,故()()max 11f x f ==.(2)不妨设120x x >>,由1122ln 2ln 2a x x a a x x a -+=-+,得1212ln ln x x a x x -=-由12ak x x <+,得121212ln ln x x k x x x x -⋅<+-,即1211221ln 0,1x x xk x x x -⋅-<+设12(1)x t t x =>,1()ln (1)1t g t k t t t -=⋅->+,则222212(1)1()(1)(1)k t k t g t t t t t '--+=-=-++记2()2(1)1(1)h t t k t t =--+>,24(1)44(2)k k k ∆=--=-(i )当0k ≤时,则()h t 图像的对称轴为11t k =-≤-,所以()h t 在()1,+∞上是增函数,又()010h =>,从而当1t >时,()0h t >,所以2()()0(1)h t g t t t '=-<+,于是()g t 在()1,+∞上是减函数,所以()()10g t g <=,此时适合题意(ii )当02k <≤时,0∆≤,则()0h t ≥恒成立,从而2()()0(1)h t g t t t '=-≤+,所以()g t 在()1,+∞上是减函数,于是()()10g t g <=,此时适合题意.(iii )当2k >时,()h t 的对称轴方程为1t k =-,且()1420h k =-<,()2410h k k =+>,所以存在()01,2t k k ∈-,使得()00h t =,于是()h t 在()1,k -+∞内只有一个零点0t ,所以当01t t <<时,()0h t <,从而2()()0(1)h t g t t t '=->+所以()g t 在()01,t 上是增函数,于是当()01,t t ∈时,()()10g t g >=,此时不适合题意.综上,实数k 的取值范围(],2-∞【点睛】恒成立问题解题思路:(1)参变量分离:(2)构造函数:①构造函数,研究函数的单调性,求出函数的最值,解不等式即可;②构造函数后,研究函数单调性,利用单调性解不等式,转化之后参数分离即可解决问题.。

高一数学寒假作业(二)一、选择题,每小题只有一项是正确的。
1.已知全集{}1,2,3,4U =,集合{}{}1,2,2A B == ,则∁U (A ∪B ) =( )A .{}134,, B .{}34, C . {}3 D . {}4 2.已知集合A ={x|a -1≤x≤a+2},B ={x|3<x <5},则使A ⊇B 成立的实数a 的取 值范围是 ( ) A.{a|3<a≤4}<a <4} D.φ3.函数 的定义域为M , 的定义域为N ,则M ∩N =( )A .[-2,+∞)B .[-2,2)C .(-2,2)D .(-∞,2) 4.下列式子中成立的是 ( )A.1122log 4log 6< B. 0.30.311()()23> C. 3.4 3.511())22<( D.32log 2log 3>5.下列函数是偶函数的是 ( )A. 2lg y x = B. 1()2x y = C. 21y x =- ,(11]x ∈- D. 1y x -= 6.已知函数()2030x x x fx x log ,,⎧>=⎨≤⎩, 则14f f ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭的值是( )A .9B .19 C .9- D .19- 7.下列各个对应中,构成映射的是 ( )8.设()f x 是定义在R 上的偶函数,对任意的x R ∈,都有(2)(2)f x f x -=+,且当[2,0]x ∈-时,1()()12x f x =-,则在区间(2,6]-内关于x 的方程2()log (2)0f x x -+=的零点的个数是( )A .1B .2C .3D .49.若函数()(1)(0xxf x k a a a -=-->且1)a ≠在R 上既是奇函数,又是减函数,则()log ()a g x x k =+的图象是( )二、填空题10.函数32,1()log 1x x f x x x ⎧≤=⎨>⎩,,则(f f =__________11.若}4,3,2,2{-=A ,},|{2A t t x xB ∈==,用列举法表示B 。

高一寒假作业数学注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)一、选择题1.已知集合{}1,2,3A =, ()(){}|120, B x x x x =+−<∈Z ,则A B 等于( )A . {}1B . {}1,2C . {}0,1,2,3D . {}1,0,1,2,3−2.点)在直线:10l ax y −+=上,则直线l 的倾斜角为( )A . 120°B . 60°C .45°D . 30°3.函数()f x =的定义域是( )A . {|23}x x <<B .{|23}x x x <>或C .{|23}x x x ≤≥或D .{|23}x x x <≥或4.一个球被两个平行平面截后所得几何体形如我国的一种民族打击乐器“鼓”,该“鼓”的三视图如图所示,则球的表面积为( ) A . 5π B . 10π C . 20πD .5.设,x y 为正数,且34x y =,当3x py =时,p 的值为( ) A . 3log 4 B . 4log 3 C . 36log 2 D . 3log 26.定义域为D 的奇函数()f x ,当0x >时,()()12f x f ≤=.给出下列命题:①[1,1]D −;②对任意, |()|2x D f x ∈≤;③存在0x D ∈,使得0()0f x =;④存在1x D ∈,使得1()1f x =.其中所有正确的命题的个数为( )A .0B .1C . 2D .37.如图,1111ABCD A B C D −为正方体,下列结论错误..的是( )A . 11BD CB D ∥平面 B . 1AC BD ⊥C . 111AC CBD ⊥平面 D . 异面直线AD 与1CB 所成角为60°8.定义在R 上的偶函数()f x 的图象关于直线1x =对称,当[0,1]x ∈时,()21f x x =−+,设函数|1|1()(13)2x g x x − =−<<,则函数()f x 与()g x 的图象交点个数为( )A . 3B . 4C . 5D . 69.如图1,直线EEEE 将矩形纸AAAAAAAA 分为两个直角梯形AAAAEEEE 和AAAAEEEE ,将梯形AAAAEEEE 沿边EEEE 翻折,如图2,在翻折的过程中(平面AAAAEEEE 和平面AAAAEEEE 不重合),下面说法正确的是( )图1 图2A . 存在某一位置,使得AAAA ∥平面AAAAEEEEB . 在翻折的过程中,AAEE ∥平面AAAAEE 恒成立C . 存在某一位置,使得AAEE ⊥平面AAAAEEEE D.在翻折的过程中,AAEE ⊥平面AAAAEEEE 恒成立10.我国魏晋时期的数学家刘徽创立了割圆术,也就是用内接正多边形去逐步逼近圆,即圆内接正多边形边数无限增加时,其周长就越逼近圆周长,这种用极限思想解决数学问题的方法是数学史上的一项重大成就.现作出圆222x y +=的一个内接正八边形,使该正八边形的其中4个顶点在坐标轴上,则下列4条直线中不是该正八边形的一条边所在直线的为( )A .1)0x y +−−= B .1)0x y += C .1)0x y −+= D .1)0x y −−+=11.设集合{|48}x A x =>,集合2{|210,0}B x x ax a =−−≤>,若A B 中恰含有一个整数,则实数a 的取值范围是( )A .34,43B .41,3C .3,4 +∞D .(1,)+∞12.在直角坐标系内,已知(3,3)A 是C 上一点,折叠该圆两次使点A 分别与圆上不相同的两点(异于点A )重合,两次的折痕方程分别为xx −yy +1=0和xx +yy −7=0,若C 上存在点P ,使90MPN ∠=°,其中M 、N 的坐标分别为(,0)m −、(,0)m ,则m 的最大值为( )A . 4B . 5C . 6D . 7第II 卷(非选择题)二、填空题13.已知过点(1,)A m −和(,5)B m 的直线与310x y −−=平行,则m 的值为______. 14.给定下列四个命题:①过直线外一点可作无数条直线与已知直线平行;②如果一条直线不在这个平面内,那么这条直线就与这个平面平行; ③垂直于同一直线的两条直线可能相交、可能平行也可能异面; ④若两个平面分别经过两条垂直直线,则这两个平面互相垂直。
高三数学寒假作业八一、填空题(本大题共14小题,每小题5分,共计70分.不需要写出解答过程) 1.设集合A ={}2log 2x x <,B ={﹣1,0,1,2,4},则AB = .2.已知复数(1i)(13i)z =++,其中i 是虚数单位,则z 的值是 .3.已知一组数据2,4,5,6,8,那么这组数据的方差是 .4.从2男3女共5名同学中任选2名(每名同学被选中的机会均等)作为代表,则这2名代表都是女同学的概率为 .5.如图是一个算法的流程图,则输出a 的值是 . 6.在平面直角坐标系xOy 中,若抛物线22y px =的焦点与 椭圆22143x y +=的右焦点重合,则实数p 的值为 . 7.已知3sin()45x π+=,则sin 2x = . 8.已知数列{}n a 的通项公式为6(3)377n n a n n a a n ---≤⎧=⎨>⎩,,,若{}n a 是递增数列,则实数a 的取值范围为 . 9.在平面直角坐标系xOy 中,若曲线2by ax x=+(a ,b 为 常数)过点P(2,﹣5),且该曲线在点P 处的切线与直线2730x y -+=垂直,则2a +3b 的值是 . 10.已知函数21()43ln 2f x x x x =-+-在区间[t ,t +1]上不是单调函数,则实数t 的取值范围是 .11.如图,在△ABC 中,AB =AC ,BC =2,AD DC =,1AE EB 2=.若1BD AC 2⋅=-,则CE AB ⋅的值为.12.已知函数210()ln 0x x f x x x +≤⎧⎪=⎨>⎪⎩,,,则关于x 的方程[()]3f f x =的解的个数为 .13.已知正数a ,b ,c 满足22()0b a c b ac ++-=,则ba c+的最大值为 . 14.若存在正数x ,y ,使得(2)(ln ln )0y ex y x s x --+=,其中e为自然对数的底数,则实数s 的取值范围是 .二、解答题(本大题共6小题,共计90分.解答应写出文字说明,证明过程或演算步骤.) 15.(本小题满分14分)如图,在四棱锥P —ABCD 中,四边形ABCD 是矩形,平面PCD ⊥平面ABCD ,M 为PC 中点.求证:(1)PA ∥平面MDB ; (2)PD ⊥BC .16.(本小题满分14分)已知(0α∈,)2π,(2πβ∈,)π,1cos 3β=-,4sin()6αβ+=(1)求tan 2β的值; (2)求α的值.如图,某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(管道构成Rt△FHE,H是直角项点)来处理污水.管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,E,F分别落在线段BC,AD上.已知AB=20米,AD=米,记∠BHE=θ.(1)试将污水净化管道的长度L表示为θ的函数,并写出定义域;(2)当θ取何值时,污水净化效果最好?并求出此时管道的长度L.在平面直角坐标系xOy 中,圆O :224x y +=与坐标轴分别交于A 1,A 2,B 1,B 2(如图).(1)点Q 是圆O 上除A 1,A 2外的任意点(如图1),直线A 1Q ,A 2Q 与直线30y +=交于不同的两点M ,N ,求线段MN 长的最小值;(2)点P 是圆O 上除A 1,A 2,B 1,B 2外的任意点(如图2),直线B 2P 交x 轴于点F ,直线A 1B 2交A 2P 于点E .设A 2P 的斜率为k ,EF 的斜率为m ,求证:2m ﹣k 为定值.19.(本小题满分16分)设函数33()ln x e kf x k x x x=--,其中x >0,k 为常数,e 为自然对数的底数. (1)当k ≤0时,求()f x 的单调区间;(2)若函数()f x 在区间(1,3)上存在两个极值点,求实数k 的取值范围;(3)证明:对任意给定的实数k ,存在0x (00x >),使得()f x 在区间(0x ,+∞)上单调递增.20.(本小题满分16分)若数列{}n a 同时满足:①对于任意的正整数n ,1n n a a +≥恒成立;②若对于给定的正整数k , 2n k n k n a a a -++=对于任意的正整数n (n >k )恒成立,则称数列{}n a 是“R(k )数列”.(1)已知212n n n a n n -⎧=⎨⎩,为奇数,为偶数,判断数列{}n a 是否为“R(2)数列”,并说明理由;(2)已知数列{}n b 是“R(3)数列”,且存在整数p (p >1),使得33p b -,31p b -,31p b +,33p b +成等差数列,证明:{}n b 是等差数列.附加题21.(本小题满分10分)二阶矩阵M 对应的变换将点(1,﹣1)与(﹣2,1)分别变换成点(﹣1,﹣1)与(0,﹣2).(1)求矩阵M 的逆矩阵1M -;(2)设直线l 在变换M 作用下得到了直线m :24x y -=,求l 的方程. 22.(本小题满分10分)在极坐标系中,设圆3ρ=上的点到直线(cos )2ρθθ+=的距离为d ,求d 的最大值. 23.(本小题满分10分)如图,已知三棱锥O —ABC 的侧棱OA ,OB ,OC 两两垂直,且OA =1,OB =OC =2,E 是OC 的中点.(1)求异面直线BE 与AC 所成角的余弦值; (2)求二面角A —BE —C 的余弦值.24.(本小题满分10分)已知()(1n n f x =,n N *∈.(1)若456()()2()3()g x f x f x f x =++,求()g x 中含x 2项的系数;(2)若n p 是()n f x 展开式中所有无理项的系数和,数列{}n a 是由各项都大于1的数组成的数列,试用数学归纳法证明:1212(1)(1)(1)(1)n n n p a a a a a a +≥+++.高三数学寒假作业八参考答案1.{1,2} 2.3.4 4.3105.106.2 7.257-8.(2,3) 9.﹣8 10.(0,1)(2,3)11.43-12.5 1314.(-∞,0)[1e,+∞)15.16.17.18.19.20.21.22.23.24.。
寒假作业(12)同角三角函数的基本关系与诱导公式1、21(tan )sin tan x x x+=( ) A.tan xB.sin xC.cos xD.1tan x2、若cos sin αα+=则tan α=( ) A.12B.2C.12-D.-23、已知sin α=则44sin cos αα-的值为( ) A.15-B.35- C.15 D.354、已知1sin cos 8αα⋅=,且ππ42α<<,则cos sin αα-=( )B.34C.D.5、若tan 2α=,则22sin cos αα-=( )A.35B.35-C.45D.45-6、若()πsin πcos 2m αα⎛⎫+++=-⎪⎝⎭,则()3cos π2sin 2π2αα⎛⎫-+- ⎪⎝⎭的值为( ) A. 23m-B. 23mC. 32m -D. 32m7、sin 600tan(300)︒+-︒的值是( )A.2-B.2C.12-D.12+8、化简:= ( )A. sin αB. sin αC. cos αD.cos α9、已知tan 2,θ=则()()πsin cos π2πsin sin π2θθθθ⎛⎫+-- ⎪⎝⎭⎛⎫--- ⎪⎝⎭等于( ) A.2 B.-2 C.0 D.3 10、已知α为第二象限角,且3sin 5α=,则()tan πα+的值是( ) A.43 B. 34C. 43-D. 34-11、()43sin ,sin ,525ππθθ⎛⎫+=+= ⎪⎝⎭则θ角的终边在第__________象限12、若()()sin180cos 90a αα︒++︒+=-,则()()cos 2702sin 360αα︒-+︒-的值是__________13、已知角α终边上一点()4,3,P -则()πcos sin π211π9πcos sin 22αααα⎛⎫+-- ⎪⎝⎭⎛⎫⎛⎫-+ ⎪ ⎪⎝⎭⎝⎭的值为__________ 14、若sin cos x x +=那么44sin cos x x +的值为___________.15、已知sin 2cos 0αα+=,则22sin cos cos ααα-的值是_______________. 16、计算()()()sin1 560cos 930cos 1380sin1410-︒-︒-⋅-︒︒等于__________17、7sin(2)cos()cos cos 225cos()sin(3)sin()sin 2ααααααααππ⎛⎫⎛⎫π+π--- ⎪ ⎪⎝⎭⎝⎭=π⎛⎫π-π--π++ ⎪⎝⎭__________.答案以及解析1答案及解析: 答案:A解析:21(tan )sin tan x x x+ 2sin cos ()sin cos sin x x x x x =+ 21sin sin tan sin cos cos x x x x x x =⋅==.2答案及解析:答案:B解析:由已知可得2(cos 2sin )5αα+=,即22224sin 4sin cos cos 5(sin cos )αααααα++=+, 所以2tan 4tan 40αα-+=,故tan 2α=.3答案及解析: 答案:B解析:因为sin α=所以2214cos 1sin 155αα=-=-=. 442222sin cos (sin cos )(sin cos )αααααα-=+-2224143sin cos 5555αα=-=-=-=-.故选B.4答案及解析: 答案:C解析:23(cos sin )12sin cos 4αααα-=-=.因为ππ42α<<,所以sin cos αα>,所以cos sin αα-=故选C.5答案及解析: 答案:A解析:22222222sin cos tan 1sin cos sin cos tan 1αααααααα---==++,因为tan 2α=.所以223sin cos 5αα-=.故选A.6答案及解析: 答案:C解析:因为()πsin πcos 2αα⎛⎫+++ ⎪⎝⎭sin sin ,m αα=--=-所以sin ,2m α= 故()3cos 2sin 22παπα⎛⎫-+-=⎪⎝⎭3sin 2sin 3sin .2m ααα--=-=-7答案及解析: 答案:B解析:原式sin(54060)tan(36060)=︒+︒+-︒+︒sin 60tan 602=-︒+︒=.8答案及解析: 答案:B解析:原式sin α===9答案及解析: 答案:B解析:()()πsin cos π2πsin sin π2θθθθ⎛⎫+-- ⎪⎝⎭⎛⎫--- ⎪⎝⎭cos cos 22cos sin 1tan θθθθθ+===---10答案及解析: 答案:D解析:因为α为第二象限角,所以4cos 5α==-所以sin 3tan(π)tan cos 4αααα+===-11答案及解析:答案:四解析:因为()4sin ,5πθ+=所以4sin 05θ=-<, 因为3sin ,25πθ⎛⎫+=⎪⎝⎭所以3cos 0,5θ=>所以θ角的终边在第四象限12答案及解析: 答案:32a-解析:由已知得sin ,2a α=∴()()cos 2702sin 360αα︒-+︒-3sin 2sin 322a aαα=--=-⨯=-13答案及解析: 答案:34-解析:∵角终边上一点()4,3P-,3tan 4y xα==-∴()πcos sin π211π9πcos sin 22αααα⎛⎫+-- ⎪⎝⎭⎛⎫⎛⎫-+ ⎪ ⎪⎝⎭⎝⎭sin sin 3tan sin cos 4ααααα-⋅===--⋅14答案及解析: 答案:12解析:由sin cos x x +=得2sin cos 1x x =,由22sin cos 1x x +=,得4422sin cos 2sin cos 1x x x x ++=.所以4421sin cos 1(2sin cos )2x x x x +=-111122=-⨯=.15答案及解析:答案:-1解析:由sin 2cos 0αα+=,得tan 2α=-.所以222222sin cos cos 2tan 1412sin cos cos 1sin cos tan 141αααααααααα-----====-+++.16答案及解析:答案:1解析:sin(1560)cos(930)cos(1380)sin1410----⋅°°°°sin(4360120)cos(3360150)=-⨯--⨯+°°°°cos(436060)sin(436030)--⨯+⨯-°°°° sin(120)cos150cos 60sin(30)=---°°°°1131() 1.222244=--+⨯=+=17答案及解析: 答案:tan α解析:原式[][]sin (cos )sin cos 22cos sin 2()sin ()sin 22αααααααα⎡π⎤⎛⎫-π+π+- ⎪⎢⎥⎝⎭⎣⎦=⎡π⎤⎛⎫-π+π--π-π++ ⎪⎢⎥⎝⎭⎣⎦[]sin sin cos 2sin()sin()sin 2αααααα⎡π⎤⎛⎫π+- ⎪⎢⎥⎝⎭⎣⎦=π⎛⎫π--π-+ ⎪⎝⎭sin sin cos 2sin (sin )cos αααααα⎡π⎤⎛⎫-- ⎪⎢⎥⎝⎭⎣⎦=-sin (sin )tan (sin )cos ααααα-==-.。
高一数学(必修二)寒假作业(立体几何)第Ⅰ卷(选择题,48分)一、选择题(本大题共12小题,每小题4分,共48分,在每小题给出的四个选项中,只有一项符合题目要求。
)1.若α、β是不重合的平面,a 、b 、c 是互不相同的空间直线,则下列命题中为真命题的是 ( ) ① 若α//a ,α//b ,则b a // ; ② 若α//c ,α⊥b ,则b c ⊥ ; ③ 若α⊥c ,β//c ,则βα⊥ ;④ 若α⊂b ,α⊂c 且b a ⊥,c a ⊥,则α⊥a A.③④ B. ①② C. ①④ D. ②③2.下列四个命题:①平行于同一平面的两条直线相互平行 ②平行于同一直线的两个平面相互平行 ③垂直于同一平面的两条直线相互平行 ④垂直于同一直线的两个平面相互平行 其中正确的有A .4个 B.3个 C.2个 D.1个3.某几何体的三视图如图所示,则该几何体的体积为( )A 、163πB 、203πC 、403πD 、5π4.已知正四棱锥的各棱棱长都为23,则正四棱锥的外接球的表面积为( ) A .π12B .π36C .π72D .π1085.某几何体的三视图如图所示,则该几何体的体积为A.168π+B.88π+C.1616π+D.816π+6..a ,b 表示空间不重合两直线,α,β表示空间不重合两平面,则下列命题中正确的是( )A.若α⊂a ,β⊂b ,且b a ⊥,则βα⊥B.若βα⊥,α⊂a ,β⊂b 则b a ⊥C.若α⊥a ,β⊥b ,βα//则b a //D.若βα⊥,α⊥a ,β⊂b ,则b a //7.下列命题中为真命题的是( ) A .平行于同一条直线的两个平面平行 B .垂直于同一条直线的两个平面平行C .若—个平面内至少有三个不共线的点到另—个平面的距离相等,则这两个平面平行.D .若三直线a 、b 、c 两两平行,则在过直线a 的平面中,有且只有—个平面与b ,c 均平行.8.如图是一个组合几何体的三视图,则该几何体的体积是 . A 36128π+ B 3616π+ C 72128π+ D 7216π+9.设l ,m 是两条不同的直线,α是一个平面,则下列命题正确的是( ) A .若l m ⊥,m α⊂,则l α⊥ B .若l α⊥,l m //,则m α⊥ C .若l α//,m α⊂,则l m // D .若l α//,m α//,则l m //10.已知某几何体的三视图如右图所示,其中,主(正)视图,左(侧)视图均是由直角三角形与半圆构成,俯视图由圆与内接直角三角形构成,根据图中的数据可得此几何体的 体积为( )16+ (B) 4136π+12+ (D)2132π+11.已知圆柱1OO 底面半径为1,高为π,ABCD 是圆柱的一个轴截面.动点M 从点B 出发沿着圆柱的侧面到达点D ,其距离最短时在侧面留下的曲线Γ如图所示.现将轴截面ABCD 绕着轴1OO 逆时针旋转 (0)θθπ<≤后,边11B C 与曲线Γ相交于点P ,设BP 的长度为()f θ,则()y f θ=的图象大致为( )12.某三棱锥的侧视图和俯视图如图--1所示,则该三棱锥的体积为( )A .4 3B .8 3C .12 3D .243第Ⅱ卷(非选择题,共72分)二、填空题(本大题共4个小题,每小题4分,共16分)13.如图,在三棱柱ABC C B A -111中, F E D ,,分别是1AA AC AB ,,的中点,设三棱锥ADE F -的体积为1V ,三棱柱ABC C B A -111的体积为2V ,则=21:V V _____.14. 已知圆的方程为22680x y x y +--=.设该圆过点(3,5)的最长弦和最短弦分别为AC 和BD ,则四边形ABCD 的面积为 .15.如右图为长方体积木块堆成的几何体的三视图,此几何体共由________块木块堆成..ABC1ADE F1B1C16.已知某个几何体的三视图如图(正视图中的弧线是半圆),图中标出的尺(单位:㎝), 可得这个几何体表面是 cm 2。
本文部分内容来自网络整理,本司不为其真实性负责,如有异议或侵权请及时联系,本司将立即删除!== 本文为word格式,下载后可方便编辑和修改! ==三年级数学寒假作业参考答案数学,是研究数量、结构、变化、空间以及信息等概念的一门学科,从某种角度看属于形式科学的一种。
下面是小编为你带来的三年级数学寒假作业参考答案,欢迎阅读。
一、单选题(选择正确答案的编号填在括号里)1.一把直尺的厚度大约是2( C )A:分米 B:厘米 C:毫米 D:千米2.下列图形中,( B )不是四边形。
A:长方形 B:三角形 C:正方形 D:平行四边形3. 下面算式正确的是( D )A:56÷6=8……8 B:8-8×0=0 C:250×4=100 D:4×205=8204.小雯每天回学校要走957米,小刚每天回学校要走1205米,小刚每天回学校比小雯多走( A )米。
A:248 B:258 C:358 D:21625.下面图形中,( B )是平行四边形。
A: B: C: D:6.估计478+379的计算结果,下列说法正确的是:( C )。
A:它们的和比1000大一些; B:它们的和比700小一些;C:478不到500,379不到400,它们的和肯定不到900; D:以上说法都不对。
7.一个纸箱可以装9瓶柚子蜜,50瓶柚子蜜至少需要( B )个纸箱。
A:5 B:6 C: 4 D:78.一只身长5厘米的蚱蜢一次可跳跃的距离是它身长的75倍,那么蚱蜢一次可跳跃的距离是( A )。
A:375厘米 B:80厘米 C:70厘米 D:75厘米9.一个生日蛋糕,小华吃了蛋糕的,妈妈吃了蛋糕的,爸爸跟妈妈吃得同样多,三人一共吃了这个生日蛋糕的( C )。
A: B: C: D:10.在16届广州亚运会上,我国运动员刘翔以13( D )09的成绩获得110米栏冠军,并连续三次获得亚运会此项目的金牌。
A:日 B:时 C:分 D:秒二、填空题1. 比较两个分数的大小。
杭州钱江学校高一数学寒假作业检测(答案在最后)一、单选题:本题共8小题,每小题5分,共40分.每小题给出的选项中,只有一项是符合题目要求.1.已知集合{}|02A x x =<<,集合{}|11B x x =-<<,集合{}|10C x mx =+>,若()A B C ⊆ ,则实数m 的取值范围为()A.{}|21m m -≤≤ B.1|12m m ⎧⎫-≤≤⎨⎬⎩⎭C.1|12m m ⎧⎫-≤≤⎨⎬⎩⎭D.11|24m m ⎧⎫-≤≤⎨⎬⎩⎭【答案】B 【解析】【分析】求出A ∪B ={x |﹣1<x <2},利用集合C ={x |mx +1>0},(A ∪B )⊆C ,分类讨论,可得结论.【详解】由题意,A ∪B ={x |﹣1<x <2},∵集合C ={x |mx +1>0},(A ∪B )⊆C ,①m <0,x 1m -<,∴1m -≥2,∴m 12≥-,∴12-≤m <0;②m =0时,C =R,成立;③m >0,x 1m ->,∴1m-≤-1,∴m ≤1,∴0<m ≤1,综上所述,12-≤m ≤1,故选:B .【点睛】此题考查了并集及其运算,以及集合间的包含关系,考查分类讨论的数学思想,属于中档题.2.三角函数值1sin ,2sin ,3sin 的大小顺序是A.123sin sin sin >> B.213sin sin sin >>C.132sin sin sin >> D.3 2 1sin sin sin >>【答案】B 【解析】【分析】先估计弧度角的大小,再借助诱导公式转化到090θ<< 上的正弦值,借助正弦函数在090θ<< 的单调性比较大小.【详解】解:∵1弧度≈57°,2弧度≈114°,3弧度≈171°.∴sin 1≈sin 57°,sin 2≈sin 114°=sin 66°.sin 3≈171°=sin 9°∵y =sin x 在090θ<< 上是增函数,∴sin 9°<sin 57°<sin 66°,即sin 2>sin 1>sin 3.故选B .【点睛】本题考查了正弦函数的单调性及弧度角的大小估值,是基础题.3.设a =log 54,b =(log 53)2,c =log 45,则()A.a <c <b B.b <c <aC.a <b <cD.b <a <c【答案】D 【解析】【详解】∵a =log 54<log 55=1,b =(log 53)2<(log 55)2=1,c =log 45>log 44=1,所以c 最大单调增,所以又因为所以b<a 所以b<a<c.故选D .4.已知函数74sin 20,66ππ⎛⎫⎛⎫⎡⎤=+∈ ⎪ ⎪⎢⎥⎝⎭⎣⎦⎝⎭y x x 的图象与直线y m =有三个交点的横坐标分别为()123123,,x x x x x x <<,那么1232x x x ++的值是()A.34πB.4π3 C.5π3D.3π2【答案】C 【解析】【分析】先作出74sin 20,66ππ⎛⎫⎛⎫⎡⎤=+∈ ⎪ ⎪⎢⎝⎭⎣⎦⎝⎭y x x 的图像,结合图像利用对称性即可求得结果.【详解】先作出函数74sin 20,66y x x ππ⎛⎫⎛⎫⎡⎤=+∈ ⎪⎪⎢⎥⎝⎭⎣⎦⎝⎭的图象,如图,令4sin 246y x π⎛⎫=+=± ⎪⎝⎭,可得6x π=和23x π=,所以由对称性可得1223242,26333x x x x ππππ+=⨯=+=⨯=,故123523x x x π++=,故选:C.5.设(),0,παβ∈,()5sin 13αβ+=,1tan 22α=,则cos β的值是()A.1665-B.1665C.3365- D.3365【答案】A 【解析】【分析】根据半角公式得出α的正切值,继而得出其正弦值和余弦值,再根据α的取值范围和题意判断出π,π2αβ⎛⎫+∈ ⎪⎝⎭,并得出αβ+的余弦值,最后根据恒等变换公式计算[]cos cos ()βαβα=+-即可.【详解】22tan142tan tan 12231tan 2αααα=⇒==>- ,因为(),0,παβ∈,ππ,42α⎛⎫∴∈ ⎪⎝⎭,且4sin cos 3αα=,又223sin cos 1cos 5ααα+=⇒=,得4sin 5α=.因为()0,πβ∈,则π3π,42αβ⎛⎫+∈⎪⎝⎭,又5sin()132αβ+=<,所以π,π2αβ⎛⎫+∈ ⎪⎝⎭,12cos()13αβ∴+=-,[]16cos cos ()cos()cos sin()sin 65βαβααβααβα=+-=+++=-.故选:A.6.设函数()2sin()f x x ωϕ=+,x R ∈,其中0ω>,||ϕπ<.若5()28f π=,(08f 11π=,且()f x 的最小正周期大于2π,则A.23ω=,12πϕ= B.23ω=,12ϕ11π=-C.13ω=,24ϕ11π=- D.13ω=,724πϕ=【答案】A 【解析】【详解】由题意125282118k k ωππϕπωπϕπ⎧+=+⎪⎪⎨⎪+=⎪⎩,其中12,k k Z ∈,所以2142(2)33k k ω=--,又22T ππω=>,所以01ω<<,所以23ω=,11212k ϕ=π+π,由ϕπ<得12πϕ=,故选A.【考点】求三角函数的解析式【名师点睛】有关sin()y A x ωϕ=+问题,一种为提供函数图象求解析式或某参数的范围,一般先根据图象的最高点或最低点确定A ,再根据周期或12周期或14周期求出ω,最后再利用最高点或最低点坐标满足解析式,求出满足条件的ϕ值,另一种时根据题目用文字形容的函数图象特点,如对称轴或曲线经过的点的坐标,根据题意自己画出图象,再寻求待定的参变量,题型很活,求ω或ϕ的值或最值或范围等.7.设()|31|x f x =-,c b a <<且()()()f c f a f b >>,则下列关系中一定成立的是A .3c >3bB.3b >3aC.3c +3a >2D.3c +3a <2【答案】D 【解析】【分析】画出()|31|x f x =-的图象,利用数形结合,分析可得结果.【详解】作出()131xf x =-的图象,如图所示,要使c b a <<,且()()()f c f a f b >>成立,则有0c <且0a >,313c a ∴<<,()()13,31c a f c f a ∴=-=-,又()()f c f a >,1331c a ∴->-,即332a c +<,故选D.【点睛】通过数与形的相互转化来解决数学问题的一种重要思想方法,.函数图象是函数的一种表达形式,它形象地揭示了函数的性质,为研究函数的数量关系提供了“形”的直观性.归纳起来,图象的应用常见的命题探究角度有:1、确定方程根的个数;2、求参数的取值范围;3、求不等式的解集;4、研究函数性质.8.已知()f x 是偶函数,且()f x 在[0,)+∝上是增函数,若()()12f ax f x +≤-在1,12x ⎡⎤∈⎢⎥⎣⎦上恒成立,则实数a 的取值范围是()A.[﹣2,1] B.[﹣5,0]C.[﹣5,1]D.[﹣2,0]【答案】D 【解析】【分析】利用函数的奇偶性和单调性,可得|ax +1|≤|x ﹣2|对112x ⎡⎤∈⎢⎥⎣⎦恒成立,再分离参数利用函数单调性求最值即可求解【详解】由题意可得|ax +1|≤|x ﹣2|对112x ⎡⎤∈⎢⎥⎣⎦,恒成立,得x ﹣2≤ax +1≤2﹣x 对112x ⎡⎤∈⎢⎥⎣⎦,恒成立,从而3x a x -≥且1x a x -≤对112x ⎡⎤∈⎢⎥⎣⎦,恒成立,又3x y x -=单调递增∴a ≥﹣21xy x-=;单调递减,所以a ≤0,即a ∈[﹣2,0],故选D .【点睛】本题考查的是不等式、函数性质以及恒成立有关的综合类问题.在解答的过程当中充分体现了函数的性质、恒成立的思想以及问题转化的能力,属于中档题.二、多选题:本题共4小题,共20分.每小题给出的选项中,有多项符合题目要求.9.存在函数()f x 满足:对任意x ∈R 都有()A.()sin cos f x x =B.()sin sin 2f x x =C.()cos cos 2f x x =D.()sin sin 3f x x=【答案】CD 【解析】【分析】分别取0x =、x π=可得()01f =、()01f =-,A 错误;同理,取3x π=、23x π=可得(22f =、(22f =-,B 错误;利用三角恒等变换将cos 2x 整理为关于cos x 的二次函数可判断C ;同理可判断D.【详解】A :取0x =时,sin 0,cos 1x x ==,()01f =,取x π=时,sin 0,cos 1x x ==-,()01f =-,故A 不正确;B :取3x π=时,sin ,sin 222x x ==,(22f =,取23x π=时,sin ,sin 222x x ==-,(22f =-,故B 错误;C :()2cos cos 22cos 1f x x x ==-,令cos ,[1,1]t x t =∈-,则()221f t t =-,C 正确;D :()sin sin 3sin(2)sin 2cos cos 2sin f x x x x x x x x==+=+222sin (1sin )(12sin )sin x x x x=⨯-+-⨯3332sin 2sin sin 2sin 3sin 4sin x x x x x x=-+-=-令sin ,[1,1]t x t =∈-,则()334,[1,1]f t t t t =-∈-,D 正确.故选:CD10.下列不等式中,正确的是().A.13π13πtan tan 45< B.ππsincos 57⎛⎫<- ⎪⎝⎭C.ππsin 55> D.ππtan 55>【答案】BC 【解析】【分析】利用诱导公式及三角函数的单调性判断A 、B ,利用三角函数线证明当π02x <<时sin tan <<x x x ,即可判断C 、D.【详解】对于A :13πππtantan 3πtan 1444⎛⎫=+== ⎪⎝⎭,13π2π2πtantan 3πtan 0555⎛⎫=-=-< ⎪⎝⎭,所以13π13πtan tan 45>,故A 错误;对于B :因为ππππ7654<<<,且sin y x =在π0,2⎛⎫ ⎪⎝⎭上单调递增,cos y x =在π0,2⎛⎫⎪⎝⎭上单调递减,所以1πππ2sin sin sin 26542=<<=,又πππcos cos cos 7762⎛⎫-=>= ⎪⎝⎭,所以ππsincos 57⎛⎫<- ⎪⎝⎭,故B 正确;对于C 、D :首先证明当π02x <<时sin tan <<x x x ,构造单位圆O ,如图所示:则()1,0A ,设π0,2POA x ⎛⎫∠=∈ ⎪⎝⎭,则()cos ,sin P x x ,过点A 作直线AT 垂直于x 轴,交OP 所在直线于点T ,由=tan ATx OA,得=tan AT x ,所以()1,tan T x ,由图可知OPA TOA OPA S S S << 扇形,即21111sin 11tan 222x x x ⨯⨯<⨯⨯<⨯⨯,即sin tan <<x x x π02x ⎛⎫<< ⎪⎝⎭,所以ππsin 55>,ππtan 55<,故C 正确,D 错误;故选:BC11.关于函数()|ln |2||f x x =-,下列描述正确的有()A.()f x 在区间(1,2)上单调递增B.()y f x =的图象关于直线2x =对称C.若1212,()(),x x f x f x ≠=则124x x +=D.()f x 有且仅有两个零点【答案】ABD 【解析】【分析】作出函数()f x 的图象,由图象观察性质判断各选项.【详解】根据图象变换作出函数()f x 的图象(()ln 2f x x =-,作出ln y x =的图象,再作出其关于y 轴对称的图象,然后向右平移2个单位,最后把x 轴下方的部分关于x 轴翻折上去即可得),如图,由图象知()f x 在(1,2)是单调递增,A 正确,函数图象关于直线2x =对称,B 正确;12()()f x f x k ==,直线y k =与函数()f x 图象相交可能是4个交点,如图,如果最左边两个交点横坐标分别是12,x x ,则124x x +=不成立,C 错误,()f x 与x 轴仅有两个公共点,即函数仅有两个零点,D 正确.故选:ABD .12.设函数()f x 的定义域为R ,满足()()12f x f x +=,且当(]0,1x ∈时,()()1f x x x =-.若对任意(],x m ∈-∞,都有()89f x ≥-,则实数m 的值可以是()A.94B.73C.52D.83【答案】AB 【解析】【分析】因为(1)2()f x f x +=,可得()2(1)f x f x =-,分段求解析式,结合图象可得.【详解】解:因为(1)2()f x f x +=,()2(1)f x f x ∴=-,函数图象如下所示:(0x ∈ ,1]时,1()(1)[4f x x x =-∈-,0],(1x ∴∈,2]时,1(0x -∈,1],1()2(1)2(1)(2)[2f x f x x x =-=--∈-,0];(2x ∴∈,3]时,1(1x -∈,2],()2(1)4(2)(3)[1f x f x x x =-=--∈-,0],当(2x ∈,3]时,由84(2)(3)9x x --=-解得73x =或83x =,若对任意(x ∈-∞,]m ,都有8()9f x - ,则73m .故选:AB .【点睛】本题考查分段函数的性质的应用,解答的关键是根据函数的性质画出函数图象,数形结合即可得解;三、填空题:本题共4小题,每小题5分,共20分.13.函数()()21256f x log x x =-+-的单调减区间是______.【答案】522,⎛⎫ ⎪⎝⎭【解析】【分析】根据对数函数的定义域及复合函数单调性的判断即可求得单调递减区间.【详解】因为()()21256f x log x x =-+-所以2560x x -+->解得()2,3x ∈因为()12f x log x =为单调递减函数,所以由复合函数单调性判断可知应该取()256f x x x =-+-的单调递增区间,即5,2x ⎛⎫∈-∞ ⎪⎝⎭结合定义域可得函数()()21256f x log x x =-+-的单调减区间是522,⎛⎫⎪⎝⎭【点睛】本题考查了复合函数单调区间的求法,注意对数函数的真数大于0,属于基础题.14.已知0a >,0b >,且111a b +=,则1411a b +--的最小值为___.【答案】4【解析】【分析】由等式111a b +=可得出1a >,1b >以及1a b a =-,代入1411a b +--可得出()14141111a ab a +=+----,利用基本不等式可求得结果.【详解】0a > ,0b >,且111a b +=,得1a >,1b >以及1ab a =-,()14141414111111a a ab a a a ∴+=+=+-≥=------,当且仅当32a =时,等号成立,因此,1411a b +--的最小值为4.故答案为:4.【点睛】本题考查利用基本不等式求最值,解题时注意对定值条件进行化简变形,考查计算能力,属于中等题.15.函数f (x )=log 2(kx 2+4kx +3).①若f (x )的定义域为R ,则k 的取值范围是_____;②若f (x )的值域为R ,则k 的取值范围是_____.【答案】①.[0,34)②.k 34≥【解析】【分析】(1)根据()f x 的定义域为R ,对k 分成0,0,0k k k =><三种情况分类讨论,结合判别式,求得k 的取值范围.(2)当()f x 值域为R 时,由00k >⎧⎨∆≥⎩求得k 的取值范围.【详解】函数f (x )=log 2(kx 2+4kx +3).①若f (x )的定义域为R ,可得kx 2+4kx +3>0恒成立,当k =0时,3>0恒成立;当k >0,△<0,即16k 2﹣12k <0,解得0<k 34<;当k <0不等式不恒成立,综上可得k 的范围是[0,34);②若f (x )的值域为R ,可得y =kx 2+4kx +3取得一切正数,则k >0,△≥0,即16k 2﹣12k ≥0,解得k 34≥.故答案为:(1).[0,34)(2).k 34≥【点睛】本小题主要考查根据对数型复合函数的定义和值域求参数的取值范围,属于中档题.16.函数253sin cos 82y x a x a =+⋅+-在闭区间0,2π⎡⎤⎢⎥⎣⎦上的最大值是1,则=a __________.【答案】32【解析】【分析】令[]cos ,0,1x t t =∈,即求25218y t at a =-++-在[]0,1上的最大值,需要根据对称轴的位置进行分类讨论即可求出结果.【详解】22535sin cos cos cos 82812y x a x a x a x a =+⋅+-=-+⋅+-,令[]cos ,0,1x t t =∈,则25218y t at a =-++-,对称轴2at =,若02a ≤,即0a ≤时,25218y t at a =-++-在0=t 处取得最大值,即51821a -=,解得125a =,与0a ≤矛盾,故不合题意,舍去;若012a <<,即12a <<时,25218y t at a =-++-在2a t =处取得最大值,即25122821a a a a ⎛⎫-+⋅+-= ⎪⎝⎭,即225120a a +-=,解得4a =-或32a =,因为12a <<,所以32a =;若12a ≥,即2a ≥时,25218y t at a =-++-在1t =处取得最大值,即251=1821a a -++-,解得2013a =,与2a ≥矛盾,故不合题意,舍去;综上:32a =.故答案为:32.四、解答题:本题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.17.已知a ∈R ,集合{}2230A x x x =--≤,{}220B x x ax =--=.(1)若1a =,求A B ⋂;(2)若A B A ⋃=,求实数a 的取值范围.【答案】(1){}2,1-(2)71,3⎡⎤⎢⎥⎣⎦【解析】【分析】(1)首先解一元二次不等式求出集合A ,再根据条件求出集合B ,最后根据交集的定义计算可得;(2)依题意可得B A ⊆,则问题转化为关于x 的方程220x ax --=在区间[]1,3-上有两个不相等的实数根,结合二次函数的性质计算可得.【小问1详解】由2230x x --≤,即()()130x x +-≤,解得13x -≤≤,所以{}{}2230|13A x x x x x =--≤=-≤≤当1a =时{}{}2202,1B x x x =--==-,所以{}2,1A B =- 【小问2详解】因为A B A ⋃=,所以B A ⊆,关于x 的方程220x ax --=,因为280a ∆=+>,所以关于x 的方程220x ax --=必有两个不相等的实数根,依题意关于x 的方程220x ax --=在区间[]1,3-上有两个不相等的实数根,所以()()2213211203320a a a ⎧-<<⎪⎪⎪--⨯--≥⎨⎪--≥⎪⎪⎩,解得713a ≤≤,所以实数a 的取值范围为71,3⎡⎤⎢⎥⎣⎦.18.设集合{}12A x x =-≤≤,{}121B x m x m =-<<+.(1)若B A ⊆,求实数m 的取值范围;(2)若()R B A I ð中只有一个整数2-,求实数m 的取值范围.【答案】(1)(]1,20,2⎡⎤-∞-⎢⎥⎣⎦ ;(2)3,12⎛⎫-- ⎪⎝⎭.【解析】【分析】(1)分B =∅和B ≠∅两种情况讨论,结合B A ⊆列出关于实数m 的不等式(组),解出即可得出实数m 的取值范围;(2)求出集合R A ð,由题意得知B ≠∅,且有1213122213m m m m -<+⎧⎪-≤-<-⎨⎪-<+≤⎩,解该不等式组即可得出实数m 的取值范围.【详解】(1)集合{}12A x x =-≤≤,{}121B x m x m =-<<+.①当B =∅时,121m m -≥+,解得2m ≤-,符合要求;②当B ≠∅时,若B A ⊆,121m m -<+,则12111212m m m m -<+⎧⎪-≥-⎨⎪+≤⎩,解得102m ≤≤.综上,实数m 的取值范围是(]1,20,2⎡⎤-∞-⎢⎥⎣⎦;(2) 集合{}12A x x =-≤≤,{1R A x x ∴=<-ð或}2x >,若()B A R ð中只有一个整数2-,则必有B ≠∅,1213122213m m m m -<+⎧⎪∴-≤-<-⎨⎪-<+≤⎩,解得312m -<<-,因此,实数m 的取值范围是3,12⎛⎫-- ⎪⎝⎭.【点睛】本题考查利用集合的包含关系求参数的取值范围,同时也考查了利用交集与补集的混合运算求参数,解题时要结合题意列出不等式组进行求解,考查分析问题和解决问题的能力,属于中等题.19.设函数()sin ,f x x x =∈R .(1)已知[0,2),θ∈π函数()f x θ+是偶函数,求θ的值;(2)求函数22[()][()]124y f x f x ππ=+++的值域.【答案】(1)3,22ππ;(2)331,122⎡-+⎢⎣⎦.【解析】【分析】(1)由函数的解析式结合偶函数的性质即可确定θ的值;(2)首先整理函数的解析式为()sin y a x b ωϕ=++的形式,然后确定其值域即可.【详解】(1)由题意结合函数的解析式可得:()()sin f x x θθ+=+,函数为偶函数,则当0x =时,()02k k Z πθπ+=+∈,即()2k k Z πθπ=+∈,结合[)0,2θ∈π可取0,1k =,相应的θ值为3,22ππ.(2)由函数的解析式可得:22sin sin 124y x x ππ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭1cos 21cos 26222x x ππ⎛⎫⎛⎫-+-+ ⎪ ⎪⎝⎭⎝⎭=+11cos 2cos 2226x x ππ⎡⎤⎛⎫⎛⎫=-+++ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦111cos 2sin 2sin 2222x x x ⎛⎫=--- ⎪ ⎪⎝⎭1331cos 2sin 2222x x ⎛⎫=-- ⎪ ⎪⎝⎭31sin 226x π⎛⎫=+- ⎪⎝⎭.据此可得函数的值域为:1,122⎡-+⎢⎣⎦.【点睛】本题主要考查由三角函数的奇偶性确定参数值,三角函数值域的求解,三角函数式的整理变形等知识,意在考查学生的转化能力和计算求解能力.20.已知函数())2πcos 204f x x x ωωω⎛⎫=-++> ⎪⎝⎭的最小正周期是π.(1)求函数()y f x =的单调递增区间;(2)若对任意的π5π,1212x ⎡⎤∈-⎢⎥⎣⎦,都有()2f x m -≤,求m 的取值范围.【答案】(1)62ππ,π,Zπ3k k k ⎡⎤-+-+∈⎢⎥⎣⎦(2)2,0⎤-⎦【解析】【分析】(1)利用二倍角公式及两角和的余弦公式化简,再根据周期公式求出ω,即可得到函数解析式,最后根据余弦函数的性质求出单调递增区间;(2)由x 的取值范围求出π23x +的范围,即可求出()f x 的值域,由()22m f x m -≤≤+恒成立得到关于m 的不等式组,解得即可.【小问1详解】因为()2πcos 24f x x x ωω⎛⎫=-++ ⎪⎝⎭πcos 224x x ωω⎛⎫=+ ⎪⎝⎭πcos 222x x ωω⎛⎫=++ ⎪⎝⎭cos 22x xωω=132cos 2sin 222x x ωω⎛⎫=- ⎪ ⎪⎝⎭π2cos 23x ω⎛⎫=+ ⎪⎝⎭,又0ω>且函数的最小正周期是π,所以2ππ2T ω==,解得1ω=,所以()π2cos 23f x x ⎛⎫=+ ⎪⎝⎭,令Z ππ2π22π,3k x k k -+≤+≤∈,解得2ππππ,Z 36k x k k ≤--+≤+∈,所以函数()y f x =的单调递增区间为62ππ,π,Z π3k k k ⎡⎤-+-+∈⎢⎥⎣⎦.【小问2详解】当π5π,1212x ⎡⎤∈-⎢⎣⎦,则ππ7π2,366x ⎡⎤+∈⎢⎥⎣⎦,所以πcos 21,32x ⎡⎛⎫+∈-⎢ ⎪⎝⎭⎣⎦,则()f x ⎡∈-⎣,因为对任意的π5π,1212x ⎡⎤∈-⎢⎥⎣⎦,都有()2f x m -≤,即对任意的π5π,1212x ⎡⎤∈-⎢⎣⎦,都有()22f x m -≤-≤,即对任意的π5π,1212x ⎡⎤∈-⎢⎣⎦,都有()22m f x m -≤≤+,所以222m m ⎧+≥⎪⎨-≤-⎪⎩20m ≤≤,即m的取值范围为2,0⎤-⎦.21.已知函数()ln (0,e 2.71828e xaf x x a =->=L 为自然对数的底数).(1)当1a =时,判断函数()f x 的单调性和零点个数,并证明你的结论;(2)当[]1,e x ∈时,关于x 的不等式()2ln f x x a >-恒成立,求实数a 的取值范围.【答案】(1)函数()f x 的零点个数为1个,证明见解析(2)()e 1e,∞++【解析】【分析】(1)利用函数单调性证明,再利用零点存在性定理即可知零点个数.(2)将()2ln f x x a >-转化为ln ln e ln e ln a x x a x x -+-+>,构造函数()e xg x x =+,转化为ln ln a x x ->,即ln ln a x x >+,即()max ln ln a x x >+,求解即可.【小问1详解】函数()f x 的定义域为()0,∞+.当1a =时,函数()e1ln x f x x =-在()0,∞+上单调递减,证明如下:任取()12,0,x x ∈+∞,且12x x <,()()12121212211111ln ln ln ln e e e ex x x x f x f x x x x x -=--+=--211221e e ln e e x x x x x x -=+⋅∵120x x <<,∴21211,e e 0x x x x >->,21ln 0xx ∴>∴()()120f x f x ->,即()()12f x f x >.所以函数()e1ln x f x x =-在()0,∞+上单词递减.又1111(1)ln10,(e)ln e 10e e e ex x f f =-=>=-=-<∴()e 1ln xf x x =-在区间()1,e 上存在零点,且为唯一的零点.∴函数()f x 的零点个数为1个【小问2详解】()2ln f x x a >-可化为ln 2ln e xaa x x +>+.可化为ln e ln ln a x a x x x -+->+.可化为ln ln e ln e ln a x x a x x -+-+>.令()e xg x x =+,可知()e x g x x =+在R 单调递增,所以有ln ln a x x ->,即ln ln a x x>+令()ln h x x x =+,可知()ln h x x x =+在(0,)+∞上单调递增.即()ln h x x x =+在[]1,e 上单调递增,max ()(e)ln e e 1eh x h ==+=+e 1max ln ()e 1ln e a h x +∴>=+=,e 1e a +∴>所以实数a 的取值范围是()e 1e,∞++.【点睛】方法点睛:本题考查不等式的恒成立问题,不等式恒成立问题常见方法:①分离参数()a f x ≥恒成立(()max a f x ≥即可)或()a f x ≤恒成立(()min a f x ≤即可);②数形结合(()y f x =图像在()y g x =上方即可);③讨论最值()min 0f x ≥或()max 0f x ≤恒成立.22.已知函数2()|2|f x x x x a =+-,其中a 为实数.(Ⅰ)当1a =-时,求函数()f x 的最小值;(Ⅱ)若()f x 在[1,1]-上为增函数,求实数a 的取值范围;(Ⅲ)对于给定的负数a ,若存在两个不相等的实数12,x x (12x x <且20x ≠)使得12()()f x f x =,求112x x x +的取值范围.【答案】(Ⅰ)12-(Ⅱ)2a ≤-或0a >;(Ⅲ)见解析【解析】【分析】(Ⅰ)由题可知2222,2()22,2x ax x af x x x x a ax x a⎧-≥=+-=⎨<⎩当1a =-时,222,2()2,2x x x f x x x ⎧+≥-=⎨-<-⎩,分别讨论该函数在各段上的最小值和区间端点值,进而求出在整个定义域上的最小值;(Ⅱ)因为()f x 在[1,1]-上为增函数,分0a >,0a =,0a =三种情况讨论即可(Ⅲ)因为a<0,则()f x 在(,)2a -∞上为减函数,在(,)2a +∞上为增函数,所以122ax x <<,令112x x M x +=,分122aa x ≤<,12x a <两种情况具体讨论即可.【详解】解:2222,2()22,2x ax x a f x x x x a ax x a⎧-≥=+-=⎨<⎩(Ⅰ)当1a =-时,222,2()2,2x x x f x x x ⎧+≥-=⎨-<-⎩所以当12x =-时()()2222f x x x x +=≥-有最小值为1122f ⎛⎫-=- ⎪⎝⎭;当2x =-时,由()()22f x x x =-<-得()1242f -=>-,所以当1a =-时,函数()f x 的最小值为12-(Ⅱ)因为()f x 在[1,1]-上为增函数,若0a >,则()f x 在R 上为增函数,符合题意;若0a =,不合题意;若a<0,则12a≤-,从而2a ≤-综上,实数a 的取值范围为2a ≤-或0a >.(Ⅲ)因为a<0,则()f x 在(,)2a -∞上为减函数,在(,)2a +∞上为增函数,所以122ax x <<,令112x x M x +=1、若122a a x ≤<,则12x x a +=,由20x ≠知22a x a <≤-且20x ≠所以121222221x a x a x a x x a x x x -+=+-=--+令()1ag x x a x=--+,则()g x 在,[上为增函数,在)+∞,(-∞上为减函数(1)当4a ≤-时,2a≤a ->,则()g x 在,[上为增函数,在]a -,[2a上为减函数从而当22ax a <<-且20x ≠所以2()1g x a ≥-+或2()1g x a≤--+(2)当41a -<<-时,2a>且a ->,则()g x 在,[,0)2a上为增函数,在]a -上为减函数从而当22ax a <<-且20x ≠所以2()12ag x >+或2()1g x a ≤-+(3)当10a -≤<时,2a >且a -<,则()g x 在(0,]a -,[,0)2a上为增函数,从而当22ax a <<-且20x ≠所以2()12ag x >+或2()22g x a <-2、若12x a <,则2122222ax x ax =-,2212x x x a=-且2x a>-第21页/共21页2222222211222(,22)(11)1x x x x a x a a x a x x x x a+=+=--∞-∈+---因为221a a-≤-+综上所述,当4a ≤-时,112x x x +的取值范围为(,1]1,)a a -∞--+-++∞ ;当41a -<<-时,112x x x +的取值范围为(,1](1,)2a a +-∞--++∞ ;当10a -≤<时,112x x x +的取值范围为(,22)(1,)2a a -∞-++∞ .【点睛】本题考查函数的综合应用,包括求最值,单调性,分类讨论思想等,属于偏难题目.。
15高三数学寒假作业十五(含答案)一、填空题1.A={x|x≤2},B={-1,1,2},则A∩B={-1,1,2}。
2.z=1+i。
3.输出结果为12.4.y=3x²/31.5.m=1/2.6.概率为2/5.7.最大值为5.8.g(x)=2cos(2(x+π))/π。
9.1/3.10.a1=3,q=2/3.11.b-a=π/6.12.m≤-3或m≥-1.13.x-y=3.14.最大值为5.二、解答题15.证明:设a,b,c,d为正整数,且a<b<c<d,且a+d=b+c,则d-a=b-c。
因为a+d=b+c,所以a+c=b+d。
又因为a<b<c<d,所以a+c<b+c<d+c,即a+c<d+c。
所以d-a<b-c,即d-a≤b-c-1.因为d-a和b-c都是正整数,所以d-a≤b-c-2.所以d-a≤(b-a)-(c-b)≤2.因为a<b<c<d,所以d-a≥3.所以d-a=3,b-c=2,即d=b+2,c=b+1,a=b-1.所以a=11,b=12,c=13,d=14.因此,满足条件的四个正整数为11,12,13,14.1) 数列 $\{a_n\}$ 的通项公式为 $a_n =n(1+\frac{1}{n+1})$。
2) 数列 $\{b_n\}$ 的通项公式为 $b_n =\sqrt{\frac{a_{n+1}}{n}}$。
3) 数列 $\{c_n\}$ 中不存在不同两项 $c_i。
c_j$ ($1\leq i<j。
i,j\in \mathbb{N}$),使得 $c_i+c_j$ 是数列 $\{c_n\}$ 的项。
解析:1) 首先对 $a_{n+1}$ 进行变形,得到 $a_{n+1} =(n+1)(1+\frac{1}{n+2})$。
然后将 $a_{n+1}$ 带入 $a_n$ 的式子中,得到 $a_n =n(1+\frac{1}{n+1})$。