学生 第2讲 相似三角形培优讲义2

相似三角形知识点总结知识点1、三角对应相等，三边对应成比例的三角形叫相似三角形。

如△ABC 与△A /B /C /相似，记作: △ABC ∽△A /B /C / 。

相似三角形的比叫相似比相似三角形的定义既是相似三角形的性质，也是三角形相似的判定方法。

注意：（1）相似比是有顺序的。

（2）对应性，两个三角形相似时，通常把对应顶点写在对应位置，这样写比较容易找到相似三角形的对应角和对应边。

（3）顺序性：相似三角形的相似比是有顺序的，若△ABC ∽△A /B /C /，相似比为k ，则△A /B /C /与△ABC 的相似比是1k知识点2、相似三角形与全等三角形的关系（1）两个全等的三角形是相似比为1的相似三角形。

（2）两个等边三角形一定相似，两个等腰三角形不一定相似。

（3）二者的区别在于全等要对应边相等，而相似要求对应边成比例。

知识点3、平行线分线段成比例定理1. 比例线段的有关概念： 在比例式：：中，、叫外项，、叫内项，、叫前项，a b cda b c d a d b c a c ==() b 、d 叫后项，d 叫第四比例项，如果b=c ，那么b 叫做a 、d 的比例中项。

把线段AB 分成两条线段AC 和BC ，使AC 2=AB ·BC ，叫做把线段AB 黄金分割，C 叫做线段AB 的黄金分割点。

2. 比例性质： ①基本性质：a b c d ad bc =⇔= ②合比性质：±±a b c d a b b c dd=⇒=③等比性质：……≠……a b c d m n b d n a c m b d n a b===+++⇒++++++=()0 3. 平行线分线段成比例定理（1）平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.已知l1∥l2∥l3,A D l1B E l2C F l3可得EF BC DE AB DF EF AC BC DF EF AB BC DF DE AC AB EF DE BC AB =====或或或或等.（2）推论:平行于三角形一边的直线截其它两边(或两边的延长线)所得的对应线段成比例. AD EB C由DE ∥BC 可得：AC AEAB AD EA EC AD BD EC AE DB AD ===或或.此推论较原定理应用更加广泛,条件是平行.（3）推论的逆定理：如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例.那么这条直线平行于三角形的第三边.此定理给出了一种证明两直线平行方法,即：利用比例式证平行线. （4）定理:平行于三角形的一边,并且和其它两边相交的直线,所截的三角形的三边与原三角形三边对应成比例.知识点4：相似三角形的性质①相似三角形的对应角相等 ②相似三角形的对应边成比例③相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比 ④相似三角形周长的比等于相似比⑤相似三角形面积的比等于相似比的平方知识点5：相似三角形的判定：①两角对应相等，两个三角形相似②两边对应成比例且夹角相等，两三角形相似 ③三边对应成比例，两三角形相似④如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角形相似⑤平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似⑥直角三角形被斜边上的高分成的两个直角三角形和原三角形相似如果两个三角形的两角分别于另一个三角形的两角对应相等，那么这两个三角形相似。

相似三角形培优备课老师：梁老师 学生：王子建【核心知识梳理】一、比例线段和三角形一边的平行线知识要点1. 比例线段的有关概念：在比例式：：中，、叫外项，、叫内项，、叫前项，a b cda b c d a d b c a c ==()b 、d 叫后项，d 叫第四比例项，如果b=c ，那么b 叫做a 、d 的比例中项。

把线段AB 分成两条线段AC 和BC ，使AC 2=AB ²BC ，叫做把线段AB 黄金分割，C 叫做线段AB 的黄金分割点。

2. 比例性质：①基本性质：a b cd ad bc=⇔=②合比性质：±±a b c d a b b c d d =⇒=③等比性质：……≠……a b c d m n b d n a c m b d n a b ===+++⇒++++++=()03. 平行线分线段成比例定理：①定理：三条平行线截两条直线，所得的对应线段成比例，如图：l 1∥l 2∥l 3。

则，，，…AB BC DE EF AB AC DE DF BC AC EFDF ===②推论：平行于三角形一边的直线截其他两边（或两边的延长线）所得的对应线段成比例。

③定理：如果一条直线截三角形的两边（或两边的延长线）所得的对应线段成比例，那么这条直线平行于三角形的第三边。

编号3二、归纳导入(呈现知识)1、相似三角形的概念（1）对应角相等，对应边成比例的三角形，叫做相似三角形。

相似用符号“∽”表示，读作“相似于” 。

（2）相似三角形对应角相等，对应边成比例。

（3）相似三角形对应边的比叫做相似比(或相似系数)。

（4）全等三角形是相似比为1的相似三角形．二者的区别在于全等要求对应边相等，而相似要求对应边成比例。

（5）相似三角形的等价关系①反身性：对于任一ABC ∆有ABC ∆∽ABC ∆。

②对称性：若ABC ∆∽'''C B A ∆，则'''C B A ∆∽ABC ∆。

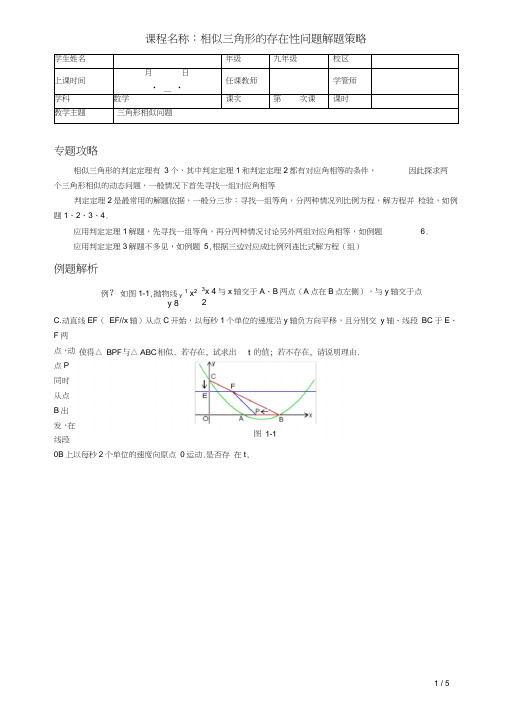
课程名称：相似三角形的存在性问题解题策略学生姓名年级九年级 校区上课时间 月日• __ •任课教师学管师学科数学课次第次课课时教学主题三角形相似问题专题攻略相似三角形的判定定理有 3个，其中判定定理1和判定定理2都有对应角相等的条件， 因此探求两个三角形相似的动态问题，一般情况下首先寻找一组对应角相等判定定理2是最常用的解题依据，一般分三步：寻找一组等角，分两种情况列比例方程，解方程并 检验，如例题1、2、3、4.应用判定定理1解题，先寻找一组等角，再分两种情况讨论另外两组对应角相等，如例题 6. 应用判定定理3解题不多见，如例题 5,根据三边对应成比例列连比式解方程（组）例题解析3x 4与x 轴交于A 、B 两点（A 点在B 点左侧），与y 轴交于点2C.动直线EF （ EF//x 轴）从点C 开始，以每秒1个单位的速度沿y 轴负方向平移，且分别交 y 轴、线段 BC 于E 、F 两点，动点P 同时从点B 出发，在线段0B 上以每秒2个单位的速度向原点 0运动.是否存 在t ,例？ 如图1-1,抛物线y 1 x 2 y 8例？ 如图2-1,在平面直角坐标系中，顶点为 M 的抛物线y = ax 2 + bx (a > 0)经过点A 和x 轴正半轴上的点 B ，AO = BO = 2,Z AOB = 120°.(1) 求这条抛物线的解析式； (2) 连结OM ,求/ AOM 的大小；(3) 如果点 C 在x 轴上，且△ ABC 与厶AOM 相似，求点 C 的坐标.例？ 如图3-1，抛物线y = ax 2 + bx — 3与x 轴交于A(1,0)、B(3, 0)两点，与y 轴交于点D ,顶点为C . (1 )求此抛物线的解析式；(2)在x 轴下方的抛物线上是否存在点M ，过M 作MN 丄x 轴于点N ,使以A 、M 、N 为顶点的三角形与△ BCD 相似？若存在，求出点 M 的坐标；若不存在，请说明理由.例？ 如图4-1，在平面直角坐标系中，A(8,0), B(0,6)，点C 在x 轴上，BC 平分/ OBA .点P 在直线图2-MAB上，直线CP与y轴交于点F,如果△ ACP与厶BPF相似，求直线CP的解析式.例？如图5-1,二次函数y= x2+ 3x的图象经过点A(1,a),线段AD平行于x轴，交抛物线于点D.在y轴上取一点C(0, 2)，直线AC交抛物线于点B，连结OA、OB、OD、BD.求坐标平面内使厶EOM A AOB 的点E的坐标；例？如图6-1，在△ ABC中，AB= AC= 4 2 , BC= 8. CA的半径为2，动点P从点B出发沿BC 方向以每秒1个单位的速度向点C运动.延长BA交G A于点D,连结AP交GA于点E,连结DE并延长交BC于点F.设点P运动的时间为t秒，当△ ABP与厶FBD相似时，求t的值.课后练习：1.如图5- 1-3,已知二次函数y= —x2+ bx+ c(b, c为常数)的图象经过点A(3, 1),点C(0, 4),顶点为M，过点A作AB// x轴，交y轴于点D，交该二次函数图象于点B,连结BC.(1) 求该二次函数的表达式及点M的坐标；(2) 若将该二次函数图象向下平移m(m>0)个单位，使平移后得到的二次函数图象的顶点落在△ ABC的内部(不包括△ ABC的边界)，求m的取值范围;⑶点P是直线AC上的动点，若点P, C, M所构成的三角形与△ BCD相似，请直接写出所有点P的坐标.。

相似三角形知识点总结知识点1、三角对应相等，三边对应成比例的三角形叫相似三角形。

如△ABC 与△A /B /C /相似，记作: △ABC ∽△A /B /C / 。

相似三角形的比叫相似比相似三角形的定义既是相似三角形的性质，也是三角形相似的判定方法。

注意：（1）相似比是有顺序的。

（2）对应性，两个三角形相似时，通常把对应顶点写在对应位置，这样写比较容易找到相似三角形的对应角和对应边。

（3）顺序性：相似三角形的相似比是有顺序的，若△ABC ∽△A /B /C /，相似比为k ，则△A /B /C /与△ABC 的相似比是1k知识点2、相似三角形与全等三角形的关系（1）两个全等的三角形是相似比为1的相似三角形。

（2）两个等边三角形一定相似，两个等腰三角形不一定相似。

（3）二者的区别在于全等要对应边相等，而相似要求对应边成比例。

知识点3、平行线分线段成比例定理1. 比例线段的有关概念： 在比例式：：中，、叫外项，、叫内项，、叫前项，a b cda b c d a d b c a c ==() b 、d 叫后项，d 叫第四比例项，如果b=c ，那么b 叫做a 、d 的比例中项。

把线段AB 分成两条线段AC 和BC ，使AC 2=AB ·BC ，叫做把线段AB 黄金分割，C 叫做线段AB 的黄金分割点。

2. 比例性质： ①基本性质：a b c d ad bc =⇔= ②合比性质：±±a b c d a b b c dd=⇒=③等比性质：……≠……a b c d m n b d n a c m b d n a b===+++⇒++++++=()0 3. 平行线分线段成比例定理（1）平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例. 已知l1∥l2∥l3,A D l1B E l2C F l3可得EF BC DE AB DF EF AC BC DF EF AB BC DF DE AC AB EF DE BC AB =====或或或或等.（2）推论:平行于三角形一边的直线截其它两边(或两边的延长线)所得的对应线段成比例. AD EB C由DE ∥BC 可得：AC AEAB AD EA EC AD BD EC AE DB AD ===或或.此推论较原定理应用更加广泛,条件是平行.（3）推论的逆定理：如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例.那么这条直线平行于三角形的第三边.此定理给出了一种证明两直线平行方法,即：利用比例式证平行线.（4）定理:平行于三角形的一边,并且和其它两边相交的直线,所截的三角形的三边与原三角形三边对应成比例.知识点4：相似三角形的性质①相似三角形的对应角相等 ②相似三角形的对应边成比例③相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比 ④相似三角形周长的比等于相似比⑤相似三角形面积的比等于相似比的平方知识点5：相似三角形的判定：①两角对应相等，两个三角形相似②两边对应成比例且夹角相等，两三角形相似 ③三边对应成比例，两三角形相似④如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角形相似⑤平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似ABC⑥直角三角形被斜边上的高分成的两个直角三角形和原三角形相似如果两个三角形的两角分别于另一个三角形的两角对应相等，那么这两个三角形相似。

相似三角形综合培优题型基础知识点梳理：知识点1 有关相似形的概念(1)形状相同的图形叫相似图形，在相似多边形中，最简单的是相似三角形.(2)如果两个边数相同的多边形的对应角相等，对应边成比例，这两个多边形叫做相似多边形．相似多边形对应边长度的比叫做相似比(相似系数)． 知识点2 比例线段的相关概念（1）如果选用同一单位量得两条线段b a ,的长度分别为n m ,，那么就说这两条线段的比是nmb a =，或写成n m b a ::=．注：在求线段比时，线段单位要统一。

（2）在四条线段dc b a ,,,中，如果b a 和的比等于d c 和的比，那么这四条线段d c b a ,,,叫做成比例线段，简称比例线段．注：①比例线段是有顺序的，如果说a 是d c b ,,的第四比例项，那么应得比例式为：ad c b =．②()a ca b c d b d==在比例式：：中，a 、d 叫比例外项，b 、c 叫比例内项, a 、c 叫比例前项，b 、d 叫比例后项，d 叫第四比例项，如果b=c ，即 a b b d =：：那么b 叫做a 、d 的比例中项， 此时有2b ad =。

知识点3 比例的性质（注意性质立的条件：分母不能为0） （1） 基本性质：①bc ad d c b a =⇔=::；②2::a b b c b a c =⇔=⋅．注：由一个比例式只可化成一个等积式，而一个等积式共可化成八个比例式，如bc ad =，除了可化为d c b a ::=，还可化为d b c a ::=，b a d c ::=，c a d b ::=，c d a b ::=，b d a c ::=，a b c d ::=，a c b d ::=．（2） 更比性质(交换比例的内项或外项)：()()()a bc d a c d c b db a d bc a ⎧=⎪⎪⎪=⇔=⎨⎪⎪=⎪⎩，交换内项，交换外项．同时交换内外项（3）反比性质(把比的前项、后项交换)：a cb d b da c=⇔=．知识点4 比例线段的有关定理1.三角形中平行线分线段成比例定理:平行于三角形一边的直线截其它两边(的延长线)所得的对应线段成比例.B由DE ∥BC 可得：ACAEAB AD EA EC AD BD EC AE DB AD ===或或2.平行线分线段成比例定理:三条平行线截两条直线,已知AD ∥BE ∥CF,可得AB DE AB DE BC EF BC EF AB BCBC EF AC DF AB DE AC DF DE EF=====或或或或等. 知识点5 相似三角形的概念①对应性：即两个三角形相似时，一定要把表示对应顶点的字母写在对应位置上，这样写比较容易找到相似三角形的对应角和对应边． ②顺序性：相似三角形的相似比是有顺序的．③两个三角形形状一样，但大小不一定一样．④全等三角形是相似比为1的相似三角形．二者的区别在于全等要求对应边相等，而相似要求对应边成比例． 知识点6 三角形相似的等价关系与三角形相似的判定定理的预备定理(1)相似三角形的等价关系：①反身性：对于任一ABC ∆有ABC ∆∽ABC ∆．②对称性：若ABC ∆∽'''C B A ∆，则'''C B A ∆∽ABC ∆．③传递性：若ABC ∆∽C B A '∆''，且C B A '∆''∽C B A ''''''∆，则ABC ∆∽C B A ''''''∆ (2) 三角形相似的判定定理的预备定理：平行于三角形一边的直线和其它两边(或两边延长线)相交，所构成的三角形与原三角形相似．定理的基本图形：用数学语言表述是：BC DE // ， ∴ ADE ∆∽ABC ∆． 知识点7 三角形相似的判定方法1、定义法：三个对应角相等，三条对应边成比例的两个三角形相似．2、平行法：平行于三角形一边的直线和其它两边(或两边的延长线)相交，所构成的三角形与原三角形相似．3、判定定理1：如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似．简述为：两角对应相等，两三角形相似．4、判定定理2：如果一个三角形的两条边与另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似．简述为：两边对应成比例且夹角相等，两三角形相似．5、判定定理3：如果一个三角形的三条边与另一个三角形的三条边对应成比例，那么这两个三角形相似．简述为：三边对应成比例，两三角形相似．6、判定直角三角形相似的方法： (1)以上各种判定均适用．(2)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似．(3)直角三角形被斜边上的高分成的两个直角三角形与原三角形相似．：射影定理：在直角三角形中，斜边上的高是两直角边在斜边上射影的比例中项。

相似三角形复习讲义一、相似三角形的定义如果两个三角形的对应角相等，对应边成比例，那么这两个三角形就叫做相似三角形。

相似三角形对应边的比叫做相似比。

需要注意的是，全等三角形是相似比为 1 的特殊相似三角形。

二、相似三角形的判定1、两角分别相等的两个三角形相似。

比如在三角形 ABC 和三角形 A'B'C'中，如果角 A ＝角 A'，角 B ＝角 B'，那么三角形 ABC 相似于三角形 A'B'C'。

2、两边成比例且夹角相等的两个三角形相似。

假设在三角形 ABC 和三角形 A'B'C'中，AB ／ A'B' ＝ AC ／ A'C'，且角 A ＝角 A'，则这两个三角形相似。

3、三边成比例的两个三角形相似。

若三角形 ABC 和三角形 A'B'C'的三条边对应成比例，即 AB ／ A'B' ＝ BC ／ B'C' ＝ AC ／ A'C'，那么它们相似。

三、相似三角形的性质1、相似三角形的对应角相等。

这意味着如果两个三角形相似，那么它们对应的角大小是相同的。

2、相似三角形的对应边成比例。

相似比等于对应边的比值，且这个比值是固定的。

3、相似三角形的对应高、对应中线、对应角平分线的比都等于相似比。

例如，三角形 ABC 相似于三角形 A'B'C'，AD 和 A'D'分别是它们的高，那么 AD ／ A'D'等于相似比。

4、相似三角形的周长比等于相似比。

假设三角形 ABC 与三角形 A'B'C'相似，相似比为 k，那么它们的周长比也是 k。

5、相似三角形的面积比等于相似比的平方。

若相似比为 m，那么面积比就是 m²。

四、常见的相似三角形模型1、“A”字型在这种模型中，有一条平行线与三角形的两边相交，形成两个相似三角形。

暑假讲义九年级数学相似三角形第1讲相似图形与成比例线段【学习目标】1、从生活中形状相同的图形的实例中认识图形的相似,理解相似图形概念。

2、了解成比例线段的概念，会确定线段的比。

【学习重点】相似图形的概念与成比例线段的概念。

【学习难点】成比例线段概念。

【学习过程】知识点一：比例线段定义：对于四条线段a、b、c、d，如果其中两条线段的比（即它们长度的比）与另外两条线段的比，如果段，简称比例线段。

a cb d，那么就说这四条线段a、b、c、d 叫做成比例线例：如四条线段的长度分别是4cm、8cm、3cm、6cm 判断这四条线段是否成比例？解：练习一：AB CD AC AC1、如图所示：（1）求线段比BC 、DE 、BE 、CD（2）试指出图中成比例线段2、线段a、b、c、d 的长度分别是30mm、2cm、0.8cm、12mm 判断这四条线段是否成比例？3、线段a、b、c、d 的长度分别是 2 、 3 、2、 6 判断这四条线段是否成比例？4、已知A、B 两地的实际距离是250m 若画在图上的距离是5cm，则图上距离与实际距离的比是___________5、已知线段a= 12、 b = 2 3 、c= 2 3 、若a cb xb y，则x =_________若y 0y c，1暑假讲义九年级数学相似三角形则y =__________6、下列四组线段中，不成比例的是（）A a=3 b=6 c=2 d=4B a=1 b= 2 c= 3 d= 6C a=4 b=6 c=5 d=10D a= 2 b= 3 c=2 d= 6知识点二：比例线段的性质比例性质是根据等式的性质得到的，推理过程如下：（1）基本性质：如果a cb d，那么ad bc （两边同乘bd ，bd 0 ）在abcd 0的情况下，还有以下几种变形b da c、a bc d、c da b（2）合比性质：如果a cb d，那么a b c db d（3）等比性质：如果a c e mb d f nb d f n0，那么a c e m ab d f n b例2 填空：如果练习二：ab23，则a =2a= 、a bb= 、a bb=1、已知ab35，求a ba b2、若a b c2 3 4，则a2b 3ca=_________3、已知mx ny ，则下列各式中不正确的是（）A m xn yBm ny xCy mx nDx yn m4、已知5x 7y0 ，则xy=_______5、已知x y z3 4 5，求x y zx y z=________暑假讲义九年级数学 相似三角形第 2 讲平行线分线段成比例【学习目标】1. 理解掌握平行线分线段成比例定理，会用符号“∽”表示相似三角形， 如△ ABC ∽△ A B C ;2. 知道相似多边形的主要特征3. 会根据相似多边形的特征识别两个多边形是否相似，并会运用其性质进行相关的计算。