Experimental study on turbulent mixing of spray droplets in crossflow

空气辅助雾化喷嘴的数值模拟研究刘海军;宋来武;吴华【摘要】基于欧拉-拉格朗日两相流模型,数值模拟研究了一种带有螺纹通道的空气辅助雾化喷嘴的雾化过程.分析了喷嘴内空气流动特性和雾化场中的雾化特性,结果表明喷嘴内空气速度、压力和温度等参数随着流动截面变化时会发生剧烈变化,并在喷嘴出口处达到超音速状态,雾化场中雾滴具有较大的轴向速度和较小的径向速度,雾滴直径分布均匀,雾化效果良好.【期刊名称】《节能技术》【年(卷),期】2015(033)003【总页数】5页(P207-210,215)【关键词】空气辅助;雾化;欧拉-拉格朗日;数值模拟;硝酸铀酰【作者】刘海军;宋来武;吴华【作者单位】中国核电工程有限公司,北京100840;中国核电工程有限公司,北京100840;中国核电工程有限公司,北京100840【正文语种】中文【中图分类】TH133;TP183利用核能发电是性价比高、碳排量低的新型发电方式，是化石能源和水力资源之后的世界第三种主要能源。

核燃料在发电过程中会慢慢裂变，以致无法使用，出于节能经济性和减少污染排放的要求，对核燃料进行后处理和循环利用尤为重要。

在已经确定的水法后处理中，铀以硝酸铀酰水溶液的形式被回收，浓缩的硝酸铀酰溶液在流化床中脱硝生成三氧化铀，进一步还原生成二氧化铀，然后转变成四氟化铀，最后还原成金属铀循环使用［1］。

硝酸铀酰水溶液的雾化能够使液料形成尺寸均匀，颗粒直径小的液雾，以增加硝酸铀酰水溶液与流化气和流化底料之间的接触面积，提高反应速度。

由于硝酸铀酰水溶液粘度较大，因此适合雾化高粘度液体的空气辅助雾化喷嘴是其常用的雾化设备之一。

空气雾化喷嘴具有很多突出特点，在较低的油压下可以获得良好的雾化效果，尤其是对雾化高粘度的液体有很好的雾化质量，流量调节范围广，且能在较大的燃油流量范围内得到良好的雾化质量，因此它在石油、化工、电力等众多领域应用广泛［2－4］。

国内外许多学者对其进行了大量研究［5－9］。

2005 年 4 月 The Chinese Journal of Process Engineering Apr. 2005收稿日期：2004−07−29，修回日期：2004−09−27作者简介：洪厚胜(1965−)，男，江西省鄱阳市人，博士，副教授，主要从事生化工程及生化反应器的研究.搅拌生物反应器混合特性的数值模拟与实验研究　洪厚胜，　张庆文，　万红贵，　欧阳平凯　(南京工业大学制药与生命科学学院，江苏 南京 210009)摘 要：以工程流体计算软件CFX −4.4为工具，对不同规模的机械搅拌生物反应器的混合特性进行数值模拟，研究了不同操作条件下反应器混合时间的变化规律. 采用pH 电极在位监测[H +]的方法实验测定混合时间. 模拟结果与实验测定值之间的误差随反应器容积增大而逐渐减小，对容积为25 m 3的反应器误差小于11.6%. 关键词：搅拌生物反应器；混合时间；计算流体力学；数值模拟中图分类号：TQ018 文献标识码：A 文章编号：1009−606X(2005)02−0131−04１ 前　言　尽管目前已开发出许多新型的生物反应器，但机械搅拌式生物反应器因其搅拌桨结构的多样性、混合与传质方面的高弹性而具有通用性强、操作范围宽等特点，在食品发酵、生物制药等生物技术行业中的应用仍占统治地位，而且这种趋势在近期不会改变[1]. 反应器的混合时间是衡量其混合传质性能的重要指标，主要受反应器的结构与操作条件的影响[2]，对反应器的设计放大及操作优化具有重要的参考价值.传统的混合时间测量方法主要有脱色法[3]、光学法[4]及电导法[5,6]等，这些测量方法都存在着一定的局限性，应用于大型生物反应器混合传质研究往往成本高、精度低、操作困难. 本工作用计算流体力学(Computational Fluid Dynamics ，简称CFD)技术对0.05, 1.0, 25.0 m 3三种规模的机械搅拌式生物反应器的混合行为进行数值模拟，研究在不同操作条件下混合时间的变化规律，并将模拟结果与实测结果进行比较，验证CFD 模拟技术用于机械搅拌生物反应器混合性能研究的可行性，以期为工程应用建立基础.２ 实　验　２．１　实验设备　实验设备是常用的机械搅拌式通风发酵罐，又称标准罐，如图1所示，主要由椭圆封头、挡板、标准六平叶圆盘涡轮搅拌桨(Rushton 型)构成. 挡板与器壁间空隙取反应器内径的1%，具体尺寸见表1.位点A 及B 分别为测定混合时间时的加料点和监测点，加料点A 高度在上搅拌桨的上边缘位置，监测点B 高度约在下两个搅拌桨高度的中点处，两位点均在相邻两挡板之间的中点且离器壁0.1 m 左右处. 反应器内图1 机械搅拌生物反应器几何结构示意图Fig.1 Sketch of stirred biochemical reactor 表１　实验设备主要尺寸　Table 1 Main dimensions of experimental apparatus料液装填系数为78%. ２．２　混合时间测量方法　实验在25℃下进行，用HCl 溶液作为酸性示踪剂，在加料点A 处瞬间注入，同时通过安装在监测点B 处的pH 电极和与之相联的计算机记录液体pH 值的变化，从Tank dataTank 1 Tank 2 Tank 3 Liquid volume, V (m ) 0.05 1.0 25.0 Liquid height, H L (m) 0.5 1.42 4.0 Tank diameter, D T (m) 0.3 0.8 2.4 Number of baffles, N B 3 4 4 Number of impellers, N I 2 3 3 Baffle width, W (m) 0.03 0.06 0.24 Baffle depth, H B (m) 0.425 1.3 4.03 Impeller diameter, D I (m)0.125 0.28 0.75 Space between impellers, S I (m) 0.25 0.56 1.4 Bottom-impeller elevation, S B (m)0.025−0.165而反映液体中[H +]浓度的变化. 典型的[H +]变化过程如图2所示[7]. 一般混合过程中示踪剂浓度变化曲线的振幅随时间指数递减，而其频率与时间无关，混合时间可以从曲线上读出. 混合时间t m 是指示踪剂注入反应器至达到一定混匀程度的时间. 混匀程度的定义为0.5100%C Cm C ∝∝−∆=×. 通常认为m 达到95%时，流体即混合均匀，此时的混合时间常用t 95来表示.３ ＣＦＤ数值模拟　３．１　基本原理　3.1.1 基本数学模型在工业生产常用的操作条件下，生物反应器内液体湍流运动可由时均方程组来描述，其流动守恒方程组由张量表示的通用形式描述如下：()()()k k k kv S t x x x φφφρφρφΓ∂∂∂∂+=+∂∂∂∂, 式中，φ表示质量组分、速度、压力、湍流动能、湍流耗散等变量，S φ为源项，Γφ为湍流扩散，在计算示踪剂浓度场时，Γφ=ρD φ+µT /σφ, D φ为示踪剂分子扩散系数，µT 为湍流动力粘度，其值取于速度场湍流k −ε双方程模型，σφ为湍流Prandtl 数. 3.1.2 混合时间模拟生物反应器中物料在混合过程中的浓度分布随时间变化的非稳态过程通常有两种数值计算方法，一种是联立所有方程进行求解，另一种是假设速度场稳定，单独进行流场计算. 本研究的混合时间计算采用后一种方法. 具体模拟分两步进行：第一步，用单物质模型计算稳态流场，模拟的单物质是水；第二步，在上述稳态流场的基础上引入双物质模型(如水和示踪剂)进行非稳态计算. 在加料点设置初始示踪剂的注入量，在计算过程中求解监测点示踪剂的浓度变化，当混匀程度达到95%时，即认为达到了完全混合. 这段时间就称为搅拌反应器的混合时间，记为t 95. ３．２　数值计算　3.2.1 几何模型的构建及网格划分对于带有六平叶圆盘涡轮桨及挡板的搅拌生物反应器，由于其结构的对称性，故可以用通过轴心的垂直截面将其分成对称的若干部分. 如1.0 m 3机械搅拌发酵罐就可以对称地分成两部分，只对其中一部分进行几何体构建及网格划分. 机械搅拌生物反应器中搅拌桨与挡板之间相对移动的动界面可采用滑移网格法处理. 这种方法将计算区域分为两部分，如图3所示，一部分包含了运动的搅拌桨叶，另一部分包含反应器的其他静止部分，两部分网格之间要求彼此独立，两者之间的物质、动量传递通过定义接触边界面的粘联来实现.网格划分采用在正交圆柱坐标下的结构化网格，同时采用分块网格技术，在反应器中心部位网格线较密、外围较疏，这也是由流动的特点决定的. 这样可以减少假扩散，对解的收敛和求解速度都十分有利. 其对应的3种反应器(0.05, 1.0, 25.0 m 3)几何体划分的网格总数分别为158268, 215712和246996，网格的划分对求解已经达到了无关性标准. 1.0 m 3反应器具体网格空间划分见图3所示.设定流体在反应器壁处的流动速度为0，即无滑移边界条件；假定流体表面与大气无摩擦，在反应器的液体表面采用所谓的自由滑移边界条件；在轮轴处采用无移动及轴对称设定. 3.2.3 数值求解整个方程组的求解通过流体工程软件CFX −4.4完(a)(b)第2期 洪厚胜等：搅拌生物反应器混合特性的数值模拟与实验研究 133　成，通过有限体积法将微分方程组离散成差分代数方程组后，各变量差分方程用沿主流方向逐线扫描的低松弛迭代求解. 压力−速度耦合求解采用SIMPLEC 算法.４ 结果与讨论　对于大多数生化反应，物料的混匀效果和混合速率决定着反应效率和生产成本，对生物反应器的混合特性的研究具有现实意义. 在搅拌生物反应器中，物料的混合作用主要由主体流动、湍流及分子扩散这3种机理的协同作用引起. 图4所示是0.05 m 3反应器在230 r/min 的搅拌转速下不同时刻示踪剂浓度值的分布. 从图中可以很直观地观察到示踪剂的混合过程. 图5为不同体积搅拌生物反应器的混合时间模拟结果与实验结果的比较. 从图中可以看出，模拟结果在趋势上与实验结果有很好的一致性，随着搅拌转速的提高，反应器混合时间逐渐变小. 从图也清楚地看出数值模拟得到的搅拌混合时间均比实验验证值要大，产生此误差的原因有很多，主要是由采用的计算方法所引起的. 因为这种方法计算首先要假设流场稳定，而实际搅拌反应器内流场并不是稳定不变的，而是呈无规则变化的非稳态过程，但流场的不稳定可以促进传质的进行，从而使混合时间减小. 就这一点来看，本研究的模拟结果与Schmalzriedt 等[8]、Bujalski 等[9]所描述的情况基本一致. 混合时间的模拟与实验结果的误差比较见表2.图5 混合时间的模拟与实验结果比较Fig.5 Comparison between simulative and experimental mixing timest =20 s10020030040020406080100120140t 95 (s )R (r/min)6080100120140160100110120130140150160170R (r/min)14016018020022024040455055606570758085R (r/min)134 过 程 工 程 学 报 第5卷表２　混合时间的模拟与实验误差比较　Table 2 Comparison of deviations between simulative and experimental mixing timesTank 1 Tank 2 Tank 3 .50 230 400 150170 190 210 230 70 90 110 130 150 Simulation value (s) 137.5 27.9 18.0 81.9 72.2 64.6 57.2 51.1 167.4 151.1 135.3 118.3 105.0 Experiment value (s) 104.0 17.0 11.0 73.0 60.0 53.0 49.0 43.0 165.0 140.0 129.0 106.0 102.0 Deviation (%)32.264.1 63.612.220.321.916.7 18.8 1.5 7.94.911.6 2.9分析比较图5和表2所给数据还可以得知，它们的误差分别在64.1%, 21.9%及11.6%以下. 随着搅拌生物反应器容积的增大，数值模拟与实验结果之间的误差逐渐变小，模拟的可靠性逐渐增大. 对容积为25 m 3的工业规模的生物反应器，模拟与验证之间的误差值小于11.6%，完全符合当前数值模拟的工程应用要求. 产生这种现象可能是小反应器中流场的无规则周期性振荡更甚，偏离本研究数值计算的第一步流场稳定的假设条件更远所致.５ 结　论　以流体工程软件CFX −4.4为工具，对不同规模的机械搅拌生物反应器的混合特性进行了数值模拟，建立了最大容积为25 m 3的工业规模冷模实验装置和混合时间测定方法，并对模拟结果进行了验证. 研究结果表明，本工作建立的数学模型及采用的算法是可行的；CFD 技术可用于机械搅拌式生物反应器混合传质的基础研究和反应器的优化设计及工程放大的应用研究.符号表：S L两搅拌桨间距 (m)W挡板宽度 (m)t 时间 (s) x k 坐标位置 (m) t m 混合时间 (s) ρ 流体密度 (kg/m 3)t 95 混匀程度95%的混合时间 (s) ∆C信号波峰值波动范围 (mol/L) v 流体质点的速度 (m/s) µT 湍流动力粘度 [kg/(m ⋅s)] V反应器体积 (m 3)σφ湍流Prandtl 数参考文献：[1] 赵学明. 搅拌生物反应器的结构模型、放大及搅拌器改型 [J]. 化学反应工程与工艺, 1996, 12(1): 80−90.[2] 韦朝海，谢波，吴超飞，等. 三重环流生物流化床反应器的混合特性 [J]. 化学反应工程与工艺, 1999, 15(2): 174−178.[3] 武斌，戴干策. 搅拌槽内粘稠物系的混合过程 [J]. 高校化学工程学报, 1997, 11(2): 143−149.[4] 林猛流，王英琛，施力田. 激光法测定搅拌器的混合特性 [J]. 化学工程, 1986, 14(3): 52−56.[5] Nienow A W. On Impeller Circulation and Mixing Effectiveness inthe Turbulent Flow Regime [J]. Chem. Eng. Sci., 1997, 52(15): 2557−2565.[6] Manna L. Comparison between Physical and Chemical Methods forthe Measurement of Mixing Times [J]. Chem. Eng. J., 1997, 67(3): 167−173.[7] 戚以政，汪叔雄. 生化反应动力学与反应器，第二版 [M]. 北京：化学工业出版社, 1999. 391−392.[8] Schmalzriedt S, Reuss M. Application of Computational FluidDynamics to Simulations of Mixing and Biotechnical Conversion Processes in Stirred T ank Bioreactors [J]. Recents Progres en Genie des Procedes, 1997, 11(51): 171−178.[9] Bujalski W, Jaworski Z, Nienow A W. CFD Study of Homogenizationwith Dual Rushton Turbines Comparison with Experimental Results: Part II: The Multiple Reference Frame [J]. Chem. Eng. Res. Des., 2002, 80(A1): 97−104.Numerical Simulation and Experimental Study on Mixing Characteristics of Stirred BioreactorHONG Hou-sheng, ZHANG Qing-wen, WAN Hong-gui, OUYANG Ping-kai(College of Pharmacy and Life Science, Nanjing University of Technology, Nanjing, Jiangsu 210009, China )Abstract: By commercial CFD package CFX-4.4, mixing characteristics of stirred bioreactor were simulated and the mixing time variation under various operation conditions was investigated. The liquid mixing time was measured by means of detecting the concentration variety of [H +] with a pH probe. The deviation between simulation and experiment becomes smaller as the bioreactor volume is increased, and the error for 25 m 3 bioreactor is less than 11.6%.Key words: stirred bioreactor; mixing time; computational fluid dynamics; numerical simulationC ∝ 理想完全混匀浓度 (mol/L) m混匀程度 D I 搅拌桨直径 (m) N B 挡板个数 D T 反应器内径 (m) N L 搅拌桨个数 H B 挡板深度 (m) R 搅拌转速 (r/min)H L液位高度 (m)S B下搅拌桨距筒体底间距 (m)。

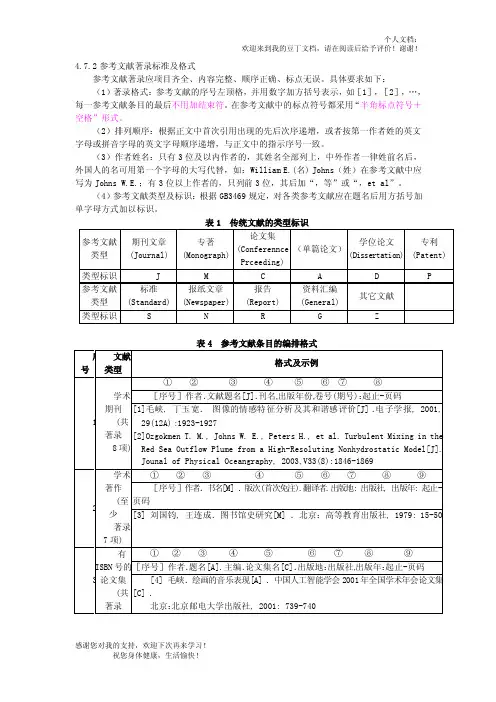
4.7.2参考文献著录标准及格式参考文献著录应项目齐全、内容完整、顺序正确、标点无误。

具体要求如下：（1）著录格式：参考文献的序号左顶格，并用数字加方括号表示，如［1］，［2］，…，每一参考文献条目的最后不用加结束符。

在参考文献中的标点符号都采用“半角标点符号＋空格”形式。

（2）排列顺序：根据正文中首次引用出现的先后次序递增，或者按第一作者姓的英文字母或拼音字母的英文字母顺序递增，与正文中的指示序号一致。

（3）作者姓名：只有3位及以内作者的，其姓名全部列上，中外作者一律姓前名后，外国人的名可用第一个字母的大写代替，如：William E.(名) Johns（姓）在参考文献中应写为Johns W.E.；有3位以上作者的，只列前3位，其后加“，等”或“，et al”。

（4）参考文献类型及标识：根据GB3469规定，对各类参考文献应在题名后用方括号加单字母方式加以标识。

表1 传统文献的类型标识标签：杂谈1. 问：WORD 里边怎样设置每页不同的页眉？如何使不同的章节显示的页眉不同？答：分节，每节可以设置不同的页眉。

文件――页面设置――版式――页眉和页脚――首页不同。

2. 问：请问word 中怎样让每一章用不同的页眉？怎么我现在只能用一个页眉，一改就全部改了？答：在插入分隔符里，选插入分节符，可以选连续的那个，然后下一页改页眉前，按一下“同前”钮，再做的改动就不影响前面的了。

简言之，分节符使得它们独立了。

这个工具栏上的“同前”按钮就显示在工具栏上，不过是图标的形式，把光标移到上面就显示出”同前“两个字来。

3. 问：如何合并两个WORD 文档，不同的页眉需要先写两个文件，然后合并，如何做？答：页眉设置中，选择奇偶页不同与前不同等选项。

4. 问：WORD 编辑页眉设置，如何实现奇偶页不同比如：单页浙江大学学位论文，这一个容易设；双页：（每章标题），这一个有什么技巧啊？答：插入节分隔符，与前节设置相同去掉，再设置奇偶页不同。

双锥干燥机定位原理A double cone dryer is a type of rotating, horizontal cylinder that is used to dry powders, granules, and other materials in the pharmaceutical, food, chemical, and other industries. This type of dryer operates on the principle of conduction, where heat is transferred to the materials being dried through direct contact with the dryer's heated surface.双锥干燥机是一种旋转的、水平的圆筒，用于在制药、食品、化工等行业中干燥粉末、颗粒和其他材料。

这种类型的干燥机是根据传导的原理运作的，即热量通过与干燥机加热表面的直接接触传递给被干燥的材料。

The double cone dryer consists of two conical sections that are joined at the top and separated by a small angle, creating a V-shaped chamber. The materials to be dried are loaded into the dryer through a wide opening at the top, and the dryer is then rotated, allowing the materials to cascade and mix as they move from one end of the chamber to the other. This movement promotes uniform drying and prevents the materials from forming lumps or sticking to the dryer's heated surface.双锥干燥机由两个圆锥形部分组成，顶部连接并通过一个小角度分开，形成一个V形的室内。

第35卷第1期燃气涡轮试验与研究Vol.35,No.1 2022年2月Gas Turbine Experiment and Research Feb.,2022严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严严收稿日期：2021-01-09作者简介：文璧(1983-)，男，四川绵阳人，高级工程师，硕士，主要从事发动机噪声测试及故障诊断技术研究。

1引言航空发动机中央锥齿轮是匹配发动机和附件机构的重要部件，其主要作用是将发动机主轴转速按一定比例与转向传递给发动机附件装置[1]。

目前，中央锥齿轮在设计中主要是作为刚体处理，忽略轮齿受载后的弹性变形，这种方法满足强度、疲劳寿命、质量、体积等条件的静态设计，但其工作在高温、高转速、交变大载荷等恶劣环境，锥齿轮盘形结构易在工作中产生行波共振的动态现象，造成齿轮成块破裂失效故障。

因此，开展锥齿轮的声振特性研究就摘要：航空发动机锥齿轮声振特性的确定对于锥齿轮的研制具有重要意义。

为研究航空发动机中央锥齿轮的声振特性，根据齿轮声振信息辨识原理，利用声导管技术在齿轮部件试验器中获取原始空气声。

分析发现，啮合频率幅值的变化能够对齿轮行波共振特性实现完全表述，不仅可反映从动轮的声振特性，同时也能反映主动轮的声振特性，边频信息则反映了齿轮的故障信息。

与应变片测量结果和设计计算结果对比分析证明，声学测试是获取齿轮声振特性的有效方法。

关键词：航空发动机；中央锥齿轮；声振特性；声学测试；行波共振中图分类号：V223文献标识码：A文章编号：1672-2620(2022)01-0036-05Experimental study on acoustic and vibration characteristicsof central bevel gears of aero-enginesWEN Bi1，3，LIU Yuan-shi2，XU Yong-qiang2，DU Jun2（1.Areo Engine High Altitude Simulation Key Laboratory，Mianyang621000China；2.AECCSichuan Gas Turbine Research Institute，Mianyang621000China；3.School ofMechanical Engineering，Xi’an Jiaotong University，Xi’an710049China）Abstract:The determination of the acoustic and vibration characteristics of aero-engine bevel gears is of great significance for the development of bevel gears.In order to study the acoustic and vibration character⁃istics of the aero-engine central bevel gear,the original air sound was obtained in the gear component tester using the acoustic dust technology according to the principle of the gear acoustic information identification. Analysis results show that the variation of the meshing frequency amplitude can fully express the traveling wave resonance characteristics of the gear,which can not only reflect the acoustic and vibration characteris⁃tics of the driving wheel,but also reflect the acoustic and vibration characteristics of the driven wheel,while the side frequency information reflects the gear fault pared with the measurement results of the strain gauges and the design calculations,the acoustics test is an effective method to obtain the acoustic vibration characteristics of the teeth.Key words:aero-engine；bevel gears；acoustic and vibration characteristics；acoustic test；traveling wave resonance36燃气涡轮试验与研究第35卷显得十分重要。

大气边界层的国内外研究现状宁志远;刘厚凤【摘要】对大气边界层的理论基础、确定方法、特征要素、影响因子、时空变化特征以及与大气污染间的相互作用进行总结,得出以下结论:大气边界层的理论体系较为完备,但理论研究进展缓慢;廓线测量是确定大气边界层结构最常用的方法,雷达、数值模拟等方法仍需对比验证;大气边界层日变化、季节变化特征十分明显,海陆间边界层变化特征差异明显,戈壁、高原等地区的大气边界层特征较为特殊;大气边界层结构,尤其是风速风向、混合层高度对大气环境有明显的影响;大气污染对大气边界层的影响和区域大气边界层特征的研究较少,可作为今后的研究重点.【期刊名称】《中国环境管理干部学院学报》【年(卷),期】2017(027)002【总页数】4页(P22-25)【关键词】大气边界层;理论基础;确定方法;时空变化特征;大气边界层结构与大气污染的相互影响【作者】宁志远;刘厚凤【作者单位】山东师范大学地理与环境学院, 山东济南 250014;山东师范大学地理与环境学院, 山东济南 250014【正文语种】中文【中图分类】X51大气边界层（Atmospheric Boundary Layer，ABL）位于大气圈与地球表面交界区，是对流层下部直接受地面影响的部分，平均高度约为1～2 km，也是大气热量、动量和各种物质（水汽、污染物）上下输送的重要通道，能在一小时或更短时间内响应地面作用[1]，影响因素包括地表摩擦、热量输送、污染物排放及地形扰动等，对某区域的大气环境质量有着至关重要的作用。

20世纪初，Prandtl、Ekman提出的边界层理论和Ekman螺线奠定了大气边界层理论基础[2]；20世纪中期，随着Monin-Obukhov相似性理论和自由对流大气湍流理论的提出，经典湍流理论基本形成[3]。

20世纪60年代，Lorenz发现了新的湍流发生机制[4]；70年代，Deardorff、Wyngaard和Dyer等人将相似性原理引入混合层和对流层的研究并逐渐完善，使其有了极大的应用价值[5]。

第63卷第3期有色金属(矿山部分)2011年5月欞欞欞欞欞欞欞欞欞欞欞欞欞欞欞欞欞欞欞欞欞欞欞欞欞欞欞欞欞欞欞欞欞欞欞欞欞欞欞欞欞欞欞欞欞欞欞DOI :10．3969/j．issn．1671－4172．2011．03．015大红山铜矿岩石物理力学性质试验研究陈超1，李争荣1，邱宇2(1.昆明理工大学，昆明650093;2.江西理工大学，江西赣州341000)摘要:对大红山铜矿435中段矿岩的单轴抗拉强度、抗压强度、抗剪强度、泊松比、弹性模量、内摩擦角以及内聚力进行了室内试验研究。

试验得出一系列岩石物理力学参数，为矿山下一步生产实践做好了准备。

关键词:岩石力学;抗压强度;抗拉强度;弹性模量;泊松比中图分类号:TD315文献标识码:A文章编号:1671－4172(2011)03－0058－04Experimental study on physical-mechanical properties of rocks in Dahongshan copper mineCHEN Chao 1，LI Zhengrong 1，QIU Yu 2(1．Kunming University of Science and Technology ，Kunming 650093，China ;2．Jiangxi University of Science and Technology ，Ganzhou Jiangxi 341000，China )Abstract :Through the study on uniaxial tensile strength ，compressive strength ，shear strength ，Poisson＇s ratio ，elastic moduls ，internal friction angle and cohesion of rock in the 435middle section of Dahongshan copper mine ，a series of phys-ical and mechanical parameters has been obtained in this paper ，which can provide preparation for the production of the next step．Key words :rock mechanics ;compressive strength ;tensile strength ;elastic modulus ;Poisson＇s ratio作者简介:陈超(1985－)，男，硕士研究生，岩石力学专业。

床形结构对气固流化床流化质量和气体返混特性的影响张永民;卢春喜【摘要】用实验方法比较了一个二维床和一个大型三维床内FCC颗粒流化床在鼓泡域和湍动域内的流化质量和气体返混特性.实验结果表明,床形对A类颗粒气固流化床具有非常大的影响.二维床和三维床的流动和气固混合行为既具有相似性,如床膨胀随气速的变化趋势;也具有很大的差异性,既包括三维床流化质量差、轴向气体扩散系数大等量上的不同,又包括压力脉动、轴向气体扩散系数的变化趋势以及湾流模式等质上的不同.总之,在本研究中,二维床体现的是一种具有强烈壁效应的小型流化床的特征,而三维床则体现的是静床高度具有很大影响的大型流化床的特征.【期刊名称】《化工学报》【年(卷),期】2010(061)009【总页数】9页(P2296-2304)【关键词】床形;流化床;二维;三维;流化质量;返混【作者】张永民;卢春喜【作者单位】中国石油大学(北京)重质油国家重点实验室,北京,102249;中国石油大学(北京)重质油国家重点实验室,北京,102249【正文语种】中文【中图分类】O6-332Abstract：The fluidization quality and gas back-mixing property in a two-dimensional and a large-scale three dimensional gas-solids fluidized bedsof FCC particles were compared in the range containing both bubbling and turbulent flow regimes.The experimental results indicated bed shape’s sound effects on fluidized beds of Geldart A particles.The hydrodynamics and gas-solids mixing demonstrated both similar and different properties in the two-dimensional and three dimensional beds.The bed expansion with increasing superficial gas velocity showed similar trends in both beds.However,the fluidization quality and axial gas dispersion coefficient were much lower in the three-dimensional beds.Moreover,there were different trends of pressure fluctuation and axial gas dispersion coefficient with increasing superficial gas velocity and even different gulf streaming patterns in the two beds.In general,it can be concluded that the two-dimensional bed in this study represented a small-scale bed with strong wall effect,while the threedimensional bed represented a large-scale bed with strong effect from static bed height.Key words：bed shape;fluidized bed;two-dimensional;three-dimensional;fluidization quality;backmixing作为一种重要的两相接触方式,气固流态化已经广泛应用于石化、能源、化工等众多国民经济支柱产业中。

With y y x x R J R J 1,1== and ()y x y x x yk k k J k J Q −+=22, the coefficients i a in the equation (9’) are:()()()()y x y x x y y x y x y x y x y x k k k J k J k k J J J J J J Q k k g a +−−+−++−=2222209991418()()()()(()()()()()())y y x x y x y x x y y x y x y x y x x y y x y x y x y x x y y x y x x y y x y x x y y x y y x x y x k J k J k k k J k J k k J J k k k J k J J J k k J J k J k J J J k J k J J J k J k J J J k J k J J J Q g a ++++++−+−+−+−−+++++=593576286332323223322222/31()()()(()()()())y x y x x y y x y x x y y x y x y x y x y x x y y x y x y x k k k k k J k J k J k J k k J J J J k k k J k J J J k k J J Q g a +++++−−−+−+++=4422222222222330141813()()()()()x y y x y x y x y x x y y x k J k J J J k k k J k J J J Q g a 332/13233+++−+=14=a1. Lord Rayleigh, “Investigations of the character of the equilibrium of an incompressible heavy fluid of variable density” Proc.Lond.Math.Soc. 14, 170 (1883)2. R.M.Davies, G.I.Taylor, “The mechanics of large bubbles rising through extended liquids and through liquids in tubes” Proc.Roy.Soc. A200, 375 (1950)3. D.H.Sharp, “An overview of Rayleigh-Taylor instability” Physica D 12, 3 19844. S.Chandrasekhar, Hydrodynamic and hydromagnetic stability, 3d ed. (Dover Publications Inc., New York, 1981), pp.428-477; K.O.Mikaelian, “Effect of viscosity on Rayleigh-Taylor and Richtmeyer-Meshkov instabilities” Phys.Rev.E 47, 375 (1993)5. K.I.Read, “Experimental investigation of turbulent mixing by Rayleigh-Taylor instability” Physica D 12, 45 (1984); Yu.A.Kucherenko at al, “Experimental study into the asymptotic stage of separation of the turbulized mixtures in gravitationally stable mode” Laser Part. Beams 15, 17 (1997); Izv. Akad. Nauk SSSR, Mekh. Zhidk. Gaza 6, 157 (1978)6. G.Dimonte M.Schneider, “Density ratio dependence of Rayleigh-Taylor mixing for sustained and impulsive acceleration histories” Phys.Fluids 12, 304 (2000);M.Schneider, G.Dimonte, B.Remington, “Large and small scale structures in Rayleigh-Taylor mixing” Phys.Rev.Lett. 80, 3507 (1998)7. F.H.Harlow, J.E.Welch, “Numerical study of large-amplitude free-surface motion” Phys.Fluids 9,842 (1966); D.L.Youngs, “Numerical simulations of turbulent mixing by Rayleigh-Taylor instability” Physica D 12, 32, (1984); R.Menikoff, C.Zemach,“Rayleigh-Taylor instability and the use of conformal maps for ideal fluid flow”p.Phys. 51, 28 (1983); G.R.Baker, D.I.Meiron, S.A.Orszag, “Vortexsimulations of the Rayleigh-Taylor instability” Phys.Fluids 23, 1485 (1980); G.Gardner, J.Glimm, O.McBryan, R.Menikoff, D.H.Sharp, Q.Zhang, “The dynamics of bubble growth for Rayleigh-Taylor instability” Phys.Fluids 31, 447 (1988)8. X.L.Li, “Study of three-dimensional Rayleigh-Taylor instability” Phys.FluidsA5, 1904 (1993); X.L.Li, “A numerical study of three-dimensional bubble merger in the Rayleigh-Taylor instability” Phys.Fluids 8, 336 (1996)9. D.L.Youngs, “Three-dimensional numerical simulations of turbulent mixing by Rayleigh-Taylor instability” Phys.Fluids A 3, 1312 (1991)10. U.Alon, J.Hecht, D.Offer, D.Sharts, “Power-laws and similarity of Rayleigh-Taylor and Richtmyer-Meshkov mixing fronts at all density ratios” Phys.Rev.Lett.74, 534 (1995)11. S.I.Abarzhi, “Stable steady flows in Rayleigh-Taylor instability”Phys.Rev.Lett.89, 1332 (1998); “Non-linear three-dimensional Rayleigh-Taylor instability” Phys.Rev.E, 59, 1729 (1999)12. A.V.Shubnikov and V.A.Koptsik, Symmetry in science and art, Plenum New York, 197413. yzer, “On the instability of superposed fluids in a gravitational field”Astrophys.Jour. 122, 1 (1955); P.R.Garabedian, “On steady-state bubbles generated by Taylor instability” Proc.Roy.Soc. A241, 423 (1957)14. S.I.Abarzhi, “The stationary spatially periodic flows in Rayleigh-Taylor instability: solutions multitude and its dimension” Physica Scripta T66, 238 (1996);“Stationary solutions of the Rayleigh-Taylor instability for spatially periodic flows:questions of uniqueness, dimensionality and universality” Zh.Eksp.Teor.Fiz. 110,1841 (1996) (Sov.Phys.JETP 83, 1012)15. S.I.Abarzhi and N.A.Inogamov, “Stationary solutions in the Rayleigh-Taylor instability for spatially periodic flow” Zh.Eksp.Teor.Fiz. 107,245 (1995) (Sov.Phys.JETP 80,132 (1995)); N.A.Inogamov, “Stationary solutions in the theory of the hydrodynamic Rayleigh-Taylor instability” Pis’ma Zh.Eksp.Teor.Fiz. 55, 505 (1992) (Sov.Phys.JETP Lett. 55, 521 (1992))16. A.Oparin, “Numerical simulations of Rayleigh-Taylor instability using quasi-monotonic grid-characteristic approach” private communication, 1998; M.F.Ivanov,A.M.Oparin, V.G.Sultanov, V.E.Fortov, “Certain features of development of the Rayleigh-Taylor instability in 3D geometry” Doklady Physics 44, 491 (1999) (Doklady Akademii Nauk 367, 464 (1999))17. R.J.Taylor, J.P.Dahlburg, A.Iwase, J.J.Gardner, D.E.Fyfe O.Willi,“Measurement and Simulation of Laser Imprinting and Consequent Rayleigh-Taylor growth” Phys.Rev.Lett.76, 1643 (1996); M.M.Marinak, S.G.Gledinning, R.J.Wallace, B.A.Remington, et al, “Non-linear evolution of a three-dimensional multimode perturbation” Phy.Rev.Lett. 80, 4426 (1998);18. Dalziel SB, Linden PF, Youngs DL, “Self-similarity and internal structure of turbulence induced by Rayleigh-Taylor instability” Jour.Fluid Mechanics, 399, 1 (1999)19. V.E.Zakharov, “Stability of periodic waves of finite amplitude on deep fluid surface” Prikl.Mat.Teor.Fiz 2, 86 (1968) (Sov.Math. Appl. Math. and Theor. Phys. 2, 86 (1968)); E.Fermi and J.von Newman, “Taylor instability of an incompressible liquid”(1951) in book: E.Fermi, Collected papers, The University of Chicago Press, Chicago 1962, v.2, 81620. J.W.Jacobs and I.Catton, “Three-dimensional Rayleigh-Taylor instability. Part I. Weakly nonlinear theory” Jour. Fluid Mech. 187, 329 (1988)21. X.Y.He, R.Y.Zhang, S.Y.Chen, G.D.Doolen, “On three-dimensional Rayleigh-Taylor instability” Phys.Fluids 11, 1143 (1999)22. J.Hecht, U.Alon, D.Shvarts, "Potential flow models of Rayleigh-Taylor and Richtmeyer-Meshkov bubble fronts" Phys.Fluids 6, 4019 (1994)23. V.S.Arpachi, A.Asmaeeli, “On interface dynamics” Phys.Fluids 12, 1244 (2000)Figure captionsFIG.1. Bubbles generated by the Rayleigh-Taylor instability. Flow symmetry group is p2mm , λx,y are spatial periods in the plane (x, y ), rotation axis 2 and mirror planes m are perpendicular to the plane of translations. Black circle marks the positions of bubble top.FIG.2.(a). Plane of parameters R x,y of steady solutions family, finite values of aspect ratio x y k k . Physical region is bounded by the flattened bubbles (“solitary spikes”) ∞→y x R ,and by the edge solutions cr y x R ,. Dashing line relates to bubbles with circular contour ()()2x y y x k k R R=. Bubbles are y -elongated at ()()2x y y x k R R < and x -elongated at ()()2x y y x k k R R >.(b). Low-symmetric steady solutions under the dimensional crossover 0→x y k k : the solutions with ()2x y y x k k R R ≥ are restricted to region of flattened bubbles (“solitary spikes”), while solutions with ()2x y y x k k R R < become solutions of the 2D flow.FIG.3. The real parts of the Lyapunov exponents for low-symmetric steady solutions.(a). Aspect ratio 2/1=x y k k and the radius of curvature ∞≡y R .(b). Limiting case of “square flow” p4mm , 1=x y k k and x y R R =.FIG.4. Stability region for the low-symmetric bubbles in first approximation (dashing area). Finite values of aspect ratio x y k k , dashing line relates to the bubbles with circular contour, ()()2x y y x k k R R =.FIG.5. Stability of steady solutions under dimensional crossover 0→x y k k .Dashing lines are real parts of the Lyapunov exponents of the 2D flow, unstable mode D D w 23− is plotted at 1.0=x y k k and 001.0=δ. cr c R k R ≈=2. Black points are the Hopf bifurcations, which bound the region of stability of the 2D flow at N =2.FIG.6. Secondary instabilities of the low-symmetric bubbles under spatial modulations: merging and splitting.。

Experimental study on convective heat transfer and flow resistance characteristics of water flow in twisted elliptical tubesSheng Yang,Li Zhang *,Hong XuState-Key Laboratory of Chemical Engineering,School of Mechanical and Power Engineering,East China University of Science and Technology,Shanghai 200237,PR Chinaa r t i c l e i n f oArticle history:Received 15January 2011Accepted 21May 2011Available online 30May 2011Keywords:Twisted elliptical tubeHeat transfer enhancement Flow resistanceField synergy principlea b s t r a c tHeat transfer and flow resistance characteristics of water flow inside the twisted elliptical tubes (TETs)with different structural parameters were experimentally investigated.Effects of tube structural parameters (aspect ratio and twist pitch)on the performance of TETs were analyzed and the overall thermal-hydraulic performance of TETs was evaluated.Experimental results showed that the TETs can provide considerable heat transfer augmentation and also high pressure drop inside rger tube aspect ratios and smaller twist pitches resulted in higher heat transfer coef ficients and friction factors.The best operating regime for TETs is at lower Reynolds numbers.It was also discovered that the experimental Nusselt numbers/friction factors can be expressed with one uni fied equation for entire Reynolds number range,which con firms the early flow transition from laminar to turbulent in TETs.Experimental results were compared with some existing correlations,and the causes for the differences between them were analyzed.Heat transfer enhancement mechanism of TETs was discussed from the viewpoint of field synergy.The longitudinal vortex induced by the twisted tube wall improves the synergy between the velocity vector and temperature gradient,which in turn results in a better heat transfer performance.Ó2011Elsevier Ltd.All rights reserved.1.IntroductionShell and tube heat exchangers are widely used in many engi-neering fields.Heat transfer enhancement techniques inside tubes are very important for improving the ef ficiency of heat exchangers and many important progresses have been made during the past 30years.In general,heat transfer enhancement techniques can be divided into two groups,namely active and passive techniques.The active technique requires external forces such as an electric field,acoustic or surface vibration,whereas the passive technique requires special surface geometries such as a rough surface,extended surface,or fluid additives.Both active and passive tech-niques were used by researchers over a century ago to increase the heat transfer rate in heat exchangers [1e 3].The twisted tube is one of the passive heat transfer enhance-ment tubes.It is formed into an elliptical or oblate cross section with a superimposed twist as illustrated in Fig.1and is left round at two ends for conventional fixing into the tube sheet.The geomet-rical features of a twisted tube include the 360 twist pitch (S ),major dimension of the cross section (A ),and minor dimension of the cross section (B ).Besides,the severity of tube twisting is described by the dimensionless twist ratio (S /d or S /d e ),where d is the diameter of the smooth round tube used to produce the twisted tubes and d e is the equivalent hydraulic diameter of the twisted tube.The severity of tube flattening is described by dimensionless aspect ratio (A/B).Twisted tubes are sometimes chosen in the design of industrial shell and tube heat exchangers,which can considerably reduce the size of the heat exchangers.2.Brief review of previous workThermal-hydraulic performance of twisted tubes has been studied by a few researchers as shown in Table 1.Ievlev et al.[4]presented the experimental results of heat transfer and hydraulic resistance of a heat transfer agent flowing inside the twisted flat tubes and inter-tube space.The working fluid used in their study was air,and Reynolds numbers ranged from 6000to 100,000for the tube side and from 3000to 60,000for the inter-tube side.The effectiveness of using these tubes in heat exchange equipment was analyzed,and the results showed that the replacement of smooth tubes by twisted ones leads to a 20%e 40%increase in heat transfer with a 50%e 80%increase in hydraulic resistance which allows*Corresponding author.Tel./fax:þ862164253810.E-mail address:lzhang@ (L.Zhang).Contents lists available at ScienceDirectApplied Thermal Engineeringjournal ho mepage:www.elsevier.co m/locate/apthermeng1359-4311/$e see front matter Ó2011Elsevier Ltd.All rights reserved.doi:10.1016/j.applthermaleng.2011.05.030Applied Thermal Engineering 31(2011)2981e 2991a reduction in the heat exchanger volume of up to 30%.Thecorrelations for Nusselt number and friction factor were proposed.Asmantas et al.[5]experimentally studied the heat transfer and flow resistance characteristics of air flow inside twisted flat tubes over a range of S /d o from 6.2to 12.2,Reynolds number from 7000to 200,000.The heat transfer coef ficient for a twisted flat tube is larger than that for a smooth tube over the entire Reynolds number range.The heat transfer is augmented by as much as 40%and the hydraulic resistance also increases by a factor of 1.7on an average at S /d o ¼62.The correlations for the Nusselt numbers and friction factors were also presented.Dzyubenko and Yakimenko [6]also presented the formulas for calculating the Nusselt numbers and friction factors for flow inside twisted oval tubes and inter-tube space respectively.It was discovered that the heat transfer is enhanced obviously when the Reynolds number is smaller than 7000.By means of a method of effective parameters,it was discovered that the thermal-hydraulic ef ficiency of twisted tubes is higher than that of smooth round tubes and smooth tubes with annular knurling.Si et al.[7]experimentally studied the heat transfer and pres-sure drop characteristics of diesel oil flowing in twisted flat tubes.Three kinds of twisted flat tubes with different structural param-eters were tested.It was found that the tube side heat transfer coef ficient and friction factors for these tubes were higher than those for the smooth tube.The twisted tubes have better heat transfer performance at smaller Reynolds number from around 2000to 7000.And the smaller the twist pitch,the better the heat transfer performance.The flow resistance for the twisted tube has a greater increase at smaller Reynolds number from 2000to 7000compared with that of the smooth tube,and with the decrease of the twist pitch,the flow resistance increases.The author analyzed that the swirling flow in the twisted tube increase the fluid turbulence,which enhances the heat transfer while increasing the flow resistance.Zhang et al.[8]conducted an experimental investigation on the heat transfer and flow resistance of water flow inside different twisted tubes.The tests were conducted at Reynolds numbers ranging between 7900and 26,500.Both heat transfer coef ficients and friction factors increase with the decrease of twist pitch or with the increase of aspect ratio at the same Reynolds number.The thermal-hydraulic performance of the twisted tube is better when the Reynolds number is smaller than 10,000.Based on the exper-imental results,correlations for the Nusselt number and friction factor were also obtained.Gao et al.[9]experimentally investigated the heat transfer and flow resistance characteristics of water flow inside twisted tubes with large twist ratio in transition and turbulent flow regime.Nusselt numbers and friction factors for twisted tubes are 1.3e 2.5times and 1.2e 1.5times of those for the smooth tube,respectively.It was also discovered that the Nusselt numbers and friction factors increase with the decrease of twist pitch or with the increase of aspect ratio,which is in agreement with the findings in Ref.[8].Yang et al.[10]studied the heat transfer and flow resistance of fluid flowing inside a twisted elliptical tube in laminar flow regime using the CFD method.The major axis,minor axis and twist pitch of the tube are 23mm,14mm and 320mm,respectively.The Rey-nolds number ranges from 100to 500,and the Prandtl number is less than 200.Results showed that the twisted ellipticaltubeFig.1.Twisted tube section.S.Yang et al./Applied Thermal Engineering 31(2011)2981e 29912982provide a remarkable heat transfer enhancement performance,and the greater the Prandtl number,the better the heat transfer performance.Thefindings about effects of tube structural param-eters(S and A/B)on the heat transfer andflow resistance charac-teristics of the tube were the same with those in Refs.[8,9].Reason for heat transfer enhancement was concluded that the secondary flow induced by thefluid swirling directlyflushes some part of the inner tube wall,temperature gradient near the tube is higher,the distribution offluid velocity and temperature is more uniform, which enhances the heat transfer effectively.Bishara et al.[11]also used the CFD method to obtain the temperature and velocity distribution offluid in the cross section of a twisted elliptical tube with a twist ratio of6.0and an aspect ratio of1.43.According to the temperature and velocity plots,the paper indicates that the secondaryflows promote mixing in the plane normal to the bulkflow direction.This mixing works to maintain a high temperature gradient close to tube wall and then increase the Nusselt number.In the above literatures,heat transfer andflow resistance char-acteristics offluidflow inside the twisted tubes and the inter-tube space have been studied,and wherein tube side is the research emphasis.Experimental and CFD methods were employed,and the workingfluid covered air,diesel oil and water.Effects of tube structural parameters on heat transfer andflow resistance perfor-mance were analyzed,and correlations to predict Nusselt number and friction factor were presented.However,little experimental research was associated with the thermal-hydraulic performance of twisted tubes in laminarflow regime.Equations presented for calculating Nusselt numbers and friction factors had various forms and often there were significant differences among the predicted values for the same twisted tube under the same operational condition.Mechanism of heat transfer enhancement is explored from the traditional point of view,which can be summarized by increasingflow turbulence or decreasing thickness of the devel-oping thermal boundary layer.In view of this,the present work conducts an experimental research on the thermal-hydraulic performance offive twisted elliptical tubes with different struc-tural parameters.The workingfluid is water,and the Reynolds number ranges from around600to55,000,covering the laminar, transition and turbulentflow regime.Correlations for heat transfer andflow resistance are obtained and compared with those existing ones.In addition,temperaturefield and velocityfield of water in TETs are numerically investigated;and the heat transfer enhance-ment mechanism of TETs is further explored from the viewpoint of field synergy principle.3.Experimental apparatus and data reduction3.1.Experimental apparatusA schematic diagram of the experimental apparatus is shown in Fig.2.The experimental apparatus mainly consisted of a cold medium loop,a hot medium loop,a test section and a measure-ment system.The test section was a double tube exchanger.Each tested tube had an effective length of1.75m.The workingfluid on both tube side and shell side was deionized water.The hot water tank had a maximum heating power of20kW and a temperature control system was equipped for it to adjust the heating power to keep a constant water temperature at a givenflow rate,and the hot water temperature can range from30to95 C.Hot water was conveyed to the test section by a centrifugal pump and cooled in the tested tube via counterflow heat exchange with the cold waterTable1Investigations on the twisted tubes with various workingfluid and tube configurations.Sources Tube parameters Workingfluid Tube side correlationsd o(mm)S(mm)A i(mm)B i(mm)S/A oIevlev[4]e12.1e 6.2e16.7air Nu¼0:019Re0:8h1þ0:547=ðs=AÞ0:83if¼0:316h1þ3:27ðs=AÞÀ0:87iReÀ0:256Â103<Re<105Asmantas[5]e12.1e 6.2e12.2airNu¼0:021Re0:8Pr0:4h1þ2:1ðs=AÞÀ0:91i TwT f!nn¼À0:17À0:27Â10À5ðx=d eÞ1:37hðs=d eÞ2:1À109:6if¼0:82ðs=AÞÀ0:63ReÀ0:18 7Â103<Re<2Â105Si[7]19144,192,25021e 6.86,9.14,11.9dieselNu¼0:396Re0:544se!0:161s!À0:519Pr0:33 lg f¼a1þa2lgReþa3ðlgReÞ21000<Re<17,000Zhang[8]25160,200,25024,2614,9e waterNu¼1:50618Re0:51825PrÀ1:2446A ii !1:12252se!À0:32367f¼0:71497Re0:07777PrÀ1:03974A iB i!À0:76212sd e!À0:333937900<Re<26,500Gao[9]19200,300,40019.8,21.2,21.89.4,7.0,5.8e waterNu¼0:034Re0:784Pr0:333B iA i!À0:590sd e!À0:165f¼4:572ReÀ0:521B ii!À0:334se!À0:0825000<Re<20,000Yang[10]19e e e10e17e Nu¼3:66þ0:512Re0:477Pr0:9751ÀB iA i!1:532sB!À0:609100<Re<500S.Yang et al./Applied Thermal Engineering31(2011)2981e29912983flowing on shell side.The upstream tube section of the tested tubewas made long and straight in order to ensure a fully developed flow in tube.An inverted U-bend was mounted on the downstream side to ensure that the tested tube can always be flooded with fluid at any given flow rate.Cold water was pumped through shell side and a plate heat exchanger in a closed loop,heated outside the tested tube and then cooled in the plate heat exchanger by means of water from an independent external cooling tower.A thermo-static control valve adjusts the flow rate of the cooling water to control the inlet temperature of cold water to be constant.The cold water temperature ranged from 30 C to 60 C.Finally,to reduce the heat loss to the ambient,the whole apparatus was well insulated.The experimental apparatus was equipped with a data acquisi-tion system (DAS)based on an Agilent Data Acquisition Unit 34970A and a PC.Parameters required to be measured includes flow rates of hot/cold water,bulk temperatures of hot/cold water at the inlet/outlet of the tested tube/shell,and pressure drop across the tested tube.Two sheathed T-type thermocouples were utilized to measure the hot/cold water bulk temperatures.All thermocou-ples were calibrated in the same constant temperature bath with an accuracy of Æ0.1 C within the tested range.Two turbine flowme-ters were employed to measure the flow rates of hot/cold water,and the uncertainty was estimated as Æ0.2%.Pressure drop across the tested tube is measured using the differential pressure trans-ducer GE Druck PMP 4170with an accuracy of Æ0.04%.For each test run,the whole system was first stabilized for about 30min by continuously running the working fluid.Steady state conditions were assured by checking both temperature and differential pressure readings.The flow rates of hot water and cold water were set to certain values during each test run.The hot water tank was thermostatic with adjustable heating power,thus the hot water could be maintained at a desired temperature at the inlet of the tested tube.Cold water flowing on shell side was heated and then conveyed back to the cold water tank passing through a plate heat exchanger.By adjusting the control valve of the plate heat exchanger,constant temperature of water that flowed back to the cold water tank could be obtained,as well as a constant inlet temperature of the cold water.Besides,the differential pressure across the tested tube was monitored.If the fluctuation of watertemperature at the inlet/outlet of tube/shell side did not exceed Æ0.1 C within 2min,and the fluctuation of the differential pres-sure was less than Æ5%,a steady state for heat transfer and fluid flow was achieved,and then the data collection began.Experi-mental data were acquired by the DAS every 3s,and the average values over 2min were used for calculating both friction factor and heat transfer coef ficient.A smooth tube and five twisted tubes were tested,and all tubes were made from commercially pure copper.The mean outside diameter,wall thickness and length of the smooth tube are 19.02mm,1.01mm and 1880mm,respectively.The twisted tubes were manufactured from smooth tubes and have an elliptical cross section.Geometrical speci fications and pro file of the twisted elliptical tubes are shown in Table 2and Fig.3.3.2.Data reductionConvective heat transfer coef ficients of tube side are obtained by the method suggested by J.A.Meng [12].First,the exponential correlation of Nusselt numbers,Nu,for the outer surface of the tested tube is obtained by varying the flow rate of cold water outside tube and keeping the hot water flow rate inside the tube at its maximum value.Then set the cold water flow rate outside tube at its maximum value and measure the overall thermal resistance.The heat transfer coef ficients for hot water inside tube can be determined by subtracting the convection resistance outside the tube and the conduction resistance through tube wall from the overall thermal resistance.Following are the detailed procedure.Table 2Speci fications of the tested TETs.Tube No.Twist pitch,S (mm)Aspect ratio,A /B 1104 1.602152 1.903192 2.154192 1.7651921.49cooling waterhot water temperature measuring point measurement pressure measuring pointFig.2.Schematic diagram of the experimental apparatus.S.Yang et al./Applied Thermal Engineering 31(2011)2981e 29912984The first step is to obtain the correlation for calculation of theheat transfer coef ficients outside the tube.The logarithmic mean temperature difference,D T LMTD ,between the hot and cold fluid can be derived from Eq.(1)D T LMTD¼ÀT h ;in ÀT c ;out ÁÀÀT h ;out ÀT c ;in ÁlnT h ;in ÀT c ;out T h ;out ÀT c ;in(1)Where T h,in and T h,out are the temperatures of hot water at the inlet and outlet of the tested tube,respectively.T c,in and T c,out are the temperatures of cold water at the inlet and outlet of the shell side,respectively.This temperature difference is kept 10e 25 C in the experiments.Heat transfer rates of tube side and shell side,Q h and Q c are calculated by Eqs.(2)and (3),and their arithmetic mean value is considered as the heat transfer rate of the experiment.Q h ¼_mh c p ;h ÀT h ;in ÀT h ;out Á(2)Q c ¼_m c c p ;c ÀT c ;out ÀT c ;in Á(3)Q ¼Q h þQ c (4)Where _mh and _m c are the mass flow rates of hot and cold water,respectively.The overall heat transfer coef ficient is determined by Eq.(5)U ¼QF o D T LMTD(5)The hot water flow rate inside tube is fixed at its maximum value while the cold water flow rate outside tube is regulated.Fit the heat transfer correlation for the shell side with an exponential relation as the following form of Eq.(6):Nu o ¼c Re 0:8Pr 0:4(6)In the present work,the fouling resistance is neglected since all the tubes are cleaned before each experiment.Then,the overall thermal resistance can be expressed as the sum of the partial thermal resistances corresponding to the inner convection,the heat conduction through tube wall and the outer convection,according to Eq.(7)1U ¼1h o þd o 2k w ln d o d i þd oh i d i(7)Submitting Eq.(6)into Eq.(7),the overall thermal resistance can be written as:1U ¼1cd o k cRe À0:8Pr À0:4 þ d o 2k w ln d o d i þd od i h i (8)Where h i and h o are the heat transfer coef ficient for the tube side and shell side,respectively.d i and d o are the inner diameter and outer diameter of the tube,respectively.k c is the thermal conduc-tivity of the cold water,and k w is the thermal conductivity of tubematerial.dow ln d o iis the conductive thermal resistance across the tube wall.In the experiments,the flow rate of hot water inside the tested tube is fixed at its maximum value and the bulk temperature of the hot water is basically kept constant,therefore the heat transfer coef ficient for the tube side is almost constant.It could be seen from Eq.(8)that 1/U only varies with Re À0.8Pr À0.4linearly.Take X ¼d o =k c Re À0:8Pr À0:4as abscissa and Y ¼1/U as ordinate,one can obtain a linear relation between Y and X by changing the flow rate outside the tube.The constant c can be determined by a curve fitting method.Once c is obtained,the heat transfer coef ficient outside the tube can be calculated by Eq.(9)h o ¼c k coRe 0:8Pr 0:4(9)The internal heat transfer performance can be determined experimentally after the thermal resistance outside tube is known.In such experiments,the flow rate of the cold water outside tube is fixed at its maximum to reduce the external convection resistance while the flow rate of the hot water inside tube is regulated.The overall heat transfer coef ficient U can be decided by Eqs.(1)e (5).Then the heat transfer coef ficient for the tube side,h i ,can be obtained by Eq.(10)1h i¼d i d o 1U À1h o Àd o 2k w ln d od i(10)The Nusselt number inside the tube isNu ¼h i d i k h(11)The friction factor for the tube side is easy to be calculated according to Eq.(12):f ¼d i L $2D p r u 2(12)Where D p is the pressure drop of hot water across the tested tube;L is the tube length;u is the mean flow rate of water inside tube.The uncertainty is estimated with the method suggested by Moffat [13]and Kline [14].As mentioned above,the measurement error of temperature is 0.1 C,the turbine flow meter has a preci-sion of 0.2%,and the measurement accuracy of the differential pressure meter is 0.04%.In addition,the measurement uncer-tainties of tube diameter and tube length are about 0.6%and 0.08%,respectively.The relative error of each physical parameter (e.g.,density,speci fic heat of fluid)is about 0.5%.According to the uncertainty propagation equation,the maximum relative uncer-tainties for the experimental Nusselt number and friction factor are 11.4%and 8.2%,respectively.Fig.3.Photograph of tested TETs.S.Yang et al./Applied Thermal Engineering 31(2011)2981e 299129854.Experimental results4.1.Verification of smooth tubeIn order to validate the reliability of the experimental system, heat transfer andflow resistance characteristics of waterflowing inside a smooth tube werefirst investigated.The Nusselt numbers for laminar,transition and turbulentflow in a smooth tube obtained from the present experiments were compared with predictions of the Sieder e Tate correlation[15,16],Eq.(13),and Gnielinski corre-lation[11,17],Eq.(14),respectively.The experimental friction factors were compared with the Darcy friction factors(f¼64=Re)and predictions of the Petukhov correlation[18],Eq.(15).Nu¼1:86Re1=3Pr1=3fd iL1=3 mfm w0:14(13)Nu¼ðf=8Þ$ðReÀ1000Þ$Pr f1þ12:7ffiffiffiffiffiffiffiffif=8p$Pr2=3fÀ11þd iL2=3!Pr fPr w0:11ð14Þf¼ð1:82lgReÀ1:64ÞÀ2(15) Fig.4shows the comparison of experimental Nusselt numbers and friction factors with those from correlations of Eqs.(13)e(15). The experimental Nusselt numbers for laminarflow agree with the Sieder e Tate correlation with a deviation betweenÀ6.5%and11%, and the average deviation is 1.6%.The experimental Nusselt numbers for transition and turbulentflow agree with the Gnielinski correlation with a deviation betweenÀ6.1%and10.6%,and the average deviation isÀ2.6%.For the friction factors,the deviation is betweenÀ9.3%and3.5%,and the average deviation is1.8%.The results prove the reliability of the experimental system.4.2.Heat transfer performance of the TETsThe heat transfer performance of TETs is presented in the form of Nusselt number.Variation of Nusselt numbers with Reynolds numbers for the tested TETs and smooth tube are given in Fig.5. Reynolds numbers are from around600to55,000,which covers the threeflow patterns of laminarflow,transitionflow and turbulentflow.Referring to Fig.5,one can observe that the Nusselt numbers for all the tested tubes increase as the rise of Reynolds numbers.The increase in Nusselt number indicates an enhance-ment in heat transfer coefficient due to the increase of convection. All the tested TETs have a better heat transfer performance than the smooth tube.TET No.1has the best heat transfer performance amongst thefive TETs and followed successively by TET No.2,TET No.3,TET No.4and TET No.5.It should be noted that the Nusselt number for TET No.5is only slightly higher than that for the smooth tube especially when Reynolds numbers exceed around 10,paring the structural parameters of TET No.3,TET No.4 and TET No.5listed in Table1,one can discover that these three tubes have same twist pitch of192mm but different aspect ratios. The Nusselt numbers increase with the rise of tube aspect ratios.TET No.3has the largest aspect ratio of2.15among these three tubes and has the highest Nusselt number,or best heat transfer performance.Thisfinding about effect of tube aspect ratio on tube heat transfer performance is in agreement with the reports in literatures[8,9].Comparing with TET No.3,both TET No.1and TET No.2have smaller tube aspect ratio but better heat transfer performance,which is due to the smaller twist pitch of TET No.1 and TET No.2.The conventional view believes that the swirling flow,that is the secondaryflow induced by the twisted tube wall,intensifies the turbulence and promotes the radial mixing of the bulkflow.The mixing works to maintain a high temperature gradient close to the tube wall and in turn enhance the heat transfer.Both a larger tube aspect ratio and a smaller twist pitch can lead to a more intensive turbulence and effective mixing to obtain a better heat transfer performance.From the experimental results, one can also discover that the effect of the twist pitch on the heat transfer performance of a TET is more notable than that of the tube aspect ratio.Nu/[Pr1/3(µf/µw)1/3]ReNu/F(f,Pr)ReRefabcFig.4.Experimental results of heat transfer andflow resistance for smooth tube:(a), (b)Nusselt number;(c)friction factor.(a)Comparison of Nusselt numbers in laminar flow regime(b)Comparison of Nusselt numbers in transition and turbulentflow regime(c)Comparison of friction factors.S.Yang et al./Applied Thermal Engineering31(2011)2981e2991 2986The effectiveness of heat transfer enhancement for the TETs relative to the smooth tube was compared in Fig.6.The effective-ness is indexed by a ratio of the Nusselt number for the enhanced tube to that for the smooth tube,in terms ofNu e =Nu s.As shown inFig.6,the Nusselt number ratios for all the tested TETs tend to increase when Reynolds number increase from around 600to 2300,then to decrease with the rise of Reynolds number from around 2300to 10,000,and finally shows a slightly decrease for higher Reynolds numbers.This indicates that the heat transfer enhance-ment of the TETs is more signi ficant at lower fluid velocities cor-responding to the laminar and transition flow regime.The Nusselt number ratios for TET No.1that has the best heat transfer perfor-mance are around 3.9e 4.8for Reynolds numbers from 600to 2300and 2.8e 1.4for Reynolds number higher than 2300.The corre-sponding Nusselt number ratios are 3.6e 4.6,2.5e 1.3for TET No.2,3.4e 4.3,2.2e 1.2for TET No.3,2.8e 3.5,2.0e 1.1for TET No.4and 2.5e 3.0,1.5e 1.0for TET No.5.For the TETs,it is found that the experimental results for the Nusselt number can be correlated with an uni fied equation,which is a function of the Reynolds number (Re),Prandtl number (Pr),twist ratio (S /d e )and aspect ratio(A i /B i ),for Reynolds numbers from 600to 55,000as shown in Eq.(16):Nu ¼0:3496Re 0:615Pr 1=3 A iB i0:490 Sd e À0:394(16)4.3.Hydraulic performance of the TETsThe hydraulic performance of the TETs is presented in the form of friction factor.Variation of the friction factor with Reynolds numbers for the TETs and the smooth tube is presented in Fig.7.In the figure,it is apparent that the friction factors for all the TETs are greater than those for the smooth tube.Friction factors are higher at lower Reynolds number and tend to decrease with the rise of Reynolds numbers from around 600to 15,000,then show a slightly decrease for higher Reynolds numbers.The difference in friction factors for TET No.1to TET No.4are trivial,therefore a partial enlarged drawing was employed to show the details of difference.From the partial enlarged drawing,one can clearly discover that the TET No.3has the greatest friction factors and followed successively by the TET No.2,TET No.4,TET No.1and TET No.5,which is just in accordance with the order of the tube aspect ratios from large to small.This demonstrates that the TET with a larger tube aspect ratio has a larger friction factor,which is in agreement with the finding in previous literatures,Refs.[8,9].The increase of flow resistance in TET can be attributed to the swirling flow caused by the twist channel and the blocking effect of the special tube wall.Just as mentioned above,when fluid flows in the TET with larger tube aspect ratio,a more intensive turbulence is induced to increase the flow resistance.In theory,a smaller twist pitch can improve the blocking effect to cause a greater friction factor.However,the effect of twist pitch on the friction factor for the TETs is not obvious in the present experiment.The effect of tube aspectReN u e /N u sFig.6.Variation of Nusselt number ratio (Nu e /Nu s )with Reynolds number for the TETs.0.000.050.100.150.200.250.30RefSmooth tube Tube No.1Tube No.2Tube No.3Tube No.4Tube No.5Fig.7.Variation of friction factor with Reynolds number for the TETs.Ref e /f sFig.8.Variation of friction factor ratio (f e =f s )with Reynolds number for the TETs.ReN u /[P r 1/3(µf /µw )0.14]Fig.5.Variation of Nusselt number with Reynolds number for various tubes.S.Yang et al./Applied Thermal Engineering 31(2011)2981e 29912987。