专题05+平面向量+5.1 平面向量的概念及线性运算讲义(无解析)

§5.1　平面向量的概念及线性运算考试要求　1.理解平面向量的意义、几何表示及向量相等的含义.2.掌握向量的加法、减法运算，并理解其几何意义及向量共线的含义.3.了解向量线性运算的性质及其几何意义．知识梳理1．向量的有关概念(1)向量：既有大小又有方向的量叫做向量，向量的大小叫做向量的长度(或模)．(2)零向量：长度为0的向量，记作0.(3)单位向量：长度等于1个单位长度的向量．(4)平行向量：方向相同或相反的非零向量，也叫做共线向量，规定：零向量与任意向量平行．(5)相等向量：长度相等且方向相同的向量．(6)相反向量：长度相等且方向相反的向量．2．向量的线性运算向量运算法则(或几何意义)运算律加法交换律：a ＋b ＝b ＋a ；结合律：(a ＋b )＋c ＝a ＋(b ＋c )减法a －b ＝a ＋(－b )数乘|λ a |＝|λ||a |，当λ>0时，λa 的方向与a 的方向相同；当λ<0时，λa 的方向与a 的方向相反；当λ＝0时，λa ＝0λ(μ a )＝(λμ)a ；(λ＋μ)a ＝λa ＋μa ；λ(a ＋b )＝λa ＋λb3.向量共线定理向量a (a ≠0)与b 共线的充要条件是：存在唯一一个实数λ，使得b ＝λa .常用结论1．一般地，首尾顺次相接的多个向量的和等于从第一个向量起点指向最后一个向量终点的向量，即A 1A 2—→ ＋A 2A 3—→ ＋A 3A 4—→ ＋…＋A n －1A n ———→ ＝A 1A n —→，特别地，一个封闭图形，首尾连接而成的向量和为零向量．2．若F 为线段AB 的中点，O 为平面内任意一点，则OF → ＝12(OA →＋OB →)．3．若A ，B ，C 是平面内不共线的三点，则PA → ＋PB → ＋PC → ＝0⇔P 为△ABC 的重心，AP → ＝13(AB→＋AC →)．4．若OA → ＝λOB → ＋μOC →(λ，μ为常数)，则A ，B ，C 三点共线的充要条件是λ＋μ＝1.5．对于任意两个向量a ，b ，都有||a |－|b ||≤|a ±b |≤|a |＋|b |.思考辨析判断下列结论是否正确(请在括号中打“√”或“×”)(1)|a |与|b |是否相等，与a ，b 的方向无关．(　√　)(2)若向量a 与b 同向，且|a |>|b |，则a >b .(　×　)(3)若向量AB → 与向量CD →是共线向量，则A ，B ，C ，D 四点在一条直线上．(　×　)(4)起点不同，但方向相同且模相等的向量是相等向量．(　√　)教材改编题1．(多选)下列命题中，正确的是( )A ．若a 与b 都是单位向量，则a ＝b B ．直角坐标平面上的x 轴、y 轴都是向量C ．若用有向线段表示的向量AM → 与AN →不相等，则点M 与N 不重合D ．海拔、温度、角度都不是向量答案　CD解析　A 错误，由于单位向量长度相等，但是方向不确定；B 错误，由于只有方向，没有大小，故x 轴、y 轴不是向量；C 正确，由于向量起点相同，但长度不相等，所以终点不同；D 正确，海拔、温度、角度只有大小，没有方向，故不是向量．2．下列各式化简结果正确的是( )A.AB → ＋AC → ＝BC →B.AM → ＋MB → ＋BO → ＋OM → ＝AM →C.AB → ＋BC → －AC → ＝0D.AB → －AD → －DC → ＝BC → 答案　B3．已知a 与b 是两个不共线的向量，且向量a ＋λb 与－(b －3a )共线，则λ＝________.答案　－13解析　由题意知存在k ∈R ，使得a ＋λb ＝k [－(b －3a )]，所以Error!解得Error!题型一　向量的基本概念例1　(1)(多选)给出下列命题，不正确的有( )A ．若两个向量相等，则它们的起点相同，终点相同B ．若A ，B ，C ，D 是不共线的四点，且AB → ＝DC →，则四边形ABCD 为平行四边形C ．a ＝b 的充要条件是|a |＝|b |且a ∥bD ．已知λ，μ为实数，若λa ＝μb ，则a 与b 共线答案　ACD解析　A 错误，两个向量起点相同，终点相同，则两个向量相等，但两个向量相等，不一定有相同的起点和终点；B 正确，因为AB → ＝DC → ，所以|AB → |＝|DC → |且AB → ∥DC →，又A ，B ，C ，D 是不共线的四点，所以四边形ABCD 为平行四边形；C 错误，当a ∥b 且方向相反时，即使|a |＝|b |，也不能得到a ＝b ，所以|a |＝|b |且a ∥b 不是a ＝b 的充要条件，而是必要不充分条件；D 错误，当λ＝μ＝0时，a 与b 可以为任意向量，满足λa ＝μb ，但a 与b 不一定共线．(2)如图，在等腰梯形ABCD 中，对角线AC 与BD 交于点P ，点E ，F 分别在腰AD ，BC 上，EF 过点P ，且EF ∥AB ，则下列等式中成立的是( )A.AD → ＝BC →B.AC → ＝BD →C.PE → ＝PF →D.EP → ＝PF →答案　D 教师备选(多选)下列命题为真命题的是( )A ．若a 与b 为非零向量，且a ∥b ，则a ＋b 必与a 或b 平行B ．若e 为单位向量，且a ∥e ，则a ＝|a |eC ．两个非零向量a ，b ，若|a －b |＝|a |＋|b |，则a 与b 共线且反向D ．“两个向量平行”是“这两个向量相等”的必要不充分条件答案　ACD思维升华　平行向量有关概念的四个关注点(1)非零向量的平行具有传递性．(2)共线向量即为平行向量，它们均与起点无关．(3)向量可以平移，平移后的向量与原向量是相等向量．(4)a|a |是与a 同方向的单位向量．跟踪训练1　(1)(多选)下列命题正确的是( )A ．零向量是唯一没有方向的向量B ．零向量的长度等于0C ．若a ，b 都为非零向量，则使a|a |＋b|b |＝0成立的条件是a 与b 反向共线D ．若a ＝b ，b ＝c ，则a ＝c 答案　BCD解析　A 项，零向量是有方向的，其方向是任意的，故A 错误；B 项，由零向量的定义知，零向量的长度为0，故B 正确；C 项，因为a|a |与b|b |都是单位向量，所以只有当a|a |与b|b |是相反向量，即a 与b 是反向共线时才成立，故C 正确；D 项，由向量相等的定义知D 正确．(2)对于非零向量a ，b ，“a ＋b ＝0”是“a ∥b ”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件答案　A解析　若a ＋b ＝0，则a ＝－b ，则a ∥b ，即充分性成立；若a ∥b ，则a ＝－b 不一定成立，即必要性不成立，即“a ＋b ＝0”是“a ∥b ”的充分不必要条件．题型二　平面向量的线性运算命题点1　向量加、减法的几何意义例2　(2022·济南模拟)已知单位向量e 1，e 2，…，e 2 023，则|e 1＋e 2＋…＋e 2 023|的最大值是________，最小值是________．答案　2 023　0解析　当单位向量e 1，e 2，…，e 2 023方向相同时，|e 1＋e 2＋…＋e 2 023|取得最大值，|e 1＋e 2＋…＋e 2 023|＝|e 1|＋|e 2|＋…＋|e 2 023|＝2 023；当单位向量e 1，e 2，…，e 2 023首尾相连时，e 1＋e 2＋…＋e 2 023＝0，所以|e 1＋e 2＋…＋e 2 023|的最小值为0.命题点2　向量的线性运算例3　(多选)如图，在四边形ABCD 中，AB ∥CD ，AB ⊥AD ，AB ＝2AD ＝2CD ，E 是BC 边上一点，且BC → ＝3EC →，F 是AE 的中点，则下列关系式正确的是( )A.BC →＝－12AB → ＋AD → B.AF → ＝13AB → ＋13AD → C.BF →＝－13AB → ＋23AD →D.CF →＝－16AB → －23AD → 答案　ABD解析　因为BC → ＝BA → ＋AD → ＋DC → ＝－AB → ＋AD → ＋12AB →＝－12AB → ＋AD → ，所以选项A 正确；因为AF → ＝12AE → ＝12(AB → ＋BE →)＝12(AB →＋23BC → )，而BC →＝－12AB → ＋AD → ，代入可得AF → ＝13AB → ＋13AD → ，所以选项B 正确；因为BF → ＝AF → －AB →，而AF → ＝13AB → ＋13AD → ，代入得BF →＝－23AB → ＋13AD → ，所以选项C 不正确；因为CF → ＝CD → ＋DA → ＋AF→＝－12AB → －AD → ＋AF → ，而AF → ＝13AB → ＋13AD →，代入得CF →＝－16AB → －23AD → ，所以选项D 正确．命题点3　根据向量线性运算求参数例4　(2022·青岛模拟)已知平面四边形ABCD 满足AD → ＝14BC → ，平面内点E 满足BE → ＝3CE →，CD与AE 交于点M ，若BM → ＝xAB → ＋yAD →，则x ＋y 等于( )A.52B ．－52C.43 D ．－43答案　C解析　如图所示，易知BC ＝4AD ，CE ＝2AD ，BM → ＝AM → －AB → ＝13AE → －AB→ ＝13(AB → ＋BE → )－AB→＝13(AB → ＋6AD → )－AB→＝－23AB → ＋2AD →，∴x ＋y ＝43.教师备选1．(2022·太原模拟)在△ABC 中，AD 为BC 边上的中线，若点O 满足AO → ＝2OD → ，则OC →等于( )A.－13AB → ＋23AC →B.23AB → －13AC →C.13AB → －23AC →D.－23AB → ＋13AC→答案　A解析　如图所示，∵D 为BC 的中点，∴AD → ＝12(AB → ＋AC → )，∵AO → ＝2OD →，∴AO → ＝23AD → ＝13AB → ＋13AC → ，∴OC → ＝AC → －AO → ＝AC →－(13AB → ＋13AC →)＝－13AB → ＋23AC →.2．(2022·长春调研)在△ABC 中，延长BC 至点M 使得BC ＝2CM ，连接AM ，点N 为AM 上一点且AN → ＝13AM → ，若AN → ＝λAB → ＋μAC →，则λ＋μ等于( )A.13 B.12C ．－12D ．－13答案　A解析　由题意，知AN → ＝13AM → ＝13(AB → ＋BM →)＝13AB → ＋13×32BC →＝13AB → ＋12(AC → －AB → )＝－16AB → ＋12AC →，又AN → ＝λAB → ＋μAC →，所以λ＝－16，μ＝12，则λ＋μ＝13.思维升华　平面向量线性运算的常见类型及解题策略(1)向量求和用平行四边形法则或三角形法则；求差用向量减法的几何意义．(2)求参数问题可以通过向量的运算将向量表示出来，进行比较，求参数的值．跟踪训练2　(1)点G 为△ABC 的重心，设BG → ＝a ，GC → ＝b ，则AB →等于( )A ．b －2aB.32a －12bC.32a ＋12b D ．2a ＋b答案　A解析　如图所示，由题意可知12AB → ＋BG → ＝12GC → ，故AB → ＝GC → －2BG →＝b －2a .(2)(2022·大连模拟)在△ABC 中，AD → ＝2DB → ，AE → ＝2EC → ，P 为线段DE 上的动点，若AP → ＝λAB→ ＋μAC →，λ，μ∈R ，则λ＋μ等于( )A ．1 B.23 C.32 D ．2答案　B解析　如图所示，由题意知，AE → ＝23AC → ，AD → ＝23AB →，设DP → ＝xDE →，所以AP → ＝AD → ＋DP → ＝AD → ＋xDE→ ＝AD → ＋x (AE → －AD → )＝xAE → ＋(1－x )AD→ ＝23xAC → ＋23(1－x )AB → ，所以μ＝23x ，λ＝23(1－x )，所以λ＋μ＝23x ＋23(1－x )＝23.题型三　共线定理及其应用例5　设两向量a 与b 不共线．(1)若AB → ＝a ＋b ，BC → ＝2a ＋8b ，CD →＝3(a －b )．求证：A ，B ，D 三点共线；(2)试确定实数k ，使k a ＋b 和a ＋k b 共线．(1)证明　∵AB → ＝a ＋b ，BC →＝2a ＋8b ，CD →＝3(a －b )．∴BD → ＝BC → ＋CD → ＝2a ＋8b ＋3(a －b )＝2a ＋8b ＋3a －3b ＝5(a ＋b )＝5AB → .∴AB → ，BD →共线，又它们有公共点B ，∴A ，B ，D 三点共线．(2)解　∵k a ＋b 与a ＋k b 共线，∴存在实数λ，使k a ＋b ＝λ(a ＋k b )，即k a ＋b ＝λa ＋λk b ，∴(k －λ)a ＝(λk －1)b .∵a ，b 是不共线的两个向量，∴k －λ＝λk －1＝0，∴k 2－1＝0，∴k ＝±1.教师备选1．已知P 是△ABC 所在平面内一点，且满足PA → ＋PB → ＋PC → ＝2AB →，若S △ABC ＝6，则△PAB 的面积为( )A ．2 B ．3C ．4 D ．8答案　A解析　∵PA → ＋PB → ＋PC → ＝2AB → ＝2(PB → －PA →)，∴3PA → ＝PB → －PC → ＝CB →，∴PA → ∥CB →，且两向量方向相同，∴S△ABCS △PAB ＝BC AP ＝|CB →||PA →|＝3，又S △ABC ＝6，∴S △PAB ＝63＝2.2．设两个非零向量a 与b 不共线，若a 与b 的起点相同，且a ，t b ，13(a ＋b )的终点在同一条直线上，则实数t 的值为________．答案　12解析　∵a ，t b ，13(a ＋b )的终点在同一条直线上，且a 与b 的起点相同，∴a －t b 与a －13(a ＋b )共线，即a －t b 与23a －13b 共线，∴存在实数λ，使a －t b ＝λ(23a －13b )，又a ，b 为两个不共线的非零向量，∴Error!解得Error!思维升华　利用共线向量定理解题的策略(1)a ∥b ⇔a ＝λb (b ≠0)是判断两个向量共线的主要依据．(2)若a 与b 不共线且λa ＝μb ，则λ＝μ＝0.(3)OA → ＝λOB → ＋μOC →(λ，μ为实数)，若A ，B ，C 三点共线，则λ＋μ＝1.跟踪训练3　(1)若a ，b 是两个不共线的向量，已知MN → ＝a －2b ，PN → ＝2a ＋k b ，PQ →＝3a －b ，若M ，N ，Q 三点共线，则k 等于( )A ．－1 B ．1 C.32 D ．2答案　B解析　由题意知，NQ → ＝PQ → －PN →＝a －(k ＋1)b ，因为M ，N ，Q 三点共线，故存在实数λ，使得MN → ＝λNQ →，即a －2b ＝λ[a －(k ＋1)b ]，解得λ＝1，k ＝1.(2)如图，已知A ，B ，C 是圆O 上不同的三点，线段CO 与线段AB 交于点D (点O 与点D 不重合)，若OC → ＝λOA → ＋μOB →(λ，μ∈R )，则λ＋μ的取值范围是( )A ．(0,1)B ．(1，＋∞)C ．(1，2]D ．(－1,0)答案　B解析　因为线段CO 与线段AB 交于点D ，所以O ，C ，D 三点共线，所以OC → 与OD →共线，设OC → ＝mOD →，则m >1，因为OC → ＝λOA → ＋μOB → ，所以mOD → ＝λOA → ＋μOB → ，可得OD → ＝λm OA → ＋μm OB →，因为A ，B ，D 三点共线，所以λm ＋μm ＝1，可得λ＋μ＝m >1，所以λ＋μ的取值范围是(1，＋∞)．课时精练1．(多选)下列选项中的式子，结果为零向量的是( )A.AB → ＋BC → ＋CA → B.AB → ＋MB → ＋BO → ＋OM → C.OA → ＋OB → ＋BO → ＋CO → D.AB → －AC → ＋BD → －CD → 答案　AD解析　利用向量运算，易知A ，D 中的式子结果为零向量．2．若a ，b 为非零向量，则“a|a |＝b|b |”是“a ，b 共线”的( )A ．充要条件B ．充分不必要条件C ．必要不充分条件D ．既不充分也不必要条件答案　B解析　a |a |，b |b |分别表示与a ，b 同方向的单位向量，a |a |＝b|b |，则有a ，b 共线，而a ，b 共线，则a |a |，b |b |是相等向量或相反向量，所以“a |a |＝b|b |”是“a ，b 共线”的充分不必要条件．3．设a ＝(AB → ＋CD → )＋(BC → ＋DA →)，b 是一个非零向量，则下列结论不正确的是( )A ．a ∥bB ．a ＋b ＝aC ．a ＋b ＝bD ．|a ＋b |＝|a |＋|b |答案　B解析　由题意得，a ＝(AB → ＋CD → )＋(BC → ＋DA → )＝AC → ＋CA →＝0，且b 是一个非零向量，所以a ∥b成立，所以A 正确；由a ＋b ＝b ，所以B 不正确，C 正确；由|a ＋b |＝|b |，|a |＋|b |＝|b |，所以|a ＋b |＝|a |＋|b |，所以D 正确．4．(2022·汕头模拟)下列命题中正确的是( )A ．若a ∥b ，则存在唯一的实数λ使得a ＝λb B ．若a ∥b ，b ∥c ，则a ∥c C ．若a·b ＝0，则a ＝0或b ＝0D ．|a |－|b |≤|a ＋b |≤|a |＋|b |答案　D解析　若a ∥b ，且b ＝0，则可有无数个实数λ使得a ＝λb ，故A 错误；若a ∥b ，b ∥c (b ≠0)，则a ∥c ，若b ＝0，则a ，c 不一定平行，故B 错误；若a·b ＝0，也可以为a ⊥b ，故C 错误；根据向量加法的三角形法则和向量减法的几何意义知，|a |－|b |≤|a ＋b |≤|a |＋|b |成立，故D 正确．5．在平行四边形ABCD 中，AC → 与BD → 交于点O ，E 是线段OD 的中点．若AC → ＝a ，BD →＝b ，则AE →等于( )A.14a ＋12bB.23a ＋13b C.12a ＋14b D.13a ＋23b 答案　C解析　如图所示，∵AC → ＝a ，BD →＝b ，∴AD → ＝AO → ＋OD → ＝12a ＋12b ，∴AE → ＝AD → －ED → ＝12a ＋12b －14b ＝12a ＋14b .6．下列说法正确的是( )A ．向量AB → 与向量BA →的长度相等B ．两个有共同起点，且长度相等的向量，它们的终点相同C ．向量a 与b 平行，则a 与b 的方向相同或相反D ．向量的模是一个正实数答案　A解析　A 项，AB → 与BA →的长度相等，方向相反，正确；B 项，两个有共同起点且长度相等的向量，若方向也相同，则它们的终点相同，故错误；C 项，向量a 与b 平行时，若a 或b 为零向量，不满足条件，故错误；D 项，向量的模是一个非负实数，故错误.7.如图，在平行四边形ABCD 中，E 为BC 的中点，F 为DE 的中点，若AF → ＝xAB → ＋34AD →，则x 等于( )A.34 B.23C.12D.14答案　C解析　连接AE (图略)，因为F 为DE 的中点，所以AF → ＝12(AD →＋AE → )，而AE → ＝AB → ＋BE → ＝AB → ＋12BC → ＝AB → ＋12AD → ，所以AF → ＝12(AD → ＋AE → )＝12(AD →＋AB → ＋12AD→ )＝12AB → ＋34AD →，又AF → ＝xAB → ＋34AD → ，所以x ＝12.8．(多选)已知4AB → －3AD → ＝AC →，则下列结论正确的是( )A ．A ，B ，C ，D 四点共线B ．C ，B ，D 三点共线C ．|AC → |＝|DB →|D ．|BC → |＝3|DB → |答案　BD解析　因为4AB → －3AD → ＝AC → ，所以3AB → －3AD → ＝AC → －AB →，所以3DB → ＝BC →，因为DB → ，BC →有公共端点B ，所以C ，B ，D 三点共线，且|BC → |＝3|DB → |，所以B ，D 正确，A 错误；由4AB → －3AD → ＝AC →，得AC → ＝3AB → －3AD → ＋AB → ＝3DB → ＋AB → ，所以|AC → |≠|DB →|，所以C 错误．9．(2022·太原模拟)已知不共线向量a ，b ，AB → ＝t a －b (t ∈R )，AC →＝2a ＋3b ，若A ，B ，C 三点共线，则实数t ＝__________.答案　－23解析　因为A ，B ，C 三点共线，所以存在实数k ，使得AB → ＝kAC →，所以t a －b ＝k (2a ＋3b )＝2k a ＋3k b ，即(t －2k )a ＝(3k ＋1)b .因为a ，b 不共线，所以Error!解得Error!10．已知△ABC 的重心为G ，经过点G 的直线交AB 于D ，交AC 于E ，若AD → ＝λAB → ，AE →＝μAC →，则1λ＋1μ＝________.答案　3解析　如图，设F 为BC 的中点，则AG → ＝23AF → ＝13(AB → ＋AC → )，又AB → ＝1λAD → ，AC → ＝1μAE → ，∴AG → ＝13λAD → ＋13μAE → ，又G ，D ，E 三点共线，∴13λ＋13μ＝1，即1λ＋1μ＝3.11．若正六边形ABCDEF 的边长为2，中心为O ，则|EB → ＋OD → ＋CA →|＝________.答案　23解析　正六边形ABCDEF 中，EB → ＋OD → ＋CA → ＝EO → ＋DC → ＋OD → ＋CA → ＝ED → ＋DA → ＝EA →，在△AEF 中，∠AFE ＝120°，AF ＝EF ＝2，∴|EA →|＝22＋22－2×2×2×cos 120°＝23，即|EB → ＋OD → ＋CA →|＝23.12．在平行四边形ABCD 中，点M 为BC 边的中点，AC → ＝λAM → ＋μBD →，则λ＋μ＝________.答案　53解析　AC → ＝λ(AB → ＋12AD →)＋μ(AD → －AB → )＝(λ－μ)AB → ＋(λ2＋μ)AD →，又因为AC → ＝AB → ＋AD →，所以Error!解得Error!所以λ＋μ＝53.13．(多选)点P 是△ABC 所在平面内一点，且满足|PB → －PC → |－|PB → ＋PC → －2PA →|＝0，则△ABC不可能是( )A ．钝角三角形 B ．直角三角形C ．等腰三角形 D ．等边三角形答案　AD解析　因为点P 是△ABC 所在平面内一点，且|PB → －PC → |－|PB → ＋PC → －2PA →|＝0，所以|CB → |－|(PB → －PA → )＋(PC → －PA →)|＝0，即|CB → |＝|AB → ＋AC → |，所以|AB → －AC → |＝|AC → ＋AB → |，等式两边平方并化简得AC → ·AB →＝0，所以AC → ⊥AB →，∠BAC ＝90°，则△ABC 一定是直角三角形，也有可能是等腰直角三角形，不可能是钝角三角形和等边三角形．14．在△ABC 中，∠A ＝60°，∠A 的平分线交BC 于点D ，若AB ＝4，且AD → ＝14AC →＋λAB →(λ∈R )，则λ＝________，AD 的长为________．答案　34　33解析　∵B ，D ，C 三点共线，∴14＋λ＝1，解得λ＝34.如图，过D 分别作AC ，AB 的平行线交AB ，AC 于点M ，N ，则AN → ＝14AC → ，AM → ＝34AB → ，∵在△ABC 中，∠A ＝60°，∠A 的平分线交BC 于D ，∴四边形AMDN 是菱形，∵AB ＝4，∴AN ＝AM ＝3，∴AD ＝33.15．(2022·滁州模拟)已知P 为△ABC 所在平面内一点，AB → ＋PB → ＋PC → ＝0，|AB → |＝|PB → |＝|PC → |＝2，则△ABC 的面积为( )A.3B ．23C ．33D ．43答案　B解析　设BC 的中点为D ，AC 的中点为M ，连接PD ，MD ，BM ，如图所示，则有PB → ＋PC → ＝2PD →.由AB → ＋PB → ＋PC →＝0，得AB → ＝－2PD →，又D 为BC 的中点，M 为AC 的中点，所以AB → ＝－2DM → ，则PD → ＝DM →，则P ，D ，M 三点共线且D 为PM 的中点，又D 为BC 的中点，所以四边形CPBM 为平行四边形．又|AB → |＝|PB → |＝|PC →|＝2，所以|MC → |＝|BP → |＝2，则|AC →|＝4，且|BM → |＝|PC →|＝2，所以△AMB 为等边三角形，∠BAC ＝60°，则S △ABC ＝12×2×4×32＝23.16．若2OA → ＋OB → ＋3OC →＝0，S △AOC ，S △ABC 分别表示△AOC ，△ABC 的面积，则S △AOC ∶S △ABC＝________.答案　1∶6解析　若2OA → ＋OB → ＋3OC →＝0，设OA ′——→ ＝2OA → ，OC ′——→ ＝3OC →，可得O 为△A ′BC ′的重心，如图，设S △AOB ＝x ，S △BOC ＝y ，S △AOC ＝z ，则S △A ′OB ＝2x ，S △BOC ′＝3y ，S △A ′OC ′＝6z ，由2x ＝3y ＝6z ，可得S △AOC ∶S △ABC ＝z ∶(x ＋y ＋z )＝1∶6.。

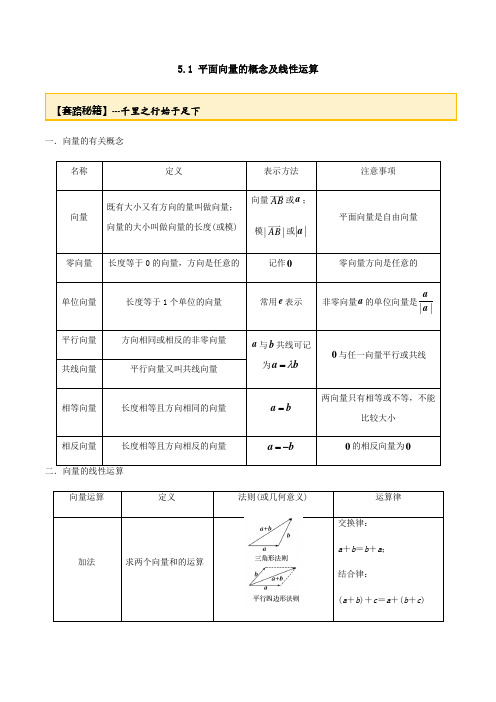
5.1 平面向量的概念及线性运算一．向量的有关概念|λ a |＝|λ||a |，当λ>0时，口诀：(加法三角形)首尾连，连首尾； (加法平行四边形)起点相同连对角； (减法三角形)共起点，连终点，指向被减． 三．向量共线定理向量b 与非零向量a 共线的充要条件是有且只有一个实数λ，使得b ＝λa . 四．平面向量基本定理如果e 1，e 2是同一平面内的两个不共线向量，那么对于这一平面内的任意向量a ，有且只有一对实数λ1，λ2，使a ＝λ1e 1＋λ2e 2.其中，不共线的向量e 1，e 2叫做表示这一平面内所有向量的一组基底．考向一 概念辨析【例1】判断下列各命题正确的是 ： (1)单位向量都相等；(2)|a |与|b |是否相等，与a ，b 的方向无关；(3)若A ，B ，C ，D 是不共线的四点，则AB →＝DC →是四边形ABCD 为平行四边形的充要条件； (4)若a 与b 共线，b 与c 共线，则a 与c 也共线；(5)两向量a ，b 相等的充要条件是|a |＝|b |且a ∥b . 【答案】（2）（3) 【解析】(1)不正确．(2)正确，两个向量的长度相等，但它们的方向不一定相同．(3)正确，∵AB →＝DC →，∴|AB →|＝|DC →|且AB ∥DC .又∵A ，B ，C ，D 是不共线的四点，∴四边形ABCD 是平行四边形．反之，若四边形ABCD 是平行四边形，则AB 綊DC ，且AB →与DC →方向相同．因此AB →＝DC →.(4)不正确，当b ＝0时，a 与c 可以不共线．(5)不正确，当a ∥b ，但方向相反时，即使|a |＝|b |，也不能得到a ＝b .【举一反三】 1．给出下列命题：①若两个向量相等，则它们的起点相同，终点相同； ②若a 与b 共线，b 与c 共线，则a 与c 也共线；③若A ，B ，C ，D 是不共线的四点，且AB →＝DC →，则四边形ABCD 为平行四边形； ④a ＝b 的充要条件是|a |＝|b |且a ∥b ；⑤已知λ，μ为实数，若λa ＝μb ，则a 与b 共线． 其中真命题的序号是________． 【答案】 ③【解析】 ①错误，两个向量起点相同，终点相同，则两个向量相等；但两个向量相等，不一定有相同的起点和终点；②错误，若b ＝0，则a 与c 不一定共线；③正确，因为AB →＝DC →，所以|AB →|＝|DC →|且AB →∥DC →；又A ，B ，C ，D 是不共线的四点，所以四边形ABCD 为平行四边形；④错误，当a ∥b 且方向相反时，即使|a |＝|b |，也不能得到a ＝b ，所以|a |＝|b |且a ∥b 不是a ＝b 的充要条件，而是必要不充分条件；⑤错误，当λ＝μ＝0时，a 与b 可以为任意向量，满足λa ＝μb ，但a 与b 不一定共线．考向二 平面向量的线性运算【例2】在△ABC 中，AB →＝c ，AC →＝b ，若点D 满足BD →＝2DC →，则AD →等于( ) A.23b ＋13c B.53c －23b C.23b －13c D.13b ＋23c (2)在△ABC 中，点M ，N 满足AM →＝2MC →，BN →＝NC →.若MN →＝xAB →＋yAC →，则x ＝________，y ＝______. (3)在△ABC 中，点D 在线段BC 的延长线上，且BC →＝3CD →，点O 在线段CD 上(与点C ，D 不重合)，若AO →＝xAB →＋(1－x )AC →，则x 的取值范围是( )A.⎝ ⎛⎭⎪⎫0，12B.⎝ ⎛⎭⎪⎫0，13C.⎝ ⎛⎭⎪⎫－12，0 D.⎝ ⎛⎭⎪⎫－13，0【答案】（1） A （2） 12 －16（3）D【解析】（1） ∵BD →＝2DC →，∴AD →－AB →＝BD →＝2DC →＝2(AC →－AD →)， ∴3AD →＝2AC →＋A B →，∴AD →＝23AC →＋13AB →＝23b ＋13c .（2）MN →＝MC →＋CN →＝13AC →＋12CB →＝13AC →＋12(AB →－AC →)＝12AB →－16AC →＝xAB →＋yAC →，∴x ＝12，y ＝－16.（3）设CO →＝yBC →，∵AO →＝AC →＋CO →＝AC →＋yBC →＝AC →＋y (AC →－AB →)＝－yAB →＋(1＋y )AC →. ∵BC →＝3CD →，点O 在线段CD 上(与点C ，D 不重合)，∴y ∈⎝ ⎛⎭⎪⎫0，13，∵AO →＝xAB →＋(1－x )AC →，∴x ＝－y ，∴x ∈⎝ ⎛⎭⎪⎫－13，0.【举一反三】1.如图，在△ABC 中，点D 在BC 边上，且CD ＝2DB ，点E 在AD 边上，且AD ＝3AE ，则用向量AB →，AC →表示CE →为( )A.29AB →＋89AC →B.29AB →－89AC →C.29AB →＋79AC →D.29AB →－79AC → 【答案】 B【解析】 由平面向量的三角形法则及向量共线的性质可得CE →＝AE →－AC →＝13AD →－AC →＝13(AB →＋13BC →)－AC →＝13⎣⎢⎡⎦⎥⎤AB →＋13(AC →－AB →)－AC →＝29AB →－89AC →.2.如图，在平行四边形ABCD 中，AC ，BD 相交于点O ，E 为线段AO 的中点．若BE →＝λBA →＋μBD →(λ，μ∈R)，则λ＋μ＝________.【答案】 34【解析】 ∵E 为线段AO 的中点，∴BE →＝12BA →＋12BO →＝12BA →＋12⎝ ⎛⎭⎪⎫12BD →＝12BA →＋14BD →＝λBA →＋μBD →，∴λ＋μ＝12＋14＝34.3.在直角梯形ABCD 中，∠A ＝90°，∠B ＝30°，AB ＝23，BC ＝2，点E 在线段CD 上，若AE →＝AD →＋μAB →，则μ的取值范围是________．【答案】 ⎣⎢⎡⎦⎥⎤0，12【解析】 由题意可求得AD ＝1，CD ＝3，∴AB →＝2DC →. ∵点E 在线段CD 上，∴DE →＝λDC →(0≤λ≤1)．∵AE →＝AD →＋DE →＝AD →＋λDC →，又AE →＝AD →＋μAB →＝AD →＋2μDC →，∴2μ＝λ，即μ＝λ2.∵0≤λ≤1，∴0≤μ≤12.4.在平行四边形ABCD 中，E ，F 分别为边BC ，CD 的中点，若AB →＝xAE →＋yAF →(x ，y ∈R)，则x －y ＝________. 【答案】 2【解析】 由题意得AE →＝AB →＋BE →＝AB →＋12AD →，AF →＝AD →＋DF →＝AD →＋12AB →，因为AB →＝xAE →＋yAF →，所以AB →＝⎝ ⎛⎭⎪⎫x ＋y 2AB →＋⎝ ⎛⎭⎪⎫x 2＋y AD →，所以⎩⎪⎨⎪⎧x ＋y2＝1，x2＋y ＝0，解得⎩⎪⎨⎪⎧x ＝43，y ＝－23，所以x －y ＝2.考向三 共线定理及其运用【例3-1】 已知O ，A ，B 是不共线的三点，且OP →＝mOA →＋nOB →(m ，n ∈R)．(1)若m ＋n ＝1，求证：A ，P ，B 三点共线； (2)若A ，P ，B 三点共线，求证：m ＋n ＝1. 【答案】见解析【解析】(1)若m ＋n ＝1，则OP →＝mOA →＋(1－m )OB →＝OB →＋m (OA →－OB →)，∴OP →－OB →＝m (OA →－OB →)，即BP →＝mBA →，∴BP →与BA →共线．又∵B P →与B A →有公共点B ，∴A ，P ，B 三点共线．(2)若A ，P ，B 三点共线，存在实数λ，使BP →＝λBA →，∴OP →－OB →＝λ(OA →－OB →)． 又OP →＝mOA →＋nOB →.故有mOA →＋(n －1)OB →＝λOA →－λOB →，即(m －λ)OA →＋(n ＋λ－1)OB →＝0. ∵O ，A ，B 不共线，∴OA →，OB →不共线，∴⎩⎪⎨⎪⎧m －λ＝0，n ＋λ－1＝0，∴m ＋n ＝1.【例3-2】 (1)已知D 为△ABC 的边AB 的中点．点M 在DC 上且满足5AM →＝AB →＋3AC →，则△ABM 与△ABC 的面积比为________．（2）已知ABC ∆的重心为O ，过O 任做一直线分别交边,AB AC 于,P Q 两点，设,AP mAB AQ nAC ==，则49m n +的最小值是________．（3）已知数列{}n a 为等差数列，且满足12107OA a OB a OC =+，若AB AC λ=（R λ∈），点O 为直线BC 外一点，则1009a =（ ）【答案】（1） 3∶5 （2）253 （3）12【解析】（1）由5AM →＝AB →＋3AC →，得2AM →＝2AD →＋3AC →－3AM →，即2(AM →－AD →)＝3(AC →－AM →)，即2DM →＝3MC →，故DM →＝35DC →，故△ABM 与△ABC 同底且高的比为3∶5，故S △ABM ∶S △ABC ＝3∶5.11111343494()9()333333m n λλλλ+=+++=++≥1343252333λλ+⋅=，当且仅当32λ=时等号成立，即55,69m n ==时49m n +取得最小值253．（3）∵数列{a n }为等差数列，满足12107OA a OB a OC =+，其中A ，B ，C 在一条直线上，O 为直线AB 外一点，∴a 1+a 2017=1，∵数列{a n }是等差数列，∴{a n }的1009121072a a a =+=1， 100912a =【举一反三】1.如图，△ABC 中，在AC 上取一点N ，使AN ＝13AC ；在AB 上取一点M ，使AM ＝13AB ；在BN 的延长线上取点P ，使得NP ＝12BN ；在CM 的延长线上取点Q ，使得MQ →＝λCM →时，AP →＝QA →，试确定λ的值．b ，若存在实数λ，使，使AB AC λ=，则A 求参数的值：利用共线向量定理及向量相等的条件列方程【答案】12【解析】∵AP →＝NP →－NA →＝12(BN →－CN →)＝12(BN →＋NC →)＝12BC →，QA →＝MA →－MQ →＝12BM →＋λMC →，又AP →＝QA →，∴12BM →＋λMC →＝12BC →，即λMC →＝12MC →，∴λ＝12.2.在△ABC 中，O 为其内部一点，且满足OA →＋OC →＋3OB →＝0，则△AOB 和△AOC 的面积比是( )A ．3∶4B ．3∶2C ．1∶1D ．1∶3 【答案】 D【解析】 根据题意，如图，在△ABC 中，M 为AC 的中点，则OA →＋OC →＝2OM →，又由OA →＋OC →＋3OB →＝0，则有2OM →＝－3OB →； 从而可得B ，O ，M 三点共线，且2OM ＝3BO ；由2OM ＝3BO 可得，S △AOC S △ABC＝OM BM ＝35，S △AOB ＋S △BOC ＝25S △ABC ， 又由S △AOB ＝S △BOC ，则S △AOB ＝15S △ABC ，则S △AOB S △AOC＝13.故选D. 3．已知点D 为△ABC 所在平面上一点，且满足A D →＝15A B →－45C A →，若△ACD 的面积为1，则△ABD 的面积为( )A ．1B ．2C ．3D ．4 【答案】D【解析】 由A D →＝15A B →－45C A →，得5AD →＝A B →＋4A C →，所以A D →－A B →＝4(A C →－A D →)，即B D →＝4D C →.所以点D 在边BC 上，且|B D →|＝4|D C →|，所以S △ABD ＝4S △ACD ＝4.4.已知等差数列{}n a 的前n 项和为n S ， P 、A 、B 三点共线，且32016OP a OA a OB =+，则2018S =__________． 【答案】10091．下列说法正确的是（ ）A ．若||=||a b ，则a 、b 的长度相等且方向相同或相反B ．若向量AB 、CD 满足||||AB CD >，且AB 与CD 同向，则AB CD >C ．若a b ≠，则a 与b 可能是共线向量D ．若非零向量AB 与CD 平行，则A 、B 、C 、D 四点共线 【答案】C【解析】对于A 选项，模相等的向量，方向不一定相同或者相反，也可能垂直，或者成其它的角度，故A 选项错误.对于B 选项，向量不能用大于或者小于号相连，向量的模可以比较大小，故B 选项错误.对于C 选项，不相等的向量可以共线，故C 选项正确.对于D 选项，平行向量,对应的四点不一定是共线的，故D 选项错误.综上所述，本小题选C.2．在四边形ABCD 中，AB AD =且BA CD =，则四边形ABCD 的形状一定是（ ）A ．正方形B ．矩形C ．菱形D ．等腰梯形【答案】C【解析】因为BA CD =，所以//,BA CD BA CD =,四边形是平行四边形又AB AD =，所以AB AD =,四边形是菱形，故选C. 3．下列说法中正确的是（ ） A ．单位向量都相等B ．平行向量不一定是共线向量C ．对于任意向量a ，b ，必有a b a b +≤+D ．若a ，b 满足a b >且a 与b 同向，则a b >【答案】C【解析】对于A,单位向量模都相等，方向不一定相同，故错误，对于B,平行向量就是共线向量，对于C,若a ，b 同向共线，a b a b +=+，若a ，b 反向共线，a b a b +<+，若a ，b 不共线，根据向量加法的三角形法则及两边之和大于第三边知a b a b +<+，综上可知对于任意向量a ，b ，必有a b a b +≤+正确，对于D,两个向量不能比较大小，故错误.故选C.4．下列结论正确的是（ ） A ．a ⃗=b ⃗⃗⇒|a ⃗|=|b ⃗⃗| B ．a ⃗⋅b ⃗⃗=a ⃗⋅c ⃗⇒b ⃗⃗=c ⃗ C ．a ⃗//b ⃗⃗，b ⃗⃗//c ⃗⇒a ⃗//c ⃗ D ．|a ⃗|>|b ⃗⃗|⇒a ⃗>b⃗⃗ 【答案】A【解析】逐一考查所给的说法： 若a ⃗=b ⃗⃗，则|a ⃗|=|b⃗⃗|，选项A 说法正确；若a ⃑=0⃗⃑，则由a ⃗⋅b ⃗⃗=a ⃗⋅c ⃗不一定能得到b ⃗⃗=c ⃗，选项B 说法错误； 若b ⃗⃑=0⃗⃑，则由a ⃗//b ⃗⃗，b ⃗⃗//c ⃗不一定能得到a ⃗//c ⃗，选项C 说法错误； 两个向量无法比较大小，故结论a ⃗>b⃗⃗错误，选项D 说法错误；故选：A . 5．如图，在平行四边形ABCD 中，点E F 、满足2,2BE EC CF FD ==，EF 与AC 交于点G ，设AG GC λ=，则λ=（ ）A ．97B ．74C ．72D ．92【答案】C【解析】设H 是BC 上除E 点外的令一个三等分点，连接FH ，连接BD 交AC 于O ，则//BD FH .在三角形CFH 中，,CG FG 是两条中线的交点，故G 是三角形CFH 的重心，结合23CH CF BH DF ==可知24.5CG CO =，由于O 是AC 中点，故224.529CG AC ==⨯.所以72AG CG =，由此可知72λ=，故选C.6．AB BD AC +-=（ ）A ．ACB ．CDC ．ABD ．DB【答案】B【解析】依题意AB AC BD CB BD CD-+=+=，故选B.7.设D 为△ABC 的边AB 的中点，P 为△ABC 内一点，且满足，AP →＝AD →＋25BC →，则S △APD S △ABC＝( )A.35B.25C.15D.310 【答案】 C【解析】 如图∵AD →＋25BC →＝AD →＋DP →＝AP →，∴D P →＝25B C →，∠ADP ＝∠ABC ，∵D 是AB 的中点，∴AD ＝12AB .∴S △APDS △ABC ＝12·AD ·DP sin ∠ADP 12·AB ·BC sin ∠ABC ＝15.故选C.8.A ，B ，C 是圆O 上不同的三点，线段CO 与线段AB 交于点D (点O 与点D 不重合)，若OC →＝λOA →＋μOB →(λ，μ∈R)，则λ＋μ的取值范围是( )A ．(0,1)B ．(1，＋∞)C ．(1，2]D ．(－1,0) 【答案】 B【解析】 设OC →＝mOD →，则m >1，因为OC →＝λOA →＋μOB →，所以mOD →＝λOA →＋μOB →，即OD →＝λm OA →＋μmOB →，又知A ，B ，D 三点共线，所以λm ＋μm＝1，即λ＋μ＝m ，所以λ＋μ>1.故选B. 10.已知点O ，A ，B 不在同一条直线上，点P 为该平面上一点，且OP →＝3OA →－OB→2，则( ) A ．点P 在线段AB 上 B ．点P 在线段AB 的反向延长线上 C ．点P 在线段AB 的延长线上 D ．点P 不在直线AB 上【答案】 B【解析】 OP →＝3OA →－OB →2＝32OA →－12OB →＝OA →＋12(OA →－OB →)＝OA →＋12BA →，即OP →－OA →＝AP →＝12BA →，所以点P 在线段AB的反向延长线上．故选B.11．若O 为△ABC 所在平面内一点，且OA →＋2OB →＋3OC →＝0，则S △OBC ∶S △AOC ∶S △ABO ＝( )A ．3∶2∶1B ．2∶1∶3C ．1∶3∶2D ．1∶2∶3 【答案】 D【解析】 如图所示，延长OB 到D ，使得BD ＝OB ，延长OC 到E ，使得CE ＝2OC .连接AD ，DE ，AE . ∵OA →＋2OB →＋3OC →＝0，∴点O 为△ADE 的重心．∴S △OBC ＝16S △ODE ＝16×13S △ADE ＝118S △ADE ；S △AOC ＝13S △OAE ＝13×13S △ADE ＝19S △ADE ；S △ABO ＝12S △OAD ＝12×13S △ADE ＝16S △ADE .∴S △OBC ∶S △AOC ∶S △ABO ＝118∶19∶16＝1∶2∶3.故选D.12.在△ABC 中，M 为边BC 上任意一点，N 为AM 中点，AN →＝λAB →＋μAC →，则λ＋μ的值为( )A.12B.13C.14 D ．1 【答案】 A【解析】 设BM →＝tBC →，则AN →＝12AM →＝12(AB →＋BM →)＝12AB →＋12BM →＝12AB →＋12tBC →＝12AB →＋t 2(AC →－AB →)＝⎝ ⎛⎭⎪⎫12－t 2AB →＋t 2AC →∴λ＝12－t 2，μ＝t 2∴λ＋μ＝12.故选A.13在△ABC 中，点D 在线段BC 的延长线上，且BC →＝3CD →，点O 在线段CD 上(与点C 、D 不重合)，若AO →＝xAB→＋(1－x )AC →，则x 的取值范围是( )A.⎝ ⎛⎭⎪⎫0，12B.⎝ ⎛⎭⎪⎫0，13C.⎝ ⎛⎭⎪⎫－12，0 D.⎝ ⎛⎭⎪⎫－13，0 【答案】 D【解析】 设C O →＝yBC →，则AO →＝AC →＋CO →＝AC →＋yBC →＝AC →＋y (AC →－AB →)＝－yAB →＋(1＋y )AC →，∵BC →＝3CD →，点O 在线段CD 上(与点C 、D 不重合)，∴y ∈⎝ ⎛⎭⎪⎫0，13， ∵AO →＝xAB →＋(1－x )AC →，∴x ∈⎝ ⎛⎭⎪⎫－13，0.故选D.14.若M 为△ABC 内一点，AM →＝13AB →＋14AC →，则△ABM 和△ABC 的面积之比为( )A.14B.13C.12D.23 【答案】 A【解析】 设AD →＝13AB →，AE →＝14AC →，以AD ，AE 为邻边作平行四边形ADME ，延长EM 交BC 与F ，连接BM .则EF∥AB ，∴S △ABM S △ABC＝AE AC ＝14.故选A.15．在ABC ∆中，O 为其内部一点，且满足30OA OC OB ++=，则AOB ∆和AOC ∆的面积比是（ ） A ．3：4 B ．3:2 C ．1:1 D ．1:3【答案】D 【解析】取AC 中点M ,则由30OA OC OB ++= 得23OM OB =- ,所以2||3OM OB =,O 在线段BM 上,因此::2:213AOBAOCAOBAOMSSSSOB OM ===： ，选D.16．已知ABC ∆，点M 是边BC 的中点，若点O 满足230OA OB OC ++=，则（ ）A ．0OM BC •=B ．0OM AB •=C ．//OM BCD ．//OM AB【答案】D【解析】点M 是边BC 的中点，可得2OM OB OC =+，230OA OB OC ++=，可得OA OC ++2（OB OC +）23OA OBOA +=-+40OM =， 即2（OA OB -）+120OM =，可得AB =6OM ，即OM ∥AB ，故选：D ．17．如图，在ABC ∆中，设,AB a AC b ==，AP 的中点为Q ，BQ 的中点为R ，CR 的中点为P ，若AP ma nb =+，则m n +=（ ）A ．12B ．23C ．67D ．1【答案】C【解析】由题意可得2,2AP QP QB QR ==，122AB a AQ QB AP QR ==+=+，① 1322AC AP PC AP RP AP QP QR AP AP QR AP QR b =+=+=+-=+-=-=，② 由①②解方程求得2477AP a b =+. 再由AP ma nb =+可得246,,777m n m n ==+=. 18．四边形OABC 中，CB ⃗⃗⃗⃗⃗⃑=12OA ⃗⃗⃗⃗⃗⃑，若OA ⃗⃗⃗⃗⃗⃑=a ，OC ⃗⃗⃗⃗⃗⃑=b ，则AB ⃗⃗⃗⃗⃗⃑= A ．a –12b B ．12a –bC ．b +12aD ．b –12a【答案】D【解析】由CB ⃗⃗⃗⃗⃗⃑=OB ⃗⃗⃗⃗⃗⃑−OC ⃗⃗⃗⃗⃗⃑=12OA ⃗⃗⃗⃗⃗⃑，可得OB ⃗⃗⃗⃗⃗⃑=OC ⃗⃗⃗⃗⃗⃑+12OA ⃗⃗⃗⃗⃗⃑=b +12a ， 所以AB ⃗⃗⃗⃗⃗⃑=OB ⃗⃗⃗⃗⃗⃑−OA ⃗⃗⃗⃗⃗⃑=b +12a −a =b −12a ，故选D.19．点P 在ΔABC 所在平面上，且满足PA ⃗⃗⃗⃗⃗⃑+PB ⃗⃗⃗⃗⃗⃑+PC ⃗⃗⃗⃗⃗⃑=2AB ⃗⃗⃗⃗⃗⃑，则SΔPAB S ΔABC =（ ） A ．12 B ．13C ．14D ．23【答案】B【解析】因为PA⃗⃗⃗⃗⃗⃑+PB ⃗⃗⃗⃗⃗⃑+PC ⃗⃗⃗⃗⃗⃑=2AB ⃗⃗⃗⃗⃗⃑=2(PB ⃗⃗⃗⃗⃗⃑−PA ⃗⃗⃗⃗⃗⃑),所以3PA ⃗⃗⃗⃗⃗⃑=PB ⃗⃗⃗⃗⃗⃑−PC ⃗⃗⃗⃗⃗⃑=CB ⃗⃗⃗⃗⃗⃑,所以PA ⃗⃗⃗⃗⃗⃑,CB ⃗⃗⃗⃗⃗⃑共线，且3|PA ⃗⃗⃗⃗⃗⃑|=|CB ⃗⃗⃗⃗⃗⃑|，所以S ΔPAB S ΔABC=13.故选B. 20．如图所示，点O 是正六边形ABCDEF 的中心，则OA OC OE ++=（ ）A ．0B ．0C ．AED ．EA【答案】A【解析】OA OC OB +=，OB OE =- 0OA OC OE OB OE ∴++=+=本题正确选项：A21．如图所示，在正方形ABCD 中，E 为AB 的中点，F 为CE 的中点，则AF =A ．3144AB AD + B ．1344AB AD + C ．12AB AD + D ．3142AB AD + 【答案】D【解析】根据题意得：1()2AF AC AE =+，又AC AB AD =+，12AE AB =，所以1131()2242AF AB AD AB AB AD =++=+.故选D.22．已知点P 是ABC ∆所在平面内一点，且满足()()cos cos AB AC AP R AB BAC Cλλ=+∈，则直线AP 必经过ABC ∆的( ) A ．外心 B ．内心C ．重心D ．垂心【答案】D【解析】 ()cos cos AB AC AP R AB B AC C λλ⎛⎫⎪=+∈ ⎪⎝⎭两边同乘以向量BC ,得AP BC ∴⊥ t ∈即点P 在BC 边的高线上，所以P 的轨迹过△ABC 的垂心，故选D.23.在ABC ∆中，1,3AN NC P =是BN 上的点，若29AP mAB AC =+，则实数m 的值为___________. 【答案】19【解析】因为13AN NC =，所以14AN AC =，即4AC AN =，所以 2899AP mAB AC mAB AN =+=+．又因为,,P B N 三点共线，所以819m +=， 所以19m =． 24如图，直线EF 与平行四边形ABCD 的两边AB，AD 分别交于E ，F 两点，且与对角线AC 交于点K ，其中，AE →＝25AB →，AF →＝12AD →，AK →＝λAC →，则λ的值为______．【答案】 29【解析】 ∵AE →＝25AB →，AF →＝12AD →，∴AB →＝52AE →，AD →＝2AF →.由向量加法的平行四边形法则可知，AC →＝AB →＋AD →， ∴AK →＝λAC →＝λ(AB →＋AD →)＝λ⎝ ⎛⎭⎪⎫52AE →＋2AF →＝52λAE →＋2λAF →，∵E ，F ，K 三点共线，∴52λ＋2λ＝1，∴λ＝29.25.如图所示，在△ABC 中，D 为BC 边上的一点，且BD ＝2DC ，若AC →＝mAB →＋nAD →(m ，n ∈R)，则m －n ＝________.【答案】 －2【解析】 由于BD ＝2DC ，则BC →＝－3CD →，其中BC →＝AC →－AB →，CD →＝AD →－AC →， 那么BC →＝－3CD →可转化为AC →－AB →＝－3(AD →－AC →)，可以得到－2AC →＝－3AD →＋AB →，即AC →＝－12AB →＋32AD →，则m ＝－12，n ＝32，那么m －n ＝－12－32＝－2.26．A ，B ，C 是圆O 上不同的三点，线段CO 与线段AB 交于点D (点O 与点D 不重合)，若OC →＝λOA →＋μOB →(λ，μ∈R)，则λ＋μ的取值范围是________．【答案】 (1，＋∞)【解析】 设OC →＝mOD →，则m >1，因为OC →＝λOA →＋μOB →，所以mOD →＝λOA →＋μOB →，即OD →＝λm OA →＋μmOB →，又知A ，B ，D 三点共线，所以λm ＋μm＝1，即λ＋μ＝m ，所以λ＋μ>1.27．已知A ，B ，C 是平面上不共线的三点，O 是△ABC 的重心，动点P 满足OP →＝13⎝⎛⎭⎪⎫2OA →＋12OB →＋12OC →，则△ABC 的面积和△PBC 的面积之比为________．【答案】 3∶2【解析】 设BC 的中点为M ，则12OC →＋12OB →＝OM →， ∴OP →＝13(OM →＋2OA →)＝13OM →＋23OA →，即3OP →＝OM →＋2OA →，OP →－OM →＝2OA →－2OP →，也就是MP →＝2PA →， ∴P ，M ，A 三点共线，且P 是AM 上靠近A 点的一个三等分点，∴S △ABC ∶S △PBC ＝3∶2.28.如图所示，在△ABC 中，点O 是BC 的中点，过点O 的直线分别交直线AB ，AC 于不同的两点M ，N ，若AB→＝mAM →，AC →＝nAN →，则m ＋n 的值为________．【答案】 2【解析】 连接AO ，∵O 是BC 的中点，∴AO →＝12(AB →＋AC →)． 又∵AB →＝mAM →，AC →＝nAN →，∴AO →＝m 2AM →＋n 2AN →.∵M ，O ，N 三点共线，∴m 2＋n 2＝1.∴m ＋n ＝2.。

第五章 平面向量第一节 平面向量的概念及线性运算[考纲要求]1．了解向量的实际背景．2．理解平面向量的概念,理解两个向量相等的含义． 3．理解向量的几何表示．4．掌握向量加法、减法的运算,并理解其几何意义．5．掌握向量数乘的运算及其几何意义,理解两个向量共线的含义．了解向量线性运算的性质及其几何意义．突破点一 平面向量的有关概念[基本知识] 名称 定义备注向量 既有大小又有方向的量叫做向量;向量的大小叫做向量的长度(或称模) 平面向量是自由向量,平面向量可自由平移 零向量 长度为0的向量;其方向是任意的记作0单位向量长度等于1个单位的向量 非零向量a 的单位向量为±a|a|平行向量方向相同或相反的非零向量,又叫做共线向量0与任一向量平行或共线 相等向量 长度相等且方向相同的向量 两向量只有相等或不等,不能比较大小相反向量长度相等且方向相反的向量0的相反向量为0一、判断题(对的打“√”,错的打“×”)(1)向量与有向线段是一样的,因此可以用有向线段来表示向量．( ) (2)若a 与b 不相等,则a 与b 一定不可能都是零向量．( ) 答案:(1)× (2)√ 二、填空题1．如果对于任意的向量a ,均有a ∥b ,则b 为________． 答案:零向量2．若e 是a 的单位向量,则a 与e 的方向________． 解析:∵e ＝a|a |,∴e 与a 的方向相同．答案:相同3．△ABC 中,点D ,E ,F 分别为BC ,CA ,AB 的中点,在以A ,B ,C ,D ,E ,F 为端点的有向线段所表示的向量中,与EF ―→共线的向量有________个．答案:7个[典例感悟]1．(2018·海淀期末)下列说法正确的是( ) A ．方向相同的向量叫做相等向量 B ．共线向量是在同一条直线上的向量 C ．零向量的长度等于0D ．AB ―→∥CD ―→就是AB ―→所在的直线平行于CD ―→所在的直线解析:选C 长度相等且方向相同的向量叫做相等向量,故A 不正确;方向相同或相反的非零向量叫做共线向量,但共线向量不一定在同一条直线上,故B 不正确;显然C 正确;当AB ―→∥CD ―→时,AB ―→所在的直线与CD ―→所在的直线可能重合,故D 不正确．2．(2019·辽宁实验中学月考)有下列命题: ①若|a |＝|b |,则a ＝b ;②若|AB ―→|＝|DC ―→|,则四边形ABCD 是平行四边形; ③若m ＝n ,n ＝k ,则m ＝k ; ④若a ∥b ,b ∥c ,则a ∥c . 其中,假命题的个数是( ) A ．1 B ．2 C ．3D ．4解析:选C 对于①,|a |＝|b |,a ,b 的方向不确定,则a ,b 不一定相等,所以①错误;对于②,若|AB ―→|＝|DC ―→|,则AB ―→,DC ―→的方向不一定相同,所以四边形ABCD 不一定是平行四边形,②错误;对于③,若m ＝n ,n ＝k ,则m ＝k ,③正确;对于④,若a ∥b ,b ∥c ,则b ＝0时,a ∥c 不一定成立,所以④错误．综上,假命题的是①②④,共3个,故选C.3．(2019·赣州崇义中学模拟)向量AB ―→与CD ―→共线是A ,B ,C ,D 四点共线的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件解析:选B 由A ,B ,C ,D 四点共线,得向量AB ―→与CD ―→共线,反之不成立,可能AB ∥CD ,所以向量AB ―→与CD ―→共线是A ,B ,C ,D 四点共线的必要不充分条件,故选B.[方法技巧]关于平面向量的3个易错提醒(1)两个向量不能比较大小,只可以判断它们是否相等,但它们的模可以比较大小; (2)大小与方向是向量的两个要素,分别是向量的代数特征与几何特征; (3)向量可以自由平移,任意一组平行向量都可以移到同一直线上．突破点二 平面向量的线性运算[基本知识]1．向量的线性运算 向量运算定义法则(或几何意义)运算律 加法求两个向量和的运算交换律:a ＋b ＝b ＋a ; 结合律: (a ＋b )＋c ＝a ＋(b ＋c )减法求a 与b 的相反向量－b 的和的运算a －b ＝a ＋(－b )数乘求实数λ与向量a 的积的运算|λa |＝|λ||a |,当λ＞0时,λa与a 的方向相同;当λ＜0时,λa 与a 的方向相反;当λ＝0时,λa ＝0λ(μ a )＝(λ μ)a ;(λ＋μ)a ＝λa ＋μa ; λ(a ＋b )＝λa ＋λb 向量b 与a (a ≠0)共线的充要条件是有且只有一个实数λ,使得b ＝λa . 3．向量的中线公式及三角形的重心 (1)向量的中线公式:若P 为线段AB 的中点,O 为平面内一点,则OP ―→＝12(OA ―→＋OB ―→)．(2)三角形的重心:已知平面内不共线的三点A ,B ,C ,PG ―→＝13(PA ―→＋PB ―→＋PC ―→)⇔G 是△ABC 的重心．特别地,PA ―→＋PB ―→＋PC ―→＝0⇔P 为△ABC 的重心．[基本能力]一、判断题(对的打“√”,错的打“×”) (1)a ∥b 是a ＝λb (λ∈R)的充要条件．( )(2)△ABC 中,D 是BC 的中点,则AD ―→＝12(AC ―→＋AB ―→)．( )答案:(1)× (2)√ 二、填空题1．在如图所示的方格纸中有定点O ,P ,Q ,E ,F ,G ,H ,则OP ―→＋OQ ―→＝________.答案:FO ―→2．化简:(AB ―→－CD ―→)－(AC ―→－BD ―→)＝________.解析:(AB ―→－CD ―→)－(AC ―→－BD ―→)＝AB ―→－CD ―→－AC ―→＋BD ―→＝(AB ―→－AC ―→)＋(DC ―→－DB ―→)＝CB ―→＋BC ―→＝0.答案:03．已知向量a ,b 不共线,且c ＝λa ＋b ,d ＝a ＋(2λ－1)b ,若c 与d 共线反向,则实数λ的值为________．答案:－12[全析考法]考法一 平面向量的线性运算应用平面向量的加法、减法和数乘运算的法则即可．(1)加法的三角形法则要求“首尾相接”,加法的平行四边形法则要求“起点相同”; (2)减法的三角形法则要求“起点相同”且差向量指向“被减向量”; (3)数乘运算的结果仍是一个向量,运算过程可类比实数运算． [例1] (1)(2019·湖北咸宁联考)如图,在△ABC 中,点M 为AC 的中点,点N 在AB 上,AN ―→＝3NB ―→,点P 在MN 上,MP ―→＝2PN ―→,那么AP ―→＝( )A.23AB ―→－16AC ―→B.13AB ―→－12AC ―→C.13AB ―→－16AC ―→ D.12AB ―→＋16AC ―→(2)如图,在直角梯形ABCD 中,DC ―→＝14AB ―→,BE ―→＝2EC ―→,且AE ―→＝r AB ―→＋s AD ―→,则2r ＋3s ＝( )A ．1B ．2C ．3D ．4[解析] (1)AP ―→＝AM ―→＋MP ―→＝AM ―→＋23MN ―→＝AM ―→＋23(AN ―→－AM ―→)＝13AM ―→＋23AN ―→＝16AC―→＋12AB ―→.故选D. (2)根据图形,由题意可得AE ―→＝AB ―→＋BE ―→＝AB ―→＋23BC ―→＝AB ―→＋23(BA ―→＋AD ―→＋DC ―→)＝13AB ―→＋23(AD ―→＋DC ―→)＝13AB ―→＋23⎝⎛⎭⎫AD ―→＋14AB ―→＝12AB ―→＋23AD ―→.因为AE ―→＝r AB ―→＋s AD ―→,所以r ＝12,s ＝23,则2r ＋3s ＝1＋2＝3.[答案] (1)D (2)C [方法技巧]1．平面向量的线性运算技巧(1)不含图形的情况:可直接运用相应运算法则求解．(2)含图形的情况:将它们转化到三角形或平行四边形中,充分利用相等向量、相反向量、三角形的中位线等性质,把未知向量用已知向量表示出来求解．2．利用平面向量的线性运算求参数的一般思路 (1)没有图形的准确作出图形,确定每一个点的位置．(2)利用平行四边形法则或三角形法则进行转化,转化为要求的向量形式． (3)比较、观察可知所求．考法二 平面向量共线定理的应用求解向量共线问题的注意事项(1)向量共线的充要条件中,当两向量共线时,通常只有非零向量才能表示与之共线的其他向量,注意待定系数法和方程思想的运用．(2)证明三点共线问题,可用向量共线来解决,但应注意向量共线与三点共线的区别与联系,当两向量共线且有公共点时,才能得到三点共线．(3)直线的向量式参数方程:A ,P ,B 三点共线⇔OP ―→＝(1－t )·OA ―→＋t OB ―→(O 为平面内任一点,t ∈R)．[例2] (1)(2019·南昌莲塘一中质检)已知a ,b 是不共线的向量,AB ―→＝λa ＋b ,AC ―→＝a ＋μb (λ,μ∈R),若A ,B ,C 三点共线,则λ,μ的关系一定成立的是( )A ．λμ＝1B ．λμ＝－1C ．λ－μ＝－1D ．λ＋μ＝2(2)(2019·郑州模拟)设e 1与e 2是两个不共线向量,AB ―→＝3e 1＋2e 2,CB ―→＝k e 1＋e 2,CD ―→＝3e 1－2k e 2,若A ,B ,D 三点共线,则k 的值为________．[解析] (1)∵AB ―→与AC ―→有公共点A ,∴若A ,B ,C 三点共线,则存在一个实数t 使AB ―→＝t AC ―→,即λa ＋b ＝t a ＋μt b ,则⎩⎪⎨⎪⎧λ＝tμt ＝1消去参数t 得λμ＝1;反之,当λμ＝1时,AB ―→＝1μa ＋b ,此时存在实数1μ使AB ―→＝1μAC ―→,故AB ―→和AC ―→共线．∵AB ―→与AC ―→有公共点A ,∴A ,B ,C 三点共线．故选A.(2)由题意,A ,B ,D 三点共线,故必存在一个实数λ,使得AB ―→＝λBD ―→. 又AB ―→＝3e 1＋2e 2,CB ―→＝k e 1＋e 2,CD ―→＝3e 1－2ke 2, 所以BD ―→＝CD ―→－CB ―→＝3e 1－2ke 2－(ke 1＋e 2) ＝(3－k )e 1－(2k ＋1)e 2,所以3e 1＋2e 2＝λ(3－k )e 1－λ(2k ＋1)e 2, 又e 1与e 2不共线,所以⎩⎪⎨⎪⎧3＝λ(3－k )2＝－λ(2k ＋1)解得k ＝－94.[答案] (1)A (2)－94[方法技巧] 平面向量共线定理的3个应用1.[考法一]在等腰梯形ABCD 中,AB ―→＝－2CD ―→,M 为BC 的中点,则AM ―→＝( ) A.12AB ―→＋12AD ―→ B.34AB ―→＋12AD ―→C.34AB ―→＋14AD ―→D.12AB ―→＋34AD ―→解析:选B 因为AB ―→＝－2CD ―→,所以AB ―→＝2DC ―→.又M 是BC 的中点,所以AM ―→＝12(AB ―→＋AC ―→)＝12(AB ―→＋AD ―→＋DC ―→)＝12⎝⎛⎭⎫AB ―→＋AD ―→＋12 AB ―→ ＝34AB ―→＋12AD ―→,故选B. 2.[考法一]在△ABC 中,AB ＝2,BC ＝3,∠ABC ＝60°,AD 为BC 边上的高,O 为AD 的中点,若AO ―→＝λAB ―→＋μBC ―→,其中λ,μ∈R,则λ＋μ等于( )A ．1 B.12 C.13D.23解析:选D 由题意易得AD ―→＝AB ―→＋BD ―→＝AB ―→＋13BC ―→,则2AO ―→＝AB ―→＋13BC ―→,即AO ―→＝12AB ―→＋16BC ―→.故λ＋μ＝12＋16＝23.3.[考法二]设两个非零向量a 与b 不共线．(1)若AB ―→＝a ＋b ,BC ―→＝2a ＋8b ,CD ―→＝3(a －b ),求证:A ,B ,D 三点共线; (2)试确定实数k ,使ka ＋b 和a ＋kb 共线．解:(1)证明:∵AB ―→＝a ＋b ,BC ―→＝2a ＋8b ,CD ―→＝3(a －b ), ∴BD ―→＝BC ―→＋CD ―→＝2a ＋8b ＋3(a －b )＝5(a ＋b )＝5AB ―→, ∴AB ―→,BD ―→共线,又它们有公共点B , ∴A ,B ,D 三点共线． (2)∵ka ＋b 与a ＋kb 共线,∴存在实数λ,使ka ＋b ＝λ(a ＋kb ),即(k －λ)a ＝(λk －1)b . 又a ,b 是两个不共线的非零向量,∴⎩⎨⎧k －λ＝0λk －1＝0.∴k 2－1＝0.∴k ＝±1. [课时跟踪检测] 1．(2019·山东省实验中学高三摸底测试)已知a ,b 是两个非零向量,且|a ＋b |＝|a |＋|b |,则下列说法正确的是( )A ．a ＋b ＝0B ．a ＝bC ．a 与b 反向共线D ．存在正实数λ,使得a ＝λb解析:选D 由已知得,向量a 与b 为同向向量,即存在正实数λ,使得a ＝λb ,故选D.2．设a 0为单位向量,下述命题中:①若a 为平面内的某个向量,则a ＝|a |a 0;②若a 与a 0平行,则a ＝|a |a 0;③若a 与a 0平行且|a |＝1,则a ＝a 0.假命题的个数是( )A ．0B ．1C ．2D ．3解析:选D 向量是既有大小又有方向的量,a 与|a |a 0的模相同,但方向不一定相同,故①是假命题;若a 与a 0平行,则a 与a 0的方向有两种情况:一是同向,二是反向,反向时a ＝－|a |a 0,故②③也是假命题．综上所述,假命题的个数是3.3．(2019·广东仲元中学期中)在平行四边形ABCD 中,下列结论错误的是( ) A ．|AB ―→|＝|AD ―→|一定成立 B ．AC ―→＝AB ―→＋AD ―→一定成立 C ．AD ―→＝BC ―→一定成立D ．BD ―→＝AD ―→－AB ―→一定成立解析:选A 在平行四边形ABCD 中,AC ―→＝AB ―→＋AD ―→一定成立,AD ―→＝BC ―→一定成立,BD ―→＝AD ―→－AB ―→一定成立,但|AB ―→|＝|AD ―→|不一定成立．故选A.4．(2019·石家庄高三一检)在△ABC 中,点D 在边AB 上,且BD ―→＝12DA ―→,设CB ―→＝a ,CA ―→＝b ,则CD ―→＝( )A.13a ＋23bB.23a ＋13b C.35a ＋45b D.45a ＋35b 解析:选B ∵BD ―→＝12DA ―→,∴BD ―→＝13BA ―→,∴CD ―→＝CB ―→＋BD ―→＝CB ―→＋13BA ―→＝CB ―→＋13(CA ―→－CB ―→)＝23CB ―→＋13CA ―→＝23a ＋13b ,故选B.5.(2019·长春模拟)如图所示,下列结论正确的是( )①PQ ―→＝32a ＋32b ;②PT ―→＝32a －b ;③PS ―→＝32a －12b ;④PR ―→＝32a ＋b .A ．①②B ．③④C ．①③D ．②④解析:选C ①根据向量的加法法则,得PQ ―→＝32a ＋32b ,故①正确;②根据向量的减法法则,得PT ―→＝32a －32b ,故②错误;③PS ―→＝PQ ―→＋QS ―→＝32a ＋32b －2b ＝32a －12b ,故③正确;④PR ―→＝PQ ―→＋QR ―→＝32a ＋32b －b ＝32a ＋12b ,故④错误,故选C.6．(2019·嘉兴调研)已知点O 为△ABC 外接圆的圆心,且OA ―→＋OB ―→＋CO ―→＝0,则△ABC 的内角A 等于( )A ．30°B ．45°C ．60°D ．90°解析:选A 由OA ―→＋OB ―→＋CO ―→＝0得,OA ―→＋OB ―→＝OC ―→,由O 为△ABC 外接圆的圆心,结合向量加法的几何意义知,四边形OACB 为菱形,且∠CAO ＝60°,故A ＝30°.7.(2019·江西新余第一中学模拟)如图,已知△OAB ,若点C 满足AC ―→＝2CB ―→,OC ―→＝λOA ―→＋μOB ―→(λ,μ∈R),则1λ＋1μ＝( )A.13B.23C.29D.92解析:选D ∵OC ―→＝OA ―→＋AC ―→＝OA ―→＋23AB ―→＝OA ―→＋23(OB ―→－OA ―→)＝13OA ―→＋23OB ―→,∴λ＝13,μ＝23,∴1λ＋1μ＝3＋32＝92.故选D. 8．(2019·张家口月考)在四边形ABCD 中,对角线AC 与BD 交于点O ,若2OA ―→＋OC ―→＝2OD ―→＋OB ―→,则四边形ABCD 一定是( )A ．矩形B ．梯形C ．平行四边形D ．菱形解析:选B ∵2OA ―→＋OC ―→＝2OD ―→＋OB ―→,∴2(OA ―→－OD ―→)＝OB ―→－OC ―→,即2DA ―→＝CB ―→,∴DA ∥CB ,且2|DA ―→ |＝|CB ―→|,∴四边形ABCD 一定是梯形．故选B.9．(2019·甘肃诊断)设D 为△ABC 所在平面内一点,BC ―→＝－4CD ―→,则AD ―→＝( ) A.14AB ―→－34AC ―→ B.14AB ―→＋34AC ―→C.34AB ―→－14AC ―→D.34AB ―→＋14AC ―→解析:选B 法一:设AD ―→＝x AB ―→＋y AC ―→,由BC ―→＝－4CD ―→可得,BA ―→＋AC ―→＝－4CA ―→－4AD ―→,即－AB ―→－3AC ―→＝－4x AB ―→－4y AC ―→,则⎩⎪⎨⎪⎧－4x ＝－1－4y ＝－3解得⎩⎪⎨⎪⎧x ＝14y ＝34即AD ―→＝ 14AB ―→＋34AC ―→,故选B.法二:在△ABC 中,BC ―→＝－4CD ―→,即－14BC ―→＝CD ―→,则AD ―→＝AC ―→＋CD ―→＝AC ―→－14BC ―→＝AC ―→－14(BA ―→＋AC ―→)＝14AB ―→＋34AC ―→,故选B.10.(2019·曲阜模拟)如图,在△ABC 中,AN ―→＝13NC ―→,P 是BN 上的一点,若AP ―→＝m AB ―→＋29AC ―→,则实数m 的值为( )A.13B.19 C ．1D ．3解析:选B 因为AN ―→＝13NC ―→,所以AC ―→＝4AN ―→.所以AP ―→＝m AB ―→＋29AC ―→＝m AB ―→＋89AN ―→,因为B ,P ,N 共线,所以m ＋89＝1,m ＝19.11．(2019·河南三市联考)若AP ―→＝12PB ―→,AB ―→＝(λ＋1)BP ―→,则λ＝________.解析:由AP ―→＝12PB ―→可知,点P 是线段AB 上靠近点A 的三等分点,则AB ―→＝－32BP ―→,所以λ＋1＝－32,解得λ＝－52.答案:－5212．(2019·石家庄高三摸底考试)平行四边形ABCD 中,M 为BC 的中点,若AB ―→＝λAM ―→＋μDB ―→,则λμ＝________.解析:∵DB ―→＝AB ―→－AD ―→＝AB ―→－BC ―→＝AB ―→－2BM ―→＝3AB ―→－2AM ―→,∴AB ―→＝λAM ―→＋3μAB ―→－2μAM ―→,∴(1－3μ)AB ―→＝(λ－2μ)AM ―→,∵AB ―→和AM ―→是不共线向量,∴⎩⎪⎨⎪⎧1－3μ＝0λ－2μ＝0解得⎩⎪⎨⎪⎧ μ＝13λ＝23∴λμ＝29. 答案:2913．(2019·盐城一模)在△ABC 中,∠A ＝60°,∠A 的平分线交BC 于点D ,若AB ＝4,且AD―→＝14AC ―→＋λAB ―→ (λ∈R),则AD 的长为________． 解析:因为B ,D ,C 三点共线,所以14＋λ＝1,解得λ＝34,如图,过点D 分别作AC ,AB 的平行线交AB ,AC 于点M ,N ,则AN ―→＝14AC ―→,AM ―→＝34AB ―→,经计算得AN ＝AM ＝3,AD ＝3 3.答案:3 314．在直角梯形ABCD 中,∠A ＝90°,∠B ＝30°,AB ＝23,BC ＝2,点E 在线段CD 上,若AE―→＝AD ―→＋μAB ―→,则μ的取值范围是________．解析:由题意可求得AD ＝1,CD ＝3,所以AB ―→＝2DC ―→.∵点E 在线段CD 上,∴DE ―→＝λDC ―→ (0≤λ≤1)．∵AE ―→＝AD ―→＋DE ―→,又AE ―→＝AD ―→＋μAB ―→＝AD ―→＋2μDC ―→＝AD ―→＋2μλDE ―→, ∴2μλ＝1,即μ＝λ2.∵0≤λ≤1,∴0≤μ≤12, 即μ的取值范围是⎣⎢⎢⎡⎦⎥⎥⎤012. 答案:⎣⎢⎢⎡⎦⎥⎥⎤012 15．已知O ,A ,B 是不共线的三点,且OP ―→＝m OA ―→＋n OB ―→ (m ,n ∈R)．(1)若m ＋n ＝1,求证:A ,P ,B 三点共线;(2)若A ,P ,B 三点共线,求证:m ＋n ＝1.证明:(1)若m ＋n ＝1,则OP ―→＝m OA ―→＋(1－m )OB ―→＝OB ―→＋m (OA ―→－OB ―→),∴OP ―→－OB ―→＝m (OA ―→－OB ―→),即BP ―→＝m BA ―→,∴BP ―→与BA ―→共线．又∵BP ―→与BA ―→有公共点B ,∴A ,P ,B 三点共线．(2)若A ,P ,B 三点共线,则存在实数λ,使BP ―→＝λBA ―→,∴OP ―→－OB ―→＝λ(OA ―→－OB ―→)．又OP ―→＝m OA ―→＋n OB ―→.故有m OA ―→＋(n －1)OB ―→＝λOA ―→－λOB ―→,即(m －λ)OA ―→＋(n ＋λ－1)OB ―→＝0.∵O ,A ,B 不共线,∴OA ―→,OB ―→不共线,∴⎩⎪⎨⎪⎧ m －λ＝0n ＋λ－1＝0∴m ＋n ＝1.。