混沌优化细菌觅食算法的传感器节点部署策略
- 格式:pdf
- 大小:1.39 MB
- 文档页数:9

基于混沌人工蜂群算法的无线传感器网络覆盖优化
文政颖;翟红生
【期刊名称】《计算机测量与控制》
【年(卷),期】2014(22)5
【摘要】针对无线传感器网络随机播撤的节点严重冗余并且导致网络寿命短、覆盖效率不高等缺陷,提出了一种混沌人工蜂群算法的无线传感器网络覆盖优化算法;将节点的利用率和覆盖率作为优化目标函数,建立与之对应的数学模型,之后用混沌人工蜂群算法改善人工蜂群算法陷入局部最优、收敛慢等问题,提高算法收敛速度和精度,对节点覆盖模型进行求解,得出网络最优覆盖方案;通过实验仿真,提出的算法提高了无线传感器网络的覆盖率,覆盖率可达93.48%以上,减少了网络节点冗余,提高了网络寿命,降低了网络成本.
【总页数】4页(P1609-1612)
【作者】文政颖;翟红生
【作者单位】河南工程学院计算机学院,郑州 451191;河南工程学院计算机学院,郑州 451191
【正文语种】中文
【中图分类】TP393
【相关文献】
1.改进人工蜂群算法的无线传感器网络覆盖优化 [J], 李华;卢静
2.基于混沌量子粒子群算法的无线传感器网络覆盖优化 [J], 王伟;朱娟娟;万家山;
乔焰;李旸
3.基于改进人工蜂群算法的WSNs覆盖优化 [J], 王鑫;谭华忠;蒋华
4.基于混沌粒子群算法的无线传感器网络覆盖优化 [J], 刘维亭;范洲远
5.基于人工蜂群算法的WSN覆盖优化研究 [J], 张洁;苏倩;韩忠泰
因版权原因,仅展示原文概要,查看原文内容请购买。

基于遗传-细菌觅食组合算法的非线性模型优化李亚品;邹德旋;段纳【摘要】文中提出一种遗传-细菌觅食组合优化算法以解决非线性模型优化问题.该方法先使用遗传算法进行全局搜索,并缩小最优解的搜索范围;再使用细菌觅食优化算法在该局部范围内执行局部搜索.这种组合搜索策略可以增强算法的收敛性,并能有效地均衡全局搜索和局部搜索.文中利用单峰、多峰和复杂多峰等非线性函数模型验证所提算法的性能.实验结果表明,组合算法的计算精度和效率分别比遗传算法和细菌觅食优化算法提高了30%和50%,表明该组合算法具有更快的收敛速度,更高的求解精度,适用于大规模多极值的非线性问题.【期刊名称】《电子科技》【年(卷),期】2019(032)005【总页数】5页(P16-20)【关键词】遗传优化;细菌觅食优化;组合算法;全局搜索;局部搜索;非线性模型【作者】李亚品;邹德旋;段纳【作者单位】江苏师范大学电气工程及自动化学院,江苏徐州221116;江苏师范大学电气工程及自动化学院,江苏徐州221116;江苏师范大学电气工程及自动化学院,江苏徐州221116【正文语种】中文【中图分类】TP18;TP301遗传算法(Genetic Algorithm,GA)是一类借鉴生物界进化规律演化而来的随机化搜索方法,已经广泛应用于各行各业。
细菌觅食优化(Bacterial Foraging Optimization,BFO)算法是Passino教授在2002年通过模拟大肠杆菌觅食这一仿生学行为所建立的一种优化算法[1],距今只有十几年时间,研究成果与应用案例较少,国内外对其研究尚处于初始阶段。
对于大型多极值的非线性优化问题,采用遗传算法通常计算速度较慢,计算结果不够精确。
学者们针对这些缺陷进行了广泛的研究,提出了很多改进措施。
邹彦艳等引入了分裂算子来避免遗传算法在寻优过程中陷入局部最优解[2];王婷等对适应度作了标定,解决了异构多无人机任务分配问题[3];祝慧灵等基于改进的遗传算法建立了集装箱船舶全航线配载优化模型[4];雷伟军等基于数控加工问题的特点,提出了一种适用于多模型加工路径规划问题的遗传算法[5];任乃飞等在标准遗传算法的基础上引入模拟退火算法的Boltzmann 生存机制,将混合遗传算法用于协同制造系统的调度问题[6];王丽萍等提出了均匀自组织映射遗传算法,弥补了其抽样过于随机的问题[7];王飞平等改进遗传算法编码、初始种群生成、突变步骤来优化 TTCAN 系统矩阵[8];郑史雄等在传统遗传算法的基础上引入最小二乘的思想,解决了二维耦合颤振问题[9]。

基于混沌克隆遗传算法的无线传感器网络低能耗分簇方法杨瑞;周杰
【期刊名称】《石河子大学学报:自然科学版》
【年(卷),期】2022(40)5
【摘要】合理的低能耗分簇是无线传感器网络中的重要问题之一。
为了降低无线传感器网络通信能耗,提升能量利用效率,本文提出一种混沌克隆遗传算法,设计了分簇模型,提出了目标函数用于计算无线传感器网络通信能耗;设计了新的分簇编码方式,以改进低能耗分簇的性能。
设计了新的混沌算子和克隆算子,提升了算法的收敛速度,避免了算法陷入早熟收敛。
实验结果显示,当传感器节点数量增至250时,混沌克隆遗传算法优化后的网络能耗相比常用的粒子群算法和混合蛙跳算法分别降低了0.22%和0.30%,即所提方案降低了无线传感器网络通信能耗,提升了网络能量利用效率。
【总页数】6页(P655-660)
【作者】杨瑞;周杰
【作者单位】石河子大学信息科学与技术学院
【正文语种】中文
【中图分类】TN925
【相关文献】
1.基于混沌粒子群优化的无线传感器网络分簇协议
2.一种基于混沌策略的无线传感器网络分簇路由协议
3.基于混沌小生境狼群算法的高密度无线传感器网络高能效
分簇方法4.基于遗传算法的异构无线传感器网络分簇算法5.基于遗传算法的无线传感器网络非均匀分簇路由协议
因版权原因,仅展示原文概要,查看原文内容请购买。

无线传感器网络节点定位的混沌粒子群优化算法
史洪宇;燕莎;曹建忠
【期刊名称】《探测与控制学报》
【年(卷),期】2010(032)005
【摘要】针对粒子群优化算法收敛速度慢且稳定度不高的问题,把混沌寻优思想引入到粒子群优化算法中,提出一种基于混沌粒子群优化算法的无线传感器网络节点定位算法.该算法首先对当前粒子群中的最优粒子进行混沌寻优, 然后用混沌寻优的结果随机替换粒子群体中的一个粒子,通过迭代搜索最佳坐标.仿真结果表明,在参数合理设置的前提下,该算法性能稳定,并且具有较快的定位速度和较高的定位精度.【总页数】4页(P46-49)
【作者】史洪宇;燕莎;曹建忠
【作者单位】惠州学院,广东,惠州,516007;西安理工大学,陕西,西安,710082;惠州学院,广东,惠州,516007
【正文语种】中文
【中图分类】TP393
【相关文献】
1.一种降低定位误差的无线传感器网络节点定位改进算法 [J], 刘林;范平志
2.基于量子粒子群优化算法的无线传感器网络节点优化 [J], 王艳萍;张惠敏;刘新贵
3.有向异构无线传感器网络节点覆盖率优化算法 [J], 徐忠明;谭励;杨朝玉;唐小江
4.基于蝙蝠优化算法的无线传感器网络节点定位研究 [J], 赖锦辉
5.水下无线传感器网络节点混合定位与优化算法 [J], HOU Senlin;DU Xiujuan;LI Meiju;HUANG Kejun
因版权原因,仅展示原文概要,查看原文内容请购买。
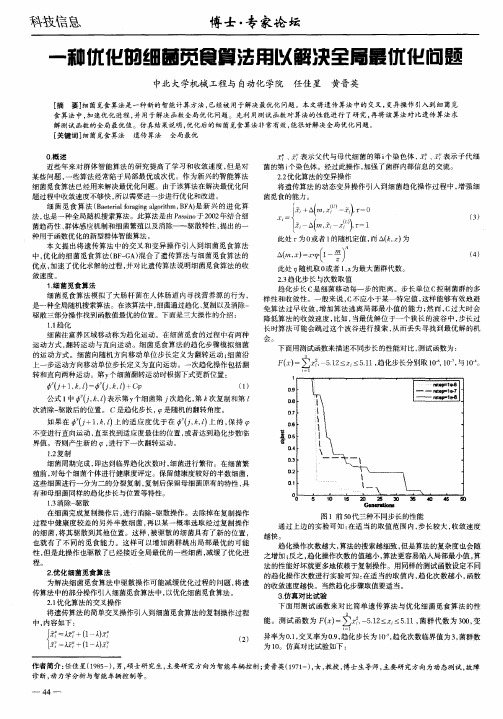

连续优化问题的细菌觅食改进算法戴秋萍;马良;郗莹【摘要】为更有效解决连续优化问题,提出了一种基于群体搜索的群智能优化算法——细菌觅食算法.该算法模拟了细菌觅食全过程,并对细菌个体的初始化、趋化操作中的搜索步长和搜索方向进行了改进.改进后的算法有效避免了算法陷入局部最优,而算法中采用的搜索步长,进一步提高了优化的收敛速度.经大量实验仿真表明,细菌觅食算法能够有效地求解连续优化问题.将仿真结果与其它算法对比,证明了细菌觅食算法的搜索质量优于其它算法.【期刊名称】《上海理工大学学报》【年(卷),期】2013(035)002【总页数】4页(P103-106)【关键词】连续优化问题;细菌觅食;局部优化【作者】戴秋萍;马良;郗莹【作者单位】上海理工大学管理学院,上海200093;上海理工大学管理学院,上海200093;上海理工大学管理学院,上海200093【正文语种】中文【中图分类】N945.15经典的优化算法在函数优化问题中,常常要求函数连续可微,因此在求解过程中需要借助一些基于梯度信息的数学技巧,并且在接近最优解时容易出现锯齿现象,造成收敛速度缓慢[1].20世纪50年代中期,人们从生物进化的机理中得到启发,创立了仿生学,并提出了许多解决复杂优化问题的智能方法,如神经网络、遗传算法[2]、进化策略、蚂蚁算法[3]等,这些方法在连续函数优化问题中取得了较好的结果.本文提出了一种新的智能优化算法——细菌觅食算法对连续函数优化问题进行求解.细菌觅食算法(bacterial foraging optimization,BFO)是由Passino[4]于2002年提出来的一种仿生随机搜索算法,该算法具有群体智能性,并可进行并行搜索.目前,BFO已被用于车间调度问题、自适应控制领域、噪声干扰下的谐波估计问题和PID(proportional integral derivative)控制器的设计等方面,并获得了较好的效果[5-6].本文对细菌觅食算法操作步骤进行了改进,有效地改善了该算法极易陷入局部最优的缺点,使其在解决复杂连续优化问题时,全局搜索能力大大增强.另外,通过大量仿真实验验证了该算法的有效性.细菌觅食算法是基于大肠杆菌在觅食过程中体现出来的智能行为的一种新型仿生优化算法,其具有群体智能性、并行性等特点.细菌觅食算法包括趋化操作(chemotaxis)、复制操作(reproduction)和迁徙(elimination and dispersal)操作.这3种操作方式是模仿细菌觅食的趋向行为、复制行为和迁移行为的抽象[7-8].a.趋化操作大肠杆菌在寻找食物源的过程中,其运动是通过表层的鞭毛实现的.当鞭毛全部逆时针摆动时,大肠杆菌将会向前行;当鞭毛全部顺时针摆动时,它会减速至停止.鞭毛的摆动对应着细菌个体对当前适应值的判断,并决定是否对其位置进行调整和确定调整的方向和力度.趋化操作模拟了大肠杆菌的这个运动过程,包括游动和翻转两个操作.设pi(j,k,l)表示细菌个体i的当前位置,j表示第j次趋化行为,k表示第k 次复制行为,l表示第l次迁徙行为.则其中,φ(j)表示游动的方向;C(i)表示前进步长.b.复制操作设群体规模为S,在完成设定次数的趋向操作之后,将群体中的个体按照其适应度值进行排序,将排在后面S/2的个体删除,剩下的个体进行自我复制,保证群体规模的稳定性.c.迁徙操作迁徙操作按照预先设定的一个概率发生,若某一个个体满足迁徙操作发生的条件,那么即将此个体删除,并生成一个新的个体代替.相当于将原来个体重新分配到一个新的位置,即以一定的概率将个体随机驱散到搜索空间.2.1 初始化操作改进在细菌觅食算法中,细菌种群的大小直接影响细菌寻求最优解的能力.种群数量越大,其初始覆盖区域越大,靠近最优解的概率就越大,能避免算法陷入局部极值,但同时增加了算法的计算量.因此,本文将初始化操作进行了改进.改进后,在细菌规模较小的情况下,能比较有效地改善初始化后细菌群体的覆盖范围(见图1、图2).确定群体规模S之后,将群体搜索的空间分成S个区域,每个细菌个体的初始位置为S个区域的中心点,随即细菌将在各自区域内搜索.由图1可知,细菌个体随机生成时,菌群可能在搜索空间内分布不均,在搜索最优解过程中,极有可能在限定的游动步长内无法找到最优解而陷入局部最优.2.2 趋化操作改进细菌觅食算法中,趋化操作是细菌觅食过程中最重要的一个步骤.基本细菌觅食算法在进行趋化操作时,细菌个体是根据历史信息按固定步长朝着食物源方向游动.在解决连续函数优化问题,尤其是多峰函数优化问题时,传统的操作方式易使得细菌个体错过最优解,本文对趋化搜索方式进行了改进.将细菌个体所在区域切分为n×n块,每个细菌在进行翻转操作时,仅在细菌周围的8个方向中随机选取,游动过程中每游动一次前进步长缩短为原来步长的0.8倍,C(i)=0.8C(i).当细菌个体游动次数并未达到设定游动次数时,细菌将再进行一次翻转操作.趋化操作步骤:a.确定细菌个体i,确定游动方向φ(j).b.细菌游动pi(j+1,k,l)=pi(j,k,l)+ C(i)φ(j).c.判断当前位置是否更优,是则个体i被新个体取代,继续步骤b,步长C(i)变为0.8C(i).d.判断是否达到设定游动次数,未达到转步骤a,达到游动次数细菌个体i趋化操作结束.2.3 复制操作改进细菌觅食过程中,一段时间后,细菌会根据个体位置的适应度值进行优劣排序.排在后面的S/2个细菌死亡,而排在前面的S/2个细菌进行自我复制,随即细菌往较小范围聚集.在求解多峰连续优化问题时,菌群极有可能跳过最优解而陷入局部最优.本算法将细菌个体首先随机与邻域周围的一个细菌进行交叉变异,变异后的细菌个体适应度值若优于原个体,原个体将被替代.通过一次改进后的复制操作后,整个菌群完成一次更新,菌群规模不变,每个细菌个体仅在各自区域及邻域内进行变异和适应度值比较,从而有效地防止了菌群向较小范围内聚集.改进后的复制操作不再只是觅食能力强的细菌个体单纯的自我繁殖过程,整个菌群群体都朝着更优的方向游动,提高了菌群整体的寻优能力.改进后复制操作过程如图3所示.前述细菌觅食算法采用Matlab 7予以实现,在PC系列机的Windows 7系统环境下运行通过.本文通过大量实例验证了此改进算法的有效性,下面给出4个算例及求解结果分析(见图4~7,图5~7见下页).算法相关参数设定:细菌规模为225,趋向操作数为10,复制操作数为4,迁徙操作数为2.算例1由函数示意图可知,该函数最优解处于中间区域,周围有很多局部极值围绕着最优解,用传统的细菌觅食算法陷入局部最优的可能性非常大.元胞蚁群算法、混沌算法均可得到最优解1,LINGO软件得到的最优解为0.646 848 8,Matlab优化工具得到的结果为0.990 3.算例2该问题的最优解被最差解包围,4个局部值点为(-5.12,5.12)、(-5.12,-5.12)、(5.12,5.12)、(5.12,-5.12),函数值均为2 748.78.运行改进后的细菌觅食算法求解该问题能够有效地获得最优解.算例3该函数在(1,1)处有最小值0,且在最优解附近存在病态,用常规方法容易陷入局部最优,难以搜索到最优解.算例4该算例可看出是典型的多峰函数,运用传统算法求解最优解相当困难.遗传算法目前所求最优解为38.827 533,运行LINGO软件与Matlab得到的解均小于38. 表1为该算法求解上述函数运行30次后的结果分析.其中平均偏差率为算法运行30次解的平均值与最优解的比值.首先对细菌初始化操作进行了改进,改变了传统的细菌觅食算法中的初始方式,使得菌群规模较小的情况下,能有较大的覆盖面.此外,本算法对细菌个体的搜索方式也进行了适当改进,增强了个体的局部搜索能力.为防止菌群在复制操作中过快地向小范围聚集而陷入局部最优,菌群进行变异性复制,不仅保证了菌群整体朝更优方向游动,同时大大提高了此算法的全局搜索能力.通过实验表明,改进后的细菌觅食算法在求解连续优化问题时,稳定性好,能够快速有效地找到最优解.通过与其它算法相比可得出以下结论:a.改进后的细菌觅食算法改进了传统细菌觅食算法的缺点,有效地改善了传统算法的收敛速度和全局寻优能力,所获最优解质量得到改善.b.改进后的细菌觅食算法能够有效解决连续优化问题,为连续优化问题提供一种新的解决方法.【相关文献】[1]马良,朱刚,宁爱兵.蚁群优化算法[M].北京:科学出版社,2008.[2]张惠珍,马良.基于变尺度混沌优化策略的混合遗传算法及在神经网络中的应用[J].上海理工大学学报,2007,29(3):215-219.[3]邱模杰,马良.约束平面选址问题的蚂蚁算法[J].上海理工大学学报,2000,22(9):61-62.[4] Passino K M.Biomimicry of bacterial foraging for distributed optimization and control[J].IEEE Control Systems Magazine,2002,22(3):52-67.[5]梁艳春,吴春国,时小虎,等.群体智能优化算法理论与应用[M].北京:科学出版社,2009.[6]张娜.细菌觅食优化算法求解车间调度问题的研究[D].吉林:吉林大学,2007.[7]胡海波,黄友锐.混合粒子群算法优化分数阶P/D控制参数研究[J].计算机应用,2009,29(9):2483 -2486.[8]李亚楠.菌群优化算法的研究[D].哈尔滨:哈尔滨工业大学,2009.。
《基于细菌群觅食优化算法的电液位置系统PID参数寻优研究》篇一一、引言在工业自动化和机器人技术中,电液位置系统作为重要的执行机构,其性能优化显得尤为重要。
PID(比例-积分-微分)控制器因其简单、稳定和响应快速的特点,广泛应用于电液位置系统的控制中。
然而,PID参数的合理配置一直是控制领域的重要问题。
传统的方法往往依赖于试错法或经验调整,这不仅效率低下,而且难以保证最佳的控制效果。
近年来,随着智能优化算法的发展,越来越多的研究者开始尝试利用这些算法对PID参数进行优化。
其中,细菌群觅食优化算法(Bacterial Foraging Optimization Algorithm, BFOA)以其优秀的全局搜索能力和较强的鲁棒性脱颖而出。
本文旨在研究基于细菌群觅食优化算法的电液位置系统PID参数寻优。
二、电液位置系统概述电液位置系统主要由液压执行机构、传感器和控制器等部分组成。
其工作原理是通过控制器对液压执行机构发出指令,驱动其按照预设的轨迹运动,从而实现位置控制。
PID控制器作为电液位置系统的核心控制部分,其参数的配置直接影响到系统的性能。
因此,对PID参数的优化对于提高电液位置系统的性能具有重要意义。
三、细菌群觅食优化算法细菌群觅食优化算法是一种模拟自然界中细菌觅食行为的智能优化算法。
它通过模拟细菌的趋化性、繁殖和扩散等行为,实现对问题的全局搜索和优化。
BFOA具有强大的全局搜索能力和较好的鲁棒性,可以有效地解决复杂非线性系统的优化问题。
在PID参数寻优中,我们可以将BFOA看作是一种“智能试探”过程,通过不断地试探和调整PID参数,寻找最优的参数组合。
四、基于BFOA的电液位置系统PID参数寻优本部分主要介绍如何将BFOA应用于电液位置系统的PID参数寻优中。
首先,建立电液位置系统的数学模型,并将PID控制器的参数作为优化对象。
然后,利用BFOA对PID参数进行智能试探和调整,通过不断迭代和优化,寻找最优的PID参数组合。
第27卷第6期2010年11月计算物理CHINESE JOURNAL OF COMPUTATIONAL PHYSICSVol.27,No.6Nov.,2010文章编号:1001-246X (2010)06-0933-07收稿日期:2009-09-07;修回日期:2010-03-04基金项目:国家自然科学基金(编号:60974082)资助项目作者简介:姜飞(1984-),女,河北保定,硕士生,主要从事最优理论与方法、决策分析及网格算法的研究.混沌系统控制与同步的细菌觅食和差分进化混合算法姜飞1,刘三阳1,张建科1,2,高卫峰1(1.西安电子科技大学理学院,陕西西安710071; 2.西安邮电学院应用数理系,陕西西安710121)摘要:将混沌系统的控制与同步问题转化为函数优化问题,提出CDEM 算法.把差分进化算法与细菌觅食算法相融合,提高DE 算法的收敛性,并利用遗传变异算子保持种群多样性;利用CDEM 算法求解混沌系统的控制与同步问题.以典型的离散混沌系统Hénon Map 为例进行数值试验,结果表明算法有效、稳定,并分析各个参数对该算法的影响.关键词:混沌系统;差分进化;细菌觅食;变异算子中图分类号:TP271文献标识码:A0引言混沌系统的控制与同步已经成为非线性科学中重要的研究方向之一,在保密通信、工程技术、电子学、生物医学、化学等方面都有极其重要的应用潜力和发展前景[1-6].近年来,人们提出了许多混沌控制与同步方法,如OGY 方法、迟延反馈控制法、线性和非线性反馈法、PC 法、自适应法等[7-11].混沌系统的控制与同步问题也可以转化为数值优化问题,故可采用智能优化算法[12-14],但现有的智能方法搜索效率很低,有待进一步提高.本文利用改进的CDE 算法[15]求解该问题.CDE 算法将细菌觅食算法(Bacteria Foraging OptimizationAlgorithm :BFOA )中的趋化算子融入到差分进化(Differential Evolution :DE )算法中,具有很强的搜索能力,但当搜索范围比较小时,易出现早熟现象.为克服这一缺点,增强种群的多样性,本文在CDE 算法的基础上结合变异算子,提出了一种新的算法———CDEM 算法.利用CDEM 算法求解混沌动态系统的控制与同步问题,以典型Hénon Map 系统为例进行仿真,验证了CDEM 算法的有效性与稳定性,并分析了各个参数对该算法的影响.1问题描述混沌系统的控制问题,即通过增加一个小而有界的扰动引导离散动态混沌系统进入预定的目标区域,该问题可以转化为在线的轨道引导问题.本文以典型的Hénon Map 离散混沌系统为例进行研究.1.1混沌系统的控制问题Hénon Map 系统中增加小的扰动u (k )∈R n 可用x (k +1)=f (x (k ))+u (k ),k =0,1,2,…,N -1(1)表示,其中x (k )∈R n ,f :R n →R n 连续可微,‖u (k )‖<μ,μ>0且为常数.不失一般性,假设u (k )只作用在f 的第一个元素,则Hénon Map 系统的控制问题可以描述为(P1):min ‖x (N )-x t ‖,s.t.x 1(k +1)=f 1(x (k ))+u (k ),x i (k +1)=f i (x (k )),i =0,1,2,…,N -1{,|u (k )|≤μ,计算物理第27卷x (0)=x 0.1.2混沌系统的同步问题反馈的混沌系统的同步,即选择一个反馈矩阵K (k )∈R n ˑn,使得‖x (N )-y (N )‖→0,其中x (0)=x 0≠y (0)=y 0,x (k +1)=f (x (k )),y (k +1)=f (y (k ))+K (k )(y (k )-x (k )){.(2)混沌同步也可用式(2)描述[16].同混沌系统的控制问题类似,可假设反馈矩阵只作用在第一个元素,即K 11(k )≠0,K (k )的其余元素均为零.为简化运算,令K 11(k )=K (k ).则Hénon Map 系统的同步问题可描述为(P2):min ‖x (N )-y (N )‖,s.t.x (k +1)=f (x (k )),y 1(k +1)=f 1(y (k ))+K (k )(y 1(k )-x 1(k )),y i (k +1)=f i (y (k )),i =0,1,2,…,N -1{,|K (k )|≤κ,x (0)=x 0≠y (0)=y 0.但(P2)并不完全等价于系统的同步问题.由于混沌系统对初始状态敏感,当x (N )≠y (N )时最终将导致两个系统彼此分离,所以应在线处理(P2):如果在第kᶄ步,有‖x (kᶄ)-y (kᶄ)‖大于给定的δ,则令x 0=x (kᶄ),y 0=y (kᶄ),重新开始.上述两个问题,需要确定合适的u (k )和K (k )使得目标函数值最小.从优化的观点来看,(P1)和(P2)均为带约束的数值优化问题.2CDE 算法和CDEM 算法2.1CDE 算法CDE 算法[15]将自适应的趋化算子融入到DE 算法中,显著提高了DE 算法的收敛性质.在CDE 算法中,首先将测试向量看作细菌,运行趋化算子,进行局部搜索;之后,整个种群进入DE 循环.重复上述操作求得最优解.2.1.1自适应的趋化算子记θ(i ,j ,t )为第i 个细菌在第j 次趋化第t 次变异时的位置,J (i ,j ,t )为θ(i ,j ,t )的目标函数值.N s 为允许细菌做趋化移动的最大次数(本文设N s =4),m 记录细菌做趋化移动的次数(初始值为0)。
细菌觅食优化算法求解物流网络问题细菌觅食优化算法求解物流网络问题随着全球化和电子商务的迅速发展,物流网络的建设和优化是一个愈发重要的问题。
物流网络的优化不仅可以降低物流成本,提高效率,还可以减少环境污染,提高资源利用率。
然而,物流网络的优化是一个复杂而且多变的问题,需要考虑到货物的运输距离、交通状况、人力资源等众多因素。
传统的物流网络优化方法往往依赖于数学建模和复杂的计算,但这些方法的计算复杂度往往很高,很难在实际应用中得到有效的解决。
为了克服这些问题,研究者们开始寻找新的优化方法,其中一种被广泛应用的方法就是基于生物学的算法。
细菌觅食优化算法就是其中一种。
细菌觅食优化算法是由模拟细菌觅食行为而来的一种算法,它的基本原理是通过模拟细菌在食物中寻找最佳位置的行为来解决实际问题。
在细菌觅食优化算法中,将解空间中的解视作食物,并通过计算每个解的适应度来模拟细菌的感知能力。
根据每个解的适应度,细菌将调整自身的位置,以寻找更适合的食物。
通过不断迭代和更新,最终能够找到问题的最优解。
在物流网络问题中,细菌觅食优化算法可以应用于优化货物的调度和路径选择。
首先,将物流网络表示为图结构,以节点表示仓库和配送点,边表示路径。
然后,通过计算每个路径的适应度来模拟细菌的感知能力。
适应度可以根据路径的长度、运输成本、交通状况等因素来确定。
根据每个路径的适应度,细菌将调整自身的位置,即调整路径的选择和货物的调度计划。
经过多次迭代和更新,细菌觅食优化算法能够找到最优的路径和货物调度方案,从而实现物流网络的优化。
与传统的物流网络优化方法相比,细菌觅食优化算法具有以下几个优点。
首先,细菌觅食优化算法是一种自适应的算法,能够自动地调整路径和货物调度方案。
其次,细菌觅食优化算法具有较高的计算效率,能够在较短的时间内得到较好的解决方案。
再次,细菌觅食优化算法不依赖于复杂的数学建模,更加符合实际应用的需求。
然而,细菌觅食优化算法也存在一些局限性。
物联网中传感器网络的部署与优化方法随着物联网的快速发展,传感器网络在其中起到了关键的作用。
传感器网络是由大量的节点组成的,这些节点通过无线通信相互连接,并将收集到的数据传输给中央服务器。
在物联网中,传感器网络的部署和优化对于系统性能和能源效率至关重要。
本文将探讨物联网中传感器网络的部署和优化方法,以提高系统的性能和能源利用效率。
1. 传感器网络的部署方法传感器网络的部署决定了网络的覆盖范围和数据采集质量。
传感器网络的部署方法可以采用以下几种方式:1.1 均匀部署方法均匀部署方法是指将传感器节点按照一定间距均匀地分布在感兴趣区域内。
这种方法可以提供全方位的覆盖,但可能导致一些区域过度覆盖,从而增加了能源的浪费。
因此,在使用均匀部署方法时,需要合理设置传感器节点之间的间距,以避免过度覆盖。
1.2 簇状部署方法簇状部署方法将传感器网络划分为多个簇,每个簇都有一个簇头节点负责数据的收集和传输。
这种方法可以减少节点之间的通信量,降低能源消耗,并提高数据传输的效率。
在选择簇头节点时,可以考虑节点的能量水平和传输距离,以实现能量均衡和覆盖范围最大化。
1.3 动态部署方法动态部署方法是根据实际需求和环境变化来部署传感器节点。
通过监测环境参数和节点的能量消耗情况,及时调整传感器节点的位置和数量。
这种方法可以根据实际情况进行灵活的调整,提高网络的适应性和灵活性。
2. 传感器网络的优化方法为了提高传感器网络的性能和能源利用效率,可以采用以下几种优化方法:2.1 路由优化方法路由优化方法是通过合理选择传感器节点之间的路径,减少数据传输的距离和能量消耗。
常用的路由优化方法包括最短路径算法、集群路由算法和多路径路由算法等。
这些算法可以根据不同的网络架构和需求选择,以实现高效的数据传输。
2.2 能量管理方法能量管理方法是通过合理利用节点的能量资源,延长网络的生命周期。
常用的能量管理方法包括动态能量分配、能量平衡和能量回收等。