下载文档原格式
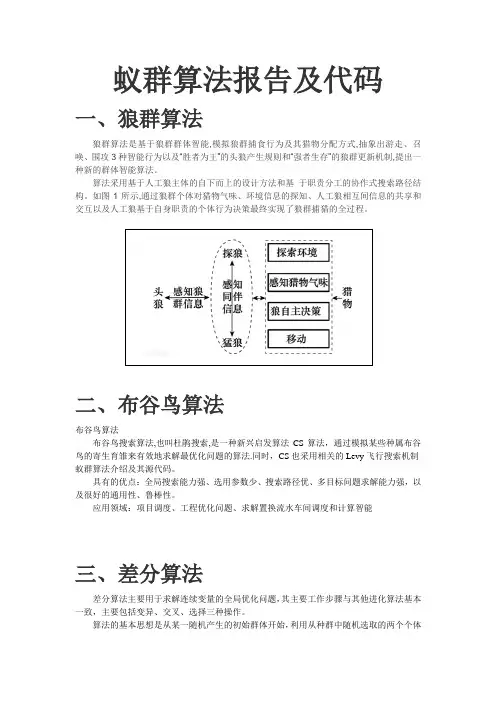
蚁群算法报告及代码一、狼群算法狼群算法是基于狼群群体智能,模拟狼群捕食行为及其猎物分配方式,抽象出游走、召唤、围攻3种智能行为以及“胜者为王”的头狼产生规则和“强者生存”的狼群更新机制,提出一种新的群体智能算法。
算法采用基于人工狼主体的自下而上的设计方法和基于职责分工的协作式搜索路径结构。
如图1所示,通过狼群个体对猎物气味、环境信息的探知、人工狼相互间信息的共享和交互以及人工狼基于自身职责的个体行为决策最终实现了狼群捕猎的全过程。
二、布谷鸟算法布谷鸟算法布谷鸟搜索算法,也叫杜鹃搜索,是一种新兴启发算法CS算法，通过模拟某些种属布谷鸟的寄生育雏来有效地求解最优化问题的算法.同时，CS也采用相关的Levy飞行搜索机制蚁群算法介绍及其源代码。
具有的优点：全局搜索能力强、选用参数少、搜索路径优、多目标问题求解能力强，以及很好的通用性、鲁棒性。
应用领域：项目调度、工程优化问题、求解置换流水车间调度和计算智能三、差分算法差分算法主要用于求解连续变量的全局优化问题，其主要工作步骤与其他进化算法基本一致，主要包括变异、交叉、选择三种操作。
算法的基本思想是从某一随机产生的初始群体开始，利用从种群中随机选取的两个个体的差向量作为第三个个体的随机变化源，将差向量加权后按照一定的规则与第三个个体求和而产生变异个体，该操作称为变异。
然后，变异个体与某个预先决定的目标个体进行参数混合，生成试验个体，这一过程称之为交叉。
如果试验个体的适应度值优于目标个体的适应度值，则在下一代中试验个体取代目标个体，否则目标个体仍保存下来，该操作称为选择。
在每一代的进化过程中，每一个体矢量作为目标个体一次，算法通过不断地迭代计算，保留优良个体，淘汰劣质个体，引导搜索过程向全局最优解逼近。
四、免疫算法免疫算法是一种具有生成+检测的迭代过程的搜索算法。
从理论上分析，迭代过程中，在保留上一代最佳个体的前提下，遗传算法是全局收敛的。
五、人工蜂群算法人工蜂群算法是模仿蜜蜂行为提出的一种优化方法，是集群智能思想的一个具体应用，它的主要特点是不需要了解问题的特殊信息，只需要对问题进行优劣的比较，通过各人工蜂个体的局部寻优行为，最终在群体中使全局最优值突现出来，有着较快的收敛速度。
c law enforcement. Therefore, c congestion was ciency of the improved algorithm with the Dijkstra algorithm. Thus, it could simulate the optimal driving path with better performance, which was targeted and innovative.关键词：蚁群算法;实际路况;最优路径Key words ：ant colony optimization; actual road conditions; optimal path文／张俊豪蚁群算法在最优路径选择中的改进及应用0 引言在国务院发布的《国家中长期科学和技术发展规划纲要（2006-2020年）》中，将交通拥堵问题列为发展现代综合交通体系亟待解决的“三大热点问题”之一。
智能交通系统作为“互联网+交通”的产物，利用先进的科学技术对车、路、人、物进行统一的管控、调配，成为了当下各国缓解交通拥堵的一个重要途径。
路径寻优是智能交通系统的一个核心研究内容，可以有效的提升交通运输效率，减少事故发生频率，降低对城市空气的污染以及提升交通警察的执法效率等。
最著名的路径规划算法是Dijkstra算法和Floyd算法，Dijkstra算法能够在有向加权网络中计算得到某一节点到其他任何节点的最短路径；Floyd算法也称查点法，该算法和Dijkstra算法相似，主要利用的是动态规划思想，寻找加权图中多源节点的最短路径。
近些年，最优路径的研究主要集中以下几个方面：（1）基于A*算法的路径寻优。
A*算法作为一种重要的路径寻优算法，其在诸多领域内都得到了应用。
随着科技的发展，A*算法主要运用于人工智能领域，特别是游戏行业，在游戏中，A*算法旨在找到一条代价（燃料、时间、距离、装备、金钱等）最小化的路径，A*算法通过启发式函数引导自己，具体的搜索过程由函数值来决定。
结构优化算法总结引言结构优化是指通过优化设计参数，使得结构在给定约束条件下具有更好的性能。
结构优化算法是解决结构优化问题的关键步骤，可以帮助工程师快速找到最优设计方案。
本文将总结几种常见的结构优化算法，并对其优缺点进行评价。
1. 遗传算法遗传算法是一种模拟自然界生物进化过程的优化方法，它通过不断演化产生出最优解。
遗传算法的基本步骤如下：1.初始化种群：随机生成一组初始设计参数。
2.适应度评估：根据适应度函数评估每个个体的适应度值。
3.选择操作：选择适应度较高的个体作为下一代的父代。
4.交叉操作：对父代个体进行交叉操作产生子代个体。
5.变异操作：对子代个体进行变异操作引入新的基因。
6.更新种群：更新种群，替换掉适应度较低的个体。
7.终止条件：达到预定的迭代次数或满足停止条件。
遗传算法的优点是可以全局搜索，避免收敛到局部最优解。
但是，由于需要对种群进行大量的评估和操作，计算复杂度较高。
2. 粒子群算法粒子群算法是一种基于群智能的优化算法，模拟了鸟群觅食的过程。
粒子群算法的基本思想是，模拟每个个体通过观察和与其他个体交互来逐渐寻找最佳位置。
粒子群算法的步骤如下：1.初始化粒子群：随机生成一组初始设计参数。
2.更新粒子速度：根据当前位置以及历史最佳位置和群体最佳位置计算新的粒子速度。
3.更新粒子位置：根据新的速度计算新的粒子位置。
4.更新历史最佳位置：根据当前位置和历史最佳位置的适应度值，更新历史最佳位置。
5.更新群体最佳位置：根据所有粒子的历史最佳位置，更新群体最佳位置。
6.终止条件：达到预定的迭代次数或满足停止条件。
粒子群算法的优点是易于实现和理解，并且具有较快的收敛速度。
然而，粒子群算法容易陷入局部最优解。
3. 人工蜂群算法人工蜂群算法是一种基于蜜蜂觅食行为的优化算法，模拟了蜜蜂在空间中搜索食物的过程。
人工蜂群算法的基本步骤如下：1.初始化蜜蜂群：随机生成一组初始设计参数。
2.对于每个蜜蜂，根据预定的搜索策略选择一个邻域位置并计算其适应度值。
蚁群算法的基本原理蚁群算法 (Ant Colony Optimization, ACO) 是一种基于群体智能的优化算法，模拟了蚂蚁在寻找食物时候的行为，被广泛应用于求解组合优化问题、路径规划等领域。
蚁群算法的基本思路蚁群算法的基本思路是通过模拟蚂蚁在寻找食物的过程中释放信息素来获取全局最优解。
具体过程如下：1.初始化信息素: 首先，需要在所有可行解的路径上放置一些信息素。
在开始时，信息素值可以选择为等量的值或一些默认值。
2.蚁群搜索: 一开始，所有的蚂蚁都分别随机选择一个节点作为起点，并开始在网络中搜索。
蚂蚁行动的过程中，会根据路径上信息素浓度的大小来选择下一步的方向。
同时，每只蚂蚁都会记录其所经过的路径和信息素值。
3.信息素更新: 每只蚂蚁到达终点之后，计算其所经过路径的费用，然后根据一定的规则更新路径上的信息素。
较优的路径上将会添加更多的信息素，使下一次蚂蚁选择该路径的概率更大。
4.重复搜索: 重复上面的步骤，直到满足一个停止条件为止。
一种常见的停止条件是达到预定的迭代次数。
蚁群算法的优势蚁群算法在解决组合优化问题时，具有以下的优势：1.全局优化能力极强: 因为每只蚂蚁都只关注自己所经过的路径上的信息素值，所以可以同时搜索并更新多个路径，从而有可能找到全局最优解。
2.能够避免陷入局部最优: 蚁群算法可以通过信息素的挥发、说长存、信息素值的启发式更新等手段来避免陷入局部最优解。
3.易于扩展和并行化: 蚁群算法通常是一种并行的算法，可以很轻松地应用于分布式计算环境中。
蚁群算法的应用蚁群算法在解决组合优化问题、路径规划、调度等方面有着广泛的应用，如下所示：1.旅行商问题: 蚁群算法可以用于解决旅行商问题。
2.线性规划问题: 蚁群算法可以用于求解线性规划问题。
3.路径规划问题: 蚁群算法可以用于车辆路径规划问题。
4.调度问题: 蚁群算法可以用于作业车间调度问题。
蚁群算法是一种基于群体智能的优化算法，模拟了蚂蚁在寻找食物时候的行为。
蚁群优化算法及其理论进展摘要:蚁群优化算法作为一种新的智能计算模式,近年来在理论研究上取得了丰硕成果。
本文主要阐述蚁群优化算法的研究成果,论述了算法在离散域、连续域问题上的理论进展,然后对收敛性研究做了介绍。
最后,阐述了蚁群优化算法的发展趋势。
关键词:蚁群算法离散域连续域收敛性中图分类号:tp301.6 文献标识码:a 文章编号:1674-098x(2012)04(a)-0032-021 引言意大利学者dorigo[1]等人根据真实蚂蚁觅食行为,提出了蚁群优化算法的(aco)最早形式—蚂蚁系统(as),并应用在tsp旅行商问题中。
该算法采用分布式并行计算机制,易与其他方法结合,具有较强的鲁棒性。
as算法提出之后,其应用范围逐渐广泛,已经由单一的tsp领域渗透到了多个应用领域[2],算法本身也不断完善和改进,形成了一系列改进aco算法。
2 蚁群算法理论研究2.1 基本蚂蚁算法与真实蚂蚁觅食行为类似,基本蚁群算法主要包括路径选择和信息素更新两个步骤。
以蚁群算法求解tsp问题为例[1]:tsp问题可表述成,旅行商走完n个城市有多种走法,每周游完所有城市可得长度为i的路径,它们构成解的集合。
而每个解是依次走过n个城市的路径距离构成的集合,可表示设是在第g次周游中城市i上的蚂蚁数。
在算法周游过程中,每只蚂蚁根据概率转换规则生成一个有n步过程的行动路线,整个算法的周游过程以g为刻度,。
其中是预先设定的算法最大周游次数,当所有蚂蚁移动一次后,周游次数计数器加1。
经过次周游,基本可找到一条最短路径。
设,np为算法中总蚂蚁数。
基本步骤为:算法开始时,每条路径上初始信息素设置为常数,并对每只蚂蚁设置随机起始城市。
蚂蚁移动过程中,从城市i选择移动到城市j主要是根据概率启发公式(1)来完成,每次选择的城市都是从可选城市列表中取出。
(1)其中为启发优先系数且。
可以改变信息素与启发优先系数的相对重要性。
如果则最近的城市容易被选择,这类似经典的随机贪婪算法。
第３８卷 第４期 ２０１０年７月 河南师范大学学报（自然科学版）
Ｊｏｕｒｎａｌ ｏｆ Ｈｅｎａｎ Ｎｏｒｍａｌ Ｕｎｉｖｅｒｓｉｔｙ（Ｎａｔｕｒａｌ Ｓｃｉｅｎｃｅ） ｆ．３８ Ｎｏ．４ Ｊｕｌｙ．２０１０
文章编号：１０００～２３６７（２０１０）０４—００４８—０３
蚁群算法迭代次数的一种优化策略 袁培燕 ，刘 萍 ，高宏卿 （河南师范大学ａ．物理与信息工程学院；ｂ．网络中心，河南新乡４５３００７） 摘 要：针对蚁群算法中后期多次迭代无法产生更优解的问题，提出了一种优化策略，当连续多次迭代没有产 生更优解时，减少迭代的总次数，加速算法的收敛性．仿真结果显示，在不影响最优解的情况下，优化后的策略明显 降低了算法的时间复杂度和空间复杂度． 关键词：蚁群算法；随机环境；性能评价；旅行商问题 中图分类号：ＴＰ３９３．０１ 文献标志码：Ａ
近年来，智能算法的研究受到了越来越多的关注．而作为继模拟退火算法、遗传算法、禁忌搜索（Ｔａｂｕ Ｓｅａｒｃｈ）算法、人工神经网络算法后的又一种应用于组合优化问题的启发式搜索算法——蚁群算法（Ａｎｔ Ａ卜 ｇｏｒｉｔｈｍ）［ ，更是研究的热点，并得到了广泛的应用．蚁群算法由意大利Ｍ．Ｄｏｒｉｇｏ等人首先提出，它模拟 蚂蚁觅食时的行为，按照启发式思想，通过信息素的诱导作用，逐步收敛到问题的最优解． 旅行商问题（Ｔｒａｖｅｌｉｎｇ Ｓａｌｅｓｍａｎ Ｐｒｏｂｌｅｍ）是ＮＰ（Ｎｏｎ—ｄｅｔｅｒｍｉｎｉｓｔｉｃ Ｐｏｌｙｎｏｍｉａ１）问题中的一个典型例 子．实际上，蚁群算法在首次提出时，就是充分利用了蚂蚁搜索食物的过程与ＴＳＰ（旅行商）问题之问的相似 性来求解ＴＳＰ的．目前，基于蚁群算法求解ＴＳＰ问题的相关文献很多Ⅲ３ ］．其中，文献［３］主要研究了蚁群算 法中蚂蚁位置的初始化问题，通过将蚂蚁边缘化而不是随机设置，来增大解的空间，提高解的质量．文献［４］ 通过将蚁群算法中的参数进行分段继而达到优化的目的．文献［５］分析了蚁群算法中最佳配置参数的问题， 文献［６］则对目前智能算法求解ＴＳＰ问题进行了归纳分类，通过不同的实验发现进化算法与局部搜索组合 求解ＴＳＰ效果最好．结合相关文献及进行的大量实验发现，在迭代中后期，多次迭代无法产生更优解的现象 明显增多，蚁群算法陷入局部最优的可能性增大．基于此，对总的迭代次数进行了优化，当多次迭代无法产生 更优解的次数超过某个界限时，减少总的迭代次数，从而降低算法的时间复杂度和空间复杂度．
１ 蚁群算法及ＴＳＰ问题 蚁群算法由意大利学者Ｍ．Ｄｏｒｉｇｏ等人首先提出，该算法利用蚂蚁搜索食物的过程与ＴＳＰ问题的相似 性，通过模拟自然界中蚂蚁寻找食物的行为，来解决ＴＳＰ等各类复杂优化问题．蚁群算法采用分布式正反馈 并行计算机制，容易与其它算法结合，具有较强的鲁棒性和适应性．由于蚂蚁在寻路时主要依据于路径上的 信息素浓度，所以不同的信息素更新策略对蚁群算法的性能影响很大．Ｄｏｒｉｇｏ Ｍ曾给出３种不同的信息素 更新模型，分别为Ａｎｔ ｃｙｃｌｅ ｓｙｓｔｅｍ（ＡＣＳ），Ａｎｔ ｑｕａｎｔｉｔｙ ｓｙｓｔｅｍ（ＡＱＳ），Ａｎｔ ｄｅｎｓｉｔｙ ｓｙｓｔｅｍ（ＡＤＳ）． 旅行商问题是一个经典的组合优化问题，它是指一个商人欲到”个城市推销产品，希望选择这样的一条 路径：使得商人经过所有城市一次又回到初始城市，并且所走的路径最短．ＴＳＰ问题是一个典型的ＮＰ一难问 题，也是验证求解组合优化问题有效性的一个间接标准．ＴＳＰ问题的数学描述为：设 一｛ｖｌ，ｖ２，…，＂ＵＹｔ｝是 个城市的集合，Ｅ一｛（ｖｉ， ），ｖｉ， ∈Ｖ｝足 中任意两个城市两两连接的边的集合，ｃ（ｉ， ）一ｃ（ｊ， ）是边（ｖｉ， ｖｊ）∈Ｅ所需要的费用．ＴＳＰ问题就是寻找一条闭合的汉密尔顿回路使之能够访问所有的城市一次，并且这
收稿日期：２００９一ｎ—ｌ０ 基金项目：河南省教育厅自然科学基金（２００９Ｂ５２００１６）；河南师范大学青年科学基会（２ＯＯ８ｑｋＯ６） 作者简介：袁培燕（１９７８一），男，河南邓州人，河南师范大学讲师，研究方向：网络协议 ｌ 程． 第４期 袁培燕等：蚁群算法迭代次数的一种优化策略 ４９ 条回路的费用最少Ｅ ］． ２ 蚁群算法的优化及仿真分析 蚁群算法最初就是为解决ＴＳＰ问题而提出的，因此用ＴＳＰ问题评价蚁群算法在不同参数体系下的相 对性能是恰当的．在大量的实验中发现，在算法的中后期，大量的迭代次数产生相同解，即存在多次迭代无法 产生更优解的现象．最坏的一次是在５００次的迭代实验中，从第４次到最后一次的值是一样的．也就是说，在 具体的实验中，大量的迭代次数是不必要的．能不能在不影响解的情况下，减少总的迭代次数，从而达到降低 算法复杂度的目的？基于这样的考虑，设置了一个统计连续多次没有产生更优解的计数器ｃｏｕｎｔｅｒ，每当当 前迭代产生的解与上一次迭代产生的解相同，ｃｏｕｎｔｅｒ的值加１，当ｃｏｕｎｔｅｒ的值大于某一规定值Ｋ时，减少 迭代次数，同时ｃｏｕｎｔｅｒ清零．算法的伪代码如下： ｗｈｅｎ（当前迭代产生的解同上一次一样） ｛总的迭代次数一总的迭代次数一Ｄ ｃｏｕｎｔｅｒ加１ ｃｏｕｎｔｅｒ＝０） ｗｈｅｎ（ｃｏｕｎｔｅｒ大于某个值Ｋ） Ｄ为每次减少的迭代次数，实验中Ｄ的变化为１、２、５、１０．仿真平台采用ＶＣ＋＋，仿真数据是ＴＳＰＬＩＢ 标准库（Ｒｅｉｎｅｌｔ，１９９１）里面的实例ｅｉｌ５１．实验中通过改变ａ，Ｊ３的值来观察蚁群算法的性能．蚂蚁个数为３４ 个，迭代次数为５００次，Ｋ的值等于６，ａ取值范围为０．１到１．０，Ｊ３取值范围为０．１到５．实验一共生成８５种 随机场境，每种场境运行１Ｏ次，最后的结果为１ｏ次的平均值．算法的评价因子有两个，一个是求得最短路径 的距离，另一个是算法的实际迭代次数． ２．１ ａ，Ｉ３对算法的影响
瀣
６００ ５５０ 蛰
５００
变动的 图Ｉ最短路彳争ＶＳ口
变动的Ｂ 图３最短路径ＶＳ ０
隶罨 杠
上＜ 较
◆＿＿Ａｎｔ—Ｄ一１—１卜Ｄ一２ ■ Ｄ一５—● Ｄ ｌ０
Ｏ．１ Ｏ．２ Ｏ．３ Ｏ．４ Ｏ．５ Ｏ．６ ０．７ Ｏ．８ Ｏ．９ １
变动的ｄ 图２实际迭代次数ＶＳ ｏ
Ｏ．１ Ｏ．２ ０．５ １ ２ ３ ４ ５ 变动的１３ 图４实际迭代次数ＶＳ１３
０ ０ ０ ０ ０ Ｏ Ｏ 鲫 ∞ ∞ ∞ 加 ５０ 河南师范大学学报（自然科学版） 图Ｉ至图４显示了当ａ，８变动时，算法求得的最短路径及迭代次数的变化情况．从图１可以看到，当ａ 小于０．６时，优化后的策略影响了最优值，当Ｄ＝＝＝１０，ａ一０．２时，误差最大，偏离最优值达到２．４６ ，而随着ａ 的增大，这种影响逐渐减小．不过从图２也可以看到，优化后的策略明显降低了算法的迭代次数，从而降低了 算法的时间和空间复杂度．从图３和图４可以看到，相对于ａ而言，Ｇ值的波动对最短路径的影响较小，两种 情况下基本一致．而对迭代次数的影响与ａ一样，显著降低了算法的迭代次数．从上面的分析可知，优化后的 策略，在不影响最优解的情况下，显著改善了算法的复杂度． ２．２ Ｄ的改变对算法的影响 从图１到图４可以同时看到，当改变Ｄ时，最短路径及迭代次数的变化情况．当迭代次数每次减少的次 数由１、２、５到１０发生变化时，最短路径的波动较小（图１和图３所示），而迭代次数的变化较为明显，即呈现 递减的趋势．说明随着Ｄ的增大，在对最优解没有产生明显影响的情况下（图１和图３各条均线粘合在一 起），总的迭代次数随之减少．当然，也不可能将Ｄ无限增大来降低问题的求解规模，否则求得的解将会严重 偏离最优解．也就是说，为了求得尽可能的最优解，一定的迭代次数是必要的，但同时也观察到，在实验中后 期，许多次的迭代是不必要的．从图２和图４可以看出，最大的迭代次数仍然没有超过４００，所以在实验初期 设置的迭代次数５００过大，浪费了系统资源．但是，对某个ＴＳＰ问题来说，在实验初期，如何设定迭代次数是 未知的，不可能设置一个恰到好处的值，所以如何合理优化蚁群算法的迭代次数，从而降低算法的时间和空 间复杂度，是一个值得认真考虑的问题．文中通过发现连续多次迭代无法产生更优解这一实验现象，继而降 低总的迭代次数以达到对算法进行优化的目的，仿真结果表明该方案是可行的，有效的．
３ 结 论 结合ＴＳＰ问题，对蚁群算法的性能进行了评价，发现在算法运行的中后期，大量的迭代次数实际上是不 必要的，通过对该阶段的研究提出了文中的优化策略，对减少蚁群算法的迭代次数，降低算法的时空复杂度 进行了有益的尝试．
参 考 文 献 ［１］Ｄｏｒｉｇｏ Ｍ，Ｍａｎｉｃｚａｏ Ｖ，Ｃｏｌｏｍ ｉ Ａ．Ａｎｔ ｓｙｓｔｅｍ：Ｏｐｔｉｍｉｚａｔｉｏｎ ｂｙ ａ ｃｏｌｏｎｙ ｏｆ ｃｏｏｐｅｒａｔｉｎｇ ａｇｅｎｔｓ［Ｊ｜］．ＩＥＥＥ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｓｙｓｔｅｍｓ Ｍａｎ ａｎｄ Ｃｙｂｅｒｎｅｔｉｃｓ Ｐａｒｔ Ｂ，１９９６，２６（１）：２９—４１． ［２３ Ｄｏｒｉｇｏ Ｍ，Ｇａｍ ｂａｒｄｅｉｌａ Ｌ Ｍ．Ａｎｔ ｃｏｌｏｎｙ ｓｙｓｔｅｍ：Ａ ｃｏｏｐｅｒａｔｉｖｅ ｌｅａｒｎｉｎｇ ａｐｐ ｒｏａｃｈ ｔｏ ｔｈｅ ｔｒａｖｅｌｉｎｇ ｓａｌｅｓｍａｎ ｐｒｏｂｌｅｍ［Ｊ］．ＩＥＥＥ Ｔｒａｎｓ． ｏｎ Ｅｖｏｌｕｔｉｏｎａｒｙ Ｃｏｍｐｕｔａｔｉｏｎ，１９９７，１（１）：５３ ６６． ［３］ 吴春明，陈治，姜明．蚁群算法中系统初始化及系统参数的研究［Ｊ］．电子学报，２００６，３４（８）：１５３０—１ ５３３． ［４］ 卢辉斌，贾兴伟，范庆辉．基本蚂蚁算法中参数的讨论与改进［Ｊ］．计算机工程，２００５，３１（２０）：１７５—１７９． Ｅ５］ 叶志伟，郑肇葆．蚁群算法中参数ａ、Ｂ、Ｐ设置的研究一以ＴＳＰ为例［Ｊ］．武汉大学学报：信息科学版，２００４，２９（７）：５９８—６０１． ［６］ 张煜东，吴乐南，韦耿，智能算法求解ＴＳＰ问题的比较［Ｊ］．计算机工程与应用，２００９，４５（１１）：１１－１ ５． ［７］ 朱颢东，钟勇基．于贝叶斯粗糙集的文本特征选择方法［Ｊ］．河南师范大学学报：自然科学版，２００９，３７（４）：３ｌ ３５ ［８］ 蒋玲艳，张军，钟树鸿．蚁群算法的参数分析啊Ｊ］．计算机工程与应用，２００７，４３（２０）：３１—３６．
Ａｎ Ｏｐｔｉｍｉｚｅｄ Ｓｔｒａｔｅｇｙ ｆｏｒ Ｉｔｅｒａｔｉｏｎ Ｎｕｍｂｅｒｓ ｉｎ Ａｎｔ Ｃｏｌｏｎｙ Ａｌｇｏｒｉｔｈｍ ＹＵＡＮ Ｐｅｉ—ｙａｎ ，ＬＩＵ Ｐｉｎｇ ，ＧＡＯ Ｈｏｎｇ—ｑｉｎｇ （ａ．Ｃｏｌｌｅｇｅ ｏｆ Ｐｈｙｓｉｃｓ ８乙Ｉｎｆ０ｒｍａｔｉｏｎ Ｅｎｇｉｎｅｅｒｉｎｇ，ｂ．Ｎｅｔｗｏｒｋ Ｃｅｎｔｅｒ，Ｈｅｎａｎ Ｎｏｒｍａｌ Ｕｎｉｖｅｒｓｉｔｙ，Ｘｉｎｘｉａｎｇ ４５３００７，Ｃｈｉｎａ） Ａｂｓｔｒａｃｔ：Ｔｈｉｓ ｐａｐｅｒ ｐｒｏｖｉｄｅｓ ａｎ ｏｐｔｉｍｉｚｅｄ ｓｔｒａｔｅｇｙ ｔｏ ｓｏｌｖｅ ｔｈｅ ｐｒｏｂｌｅｍ ｏｆ ｎｏｔ ｃａｌｃｕｌａｔｉｎｇ ｂｅｔｔｅｒ ａｎｓｗｅｒ ｉｎ ｔｈｅ ｌａｔｔｅｒ ｐｈａｓｅ ｏｆ ｓｉｍｕｌａｔｉｏｎ，ｔｈａｔ ｉｓ，ｗｈｅｎ ｍｕｃｈ Ｏｆ ｃｏｎｓｅｃｕｔｉｖｅ ｉｔｅｒａｔｉｏｎ ｃａｎ ｎｏｔ ｗｏｒｋ ｏｕｔ ｂｅｔｔｅｒ ａｎｓｗｅｒ，ｉｔ ｉｓ ｎｅｃｅｓｓａｒｙ ｔｏ ｄｅｃｒｅａｓｅ ｔｈｅ ｎｕｍｂｅｒ ｏｆ ｉｔｅｒａｔｉｏｎ ｉｎ ｏｒｄｅｒ ｔｏ ｓｐｅｅｄ ｕｐ ａｓｔｒｉｎｇｅｎｃｙ ｏｆ ｔｈｅ ａｌｇｏｒｉｔｈｍ．Ｔｈｅ ｓｉｍｕｌａｔｉｏｎ ｒｅｓｕｌｔｓ ｓｈｏｗ ｔｈａｔ ｔｈｅ ｏｐｔｉｍｉｚｅｄ ｓｔｒａｔｅｇｙ ｒｅｄｕｃｅｓ ｔｈｅ ｔｉｍｅ ａｎｄ ｓｐａｃｅ ｃｏｍｐｌｅｘｉｔｙ ｏｂｖｉｏｕｓｌｙ ｗｉｔｈｏｕｔ ｓａｃｒｉｆｉｃｉｎｇ ｔｈｅ ｂｅｓｔ ａｎｓｗｅｒ ａｔ ｔｈｅ ｓａｍｅ ｔｉｍｅ． Ｋｅｙ ｗｏｒｄｓ：ａｎｔ ｃｏｌｏｎｙ ａｌｇｏｒｉｔｈｍ；ｒａｎｄｏｍ ｅｎｖｉｒｏｎｍｅｎｔ；ｐｅｒｆｏｒｍａｎｃｅ ｅｖａｌｕａｔｉｏｎ；ＴＳＰ
