下载文档原格式
《完全平方公式》一、教材分析说课内容：《整式的乘除与因式分解》的《完全平方公式》。
教材的地位和作用：完全平方公式是初中数学中的重要公式，在整个中学数学中有着广泛的应用，重要的数学方法“配方法”的基础也是依据完全平方公式的。
而且它在整式乘法，因式分解，分式运算及其它代数式的变形中起作十分重要的作用。
本节内容共安排两个课时，这次说课是其中第一个课时。
完全平方公式这一教学内容是学生在已经掌握单项式乘法、多项式乘法及平方差公式基础上的拓展，教材从具体到抽象，由直观图形引导学生观察、实验、猜测、进而论证，最后建立数学模型，逐步培养学生的逻辑推理能力和建模思想。
教学目标和要求：由课标要求以及学生的情况我将三维目标定义为以下三点：知识与技能目标：了解公式的几何背景，理解并掌握公式的结构特征，能利用公式进行计算。
过程与方法目标：在学习的过程中使学生体会数、形结合的优势，进一步发展符号感和推理能力，培养学生数学建模的思想。
情感与态度目标：体验数学活动充满着探索性和创造性，并在数学活动中获得成功的体验与喜悦，树立自信心。
教学的重点与难点：根据对学生学习过程分析及课标要求我把重点定为：完全平方公式的结构特点及公式的直接运用。
而难点应为完全平方公式的应用以及对公式中字母a、b的广泛含义的理解与正确应用。
在教学过程中多处留有空白点以供学生独立研究思考。
二、教法与学法（1）多媒体辅助教学，将知识形象化、生动化，激发学生的兴趣。
（2）教学中逐步设置疑问，引导学生动手、动脑、动口，积极参与知识全过程。
（3）由易到难安排例题、练习，符合八年级学生的认知结构特点。
（4）课堂中，对学生激励为主，表扬为辅，树立其学习的自信心。
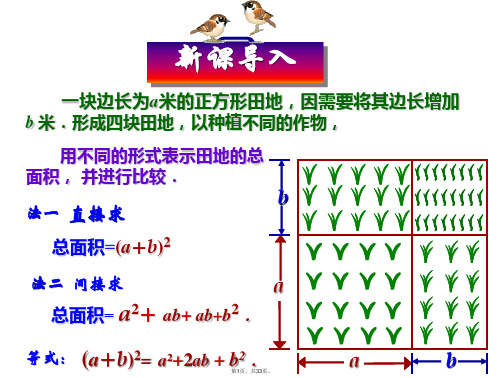
三、教学过程教师活动学生活动设计意图一、创设情景，推导公式计算103971、想一想（电脑演示）一块边长为a米的正方形实验田，因需要将其边长增加b米，形成四块实验田，以种植不同的新品种，（如图所示）（要求学生从不同的角度表示图形的面积）观察动画，学生抢答：⑴、四块实验田的面积分别为：、、、；⑵、两种形式表示实验田的总面积：复习旧知，并以问题引入。
第一课时（一） 提出问题，学生自学1．问题：根据乘方的定义，我们知道：a 2=a ·a ，那么（a+b ）2 应该写成什么样的形式呢？（a+b ）2的运算结果有什么规律？计算下列各式，你能发现什么规律？（1）（p+1）2=（p+1）（p+1）=_______； （m+2）2=_______；（2）（p-1）2=（p-1）（p-1）=________； （m-2）2=_______；2．学生探究【1】3．得到结果：（1）（p+1）2=（p+1）（p+1）=p 2+2p+1（m+2）2=（m+2）（m+2）= m 2+4m+4（2）（p-1）2=（p-1）（p-1）= p 2-2p+1（m-2）2=（m-2）（m-2=m 2-4m+44．分析推广：结果中有两个数的平方和，而2p=2·p ·1，4m=2·m ·2，恰好是两个数乘积的二倍。
（1）（2）之间只差一个符号。
推广：计算（a+b ）2=_____ ___ （a-b ）2=_____ ___ 【2】（二） 得到公式，分析公式1．结论： (a+b)2=a 2+2ab+b 2 (a-b)2=a 2-2ab+b 2 即：两数和（或差）的平方，等于它们的平方和，加（或减）它们的积的2倍． 2.几何分析：【3】图（1），可以看出大正方形的边长是a+b ，它是由两个小正方形和两个矩形组成，•所以大正方形的面积等于这四个图形的面积之和．【4】（三） 运用公式1． 直接运用【1】例：应用完全平方公式计算：（1）（4m+n ）2 （2）（y-12）2 （3）（-a-b ）2 （4）（b-a ）2 练习：P110 练习1，22． 简便计算【2】例：运用完全平方公式计算：（1）1022 （2）992练习：计算： 50.012 49.92附加练习：计算： 2)4(y x - 222)43(c ab b a - -x 5( ）2= 4210y xy +- )3)(3(b a b a --+ 2)1(x x + 2)1(xx - 在下列多项式中，哪些是由完全平方公式得来的？442+-x x 2161a + 12-x 22y xy x ++ 224139y xy x +-（四）小结完：全平方公式的结构特征．公式的左边是一个二项式的完全平方；右边是三项，其中有两项是左边二项式中每一项的平方．而另一项是左边二项式中两项乘积的2倍第二课时：（添括号法则在公式里的运用）（一） 回顾完全平方公式(a+b)2=a 2+2ab+b 2 (a-b)2=a 2-2ab+b 2（二） 提出问题，解决问题1． 在运用公式的时候，有些时候我们需要把一个多项式看作一个整体，把另外一个多项式看作另外一个整体。
