高数积分公式大全6

高等数学微积分公式大全一、基本导数公式⑴ c0 ⑵ x x 1⑶sin x cos x⑷ cos x sin x ⑸ tan x sec2x ⑹ cot x csc2 x⑺ secx sec x tan x ⑻ csc x csc x cot x⑼ e x e x⑽ a x a x ln a ⑾ ln x1x⑿ log a x1⒀ arcsin x1⒁ arccos x1x ln a1x2 1 x2⒂ arctanx12⒃ arccot x12⒄ x1⒅x11x 1 x2x二、导数的四则运算法例三、高阶导数的运算法例（1）u x v x nn v xn（2）cu x n cu n x u x（3）u ax b n ax b （4） u x v x n nc n k u n k x v(k ) xa n u nk 0四、基本初等函数的n 阶导数公式（1）x nnn! （） e ax b n(3)a x nax n n a2(4) (6)sin n a n sin ax b n(5)cos ax b nax b a n cos ax b n221n n a n n!n n 1 a n n 1 !1(7)ln ax bax axn 11axnb b b五、微分公式与微分运算法例⑴ d c 0 ⑵ d x x1 dx ⑶ d sin x cos xdx⑷ d cosx sin xdx ⑸ d tan x sec2 xdx ⑹ d cot x csc2 xdx ⑺ d secx secx tan xdx ⑻ d cscx cscx cot xdx⑼ d e x e x dx ⑽ d a x a x ln adx ⑾d ln x 1 dxx⑿⒂d log a x1dx⒀ d arcsin x11dx ⒁ d arccos x1dx x ln a x21x2d arctan x1dx ⒃ d arccot x1dx1x212x六、微分运算法例⑴ d u v du dv⑵ d cu cdu⑶ d uv vdu udv u vdu udv⑷ dv2v七、基本积分公式⑴kdx kx c ⑵x dx x 1 c ⑶dxln x c1x⑷a x dx a x c ⑸e x dx e x c ⑹ cosxdx sin x cln a⑺⑼sin xdx cosx c ⑻1dx sec2xdx tan x ccos2x1csc2 xdx cot x c ⑽1dx arctan x c sin 2 x1x2⑾1dx arcsin x c1x2八、增补积分公式九、以下常用凑微分公式积分型换元公式十、分部积分法公式⑴形如x n e ax dx ，令u x n， dv e ax dx 形如x n sin xdx 令u x n，dv sin xdx 形如x n cosxdx 令u x n，dv cosxdx⑵形如x narctan，令 u arctanx ，dvndx xdx x形如 x n ln xdx，令u ln x ，dv x n dx⑶形如 e ax sin xdx ，e ax cosxdx 令u e ax ,sin x,cos x 均可。

高等数学微积分公式大全一、基本导数公式⑴()0c '= ⑵1x xμμμ-= ⑶()sin cos x x '=⑷()cos sin x x '=- ⑸()2tan sec x x '= ⑹()2cot csc x x '=- ⑺()sec sec tan x x x '=⋅ ⑻()csc csc cot x x x '=-⋅⑼()xxee'= ⑽()ln xxaaa '= ⑾()1ln x x'=⑿()1log ln xax a'= ⒀()arcsin x '= ⒁()arccos x '=⒂()21arctan 1x x '=+ ⒃()21arccot 1x x '=-+⒄()1x '=⒅'=二、导数的四则运算法则()u v u v '''±=± ()uv u v uv '''=+ 2u u v uv v v '''-⎛⎫= ⎪⎝⎭三、高阶导数的运算法则 (1）()()()()()()()n n n u x v x u x v x ±=±⎡⎤⎣⎦ （2）()()()()n n cu x cu x =⎡⎤⎣⎦（3）()()()()n n nu ax b a uax b +=+⎡⎤⎣⎦（4）()()()()()()()0nn n k k k n k u x v x c u x v x -=⋅=⎡⎤⎣⎦∑ 四、基本初等函数的n 阶导数公式 (1）()()!n nxn = （2)()()n ax b n ax b e a e ++=⋅ （3)()()ln n x x n a a a =（4）()()sin sin 2n n ax b a ax b n π⎛⎫+=++⋅⎡⎤ ⎪⎣⎦⎝⎭ （5) ()()cos cos 2n nax b a ax b n π⎛⎫+=++⋅⎡⎤ ⎪⎣⎦⎝⎭ (6)()()()11!1n n nn a n ax b ax b +⋅⎛⎫=- ⎪+⎝⎭+ (7） ()()()()()11!ln 1n n n na n axb ax b -⋅-+=-⎡⎤⎣⎦+五、微分公式与微分运算法则 ⑴()0d c = ⑵()1d xxdx μμμ-= ⑶()sin cos d x xdx =⑷()cos sin d x xdx =- ⑸()2tan sec d x xdx = ⑹()2cot csc d x xdx =- ⑺()sec sec tan d x x xdx =⋅ ⑻()csc csc cot d x x xdx =-⋅ ⑼()xxd ee dx = ⑽()ln xxd a aadx = ⑾()1ln d x dx x=⑿()1log ln xad dx x a= ⒀()arcsin d x = ⒁()arccos d x =⒂()21arctan 1d x dx x =+ ⒃()21arccot 1d x dx x =-+ 六、微分运算法则⑴()d u v du dv ±=± ⑵()d cu cdu = ⑶()d uv vdu udv =+ ⑷2u vdu udvd v v -⎛⎫= ⎪⎝⎭七、基本积分公式⑴kdx kx c =+⎰⑸x x e dx e c =+⎰ ⑹cos sin xdx x c =+⎰ ⑺sin cos xdx x c =-+⎰⑻221sec tan cos dx xdx x c x ==+⎰⎰ ⑼221csc cot sin xdx x c x ==-+⎰⎰ ⑽21arctan 1dx x c x=++⎰ ⑾arcsin x c =+八、补充积分公式2211arctan xdx c a x a a=++⎰ 2211ln 2x adx c x a a x a-=+-+⎰arcsinxc a=+ ln x c =+九、下列常用凑微分公式十、分部积分法公式⑴形如n ax x e dx ⎰,令nu x =，axdv e dx =形如sin n x xdx ⎰令nu x =,sin dv xdx =形如cos n x xdx ⎰令nu x =,cos dv xdx = ⑵形如arctan n x xdx ⎰，令arctan u x =，ndv x dx =形如ln n x xdx ⎰，令ln u x =，ndv x dx =⑶形如sin ax e xdx ⎰，cos ax e xdx ⎰令,sin ,cos axu e x x =均可.十一、第二换元积分法中的三角换元公式(1 sin x a t = (2） tan x a t = sec x a t =【特殊角的三角函数值】（1）sin 00= (2）1sin62π=(3）sin 32π= (4)sin 12π=) (5）sin 0π=（1）cos01= （2）cos62π=（3）1cos 32π= (4）cos 02π=） （5）cos 1π=-（1)tan 00= （2）tan63π=（3)tan 3π=(4）tan 2π不存在 （5）tan 0π=（1）cot 0不存在 （2)cot 6π=（3)cot3π=(4)cot 02π=（5）cot π不存在 十二、重要公式（1）0sin lim1x xx→= （2）()10lim 1x x x e →+= (3))1n a o >=（4）1n = (5)limarctan 2x x π→∞=（6)lim tan 2x arc x π→-∞=-（7）limarccot 0x x →∞= （8）lim arccot x x π→-∞= （9）lim 0xx e →-∞=（10)lim x x e →+∞=∞ （11）0lim 1xx x +→= (12）0101101lim0n n n m m x m a n mb a x a x a n m b x b x b n m--→∞⎧=⎪⎪+++⎪=<⎨+++⎪∞>⎪⎪⎩（系数不为0的情况） 十三、下列常用等价无穷小关系（0x →）sin x x tan x x arcsin x x arctan xx 211cos 2xx - ()ln 1x x + 1x e x - 1ln x a x a - ()11x x ∂+-∂十四、三角函数公式 1.两角和公式sin()sin cos cos sin A B A B A B +=+ sin()sin cos cos sin A B A B A B -=- cos()cos cos sin sin A B A B A B +=- cos()cos cos sin sin A B A B A B -=+tan tan tan()1tan tan A B A B A B ++=- tan tan tan()1tan tan A BA B A B --=+cot cot 1cot()cot cot A B A B B A ⋅-+=+ cot cot 1cot()cot cot A B A B B A ⋅+-=- 2.二倍角公式sin 22sin cos A A A = 2222cos 2cos sin 12sin 2cos 1A A A A A =-=-=-22tan tan 21tan AA A=-3。

高数定积分公式大全在高等数学中，定积分是通过积分来求解某一特定函数的不定积分的一种特殊方法，是计算物理量变化，寻找函数极值点以及在区间内求定积分的有效工具。

定积分的定义如下：如果函数f(x)在给定区间[a,b]上可导，那么定积分的定义为：∫a^bf(x)dx = F(b) - F(a)其中F(x)是f(x)的某个不定积分，解析法求解定积分的步骤为：首先将函数f(x)分解为常数、x、x^2、x^n多项式，其次对于每一项分别求解其不定积分，最后再将每一项求得的不定积分相加，即可得出整体定积分的解析解。

定积分中常见的公式有：一、定积分中的基本公式1. 不定积分的基本公式：∫x^ndx = 1/n+1*x^n+1 + C2. 二次方程不定积分的公式：∫x^2dx = 1/3*x^3 + C3.用的其他不定积分的公式：(1)∫sinx dx = -cosx + C(2)∫cosx dx = sinx + C(3)∫1/(1+x^2)dx = arctanx + C(4)∫lnx dx = xlnx - x + C二、高阶定积分的公式1. 一阶定积分：∫ax+b dx = 1/a*(ax+b) + C2. 二阶定积分：∫ax^2 + bx + c dx = 1/3a*x^3 + 1/2b*x^2 + cx + C3.用的其他高阶定积分的公式：(1)∫sinax dx = -1/a*cosax + C(2)∫e^x dx = e^x + C(3)∫lnax dx = xlnax - x + C三、复合定积分的公式定积分可以复合求解，以求解复合定积分为例，复合定积分公式为：∫a^b f(x)dx =a^x f(x)dx +x^b f(x)dx其中f(x)为一个标量函数，[a,b]为被积函数的定积区间，求解步骤如下：1.根据f(x)的表达式求出该函数的不定积分F1(x)；2.复合定积分拆分成两部分，先求∫a^x f(x)dx，即F1(x)的定积分，再求∫x^b f(x)dx，即F2(x)的定积分；3.后将两部分求得的结果相加，即可得出复合定积分的解析解，解析解为F1(b) - F1(a) + F2(b) - F2(a)。

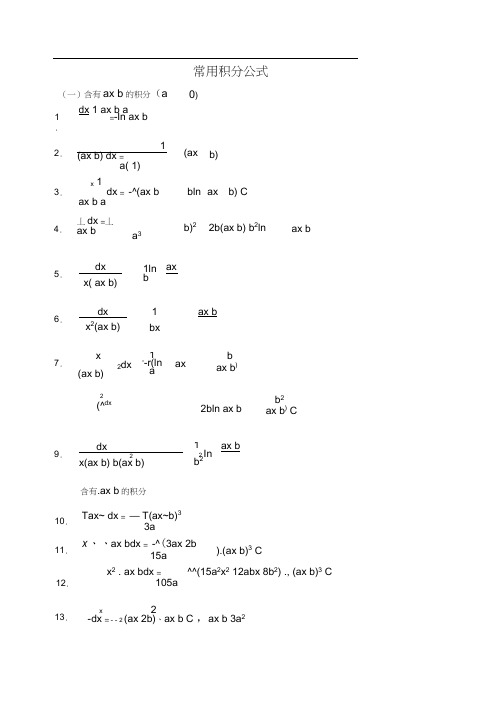
12.（一）含有ax b 的积分（a 1. dx 1 ax b a =-In ax b 2. 3. 4. 5. 6. 7.9. 10.11. 13. 常用积分公式0)1 (ax b) dx = a( 1) x 1 dx = -^(ax b ax b a 丄dx =丄ax ba 3(ax bln b)2 b)ax b) C 2b(ax b) b 2lnax bdx x( ax b) dx x 2(ax b) x 2dx (ax b)2(^dx1ln b 1 bxax ax b1=-r(ln aax bax b )2bln ax b b 2 ax b ) Cdx 2x(ax b) b(ax b)含有.ax b 的积分12In b 2ax bTax~ dx = — T(ax~b)3 3a x 、、ax bdx = -^(3ax 2b15ax 2 . ax bdx = ^^(15a 2x 2 12abx 8b 2) ., (ax b)3 C105a).(ax b)3 Cx2- d x = -- 2 (ax 2b)、ax b C ，ax b 3a 2215a 3dx x ¥ ax b dx x 21 ax bax b. dx = (3a 2x 2 4abx 8b 2)、、ax b■, ax b 、.； b .ax b.b AC (b(b 0)0)bx 2b x 丫 ax b2 ax bdx x, ax bax b ,2 dx =xa dx 2 x 、ax b14.15.16.17.18.(三)19.20.21 .(四)22.23.含有x 2 a 2的积分dx 1 x arcta n—C22 _xa a adxx2n 3 dx (x2a 2) n= 「2(n 1)a 2/22、n 1(x a )2( n 1)a 222 n 1(x a )dx~22 =x a含有ax 2 b(a 0)的积分dx ax 2 b~^= arcta n j ax C Vbax b2TZ ln(b 0) C (b 0)x2ax -dx b2aax 2 -In 2a2 34.24. x 2—- ax b dx ax 2 b25. dx x(ax 2 b) In 2b 2x 2~ ax26. dx x 2(ax 2 b) 1 bx27.dx3a l 3 2 2lnx 3(ax 2 b)2b 228. dx 2 2(ax b)29.30. (六) 31. 32. 33. dx ~2- ax2ax b2x2b(ax 2 b) 12bdx ax 2 b含有ax 2bx dx ax 2 bx cx dx ax bx c 含有■. x 2dx dx.(x 2 a 2)x7x 2" c(a 0)的积分-=2 2 arctan —2ax b _ C ■. 4ac b 、4ac ba 2 (a 丄 ln ax 2a arsh- a—dx = 2 a1dx = ----- = C/ 2 2■ x a2 ax b J b 24ac 2 ax b J b 2 4ac C b .b 2 4ac(b 2 4ac)2(b 4ac)2 bx c 0)的积分 dx ___ 2a ax 2 bx c C 1 = ln(x 、.x 2 a 2) C ■. x 2 a 2 C22—x _____ dx =7^ d,(x a )ln( x \ x 2 a 2)dx 2 2 x x a2 2x a 」 dx =xdx "x^O 2xarch 凶 aG =ln xdxx :=a 2 dx =\ x 2 a 2dx35.36.37.38.39.40.41 .42.43.44.(七)45.46.47.dxx i x 2 a 2 lln aX '. x 2 a 2dx = 、 x dx = (2x8 1 J( 3 5a 2)、.x 2X 2 X 2 a2dx = 8(2x ln( x . x 2 a 2) C 4a ln(x 8、.x 2 a 2) C2 2x a 」2 dx = x x 2 a 2ln(x、x 2 a 2)含有\ x 2a 2 (a 0)的积分—22.x a2 a xa 2)■- x 2 a 2___ x a 2 x 2.(x 2 a 2)32 ~~2, x 2x x a dx =(2x 8 aa arccos —xIn x含有、•.a 2 x 2(a 0)的积分=arcs in 仝 Cadxxx 」1dx =CJ\3I 22a ) x a2 x 2 2 x a 2r a a ln2 2 x . dx =2 2、3 x a ) x . ln2 2x a1=—arccosx 、x * 2 a 2 a dx x 2adx x 2 x^? 2 2x a 2a xC In 2 2x x a48.49.50.51 .52.53.54. 55.56.57.58.(八)59.60.4—ln 8x2a x■- x 2 2 adx =x22a . x arcs in C 2 aarcsin - C a,(a /x 2)3dxdx x 、a 2 x 2 dx x 2、a 2 x 2 lln a 心 x 2 a2 2.a x 2 a x 2a . x arcsin3a 4arcs in 仝 C8~ x = x ~x 2X 2 Ldx =評X 2 / 2 2 ax, 2 2----------- dx = '. a x _2 2 ~2 2 a x a x 2 ----dx =—x2、 2 2a ) .a x4a . x arcs in 8 aa Ina a 2 x 2 QCxarcsin 一 Ca含有i ax 2 bx c (a 0)的积分 dx 1 2= = ln 2ax b Vaxbx c 7a61.62.63.64.65.66.67.68. 69.70.71 .72. (九) 73.= 2 ax b —2=cdx = ----------- ：,ax bx c4a（十一）含有三角函数的积分82.C (a b)74.ax bx75.x ax 2 bxdx =76.dx c bx ax 277.、、c bx ax2dx4ac b 2 8 . a 3In 2ax b 2石 bxc C1Jax 2bx c a— In 2ax b 2梟罷 2府1 2 ax b —i= arcsi n = C ■ a . b 4ac2ax b - ’ 2c bx ax 4ax 2 bx cb 2 4ac . 2ax barcs inC8 . a 3 b 2 4ac78..xdx = Sc bx ax 2—空 arcsin —2ax —b — C.c bx ax 2a2 . a 3b 2 4acJ x b) Cb)F (b 加® F C=2arcsi n_a C (a b) x a)(b x)1b x(x a)(b x)的积分b 后（b曲79.83. sin xdx = cosx Ccosxdx = sinx Ccot xdx = ln si nx C sec xdx = ln ta n(- -) C 4 2 csc xdx = ln tan — C =ln2sec xdx = tan x Ccsc 2 xdx = cotx CC In cosx tan xdx = =In secx tanx cscx secx tan xdx = secx C csc x cot xdx = cscx 2x 1sin xdx = — 一 sin 2x 2 42」x 1cos xdx = sin2x 2 4n1 n 1 sin xdx = sin xcosx n n | 1 n 1 .cos xdx = cos xsinx n 1 cosx n 1n 1 sin x 1 sin x dx n sin x dxn 丄n 1cos x n 1 cos x m . n | 1cos xsin xdx = m cotx Cn 2sin xdx cos n 2 xdx dx__^"2~sin x dx彳 n 2 n 1 cos x m 1 . n 1 m 1 — cos xsi n x --------------n m n 1 m 1 . n 1 n cos xsi n x m cosm n m n 2. n .xsin xdxm ・ n 2.cos xsin xdx sin ax cosbxdx =cos(a b)xcos(a b)x C2(a b)2(a b)84. 85. 86.87.88.89. 90. 91. 92.93. 94.95. 96. 97.98. 99.100.1sin ax sin bxdx = sin(a b)x2( a b)1cosax cosbxdx = sin(a b)x(a b)dx a bsinx2a2ata n?=arcta n2b2；a2b2dx a bsinx =2l nadx a bcosx1sin (a b)x C2(a b)1sin(a b)x2(a b)b2)atan兰b 4b~a22 ___________atan^ b 4b~a22dxb a bcosxdxa2 cos2 x b2 sin2 x ______ dxa2 cos2 x b2 sin2 x(a2b2)(a2b2)CC1 arctan(— tan x)ab aab丄ln2abxsin axdx = $sin axa2 1 2x sin axdx = x cosaxax cosaxdx = $ cosaxa1x cosaxdx = x sin axa含有反三角函数的积分(其中(abta nx abta nx a1-x cos ax C a2 .2 xs in axa1 . xsi n axa22 xcosaxaa 0)arcsin x dx = xarcsin 仝Ca a23 cosaxa2 .3 sin ax C a101. 102. 103. 104. 105. 106. 107. 10 8. 109.110. 111.112. (十二) 113.X2• X, /X xarcs in dx =(—22X. /X x arccos-dx =(— a 2arctan — dx = x arcta n — a114.115.116.117.118.119. 120.121.(十三)122. 123. 124. 125. 126.127.12 8. 129.x 2arcsin ^dx a 3x . x =—arcs in 3 1 / 29(x2a 2)\ a 2x 2arccos xdx = axx arccos-ax 2arccos —dx a3x =—arc cos —3 a 1(x 2 2a 2). ax 2xarctan x dx = - (a 2 a 2 x 2 )arcta nax C23 x 2 arctan dx = arctan —a 3 x 2)含有指数函数的积分 1 a X dx = ----- a x C In a ax 1 ax e dx = e C a xe dx = 2 (ax a n ax 1 n ax x e dx = x e a ax1)e1 ax .e dx x x xxa dx = aIn a 2a(ln a)n x 1 nx a dx = x In aIn a n 1 x . x a dx e ax s in bxdx =— a e ax(as inbx bcosbx)e ax cosbxdx = b 2 2 -_ e ax (bsinbx acosbx) a b 2a . x)arcsin 4 a x -a x C 42a x)arccos 一 4 a al n(a 2a 2x 2) C144.130. e ax s in nbxdx1ax . n 1ea bnsin bx(a s inbx nbcosbx)131. ax n e cos bxdx =2n(n 1)bb 2n 2ax . n 2 e sin bxdx axbV en cos 1bx(a cosbx nbsin bx)2n(n 1)b ax e cos n 2bxdx 132. In xdx = xlnxx Cdx ,133. -lnln xCxln xn -1n 1八1134. x ln xdx -x (ln x n 1n135. (ln x)n dx - x(ln x)n n (ln x)136. x m(ln x)nd: x -1 mx 1(ln x)r含有对数函数的积分（十四） nm2 .22 1)C1dxmx (lnm 1x)n 1dx （十五）含有双曲函数的积分137.shxdx - chx C13 8. chxdx - shx C139. thxdx - lnchx :C 140. sh 2xdx -- 2 1sh2x C4141.2 x ch xdx -— 2 1 sh2x C4（十六）定积分142.cosnxdx -sin nxdx -0, m cos mxcos nxdx =143 .0 cosmxsin nxdx = 0144.= —C145.sin mxsin nxdx =0, m n146.—,m n20, m nsin mxsin nxdx =cosmxcos nxdx =0 2n = 2nxdx22cos nxdxn 0n 1 In -12nn 1 n 3L 4 2/ 一 亠厶 _4-- ~r\ 4 r^rAr 来、n— n 为大于1旳止可数），I 1 -1 n n 2 5 3 n 1 n 3 3 1（n 为正偶数），I 0 -nL -nn 24 2 22147.2x a b / —、(b a)2x a)(b x)dx =--------------------- 乂x a)(b x) arcsin4 4。

高数不定积分24个基本公式高数不定积分24个基本公式是数学学科中的重要内容。

这些基本公式涉及到多种函数的不定积分，如多项式函数、指数函数、对数函数、三角函数等。

这些公式可以方便地帮助我们求得复杂函数的不定积分。

其中一些基本公式包括：1.$\int x^n dx=\frac{1}{n+1}x^{n+1}+C$2.$\int\frac{1}{x}dx=\ln|x|+C$3.$\int e^x dx=e^x+C$4.$\int\frac{1}{1+x^2}dx=\arctan x+C$5.$\int\cos x dx=\sin x+C$6.$\int\sin x dx=-\cos x+C$7.$\int\sec^2x dx=\tan x+C$8.$\int\csc^2x dx=-\cot x+C$9.$\int\frac{1}{\sqrt{1-x^2}}dx=\arcsin x+C$10.$\int\frac{1}{\sqrt{x^2+1}}dx=\ln|x+\sqrt{x^2+1}|+C$11.$\int\ln x dx=x\ln x-x+C$12.$\int e^{ax}\cos bx dx=\frac{e^{ax}}{a^2+b^2}(a\cos bx+b\sin bx)+C$13.$\int e^{ax}\sin bx dx=\frac{e^{ax}}{a^2+b^2}(a\sin bx-b\cos bx)+C$14.$\int\frac{1}{\sqrt{a^2-x^2}}dx=\arcsin\frac{x}{a}+C$15.$\int\frac{1}{\sqrt{x^2-a^2}}dx=\ln|x+\sqrt{x^2-a^2}|+C$16.$\int\frac{1}{a^2+x^2}dx=\frac{1}{a}\arctan\frac{x}{a}+C$17.$\int\frac{1}{a^2-x^2}dx=\frac{1}{2a}\ln\frac{a+x}{a-x}+C$18.$\int\frac{1}{x^2-a^2}dx=\frac{1}{2a}\ln\frac{a+x}{a-x}+C$19.$\int\frac{1}{\cos^2x}dx=\tan x+C$20.$\int\frac{1}{\sin^2x}dx=-\cot x+C$21.$\int\frac{x}{\sqrt{a^2+x^2}}dx=\sqrt{a^2+x^2}-a\ln\left|x+\sqrt{a^2+x^2}\right|+C$22.$\int x\sin ax dx=-\frac{1}{a}x\cosax+\frac{1}{a^2}\sin ax+C$23.$\int x\cos ax dx=\frac{1}{a}x\sinax+\frac{1}{a^2}\cos ax+C$24.$\int\frac{1}{\sqrt{x^2+a^2}}dx=\ln|x+\sqrt{x^2+a^2}|+C$这24个基本公式对于高数学科的学习非常重要，我们可以通过多次练习和应用，熟练地掌握这些公式，提高自己在高数学科中的成绩和水平。

高等数学微积分公式大全一、基本导数公式 ⑴1x xμμμ-= (2)()sin cos x x '= （3）()cos sin x x '=-(4)()2tan sec x x '=(5)()1ln x x'=(6)()2cot csc x x '=- (7)()sec sec tan x x x '=⋅(8)()csc csc cot x x x '=-⋅ (9)()ln x x a a a '= (10)()1log ln x a x a '=(11)()arcsin x '=(12)()arccos x '=(13)()21arctan 1x x '=+ (14)()21arccot 1x x '=-+(15)'=二、微分公式与微分运算法那么⑴()0d c =⑵()1d x x dx μμμ-=⑶()sin cos d x xdx =⑷()cos sin d x xdx =-⑸()2tan sec d x xdx =⑹()2cot csc d x xdx =-⑺()sec sec tan d x x xdx =⋅⑻()csc csc cot d x x xdx =-⋅ ⑼()x x d e e dx =⑽()ln x x d a a adx =⑾()1ln d x dx x= ⑿()1log ln xad dx x a =⒀()arcsin d x dx =⒁()arccos d x = ⒂()21arctan 1d x dx x =+⒃()21arccot 1d x dx x=-+ 三、基本积分公式⑴kdx kx c =+⎰⑵11x x dx c μμμ+=++⎰⑶ln dxx c x=+⎰ ⑷ln xxa a dx c a=+⎰⑸x x e dx e c =+⎰⑹cos sin xdx x c =+⎰ ⑺sin cos xdx x c =-+⎰⑻221sec tan cos dx xdx x c x ==+⎰⎰ ⑼221csc cot sin xdx x c x ==-+⎰⎰⑽21arctan 1dx x c x =++⎰⑾arcsin x c =+四、补充积分公式tan ln cos xdx x c =-+⎰cot ln sin xdx x c =+⎰sec ln sec tan xdx x x c =++⎰csc ln csc cot xdx x x c =-+⎰2211arctan xdx c a x a a=++⎰2211ln 2x a dx c x a a x a -=+-+⎰arcsinxc a=+ln x c =++⎰六、分部积分法公式⑴形如n ax x e dx ⎰，令n u x =，axdv e dx =形如sin n x xdx ⎰令nu x =，sin dv xdx =形如cos n x xdx ⎰令nu x =，cos dv xdx =⑵形如arctan n x xdx ⎰，令arctan u x =，ndv x dx =形如ln nx xdx ⎰，令ln u x =，ndv x dx =⑶形如sin ax e xdx ⎰，cos axe xdx ⎰令,sin ,cos axu e x x =均可。

高数常用微积分公式24个为了更好地帮助大家理解高等数学中的微积分，本文主要介绍高数常用的微积分公式24个。

首先，介绍最基本的微积分概念。

微积分是一个广义的概念，它包括微分学和积分学。

微分学是研究变动数量的变化率，变量可以表达为函数。

积分学则是将某一函数在不同区域上的积分和运算，可以表示为面积、重量或其他距离变化的概念。

其次，介绍高数常用的微积分公式。

1、微分中的基本公式：（1）函数的定义域x的导数，表示为f′(x)（2）复合函数的导数，表示为f′(g(x))（3）二阶导数的定义，表示为f″(x)2、积分中的基本公式：（1）求解定积分，表示为∫[a, b]f(x)dx（2）定积分的换折叠公式，表示为∫[a, b]f(x)dx=[a,c]f(x)dx+[c, b]f(x)dx（3）求解不定积分，表示为∫f（4）二重积分的定义，表示为∫[a, b]∫[c, d]f(x,y)dydx （5）定义域积分，表示为∫[S]f(x,y)ds3、微分与积分的关系：微分与积分有着相互联系的关系。

积分是将函数某一段区间的值累积为某一量，而微分则是积分的反过程，求出函数在有限的区间内的变化率。

这一关系也被称为微分法和积分法的反射关系。

4、偏微分的基本公式：偏微分是指关于同一变量的偏导数。

它是微分中比较复杂的一种形式，通常与多元函数相关，旨在研究函数变化率在同一点上受其他变量影响的情况。

它的基本公式为f′(x, y)=f/x, f′(x, y)=f/y。

5、常见的微分与积分公式：（1）指数函数的求导公式，表示为f′(x)=ae^(ax)（2）对数函数的求导公式，表示为f′(x)=1/x（3）三角函数的求导公式，表示为f′(x)=cos(x),f′(x)=sin(x)（4）椭圆函数的求导公式，表示为f′(x)=2a(a+bx)/(b^2-a^2)（5）反椭圆函数的求导公式，表示为f′(x)=-2a(a+bx)/(b^2-a^2)（6）求极限的求导公式，表示为limX→0f′(x)=f(0)（7）求微积分的积分公式，表示为∫[a,b]f(x)=F(b)-F(a)最后，本文介绍了高数常用的微积分公式24个，包括微分、积分、偏微分以及极限的求导公式，利用这些公式，大家就可以更好地理解微积分的概念，从而更好地学习高等数学中的微积分内容。

微积分公式D x sin x=cos x cos x = -sin x tan x = sec 2 x cot x = -csc 2 x sec x = sec x tan x csc x = -csc x cot x⎰ sin x dx = -cos x + C ⎰ cos x dx = sin x + C ⎰ tan x dx = ln |sec x | + C ⎰ cot x dx = ln |sin x | + C⎰ sec x dx = ln |sec x + tan x | + C ⎰ csc x dx = ln |csc x – cot x | + C sin -1(-x) = -sin -1 x cos -1(-x) = π - cos -1 x tan -1(-x) = -tan -1 x cot -1(-x) = π - cot -1 x sec -1(-x) = π - sec -1 x csc -1(-x) = - csc -1 xD x sin -1 (a x )= 221xa -±cos -1 (a x)=tan -1 (a x )=22x a a +±cot -1 (ax )=sec -1 (a x )=22a x x a-±csc -1 (x/a)= ⎰ sin -1 x dx = x sin -1 x+21x -+C ⎰ cos -1 x dx = x cos -1 x-21x -+C ⎰ tan -1 x dx = x tan -1 x-½ln (1+x 2)+C ⎰ cot -1 x dx = x cot -1 x+½ln (1+x 2)+C ⎰ sec -1 x dx = x sec -1 x- ln |x+12-x |+C⎰ csc -1 x dx = x csc -1 x+ ln |x+12-x |+Csinh -1 (a x)= ln (x+22x a +) x ∈Rcosh -1 (a x)=ln (x+22a x -) x ≧1tanh -1 (a x )=a 21ln (xa xa -+) |x| <1coth -1 (a x )=a 21ln (a x a x -+) |x| >1 sech -1(a x )=ln(x 1-+221xx -)0≦x ≦1 csch -1(a x )=ln(x 1+221xx +) |x| >0 D x sinh x = cosh xcosh x = sinh xtanh x = sech 2 x coth x = -csch 2 x sech x = -sech x tanh x csch x = -csch x coth x ⎰ sinh x dx = cosh x + C ⎰ cosh x dx = sinh x + C⎰ tanh x dx = ln | cosh x |+ C ⎰ coth x dx = ln | sinh x | + C ⎰ sech x dx = -2tan -1 (e -x ) + C ⎰ csch x dx = 2 ln |xxee 211---+| + Cd uv = u d v + v d u⎰ d uv = uv = ⎰ u d v + ⎰ v d u →⎰ u d v = uv - ⎰ v d u cos 2θ-sin 2θ=cos2θ cos 2θ+ sin 2θ=1 cosh 2θ-sinh 2θ=1cosh 2θ+sinh 2θ=cosh2θD x sinh -1(a x )= 221xa + cosh -1(ax)=221ax - tanh -1(a x )= 22x a a -±coth -1(ax )=sech -1(a x )= 22x a x a --csch -1(x/a)=22xa x a +-⎰ sinh -1 x dx = x sinh -1 x-21x ++ C⎰ cosh -1 x dx = x cosh -1 x-12-x + C ⎰ tanh -1 x dx = x tanh -1 x+ ½ ln | 1-x 2|+ C⎰ coth -1 x dx = x coth -1 x- ½ ln | 1-x 2|+ C⎰ sech -1 x dx = x sech -1 x- sin -1 x + C⎰ csch -1 x dx = x csch -1 x+ sinh -1 x + Csin 3θ=3sin θ-4sin 3θ cos3θ=4cos 3θ-3cos θ →sin 3θ= ¼ (3sin θ-sin3θ) →cos 3θ=¼(3cos θ+cos3θ)sin x = j e e jxjx 2-- cos x = 2jx jx e e -+sinh x = 2x x e e -- cosh x = 2xx e e -+正弦定理:αsin a = βsin b =γsin c=2R余弦定理: a 2=b 2+c 2-2bc cos α b 2=a 2+c 2-2ac cos β c 2=a 2+b 2-2ab cos γa b cαβγ Rsin (α±β)=sin α cos β ± cos α sin β cos (α±β)=cos α cos β sin α sin β 2 sin α cos β = sin (α+β) + sin (α-β) 2 cos α sin β = sin (α+β) - sin (α-β) 2 cos α cos β = cos (α-β) + cos (α+β) 2 sin α sin β = cos (α-β) - cos (α+β)sin α + sin β = 2 sin ½(α+β) cos ½(α-β)sin α - sin β = 2 cos ½(α+β) sin ½(α-β)cos α + cos β = 2 cos ½(α+β) cos ½(α-β) cos α - cos β = -2 sin ½(α+β) sin ½(α-β)tan (α±β)=βαβαtan tan tan tan ±, cot (α±β)=βαβαcot cot cot cot ±e x=1+x+!22x +!33x +…+!n x n+ …sin x = x-!33x +!55x -!77x +…+)!12()1(12+-+n x n n + …cos x = 1-!22x +!44x -!66x +…+)!2()1(2n x nn -+ …ln (1+x) = x-22x +33x -44x +…+)!1()1(1+-+n x n n + …tan -1x = x-33x +55x -77x +…+)12()1(12+-+n x n n + …(1+x)r=1+r x+!2)1(-r r x 2+!3)2)(1(--r r r x 3+… -1<x<1 ∑=ni 11= n∑=ni i 1= ½n (n +1)∑=ni i 12=61n (n +1)(2n +1) ∑=ni i13= [½n (n +1)]2Γ(x) = ⎰∞t x-1e -t d t = 2⎰∞t 2x-12t e -d t =⎰∞)1(ln tx-1 d t β(m , n ) =⎰10x m -1(1-x)n -1 d x =2⎰20sin π2m -1x cos 2n -1x d x =⎰∞+-+01)1(nm m x x d x 希腊字母 (Greek Alphabets)大写小写读音 大写 小写读音 大写 小写读音 Α α alpha Ι ι iota Ρ ρrhoΒ β beta Κ κ kappa Σ σ, ς sigmaΓ γ gamma Λ λ lambda Τ τtau Δ δ delta Μ μ mu Υ υ upsilonΕ ε epsilon Ν ν nu Φ φphi Ζ ζ zeta Ξ ξ xi Χ χkhi Η η eta Ο ο omicron Ψ ψpsi ΘθthetaΠπpiΩω omega倒数关系: sin θcsc θ=1; tan θcot θ=1; cos θsec θ=1 商数关系: tan θ=θθcos sin ; cot θ= θθsin cos 平方关系: cos 2θ+ sin 2θ=1; tan 2θ+ 1= sec 2θ; 1+ cot 2θ= csc 2θ順位低順位高; ⎰ 顺位高d 顺位低 ;0*∞ =∞1 *∞ = ∞∞ = 0*01 = 0000 = )(0-∞e ; 0∞ = ∞⋅0e ; ∞1 = ∞⋅0e顺位一: 对数; 反三角(反双曲) 顺位二: 多项函数; 幂函数 顺位三: 指数; 三角(双曲)算术平均数(Arithmetic mean) nX X X X n+++= (21)中位数(Median) 取排序后中间的那位数字 众数(Mode)次数出现最多的数值几何平均数(Geometric mean) n n X X X G ⋅⋅⋅= (21)调和平均数(Harmonic mean))1...11(1121nx x x n H +++=平均差(Average Deviatoin)nX Xni||1-∑变异数(Variance)nX Xni21)(-∑ or1)(21--∑n X Xni标准差(Standard Deviation)nX Xni21)(-∑ or1)(21--∑n X Xni分配 机率函数f (x )期望值E(x )变异数V(x )动差母函数m (t )Discrete Uniform n1 21(n +1) 121(n 2+1) tnt t e e e n --1)1(1Continuous Uniform a b -1 21(a +b ) 121(b -a )2 ta b e e atbt )(--Bernoulli p x q 1-x (x =0, 1)p pq q +pe t Binomial ⎪⎪⎭⎫ ⎝⎛x n p x q n -x npnpq(q+ pe t )nNegative Binomial ⎪⎪⎭⎫ ⎝⎛-+x x k 1p k q x pkq 2p kq k t kqe p )1(-Multinomialf (x 1, x 2, …, x m -1)= m xm x x m p p p x x x n ...!!...!!212121np inp i (1-p i )三项 (p 1e t 1+ p 2e t 2+ p 3)nGeometric pq x-1p1 2p q ttqe pe -1 Hypergeometric⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫⎝⎛--⎪⎪⎭⎫ ⎝⎛n N x n k N x k n ⎪⎭⎫ ⎝⎛N k ⎪⎭⎫ ⎝⎛--1N n N n ⎪⎭⎫ ⎝⎛N kPoissone xλλ- λ λ)1(--t e eλNormal 2)(21 21σμπσ--x eμ σ222 21 t t eσμ+Beta 11)1(),(1---βαβαx x Bβαα+2))(1(βαβααβ+++Gammax e x λαλαλ--Γ1)()( λα 2λα αλλ-⎪⎭⎫ ⎝⎛-t Exponentxeλλ-λ121λ t-λλ Chi-Squared χ2 =f (χ2)=212222)(221χχ--⎪⎭⎫⎝⎛Γen n nE(χ2)=nV(χ2)=2n2)21(n t --Weibullαβα--x e1⎪⎭⎫⎝⎛+Γ+111λαβλ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+Γ-⎪⎭⎫ ⎝⎛+Γ111222λλαλ1 000 000 000 000 000 000 000 000 1024 yotta Y1 000 000 000 000 000 000 000 1021 zetta Z 1 000 000 000 000 000 000 1018 exa E 1 000 000 000 000 000 1015 peta P 1 000 000 000 000 1012 tera T 兆 1 000 000 000 109 giga G 十亿 1 000 000 106 mega M 百万 1 000 103 kilo K 千 100 102 hecto H 百 10 101 deca D 十0.1 10-1 deci d 分，十分之一 0.01 10-2 centi c 厘（或写作「厘」），百分之一 0.001 10-3 milli m 毫，千分之一0.000 001 10-6 micro ? 微，百万分之一 0.000 000 001 10-9 nano n 奈，十亿分之一 0.000 000 000 001 10-12 pico p 皮，兆分之一0.000 000 000 000 001 10-15 femto f 飞（或作「费」），千兆分之一 0.000 000 000 000 000 001 10-18 atto a 阿 0.000 000 000 000 000 000 001 10-21 zepto z 0.000 000 000 000 000 000 000 001 10-24 yocto y。

高等数学微积分公式大全一、基本导数公式⑴()0c '= ⑵1x xμμμ-= ⑶()sin cos x x '=⑷()cos sin x x '=- ⑸()2tan sec x x '= ⑹()2cot csc x x '=- ⑺()sec sec tan x x x '=⋅ ⑻()csc csc cot x x x '=-⋅⑼()xxee'= ⑽()ln xxaaa '= ⑾()1ln x x'=⑿()1log ln xax a'= ⒀()arcsin x '= ⒁()arccos x '=⒂()21arctan 1x x '=+ ⒃()21arccot 1x x '=-+⒄()1x '=⒅'=二、导数的四则运算法则()u v u v '''±=± ()uv u v uv '''=+ 2u u v uv v v '''-⎛⎫= ⎪⎝⎭三、高阶导数的运算法则 （1）()()()()()()()n n n u x v x u x v x ±=±⎡⎤⎣⎦ （2）()()()()n n cu x cu x =⎡⎤⎣⎦（3）()()()()n n nu ax b a uax b +=+⎡⎤⎣⎦（4）()()()()()()()0nn n k k k n k u x v x c u x v x -=⋅=⎡⎤⎣⎦∑ 四、基本初等函数的n 阶导数公式 （1）()()!n nxn = （2）()()n ax b n ax b e a e ++=⋅ (3)()()ln n x x n a a a =(4)()()sin sin 2n n ax b a ax b n π⎛⎫+=++⋅⎡⎤ ⎪⎣⎦⎝⎭ (5) ()()cos cos 2n nax b a ax b n π⎛⎫+=++⋅⎡⎤ ⎪⎣⎦⎝⎭ (6)()()()11!1n n nn a n ax b ax b +⋅⎛⎫=- ⎪+⎝⎭+ (7) ()()()()()11!ln 1n n n na n axb ax b -⋅-+=-⎡⎤⎣⎦+五、微分公式与微分运算法则 ⑴()0d c = ⑵()1d xxdx μμμ-= ⑶()sin cos d x xdx =⑷()cos sin d x xdx =- ⑸()2tan sec d x xdx = ⑹()2cot csc d x xdx =- ⑺()sec sec tan d x x xdx =⋅ ⑻()csc csc cot d x x xdx =-⋅ ⑼()xxd ee dx = ⑽()ln xxd a aadx = ⑾()1ln d x dx x=⑿()1logln xad dx x a =⒀()arcsin d x =⒁()arccos d x = ⒂()21arctan 1d x dx x =+ ⒃()21arccot 1d x dx x=-+ 六、微分运算法则⑴()d u v du dv ±=± ⑵()d cu cdu = ⑶()d uv vdu udv =+ ⑷2u vdu udvd v v -⎛⎫= ⎪⎝⎭七、基本积分公式⑴kdx kx c =+⎰ ⑵11x x dx c μμμ+=++⎰ ⑶ln dxx c x=+⎰ ⑷ln xxa a dx c a=+⎰ ⑸x x e dx e c =+⎰ ⑹cos sin xdx x c =+⎰ ⑺sin cos xdx x c =-+⎰⑻221sec tan cos dx xdx x c x ==+⎰⎰ ⑼221csc cot sin xdx x c x ==-+⎰⎰⑽21arctan 1dx x c x =++⎰ ⑾arcsin x c =+八、补充积分公式tan ln cos xdx x c =-+⎰ cot ln sin xdx x c =+⎰ sec ln sec tan xdx x x c =++⎰ csc ln csc cot xdx x x c =-+⎰2211arctan xdx c a x a a=++⎰ 2211ln 2x adx c x a a x a-=+-+⎰arcsinxc a=+ ln x c =+十、分部积分法公式⑴形如n ax x e dx ⎰，令n u x =，axdv e dx =形如sin n x xdx ⎰令nu x =，sin dv xdx =形如cos n x xdx ⎰令nu x =，cos dv xdx =⑵形如arctan nx xdx ⎰，令arctan u x =，ndv x dx =形如ln nx xdx ⎰，令ln u x =，ndv x dx =⑶形如sin ax e xdx ⎰，cos axe xdx ⎰令,sin ,cos axu e x x =均可。