4 方差分析--医学统计
- 格式:ppt
- 大小:1.04 MB
- 文档页数:42


方差分析原理方差分析(Analysis of Variance,简称ANOVA)是一种统计方法,用于比较两个或多个样本均值之间的差异。
它能够帮助我们确定多个样本的均值是否存在显著差异,并进一步了解差异来自于哪些因素。
本文将介绍方差分析的原理和应用。
一、方差分析的背景在实际问题中,我们常常需要比较不同样本的均值,以了解它们之间是否存在差异。
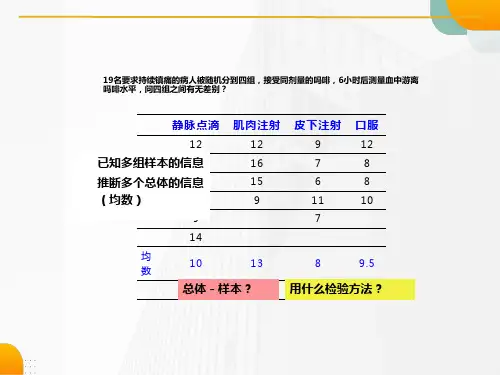
例如,我们想要知道不同药物对治疗某种疾病的疗效是否有差别,或者不同教学方法对学生成绩是否有影响等。
这时候,我们需要用到方差分析这个统计工具。
二、方差分析的基本原理方差分析的基本原理是通过比较组内变异(Within-group variation)与组间变异(Between-group variation)的大小来判断多个样本的均值是否存在显著差异。
组内变异指的是同一组内个体(观察值)之间的差异,也可以看作是测量误差或个体内部差异。
组间变异指的是不同组之间的差异,也可以理解为组与组之间的差别。
我们的目标是判断组间变异是否显著大于组内变异。
统计学家通过构建方差分析的假设检验来实现这一目标。
假设检验的零假设(null hypothesis)是所有样本的均值相等,备择假设(alternative hypothesis)则是至少存在一个样本的均值与其他样本不同。
三、方差分析的步骤进行方差分析时,一般需要按照以下步骤进行:1. 提出假设:定义零假设和备择假设。
2. 选择显著性水平:通常为0.05,表示我们要找到的结论是在5%的显著水平下成立。
3. 收集数据:需要收集多个组别的数据,并记录下来。
4. 计算方差:通过计算组内变异和组间变异。
5. 计算F统计量:F统计量用于判断组间变异是否显著大于组内变异,可以通过计算组间均方与组内均方之比得到。
6. 判断:根据F统计量与给定显著性水平的临界值进行比较,如果F统计量大于临界值,则拒绝零假设,表示至少存在一个样本均值与其他不同。
7. 进行事后分析(post hoc analysis):如果方差分析的结果是显著的,我们可以进行事后分析,以确定具体哪些组别之间存在差异。
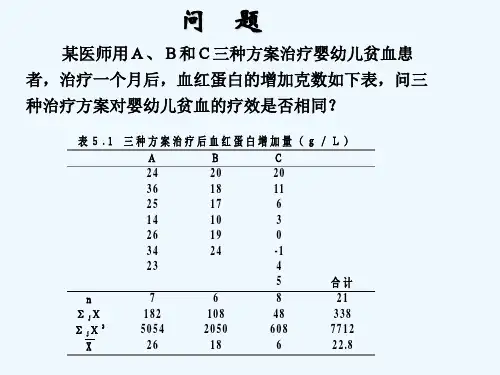







医学统计学方差分析方差分析是一种统计学方法,用于比较三个或三个以上的组之间的平均值是否存在显著差异。
在医学研究中,方差分析常用于比较不同治疗方法或不同个体群体之间的差异,以确定是否存在统计学上的显著差异。
方差分析的基本原理是比较组间离散程度与组内离散程度的比值,即组间均方与组内均方的比值。
组间方差表示不同组之间的差异性,组内方差表示同一组内个体之间的变异程度。
如果组间离散程度显著大于组内离散程度,即组间均方大于组内均方,就可以得出组间存在显著差异的结论。
在医学研究中,方差分析可以应用于很多不同的情况。
举例来说,我们可以使用方差分析来比较不同药物对同一疾病的治疗效果,或者比较不同药物剂量对同一疾病的治疗效果。
我们还可以使用方差分析比较不同年龄组、性别组或不同地区患者之间的其中一种疾病发病率。
方差分析的核心是比较组间差异与组内差异。
组间差异可以通过计算组间均方来得到。
组间均方的计算公式为组间平方和除以组间自由度。
组间平方和是每个组内数据与该组均值之差的平方的总和。
组间自由度等于组数减1、组内差异可以通过计算组内均方来得到。
组内均方的计算公式为组内平方和除以组内自由度。
组内平方和是每个组内数据与该组均值之差的平方的总和。
组内自由度等于总体样本量减去组数。
计算得到组间均方和组内均方之后,即可计算F值。
F值等于组间均方除以组内均方。
F值的计算结果可以与F分布的临界值进行比较,以判断组间均方是否显著大于组内均方。
如果F值大于F分布的临界值,就可以得出组间存在显著差异的结论。
除了F值,方差分析还可以计算一些其他的统计量。
例如,可以计算每个组的均值和标准差,以了解不同组之间的差异程度。
还可以计算方差分析表,其中包含了组间平方和、组间自由度、组间均方、组内平方和、总平方和、总自由度、组内自由度和组内均方等统计量。
需要注意的是,在进行方差分析之前,需要检验数据的正态性和方差齐性。
正态性检验可通过绘制正态概率图、Shapiro-Wilk检验或Kolmogorov-Smirnov检验进行。