ch12电工电子学1-ch12电工电子学1
- 格式:ppt
- 大小:7.32 MB
- 文档页数:96
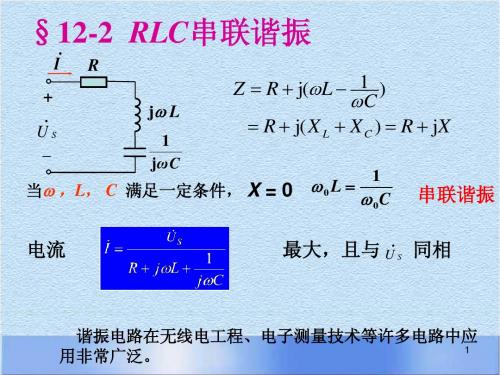




昆明理工大学硕士研究生入学考试《电工电子学》考试大纲第一部分考试形式和试卷结构一、试卷满分及考试时间试卷满分为150分,考试时间为180分钟.二、答题方式答题方式为闭卷、笔试.三、试卷的内容结构基本概念约占40%分析计算约占40%综合设计约占20%四、试卷的题型结构试卷题型结构为:问答题:约60分分析题:约30分计算题:约30分设计题:约30分合计150分第二部分考察的知识及范围1.电路的基本概念和基本定律电路的作用与组成、电路模型、电压和电流的参考方向、欧姆定律、电源有载工作状态、电源开路、电源短路、基尔霍夫电流定律、基尔霍夫电压定律、电路中电位的概念及计算2.电路的分析方法电阻的串联、电阻的并联、电阻串并联接的等效变换、电压源、电流源、电压源与电流源的等效变换、支路电流法、叠加原理、戴维宁定理、静态电阻和动态电阻的概念、非线性电阻电路的图解分析3.正弦交流电路正弦电压与电流、正弦量的相量表示法、电阻元件、电感元件、电容元件、电阻元件的交流电路、电感元件的交流电路、电容元件的交流电路、电阻电感与电容元件串联的交流电路、阻抗的串联、阻抗的并联、交流电路的频率特性(RC串联电路的频率特性、串联谐振、并联谐振)、有功功率无功功率和视在功率的概念和计算、功率因数的提高4.三相电路三相电压、负载星形联接的三相电路、负载三角形联接的三相电路、三相功率5.非正弦周期电流的电路非正弦周期量的分解、非正弦周期量的有效值、非正弦周期电流电路中的平均功率6.电路的暂态分析换路定则与电压和电流初始值的确定、RC电路的零输入响应、RC电路的零状态响应、RC电路的全响应、一阶线性电路暂态分析的三要素法、微分电路、积分电路、RL电路的零输入响应、RL电路的零状态响应、RL电路的全响应7.磁路与铁心线圈电路磁路及其基本定律、交流铁心线圈电路、变压器(变压器的工作原理、变压器的外特性、变压器损耗与效率、特殊变压器、变压器绕组的极性)、电磁铁8.半导体器件半导体的导电特性、PN结、半导体二极管(基本结构、伏安特性、主要参数)、稳压管、半导体三极管(基本结构、电流分配和放大原理、特性曲线、主要参数)、场效应管9.基本放大电路基本放大电路的组成、放大电路的静态分析(用放大电路的直流通路确定静态值、用图解法确定静态值)、放大电路的动态分析(微变等效电路法、图解法)、静态工作点的稳定、射极输出器、放大电路中负反馈(负反馈、负反馈的类型、负反馈对放大电路工作性能的影响)、多级放大电路及其级间耦合方式(阻容耦合、直接耦合)、差动放大电路(差动放大电路的工作情况、典型差动放大电路)10.集成运算放大器集成运算放大器(集成运算放大器的基本概念、特点、主要参数)、理想运算放大器及其分析依据、运算放大器在信号运算方面的应用(比例运算、加法运算、减法运算、积分运算、微分运算)、运算放大器在信号处理方面的应用(电压比较器)、集成功率放大器、运算放大器电路中的负反馈(并联电压负反馈、串联电压负反馈、串联电流负反馈、并联电流负反馈)、使用运算放大器应注意的问题11.正弦波振荡电路自激振荡、RC振荡电路、LC振荡电路12.直流稳压电源整流电路(单相半波整流电路、单相桥式整流电路)、滤波器、直流稳压电源(稳压管稳压电路、恒压源、串联型稳压电路、集成稳压电源)13.门电路和组合逻辑电路脉冲信号、晶体管的开关作用、分立元件门电路(门电路的基本概念、二极管“与”门电路、二极管“或”门电路、晶体管“非”门电路)、TTL门电路(TTL“与非”门电路、主要参数、三态输出“与非”门电路)、MOS门电路(NMOS门电路、CMOS门电路)、逻辑代数、组合逻辑电路、组合逻辑电路的分析和综合(组合逻辑电路的分析、组合逻辑电路的综合)、加法器、编码器(二进制编码器、二—十进制编码器、优先编码器)、译码器和数字显示(二进制译码器、二—十进制显示译码器)14.触发器和时序逻辑电路时序逻辑电路、双稳态触发器(R-S触发器、J-K触发器、D触发器、T触发器、T′触发器)、寄存器(数码寄存器、移位寄存器)、计数器(二进制计数器、十进制计数器)、555定时器(由555集成定时器组成的单稳态触发器、由555集成定时器组成的多谐振荡器)15.模拟量和数字量的转换数-模转换器(T型电阻网络数-模转换器、数-模转换器的主要技术指标)、模-数转换器(逐次逼近型模-数转换器、模-数转换器的主要技术指标)16. 继电器接触器控制系统与PLC低压电器、继电器接触器控制系统电路分析、继电器接触器控制系统电路设计;PLC 的基本概念、PLC系统结构、PLC控制系统电路分析、PLC控制系统电路设计。

Outline and Reading Convex Hullobstacle start endConvex hull (§12.5.2) Orientation (§12.5.1-2) Sorting by angle (§12.5.5) Graham scan (§12.5.5) Analysis (§12.5.5)6/8/2002 12:42 PMConvex Hull16/8/2002 12:42 PMConvex Hull2Convex PolygonA convex polygon is a nonintersecting polygon whose internal angles are all convex (i.e., less than π) In a convex polygon, a segment joining two vertices of the polygon lies entirely inside the polygonConvex HullThe convex hull of a set of points is the smallest convex polygon containing the points Think of a rubber band snapping around the pointsconvex6/8/2002 12:42 PM Convex Hullnonconvex3 6/8/2002 12:42 PM Convex Hull 4Special CasesThe convex hull is a segmentTwo points All the points are collinearApplicationsMotion planningFind an optimal route that avoids obstacles for a robotGeometric algorithmsConvex hull is like a two-dimensional sortingThe convex hull is a pointthere is one point All the points are coincidentobstacle start end6/8/2002 12:42 PMConvex Hull56/8/2002 12:42 PMConvex Hull6Computing the Convex HullThe following method computes the convex hull of a set of pointsPhase 1: Find the lowest point (anchor point) Phase 2: Form a nonintersecting polygon by sorting the points counterclockwise around the anchor point Phase 3: While the polygon has a nonconvex vertex, remove itOrientationThe orientation of three points in the plane is clockwise, counterclockwise, or collinear orientation(a, b, c)clockwise (CW, right turn) counterclockwise (CCW, left turn) collinear (COLL, no turn)b c a c b a c a b COLL CCW CWThe orientation of three points is characterized by the sign of the determinant ∆(a, b, c), whose absolute value is twice the area of the triangle with vertices a, b and cxa ∆(a, b, c) = xb xc6/8/2002 12:42 PM Convex Hull 7 6/8/2002 12:42 PMya 1 yb 1 yc 1Convex Hull8Sorting by AngleComputing angles from coordinates is complex and leads to numerical inaccuracy We can sort a set of points by angle with respect to the anchor point a using a comparator based on the orientation functionb < c ⇔ orientation(a, b, c) = CCW b = c ⇔ orientation(a, b, c) = COLL b > c ⇔ orientation(a, b, c) = CWRemoving Nonconvex VerticesTesting whether a vertex is convex can be done using the orientation function Let p, q and r be three consecutive vertices of a polygon, in counterclockwise orderq convex ⇔ orientation(p, q, r) = CCW q nonconvex ⇔ orientation(p, q, r) = CW or COLLr b CW c a9 6/8/2002 12:42 PMcCCW b acCOLL b arqqppConvex Hull 106/8/2002 12:42 PMConvex HullGraham ScanThe Graham scan is a systematic procedure for removing nonconvex vertices from a polygon The polygon is traversed counterclockwise and a sequence H of vertices is maintainedAnalysisfor each vertex r of the polygonLet q and p be the last and second last vertex of H while orientation(p, q, r) = CW or COLL remove q from H q←p p ← vertex preceding p in H Add r to the end of HComputing the convex hull of a set of points takes O(n log n) timeFinding the anchor point takes O(n) time Sorting the points counterclockwise around the anchor point takes O(n log n) timeUse the orientation comparator and any sorting algorithm that runs in O(n log n) time (e.g., heap-sort or merge-sort)rp q Hrqprq pThe Graham scan takes O(n) timeEach point is inserted once in sequence H Each vertex is removed at most once from sequence HHConvex Hull 11H6/8/2002 12:42 PM6/8/2002 12:42 PMConvex Hull12。