量子力学中科大课件Q10讲稿第十章势散射理论

第七讲散射理论一、散射现象的一般描述1、什么是散射？简单地说，散射就是指粒子与粒子之间或粒子与力场之间的碰撞（相互作用）过程，是一种具有重要实际意义的现象，所以散射现象也称碰撞现象，其可以示意为：粒子流散射中心如：原子物理中的α粒子散射实验。

2、散射的分类：弹性散射：一粒子与另一粒子碰撞的过程中，只有动能的交换，粒子内部状态并无改变。

非弹性散射：两粒子碰撞中粒子的内部状态有所改变（例如原子被激发或电离）。

在这里我们只讨论弹性散射，即假设碰撞过程中粒子的内部状态未变，并假设散射中心质量很大、碰撞对其运动没有影响。

3、散射的经典力学描述从经典力学来看，在散射过程中，每个入射粒子都以一个确定的碰撞参数（瞄准距离）b 和方位角0ϕ射向靶子，由于靶子的作用，入射粒子的轨道将发生偏转，沿某方向(,)θϕ出射。

例如在α粒子的散射实验中，有22cot 422M b Ze θυπε= （偏转角θ与瞄准距离之间的关系） 那些瞄准距离在b b db -和之间的α粒子，散射后，必定向着d θθθ+和之间的角度射出，如下图所示：凡通过图中所示环形面积d σ的α粒子，必定散射到角度在d θθθ+和之间的一个空心圆锥体之中。

环形面积d σ称为有效散射截面，又称微分截面。

且2222401()()4sin 2Ze d d M σθπευΩ= 然而，在散射实验中，人们并不对每个粒子的轨道感兴趣，而是研究入射粒子束经过散射后沿不同方向出射的分布。

设一束粒子流以稳定的入射流强度沿Z 轴方向射向靶粒子A ，由于靶粒子的作用，设在单位时间内有dn 个粒子沿(,)θϕ方向的立体角d Ω中射出，显然，,(,)dn Nd dn q Nd θϕ∝Ω=Ω令，即1(,)()dn q N d θϕ=Ω显然，(,)q θϕ具有面积的量纲，称为微分散射截面。

微分散射截面),(ϕθq 表示单位时间内散射到单位立体角Ωd （面积/距离平方）的粒子数占总粒子数比率，即Ω=Nd q dn ),(ϕθ。

第八章 散射理论本章介绍：前面讨论了薛定谔方程中的束缚态问题。

而对于能量连续的散射态，能级间隔趋于零，因此一般说来，不能用微扰论来处理。

另一方面，微观粒子之间的散射或称碰撞过程的研究，对于了解许多实验现象十分重要，所以，建立一套散射理论无论从实验上看，还是使理论更加完善上看，都是完全必要的。

本章将分别就弹性散射和非弹性散射，按入射粒子的能量高低，分别建立不同的散射理论，并介绍了分波法和玻恩近似两种处理散射问题的近似方法。

§8.1 散射截面§8.2 分波法§8.3 分波法应用实例§8.4 玻恩近似§8.5 质心坐标系与实验坐标系§8.6 全同粒子的散射§8.1 散射截面在经典力学中，弹性散射是按照粒子在散射过程中，同时满足动量守恒和能量守恒来定义的。

在量子力学中，一般说来，除非完全略去粒子之间的相互作用势能，否则，动量将不守恒。

因此，在量子力学中，不可能按经典力学的公式来定义弹性散射。

在量子力学中，如果在散射过程中两粒子之间只有动量交换，粒子由内部运动状态决定，则这种碰撞过程成为弹性散射。

如果在散射过程中粒子内部运动状态有所变化，如激发、电离等则称为非弹性散射。

本章只讨论弹性散射问题。

考虑一束入射粒子流向粒子A 射来，取粒子流入射方向为z 轴。

A 为散射中心。

为讨论方便起见，假定A 的质量比入射粒子大得多，由碰撞引起的A 的运动可以忽略。

应当指出，散射过程是两体问题。

因为它涉及两个互相散射的粒子。

对于两体问题，最好的处理方法是采用质心坐标系。

因为在质心坐标系中，一个两体问题将被归结为一个粒子因为与质心的相互作用而被散射。

另一粒子的运动可对称给出。

从而归结为单体问题。

如果散射中心粒子A 的质量比入射粒子大得多，可以认为质心就在A 上，这样就使问题处理简单多了。

如图所示，入射粒子受A 的作用而偏离原来的运动方向，发生散射。

图中A 角为散射粒子的方向与入射粒子方向的夹角，称为散射角。

第七章 散射理论.前面几章主要讨论了薛定谔方程中的束缚态问题，特别是微扰理论；必须要求微扰H '在无微扰表象中的矩阵元mn H '的绝对值远小于无微扰表象中相应的能级间隔00m n E E -，以保证微扰级数收敛，而对于能量连续的散射态，能级间隔趋于零，因此一般来说，不能用第五章中的方法处理。

但是，另一方面，微观粒子之间的散射或称碰撞过程的研究，对于理解许多物理现象十分重要。

例如，许多复合粒子的内部结构、电荷分布等，就是通过散射实验给出的。

核子、介子的夸克结构，由于目前在实验上还未找到自由夸克，也只能通过散射实验间接地予以论证，今年来的高能重离子碰撞之所以能引起巨大的关注，也是因为人们相信，有可能由此得出夸克、胶子等离子态。

至于高能宇宙线、气体放电、原子、分子物理的研究，散射过程更占着重要地位。

建立一套散射理论无论从实验上看，还是从使理论更加完整的角度上看，都是完全必要的。

散射过程最主要的特点是散射粒子的波函数，一般来说，在无穷远处并不为零。

而且，入射粒子的能量通常是给定的。

散射粒子在无穷元处的波函数并不为零，能谱连续。

散射过程中最感兴趣的物理结果是粒子被散射后，散射到各个不同方向，各个不同立体角的概率。

在8.1中将看到，这些物理结果可以用微分散射截面以及总散射截面描述。

本章将分别就弹散射和非弹性散射两种不同情况，按入射粒子是高能粒子还是低能粒子，分别建立各种不同的散射理论。

我们还将逐步介绍适用于各种不同情况的处理散射过程的近似方法，包括分波法、格林函数法和玻恩近似、克劳勃近似、S 矩阵、T 矩阵和形式散射微扰理论、光学势、扭曲波近似等等。

7.1散射问题的一般描述 在经典力学中，弹性散射是按照粒子在散射过程中，同时满足动量守恒和能量守恒来定义的。

在量子力学中，一般说来，除非完全略不粒子之间的相互作用能，否则，动量将不守恒。

这是因为动量算符ˆP与势能算符U(r)不对易，动量不是守恒。

量子碰撞与散射过程的描述方法引言：量子碰撞与散射过程是量子力学中的重要研究领域，涉及到微观粒子之间的相互作用以及能量转移等关键问题。

本文将介绍一些常用的描述方法，包括散射理论、波包方法和散射振幅等，以及它们在实际应用中的一些特点。

一、散射理论散射理论是研究粒子在势场中的散射过程的一种常用方法。

在散射理论中，通过求解薛定谔方程来描述粒子在势场中的运动。

这种方法可以用来计算散射截面、散射相移等散射过程的重要物理量。

散射理论的基本思想是将入射波函数分解为入射波和散射波两部分，然后通过求解薛定谔方程得到散射波的形式。

散射理论可以应用于各种势场，包括有限深势阱、库伦势等。

通过求解薛定谔方程，可以得到散射截面和散射相移等与实验结果相符的物理量。

二、波包方法波包方法是一种将散射问题转化为波包的形式进行计算的方法。

在波包方法中，将入射波函数表示为多个波包的叠加，通过求解波包的运动方程来描述散射过程。

波包方法的优点是可以将散射问题转化为经典力学中的问题，简化了计算的复杂性。

波包方法的基本思想是将波函数表示为多个高斯波包的叠加，通过求解波包的运动方程来描述散射过程。

波包方法可以用于计算散射截面、散射相移等物理量，并且可以考虑到波包的宽度和速度等因素对散射过程的影响。

三、散射振幅散射振幅是描述散射过程的重要物理量之一。

散射振幅可以通过求解薛定谔方程来得到，它描述了入射波与散射波之间的关系。

散射振幅可以用来计算散射截面、散射相移等物理量，并且可以通过实验测量来验证理论结果。

散射振幅的计算通常需要考虑到势场的形式和散射波的边界条件等因素。

通过求解薛定谔方程，可以得到散射振幅的具体形式，并且可以通过实验测量来验证理论结果。

散射振幅的计算对于理解散射过程的本质和探索微观世界的奥秘具有重要意义。

结论：量子碰撞与散射过程的描述方法包括散射理论、波包方法和散射振幅等。

这些方法在研究微观粒子之间的相互作用和能量转移等问题中起着重要作用。

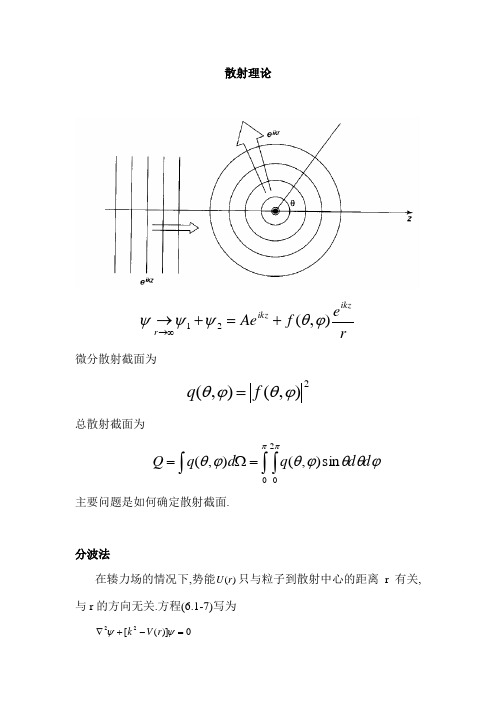
散射理论ref Ae ikz ikz r ),(21ϕθψψψ+=+→∞→微分散射截面为2),(),(ϕθϕθf q =总散射截面为⎰⎰⎰=Ω=ππϕθθϕθϕθ020sin ),(),(d d q d q Q主要问题是如何确定散射截面. 分波法在辏力场的情况下,势能)(r U 只与粒子到散射中心的距离r 有关,与r 的方向无关.方程(6.1-7)写为0)]([22=-+∇ψψr V k一般解可写为(弹性散射n 不改变)),()(),,(ϕθϕθψlm lml Y r R r ∑=因为现在ψ与ϕ角无关, m=0, 因而一般解可写为)(cos )(),(θθψl ll P r R r ∑=这个展式中的每一项成为一个分波, )(cos )(θl l P r R 是第l 个分波,每一个分波都是方程(6.2-1)的解.通常称,....2,1,0=l 的分波分别为,...,,d p s 分波.径向函数满足下列方程 0)()1()()(12222=⎥⎦⎤⎢⎣⎡+--+⎪⎭⎫ ⎝⎛r R r l l r V k dr r dR r dr d r l l 令 rr u r R l l )()(= (6.2-4)则)(r u l 满足方程0)1()(2222=⎥⎦⎤⎢⎣⎡+--+l l u r l l r V k dr u d 由于现在散射振幅f 与与ϕ角无关,只是θ的函数, ψ的渐进表示式应为 ikrikzr e rf Ae)(θψ+→∞→根据我们的假设,当r 趋向无限大时)(r V 趋近于零,所以当∞→r ,我们有0)()(222=+r u k drr u d l l 它的解是)sin()(''ll l kr A r u δ+=由此有krl kr A kr r A r R l l l lr l )2/sin()sin()(''δπδ+-=+→∞→ 为讨论方便,我们引入了,2/,''πδδl kA A l l l l +==因此渐进解为)(cos )2/sin(),(θδπθψl l l lr P l kr krA r +-→∑∞→ 利用数学公式将平面波ikz e 按球面波展开 )(cos )()12(0cos θθl l l l ikr ikzP kr j i l ee∑∞=+==式中)(kr j l 是球面贝赛尔函数,它和贝赛尔函数)(2/1kr J l +的关系,以及它的渐进表示式是 )2/sin(1)(2)(2/1ππl kr krkr J krkr j r l l -→=∞→+ 将(6.2-9)式的渐进式代入(6.2-6),并令它和(6.2-8)式相等,得到)(cos )2/sin()()(cos )2/sin(1)12(00θδπθθπl l l l ikrl l lP l kr krA e r f P l kr kr i l +-=+-+∑∑∞=∞=利用公式 )(21sin αααi i e e i--=将正弦函数写成指数函数,得)(cos )(cos )12()(cos )(cos )12()(200)2/(2/00)2/(2/=⎥⎦⎤⎢⎣⎡-++⎥⎦⎤⎢⎣⎡-++-∞=∞=--∞=∞=--∑∑∑∑ikr l l l l i l l il l ikr l l l l i l l il l e P e A P e i l eP e A P e i l kif θθθθθπδππδπ要使这个等式成立,式中ikr e 和ikr e -前得系数必须分别等于零)122.6()(cos )(cos )12()112.6()(cos )(cos )12()(200)2/(2/00)2/(2/-⎥⎦⎤⎢⎣⎡=+-⎥⎦⎤⎢⎣⎡=++∑∑∑∑∞=∞=--∞=∞=--l l l l i l l il l l l l l i l l il l P e A P e i l P e A P ei l kif θθθθθπδππδπ(6.2-12)两边乘以)(cos 'θl P ,对θ积分,并利用勒让德多项式的正交性''0122sin )(cos )(cos ll l l l d P P δθθθθπ+=⎰ (6.2-13) 可以得到l i l l e i l A δ)12(+=将这结果代入(6.2-11),并利用2/πil l e i =就得到ll i l l l i l l ie P l P e l kif δθθθδδsin 2)(cos )12()(cos )1)(12()(2002∑∑∞=∞=+=-+=ll i l l e P l k f δθθδsin )(cos )12(1)(0∑∞=+= 由上式可以看出,求散射振幅)(θf 的问题归结为求l δ, 因为)2/(πl kr -是入射波第l 个分波的位相, )2/(l l kr δπ+-是散射波第l 个分波的位相,所以l δ是入射波经过散射后第l 个分波的位相移动(简称相移), l δ的具体数值要解出方程(6.2-3)后才能求得. 由(6.2-14)得出微分散射截面的表示式222sin )(cos )12(1)()(ll i lleP l kf q δθθθδ∑∞=+==及总散射截面∑∑∑∑∑∑⎰⎰∞=∞=-∞=∞=-∞=∞=≡+=+++=⎥⎦⎤⎢⎣⎡++==022'00''2'00'0'2sin)12(4sin sin 12)1'2)(12(4sin sin sin )(cos )(cos )1'2)(12(2sin )(2''l ll l l l i i l l ll l l i i l l l l Q l k e e l l l k e e d P P l l k d q Q l l l l δπδδδπδδθθθθπθθθπδδδδππ式中l l l kQ δπ22sin )12(4+=是第l 个分波的散射截面.由(6.2-14)式,因为1)1(=l P ,所以)0(f 的虚部是l l l k f δ∑∞=+=02sin )12(1)0(Im因而)0(Im 4f kQ π=(6.2-18)这个结果称为光学定理.例题 方形势阱与势垒所产生的散射作为应用分波法的一个例子,我们讨论低能粒子受球对称方形势阱的散射,并且入射粒子能量很小,它的德布罗意波长比势场作用范围大的多.质子和中子的低能散射可以近似地归结为这种情况.方形势阱可以表示为⎩⎨⎧>≤=ar a r U r U 0)(0在势阱情况下00<U .因为1<<ka ,所以只需要讨论s 分波()0(=l 的散射就够了.在方程(6.2-5)中令0=l 得,02'22≤=+r u k dru d(6.3-1),0222>=+r u k dru d(6.3-2) 式中222Ek μ=,20222' U k k μ-=方程(6.2-1,2)得解是ar kr B r u a r r k A r u >+=≤+=),sin()(),''sin()(00δδ(6.3-3)由波函数得标准条件, r r u R )(=在0=r 处为有限,所以0'0=δ;在a r =处drdur u )(1连续,得 ak k ka k 'cot ')cot(0=+δ(6.3-4) 由此得到相移kaa tgk k karctg -⎥⎦⎤⎢⎣⎡=''0δ(6.3-5) 总散射截面为0220sin 4δπkQ Q =≈(6.3-6)在粒子能量很低0→k 得情况下,因为0,0→→arctgx x ,所以11000<<⎥⎦⎤⎢⎣⎡-≈a k a tgk ka δ 式中'200k U k ≈=μ总散射截面可化为2002202022144sin 4⎪⎪⎭⎫ ⎝⎛-≈≈≈a k a tgk a k k Q πδπδπ(6.3-7)如果散射场不是势阱而是势垒,即00>U ,那么在(6.3-7)式中将0k 换成0ik ,0→k 时的总散射截面为200214⎪⎪⎭⎫ ⎝⎛-≈a k a thk a Q π(6.3-8)当∞→0U 时,∞→0k , ∞→a thk 0,于是有24a Q π≈在这种情况下,总散射截面等于半径为a 的球面面积.它与经典情况不同.在经典情况下,总散射截面就是作为散射中心的硬球的最大截面面积2a π,所以在量子力学中计算得到的散射截面是经典值的4倍. 上面我们看到,给定粒子相互作用势后,用分波法可以求出低能散射的相移和散射截面.如果不知道势场的具体形式.则可由实验测定散射截面和相移,然后通过分波法所给出的势场和相移的关系来确定势场,这是研究基本粒子间相互作用所常用的方法.6.4 玻恩近似前面介绍的分波法在入射粒子的动能较大时,应用起来很不方便.如果入射粒子的动能比粒子与散射中心相互作用的势能大的多,以致势能)(r U 可以看作是微扰时,我们可用下面介绍的波恩近似来计算散射截面.体系的哈密顿写为 '0H H H +=其中μ2/20p H =是自由粒子的哈密顿, )('r U H =取箱归一化的动量本征函数r k ⋅-i e L 2/3作为0H 的本征函数,这种归一化描写在体积3L 内有一个粒子.微扰使粒子从动量为k 的初态跃迁到动量为'k 的末态.因为是弹性散射,根据能量守恒,有 222'k ≡=k k入射粒子流强度为3-vL , 其中μ/k v =. 根据(6.1-1)式,单位时间内散射到立体角Ωd 内的粒子数为,Ω=-d q vL dn ),(3ϕθ(6.4-1)另一方面,由(5.7-8)动量大小为k 方向在立体角Ωd 内的末态的态密度是Ω⎪⎭⎫⎝⎛=kd L m μπρ32)(将此式代入(5.7-6)也得到单位时间内散射到立体角Ωd 内的粒子数Ω-=Ω-=⎰⎰----d d e U vk vL d k L d e U L dn i i 2).'(323232).'(3)(48)(2r r r r rk k rk k πμπμπ(6.4-2)比较(6.4-1)和(6.4-2),可以得到2).'(32)(4)(⎰--=r r r k k d e U vk q i πμθ(6.4-3)(绝对值号内保留负号是因为用其它方法算出的散射振幅)(θf 有一负号). 令kk K -='(6.4-4) 它的数值是2/sin 2θk K =其中θ是散射角, K 是散射引起的动量的变化,于是(6.4-3)式的积分可以简化为⎰⎰⎰⎰⎰∞∞--==020cos 2.)sin()(4sin )()(dr Kr r rU K d d edr r r U d er U iKr i πϕθθππθrK r因而2422)sin()(4)(⎰∞=drKr r rU K q μθ(6.4-5)若势能)(r U 已知,由上式即可求得微分散射截面 如果势能可以表示为球形对称的方势垒或势阱 ⎩⎨⎧>≤=ar a r U r U 0)(0那么波恩近似条件就容易得出.根据6.2节的讨论,如果散射波的相移很小,特别是s 分波的相移很小,就说明势场对散射波的影响很小,因而把势场看作微扰是合理的,所以分析s 分波相移就可以得出波恩近似成立的条件. 由方程(6.3-4), 注意到E U k k U k k /1)2//(1'0220-=-=μ , 得[])cot()/1(cot /102/100δ+=--ka k E U ka E U k(6.4-6)当粒子能量很高时,)2/1()/1(,02/100E U E U U E -≈->>,于是上式左边余切的宗量可写为[][]E kaU ka E U ka 2/)2/1(00-=- 当此宗量与ka 只相差一小角时,则相移0δ就很小.于是波恩近似有效的条件是1/2/00<<=v aU E kaU(6.4-7)v 是入射粒子的经典速度.由此可见,波恩近似适用于粒子的高能散射.分波法则适用于低能散射,这两种方法相互补充.在势阱情况下(00<U ) 波恩近似对低能散射也可能有效.由(6.4-6)式, 当,1<<ka 0U E <<时,有⎥⎦⎤⎢⎣⎡-⎪⎪⎭⎫ ⎝⎛-≈ a U tg U E tg 2/102/100)2(μδ(6.4-8) 所以只要a U 2/10)2(μ-不是很接近于2/π.则0δ就很小,于是波恩近似就可以应用.作为应用波恩近似的一个例子,我们计算一个高速带电粒子(带电e Z ')被一中性原子散射的散射截面,原子核所产生的电场被原子内部的电子所屏蔽,这种屏蔽库仑场可以表示为a r s e r e ZZ r U /2')(--= (6.4-9)式中a 为原子半径,Z 为原子序数.将(6.4-9)式代入(6.4-5)式得2224422220/424222)/1(1'4sin '4)(a K e Z Z Krdr e K e Z Z q s a r s +==⎰∞- μμθ(6.4-10)如果12/sin 2>>=θka Ka (6.4-11)(6.4-10)可以表示为2/csc 4')(442422θμθv e Z Z q s = (6.4-12)(6.4-12)式就是卢瑟福散射公式.它首先由卢瑟福用经典力学方法计算库仑散射(不考虑屏蔽作用)得出,这说明(6.4-11)式是经典力学可以适用的条件.(6.4-11)式要求散射角比较大,这时散射在原子核附近发生,即入射粒子深入到原子内部,因而核外电子不起屏蔽作用.当θ角很小时,条件(6.4-11)式不被满足,卢瑟福公式不能成立,这时就必须用公式(6.4-10)。