上海市中学生业余数学学校招生试题 含答案

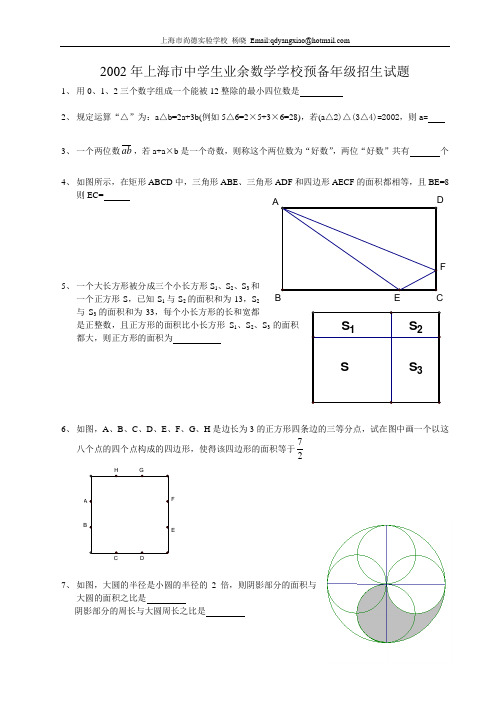
2002年上海市中学生业余数学学校预备年级招生试题1、 用0、1、2三个数字组成一个能被12整除的最小四位数是2、 规定运算“△”为：a △b=2a+3b(例如5△6=2×5+3×6=28)，若(a △2)△(3△4)=2002，则a=3、 一个两位数ab ，若a+a ×b 是一个奇数，则称这个两位数为“好数”，两位“好数”共有 个4、 如图所示，在矩形ABCD 中，三角形ABE 、三角形ADF 和四边形AECF 的面积都相等，且BE=8则EC=5、 一个大长方形被分成三个小长方形S 1、S 2、S 3和一个正方形S ，已知S 1与S 2的面积和为13，S 2与S 3的面积和为33，每个小长方形的长和宽都是正整数，且正方形的面积比小长方形S 1、S 2、S 3的面积都大，则正方形的面积为6、 如图，A 、B 、C 、D 、E 、F 、G 、H 是边长为3的正方形四条边的三等分点，试在图中画一个以这八个点的四个点构成的四边形，使得该四边形的面积等于277、 如图，大圆的半径是小圆的半径的2倍，则阴影部分的面积与大圆的面积之比是阴影部分的周长与大圆周长之比是A B CE FC DE F B A8、 一副扑克牌共有黑桃、红心、方块、草花四种花色，每种花色有A 、2，3， ，10，J ，Q ，K 各13张牌，其中J ，Q ，K 分别作11、12、13计，A 可作1也可作14计。

若在一副扑克牌中任取5张牌，使这5张牌同花色且点数顺次相连，则不同的抽法共有 种。

9、 小胡和小涂计算甲、乙两个两位数的乘积，小胡看错了甲数的个位数字，计算结果为1274，小涂看错了甲数的十位数字，计算结果为819，则甲数是10、 把一个长方形菜地分成三块，如图所示，已知第二块比第一块宽10米，第二块的面积为1000平方米；第三块比第一块窄4米，第三块的面积为650平方米，那么第一块的面积是 平方米。

上海市高中理科班、数学班招生选拔测试数学试卷一、填空题(本大题满分80分,每小题8分)本题共有10道小题,要求直接将答案写在横线上.1．= .2． 已知关于ｘ的方程2ｘ2-4ｘ+ａ-1=0至少有一个正实数根,则ａ的取值范围是. .3. 在梯形ＡＢＣＤ中,ＡＢ∥ＤＣ,ＡＢ=ＡＣ=ＡＤＢＣ,则ＢＤ= .4. 已知ａ2-ａ-1=0,且42323293,2112a xa a xa a -+=-+-则ｘ= . 5. 在凸四边形ＡＢＣＤ中,ＡＤ,ＡＢ+ＣＤ, ∠ＢＡＤ=60°,∠ＡＤＣ=120°.Ｍ是ＢＣ的中点, 则ＤＭ= .6. 在平面直角坐标系中,点Ｐ的坐标是+ｍ, +ｎ),这里ｍ,ｎ都是有理数, 过点Ｐ作ｙ轴的垂线, 垂足为Ｈ,已知△ＯＰＨ的面积为2, 其中Ｏ为坐标原点,则满足条件的有序数对(ｍ,ｎ)有对. .7. 今有浓度分别为3%、8%、11%的甲、乙、丙三种盐水50千克、70千克、60千克,现要用甲、乙、丙这三种盐水配制浓度为7%的盐水100千克,则丙种盐水最多可用. 千克.8. 已知实数ｘ,ｙ满足方程(ｘ2+2ｘ+3)(3y 2+2ｙ+1)=,43则ｘ+ｙ= . 9. 已知ＡＢ是半径为1的圆Ｏ的直径,ＣＤ是过ＯＢ中点的弦,且ＣＤ⊥ＡＢ,以ＣＤ为直径的圆交ＡＢ于Ｅ,ＤＥ的延长线交圆Ｏ于Ｆ,连结ＣＦ,则ＣＦ=. .10. 已知二次函数ｙ=ａｘ2(ａ≥1)的图象上点Ａ,Ｂ的横坐标分别为-1,2,Ｏ是坐标原点,如果△ＯＡＢ是直角三角形,则△ＯＡＢ的周长为 .二、解答题(本大题满分70分,共4小题)11. (本题满分14分)已知实数ａ,ｂ,ｃ满足不等式|ａ|≥|ｂ+ｃ|,|ｂ|≥|ｃ+ａ|,|ｃ|≥|ａ+ｂ|,求证:ａ+ｂ+ｃ=0.12. (本题满分16分)在凸四边形ＡＢＣＤ中,Ｍ是ＡＢ的中点,Ｏ是对角线ＡＣ与ＢＤ的交点,延长ＭＯ与ＣＤ交于Ｑ点,求证: BCO ADO S CQ S DQ∆∆=. 13. (本题满分20分)求满足方程ｘ2+ｙ2=2(ｘ+ｙ)+ｘｙ的所有正整数ｘ,ｙ.14 (本题满分20分)如图所示,在梯形ＡＢＣＤ中,ＡＤ∥ＢＣ,ＢＣ=ＢＤ=1,ＡＢ=ＡＣ,ＣＤ<1,且∠ＢＡＣ+∠ＢＤＣ=180°,求ＣＤ的长.。

一、解答题（共4小题，满分0分）1．菱形OABC中，OB、AC相交于M（x0，y0），y＝过点M、C，2≤x0≤4，求菱形OABC的面积最大值．2．二次函数y＝ax2+bx+c，其图象都在x轴及其上方，设t＝，则t的最值为多少？3．对于各数互不相同的数列a1，a2，a3，…，a k．若1≤m＜n≤k，a n＜a m，则（a n，a m）称为一个逆序．数列中逆序的总数称为该数列的逆序数，如3，2，1中2＜3，则称（3，2）为一个逆序，同理（3，1），（2，1）也为逆序，逆序数为2+1＝3，现有一各数互不相同的数列a1，a2，a3，…，a100，逆序数为k，则该数列颠倒后得到的a100，a99，…，a1，逆序数为多少？4．已知实数t，使得[t]＝1，[t2]＝2，[t3]＝3，…，[t n]＝n都成立，求正整数n的最大值．参考答案与试题解析一、解答题（共4小题，满分0分）1．菱形OABC中，OB、AC相交于M（x0，y0），y＝过点M、C，2≤x0≤4，求菱形OABC的面积最大值．【解答】解：∵菱形OABC中，OB、AC相交于M（x0，y0），∴直线的OM斜率为，由菱形对角线互相垂直可得：AC的斜率为﹣，∴AC：y＝﹣（x﹣x0）+y0，令y＝0，则x＝+x0＝，∴A（，0），∴C（，2y0），∵M、C在同一反比例函数上∴•2y0＝x0•y0，∴x02＝2y02，∴y0＝x0，∴S＝•2y0＝•x0＝x02，∴S最大值＝×42＝24．2．二次函数y＝ax2+bx+c，其图象都在x轴及其上方，设t＝，则t的最值为多少？【解答】解：由题意得：a＞0且Δ＝b2﹣4ac≤0，即（）2≤，故t＝＝1++≥1++3（）2＝3（）2+≥，当且仅当＝﹣时等号成立，而（）2，无最大值，故t无最大值，故t最小值为，无最大值．3．对于各数互不相同的数列a1，a2，a3，…，a k．若1≤m＜n≤k，a n＜a m，则（a n，a m）称为一个逆序．数列中逆序的总数称为该数列的逆序数，如3，2，1中2＜3，则称（3，2）为一个逆序，同理（3，1），（2，1）也为逆序，逆序数为2+1＝3，现有一各数互不相同的数列a1，a2，a3，…，a100，逆序数为k，则该数列颠倒后得到的a100，a99，…，a1，逆序数为多少？【解答】解：根据题意可知：各数互不相同的（a m，a n）和（a n，a m）中恰有一个逆序，所以在数列a1，a2，a3，…，a100与a100，a99，…，a1，中，共有：1+2+3+…+99＝＝4950个逆序，因为数列a1，a2，a3，…，a100，逆序数为k，所以a100，a99，…，a1逆序数为4950﹣k．4．已知实数t，使得[t]＝1，[t2]＝2，[t3]＝3，…，[t n]＝n都成立，求正整数n的最大值．【解答】解：∵[t]＝1，∴则1≤t＜2，∵[t2]＝2，∴2≤t2＜3，∵[t3]＝3，∴3≤t3＜4 ①，[t4]＝4，∴4≤t4＜5，此时2≤t2＜②，∵[t5]＝5，∴5≤t5＜6，由①和②，可知6≤t5＜，与5≤t5＜6矛盾，∴[t5]＝5不成立，因此n的最大值为4．。

2006年上海市中学生业余数学学校预备年级招生考试2006年上海市中学生业余数学学校预备年级招生考试（10月6日 上午8:309:30-）本卷满分100分（7'48'410'4100'⨯+⨯+⨯=）【第1题】有一列数8，88，888，…，888888 个，它们的和的百位数字是_______。

【分析与解】888888888888++++ 个的和的百位数字与88286888888888888-=++++ 个的和的百位数字相同；868888888888888888888676464++++=++⨯= 个；即86888888888888++++ 个的和的百位数字是4；故888888888888++++ 个的和的百位数字是4。

【第2题】若数20062006200620061006n个能被11整除，则n 的最小值是_______。

【分析与解】因为200611|2006200620061006n个； 所以()()062011|0606060620202010662145n n n n n ++⎛⎫⎛⎫++++++++-++++++++=+-+=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭个个； n 的最小值是7。

2006年上海市中学生业余数学学校预备年级招生考试【第3题】如图，ABCD ，AMOQ ，MBNO ，ONCP ，QOPD 都是矩形，若矩形QOPD 的面积为251cm ，矩形ONCP 的面积为217cm ，矩形MBNO 的面积为229cm ，则四边形MNPQ 的面积2_______cm 。

OQPNM DCBA【分析与解】因为()()()()OQ OP ON OM ON OP OQ OM ⨯⨯⨯=⨯⨯⨯； 所以QOPD MBNO ONCP AMOQ S S S S ⨯=⨯矩形矩形矩形矩形；所以251291787AMOQ QOPD MBNO ONCP S S S S cm =⨯÷=⨯÷=矩形矩形矩形矩形；所以251172987184ABCD QOPD ONCP MBNO AMOQ S S S S S cm =+++=+++=矩形矩形矩形矩形矩形； 因为PQO PQD S S ∆∆=，PNO PNC S S ∆∆=，MNO MNB S S ∆∆=，QMO QMA S S ∆∆=； 所以22184292MNPQ ABCD S S cm =÷=÷=四边形矩形。

2001年上海市中学生业余数学学校预备年级招生试题（2001年10月6日上午8:00~9:30）1. 某学校共有1000名学生，其中男学生人数与女学生人数的比是2:3，女学生人数与教师人数的比是8:1。

那么教师有___________名。

2. 有一筐苹果和一筐梨，如果每天吃掉1个苹果2个梨，那么梨吃完时还剩下3个苹果；如果每天吃掉2个苹果3个梨，那么苹果吃完时还剩下5个梨，这筐苹果有_________个，这筐梨有__________个。

3. 若abcd为一个四位数，且a=d，b=c，则称这个数为四位对称数。

四位对称数共有__________个。

4. 在一个圆周上有7个点，正好将圆周七等分，以这些点为顶点作三角形，可以作___________个等腰三角形。

5. 已知S n=1-2+3-4+5-6+…+(-1)n+1n，其中n是正整数。

那么S2001+S2002=________。

6. 一个两位数N具有性质：N与颠倒N的数字后的数之和为完全平方数，则这样的N有___________个。

7. 数119具有以下性质：当它被2除余1；被3除余2；被4除余3；被5除余4；被6除余5；那么，具有这样性质的三位数（包括数119在内）共有_____个。

8. 有两部自动换币机，第一部能将一枚硬币换成二枚其它硬币；第二部能将一枚硬币换成五枚其它硬币，某人进行了14次换币，将一枚硬币换成了42枚硬币。

则他在第一，第二部换币机上分别换了________，________次。

9. 某人一块手表比家里的钟每小时快15秒，已知家里的钟比标准时间每小时慢15秒，则这快手表比标准时间一昼夜____________秒（填快或慢多少秒）10. A，B，C，D，E五个人中，其中任取4个人的平均年龄再加上余下一个人的年龄所得的和分别为37，40，49，58，64，则这五个人中年龄最大的比年龄最小的大___________岁。

11. 一次乒乓球比赛有A ，B ，C ，D ，E 五名选手参加，他们来自湖北，广东，福建，北京和上海，经调查知道：（1）A 仅与另外两名运动员比赛过；（2）上海运动员与另外三名运动员比赛过；（3）B 没有和广东运动员比赛过；（4）福建运动员和C 比赛过；（5）广东，福建。

高一入学考试（2014） 第1页（共1页） 2004年上海市中学生业余数学学校高一年级招生试题（考试时间：2014年10月12日）1、如图，在直角坐标平面中，30AOX ∠=︒，AB AO ⊥，2AO =，BO =，则点B 的坐标为 ▲ ． 2、记N i k *∈，且12n k k k >>>L ，若122014222n k k k =+++L ，试求12n k k k +++L 的值为 ▲ ． 3、如图，在矩形ABCD 中，5AB =，12BC =，将矩形沿对角线AC 翻折，记D 的对应点为点E ，联结AE 交BC 于点F ，则△ECF 的面积为 ▲ ．4、若方程220x ax ++=，20x ax a +-=，2(1)0x a x a +--=中至少有一个方程有实数根，则a 的取值范围是 ▲ ．5、若111111(20)a b c d e a b c d e =++++<<<<<，满足 ,,,,N a b c d e *∈，试写出满足条件的其中一个算式 ▲ ．6、如图，四边形ABCD 是正方形，E 是边BC 上的一点，且40DME S =△，20AB =，则BE 的长为 ▲ ．7、若方程20x mx n --=的正根小于5，且,N m n *∈，则满足条件的方程共有 ▲ 个8、令函数110()10100x f x x +=-，记()()((()))n n ff x f f f f x =L 14243个，则 (2)(3)(1000)11112222f f f f ⎛⎫⎛⎫⎛⎫⎛⎫++++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭L 的值为 ▲ ． 9、若正整数n 满足如下条件：①不等式220130x x n -+>对于N x *∈恒成立；②存在N x *∈，使得220140x x n -+≤成立。

则满足条件的n 的个数是 ▲ ．10、已知x 是无理数，且满足2x x +、322x x +都是整数，则x 的值为 ▲ ．AB CD E F A B CDE M。

上海七宝中学自招数学试题今天分享几道能够比肩上海四大名校的七宝中学的自招数学试题。

题目一：计算 \frac{\sqrt{6}+4 \sqrt{3}+3\sqrt{2}}{(\sqrt{6}+\sqrt{3})(\sqrt{3}+\sqrt{2})}【详解】\frac{\sqrt{6}+4 \sqrt{3}+3\sqrt{2}}{(\sqrt{6}+\sqrt{3})(\sqrt{3}+\sqrt{2})}=\frac{\sqrt{6} +\sqrt{3}+3\sqrt{3}+3\sqrt{2}}{(\sqrt{6}+\sqrt{3})(\sqrt{3}+\sqrt{2})}=\frac{\sqrt{6}+\sqrt{3}+3(\sqrt{3}+\sqrt{2})}{(\sqrt{6}+\sqrt{3})(\sqrt{3}+\sqrt{2})}=\frac{1}{\sqrt{3}+\sqrt{2}}+\frac{3}{\sqrt{6}+\sqrt{3}}=\frac{1}{\sqrt{3}+\sqrt{2}}+\frac{\sqrt{3}}{\sqrt{2}+1}=\frac{\sqrt{3}-\sqrt{2}}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}+\frac{\sqrt{3}\cdot(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)}=\sqrt{3}-\sqrt{2}+\sqrt{6}-\sqrt{3}=\boxed{\sqrt{6}-\sqrt{2}}.\square一般我们看到分式化简第一时间想到的就是分母有理话，比如针对这道题应该分子、分母同时乘以 (\sqrt{6}-\sqrt{3})(\sqrt{3}-\sqrt{2})。

这样做也是可以的，毕竟分母变成整数，肯定是能够做出来的。

不过，这样做分子的计算量比较大，且很容易就会算错了。

1
2023年上海中学自主招生数学试卷
1．已知，求x2+y2．
2．如图，已知∠AOX＝30°，OA＝2，AB⊥OA，AB＝OA，则B的坐标为 ．

3．已知a+＝3，b+＝17，c+＝，求abc＝ ．
4．与x轴，y轴交于A，B（k为正整数），记Sk为S△AOB在对应k时的大小，则S1+S2+⋯+S
2033

＝ ．
5．有九个方格，把1到9这些正整数均填入其中，要使任意相邻的三个格子的和为3的倍数，有 种
填法．

6．在圆O中，AP＝7，BP＝3，且OP⊥CP，求CP＝ ．

7．有一数列（8项），首项与末项均为1，每一项与前一项比均为1或2或，这种数列有 种．
8．x2+y2＝|x|+|y|有 组整数解．
9．．

10．在长方形ABCD中，长为4，宽为2，N为CD的中点，M在AD上，且∠MBC＝∠BMN，求AM．
2

11．三角形三边为x，y，z，均为正整数，且符合xyz＝2（x﹣1）（y﹣1）（z﹣1），求三边长．

2004年上海市中学生业余数学学校高一年级招生试题（考试时间：2014年10月12日）1、如图，在直角坐标平面中，30AOX ∠=︒，AB AO ⊥，2AO =，BO =，则点B 的坐标为 ▲ ． 2、记N i k *∈，且12n k k k >>>L ，若122014222n k k k =+++L ，试求12n k k k +++L 的值为 ▲ ． 3、如图，在矩形ABCD 中，5AB =，12BC =，将矩形沿对角线AC 翻折，记D 的对应点为点E ，联结AE 交BC 于点F ，则△ECF 的面积为 ▲ ．4、若方程220x ax ++=，20x ax a +-=，2(1)0x a x a +--=中至少有一个方程有实数根，则a 的取值范围是 ▲ ．5、若111111(20)a b c d e a b c d e =++++<<<<<，满足 ,,,,N a b c d e *∈，试写出满足条件的其中一个算式 ▲ ．6、如图，四边形ABCD 是正方形，E 是边BC 上的一点，且40DME S =△，20AB =，则BE 的长为 ▲ ．7、若方程20x mx n --=的正根小于5，且,N m n *∈，则满足条件的方程共有 ▲ 个8、令函数110()10100x f x x +=-，记()()((()))n n ff x f f f f x =L 14243个，则 (2)(3)(1000)11112222f f f f ⎛⎫⎛⎫⎛⎫⎛⎫++++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭L 的值为 ▲ ． 9、若正整数n 满足如下条件：①不等式220130x x n -+>对于N x *∈恒成立；②存在N x *∈，使得220140x x n -+≤成立。

则满足条件的n 的个数是 ▲ ．10、已知x 是无理数，且满足2x x +、322x x +都是整数，则x 的值为 ▲ ．AB CD E F A B CDE M。