上海市中学生业余数学学校预备年级招生试题

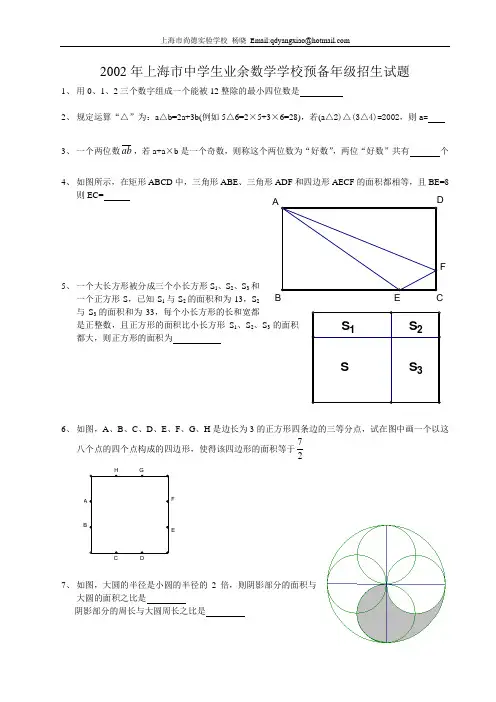
2002年上海市中学生业余数学学校预备年级招生试题1、 用0、1、2三个数字组成一个能被12整除的最小四位数是2、 规定运算“△”为：a △b=2a+3b(例如5△6=2×5+3×6=28)，若(a △2)△(3△4)=2002，则a=3、 一个两位数ab ，若a+a ×b 是一个奇数，则称这个两位数为“好数”，两位“好数”共有 个4、 如图所示，在矩形ABCD 中，三角形ABE 、三角形ADF 和四边形AECF 的面积都相等，且BE=8则EC=5、 一个大长方形被分成三个小长方形S 1、S 2、S 3和一个正方形S ，已知S 1与S 2的面积和为13，S 2与S 3的面积和为33，每个小长方形的长和宽都是正整数，且正方形的面积比小长方形S 1、S 2、S 3的面积都大，则正方形的面积为6、 如图，A 、B 、C 、D 、E 、F 、G 、H 是边长为3的正方形四条边的三等分点，试在图中画一个以这八个点的四个点构成的四边形，使得该四边形的面积等于277、 如图，大圆的半径是小圆的半径的2倍，则阴影部分的面积与大圆的面积之比是阴影部分的周长与大圆周长之比是A B CE FC DE F B A8、 一副扑克牌共有黑桃、红心、方块、草花四种花色，每种花色有A 、2，3， ，10，J ，Q ，K 各13张牌，其中J ，Q ，K 分别作11、12、13计，A 可作1也可作14计。

若在一副扑克牌中任取5张牌，使这5张牌同花色且点数顺次相连，则不同的抽法共有 种。

9、 小胡和小涂计算甲、乙两个两位数的乘积，小胡看错了甲数的个位数字，计算结果为1274，小涂看错了甲数的十位数字，计算结果为819，则甲数是10、 把一个长方形菜地分成三块，如图所示，已知第二块比第一块宽10米，第二块的面积为1000平方米；第三块比第一块窄4米，第三块的面积为650平方米，那么第一块的面积是 平方米。

2003年上海市中学生业余数学学校预备年级招生试题（10月11日上午8∶30—9∶30）本卷满分100分（7/×4+8/×4+10/×4 =100/）1、A、B两城市相距625千米，小王从A市于上午5:30出发，以每小时100千米的速度驶向B市．小王出发15分钟后，小张从B市以每小时80千米的速度驶向A市．则两人于点分在途中相遇．解：小王出发15分钟，走了100×0.25小时=25千米；余下项羽距离625-25=600千米；600÷（100+80）=10/3小时=200分钟∴215分钟后（3小时35分钟后）相遇，即9点05分2、某城市的外环公路总长61千米，为了联络需要在环路边设置应急电话亭，要求每两个电话亭之间的距离不超过2千米，那么外环路边最少需要设置个电话亭．解：[61÷2]+1=313、运相同的78箱货物，如果用能装5箱货物的大卡车运一次，运费为130元，如果用能装2箱货物的小卡车运一次，运费为60元，合理选择大、小卡车的辆数，可使得总运费最省，最省的总运费为．解：大卡车折合每箱26元、小卡车每箱30元，所以尽量要用大卡车。

4、在如图所示的街道示意图中，从A到B的最短路线共有条．解：最短路线就是不走回头路，只往右、只网上。

标数法，9条AB5、如图所示，两个等腰直角三角形ABC和DEF叠放在一起，如果BC = 10，EF = 8，CE = FC + BE，那么图中阴影部分的面积是．解：CE = FC + BE => 3 CE = BC + EF = 10+8 => CE=6、FC=2、BE=4、FB=12S阴影=S△NBF- S△FMC- S△PBE=（12×12÷2-4×4-2×2）÷2=526、某个质数与6，8，12，14之和都仍然是质数，一共有个满足上述条件的质数．解：把x依据处以5所得余数分为以下五种情况：当X=5k+1，则X+14=5×（k+3）为合数当X=5k+2，则X+8=5×(k+2) 为合数当X=5k+3，则X+12=5×（k+3）为合数当X=5k+4，则X+6=5×（k+2）为合数因此只能取X=5k，且k取1即X=5 ∴1个A BECFMNDP7、据说美国有一位铁路职员花了50多年业余时间，研究得到了一个六角形幻方，如图所示的每一个圆中分别填写了1，2，…，19中的一个数字（不同的圆中填写的数字各不相同），使得图中每一个横或斜方向的线段上几个圆内的数之和都相等，现在已知该图中七个圆内的数字，则图中的x= ．解：①确定红色的两个数比较容易(11+18=14+15;16+12=13+15)。

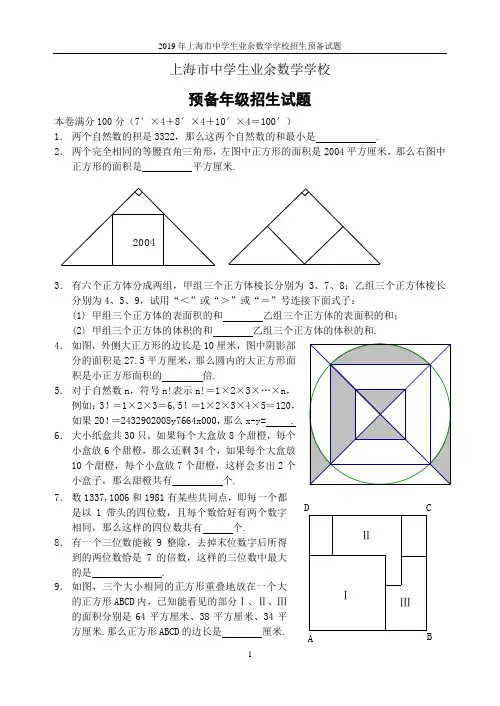
上海市中学生业余数学学校预备年级招生试题本卷满分100分（7′×4＋8′×4＋10′×4＝100′）1． 两个自然数的积是3322，那么这两个自然数的和最小是 .2． 两个完全相同的等腰直角三角形，左图中正方形的面积是2004平方厘米，那么右图中正方形的面积是 平方厘米.20043． 有六个正方体分成两组，甲组三个正方体棱长分别为3、7、8；乙组三个正方体棱长分别为4、5、9，试用“＜”或“＞”或“＝”号连接下面式子：(1) 甲组三个正方体的表面积的和 乙组三个正方体的表面积的和； (2) 甲组三个正方体的体积的和 乙组三个正方体的体积的和. 4． 如图，外侧大正方形的边长是10厘米，图中阴影部分的面积是27.5平方厘米，那么圆内的大正方形面积是小正方形面积的 倍.5． 对于自然数n ，符号n!表示n!＝1×2×3×…×n ，例如：3！＝1×2×3＝6,5！＝1×2×3×4×5＝120，如果20！＝2432902008y7664x000，那么x-y= . 6． 大小纸盒共30只，如果每个大盒放8个甜橙，每个小盒放6个甜橙，那么还剩34个，如果每个大盒放10个甜橙，每个小盒放7个甜橙，这样会多出2个小盒子，那么甜橙共有 个. 7． 数1337,1006和1981有某些共同点，即每一个都是以1带头的四位数，且每个数恰好有两个数字相同，那么这样的四位数共有 个.8． 有一个三位数能被9整除，去掉末位数字后所得到的两位数恰是7的倍数，这样的三位数中最大的是 .9． 如图，三个大小相同的正方形重叠地放在一个大的正方形ABCD 内，已知能看见的部分Ⅰ、Ⅱ、Ⅲ的面积分别是64平方厘米、38平方厘米、34平方厘米.那么正方形ABCD 的边长是 厘米.ⅢⅡⅠBD CA10.两个整数相加的和是两个数字相同的二位数aa ，并且它们的积是三个数字相同的三位数bbb ，写出所有满足条件的两个整数是 .11.如图，三角形ABC 被分成三角形BEF 和四边形AEFC 两部分，那么三角形BEF 面积和四边形AEFC 面积的比是 .5463BE CF A12.把1、2、3、…、10这十个数字分别填入下列十个空格内，每格一个数字，分别记为1210,,,a a a ，并且相邻三个数字的和不超过16，那么12345678910a a a a a a a a a a --+--+--+＝ .答案：1．1732．2254.53．(1) = (2) < 4．55．-16．2507．4328．9819．12.510. 37和18、74和311. 4:2312.13。

上海预备数学试题及答案一、选择题（每题3分，共30分）1. 下列哪个数是最小的正整数？A. 0B. -1C. 1D. 2答案：C2. 一个数的相反数是-5，这个数是多少？A. 5B. -5C. 0D. 10答案：A3. 如果一个角是直角的两倍，那么这个角的度数是多少？A. 30°B. 60°C. 90°D. 180°答案：D4. 一个等腰三角形的底角是40°，那么顶角的度数是多少？A. 100°B. 80°C. 40°D. 20°答案：B5. 一个数的绝对值是5，这个数可能是？A. 5B. -5C. 5或-5D. 0答案：C6. 下列哪个分数是最简分数？A. 2/4B. 3/6C. 4/8D. 5/10答案：A7. 一个数除以-2等于-3，这个数是多少？A. 6B. -6C. 3D. -3答案：B8. 一个数的平方是25，这个数可能是？A. 5B. -5C. 5或-5D. 0答案：C9. 一个数的立方是-8，这个数是多少？A. 2B. -2C. 8D. -8答案：B10. 一个数的倒数是1/3，这个数是多少？A. 3B. 1/3C. 3/1D. -3答案：A二、填空题（每题4分，共20分）11. 一个数的平方根是4，这个数是______。

答案：1612. 一个数的立方根是2，这个数是______。

答案：813. 一个数的绝对值是7，这个数可能是______或______。

答案：7或-714. 一个数的相反数是-7，这个数是______。

答案：715. 一个数的倒数是2，这个数是______。

答案：1/2三、解答题（每题10分，共50分）16. 计算下列表达式的值：(3+2)×(5-3)。

答案：5×2=1017. 计算下列表达式的值：(-4)×(-3)÷(-2)。

答案：12÷(-2)=-618. 计算下列表达式的值：(-2)³+4²。

2006年上海市中学生业余数学学校预备年级招生考试2006年上海市中学生业余数学学校预备年级招生考试（10月6日 上午8:309:30-）本卷满分100分（7'48'410'4100'⨯+⨯+⨯=）【第1题】有一列数8，88，888，…，888888 个，它们的和的百位数字是_______。

【分析与解】888888888888++++ 个的和的百位数字与88286888888888888-=++++ 个的和的百位数字相同；868888888888888888888676464++++=++⨯= 个；即86888888888888++++ 个的和的百位数字是4；故888888888888++++ 个的和的百位数字是4。

【第2题】若数20062006200620061006n个能被11整除，则n 的最小值是_______。

【分析与解】因为200611|2006200620061006n个； 所以()()062011|0606060620202010662145n n n n n ++⎛⎫⎛⎫++++++++-++++++++=+-+=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭个个； n 的最小值是7。

2006年上海市中学生业余数学学校预备年级招生考试【第3题】如图，ABCD ，AMOQ ，MBNO ，ONCP ，QOPD 都是矩形，若矩形QOPD 的面积为251cm ，矩形ONCP 的面积为217cm ，矩形MBNO 的面积为229cm ，则四边形MNPQ 的面积2_______cm 。

OQPNM DCBA【分析与解】因为()()()()OQ OP ON OM ON OP OQ OM ⨯⨯⨯=⨯⨯⨯； 所以QOPD MBNO ONCP AMOQ S S S S ⨯=⨯矩形矩形矩形矩形；所以251291787AMOQ QOPD MBNO ONCP S S S S cm =⨯÷=⨯÷=矩形矩形矩形矩形；所以251172987184ABCD QOPD ONCP MBNO AMOQ S S S S S cm =+++=+++=矩形矩形矩形矩形矩形； 因为PQO PQD S S ∆∆=，PNO PNC S S ∆∆=，MNO MNB S S ∆∆=，QMO QMA S S ∆∆=； 所以22184292MNPQ ABCD S S cm =÷=÷=四边形矩形。

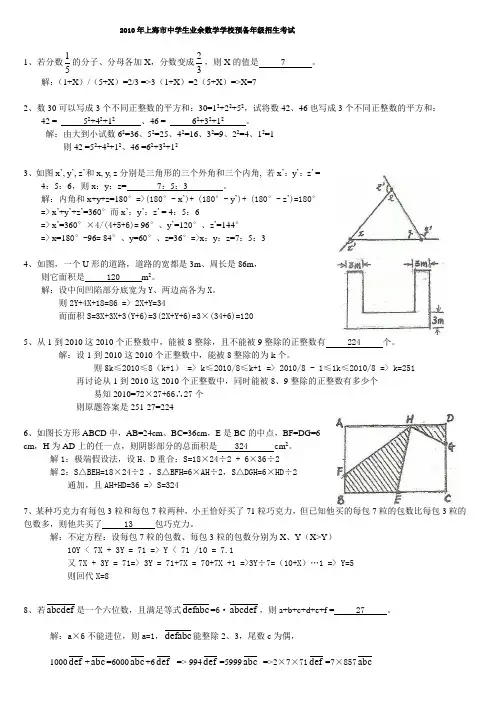
2010年上海市中学生业余数学学校预备年级招生考试1、若分数51的分子、分母各加X ，分数变成32，则X 的值是 7 。

解：（1+X ）/（5+X ）=2/3 =>3（1+X ）=2（5+X ）=>X=72、数30可以写成3个不同正整数的平方和：30=12+22+52，试将数42、46也写成3个不同正整数的平方和：42 = 52+42+12 、46 = 62+32+12 。

解：由大到小试数62=36、52=25、42=16、32=9、22=4、12=1则42 =52+42+12、46 =62+32+123、如图x ’, y ’, z ’和x, y, z 分别是三角形的三个外角和三个内角, 若x ’：y ’：z ’ =4：5：6，则x ：y ：z= 7：5：3 。

解：内角和x+y+z=180°=>(180°- x ’)+ (180°- y ’)+ (180°- z ’)=180°=> x ’+y ’+z ’=360°而x ’：y ’：z ’ = 4：5：6=> x ’=360°×4/(4+5+6)= 96°、y ’=120°、z ’=144°=> x=180°-96= 84°、y=60°、z=36°=>x ：y ：z=7：5：34、如图，一个U 形的道路，道路的宽都是3m 、周长是86m ，则它面积是 120 m 2。

解：设中间凹陷部分底宽为Y 、两边高各为X 。

则2Y+4X+18=86 => 2X+Y=34而面积S=3X+3X+3(Y+6)=3(2X+Y+6)=3×(34+6)=1205、从1到2010这2010个正整数中，能被8整除，且不能被9整除的正整数有 224 个。

解：设1到2010这2010个正整数中，能被8整除的为k 个。

上海建平中学西校预备班分班考试数学试卷（含答案）上海建平中学西校预备班分班考试数学试卷⼀、是⾮题（对的在括号⾥⾯画“√”，错的画“×”，每题 1 分，共 10 分）1、10 个 10 是 100，10 个⼗分之⼀是百分之⼀2、 0.749 保留⼀位⼩数约是 0.7 （）3、⼀个数乘⼩数，积⼀定⼩于这个数（）4、 3.5 和 3.50 的意义相同（）5、 3x 5x 8 是⽅程（）6、37÷4 的商是⽆限⼩数（）7、（ 135 1.08）÷9 = 13.5 ÷0.9 1.08 ÷0.9 （）8、9 与 x 的 4 倍的和是 9 4x（）9、⼩数点左边第⼆位是⼗位，右边第⼆位是⼗分位（）10、不等式 0.542＜0.5 □3中，□中可填 6 个数字（）⼆、选择题（每题 2 分，共 16 分）11、与 1.4 最接近的⼀个数是（）A. 0B. 1C. 1.9D. 212、⼤于 0.7 ⽽⼩于 0.9 的⼩数有（）A. 1个B. 9 个 C . ⽆数个 D. 10个13、⽤ 1、2、3 和⼀个⼩数点组成的最⼤的⼀位⼩数是（）A. 12.3B. 23.1C. 32.1D. 21.314、⼀个⼩数的⼩数点向右移动三位，再向左移动两位，原数会（ )A. 扩⼤ 10 倍B. 缩⼩ 10 倍C. 不变D. 缩⼩ 100 倍15、与 0.456 ×2.1 结果相同的算式是（ )A. 4.56 ×21B. 0.0456×21C. 45.6 ×0.21D. 456 ×0.02116、下⾯各题中，结果最⼤的是（ )A. 2.46 ×0.15B. 2.46 ÷0.15C.2.46 ×1.5D. 2.46 ÷1.517、⾷堂每天⽤⼤⽶a 千克，⽤了 2 天后还剩下 b 千克，原有⼤⽶（ )千克。

2001年上海市中学生业余数学学校预备年级招生试题（2001年10月6日上午8:00~9:30）1. 某学校共有1000名学生，其中男学生人数与女学生人数的比是2:3，女学生人数与教师人数的比是8:1。

那么教师有___________名。

2. 有一筐苹果和一筐梨，如果每天吃掉1个苹果2个梨，那么梨吃完时还剩下3个苹果；如果每天吃掉2个苹果3个梨，那么苹果吃完时还剩下5个梨，这筐苹果有_________个，这筐梨有__________个。

3. 若abcd为一个四位数，且a=d，b=c，则称这个数为四位对称数。

四位对称数共有__________个。

4. 在一个圆周上有7个点，正好将圆周七等分，以这些点为顶点作三角形，可以作___________个等腰三角形。

5. 已知S n=1-2+3-4+5-6+…+(-1)n+1n，其中n是正整数。

那么S2001+S2002=________。

6. 一个两位数N具有性质：N与颠倒N的数字后的数之和为完全平方数，则这样的N有___________个。

7. 数119具有以下性质：当它被2除余1；被3除余2；被4除余3；被5除余4；被6除余5；那么，具有这样性质的三位数（包括数119在内）共有_____个。

8. 有两部自动换币机，第一部能将一枚硬币换成二枚其它硬币；第二部能将一枚硬币换成五枚其它硬币，某人进行了14次换币，将一枚硬币换成了42枚硬币。

则他在第一，第二部换币机上分别换了________，________次。

9. 某人一块手表比家里的钟每小时快15秒，已知家里的钟比标准时间每小时慢15秒，则这快手表比标准时间一昼夜____________秒（填快或慢多少秒）10. A，B，C，D，E五个人中，其中任取4个人的平均年龄再加上余下一个人的年龄所得的和分别为37，40，49，58，64，则这五个人中年龄最大的比年龄最小的大___________岁。

11. 一次乒乓球比赛有A ，B ，C ，D ，E 五名选手参加，他们来自湖北，广东，福建，北京和上海，经调查知道：（1）A 仅与另外两名运动员比赛过；（2）上海运动员与另外三名运动员比赛过；（3）B 没有和广东运动员比赛过；（4）福建运动员和C 比赛过；（5）广东，福建。

2005年上海市中学生业余数学学校预备年级招生试题（10月6日 上午8∶30—9∶30） 本卷满分100分（7/×4+8/×4+10/×4 =100/）1、在平面上画一个长方形能把平面分成两个部分，如果画三个长方形，那么最多能把平面分成 部分。

解：1个长方形 4个角（2部分）；2个长方形 最多是八角星形（10部分）；3个长方形 最多是12角星形：新长方形把原来八角星的角分出成为新的部分（+8）， 新长方形自己新加入的角也成为新部分（+4）； 原来两角间凹陷部分有一半也成为新部分（4）； ∴共10+8+4+4=26个部分2、n ×7的积的末四位数是2005，那么n 的最小值是 。

解1 数字谜+逆推：1715解2 数论整除：设 a2005整除7，则a2-005要能被7整除。

a2最小取12 所以 n=1200÷7=17153、一只箱子装有标号为1、2、3、…、2005的2005张卡片，现从箱子中随意取出x 张卡片，但是为了确保 这x 张卡片中至少有两张卡片标号的差是5，那么x 至少是 。

解：最倒霉拿连着5个数 空5个数 再拿5个数 再空…；2000÷2+5+1=10064、一名收藏家拥有m 块宝石，如果他拿走最重的3块宝石，那么宝石的总重量会减少35％，如果他从余下的宝石中再拿走最轻的3块，那么余下宝石的重量会再减少5/13，则m ＝ 。

解：三块最重的重0.35, 平均每块重 0.107；三块最轻的重(1-0.35) ×(5/13)=0.25, 平均每块重 0.083；则剩下的共重1-0.35-0.25=0.40若剩3块，则每块重0.40/3=0.133>0.107,所以剩下的多于3块； 若剩5块，则每块重0.40/5=0.080<0.083,所以剩下的少于5块； 所以剩下的只能是4块,加最大3块，最小3块，共10块5、在正方形ABCD 中，切去四个三角形得到一个五边形EFGHI （如右图，其中所标的数表示各线段的长度），线段IJ 将五边形EFGHI 分成两个面积相等的部分，那么FJ 的长度是 。

2010年上海市中学生业余数学学校预备年级招生考试2010年上海市中学生业余数学学校预备年级招生考试【第1题】若分数15的分子、分母各加X ，分数变成23，则X 的值是_______。

【分析与解】（方法一）()()125331257X X X X X +=++=+=即X 的值是7。

（方法二）约分之前，分母比分子大514-=；分数15的分子、分母各加X ，分数的分子为()43228÷-⨯=，分母为()432312÷-⨯=；即18512X X +=+； 故X 的值是7。

【第2题】数30可以写成三个不同正整数的平方和：22230125=++试将数42，46也写成三个不同正整数的平方和： 42_____________=；46_____________=。

【分析与解】211=，224=，239=，2416=，2525=，2636=； 先考虑最大的整数的平方；经尝试，22242145=++，22246136=++。

2010年上海市中学生业余数学学校预备年级招生考试【第3题】如图，'x ，'y ，'z 和x ，y ，z 分别是三角形的三个外角和三个内角，若':':'4:5:6x y z =，则::_______x y z =。

z' y'x'yx z【分析与解】因为':':'4:5:6x y z =；所以设'4x k = ，'5y k = ，'6z k = （0k ≠）；则()180'1804x x k =-=-，()180'1805y y k =-=-，()180'1806z z k =-=-； 三角形内角和等于180 ；()()()180418051806180k k k -+-+-=； 三角形外角和等于360 ；456360k k k ++=； 24k =；84x = ，60y = ，36z = ； ::84:60:367:5:3x y z == 。

2008 年上海市中学生业余数学学校 预备年级招生考试
城隍喵
【第 6 题】 如图， 四个一样大小的正方形和七个一样的小长方形拼成一个大长方形， 如果大长方形的面积是 30 平方分 米，那么这个大长方形的周长是 _______ 分米。
【分析与解】
3 个小长方形组成的小长方形与 4 个小正方形组成的小长方形的长、宽分别相等，故面积也相等； 那么大长方形的面积相当于 10 个小长方形的面积； 小长方形的面积为 30 10 3 平方分米； 4 个小正方形的面积为 3 3 9 平方分米； 即 3 个小长方形的面积为 9 平方分米；
2008 年上海市中学生业余数学学校 预备年级招生考试
城隍喵
【第 4 题】 1 ， 2 ， 3 ，…， 2007 ， 2008 这 2008 个数中，数码 0 共有 _______ 。 【分析与解】 先考虑 0 ~ 1999 中的数； 将所有 0 ~ 1999 所有的数都看成四位数，不足四位的在前面补 0 ，即看成 0000 ~ 1999 ； 个位数字是 0 的，千位、百位、十位可以是 000 ~ 199 ，有 200 个数； 十位数字是 0 的，千位、百位、个位可以是 000 ~ 199 ，有 200 个数； 百位数字是 0 的，千位、十位、个位可以是 000 ~ 199 ，有 200 个数； 千位数字是 0 的，百位、十位、个位可以是 000 ~ 999 ，有 1000 个数； 则 0000 ~ 1999 中，一共有 200 200 200 1000 1600 个数字 0 ； 0 ~ 9 ，每个数多算了 3 个数字 0 ，一共有多算了 3 10 30 个数字 0 ； 10 ~ 99 ，每个数多算了 2 个数字 0 ，一共有多算了 2 90 180 个数字 0 ； 100 ~ 999 ，每个数多算了 1 个数字 0 ，一共有多算了 1 900 900 个数字 0 ； 0 ~ 1999 中，一共有 1600 30 180 900 490 个数字 0 ； 因为 0 有 1 个数字 0 ， 2000 ~ 2008 一共有 3 2 2 2 19 个数字 0 ；

中任取 5 张牌，使则 5 张牌同花色，且点数顺次相连，则不同的抽法共有 __________种。
9. 小胡和小涂计算甲，乙两个两位数的乘积。小胡看错了甲数的个位数字，计 算结果为 1274 ，小涂看错了甲数的十位数字，计算结果为 819 ，则甲数是 _____________。 10. 把一个长方形菜地分成三块，如图所示，已 知第二块比第一块宽 10 米，第二块面积为 1000 平方米；第三块比第一块窄 4 米，第三块面积是 650 平方米，那么第一块的面积是_____________平方米。 11. 一 条 单 轨 铁 路 线 上 有
本卷满分 100 分（7 ×4+8 ×4+10/×4 =100/）
1、A、B 两城市相距 625 千米，小王从 A 市于上午 5:30 出发，以每小时 100 千米的速 度驶向 B 市．小王出发 15 分钟后，小张从 B 市以每小时 80 千米的速度驶向 A 市．则两人 点 分在途中相遇． 于 2、某城市的外环公路总长 61 千米，为了联络需要在环路边设置应急电话亭，要求每两 个电话亭． 个电话亭之间的距离不超过 2 千米，那么外环路边最少需要设置 3、运相同的 78 箱货物，如果用能装 5 箱货物的大卡车运一次，运费为 130 元，如果用 能装 2 箱货物的小卡车运一次，运费为 60 元，合理选择大、小卡车的辆数，可使得总运费 ． 最省，最省的总运费为 4、在如图所示的街道示意图中，从 A 到 B 的最短路线共有 条．
5 ，则 m＝ 13
。
B
5
I
3
ቤተ መጻሕፍቲ ባይዱ
C
5、在正方形 ABCD 中，切去四个三角形得到一个 五边形 EFGHI （如右图， 其中所标的数表示各线段 的长度） ， 线段 IJ 将五边形 EFGHI 分成两个面积相 等的部分，那么 FJ 的长度是 。

2006年上海市中学生业余数学学校预备年级招生试题（10月6日 上午8∶30—9∶30） 本卷满分100分（7/×4+8/×4+10/×4 =100/）1、有一列数8，88，888，…，888…888（88个8），他们的和的百位数是 4 。

解：个位88个8，十位87个8，百位86个8：88×8+87×80+86×800=704+6960+68800 =。

464（或888×86+88+8）2、若数10062006 (200620062006)个n 能被11整除，则n 的最小值是 7 。

解：（6n +6）-（2n+1）=4n+5能整除11，试数n=73、如图，ABCD 、AMOQ 、MBNO 、ONCP 、QOPD 都是矩形，若矩形QOPD 的面积为51cm 2，矩形ONCP 的面积为17 cm 2，矩形MBNO 的面积为29cm 2，则四边形MNPQ 的面积为 92 cm 2。

解：矩形QOPD 的面积为a ×b=51cm 2，矩形ONCP 的面积为b ×c=17 cm 2，矩形MBNO 的面积为c ×d=29cm 2（a ×b ）（c ×d ）÷（b ×c ）=a ×d=51×29÷17=87，则平行四边形一般定理（51+17+29+87）/2=924、1到100中，满足既是4的倍数加1，又是5的倍数减1的所有质数的和为 118 。

解：5的倍数减1，尾数为9或4（舍），枚举验证：29+89=1185、一个五位数，五个数字各不相同，且是23的倍数，则符合条件的最小的数是 10235 。

解：[10234÷23]=444，试数445×23=102356、一些笔记本分给某班学生， 若只平均分给女生， 则每位女生可分得15本； 若只平均分给男生， 则每位男生可分得10本。

上海市中学生业余数学学校预备年级招生试题1. 某学校共有1000名学生，其中男学生人数与女学生人数的比是2:3，女学生人数与教师人数的比是8:1。

那么教师有___________名。

2. 有一筐苹果和一筐梨，如果每天吃掉1个苹果2个梨，那么梨吃完时还剩下3个苹果;如果每天吃掉2个苹果3个梨，那么苹果吃完时还剩下5个梨，这筐苹果有_________个，这筐梨有__________个。

3. 若为一个四位数，且a=d，b=c，则称这个数为四位对称数。

四位对称数共有__________个。

4. 在一个圆周上有7个点，正好将圆周七等分，以这些点为顶点作三角形，可以作___________个等腰三角形。

5. 已知Sn=1-2+3-4+5-6+…+(-1)n+1n，其中n是正整数。

那么S2001+S2002=________。

6. 一个两位数N具有性质：N与颠倒N的数字后的数之和为完全平方数，则这样的N有___________个。

7. 数119具有以下性质：当它被2除余1;被3除余2;被4除余3;被5除余4;被6除余5;那么，具有这样性质的三位数(包括数119在内)共有_____个。

8. 有两部自动换币机，第一部能将一枚硬币换成二枚其它硬币;第二部能将一枚硬币换成五枚其它硬币，某人进行了14次换币，将一枚硬币换成了42枚硬币。

则他在第一，第二部换币机上分别换了________，________次。

9. 某人一块手表比家里的钟每小时快15秒，已知家里的钟比标准时间每小时慢15秒，则这快手表比标准时间一昼夜____________秒(填快或慢多少秒)10. A，B，C，D，E五个人中，其中任取4个人的平均年龄再加上余下一个人的年龄所得的和分别为37，40，49，58，64，则这五个人中年龄最大的比年龄最小的大___________岁。

11. 一次乒乓球比赛有A，B，C，D，E五名选手参加，他们来自湖北，广东，福建，北京和上海，经调查知道：(1)A仅与另外两名运动员比赛过;(2)上海运动员与另外三名运动员比赛过;(3)B没有和广东运动员比赛过;(4)福建运动员和C比赛过;(5)广东，福建。

2007年上海市中学生业余数学学校预备年级招生考试2007年上海市中学生业余数学学校预备年级招生考试（10月13日 上午8:309:30-）本卷满分100分（7'48'410'4100'⨯+⨯+⨯=）【第1题】数2727272727和5454545463的最大公约数是_______。

【分析与解】 辗转相除法：5454545463272727272729÷= ； 27272727279303030303÷=；()()2727272727,54545454632727272727,99==；即数2727272727和5454545463的最大公约数是9。

【第2题】设999999999999n =++++个，则n 的十进制表示中数码1有_______个。

【分析与解】()()()99999099999999910110011000110001n ⎛⎫=++++=-+-+-++- ⎪ ⎪⎝⎭个个99197197199199010100100010001111111019911111099111011⎛⎫⎛⎫=++++-++++=-⨯=-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭ 个个个个个； 故n 的十进制表示中数码1有99个。

2007年上海市中学生业余数学学校预备年级招生考试【第3题】在平行四边形PQRS 中，点T 在边PS 上，且:3:2PT TS =，则四边形PQRT 的面积与平行四边形PQRS 的面积之比是_______。

TSRQ P【分析与解】 （方法一）PQ RST连接PR ；因为:3:2PT TS =； 所以:3:2PTR TSR S S ∆∆=； 所以:2:5TSR PSR S S ∆∆=； 因为2PSR PQRS S S ∆=⨯平行四边形； 所以:2:101:5TSR PQRS S S ∆==平行四边形； 所以:4:5PQRT PQRS S S =四边形平行四边形。

2017年上海市中学生业余数学学校预备年级招生考试试题（10月21日上午8:30~9:30）本卷满分100分（10’×10=100’）1.计算：（1）2017×20162016-2016×20172017=________.（2）1331215++++++=________.51326425865382.有一个四位正整数，在它的某位数字前加上一个小数点，再与这个四位数相加，得到数2037.17，则这个四位数是________.3.已知一列数：2017,2016,1,2015,20XX,1,20XX,20XX,1，…，3,2,1，则这一列数中，从左向右数，第2017个数是________.4.五年级某班有26名男生.在一次考试中，该班有30人得分超过85分，则这次考试中，该班女生中得分超过85分的人数比男生中得分没有超过85分的人数多________人.5.某人工作一月（按30天计算）的酬金是1800元加一台自动洗衣机.实际上，他做了12天，得到60元和一台自动洗衣机，则这台自动洗衣机的价值为________元.6.如图，在四边形ABCD中，已知AB=BC=a cm，AD=DC=b cm（a，b为整数），∠DAB=∠BCD=90°，且四边形ABCD的面积为385cm2，则四边形ABCD周长的最小值是________cm.7.有三堆棋子，每堆棋子一样多，且都由黑白两色棋子组成.已知第一堆的黑棋和第二堆的白棋数目相等，第三堆的黑.若把三堆棋占三堆全部黑棋的25棋子并成一堆，则在这一堆棋子中，白棋占全部棋子的________（填一个分数）.8.如图，由12条线段搭成一个空间框架.框架中两条没有公共端点的线段是不相交的，例如AC与BD是一对不相交的线段（这里AC，BD没有次序之分），则这个框架的12条线段中，不相交的线段有________对.9.在如图的10个小方格里分别填上1,2,3,4,5,11,12,13,14,15十个数，使三个2×2的正方形中的四个数的和都相等，则这个和的最大值是________. 10.有64个1×1×1的小正方体，其中34个是白色的，30个是黑色的.现将它们拼成一个4×4×4的大正方体，则大正方体表面黑色部分面积的最小是________.2017年上海市中学生业余数学学校高一年级招生考试试题（10月21日上午10:00~11:30）________区__________________学校，姓名___________准考证号________________得分评分 复核本卷满分100分（10’×10=100’） 1.如图，直线122y x =--与G 轴、y 轴分别交于 A 点、B 点，把△AOB （O 为坐标原点）沿直线AB翻折，点O 落在点C 处，则点C 的坐标是________.2.如图，直线AB 、AC 切圆O 于B 、C 两点，点P 在圆O 上，且到AB 、AC 的距离PM 、PN 分别为1、2，则点P 到直线BC 的距离PQ 的长为________.3.已知23()2|1|1,02f x x x x =---≤≤，则()f x 的值域是________. 4.已知a 、b 、G 、y 都是实数，且aG +by =4，aG 2+by 2=2，aG 3+by 3=1，则aG 4+by 4的值是________.5.如图，正方形DEFG 内接于△ABC ，正方形HIJ K内接于△AGF ，若BC=a ，KJ=m ，则正方形DEFG的面积为________.6.如图，在△ABC 中，∠ACB=90°，CA=CB=2，O 为AC 的中点，以AC 为直径作⊙O ，OB 交⊙O 于点D ，AD 的延长线交CB 于点E ，则CE 的长为________.7.一个五位数乘以某一整数k （28k ≤≤），得到该五位数的反序数（把一个n 位正整数的各位数码顺序颠倒过来得到的新的n 位整数称为原数的反序数. 例如12345的反序数为54321），则原来的五位数是________________.8.已知a 、b 为实数，且224a ab b ++=，则22a ab b -+的取值范围为 ________________.9.从集合{|,11000}x x N x ∈≤≤中取出k 个数，使得取出的k 个数中，任意三 个数之和总能被18整除，则k 的最大值为________.10.已知凸五边形ABCDE 的面积为1，且△ABC,△BCD,△CDE,△DEA,△EAB 的 面积都相等，则△ABC 的面积为________.2017年上海市中学生业余数学学校招生试题答案预备年级1.（1）0;（2）242.20173.6734.45.11006.927.948.36 9.3310.22高一年级 1.)516,58(-- 2.2 3.[-2,1]4.21 5.am6.15- 7.219788.[34,12] 9.5610.1055-。