齿面接触强度计算

直齿圆柱齿轮传动的齿面接触强度计算
弹性力学的Hertz公式：
分析：1. 啮合点不同，曲率半径不同；
2.一般情况下，ε＞1，1对齿，2对齿啮合时，
σH不同（Fn不同）。

应该按齿廓的哪一点来计算σH？
研究表明：
点蚀最容易发生在齿根靠近节圆处（单对齿啮合区的边界）。

故：1. 综合曲率半径按节圆处两齿廓的曲率半径计算
其中，u是大轮与小轮的齿数比
2. Fn按单对齿啮合计算
针对钢制齿轮，引入钢的泊松比μ1= μ2 =0.3，钢的弹性模量
E=2.06×105 MPa，载荷系数K，中心距a，得齿面接触强度的验算公式：令齿宽系数ψa ＝b／d1，代入上式得中心距：
分析：当一对齿轮的材料、传动比、齿宽系数一定时，接触应力σH 仅取决于分度圆直径d或中心矩a，与模数m无关。

即：两对分度圆直径对应相等的齿轮传动，具有相同的接触强度，与各自模数无关。

即：增大模数m（但d不改变），不能提高齿面接触强度。

关于齿宽系数ψa
理论上讲，ψa越大，a越小，结构越紧凑。

但实际上，ψa↑，可能降低结构的刚性，载荷分布越不均匀，轮齿更易折断。

许用接触应力按下式计算：
式中: σHlim为试验齿轮的接触疲劳强度
极限，按图11－7查得；
S H为齿面接触疲劳安全系数，查表11－4得到。

图11－7。

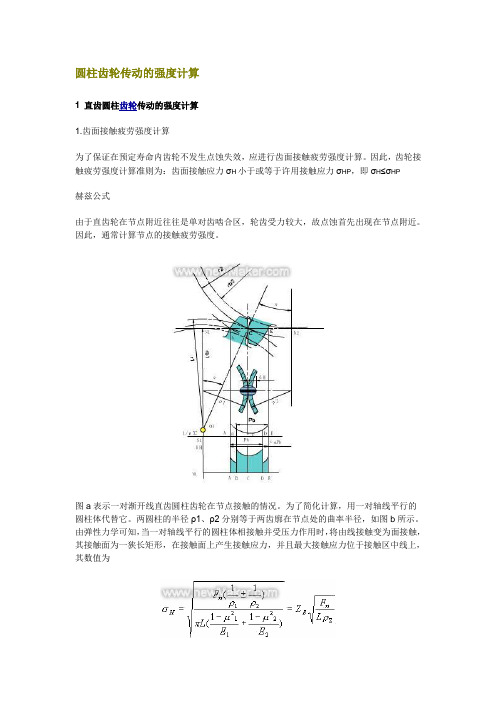
圆柱齿轮传动的强度计算1 直齿圆柱齿轮传动的强度计算1.齿面接触疲劳强度计算为了保证在预定寿命内齿轮不发生点蚀失效，应进行齿面接触疲劳强度计算。

因此，齿轮接触疲劳强度计算准则为：齿面接触应力σH小于或等于许用接触应力σHP，即σH≤σHP赫兹公式由于直齿轮在节点附近往往是单对齿啮合区，轮齿受力较大，故点蚀首先出现在节点附近。

因此，通常计算节点的接触疲劳强度。

图a表示一对渐开线直齿圆柱齿轮在节点接触的情况。

为了简化计算，用一对轴线平行的圆柱体代替它。

两圆柱的半径ρ1、ρ2分别等于两齿廓在节点处的曲率半径，如图b所示。

由弹性力学可知，当一对轴线平行的圆柱体相接触并受压力作用时，将由线接触变为面接触，其接触面为一狭长矩形，在接触面上产生接触应力，并且最大接触应力位于接触区中线上，其数值为式中σH-接触应力（Mpa）Fn-法向力（N）L-接触线长度（mm）rS-综合曲率半径（mm）；±-正号用于外接触，负号用于内接触ZE-材料弹性系数（），，其中E1、E2分别为两圆柱体材料的弹性模量（MPa）；m1、m2分别为两圆柱体材料的泊松比。

上式表明接触应力应随齿廓上各接触点的综合曲率半径的变化而不同，且靠近节点的齿根处最大（图c、d）。

但为了简化计算，通常控制节点处的接触应力。

节点处的参数（1）综合曲率半径由图可知，，代入rE公式得式中：，称为齿数比。

对减速传动，u=i；对增速传动，u=1/i。

因，则有（2）计算法向力（3）接触线长度L引入重合度系数Ze，令接触线长度将上述参数代入最大接触应力公式得接触疲劳强度计算公式令，称为节点区域系数。

则得(1) 齿面接触疲劳强度的校核公式齿面接触疲劳强度的校核公式为(2) 齿面接触疲劳强度设计公式设齿宽系数，并将代入上式，则得齿面接触疲劳强度的设计公式式中:d1-小齿轮分度圆直径（mm）；ZE-材料弹性系数()，按下表查取；注：泊松比m1＝m2＝0.3Z H-节点区域系数，考虑节点处轮廓曲率对接触应力的影响，可由下左图查取。

齿面接触强度及齿根弯曲强度核算在设计产品过程中，经常会选用齿轮作为传动力及扭矩的原件。

在大部分成型产品改造或调整过程中，关于齿轮的强度校核这一步骤就可以用类比法代替，从而节省设计人员的精力，缩短了设计周期。

但得出的结果没有书面依据以及理论方面的支持。

所以当进行多次类比之后，所设计出来的齿轮与理论计算得出的齿轮偏差会较大。

其原理类似于累计偏差。

所以应该进行强度校核方面的计算。

齿轮强度校核计算，在实际应用中，主要是两方面的核算：1、齿面接触强度的核算。

2、齿根弯曲强度的核算。

1.齿面接触强度核算-分度圆直径计算参考文献：在初步设计齿轮时，根据齿面接触强度，可按照下列公式估算齿轮传动的尺寸。

(机械设计手册P14-133)a≥A a(μ±1)·√KT1ψaσHP23①d1≥A d·√KT1ψdσHP2·μ±1μ3②公式①为两齿轮中心距的计算；公式②为齿轮分度圆直径的计算。

由于本次计算的是齿轮齿条传动。

所以，中心距a= d1/2其中：d1为齿轮分度圆直径，只需要核算齿轮分度圆直径d1首先，要确定公式②中各个符号代表的含义及数值选取。

d1—齿轮分度圆直径；A d—常系数；K—载荷系数；μ—齿数比；σHP—许用接触应力；ψd—齿宽系数；T1—电机减速机输出扭矩；d1：齿轮分度圆直径，待求；A d：常系数值；A d值在表14-1-65中，通过螺旋角角度β的数值求得。

齿轮的螺旋角β=11.655°,则A d = 756。

载荷系数K，常用值K=1.2～2（机械设计手册P14-133），当载荷平稳，齿宽系数较小，轴承对称布置，轴的刚性较大，齿轮精度较高（6级以上），以及齿轮的螺旋角较大时取较小值；反之取较大值。

根据对比后的结果在K的常用范围内选取。

此次选择K=1.8（载荷平稳，齿宽系数较小，轴为非对称分布，轴的刚性不大，齿轮精度不高）u：传动比。

当齿轮之间为外啮合的时候，选取“+”；当齿轮之间为内啮合的时候，选取“-”，本次计算为齿轮齿条，不影响计算结果。

接触强度计算的尺寸系数
（3）受载时，主、从齿轮接触力的大小相等，接触面积
也相等，故两配对齿轮接触应力是相同的，即σH1=σH2。

但因两齿轮的材料不同、热处理方法不同，其许用应力不同，即：[σH1]≠[σH2 ]。

因此按接触疲劳强度进行设计计算时，只须将[σH1]和[σH2 ]中较小者代入公式即可。

其含义
是齿轮的几何尺寸参数决定于接触强度较弱者。

（4）直齿
圆柱齿轮传动按公式计算出中心距α后，初选齿数z1 ，
z2, 然后按m=2α/(z1+z2)计算出模数m，并圆整为标准值；
斜齿圆柱齿轮传动按公式计算出中心距α后，初选齿数z1 ，z2 以及mn（或β）再按β=arccos[mn(z1+z2)/2α]计算β，或按mn= 2αcosβ/(z1+z2)计算法面模数mn，并圆整为标准值；圆锥齿轮按公式计算出锥距Re后，初选齿数z1 ，z2，再
按计算出大端模数，并圆整为标准值。

（5）在其它参数相同的条件下，齿轮的接触疲劳强度与中心距α或齿轮的分度圆直径d1和d2有关。

分度圆直径d1和d2分别相等的两对齿轮，不论其模数是否相等，均具有相同的接触强度。

模数m不能作为衡量齿轮接触强度的依据。

例如有两对齿
轮传动，其参数分别为m=2，Z1=40，Z2=80和m=4，
Z1=20，Z2=40，则此两对齿轮接触疲劳强度是相同的。

1. 齿轮接触强度计算1.1齿轮接触的计算应力βανεννπσK K K K uu bd F Z Z Z MPa E E R L FH A t E H red H1)(1111222121±⋅=-+-= 式中：A K —工况系数； νK —动载系数；αH K —接触强度的端面载荷分配系数；βK —齿向载荷分布系数；H Z —节点域系数；E Z —弹性系数； εZ 一重合度系数；1.1.1工况系数A K由于齿轮的载荷特性为工作稳定状况下，故取工况系数为A K =1.0. 1.1.2动载系数νK由于=15.96m/s齿轮重合度再根据《机械设计手册》图8-32与8.33得；)=1.48-0.44(1.48-1.22)=1.361.1.3端面载荷分配系数αH K查表8-120得21εαZ C K H H ∙=其中H C 查图8-34为0.865. 1.1.4齿向载荷分布系数βK查图8.35可得βK =1.13. 1.1.5节点域系数H Z式中：错误！未找到引用源。

为端面分度圆压力角；错误！未找到引用源。

为基圆螺旋角；错误！未找到引用源。

为端面啮合角；经计算最后得到H Z =2.254 1.1.6弹性系数E Z带入各值后，得E Z =189.87错误！未找到引用源。

1.1.7重合度系数εZ与1.13的分母约去，不需考虑。

最后得到理论接触应力为：MPaZ mm mm N Z MPa H 67.124413.11865.036.11208.2208.3776.1572.7627.5265287.189254.2=⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯=εεσ1.2 接触疲劳极限lim Hσ' W R V L N H HZ Z Z Z Z lim lim σσ=' 式中： 'H l i m σ表示计算齿轮的接触疲劳极限；H l i m σ表示试验齿轮的接触疲劳极限；N Z 表示接触强度的寿命系数；L Z 表示润滑剂系数；V Z 表示速度系数；R Z 表示光洁度系数；W Z 表示工作硬化系数。

1. 齿面接触疲劳强度的计算齿面接触疲劳强度的计算中，由于赫兹应力是齿面间应力的主要指标，故把赫兹应力作为齿面接触应力的计算基础，并用来评价接触强度。

齿面接触疲劳强度核算时，根据设计要求可以选择不同的计算公式。

用于总体设计和非重要齿轮计算时，可采用简化计算方法；重要齿轮校核时可采用精确计算方法。

分析计算表明，大、小齿轮的接触应力总是相等的。

齿面最大接触应力一般出现在小轮单对齿啮合区内界点、节点和大轮单对齿啮合区内界点三个特征点之一。

实际使用和实验也证明了这一规律的正确。

因此，在齿面接触疲劳强度的计算中，常采用节点的接触应力分析齿轮的接触强度。

强度条件为：大、小齿轮在节点处的计算接触应力均不大于其相应的许用接触应力，即：⑴圆柱齿轮的接触疲劳强度计算1）两圆柱体接触时的接触应力在载荷作用下，两曲面零件表面理论上为线接触或点接触，考虑到弹性变形，实际为很小的面接触。

两圆柱体接触时的接触面尺寸和接触应力可按赫兹公式计算。

两圆柱体接触，接触面为矩形（2axb），最大接触应力σHmax位于接触面宽中线处。

计算公式为：接触面半宽:最大接触应力:•F——接触面所受到的载荷•ρ——综合曲率半径，（正号用于外接触，负号用于内接触）•E1、E2——两接触体材料的弹性模量•μ1、μ2——两接触体材料的泊松比2）齿轮啮合时的接触应力两渐开线圆柱齿轮在任意一处啮合点时接触应力状况，都可以转化为以啮合点处的曲率半径ρ1、ρ2为半径的两圆柱体的接触应力。

在整个啮合过程中的最大接触应力即为各啮合点接触应力的最大值。

节点附近处的ρ虽然不是最小值，但节点处一般只有一对轮齿啮合，点蚀也往往先在节点附近的齿根表面出现，因此，接触疲劳强度计算通常以节点为最大接触应力计算点。

参数直齿圆柱齿轮斜齿圆柱齿轮节点处的载荷为综合曲率半径为接触线的长度为，3）圆柱齿轮的接触疲劳强度将节点处的上述参数带入两圆柱体接触应力公式，并考虑各载荷系数的影响，得到：接触疲劳强度的校核公式为：接触疲劳强度的设计公式为：•KA——使用系数•KV——动载荷系数•KHβ——接触强度计算的齿向载荷分布系数•KHα——接触强度计算的齿间载荷分配系数•Ft——端面内分度圆上的名义切向力，N；•T1——端面内分度圆上的名义转矩，N.mm；•d1——小齿轮分度圆直径，mm；•b ——工作齿宽，mm，指一对齿轮中的较小齿宽；•u ——齿数比；•ψd——齿宽系数，指齿宽b和小齿轮分度圆直径的比值（ψd=b/d1）。

齿面接触强度计算一、概念齿面接触强度是指齿轮齿面在传动过程中所承受的应力强度。

以传动过程中的一个齿对为研究对象，齿面接触强度可以用接触应力或接触压力来表示。

接触应力为单位齿宽上的接触力，接触压力为单位齿面接触面积上的接触力。

齿面接触强度计算的目的是为了确定齿面接触强度是否在允许范围内，以判断齿轮齿面的强度是否足够，从而保证传动的安全可靠。

二、计算方法1.弹性接触理论法弹性接触理论法是基于弹性力学理论推导出的一种计算方法，适用于小模数的齿轮。

该方法假设接触区域为一个等效的半椭球面，通过对接触区域的弹性变形和力学平衡关系进行求解，得到接触应力或接触压力的计算公式。

接触应力或接触压力与载荷、齿轮几何参数和材料性能有关。

2.接触应力分析法接触应力分析法是通过有限元分析等数值方法对齿轮接触区域进行分析，得到接触应力分布的方法。

首先根据齿轮的几何参数和载荷情况建立有限元模型，然后进行接触应力分析，最后通过结果分析判断齿面接触强度是否满足要求。

接触应力分析法可以得到更精确的接触应力分布，适用于大模数和复杂齿形的齿轮。

三、应用实例以一对调整齿轮为例，齿轮参数如下：模数m=2mm，齿数z1=20，z2=30，齿轮宽度b=40mm，法向载荷Ft=1000N，转速n=1000r/min。

根据给定参数，可以采用弹性接触理论法或接触应力分析法计算齿面接触强度。

采用弹性接触理论法，根据经验公式得到接触应力σt=1.2√(Ft/(m·b))=48MPa。

根据齿面接触强度的规定，该齿轮的接触应力在允许范围内，齿面接触强度满足要求。

采用接触应力分析法，建立有限元模型，进行接触应力分析，得到齿面接触应力分布。

通过结果分析，判断齿轮齿面的接触强度是否满足要求。

综上所述，齿面接触强度的计算是齿轮传动设计中的重要环节。

齿面接触强度的计算方法有弹性接触理论法和接触应力分析法。

通过合适的计算方法和实例分析，可以判断齿面接触强度是否满足要求，保证齿轮传动的安全可靠运行。

齿轮承载能力作者：佚名文章来源：网络转载点击数： 3 更新时间：2006-5-2在齿轮传动中﹐齿轮失效前所能传递的最大允许载荷。

齿轮的承载能力取决於齿轮的尺寸﹑结构﹑材质﹑製造水平﹑润滑条件﹑允许的损伤程度﹑要求的寿命和可靠度等。

失效形式齿轮的齿圈﹑轮辐和轮轂等部分通常按经验设计﹐结构尺寸的安全係数较大﹐一般很少遭受破坏。

齿轮的失效主要出现在轮齿上。

轮齿的失效形式主要有轮齿摺断﹑点蚀﹑胶合﹑磨损和塑性变形等(图1 齿轮轮齿的主要失效形式 )。

不过﹐轮齿每一种失效形式的出现并不是孤立的﹐齿面一旦出现了点蚀或胶合﹐就会加剧齿面的磨损﹔齿面的严重磨损又将导致轮齿的摺断等。

轮齿摺断轮齿受载后齿根处的弯曲应力最大﹐当轮齿弯曲应力超过其极限应力时就会发生过载摺断或疲劳摺断。

轮齿摺断一般发生在齿根部分﹐可能一个或多个齿沿齿长整体摺断﹐也可能发生局部摺断。

点蚀在润滑良好的闭式传动中﹐齿面在过高的循环变化的接触应力作用下產生疲劳裂纹﹐裂纹不断扩展蔓延﹐导致工作齿面小块金属剥落﹐形成麻点﹐即点蚀。

点蚀严重时会產生强烈振动和机械噪声﹐使齿轮不能正常工作。

点蚀一般首先出现在节线附近的齿根表面。

胶合在高速重载齿轮传动中﹐油膜会因瞬时高温而破坏﹐相嚙合齿面的金属形成局部熔焊﹐导致较软齿面上的金属撕落﹐形成沟痕。

在低速重载齿轮传动中﹐有时也常因局部压应力很高﹐两接触齿面间油膜被刺破而黏著。

胶合时振动和噪声增大﹐轮齿很快失效。

磨损在闭式传动中﹐润滑油供应不足﹐油不清洁﹐齿面易產生磨损。

在开式传动中﹐灰尘和各种颗粒等进入嚙合齿面会造成磨料磨损。

磨损使齿厚减薄﹑侧隙加大﹐造成衝击﹐降低弯曲强度﹐严重时使轮齿过载摺断。

塑性变形在过大的应力作用下﹐轮齿材料因屈服而產生的塑性流动﹐如齿面碾击塑变﹑鳞皱﹑起脊﹑齿体的歪扭和齿形剧变等。

这些现象多发生在硬度低的齿轮上﹐严重时会破坏正常齿廓﹐使之失去工作能力。

强度计算在机械工程中﹐轮齿的强度计算方法主要有两种。

齿面接触疲劳强度计算由齿面接触疲劳强度计算公式：d≥1、材料弹性系数ZE根据参考文献《机械设计》表8.5查取，材料都为铸铁。

查取ZE =188.0。

2、节点区域系数ZH根据参考文献《机械设计》图8.14查取，此系数反映了节点齿廓形状对接触应力的影响。

查取ZH=2.5。

3、重合度系数Zε根据参考文献《机械设计》图8.15查取，次系数是考虑重合度对齿面接触应力影响的系数。

查处Zε=0.975。

4、齿宽系数dφ，根据参考文献《机械设计》表8.6查取，dφ=0.6。

5、齿宽b根据计算公式b=dφ*d= 0.6×30=18mm。

6、齿轮传递的转矩T1根据计算公式T1= 2F1d1=2×1.2×9.8×50=1176N·mm ZN接触强度计算的寿命系数根据参考文献《机械设计》图8.29查取，ZN=1.15齿面接触疲劳极限minHσ根据参考文献《机械设计》图8.28查取，minHσ=750MPa9接触强度计算的安全系数SH根据参考文献《机械设计》表8.7查取，一般选取SH=1.0。

10许用接触应力[]H σ根据参考文献《机械设计》公式8.26min []/H H N H Z S σσ=代入数据[]H σ=862.5MPa 。

11、设计计算根据公式 其中数据由上可知，带入数据：d=30≥ =11.4所求得满足齿面接触疲劳强度要求。

则可取齿轮的标准分度圆直径d=30。

齿轮齿面强度引言齿轮是一种常用的机械传动元件，它通过齿与齿之间的啮合来实现转动传动。

在齿轮传动中，齿面强度是一个重要的参数，它决定了齿轮的承载能力和使用寿命。

本文将介绍齿轮齿面强度的概念、计算方法和影响因素。

1. 齿面强度的定义齿面强度是指齿轮表面承受外部载荷时不发生破坏的能力。

通常用材料的弹性极限来表示，即当应力达到材料的弹性极限时，就会发生塑性变形或破坏。

2. 齿面强度计算方法2.1 动载荷法动载荷法是一种常用的计算齿面强度的方法。

它基于对啮合过程中产生的接触应力进行分析，并考虑了材料疲劳寿命和安全系数等因素。

具体计算步骤如下： 1. 根据输入功率、转速和传动比等参数计算出实际扭矩； 2. 根据齿轮的模数、齿数和齿轮材料的弹性模量等参数，计算出齿轮的几何参数； 3. 根据几何参数和实际扭矩计算出啮合面上的接触应力； 4. 根据材料的疲劳极限和安全系数，判断是否满足强度要求。

2.2 静载荷法静载荷法是一种简化的计算方法，它假设齿轮在传动过程中只受静态载荷作用，并忽略了动态载荷的影响。

这种方法适用于负载比较小、转速较低或工作环境稳定的情况。

具体计算步骤如下： 1. 根据输入功率、转速和传动比等参数计算出实际扭矩； 2. 根据齿轮的模数、齿数和齿轮材料的弹性模量等参数，计算出齿轮的几何参数； 3. 根据实际扭矩和几何参数计算出啮合面上的接触应力； 4. 根据材料的强度极限，判断是否满足强度要求。

3. 影响齿面强度的因素齿轮齿面强度受到多种因素的影响，包括材料性能、几何参数、工作条件等。

3.1 材料性能材料的硬度、弹性模量和疲劳寿命等性能对齿面强度有重要影响。

一般来说，材料的硬度越高、弹性模量越大，齿轮的齿面强度越高。

同时，材料的疲劳寿命也是一个关键因素，它决定了齿轮在长期使用中是否会发生疲劳破坏。

3.2 几何参数齿轮的几何参数包括模数、齿数、压力角等。

这些参数决定了齿轮的尺寸和形状，直接影响着啮合过程中产生的接触应力和挤压应力。

三、蜗杆传动的强度计算1、蜗轮齿面接触疲劳强度计算，由赫其公式（Hertz)按主平面内斜齿轮与齿条啮合进行强度计算 H n E H L KF Z ][σρσ≤=∑Fn ——法向载荷（N ）;L ——接触线长度（注意蜗杆蜗轮接触线是倾斜的，并计入重合度）；∑ρ——综合曲率半径；Z E ——材料弹性线数，对钢蜗杆↔配青铜蜗轮αMP Z E 160=，代入蜗杆传动有关参数，并化简得 校核公式：H P E H a KT Z Z ][/32σσ≤⋅= Mpa式中，Z E -—材料的弹性系数，钢蜗杆配青铜蜗轮αMP Z E 160=Z P ——接触系数,Z P 为反映蜗杆传动接触线长度和曲率半径对接触强度的影响系数βK K K K V A ⋅⋅=--载荷系数K A ——工况系数βK -—齿面载荷分布系数：1=βK —-载荷平稳6.1~3.1=βK —-载荷变化较大，或有冲击、振动时K V —-动载荷系数 s m V K V /3,1.1~0.12≤=——精制蜗杆s m V K V /3,2.1~1.12>=—-一般蜗杆设计公式：322][⎪⎪⎭⎫ ⎝⎛≥H P E Z Z KT a σmm ⇒定m ，q ，H ][σ——蜗轮齿面许用接触应力(1)当蜗轮材料为铸铁或高强度青铜,ασMP B 300≥—-失效形式为胶合(不属于疲劳失效），∴许用应力H ][σ与应力循环次数N 无关。

（2）若蜗轮材料ασMP B 300<(锡青铜）-—失效形式为点蚀，H ][σ与应力循环次数N 有关。

OH HN H K ][][σσ=OH ][σ——基本许用接触应力HN K —-接触强度寿命系数，8710NK HN =，N 为应力循环次数，h L jn N 260=,n 2为蜗轮转速（r/min ），L h 为蜗轮总工作时数h ，j 为每转一圈每个轮齿啮合次数。

2、蜗轮齿根弯曲疲劳强度计算齿根折断一般发生在Z 2〉90，及开式传动中，∴在闭式传动中弯曲强度计算作为校核计算对于重载传动，通过计算还可差别由于轮齿的弯曲变形量引起的轮齿弹性变形量是否过大而影响蜗杆传动的平稳性。