标准直齿圆柱齿轮齿面接触疲劳强度计算

11-4直齿圆柱齿轮传动的作用力及计算载荷：一、齿轮上的作用力：为了计算齿轮的强度，设计轴和选用轴承，有必要分析轮齿上的作用力。

当不计齿面的摩擦力时，作用在主动轮齿上的总压力将垂直于齿面，（因为齿轮传动一般都加以润滑，齿轮在齿啮合时，摩擦系数很小，齿面所受的摩擦力相对载荷很小，所以不必考虑），即为P175图11-5b所示的Fn（沿其啮合线方向），Fn可分解为两个分力：圆周力：Ft=2T1/d1 N径向力：Fr=Fttgα N而法向力：Fn=Ft/cosα NT1：小齿轮上的扭矩 T1=9550000p/n1 n·mmP：传递的功率（KW） d1：小齿轮分度圆直径 mmα：压力角 n1：小齿轮的转速(r·p·m)Ft1：与主动轮运动方向相反；Ft2与从动轮运动方向一致。

各力的方向 Fr：分别由作用点指向各轮轮心。

Fn：通过节点与基圆相切（由法切互为性质）。

根据作用力与反作用力的关系，主从动轮上各对的应力应大小相等，方向相反。

二、计算载荷：Fn是根据名义功率求得的法向力，称为名义载荷，理论上Fn沿齿宽均匀分布，但由于轴和轴承的变形，传动装置的制造安装误差等原因，载荷沿齿宽的分布并不均匀，即出现载荷集中现象（如P176图11-6所示，齿轮相对轴承不对称布置，由于轴的弯曲变形，齿轮将相互倾斜，这时，轮齿左端载荷增大，轴和轴承刚度越小，b越宽，载荷集中越严重。

此外，由于各种原动机和工作机的特性不同，齿轮制造误差以及轮齿变形等原因，还会引起附加动载荷。

精度越低，圆周速度V越大，附加载荷越大。

因此在计算强度时，通常以计算载荷K·Fn代替名义载荷Fn，以考虑上两因素的影响。

K—载荷系数表达式11-311-5 直齿圆柱齿轮的齿面接触强度计算：一、设计准则：齿轮强度计算是根据齿轮失效形式来决定的，在闭式传动中，轮齿的失效形式主要是齿面点蚀，开式传动中，是齿轮折断，在高速变截的齿轮传动中，还会出现胶合破坏，因胶合破坏的计算方法有待进一步验证和完善。

① 按齿面接触的疲劳强度设计齿轮是一种常见的传动装置，不仅广泛应用于机床、汽车、船舶、飞机等工业领域，也被用于农业机械和家用电器等领域。

齿轮的设计需要综合考虑多种因素，其中疲劳强度是一项重要的考虑因素。

本文主要讨论按齿面接触的疲劳强度设计。

1. 齿轮疲劳破坏的原因齿轮在长时间使用过程中，可能会发生疲劳破坏，主要原因有以下三点。

1.1 循环载荷作用循环载荷是齿轮疲劳破坏的主要原因之一。

齿轮在运行过程中，由于受到循环载荷的作用，导致齿表表面和内部产生裂纹，最终导致齿轮疲劳破坏。

1.2 齿面接触疲劳齿轮在运行过程中，齿面之间不断摩擦接触，产生接触疲劳。

长时间的齿面摩擦作用会导致齿面磨损和裂纹，从而加速齿轮的疲劳破坏。

1.3 齿轮微小杂质齿轮制造过程中，可能会留下一些微小的杂质，这些杂质会影响齿轮的强度和寿命。

在齿轮运转过程中，这些杂质可能被挤入齿轮表面和内部，从而导致齿轮疲劳破坏。

2. 按齿面接触的疲劳强度指标2.1 等效应力法等效应力法基于最大主应力和平均应力在作用方向上的不同，通过等效应力来判断齿轮的疲劳寿命。

等效应力法是一种基于静态强度计算经验公式修正的方法，适用于齿轮低速、半精度、低载荷情况下的疲劳寿命预测。

等效应力法无法同时考虑多种载荷作用下的疲劳寿命，无法准确反映实际疲劳寿命。

2.2 AGMA方法AGMA方法是由美国齿轮制造商协会（AGMA）提出的一种疲劳分析方法。

通过综合考虑齿轮中各种载荷的作用，将其合成为一个等效载荷，然后根据这个等效载荷计算齿轮的疲劳寿命。

AGMA方法具有比等效应力法更高的精度和适用范围，适用于不同载荷作用下的齿轮疲劳分析。

3. 基于齿面接触的疲劳强度设计3.1 齿轮材料的选择齿轮材料的选择与齿轮的设计和使用相关联。

通常情况下，齿轮材料需要具有高强度、高韧性和高疲劳强度等特性。

传统的齿轮材料有合金钢、碳素钢和铸铁等，而现代材料则有硬质合金、陶瓷和高分子材料等。

同时需要考虑的是，齿轮材料的选择还应考虑到齿轮生产成本、机械加工性能和耐热性能等方面。

1.选定齿轮类型、精度等级、材料级齿数1）选用直齿圆柱齿轮齿条传动。

2）速度不高，故选用7级精度（GB10095-88）。

3）材料选择。

由表10-1选择小齿轮材料为40Cr(调质)，硬度为280HBS，齿条材料为45钢（调质）硬度为240HBS。

4）选小齿轮齿数Z1=24，大齿轮齿数Z2=∞。

2.按齿面接触强度设计由设计计算公式进行计算，即d1t ≥2.32√K t T1φd∙u+1u(Z E[σH])23(1)确定公式内的各计算数值1）试选载荷系数K t =1.3。

2）计算小齿轮传递的转矩。

（预设齿轮模数m=8mm,直径d=160mm）T1=95.5×105P1n1=95.5×105×0.24247.96=2.908×105N∙mm3) 由表10-7选齿宽系数φd=0.5。

4）由表10-6查得材料的弹性影响系数Z E=189.8MPa 1 2。

5）由图10-21d按齿面硬度查得小齿轮的接触疲劳强度极限σHlim1=600MPa;齿条的接触疲劳强度极限σHlim2=550MPa。

6）由式10-13计算应力循环次数。

N1=60n1jL h=60×7.96×1×(2×0.08×200×4)=6.113×1047)由图10-19取接触疲劳寿命系数K HN1=1.7。

8）计算接触疲劳许用应力。

取失效概率为1%，安全系数S=1，由式（10-12）得[σH]1=K HN1σHlim1S=1.7×600MPa=1020MPa(2)计算1）试算小齿轮分度圆直径d t1,代入[σH]1。

d 1t ≥2.32√K t T 1φd ∙u +1u (Z E [σH ])23=2.32√1.3×2.908×1050.5∙∞+1∞ (189.81020)23=68.89mm2）计算圆周速度v 。

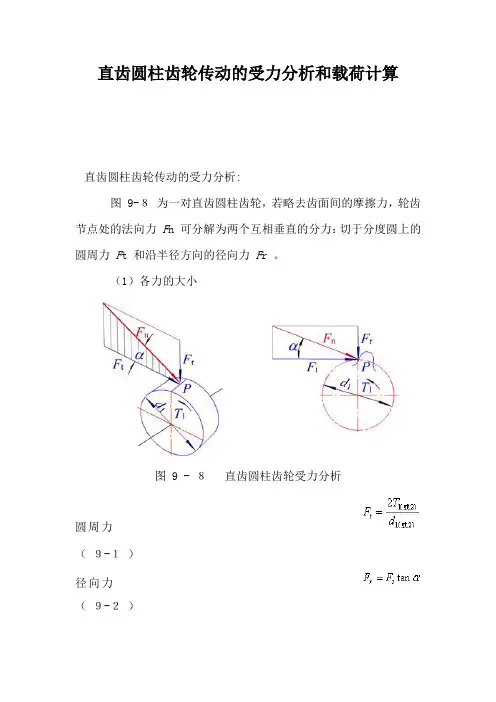
直齿圆柱齿轮传动的受力分析和载荷计算直齿圆柱齿轮传动的受力分析:图 9-８为一对直齿圆柱齿轮，若略去齿面间的摩擦力，轮齿节点处的法向力F n 可分解为两个互相垂直的分力：切于分度圆上的圆周力F t 和沿半径方向的径向力F r 。

（1）各力的大小图 9 - ８直齿圆柱齿轮受力分析圆周力（９-１）径向力（９-２）法向力（９-３）其中转矩（９-４）式中：T1 ，T2 是主、从动齿轮传递的名义转矩，N.mm ；d1 ，d2 是主、从动齿轮分度圆直径， mm ；为分度圆压力角；P是额定功率， kW ；n1 ，n2 是主动齿轮、从动轮的转速， r/min 。

作用在主动轮和从动轮上的各对应力大小相等，方向相反。

即：，，（2）各力的方向主动轮圆周力的方向与转动方向相反；从动轮圆周力的方向与转动方向相同；径向力F r 分别指向各自轮心 ( 外啮合齿轮传动 ) 。

9.4.2 计算载荷前面齿轮力分析中的F n 、F t 和F r 及F a 均是作用在轮齿上的名义载荷。

原动机和工作机性能的不同有可能产生振动和冲击；轮齿在啮合过程中会产生动载荷；制造安装误差或受载后轮齿的弹性变形以及轴、轴承、箱体的变形，会使载荷沿接触线分布不均，而同时啮合的各轮齿间载荷分配不均等，因此接触线单位长度的载荷会比由名义载荷计算的大。

所以须将名义载荷修正为计算载荷。

进行齿轮的强度计算时，按计算载荷进行计算。

（９－４）计算载荷(９ - ５)载荷系数(９- ６)式中：K是载荷系数；K A 是使用系数；K v 是动载系数；是齿向载荷分布系数；是齿间载荷分配系数。

1 ．使用系数K A使用系数K A 是考虑由于齿轮外部因素引起附加动载荷影响的系数。

其取决于原动机和工作机的工作特性、轴和联轴器系统的质量和刚度以及运行状态。

其值可按表 9 - ３选取。

表 9-３使用系数K A工作机的工作特性工作机器原动机的工作特性及其示例电动机、均匀运转的蒸气机、燃气轮机蒸气机、燃气轮机液压装置电动机（经多缸内燃机单缸内燃机（小的，启动转矩大）常启动启动转矩大）均匀平稳发电机、均匀传送的带式或板式运输机、螺旋输送机、轻型升降机、机床进给机构、通风机、轻型离心机、均匀密度材料搅拌机等1.00 1.101.251.50轻微冲击不均匀传送的带式输送机、机床的主传动机构、重型升降机、工业与矿用风机、重型离心机、变密度材料搅拌机、给水泵、转炉、轧机、1.25 1.351.51.75中等冲击橡木工机械、胶积压机、橡胶和塑料作间断工作的搅拌机、轻型球磨机、木工机械、钢坯初轧机、提升装置、单缸活塞泵等1.50 1.601.752.00严重挖掘机、重型球磨机、橡 1.75 1.85 2.0 2.25冲击胶揉合机、落沙机、破碎机、重型给水泵、旋转式钻探装置、压砖机、带材冷轧机、压坯机等0或更大注： 1. 对于增速传动，根据经验建议取表中值的 1.1 倍。

齿面接触强度及齿根弯曲强度核算在设计产品过程中，经常会选用齿轮作为传动力及扭矩的原件。

在大部分成型产品改造或调整过程中，关于齿轮的强度校核这一步骤就可以用类比法代替，从而节省设计人员的精力，缩短了设计周期。

但得出的结果没有书面依据以及理论方面的支持。

所以当进行多次类比之后，所设计出来的齿轮与理论计算得出的齿轮偏差会较大。

其原理类似于累计偏差。

所以应该进行强度校核方面的计算。

齿轮强度校核计算，在实际应用中，主要是两方面的核算：1、齿面接触强度的核算。

2、齿根弯曲强度的核算。

1.齿面接触强度核算-分度圆直径计算参考文献：在初步设计齿轮时，根据齿面接触强度，可按照下列公式估算齿轮传动的尺寸。

(机械设计手册P14-133)a≥A a(μ±1)·√KT1ψaσHP23①d1≥A d·√KT1ψdσHP2·μ±1μ3②公式①为两齿轮中心距的计算；公式②为齿轮分度圆直径的计算。

由于本次计算的是齿轮齿条传动。

所以，中心距a= d1/2其中：d1为齿轮分度圆直径，只需要核算齿轮分度圆直径d1首先，要确定公式②中各个符号代表的含义及数值选取。

d1—齿轮分度圆直径；A d—常系数；K—载荷系数；μ—齿数比；σHP—许用接触应力；ψd—齿宽系数；T1—电机减速机输出扭矩；d1：齿轮分度圆直径，待求；A d：常系数值；A d值在表14-1-65中，通过螺旋角角度β的数值求得。

齿轮的螺旋角β=11.655°,则A d = 756。

载荷系数K，常用值K=1.2～2（机械设计手册P14-133），当载荷平稳，齿宽系数较小，轴承对称布置，轴的刚性较大，齿轮精度较高（6级以上），以及齿轮的螺旋角较大时取较小值；反之取较大值。

根据对比后的结果在K的常用范围内选取。

此次选择K=1.8（载荷平稳，齿宽系数较小，轴为非对称分布，轴的刚性不大，齿轮精度不高）u：传动比。

当齿轮之间为外啮合的时候，选取“+”；当齿轮之间为内啮合的时候，选取“-”，本次计算为齿轮齿条，不影响计算结果。

机械设计复习题一、选择题、填空题及判断题1．一般机械中，若两根被连接轴间存在较大的综合位移，可采用联轴器。

①齿式②凸缘③套筒④滑块2.牙嵌离合器只能在结合。

①．单向转动时②.高速转动时③. 正反转工作时④.两轴转速差很小或停车时3．齿式联轴器允许轴线具有位移；十字滑块联轴器允许轴线具有位移。

（均答一种主要位移）4. 牙嵌式离合器的常用牙形有矩形、梯形、锯齿形和三角形等，在传递较大转矩时，因为。

①. 梯形牙齿与齿接触面间有轴向分力②. 结合后没有相对滑动③.梯形牙强度高，结合或分离较容易且磨损能补偿5．非液体摩擦滑动轴承的主要失效形式是。

6.设计动压向心滑动轴承时，若宽径比L/D取得较小，则有。

①轴承端泄量大，承载能力低，温度高②轴承端泄量大，承载能力低，温度低③轴承端泄量小，承载能力高，温度高④轴承端泄量小，承载能力高，温度低7.计算滑动轴承的最小油膜厚度h min，其目的是。

①计算轴承的耗油量②计算轴承的内部摩擦力③验算轴承是否获得液体摩擦④计算轴承的发热量8.为使润滑油容易进入滑动轴承的承载区以形成油膜，最好。

①在承载区开油槽②在非承载区开油槽③在承载区和非承载区均开油槽④在轴向中间，开周向油槽9.在情况下，滑动轴承润滑油的粘度不宜取得太高①低速重载②高速轻载③人工滴油润滑④环境温度高10.滑动轴承设计中，适当选用较大的宽径比可以提高承载能力。

（A．正确B。

错误）11．不完全液体润滑滑动轴承中，为防止轴承的过度磨损应该校核、，为防止轴承温升过高产生胶合，应该校核。

12. 不完全液体润滑滑动轴承中，限制pv≤[pv]的主要目的主要是为了。

①防止金属接触②防止轴承温升过高③防止轴瓦变形④防止轴瓦压溃13．普通平键连接是根据来选出键的剖面尺寸b×h，而键的长度L是参考来确定的。

14.平键联接的主要失效形式是键的工作面。

①胶合②压溃③疲劳点蚀④磨损15.轴和轴向零件广泛采用平键连接的主要原因是。

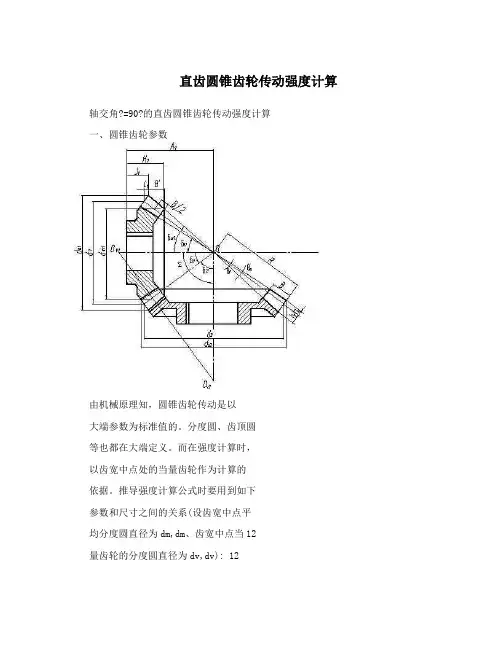
直齿圆锥齿轮传动强度计算轴交角?=90?的直齿圆锥齿轮传动强度计算一、圆锥齿轮参数由机械原理知，圆锥齿轮传动是以大端参数为标准值的。

分度圆、齿顶圆等也都在大端定义。

而在强度计算时，以齿宽中点处的当量齿轮作为计算的依据。

推导强度计算公式时要用到如下参数和尺寸之间的关系(设齿宽中点平均分度圆直径为dm,dm、齿宽中点当12量齿轮的分度圆直径为dv,dv): 12令φ=b/R，称为锥齿轮传动的齿宽系数(通常取φ=0.25-0.35,最常用的值为φ=1/3)于是: RRR二、齿根弯曲疲劳强度计算直齿锥齿轮的弯曲疲劳强度可近似地按平均分度圆处的当量圆柱齿轮进行计算。

因而可直接沿用直齿轮弯曲强度校核公式，得直齿锥齿轮的载荷系数同样为，其中使用系数KA可由表1查取;动载系数Kv 可由图5按低一级的精度线及vm(m/s)查取;齿间载荷分配系数及可取为1;齿向载荷分布系数可按下式计算:= =1.5式中是轴承系数，可从表10中查取Y,Y分别为齿轮系数及应力校正系数，按当量齿数z查表5。

FaSav将:代入校核公式，得设计公式:三、齿面接触疲劳强度计算直齿锥齿轮的齿面接触疲劳强度，仍按平均分度圆处的当量圆柱齿轮计算，工作齿宽即为锥齿轮的齿宽b。

按赫兹公式计算齿面接触疲劳强度时，式中的综合曲率为:将式(l)及代入赫兹公式，并令接触线长度L=b,得:对α=20?的直齿锥齿轮，Z=2.5，于是可得: H上面两式分别为校核式和设计式。

四、曲齿锥齿轮传动简介曲齿锥齿轮传动较之直齿锥齿轮传动具有重合度大、承载能力高、传动效率高、传动平稳、噪音小等优点，因而获得了日益广泛的应用。

曲齿锥齿轮有圆弧齿(简称弧齿，为格里森制齿轮)及长幅外摆线齿(为奥里康制齿轮)等。

格里森制弧齿锥齿轮传动的压力角α取为=20?，平均分度圆处的齿轮螺旋角βm(如右图)取为30?或0?(零度弧齿锥齿轮)。

零度弧齿锥齿轮传动较之直齿锥齿轮传动，平稳性及生产率都高，并因βm=0，轴向力的方向亦不随转矩方向的改变而改变。

齿轮传动典型例题（设计）一、应熟记的公式：6021n πω=；;1055.91161n P T ⨯= η⋅⋅=1212i T T1）直齿：112d T F t =； αtan ⋅=t r F F ； αcos tn F F = 。

21t t F F -=；21r r F F -=。

2）斜齿：21t t F F -=； 21r r F F -=； 21a a F F -=。

1212d T F t =；βs c Zm d n 011=。

βαcos /tan 11n t r F F ⋅=； βtan 11⋅=t a F F 。

3）圆锥：21t t F F -=；21a r F F -=；21r a F F -=。

1112m t d T F =, )5.01(sin 1111R m d b d d φδ-=-=； 111cos tan δα⋅=t r F F ； 111sin tan δα⋅⋅=t a F F 。

R b R =φ，22222212221d d Z Z m R +=+=；121221tan tan δδc Z Z n n i ==== 4）蜗轮蜗杆：21a t F F -=；21r r F F -=； 21t a F F -=。

1112d T F t =，mq d =1； 22212d TF F t a ==； αtan 221t r r F F F == 二、习题1． 判断下列圆锥齿轮受力，设驱动功率为P ，主动轮转速为1n （方向如图示）。

各齿轮几何参数均已知。

求：（1）两轮各力的方向；（2）各力计算表达式。

解：（1）如图所示；（2）;1055.91161nP T ⨯=η⋅⋅=1212i T T ； 21112t m t F d T F -==，)5.01(sin 1111R m d b d d φδ-=-=； 111cos tan δα⋅=t r F F ；111sin tan δα⋅⋅=t a F F 。