中考数学专题复习初三数学第二轮复习练习试卷

初三数学第二轮复习练习试卷（二）1、如图，一张长方形纸片ABCD ，其长 AD=a ，宽 AB=b(a>b) ，在 BC 边上选用一点 M ，将 ABM 沿 AM 翻折后 B 至 B ′的地点， 若 B ′为长方形纸片 ABCD 的对称中心， 则 a的ADb值是.B ′BMCy2、在方格纸中，每个小格的极点称为格点，以格点为极点的三角形叫做格点三角形．在如图5× 5 的方格纸中，以AA 、B 为极点作格点三角形与△ OAB 相像（相像比不可以为１） ，则另一个极点 C 的坐标为．OBx3、 (1)命题“ a 、 b 是实数，若 a>b ，则 a 2>b 2”若结论保持不变，如何改变条件， 命题才是真命题，以下四种改法：①a 、b 是实数，若 a>b>0，则 a 2>b 2；② a 、 b 是实数，若 a>b 且 a+b>0，则 a 2>b 2 ；③ a 、b 是实数，若 a<b<0，则 a 2>b 2；④ a 、b 是 实数，若 a<b 且 a+b<0，则 a 2>b 2. 此中真命题的个数是（ ） A ．1 个B ．2 个C ．3 个D ．4 个4、近视眼镜的度数 y （度）与镜片焦距 x （ m ）成反比率，已知 400°近视眼镜片的焦距为 0.25m ，则眼镜度数y 与镜片焦距 x 之间的函数关系式为5、鞋子的“鞋码”和鞋长（厘米）存在一种换算关系，下表是几组“鞋码”和“鞋 长”的对应1523 25 26 表：鞋长鞋码20364042（ 1）经过绘图计算、比较、察看等方法，猜想这类换算可能切合哪一种函数关系？试写出鞋长 x 与鞋码 y 的关系式。

（ 2）考证你所求的换算关系式能否正确。

（ 3）假如篮球巨人姚明的脚长31 厘米，那么他穿多大码的鞋？6、某生产“科学计算器”企业有100 名员工，该企业生产的计算器有百货企业代理销售。

中考二轮专题复习练习题-5创新作图专题一、用三角形的有关性质作图1．如图，在△ABE中，AE＝BE，请你仅用无刻度的直尺按要求作图．（不写作法，保留作图痕迹）（1）如图1，点C，D分别为AE，BE的中点，作出AB的垂线；（2）如图2，EF⊥AB于点F，点C为AE上任意一点，在BE上找出一点D，使ED＝EC．2．如图，在△ABC中，已知AB＝AC，AD⊥BC于点D．（1）如图①，点P为AB上任意一点，请你用无刻度的直尺在AC上找出一点P′，使AP＝AP′．（2）如图②，点P为BD上任意一点，请你用无刻度的直尺在CD上找出一点P′，使BP＝CP′．3．如图，在四边形ABCD中，AD∥BC，AD＝2BC，点E是AD的中点，请仅用无刻度的直尺分别按下列要求画图．（不写画法，保留画图痕迹）（1）在图1中，画出△ACD的边AC上的中线DM；（2）在图2中，若AC＝AD，画出△ACD的边CD上的高AN．4．在Rt△ABC中，∠ACB＝90°，AC＝2BC，将△ABC绕点O按逆时针方向旋转90°得到△DEF，点A，B，C的对应点分别是点D，E，F．请仅用无刻度直尺分别在下面图中按要求画出相应的点（保留画图痕迹）．（1）如图1，当点O为AC的中点时，画出BC的中点N；（2）如图2，旋转后点E恰好落在点C，点F落在AC上，点N是BC的中点，画出旋转中心O．5．如图，在△ABC和△DCB中，∠A＝∠D＝90°，AC＝BD，AC与BD相交于点O，限用无刻度直尺完成以下作图：（1）在图1中作线段BC的中点P；（2）在图2中，在OB、OC上分别取点E、F，使EF∥BC．6．已知Rt△ABC中，∠ACB＝90°，点E为BC的中点，以BC为底边的等腰△BCD按如图所示位置摆放，且∠DBC＝∠ABC．请仅用无刻度的直尺分别按下列要求作图（保留作图痕迹）：（1）如图①，在AB上求作一点F，使四边形BDCF为菱形；（2）如图②，过点C作线段CP，使得线段CP将△BCD的面积平分．二、用特殊四边形的性质作图7．如图，四边形ABCD是平行四边形，点E在AD上，请仅用无刻度直尺按要求作图（保留作图痕迹，不写作法）（1）在图1中，过点E作直线EF将四边形ABCD的面积平分；（2）在图2中，DE＝DC，作∠A的平分线AM；8．如图，在矩形ABCD中，请仅用无刻度的直尺按要求作图．（1）如图①，当E为AD的中点，在BC上找一点F，使得F是BC的中点；（2）如图②，当E为AD上任意一点，在BC上找一点F，使得BF＝DE．9．已知正方形ABCD如图所示，M、N在直线BC上，MB＝NC，试分别在图1、图2中仅用无刻度的直尺画出一个不同的等腰三角形OMN．10．请仅用无刻度的直尺在下列图1和图2中按要求画菱形．（1）图1是矩形ABCD，E，F分别是AB和AD的中点，以EF为边画一个菱形；（2）图2是正方形ABCD，E是对角线BD上任意一点（BE＞DE），以AE为边画一个菱形．11．如图，四边形ABCD是菱形，BE是AD边上的高，请仅用无刻度的直尺作图（保留作图痕迹）（1）在图①中，BD＝AB，作△BCD的边BC上的中线DF；（2）在图②中，BD≠AB作△ABD的边AB上的高DF．12．分别在图①，图②中按要求作图（保留作图痕迹，不写作法）（1）如图①，已知四边形ABCD为平行四边形，BD为对角线，点P为AB 上任意一点，请你用无刻度的直尺在CD上找出另一点Q，使AP＝CQ；（2）如图②，已知四边形ABCD为平行四边形，BD为对角线，点P为BD 上任意一点，请你用无刻度的直尺在BD上找出一点Q，使BP＝DQ．13．如图，在正方形ABCD中，点M是BC边上任意一点，请你仅用无刻度直尺、用连线的方法，分别在图（1）、图（2）中按要求作图（保留作图痕迹，不写作法）．（1）在图（1）中，在AB边上求作一点N，连接CN，使CN＝AM；（2）在图（2）中，在AD边上求作一点Q，连接CQ，使CQ∥AM．14．请你按照下列要求用无刻度的直尺作图：（不写作法，保留作图痕迹）（1）如图1，请你作一条直线（但不过A、B、C、D四点）将平行四边形的面积平分；（2）如图2，在平行四边形ABCD中挖去一个矩形，准确作出一条直线将剩下图形的面积平分．15．如图，在▱ABCD中，点E为边BC上的中点，请仅用无刻度的直尺，按要求画图（保留画图痕迹，不写画法）．（1）在图1中，作EF∥AB交AD于点F；（2）在图2中，若AB＝BC，作一矩形，使得其面积等于▱ABCD的一半．16．如图，AE为菱形ABCD的高，请仅用无刻度的直尺按要求画图．（不写画法，保留作图痕迹）．（1）在图1中，过点C画出AB边上的高；（2）在图2中，过点C画出AD边上的高．三、用圆或多边形有关性质作图17．如图，AB、AD是⊙O的弦，△ABC是等腰直角三角形，△ADC≌△AEB，请仅用无刻度直尺作图：（1）在图1中作出圆心O；（2）在图2中过点B作BF∥AC．18．在⊙O中，点A，B，C在⊙O上，请仅用无刻度的直尺作图：（1）在图1中，以点C或点B为顶点作一锐角，使该锐角与∠CAB互余；（2）在图2中，已知AD∥BC交⊙O于点D，过点A作直线将△ACB的面积平分．19．已知四边形ABCD内接于⊙O，且已知∠ADC＝120°；请仅用无刻度直尺完成以下作图（保留作图痕迹，不写作法，写明答案）．（1）在图1中，已知AD＝CD，在⊙O上求作一个度数为30°的圆周角；（2）在图2中，已知AD≠CD，在⊙O上求作一个度数为30°的圆周角．20．仅用无刻度的直尺．．．．．．．．，按要求画图（保留画图痕迹，不写作法）（1）如图①，画出⊙O的一个内接矩形；（2）如图②，AB是⊙O的直径，CD是弦，且AB∥CD，画出⊙O的内接正方形．21．如图，△ABC是⊙O的内接三角形，请仅用无刻度的直尺在下列图形中按要求画图．（1）在图1中，已知OD⊥BC于点D，画出∠A的角平分线；（2）在图2中，已知OE⊥AB于点E，OF⊥AC于点F，画出∠A的角平分线．22．如图，在正五边形ABCDE中，请仅用无刻度的直尺，分别按下列要求作，（1）在图1中，画出过点A的正五边形的对称轴；（2）在图2中，画出一个以点C为顶点的72°的角．23．在如图的正方形网格中，点O在格点上，⊙O的半径与小正方形的边长相等，请利用无刻度的直尺完成作图，在图（1）中画出一个45°的圆周角，在图（2）中画出一个22.5°的圆周角．24．如图，线段AB是⊙O的直径，BC⊥CD于点C，AD⊥CD于点D，请仅用无刻度的直尺按下列要求作图．（1）在图1中，当线段CD与⊙O相切时，请在CD上确定一点E，连接BE，使BE平分∠ABC；（2）在图2中，当线段CD与⊙O相离时，请过点O作OF⊥CD，垂足为F．25．如图，⊙O是△ABC的外接圆，AB＝AC，P是⊙O上一点，请你只用无刻度的直尺，分别画出图①和图②中∠P的平分线．26．如图（甲、乙），AB为半圆⊙O1的直径，AO1为半圆⊙O2的直径，仅用无刻度的直尺完成下列作图：（1）如图甲，C为半圆⊙O1上一点，请在半圆⊙O1找个点D，使得D恰为的中点；（2）如图乙，E为半圆⊙O2上一点，请在半圆⊙O2找个点F，使得F恰为的中点．27．如图，四边形ABCD为菱形，且∠BAD＝120°，以AD为直径作⊙O，与CD交于点P．请仅用无刻度的直尺按下列要求画图．（保留作图痕迹）（1）在图1中，过点C作AB边上的高CE；（2）在图2中，过点P作⊙O的切线PQ，与BC交于点Q．28．等腰△ABC中，AB＝AC，以AB为直径作圆交BC于点D，请仅用无刻度的直尺，根据下列条件分别在图1、图2中画一条弦，使这条弦的长度等于弦BD．（保留作图痕迹，不写作法）（1）如图1，∠A＜90°；（2）如图2，∠A＞90°．29．在△ABC中，AB＝AC，点A在以BC为直径的半圆内．请仅用无刻度的直尺分别按下列要求画图（保留画图痕迹）．（1）在图1中作弦EF，使EF∥BC；（2）在图2中以BC为边作一个45°的圆周角．30．如图在⊙O中，图1中△ABC内接于⊙O且∠ABC＝90°，图2中△A1BC1，内接于⊙O，AC是直径且AC∥A1C1，请仅用无刻度的直尺按要求画图．（1）在图1中，画出将△ABC的面积平分为两等份的弦．（2）在图2中，画出将△A1BC1的面积平分为两等份的弦．四、用网格的有关性质作图31．如图所示，在正方形网格中，每个小正方形的边长都是1，每个小格点的顶点叫做格点，以格点为顶点分别按下列要求画三角形．（1）使三角形的三边长分别为3，2，．（2）使三角形为边长都为无理数的钝角三角形且面积为4．32．在正方形网格中，点A、B、C都是格点，仅用无刻度的直尺按下列要求作图．（1）在图1中，作线段AB的垂直平分线；（2）在图2中，作∠ABC的角平分线．33．请在如图所示的正方形和等边三角形网格内，仅用无刻度的直尺完成下列作图，过点P向线段AB引平行线．34．已知△ABC，请用无刻度直尺画图．（1）在图1中，画一个与△ABC面积相等，且以BC为边的平行四边形；（2）在图2中，画一个与△ABC面积相等，且以点C为一顶点的正方形．35．图1、图2是两张形状、大小完全相同的方格纸，方格纸中的每个小正方形的边长均为1，每个小正方形的顶点叫做格点．（1）在图1中画出等腰直角三角形MON，使点N在格点上，且∠MON＝90°；（2）在图2中以格点为顶点画一个正方形ABCD，使正方形ABCD面积等于（1）中等腰直角三角形MON面积的4倍，并将正方形ABCD分割成以格点为顶点的四个全等的直角三角形和一个正方形，且正方形ABCD面积没有剩余（画出一种即可）．36．如图是一个正方形网格图，图中已画了线段AB和线段EG，请使用无刻度的直尺在正方形网格中画图．（1）画一个以AB为边的正方形ABCD；（2）画一个以EG为一条对角线的菱形EFGH，且面积与（1）中正方形的面积相等．37．图1，图2均为正方形网络，每个小正方形的面积均为1．在这个正方形网格中，各个小正方形的顶点叫做格点．在网格中画图，使得每个形图的顶点均在格点上．（1）画一个边长为整数的菱形，且面积等于24．（2）画一个直角三角形，使其一边长为2，且一个角为45°．38．如图，网格中每个小正方形的边长均为1，请你按下列要求在网格中画图．（1）在图1中画出以AB为对角线、面积是24的平行四边形ACBD；（2）在图2中画出以AB为对角线、面积是24的矩形AEBF．（所画四边形的顶点都在小正方形的顶点上）39．在5×5的网格中有线段AB，在网格线的交点上找一点C，使三角形ABC 满足如下条件．（仅用直尺作图）（1）在网格①中作一个等腰三角形ABC；（2）在网格②中作一个直角三角形ABC，使两直角边的长为无理数．40．在10×10的正方形网格中（每个小正方形的边长为1）线段AB在网格中的位置如图所示，请仅用无刻度直尺，按要求分别完成以下画图．（1）在图1中，画出一个以AB为边，另两个顶点C、D也在格点上的菱形ABCD；（2）在图2中，画出一个以A、B为顶点，另两个顶点C、D也在格点上的菱形，且使这个菱形的面积最大或最小（仅选其一，即可）：其面积值是．中考二轮专题复习练习题-5创新作图专题（参考答案）1.解：（1）如图1，直线EM即为所求；（2）如图2，点D即为所求．2．解：（1）如图①，点P'为所求作的图形，（2）如图②，点P'为所求作的图形，3．解：（1）如图，DM为所作；（2）如图，AN为所作．4．解：（1）如图，点N即为所求．（2）如图，点O为所作；5．解：（1）如图1，点P为所作；（2）如图2，EF为所作．6．解：（1）如图①，点F为所作；（2）如图②，CP为所作．7．解：（1）如图1，直线EF即为所求；（2）如图2，射线AM即为所求．8．解：（1）连接AC、BD交于点O，作直线EO交BC于F，点F即为所求．（2）连接AC、BD交于点O，作直线EO交BC于F，点F即为所求．9．解：如图1、2，△OMN为所作．10．解：（1）如图所示：四边形EFGH即为所求的菱形；（2）如图所示：四边形AECF即为所求的菱形．11．解：（1）如图1中，线段DF即为所求．（2）如图2中，线段DF即为所求．12．解：（1）如图①，点Q即为所求；（2）如图②，点Q即为所求．13．解：（1）连接BD，BD与AM交于点O，连接CO并延长交于AB，则CO 与AB的交点为点N，如图1，（2）延长MO交ADE于Q，连结CQ，则CQ为所作，如图2．14．解：（1）如图1，直线l为所作；（2）如图2，直线MN为所作．15．解：（1）如图1，F点就是所求作的点；（2）如图2，矩形EGFH就是所求作的四边形．16．解：（1）如图1所示，线段CG即为所求；（2）如图2所示，线段CG即为所求．17．解：（1）设AC交⊙O于K，连接BK，DE，BK交DE于点O，点O即为所求．（2）如图2中，作直线AO交⊙O于F，直线直线BF，直线BF即为所求．18．解：（1）如图1，∠BCE为所作；（2）如图2，AF为所作．19．解：（1）如图1所示：∠ABD＝30°或∠CBD＝30°；（2）如图2所示：∠CAE＝30°．20．解：（1）如图所示，过O作⊙O的直径AC与BD，连接AB，BC，CD，DA，则四边形ABCD即为所求；（2）如图所示，延长AC，BD交于点E，连接AD，BC交于点F，连接EF 并延长交⊙O于G，H，连接AH，HB，BG，GA，则四边形AHBG即为所求．21．解：（1）如图1所示：AM即为所求；（2）如图2所示：AN即为所求．22.解：（1）如图1，连接BD，CE，交于点F，过A、F作直线AF，则AF即为所求；（2）如图2，连接AC，则∠ACB＝36°，∠BCD＝108°，∴∠ACD＝72°．同理，连接CE，则∠BCE＝72°．23．解：（1）如图1，连接OA、OB，在优弧AB上任意找一点C，连接AC、AB ∠ACB为所求作（2）如图2，连接OA交圆O于点C，在优弧BC上任意找一点D，连接CD、BD，∠CDB为所求作24.解：（1）如图1；（2）如图2.25.解：如图①中，连接P A，P A就是∠P的平分线．如图②中，连接AO延长交⊙O于E，连接PE，PE就是∠P的平分线．26．解：（1）如图甲所示：（2）如图乙所示：27．解：（1）如图1，CE为所；（2）如图2，PQ为所作．28．解：（1）如图1，DE为所作：（2）如图2，DE为所作：29．解：（1）如图1，EF为所作；（2）如图2，∠DBC为所作．30．解：（1）如图所示：（2）如图所示：31．解：（1）满足条件的△ABC如图所示．（2）满足条件的△DEF如图所示．32．解：（1）如图所示：直线CD即为所求；（2）如图所示：射线BD即为所求．33．解：如图所示，PQ即为所求．34．解：（1）如图1所示：平行四边形BCDE即为所求；（2）如图2所示：正方形CDEF即为所求．35．解：（1）如图1所示；（2）如图2、3所示；36．解：（1）如图所示：正方形ABCD，即为所求；（2）如图所示：菱形EFGH，即为所求．37．解：（1）菱形ABCD即为所求．（2）Rt△EFG即为所求．38．解：（1）如图1中，平行四边形ACBD即为所求．（2）如图2中，矩形AEBF即为所求．39．解：（1）∵＝5，AB＝5，∴作AC＝5，或BC＝5，△ABC如图1所示：（2）∵＝，＝2，（）2+（2）2＝5+20＝25＝AB2，∴画出△ABC和△ABC1是直角三角形，如图2所示．40．解：（1）如图1所示：四边形ABCD即为所求；（2）如图2所示：以线段AB为对角线得到菱形ADBC此时面积最大，其面积为：××3＝15．当AB为正方形对角线时，最小面积为：5．答案为：15．。

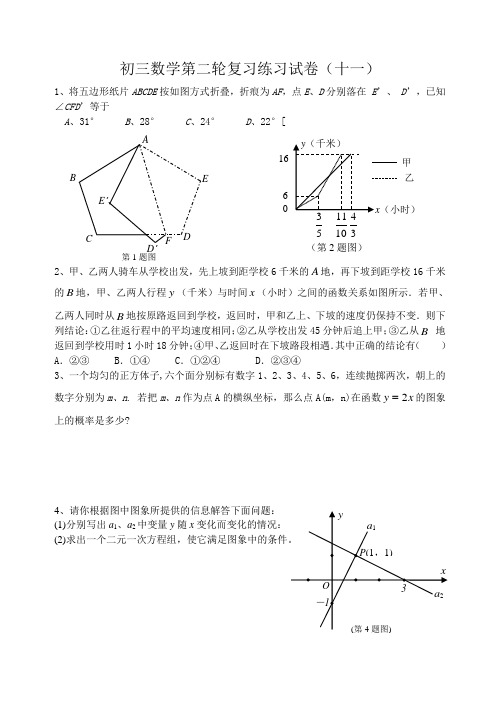
初三数学第二轮复习练习试卷（十一）1、将五边形纸片ABCDE 按如图方式折叠，折痕为AF ，点E 、D 分别落在 E ’、 D ’，已知∠CFD ’等于A 、31°B 、28°C 、24°D 、22°[2、甲、乙两人骑车从学校出发，先上坡到距学校6千米的A 地，再下坡到距学校16千米的B 地，甲、乙两人行程y （千米）与时间x （小时）之间的函数关系如图所示．若甲、乙两人同时从B 地按原路返回到学校，返回时，甲和乙上、下坡的速度仍保持不变．则下列结论：①乙往返行程中的平均速度相同；②乙从学校出发45分钟后追上甲；③乙从B 地返回到学校用时1小时18分钟；④甲、乙返回时在下坡路段相遇．其中正确的结论有（ ）A ．②③B ．①④C ．①②④D ．②③④3、一个均匀的正方体子,六个面分别标有数字1、2、3、4、5、6，连续抛掷两次，朝上的数字分别为m 、n . 若把m 、n 作为点A 的横纵坐标，那么点A(m ，n)在函数x y 2 的图象上的概率是多少?4、请你根据图中图象所提供的信息解答下面问题：(1)分别写出a 1、a 2中变量y 随x 变化而变化的情况：(2)E DF D ’ E ’ A BC 第1题图5 10 36 0 16 （第2题图） 甲 乙5、如图，一天早上，小张正向着教学楼AB 走去，他发现教学楼后面有一水塔DC ，可过了一会抬头一看：“怎么看不到水塔了？”心里很是纳闷。

经过了解，教学楼、水塔的高分别为20m 和30m ，它们之间的距离为30m ，小张身高为1.6m 。

小张要想看到水塔，他与教学楼的距离至少应有多少m ？6、在Rt △ABC 中，90=∠C °，60=∠A °，6=BC ，等边三角形DEF从初始位置（点E 与点B 重合，EF 落在BC 上，如图1所示）在线段BC 上沿BC 方向以每秒1个单位的速度平移，DF DE 、分别与AB 相交于点NM 、.当点F 运动到点C 时，△DEF 终止运动，此时点D 恰好落在AB 上，设△DEF 平移的时间为x .（1）求△DEF 的边长；（2）求M 点、N 点在BA 上的移动速度；（3）在△DEF 开始运动的同时，如果点P 以每秒2个单位的速度从D 点出发沿 DE →EF 运动，最终运动到F 点.若设△PMN 的面积为y ，求y 与x 的函数关系式，写出自变量的取值范围；并说明当P 点在何处时，△PMN 的面积最大？(第5题图)B C （E ）F B C E F （图1） （图2）(第6题图)。

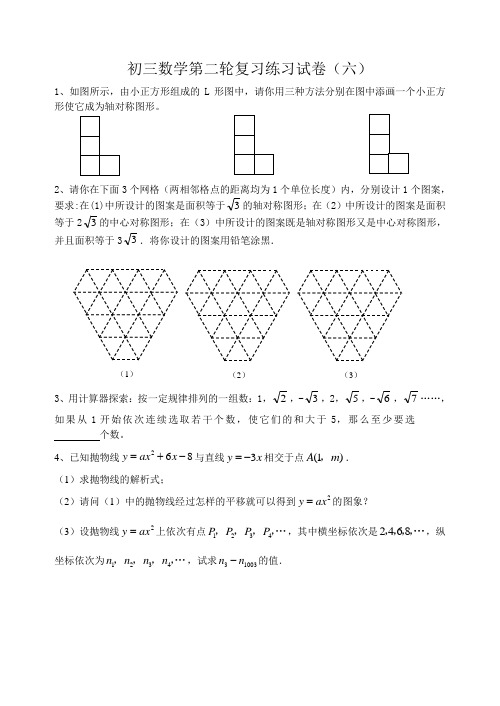
初三数学第二轮复习练习试卷（六）1、如图所示，由小正方形组成的L 形图中，请你用三种方法分别在图中添画一个小正方形使它成为轴对称图形。

2、请你在下面3个网格（两相邻格点的距离均为1个单位长度）内，分别设计1个图案，要求:在(1)中所设计的图案是面积等于3的轴对称图形；在（2）中所设计的图案是面积等于23的中心对称图形；在（3）中所设计的图案既是轴对称图形又是中心对称图形，并且面积等于33．将你设计的图案用铅笔涂黑．3、用计算器探索：按一定规律排列的一组数：1，2，-3，2，5，-6，7……，如果从1开始依次连续选取若干个数，使它们的和大于5，那么至少要选 个数。

4、已知抛物线268y ax x =+-与直线3y x =-相交于点(1)A m ，．（1）求抛物线的解析式；（2）请问（1）中的抛物线经过怎样的平移就可以得到2y ax =的图象？ （3）设抛物线2y ax =上依次有点1234P P P P ，，，，…，其中横坐标依次是2468，，，，…，纵坐标依次为1234n n n n ，，，，…，试求31003n n -的值．（1） （2） （3）5、如图①，有两个形状完全相同的直角三角形ABC和EFG叠放在一起（点A与点E重合），已知AC＝8cm，BC＝6cm，∠C＝90°，EG＝4cm，∠EGF＝90°，O 是△EFG斜边上的中点．如图②，若整个△EFG从图①的位置出发，以1cm/s 的速度沿射线AB方向平移，在△EFG 平移的同时，点P从△EFG的顶点G出发，以1cm/s 的速度在直角边GF上向点F运动，当点P到达点F时，点P停止运动，△EFG也随之停止平移．设运动时间为x（s），FG 的延长线交AC于H，四边形OAHP的面积为y（cm2)（不考虑点P与G、F重合的情况）．（1）当x为何值时，OP∥AC ?（2）求y与x 之间的函数关系式，并确定自变量x的取值范围．（3）是否存在某一时刻，使四边形OAHP面积与△ABC面积的比为13∶24？若存在，求出x的值；若不存在，说明理由．（参考数据：1142＝12996，1152＝13225，1162＝13456或4.42＝19.36，4.52＝20.25，4.62＝21.16）。

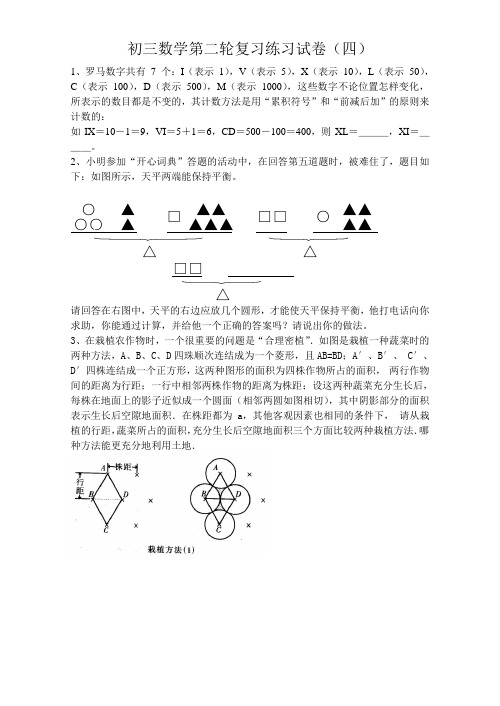
初三数学第二轮复习练习试卷（四）1、罗马数字共有 7 个：I （表示 1），V （表示 5），X （表示 10），L （表示 50），C （表示 100），D （表示 500），M （表示 1000），这些数字不论位置怎样变化，所表示的数目都是不变的，其计数方法是用“累积符号”和“前减后加”的原则来计数的：如IX ＝10－1＝9，VI ＝5＋1＝6，CD ＝500－100＝400，则XL ＝＿＿＿，XI ＝＿＿＿。

2、小明参加“开心词典”答题的活动中，在回答第五道题时，被难住了，题目如下：如图所示，天平两端能保持平衡。

请回答在右图中，天平的右边应放几个圆形，才能使天平保持平衡，他打电话向你求助，你能通过计算，并给他一个正确的答案吗？请说出你的做法。

3、在栽植农作物时，一个很重要的问题是“合理密植”．如图是栽植一种蔬菜时的两种方法，A 、B 、C 、D 四珠顺次连结成为一个菱形，且AB=BD ；A ′、B ′、•C ′、D ′四株连结成一个正方形，这两种图形的面积为四株作物所占的面积，•两行作物间的距离为行距；一行中相邻两株作物的距离为株距；设这两种蔬菜充分生长后，每株在地面上的影子近似成一个圆面（相邻两圆如图相切），其中阴影部分的面积表示生长后空隙地面积．在株距都为a ，其他客观因素也相同的条件下，•请从栽植的行距，蔬菜所占的面积，充分生长后空隙地面积三个方面比较两种栽植方法．哪种方法能更充分地利用土地．○ ▲▲ ▲▲ □□ □ ▲▲▲ ▲▲ ▲ ▲ ○○ ○ △ △□□ △4、观察图2－6－10中⑴）至⑸中小黑点的摆放规律，并按照这样的规律继续摆放．记第n个图中小黑点的个数为y．解答下列问题：⑴填下表：⑵当n=8时，y=___________；⑶请你猜一猜上述各点会在某一函数的图象上吗？如果在某一函数的图象上，请求出该函数的解析式．5、如图2－3－5所示，抛物线2y ax bx c=++与x轴交于A、B两点（点A在点B 的左侧），与y轴交于点C，且当x=0和x=2时y的值相等，直线y=3x—7与这条抛物线相交于两点．其中一点的横坐标是4，另一点是这条抛物线的顶点M。

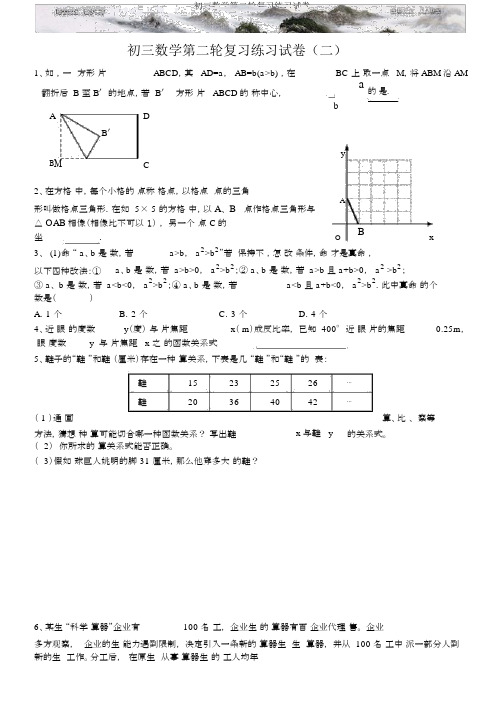
初三数学第二轮复习练习试卷（二）1、如 ，一 方形 片ABCD ，其 AD=a ， AB=b(a>b) ，在 BC 上 取一点 M ，将 ABM 沿 AM翻折后 B 至 B ′的地点，若 B ′ 方形 片 ABCD 的 称中心， a的 是.AD bB ′B MCy2、在方格 中，每个小格的 点称 格点，以格点 点的三角形叫做格点三角形．在如 5× 5 的方格 中，以 A 、 B 点作格点三角形与△ OAB 相像（相像比不可以 １） ， 另一个 点 C 的坐 ．AOBx3、 (1)命 “ a 、b 是 数，若 a>b ， a 2>b 2”若 保持不 ，怎 改 条件，命 才是真命 ，以下四种改法：① a 、b 是 数，若 a>b>0， a 2>b 2；② a 、b 是 数，若 a>b 且 a+b>0， a 2 >b 2；③ a 、 b 是 数，若 a<b<0， a 2>b 2；④ a 、b 是 数，若a<b 且 a+b<0， a 2>b 2. 此中真命 的个数是（ ）A ．1 个B ．2 个C ．3 个D ．4 个4、近 眼 的度数 y （度） 与 片焦距 x （ m ）成反比率， 已知 400°近 眼 片的焦距0.25m ，眼 度数y 与 片焦距 x 之 的函数关系式5、鞋子的“鞋 ”和鞋 （厘米）存在一种 算关系，下表是几 “鞋 ”和“鞋 ”的 表：鞋 15 23 25 26 ⋯鞋20364042 ⋯（ 1 ）通 画算、比 、 察等方法，猜想 种 算可能切合哪一种函数关系？ 写出鞋 x 与鞋 y的关系式。

（ 2） 你所求的 算关系式能否正确。

（ 3）假如 球巨人姚明的脚 31 厘米，那么他穿多大 的鞋？6、某生 “科学 算器”企业有 100 名 工， 企业生 的 算器有百 企业代理 售。

初三数学第二轮复习练习试卷（二）1、如 ，一 方形 片ABCD ，其 AD=a ， AB=b(a>b) ，在 BC 上 取一点 M ，将 ABM 沿 AM翻折后 B 至 B ′的位置，若 B ′ 方形 片 ABCD 的 称中心， a的 是.AD bB ′B MCy2、在方格 中，每个小格的 点称 格点，以格点 点的三角形叫做格点三角形．在如 5× 5 的方格 中，以 A 、 B 点作格点三角形与△ OAB 相似（相似比不能 １） ， 另一个 点 C 的坐 ．AOBx3、 (1)命 “ a 、b 是 数，若 a>b ， a 2>b 2”若 保持不 ，怎 改 条件，命 才是真命 ，以下四种改法：① a 、b 是 数，若 a>b>0， a 2>b 2；② a 、b 是 数，若 a>b 且 a+b>0， a 2 >b 2；③ a 、 b 是 数，若 a<b<0， a 2>b 2；④ a 、b 是 数，若a<b 且 a+b<0， a 2>b 2. 其中真命 的个数是（ ）A ．1 个B ．2 个C ．3 个D ．4 个4、近 眼 的度数 y （度） 与 片焦距 x （ m ）成反比例， 已知 400°近 眼 片的焦距0.25m ，眼 度数y 与 片焦距 x 之 的函数关系式5、鞋子的“鞋 ”和鞋 （厘米）存在一种 算关系，下表是几 “鞋 ”和“鞋 ”的 表：鞋 15 23 25 26 ⋯鞋20364042 ⋯（ 1 ）通 画算、比 、 察等方法，猜想 种 算可能符合哪种函数关系？ 写出鞋 x 与鞋 y的关系式。

（ 2） 你所求的 算关系式是否正确。

（ 3）如果 球巨人姚明的脚 31 厘米，那么他穿多大 的鞋？6、某生 “科学 算器”公司有 100 名 工， 公司生 的 算器有百 公司代理 售。

公司多方考察， 公司的生 能力受到限制， 决定引入一条新的 算器生 生 算器， 并从 100 名 工中 派一部分人到新的生 工作。

方案设计型试题例1、（常州）七（２）班共有50名学生，老师安排每人制作一件A 型或B 型的陶艺品，学校现有甲种制作材料36kg ，乙种制作材料29kg ，制作A 、B 两种型号的陶（1）设制作型陶艺品件，求的取值范围；（2）请你根据学校现有材料，分别写出七（2）班制作A 型和B 型陶艺品的件数． 分析：本题的背景是与人们的生活息息相关的现实问题，本题的条件较多，要分清楚每个量之间的关系，还有，弄清楚这些陶艺品并不能将料全部用完后，本题目就较容易解决了。

解：（1）由题意得：⎩⎨⎧⋯⋯⋯⋯≤+-⋯⋯⋯≤+-②x x ①x x 27)50(3.0364.0)50(9.0 由①得，x ≥18，由②得，x ≤20，所以x 的取值得范围是18≤x ≤20（x 为正整数） （2）制作A 型和B 型陶艺品的件数为：①制作A 型陶艺品32件，制作B 型陶艺品18件； ②制作A 型陶艺品31件，制作B 型陶艺品19件； ③制作A 型陶艺品30件，制作B 型陶艺品20件； 说明：1.本题考察的是不等式组的应用及解不等式。

练习一1、（黑龙江）某房地产开发公司计划建A、B两种户型的住房共80套，该公司所筹资金不少于万元，但不超过万元，且所筹资金全部用于建房，两种户型的建房成本和售价如下表：(1)该公司对这两种户型住房有哪几种建房方案?(2)该公司如何建房获得利润最大?(3)根据市场调查，每套B型住房的售价不会改变，每套A型住房的售价将会提高a万元(a>0)，且所建的两种住房可全部售出，该公司又将如何建房获得利润最大?注：利润=售价-成本2．（哈尔滨）双蓉服装店老板到厂家选购A、B两种型号的服装，若购进A种型号服装9件，B种型号服装10件，需要1810元；若购进A种型号服装12件，B种型号服装8件，需要1880元。

(1)求A、B两种型号的服装每件分别为多少元?(2)若销售1件A型服装可获利18元，销售1件B型服装可获利30元，根据市场需求，服装店老板决定，购进A型服装的数量要比购进B型服装数量的2倍还多4件，且A 型服装最多可购进28件，这样服装全部售出后，可使总的获利不少于699元，问有几种进货方案?如何进货?3．（河南）某公司为了扩大经营，决定购进6台机器用于生产某种活塞。

初三数学第二轮复习练习试卷（二十）1、售货员：“快来买啦，特价鸡蛋，原价每箱14元，现价每箱12元，每箱有鸡蛋30个．” 顾客甲：“我店里买了一些这种特价鸡蛋，花的钱比按原价买同样多鸡蛋花的钱的2倍少96元．” 乙顾客：“我家买了两箱相同特价的鸡蛋，结果18天后，剩下的20个鸡蛋全坏了．” 请你根据上面的对话，解答下面的问题：（1）顾客乙买的两箱鸡蛋合算吗？说明理由．（2）请你求出顾客甲店里买了多少箱这种特价鸡蛋，假设这批特价鸡蛋的保质期还有18天，那么甲店里平均每天要消费多少个鸡蛋才不会浪费？2、据了解，火车票价按“总里程数实际乘车里程数全程参考价⨯”的方法来确定．已知A 站至H例如，要确定从B 站至E 站火车票价，其票价为8736.8715004021130180≈=-⨯(元)．(1) 求A 站至F 站的火车票价(结果精确到1元)；(2) 旅客王大妈乘火车去女儿家，上车过两站后拿着火车票问乘务员：我快到站了吗？乘务员看到王大妈手中票价是66元，马上说下一站就到了．请问王大妈是在哪一站下车的？（要求写出解答过程）．3、如今，餐馆常用一次性筷子，有人说这是浪费资源，破坏生态环境．已知用来生产一次性筷子的大树的数量（万棵）与加工后一次性筷子的数量（亿双）成正比例关系，且100万棵大树能加工成18亿双一次性筷子．（1）求用来生产一次性筷子的大树的数量y （万棵）与加工后一次性筷子的数量x （亿双）的函数关系式．（2）据统计，我国一年要耗费一次性筷子约450亿双，生产这些一次性筷子约需要多少万棵大树？每1万棵大树占地面积约为0.08平方千米，照这样计算，我国的森林面积每年因此将会减少大约多少平方千米？4、如图2－5-16，在矩形ABCD中，AB=10。

cm，BC=8cm．点P从A出发，沿A→B→C→D 路线运动，到D停止；点Q从D出发，沿D→C→B→A路线运动，到A停止，若点P、点Q同时出发，点P的速度为1cm/s，点Q的速度为2cm/s，a s时点P、点Q同时改变速度，点P的速度变为bcm/s，点Q的速度变为d cm/s，图2－5－17是点P出发x秒后△APD 的面积S1（cm2）与x（s）的函数关系图象；图2－5－18是点Q出发xs后面AQD的面积S2（cm2）与x（s）的函数关系图象．⑴参照图2－5－17，求a、b及图中c的值；⑵求d的值；⑶设点P离开点A的路程为y1(cm)，点Q到点A还需走的路程为y2(cm)，请分别写出动点P、Q改变速度后，y1、y2与出发后的运动时间x（s）的函数解析式，并求出P、Q相遇时x的值．⑷当点Q出发_______s时，点P、点Q在运动路线上相距的路程为25cm．5、某校数学研究性学习小组准备设计一种高为60cm 的简易废纸箱．如图1，废纸箱的一面利用墙，放置在地面上，利用地面作底，其它的面用一张边长为60cm 的正方形硬纸板围成．经研究发现：由于废纸箱的高是确定的，所以废纸箱的横截面图形面积越大，则它的容积越大．（1）该小组通过多次尝试，最终选定下表中的简便且易操作的三种横截面图形，如图2，是根据这三种横截面图形的面积2(cm )y 与(cm)x （见表中横截面图形所示）的函数关系式而绘制出的图象．请你根据有信息，在表中空白处填上适当的数、式，并完成y 取最大值时的设计示意图；（2）在研究性学习小组展示研究成果时，小华同学指出：图2中“底角为60的等腰梯形”说明理由．60图16、二次函数2y ax bx c=++的图象的一部分如图2－3－1所示。

初三数学第二轮复习练习试卷（二十一）1、某学校举行理科（含数学、物理、化学、生物四科）综合能力比赛，四科的满分都为综合成绩按照数学、物理、化学、生物四科测试成绩的的比例计分，则综合成绩的第一名是（ ）A ．甲B ．乙C ．丙D ．不确定 2、观察下列图形,按规律填空:● 1 1+3 4+5 9+7 16+___ … 36+____3、如图，已知直角坐标系中一条圆弧经过正方形网格的格点A 、B 、C 。

（1）用直尺画出该圆弧所在圆的圆心M 的位置； （2）若A 点的坐标为（0，4），D 点的坐标为（7，0），试验证点D 是否在经过点A 、B 、C 的抛物线上；（3）在（2）的条件下，求证直线CD 是⊙M 的切线。

4、南博汽车城销售某种型号的汽车，每辆进货价为25万元，市场调研表明：当销售价为29万元时，平均每周能售出8辆，而当销售价每降低0.5万元时，平均每周能多售出4辆．如果设每辆．．汽车降价x 万元，每辆汽车的销售利润．．．．为y 万元．（销售利润=销售价-进货价） （1）求y 与x 的函数关系式；在保证商家不亏本的前提下，写出x 的取值范围； （2）假设这种汽车平均每周．．的销售利润为z 万元，试写出z 与x 之间的函数关系式； （3）当每辆汽车的定价为多少万元时，平均每周的销售利润最大？最大利润是多少？● ● ● ● ● ● ●● ● ●● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● … … …5、如图，在等腰梯形ABCD 中，AB DC ∥，45A =∠，10cm AB =，4cm CD =．等腰直角三角形PMN 的斜边10cm MN =，A 点与N 点重合，MN 和AB 在一条直线上，设等腰梯形ABCD 不动，等腰直角三角形PMN 沿AB 所在直线以1cm/s 的速度向右移动，直到点N 与点B 重合为止．（1）等腰直角三角形PMN 在整个移动过程中与等腰梯形ABCD 重叠部分的形状 由 形变化为 形；（2）设当等腰直角三角形PMN 移动(s)x 时，等腰直角三角形PMN 与等腰梯形ABCD 重叠部分的面积为2(cm )y ，求y 与x 之间的函数关系式；（3）当4(s)x =时，求等腰直角三角形PMN 与等腰梯形ABCD 重叠部分的面积．A （N ）MA NM6、有一种笔记本原售价为每8元,甲商场用如下办法促梢,每次购买1～8本打九折、9～16本打八五折、17～25本打八折、超过25本打七五折. 乙商场用如下办法促销:①.请仿照乙商场的促销列表,列出甲商场促销笔记本的购买本数与本价格的对照表 ②.某学校有A 、B 两个班都需要买这种笔记本,A 班需要8本,B 班需要15本,问他们到哪家商场购买花钱较少?③设某班需要购买这种笔记本本数为x 且9 ≤x ≤40,总花费为y 元,从最省钱的角度出发,写出y 与x 的函数关系式.7、如图，45AOB ∠，过OA 上到点O 的距离分别为1，2，3，4，5的点作OA 的垂线与OB 相交，再按一定规律标出一组如图所示的黑色梯形．设前n 个黑色梯形的面积和为n S ．（1）请完成下面的表格：（2）已知n S 与n 之间满足一个二次函数关系，试求出这个二次函数的解析式．8、如图，在平面直角坐标系中，两个函数621,+-==x y x y 的图象交于点A 。