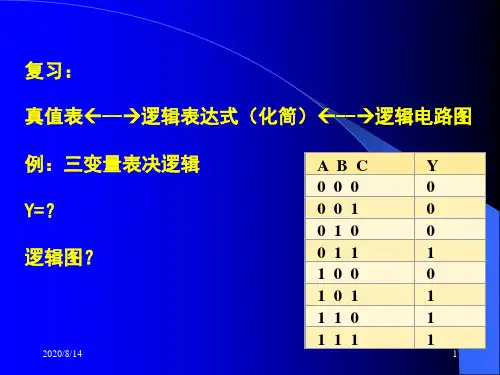
逻辑函数卡诺图化简

利用卡诺图化简逻辑函数的基本原理
1.“相邻”的判断
⑴相邻最小项：任意两个最小项中只有一个变量不同(同一变量名但一个为原变量，另一个为反变量)，其余变量完全相同，在图上反映的是两个相邻的小方格。

⑵卡诺图相邻小方格：是指只隔一条边界的两个小方格。

在n变量的卡诺图上，每个小方格具有n个相邻的小方格，它们是：•具有共同边界的小方格(几何相邻)
•同一幅卡诺图中分别处于行(或列)两端的小方格
(相对相邻)
•在相邻两幅卡诺图中，处于相同位置的两个小方格
(相重相邻)
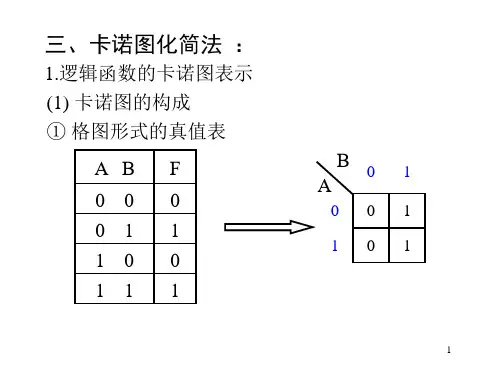
2画卡诺圈的原则
寻找相邻块的目的是为了在图上进行函数化简。

•任何2i个（i≤n）标1的相邻小方格均可画在一个卡诺圈内；
•任何2i个标1的非相邻的小方格不能画入一个卡诺圈内，它们至少画在两个圈内。

下面看几种情况的例子：。

逻辑函数的卡诺图化简法211.6 逻辑函数的卡诺图化简法2【预习】第三册课本第26⾄28页内容.【预习⽬标】了解逻辑函数的卡诺图的概念，了解卡诺图作图的作图⽅法及注意点. 【导引】1．卡诺图：卡诺图是根据最⼩项真值表按相邻原则（⼏何位置上相邻的⼩⽅格只有⼀个因⼦互为反变量，⽽且⽔平、垂直⽅向的两端也如此）排列⽽成的⽅格图，即每⼀个⼩⽅格表⽰⼀个最⼩项．对于含有两个逻辑变量（记为A,B ）的逻辑函数,⽤00表⽰B A ?，01表⽰B A ?，10表⽰B A ?，11表⽰B A ?，其卡诺图的形式如下：将逻辑函数表⽰成最⼩项表达式后，只要在出现的最⼩项对应的⽅格内填上1，其余的填上0即可.对于含有三个逻辑变量（记为A,B,C ）的逻辑函数，可以仿照两个变量的符号表⽰⽅法，得到其卡诺图形式如下：将逻辑函数表⽰成最⼩项表达式后，只要在出现的最⼩项对应的⽅格内填上1，其余的填上0即可.对于含有四个逻辑变量（记为A,B,C,D ）的逻辑函数，仿照上⾯的⽅法可以得到其卡诺图形式如下：将逻辑函数表⽰成最⼩项表达式后，只要在出现的最⼩项对应的⽅格内填上1，其余的填上0即可.【试试看】1.卡诺图的每⼀个⼩⽅格对应着函数的（） A ．最⼤项B ．最⼩项C ．最简函数项D ．输⼊项2.变量为A 、B 、C 的逻辑函数其最⼩项有个，对应的卡诺图⼩⽅格有个.【本课⽬标】了解卡诺图的概念，能根据给定的逻辑函数，画出其对应的卡诺图. 【重点】卡诺图的概念，给定逻辑函数，画出其对应的卡诺图. 【难点】由逻辑函数画卡诺图. 【导学】任务1：学会画出逻辑函数对应的卡诺图.【例1】例1 画出逻辑函数()C B A C B A BC A C AB ABC C B A f ++++=,,对应的卡诺图．【试⾦⽯】画出逻辑函数()C AB C B A BC A ABC C B A f +++=,,对应的卡诺图．【例2】画出逻辑函数()C A C B ABC C B A f ++=,,对应的卡诺图．【试⾦⽯】画出逻辑函数()C B A C B A A C B A f ++=,,对应的卡诺图．【检测】画出逻辑函数(),,f A B C AB BC AB =++对应的卡诺图．【导练】⼀、选择题1.关于作卡诺图说法错误的是（）A.卡诺图是根据最⼩项真值表按相邻原则排列⽽成的⽅格图B.根据变量数的不同，卡诺图可画成2⾏2列、2⾏4列、4⾏4列的形式C.三个变量的卡诺图第⼀⾏的4个取值依次为 00、01、10、11D.卡诺图中每⼀个⼩⽅格表⽰⼀个最⼩项2. 逻辑函数C B A C B A C AB Y ++=的卡诺图为（）A. B.C. D.3.最⼩项D C AB 的逻辑相邻项为（）A. D C B AB. ABCDC. D ABCD. D C B A ⼆、填空题4.将逻辑函数C B A B A Y +=展开为最⼩项表达式为．5.将逻辑函数()C B A Y +=展开为最⼩项表达式为．三、解答题6. 画出逻辑函数()CD B A D C B A CD B A D C AB D C B A f +++=,,,对应的卡诺图．7. 画出逻辑函数()C B C B C A C A C B A f +++=,,对应的卡诺图．。

用卡诺图化简或——与表达式引言：随着电子技术的飞快发展，卡诺图已经变成了逻辑设计中十分重要的数学工具。

卡诺图因为它能用图形将复杂的逻辑函数形象直观的表示出来。

所以，卡诺图在数字电子技术当中应用十分的广泛。

数字电子技术当中的逻辑函数是“或”、“与”、“非”复合而成，所以使用卡诺图分析逻辑函数是具有现实意义的。

1.使用卡诺图的优点化简或——与函数可以使用卡诺图化简法和公式分析法来进行化简。

但是在现实当中的逻辑函数化简当中，逻辑函数可能十分复杂，化简需要熟记大量的基本公式。

不仅如此还需要能够灵活巧妙的使用基本公式、方法，所以使公式化简法显得十分繁琐，所需的技巧性十分强。

但是使用卡诺图时不仅可以用于多输入变量的逻辑函数化简，还可以用图像来直观、快速表示出最简表达式，所以卡诺图是一种十分实用的化简方法。

2. 卡诺图2.1卡诺图概述一个逻辑函数的卡诺图就是讲此函数的最小项表达式中的各最小项相应地填入一个特定的方格图内，从此方格图称为卡诺图。

卡诺图的实质就是真值表的图形化，使得最小项排列得更紧凑，更便于化简。

卡诺图中最小项的排列方案不是惟一的；变量的坐标值0表示相应变量的反变量，1表示相应变量的原变量；各小方格依变量顺序取坐标值，所得二进制数对应的十进制数即相应最小项的下标i。

对于n个变量的逻辑函数有2^n个最小项。

如果把每个最小项用一个小方格表示，再讲这些小方格按格雷码顺序排列，就可以构成n个变量的卡诺图。

以4变量为例的卡诺图表一2.2卡诺图特点卡诺图的特点是：几何位置相邻的最小项在逻辑上也是相邻的。

即相邻的两个最小项只有一个变量不同，这是用卡诺图化简逻辑函数的主要依据。

正如表一中m4与m5两个相邻相中只有D与非D两的差别。

2.3卡诺图化简逻辑函数依据卡诺图具有相邻性，若两个相邻的方格均为1，则这两个最小项之和有一个变量可以被消去。

以此为依据通过把卡诺图上相邻最小项的相邻小方格圈起来进行合并，达到用“与”项来代替。

1.4 用卡诺图化简逻辑函数本次重点内容1、卡诺图的画法与性质2、用卡诺图化简函数教学过程应用卡诺图化简一、卡诺图逻辑函数可以用卡诺图表示。

所谓卡诺图，就是逻辑函数的一种图形表示。

对n个变量的卡诺图来说，有2n个小方格组成，每一小方格代表一个最小项。

在卡诺图中，几何位置相邻（包括边缘、四角）的小方格在逻辑上也是相邻的。

二、最小项的定义及基本性质：1、最小项的定义在n个变量的逻辑函数中，如乘积项中包含了全部变量，并且每个变量在该乘积项中或以原变量或以反变量的形式但只出现一次，则该乘积项就定义为该逻辑函数的最小项。

通常用m表示最小项，其下标为最小项的编号。

编号的方法是：最小项的原变量取1，反变量取0，则最小项取值为一组二进制数，其对应的十进制数便为该最小项的编号。

如最小项CBA对应的变量取值为000，它对应十进制数为0。

因此，最小项CBA的编号为m0，如最小项CBA的编号为m4，其余最小项的编号以此类推。

2、最小项的基本性质：（1）对于任意一个最小项，只有一组变量取值使它的值为1，而其余各种变量取值均使它的值为0。

（2）不同的最小项，使它的值为1的那组变量取值也不同。

（3）对于变量的任一组取值，全体最小项的和为1。

图1.4.1分别为二变量、三变量和四变量卡诺图。

在卡诺图的行和列分别标出变量及其状态。

变量状态的次序是00，01，11，10，而不是二进制递增的次序00，01，10，11。

这样排列是为了使任意两个相邻最小项之间只有一个变量改变（即满足相邻性）。

小方格也可用二进制数对应于十进制数编号，如图中的四变量卡诺图，也就是变量的最小项可用m0, m１,m２,……来编号。

01 0100011110 01ABCABCDBA0001111000011110m m m mm m m mm mm m01230112233mmmmmmmmmmmmmmmm456789101112131415图1.4.1 卡诺图二、应用卡诺图表示逻辑函数应用卡诺图化简逻辑函数时，先将逻辑式中的最小项(或逻辑状态表中取值为1的最小项)分别用1填入相应的小方格内，其它的则填0或空着不填。

10.3逻辑函数的表示及化简169 例2：Y AD AD AB AC BD ABEF BEF A AB AC BD ABEF BEF A BD BEF=++++++=+++++=++ 例3： ()()()()()()()()()(1)(1)()Y AC ABC BC ABC AC ABC BC ABCA C ABC B C ABCA ABC B C C A B C B C ABCA B C B C C A B B ABCA BC BC C C ABC AC C ABC =+++=+=+++++=++++++++=+++++++=++++=++=+=i i在数字电路中大量使用与非门，所以如何把一个化简了的与或表达式转换为与非-与非式，并用与非门去实现它是十分重要的。

一般，用两次求反法可以将一个化简了的与或式转换成与非-与非式。

例 Y AB BC CD AB BC CD AB BC CD =++=++=⋅⋅ 10.3.5 逻辑函数的卡诺图化简1．最小项（1）最小项的定义对于N 个变量，如果P 是一个含有N 个因子的乘积项，而在P 中每一个变量都以原变量或反变量的形式出现一次，且仅出现一次，那么就称P 是N 个变量的一个最小项。

因为每个变量都以原变量和反变量两种可能的形式出现，所以N 个变量有2N 个最小项。

（2）最小项的性质表10-11列出了三个变量的全部最小项真值表。

由表可以看出最小项具有下列性质。

表10-11三变量最小项真值表性质1：每个最小项仅有一组变量的取值会使它的值为“1”，而其他变量取值都使它的值为“0”。

性质2：任意两个不同的最小项的乘积恒为“0”。

性质3：全部最小项之和恒为“1”。

由函数的真值表可以很容易地写出函数的标准与或式，此外，利用逻辑代数的定律、公式，可以将任何逻辑函数式展开或变换成标准与或式。

例1：将逻辑函数式变换成标准与或式。