三角函数综合复习

中考锐角三角函数复习教案教案标题：中考锐角三角函数复习一、教学目标：1.复习三角函数的定义及性质；2.复习与锐角三角函数相关的公式和计算方法；3.提高学生的综合应用能力。

二、教学重点：1.锐角三角函数的定义；2.锐角三角函数的性质；3.锐角三角函数的计算。

三、教学难点：1.锐角三角函数的综合应用；2.解决与锐角三角函数相关的实际问题。

四、教学流程：1.复习预习：复习三角函数的定义及性质；2.引入新知识：引入锐角三角函数的定义；3.讲解锐角三角函数的性质；4.讲解与锐角三角函数相关的公式和计算方法；5.练习锐角三角函数的计算；6.进行综合应用练习；7.提问与解答；8.作业布置。

五、教学内容详细说明：1.复习预习：复习三角函数的定义及性质，包括正弦函数、余弦函数和正切函数的定义及其周期性、奇偶性、增减性等性质。

2.引入新知识：介绍锐角三角函数的定义，包括正弦定理、余弦定理和正切函数的定义。

通过几何图形的展示和实例的计算，让学生感受到锐角三角函数在实际问题中的应用。

3.讲解锐角三角函数的性质：详细讲解正弦、余弦和正切函数的周期性、奇偶性、增减性等性质。

通过图形展示和实例计算，让学生理解和掌握这些性质。

4.讲解与锐角三角函数相关的公式和计算方法：讲解正弦、余弦和正切函数之间的关系及计算方法，包括倍角、半角、和差等公式。

通过实例计算，让学生掌握这些公式和计算方法。

5.练习锐角三角函数的计算：提供一些锐角三角函数的计算题目，让学生进行练习和巩固。

教师可以给予指导和解答，让学生通过练习提高计算能力。

6.进行综合应用练习：提供一些与锐角三角函数相关的实际问题，让学生进行综合应用练习。

学生可以通过解决这些问题来巩固所学的知识，并培养解决实际问题的能力。

7.提问与解答：教师可以进行提问，引导学生回顾和总结所学内容，回答问题和解决疑惑。

8.作业布置：布置一些与锐角三角函数相关的作业，让学生巩固所学的知识。

作业可以包括计算题目、应用题目和综合问题。

2025年中考数学二轮复习专题圆与锐角三角函数综合题（第二课时）练习例1.已知，如图，AB是⊙O的直径，点C为⊙O上一点，OF⊙BC于点F，交⊙O于点E，AE与BC交于点H，点D为OE的延长线上一点，且⊙ODB＝⊙AEC．（1）求证：BD是⊙O的切线；（2）求证：CE2＝EH•EA；（3）若⊙O的半径为5，sin A＝，求BH的长．练习1.如图，AB为⊙O的直径，直线CD切⊙O于点M，BE⊙CD于点E．（1）求证：⊙BME＝⊙MAB；（2）求证：BM2＝BE•AB；（3）若BE＝，sin⊙BAM＝，求线段AM的长．例2.如图，AB是⊙O的直径，点P是BA延长线上一点，过点P作⊙O的切线PC，切点是C，过点C作弦CD⊙AB于E，连接CO，CB．（1）求证：PD是⊙O的切线；（2）若AB＝10，tan B＝，求P A的长；（3）试探究线段AB，OE，OP之间的数量关系，并说明理由．练习2．如图，AB是⊙O的直径，弦CD⊙AB，垂足为H，连结AC，过上一点E作EG⊙AC交CD的延长线于点G，连结AE交CD于点F，且EG＝FG，连结CE．（1）求证：⊙ECF⊙⊙GCE；（2）求证：EG是⊙O的切线；（3）延长AB交GE的延长线于点M，若tan G＝，AH＝3，求EM的值．例3.如图，BM是以AB为直径的⊙O的切线，B为切点，BC平分⊙ABM，弦CD交AB于点E，DE＝OE．（1）求证：⊙ACB是等腰直角三角形；（2）求证：OA2＝OE•DC：（3）求tan⊙ACD的值．练习3如图，AB为⊙O的直径，C为⊙O上一点，D是弧BC的中点，BC与AD、OD分别交于点E、F．（1）求证：DO⊙AC；（2）求证：DE•DA＝DC2；（3）若tan⊙CAD＝，求sin⊙CDA的值．例4.如图，已知在⊙ABP中，C是BP边上一点，⊙P AC＝⊙PBA，⊙O是⊙ABC的外接圆，AD是⊙O的直径，且交BP于点E．（1）求证：P A是⊙O的切线；（2）过点C作CF⊙AD，垂足为点F，延长CF交AB于点G，若AG•AB＝12，求AC的长；（3）在满足（2）的条件下，若AF：FD＝1：2，GF＝1，求⊙O的半径及sin⊙ACE的值．练习4.如图1所示，已知AB，CD是⊙O的直径，T是CD延长线的一点，⊙O的弦AF交CD于点E，且AE＝EF，OA2＝OE•OT．（1）如图1，求证：BT是⊙O的切线；（2）在图1中连接CB，DB，若＝，求tan T的值；（3）如图2，连接DF交AB于点G，过G作GP⊙CD于点P，若BT＝6，DT＝6．求：DG的长．例5.如图，已知AO为Rt⊙ABC的角平分线，⊙ACB＝90°，，以O为圆心，OC为半径的圆分别交AO，BC于点D，E，连接ED并延长交AC于点F．（1）求证：AB是⊙O的切线；（2）求tan⊙CAO的值；（3）求的值．课后练习1.如图1，以AB为直径作⊙O，点C是直径AB上方半圆上的一点，连结AC，BC，过点C作∠ACB的平分线交⊙O于点D，连结AD，过点D作⊙O的切线交CB的延长线于点E．（1）求证：DE∥AB．（2）若⊙O的半径为1，求CA•CE的最大值．（3）如图2，连结AE，若，求tan∠AEC的值．2.如图，点A，B，C在⊙O上运动，满足AB2＝BC2+AC2，延长AC至点D，使得∠DBC＝∠CAB，点E是弦AC上一动点（不与点A，C重合），过点E作弦AB的垂线，交AB于点F，交BC的延长线于点N，交⊙O于点M（点M在劣弧上）．（1）BD是⊙O的切线吗？请作出你的判断并给出证明；（2）记△BDC，△ABC，△ADB的面积分别为S1，S2，S，若S1•S＝（S2）2，求（tan D）2的值；（3）若⊙O的半径为1，设FM＝x，FE•FN•＝y，试求y关于x的函数解析式，并写出自变量x的取值范围．3.如图，点O为以AB为直径的半圆的圆心，点M，N在直径AB上，点P，Q在上，四边形MNPQ为正方形，点C在上运动（点C与点P，Q不重合），连接BC并延长交MQ的延长线于点D，连接AC交MQ于点E，连接OQ．（1）求sin∠AOQ的值；（2）求的值；（3）令ME＝x，QD＝y，直径AB＝2R（R＞0，R是常数），求y关于x的函数解析式，并指明自变量x的取值范围．4.如图，已知等腰三角形ABC内接于⊙O，AB＝AC，点D为上一点（不与点A，C重合），连接AD，BD，CD，且BC＝3CD＝18．（1）如图1，若BD为⊙O直径．①求tan∠BAC的值；②求四边形ABCD的面积．（2）如图2，在上取一点E，使，连接CE，交AB于点F，若∠BDC＝∠AFC，求AD的长度．5.如图1，AB是⊙O的直径，点P是直径AB上一动点，过点P作直径AB的垂线交⊙O于C，D两点．（1）若⊙O的半径为2，，连接CO，DO，求劣弧的长度；（2）如图2，点K是劣弧上一点，连接AK，BK，AK交CD于点Q，连接BQ，记∠BAK＝α，∠ABQ＝β，若BQ恰好平分∠ABK，且，求β的正切值；（3）如图3，当动点P移动到点O时，点K是劣弧上一点，连接AK，DK，AK交CD于点Q，DK交AB于点N，连接AD，QN．①求证：△DAQ∽△AND；②记∠OND＝θ，△ANQ的面积为S1，△DON的面积为S2，求的值（结果用含有θ的三角函数值的式子进行表示）．。

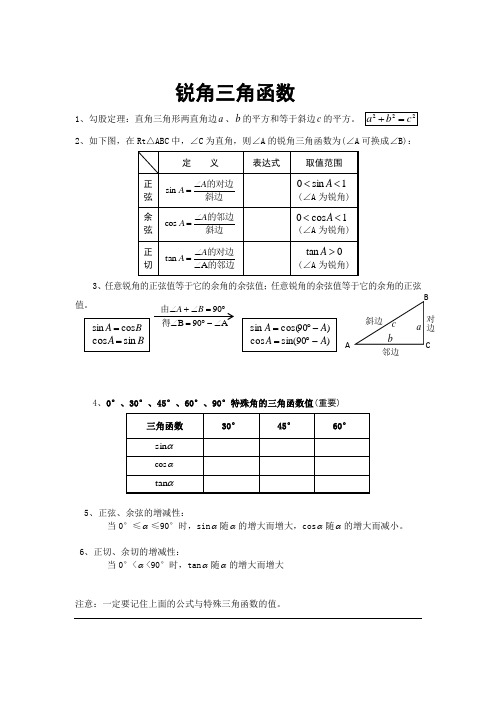
锐角三角函数1、勾股定理：直角三角形两直角边a 、b 的平方和等于斜边c 的平方。

2、如下图，在Rt △ABC 中，∠C 为直角，则∠A 的锐角三角函数为(∠A 可换成∠B)：3、任意锐角的正弦值等于它的余角的余弦值；任意锐角的余弦值等于它的余角的正弦值。

4、0°、30°、45°、60°、90°特殊角的三角函数值(重要)5、正弦、余弦的增减性：当0°≤α≤90°时，sin α随α的增大而增大，cos α随α的增大而减小。

6、正切、余切的增减性：当0°<α<90°时，tan α随α的增大而增大注意：一定要记住上面的公式与特殊三角函数的值。

A90B 90∠-︒=∠︒=∠+∠得由B A对边邻边AC解直角三角形1、解直角三角形的定义：已知边和角（两个，其中必有一边）→所有未知的边和角。

依据：①边的关系：222c b a =+；②角的关系：A+B=90°； ③边角关系：三角函数的定义。

斜边的对边A A ∠=sin 斜边的邻边A A ∠=cos的邻边的对边A tan ∠∠=A A2、应用举例：(1)仰角：视线在水平线上方的角；俯角：视线在水平线下方的角。

(2)坡面的铅直高度h 和水平宽度l 的比叫做坡度(坡比)。

用字母i 表示，即hi l=。

坡度一般写成1:m 的形式，如1:5i =等。

把坡面与水平面的夹角记作α(叫做坡角)，那么tan hi lα==。

3、从某点的指北方向按顺时针转到目标方向的水平角，叫做方位角。

如图3，OA 、OB 、OC 、OD 的方向角分别是：45°、135°、225°。

4、指北或指南方向线与目标方向 线所成的小于90°的水平角，叫做方向角。

如图4,OA 、OB 、OC 、OD 的方向角分别是：北偏东30°（东北方向） ， 南偏东45°（东南方向）， 南偏西60°（西南方向）， 北偏西60°（西北方向）。

专题复习：三角函数的综合应用题编(推荐时间：推荐时间：7070分钟分钟) )1． 设函数f (x )＝a ·b ，其中向量a ＝(2cos x,1)1)，，b ＝(cos x ，3sin 2x )，x ∈R .(1)(1)若函数若函数f (x )＝1－3，且x ∈ëêéûúù－π3，π3，求x 的值；的值；(2)(2)求函数求函数y ＝f (x )的单调增区间，的单调增区间，并在给出的坐标系中画出并在给出的坐标系中画出y ＝f (x )在区间[0[0，，π]上的图象．上的图象．解 (1)(1)依题设得依题设得f (x )＝2cos 22x ＋3sin 2x ＝1＋cos 2x ＋3sin 2x ＝2sin èçæø÷ö2x＋π6＋1.由2sin èçæø÷ö2x ＋π6＋1＝1－3，得sin èçæø÷ö2x ＋π6＝－32.∵－π3≤x ≤π3，∴－π2≤2x ＋π6≤5π6， ∴2x ＋π6＝－π3，即x ＝－π4. (2)(2)当－当－π2＋2k π≤2x ＋π6≤π2＋2k π(k ∈Z )， 即－π3＋k π≤x ≤π6＋k π(k ∈Z )时，函数y ＝f (x )单调递增，即函数y ＝f (x )的单调增区间为ëêéûúù－π3＋k π，π6＋k π(k ∈Z )，x 0 π6 π3 π2 2π3 5π6 π y232－122． 已知向量a ＝(cosx ＋3sin x ，3sin x )，b ＝(cos x －3sin x ，2cos x )，函数f (x )＝a ·b －cos 2x . (1)(1)求函数求函数f (x )的值域；的值域；(2)(2)若若f (θ)＝15，θ∈ëêéûúùπ6，π3，求sin 2θ的值．的值．解 (1)f (x )＝a ·b －cos 2x＝(cos x ＋3sin x )(cos x －3sin x )＋3sin x ·2cos x －cos 2x ＝cos 2x －3sin 2x ＋23sin x cos x －cos 2x ＝cos 2x －sin 2x －2sin 2x ＋23sin x cos x －cos 2x ＝cos 2x ＋3sin 2x －1 ＝2sin èçæø÷ö2x ＋π6－1，f (x )的值域为的值域为[[－3,1]3,1]．．(2)(2)由由(1)(1)知知f (θ)＝2sin èçæø÷ö2θ＋π6－1，由题设2sin èçæø÷ö2θ＋π6－1＝15，即sin èçæø÷ö2θ＋π6＝35，∵θ∈ëêéûúùπ6，π3，∴，∴22θ＋π6∈ëêéûúùπ2，5π6， ∴cos èçæø÷ö2θ＋π6＝－45，∴sin 2θ＝sin ëêéûúùèçæø÷ö2θ＋π6－π6＝sin èçæø÷ö2θ＋π6cos π6－cos èçæø÷ö2θ＋π6sinπ6＝35×32－èçæø÷ö－45×12＝33＋410.3． 已知向量m ＝èçæø÷ösin A ，12与n ＝(3(3，，sin A ＋3cos A )共线，其中A 是△ABC的内角．的内角．(1)(1)求角求角A 的大小；的大小；(2)(2)若若BC ＝2，求△ABC 面积S 的最大值．的最大值．解 (1)(1)∵∵m ∥n ，∴，∴sin sin A ·(sin A ＋3cos A )－32＝0.∴1－cos 2A 2＋32sin 2A －32＝0， 即32sin 2A －12cos 2A ＝1， 即sin èçæø÷ö2A －π6＝1.∵A ∈(0(0，，π)，∴，∴22A －π6∈èçæø÷ö－π6，11π6. 故2A －π6＝π2，A ＝π3. (2)(2)∵∵BC ＝2，由余弦定理得b 22＋c 22－bc ＝4，又b 22＋c 22≥2bc ，∴bc ≤4(4(当且仅当当且仅当b ＝c 时等号成立时等号成立))， 从而S △ABC ＝12bc sin A ＝34bc ≤34×4＝ 3.即△ABC 面积S 的最大值为 3.4． 在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c 已知cos A －3cos C cos B＝3c －ab . (1)(1)求求sin Csin A的值；的值；(2)(2)若若B 为钝角，b ＝1010，求，求a 的取值范围．的取值范围． 解 (1)(1)由正弦定理，设由正弦定理，设asin A ＝bsin B ＝csin C＝k ，则3c －a b ＝3k sin C －k sin A k sin B ＝3sin C －sin Asin B ， 所以cos A －3cos C cos B ＝3sin C －sin Asin B，即(cos A －3cos C )sin B ＝(3sin C －sin A )cos B ， 化简可得sin(A ＋B )＝3sin(B ＋C )． 又A ＋B ＋C ＝π，所以sin C ＝3sin A ， 因此sin Csin A＝3. (2)(2)由由sin C sin A ＝3得c ＝3a . 由题意知îíìa ＋c >ba 2＋c 2<b2，又b ＝1010，所以，所以52<a <10.5． 已知函数f (x )＝A sin(ωx ＋φ)èçæø÷ö其中x ∈R ，A >0>0，，ω>0>0，－，－π2<φ<π2的部分图象如图所示．图象如图所示．(1)(1)求函数求函数f (x )的解析式；的解析式；(2)(2)已知函数已知函数f (x )的图象上的三点M ，N ，P 的横坐标分别为－的横坐标分别为－1,1,51,1,5，，求sin ∠MNP 的值．的值．解 (1)(1)由图可知，由图可知，A ＝1，最小正周期T ＝4×2＝8. 由T ＝2πω＝8，得ω＝π4.又f (1)(1)＝＝sin èçæø÷öπ4＋φ＝1，且－π2<φ<π2，所以π4＋φ＝π2，解得φ＝π4. 所以f (x )＝sin èçæø÷öπ4x ＋π4. (2)(2)因为因为f (－1)1)＝＝0，f (1)(1)＝＝1，f (5)(5)＝＝sin èçæø÷ö5π4＋π4＝－＝－11， 所以M (－1,0)1,0)，，N (1,1)(1,1)，，P (5(5，－，－1)1)．．所以所以||MN |＝5，|PN |＝2020，，|MP |＝37. 由余弦定理得由余弦定理得cos cos∠∠MNP ＝5＋2020－－3725×20＝－35. 因为∠MNP ∈(0(0，，π)， 所以sin sin∠∠MNP ＝45.6． 已知向量a ＝(cos α，sin α)，b ＝(cosx ，sin x )，c ＝(sin x ＋2sin α，cos x ＋2cos α)，其中0<α<x <π. (1)(1)若若α＝π4，求函数f (x )＝b ·c 的最小值及相应x 的值；的值； (2)(2)若若a 与b 的夹角为π3，且a ⊥c ，求tan 2α的值．的值．解 (1)(1)∵∵b ＝(cos x ，sin x )，c ＝(sin x ＋2sin α，cos x ＋2cos α)，α＝π4， ∴f (x )＝b ·c ＝cos x sin x ＋2cos x sin α＋sin x cos x ＋2sin x cos α＝2sin x cos x ＋2(sin x ＋cos x )．令t ＝sin x ＋cos x èçæø÷öπ4<x <π，则2sin x cos x ＝t 2－1，且－，且－1<1<t < 2.则y ＝t 2＋2t －1＝èçæø÷öt ＋222－32，－，－1<1<t <2，∴t ＝－22时，y min ＝－32，此时sin x ＋cos x ＝－22，即2sin èçæø÷öx ＋π4＝－22，∵π4<x <π，∴π2<x ＋π4<54π， ∴x ＋π4＝76π，∴x ＝11π12. ∴函数f (x )的最小值为－32，相应x 的值为11π12.的夹角为，cos＝a·b＝＝π.ø÷ö＋π3＋∴52sin 2＋32cos 2＝－35.。

三角函数综合练习题考查单调性，单调区间，最大最小值，周期，零点，对称性，对称中心一、解答题（本大题共30小题，共360.0分）1.已知函数f(x)=cosxsin(x−π3)+√34(x∈R)．(1)求f(x)的最小正周期及单调递增区间；(2)求f(x)在区间[−π4,π4]上的最大值和最小值．2.已知函数f(x)=cos(2x+π3)．(1)求函数y=f(x)的对称轴方程；(2)求函数f(x)在区间[−π12,π2]上的最大值和最小值．3.设函数f(x)=cosx⋅sin(x+π3)−√3cos2x+√34．(1)求f(x)的最小正周期和对称中心；(2)当x∈[0,π3]时，求函数f(x)的最值．4.已知函数f(x)=cos2x−sin2x−2√3sinxcosx(x∈R)．(2)求f(x)的最小正周期及单调递减区间．5.已知函数f(x)=cos(2x−π3)+2sin(x−π4)sin(x+π4)．(Ⅰ)求函数f(x)的最小正周期；(Ⅱ)若将函数f(x)图象上每点的横坐标变为原来的2倍，纵坐标不变，得到函数y=g(x)的图象，求g(x)在区间[−π12,π]上的值域．6.已知函数f(x)=2sinx⋅sin(π2−x)+√3(cos2x−sin2x)．(Ⅰ)求函数f(x)的最小正周期；(Ⅱ)求方程f(x)=2的解构成的集合．7.已知函数f(x)=2sin2x+2√3sinxcosx．(Ⅰ)求函数f(x)的最小正周期；(Ⅱ)若x∈[0,5π12]，求函数f(x)的值域．8.已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π2)的图象过点P(−5π12,0)，且图象上与P点最近的一个最低点坐标为(−π6,−2)．(1)求函数的解析式；(2)若将此函数的图象向左平移π6个单位长度后，再向上平移2个单位长度得到g(x)的图象，求g(x)在[−π6,π3]上的值域．9.已知f(x)=2sin(2x+π3)．(1)求f(x)的最大值，并写出f(x)取最大值时，x值的集合．(2)求f(x)的单调递增区间．10.已知函数f(x)=cosx(2sinx+√3cosx)−√3sin2x．(Ⅰ)求函数f(x)的最小正周期和单调递减区间；(Ⅱ)若当x∈[0,π2]时，关于x的不等式f(x)≥m有解，求实数m的取值范围．11.已知函数f(x)=2sin(2x−π6).(1)求函数f(x)的对称轴；(2)当x∈[0,π2]时，求函数f(x)的最大值与最小值．12.已知函数f(x)=4sinxcos(x−π3)−√3．(Ⅰ)求f(x)的最小正周期和单调递增区间；(Ⅱ)若方程f(x)=m在(π2,5π3)有两个不同的实根，求m的取值范围．13.已知向量a⃗=(3sinx,cos2x)，b⃗ =(cosx,12)，x∈R，设函数f(x)=a⃗⋅b⃗ ．(Ⅰ)求函数f(x)的最小正周期；(Ⅱ)求函数f(x)在[0,π2]上的最大值和最小值．14.已知函数f(x)=sinωx(sinωx+cosωx)的最小正周期为π，ω为正实数．(1)求ω的值；(2)求函数f(x)的单调递减区间及对称轴方程．15.已知向量m⃗⃗⃗ =(cosx,−1)，n⃗=(√3sinx,cos2x)，设函数f(x)=m⃗⃗⃗ ⋅n⃗+1．(1)求函数y=f(x)的单调递减区间，并说明由函数y=sinx的图象如何变换可得到函数y=f(x)的图象．(2)若x∈[0,π2]，f(x)=56，求cos2x的值．16.已知函数f(x)=(sinx+cosx)2+cos2x．(I)求f(x)的最小正周期；(Ⅱ)求f(x)在[0,π2]上的单调递增区间．17.已知向量a⃗=(√3sinx,cosx)，b⃗ =(−cosx,cosx)，c⃗=(2,1)．(Ⅰ)若a⃗//c⃗，求a⃗⋅b⃗ 的值；(Ⅱ)若x∈[0,π2]，求f(x)=a⃗⋅b⃗ 的值域．18.已知函数f(x)=2asinωxcosωx+2√3cos2ωx−√3(a>0,ω>0)的最大值为2，且最小正周期为π．(1)求函数f(x)的对称轴方程；(2)若f(α)=43,求sin(4α+π6)的值．19.设函数f(x)=sinx+√3cosx(x∈R)．(1)求函数f(x)的最值和最小正周期；(2)将函数f(x)的图像先保持纵坐标不变，横坐标伸长为原来的2倍，再将图像向π20.已知函数f(x)=Asin(ωx+φ)，其中A>0，ω>0，−π2<φ<π2，x∈R其部分图象如图所示．(1)求函数y=f(x)的解析式与单调增区间；(2)当x∈[0,π]时，求函数y=f(x)的最大值与最小值及此时相应x的值．21.已知函数f(x)=2sinx(√3cosx+sinx)−1．(I)求f(x)的单调递增区间；(II)若f(α2)=25，求sin(2α+π6)的值．22.已知函数f(x)=12cos2x+√32sinxcosx+1．(1)求函数f(x)的最小正周期和其图象对称中心的坐标；(2)求函数f(x)在[π12,π4]上的值域．23.已知f(x)=sin(2x+π6)+3cos(2x−π3).(1)求f(x)的最小正周期及单调递减区间;(2)若f(α2)=45，α∈(0,π)，试求cosα的值．24.已知函数f(x)=cos2x+2√3sinxcosx−sin2x.(1)求函数f(x)的最小正周期；(2)求f(x)在区间[−π3,π3]上的最大值和最小值．25.已知函数f(x)=(cosx+√3sinx)⋅sin(π2−x)+12．(1)求函数f(x)的最小正周期和单调增区间；(2)求函数f(x)在区间[712π,56π]上的最小值以及取得该最小值时x的值．26.已知函数f(x)=√3sin(ωx+φ)(ω>0,|φ|≤π2)的图像关于直线x=π3对称，且图像上相邻两个最高点的距离为π．(1)求ω和φ的值；(2)若f(α2)=√34(π6<α<2π3)，求sin (α+π3)的值．27.已知函数f(x)=cos2x+√3sinxcosx−12(x∈R)．(1)求f(x)的最小正周期；(2)讨论f(x)在区间[−π4,π4]上的单调性；28.已知函数f(x)=2cosx(λsinx−cosx)+sin2x+1(λ<0)，且f(x)的最小值为−2．(1)求实数λ的值及函数f(x)的单调递减区间;(2)当x∈[−π12,π2]时，若函数g(x)=f(x)−k有且仅有一个零点，求实数k的取值范围．29. 已知函数f(x)=Acos(ωx +φ)+B(A >0,ω>0,|φ|<π2)的部分图像如下图所示．(Ⅰ)求f (x )的解析式及对称中心坐标；(Ⅱ)先将f (x )的图像纵坐标缩短到原来的12倍，在向右平移π6个单位，最后将图像向上平移1个单位后得到g (x )的图像，求函数y =g (x )在x ∈[π12,3π4]在上的单调减区间和最值．)(x∈R)．30.已知函数f(x)=2sinxsin(x+π2(Ⅰ)求f(0)的值；(Ⅱ)求f(x)的最小正周期；)为偶函数，求φ的值．(Ⅲ)若y=f(x+φ)(0<φ<π2答案和解析1.【答案】解：(1)因为f(x)=cosxsin(x−π3)+√34，=12sinxcosx−√32cos2x+√34=14sin2x+√34(1−2cos2x)，=14sin2x−√34cos2x，=12sin(2x−π3)所以最小正周期为：T=π；由−π2+2kπ≤2x−π3≤π2+2kπ，k∈Z得−π12+kπ≤x≤5π12+kπ，k∈Z，即单调递增区间是：[−π12+kπ,5π12+kπ]，k∈Z，(2)因为x∈[−π4,π4]，所以2x−π3∈[−5π6,π6]，因此sin(2x−π3)∈[−1,12]，当2x−π3=−π2即x=−π12时，取最小值−12；当2x−π3=π6即x=π4时，取最大值14；【解析】(1)先利用和差角公式及辅助角公式进行化简，然后结合周期公式即可求解；(2)结合正弦函数的性质即可直接求解．本题主要和差角公式，辅助角公式在三角化简求值中的应用2.【答案】解：(1)函数f(x)=cos(2x+π3)．由2x+π3=kπ得x=kπ2−π6，即函数的对称轴方程为x=kπ2−π6，k∈Z，(2)当−π12≤x≤π2时，−π6≤2x≤π，π6≤2x+π3≤4π3，所以当2x+π3=π，即x=π3时，函数f(x)取得最小值，最小值为f(x)=cosπ=−1，当2x+π3=π6，即x=−π12时，函数f(x)取得最大值，最大值为f(x)=cosπ6=√32．【解析】(1)直接利用余弦型函数的性质和整体思想求出函数的对称轴方程．(2)利用整体思想，进一步利用函数的定义域求出函数的值域，再求出函数的最值．本题考查的知识要点：三角函数关系式的变换，余弦型函数的性质的应用，主要考查学生的运算能力和转换能力及思维能力，属于基础题型．3.【答案】解：(1)f(x)=cosx⋅sin(x+π3)−√3cos2x+√34=cosx(12sinx+√32cosx)−√3cos2x+√34=14sin2x−√34cos2x=12sin(2x−π3)，∴f(x)的最小正周期是2π2=π，令2x−π3=kπ，k∈Z，解得x=12kπ+π6，k∈Z，可得对称中心为(12kπ+π6,0)，k∈Z．(2)当x∈[0,π3]时，2x−π3∈[−π3,π3]，可得sin(2x−π3)∈[−√32,√32]，可得函数f(x)=12sin(2x−π3)∈[−√34,√34]，即函数f(x)的最小值为−√34，最大值为√34．【解析】(1)利用三角函数恒等变换的应用可求函数解析式f(x)=12sin(2x−π3)，利用三角函数周期公式可求f(x)的最小正周期，利用正弦函数的性质可求其对称中心．(2)由已知可求范围2x−π3∈[−π3,π3]，进而根据正弦函数的性质即可求其最值．本题主要考查了三角函数恒等变换的应用，正弦函数的图象和性质，考查了转化思想和函数思想，属于基础题．4.【答案】解：(1)f(x)=cos2x−sin2x−2√3sinxcosx=cos2x−√3sin2x=2cos(2x+π3)，则f(π6)=2cos2π3=2×(−12)=−1．(2)f(x)的最小正周期T=2π2=π，令2kπ≤2x+π3≤2kπ+π，k∈Z，得kπ−π6≤x≤kπ+π3，k∈Z，即f(x)的单调递减区间为[kπ−π6,kπ+π3]，k∈Z．【解析】(1)利用辅助角公式进行化简，然后代入求值即可．(2)结合三角函数的周期公式，以及单调递减区间的性质建立不等式进行求解．本题主要考查三角函数的图象和性质，利用辅助角公式进行化简，然后结合三角函数的性质是解决本题的关键．难度不大．5.【答案】解：(Ⅰ)函数f(x)=cos(2x−π3)+2sin(x−π4)sin(x+π4)=cos(2x−π3)+sin(2x−π2)=12cos2x+√32sin2x−cos2x=sin(2x−π6)，故它的最小正周期为2π2=π．(Ⅱ)若将函数f(x)的图象上每点的横坐标变为原来的2倍，纵坐标不变，得到函数y=g(x)=sin(x−π6)的图象．在区间[−π12,π]上，x−π6∈[−π4,5π6]，故g(x)在区间[−π12,π]上的值域为[−√22,1]．【解析】(Ⅰ)由题意利用三角恒等变换花简f(x)的解析式，再利用正弦函数的周期性，得出结论．(Ⅱ)由题意利用函数y=Asin(ωx+φ)的图象变换规律，求得g(x)的解析式，再利用正弦函数的定义域和值域，得出结论．本题主要考查三角恒等变换，函数y=Asin(ωx+φ)的图象变换规律，正弦函数的周期性、定义域和值域，属于中档题．6.【答案】解：(Ⅰ)∵函数f(x)=2sinx⋅sin(π2−x)+√3(cos2x−sin2x)=sin2x+√3cos2x=2sin(2x+π3)，故f(x)的最小正周期为2π2=π．(Ⅱ)方程f(x)=2，即sin(2x+π3)=1，2x+π3=2kπ+π2，即x=kπ+π12，k∈Z．故方程f(x)=2的解构成的集合为{x|x═kπ+π12,k∈Z}．【解析】(Ⅰ)由题意利用三角恒等变换化简函数的解析式，再根据正弦函数的周期性，得出结论．(Ⅱ)根据方程f(x)=2，可得2x+π3=2kπ+π2，由此求得x的取值集合．本题主要考查三角恒等变换，正弦函数的周期性，解三角方程，属于中档题．7.【答案】解：(Ⅰ)∵f(x)=2sin2x+2√3sinxcosx=1−cos2x+√3sin2x=2sin(2x−π6)+1，∴函数f(x)的最小正周期T=2π2=π．(Ⅱ)∵x∈[0,5π12]，∴2x−π6∈[−π6,2π3]，∴sin(2x−π6)∈[−12,1]，∴f(x)=2sin(2x−π6)+1∈[0,3]，即函数f(x)的值域为[0,3]．【解析】(Ⅰ)利用三角函数的恒等变换化简函数的解析式，再利用正弦函数的周期性求得f(x)的最小正周期．(Ⅱ)利用正弦函数的定义域和值域，即可求解．本题主要考查三角函数的恒等变换，正弦函数的周期性、定义域和值域，属于基础题．8.【答案】解：(1)由题可知，A=2，|−5π12+π6|=14T，∴最小正周期T=π，∴ω=2πT=2，∵函数f(x)过点(−π6,−2)，∴−2=2sin[2×(−π6)+φ]，∴φ=−π6+2kπ，k∈Z，又|φ|<π2，∴φ=−π6，∴函数的解析式y=2sin(2x−π6).(2)g(x)=2sin[2(x+π6)−π6]+2=2sin(2x+π6)+2，∵x∈[−π6,π3]，∴2x+π6∈[−π6,5π6]，∴sin(2x+π6)∈[−12,1]，g(x)∈[1,4]．故g(x)在[−π6,π3]上的值域为[1,4]．【解析】(1)由题可知，A=2，|−5π12+π6|=14T，再结合ω=2πT可求得ω的值，然后将点(−π6,−2)代入函数f(x)的解析式中，并利用|φ|<π2，可求出φ的值，故而得解．(2)根据函数图象的变换法则可得g(x)=2sin(2x+π6)+2，然后根据x∈[−π6,π3]，求出2x+π6的取值范围，再结合正弦函数的图象即可得解．本题考查正弦型函数解析式的求法、正弦函数的图象变换与性质，考查学生的数形结合思想、逻辑推理能力和运算能力，属于基础题．9.【答案】解：(1)f(x)max=2，当f(x)=2时，有sim(2x+π3)=1∴2x+π3=2kπ+π2(k∈z)，解得x=kπ+π12，∴f(x)取最大值时x值的集合为{x|x=kπ+π12,k∈z}．(2)由2kπ−π2≤2x+π3≤2kπ+π2,k∈z，解得kπ−5π12≤x≤kπ+π12∴f(x)的单调递增区间为：[kπ−5π12,kπ+π12],k∈z．【解析】(1)由正弦函数的有界性得出函数的最值，再整体代换解出x的值，写成集合形式；(2)将2x+π3整体代入正弦函数的单调递增区间，解出x的范围写成区间形式．本题考查复合三角函数的单调性与三角函数的最值，考查正弦函数的性质，考查分析与运算能力，属于中档题．10.【答案】解：(Ⅰ)因为f(x)=2sinxcosx+√3cos2x−√3sin2x=sin2x+√3cos2x=2sin(2x+π3)，所以函数f(x)的最小正周期T=π，因为函数y=sinx的的单调递减区间为[2kπ+π2,2kπ+3π2],k∈Z，所以2kπ+π2≤2x+π3≤2kπ+3π2(k∈Z)，解得kπ+π12≤x≤kπ+7π12(k∈Z)，所以函数f(x)的单调递减区间是[kπ+π12,kπ+7π12],(k∈Z)．(Ⅱ)由题意可知，不等式f(x)≥m有解，即m≤f(x)max．由(Ⅰ)可知f(x)=2sin(2x+π3)，当x∈[0,π2]时，2x+π3∈[π3,4π3]，故当2x+π3=π2，即x=π12时，f(x)取得最大值，最大值为2．所以m≤2.故实数m的取值范围是(−∞,2]．【解析】(Ⅰ)先将函数f(x)进行化简，然后根据三角函数的图象和性质即可求函数f(x)的最小正周期和单调递减区间；(Ⅱ)转化为m≤f(x)max.结合变量的范围求出其最大值即可求解结论．本题主要考查三角函数的图象和性质，利用三角化简公式将函数化简是解决本题的关键．11.【答案】解：(1)函数f(x)=2sin(2x−π6).令2x−π6=kπ+π2(k∈Z)，解得x=kπ2+π3(k∈Z)，所以函数f(x)的对称轴方程为：x=kπ2+π3(k∈Z)．(2)由于x∈[0,π2]，所以2x−π6∈[−π6,5π6]，故sin(2x−π6)∈[−12,1]．则：−1≤f(x)≤2．故：当x=0时，函数的最小值为−1．当x=π3时，函数的最大值为2．【解析】(1)直接利用正弦型函数的性质的应用求出函数的对称轴方程．(2)利用函数的定义域的应用求出函数的值域，进一步求出函数的最大和最小值．本题考查的知识要点：正弦型函数的性质的应用，主要考查学生的运算能力和转换能力及思维能力，属于基础题型．12.【答案】解：(Ⅰ)f(x)=4sinxcos(x −π3)−√3，=4sinx(12cosx +√32sinx)−√3=2sinxcosx +2√3sin 2x −√3，=sin2x −√3cos2x =2sin(2x −π3)， 所以f(x)的最小正周期T =2π2=π，由−π2+2kπ≤2x −π3≤π2+2kπ,k ∈Z 得 −π12+kπ≤x ≤5π12+kπ,k ∈Z ，所以f(x)的单调递增区间是[−π12+kπ,5π12+kπ],k ∈Z ， (Ⅱ)令t =2x −π3，因为x ∈(π2,5π3)，所以t ∈(2π3,3π)， 即方程2sint =m 在t ∈(2π3,3π)有两个不同的实根，由函数y =2sint 的图象可知，当m ∈(−2,0]∪[√3,2)时满足题意，所以m 的取值范围为(−2,0]∪[√3,2)．【解析】(I)先结合和差角公式及辅助角公式进行化简，然后结合正弦函数的性质即可求解；(II)由已知可转化为函数图象的交点，结合正弦函数的性质可求．本题主要考出来和差角公式，辅助角公式在三角化简中的应用，体现了转化思想的应用，属于中档试题．13.【答案】解：(1)∵a ⃗ =(3sinx,cos2x)，b ⃗ =(cosx,12)，x ∈R ， ∴函数f(x)=a⃗ ⋅b ⃗ =(3sinx,cos2x)⋅(cosx,12)=3sinxcosx +12cos2x =32sin2x +12cos2x =√102sin(2x +φ)(tanφ=13，取φ为锐角)．∴函数f(x)的最小正周期为2π2=π；(2)由(1)得f(x)=√102sin(2x +φ)(tanφ=13，取φ为锐角)．∵x ∈[0,π2]，∴2x +φ∈[φ,π+φ]．则当2x +φ=π+φ时，f(x)取得最小值为√102sin(π+φ)=−√102sinφ=−√102×√1010=−12；当2x +φ=π2时，f(x)取得最大值为√102sin π2=√102．∴函数f(x)在[0,π2]上的最大值和最小值分别为√102，−12．【解析】(Ⅰ)利用平面向量的数量积的坐标运算可得f(x)的解析式，利用周期公式求周期；(Ⅱ)由x 的范围求得相位的范围，进一步求得函数的最值．本题考查平面向量数量积的坐标运算，训练了三角函数最值的求法，是中档题． 14.【答案】解：(1)∵函数f(x)=sinωx(sinωx +cosωx)=sin 2ωx +sinωxcosωx =1−cos2ωx2+12sin2ωx=√22sin(2ωx −π4)+12 的最小正周期为2π2ω=π，∴ω=1，f(x)=√22sin(2x −π4)+12．(2)对于函数f(x)=√22sin(2x −π4)+12，令2kπ+π2≤2x −π4≤2kπ+3π2，求得kπ+3π8≤x ≤π+7π8，可得函数的减区间为[kπ+3π8,π+7π8]，k ∈Z ．令2x −π4=kπ+π2，求得x =kπ2+3π8，可得函数的图象的对称轴方程为x =kπ2+3π8，k ∈Z ．【解析】(1)利用三角恒等变换化简函数的解析式，再利用正弦函数的周期性求出ω的值．(2)由题意利用正弦函数的单调性、以及它的图象的对称性，得出结论．本题主要考查三角恒等变换，正弦函数的周期性和单调性、以及它的图象的对称性，属于中档题．15.【答案】解：(1)由题可知，f(x)=m ⃗⃗⃗ ⋅n ⃗ +1=√3sinxcosx −cos 2x +1 =√32sin2x −12cos2x +12=sin(2x −π6)+12．令π2+2kπ≤2x −π6≤3π2+2kπ，则π3+kπ≤x ≤5π6+kπ,k ∈Z ，∴y =f(x)的单调递减区间为[π3+kπ,5π6+kπ],k ∈Z ．由y =sinx 变换成y =f(x)的过程如下所示：y =sinx 的图象纵坐标不变，横坐标先向右平移π6个单位，再缩小为原来的12，然后横坐标不变，纵坐标向上平移12个单位．(2)令f(x)=sin(2x −π6)+12=56，则sin(2x −π6)=13， ∵x ∈[0,π2]，∴2x −π6∈[−π6,5π6]，∴cos(2x −π6)=±2√23， 而cos2x =cos[(2x −π6)+π6]=√32cos(2x −π6)−12sin(2x −π6)，∴当cos(2x −π6)=2√23时，cos2x =√32×2√23−12×13=2√6−16； 当cos(2x −π6)=−2√23时，cos2x =√32×(−2√23)−12×13=−2√6−16， 综上，cos2x 的值为2√6−16或−2√6−16．【解析】(1)结合平面向量数量积的坐标运算和二倍角公式、辅助角公式可将函数f(x)化简为f(x)=sin(2x−π6)+12，再利用正弦函数的单调性即可求得f(x)的单调递减区间；结合三角函数的平移变换与伸缩变换法则即可得解．(2)由题可知，sin(2x−π6)=13，由于x∈[0,π2]，所以2x−π6∈[−π6,5π6]，利用平方关系可求得cos(2x−π6)=±2√23，然后结合拼凑角的方法可知cos2x=cos[(2x−π6)+π6]，利用余弦的两角和公式展开后，代入数据进行运算即可得解．本题主要考查三角恒等变换与三角函数图象的综合，还涉及平面向量数量积的坐标运算，熟练运用二倍角公式、辅助角公式等基本公式是解题的关键，考查学生的分析能力和运算能力，属于基础题．16.【答案】解：f(x)=(sinx+cosx)2+cos2x=1+sin2x+cos2x=√2sin(2x+π4)+1．(I)f(x)的最小正周期T=2π2=π．(Ⅱ)令2kπ−π2≤2x+π4≤2kπ+π2,k∈Z，解得kπ−3π8≤x≤kπ+π8,k∈Z，∴f(x)的单调递增区间为[kπ−3π8,kπ+π8],k∈Z，∵x∈[0,π2]，∴k=0，f(x)在[0,π2]上的单调递增区间为[0,π8]．【解析】利用平方关系、辅助角公式将函数化简为f(x)=√2sin(2x+π4)+1．(I)根据正弦函数的周期性即可得解；(Ⅱ)根据正弦函数的单调性即可得解，需要注意限定了区间[0,π2].本题考查三角恒等变换与三角函数的综合，考查学生的逻辑推理能力和运算能力，属于基础题．17.【答案】解：(Ⅰ)由a⃗//c⃗可得，√3sinx=2cosx，∴tanx=2√33，∴a⃗⋅b⃗ =−√3sinxcosx+cos2x=−√3sinxcosx+cos2xcos2x+sin2x =−√3tanx+1tan2x+1=−173=−37．(Ⅱ)函数f(x)=a⃗⋅b⃗ =−√3sinxcosx+cos2x=−√32sin2x+1+cos2x2=−sin (2x−π6)+12，∵x∈[0,π2]，，∴sin (2x−π6)∈[−12,1]，∴−sin (2x−π6)+12∈[−12,1]，即f(x)的值域为[−12,1]．【解析】本题主要考查两个向量的数量积的运算，三角函数的恒等变换，函数y= Asin(ωx+φ)的图象与性质，平面向量共线的充要条件，属于中档题．(Ⅰ)由a⃗//c⃗求得tanx=2√33，再利用同角三角函数的基本关系以及两个向量的数量积公式求出a⃗⋅b⃗ 的值．(Ⅱ)利用两个向量的数量积公式以及三角恒等变换求出函数f(x)=a⃗⋅b⃗ =−sin (2x−π6)+12，再由x的范围，求出f(x)的值域．18.【答案】解：，其中tanφ=√3a．∵f(x)的最小正周期为T=π，∴2ω=2πT=2，即ω=1．又∵f(x)的最大值为2，∴√a2+3=2，即a=±1，∵a>0，∴a=1．所以不妨取φ=π3，因此，(1)令2x+π3=π2+kπ，(k∈Z)．对称轴方程为x=π12+kπ2，(k∈Z)．(2)由f(α)=43，得，即，则．【解析】本题考查了两角和与差的三角函数公式，二倍角公式及应用，辅助角公式和函数y=Asin(ωx+φ)的图象与性质．(1)根据条件函数最值和周期，利用三角函数的公式进行化简，即可求a和ω的值，即可求出函数的解析式和对称轴方程；(2)根据f(α)=43，利用余弦函数的倍角公式进行化简即可求sin(4α+π6)的值．19.【答案】解：(1)由辅助角公式得：f(x)=sinx+√3cosx=2sin (x+π3)，当sin (x+π3)=±1，故最大值为2，最小值为−2．最小正周期为T=2π|ω|=2π．，令2kπ+π2⩽x2+π4⩽2kπ+3π2(k ∈Z)，则4kπ+π2⩽x ⩽4kπ+5π2(k ∈Z)，即单调递减区间为：[4kπ+π2,4kπ+5π2](k ∈Z)．【解析】本题考查了函数y =Asin(ωx +φ)的图象与性质，是基础题． (1)先由辅助角公式化简f(x)，由三角函数性质可得最值和最小正周期；； (2)由三角函数图象变换得g(x)=2sin(x2+π4)，令2kπ+π2⩽x2+π4⩽2kπ+3π2(k ∈Z)，可得g(x)的单调递减区间．20.【答案】解：(1)根据函数f(x)=Asin(ωx +φ)，其中A >0，ω>0，−π2<φ<π2，x ∈R 其部分图象，可得A =2，14⋅2πω=5π6−π3，∴ω=1． 再根据五点法作图，可得1×π3+φ=π2，求得φ=π6， ∴函数f(x)=2sin(x +π6). (2)当x ∈[0,π]时，x +π6∈[π6,7π6]，故当x +π6=π2时，即x =π3时，函数f(x)取得最大值为2； 当x +π6=7π6时，即x =π时，函数f(x)取得最小值为−1．【解析】(1)由题意利用由函数的图象的顶点坐标求出A ，由周期求出ω，由五点法作图求出φ的值，可得函数的解析式．(2)根据函数的解析式、正弦函数的最值，求出函数y =f(x)的最大值与最小值及此时相应x 的值．本题主要考查由函数y =Asin(ωx +φ)的部分图象求解析式，由函数的图象的顶点坐标求出A ，由周期求出ω，由五点法作图求出φ的值，正弦函数的最值，属于中档题． 21.【答案】解：(I)f(x)=2√3sin xcos x +2sin 2x −1=√3sin2x −cos2x=2(√32sin2x −12cos2x)=2sin(2x −π6)，令−π2+2kπ⩽2x −π6⩽π2+2kπ，k ∈Z ，解得−π6+kπ⩽x ⩽π3+kπ,k ∈Z ， 故所求单调增区间为[−π6+kπ,π3+kπ](k ∈Z)；(Ⅱ)由题意得：f(α2)=25，得sin(α−π6)=15，所以sin(2α+π6)=sin[2(α−π6)+π2]=cos2(α−π6)=1−2sin2(α−π)=2325．【解析】本题考查两角和与差的三角函数，二倍角公式，函数的单调性以及函数求值，考查转化思想以及计算能力，属于中档题．(I)利用二倍角公式、两角和与差的三角函数化简函数的解析式，利用正弦函数的单调性求解函数f(x)的单调递增区间；(II)由(I)可得sin(α−π6)=15，由角之间的关系、诱导公式、二倍角余弦公式的变形求出答案．22.【答案】解：函数f(x)=12cos2x+√32sinxcosx+1，化简可得：f(x)=1+cos2x4+√34sin2x+1=12sin(2x+π6)+54．(1)∴函数f(x)的最小正周期T=2π2=π．令2x+π6=kπ,k∈Z，可得，对称中心的坐标：x=kπ2−π12,k∈Z．∴函数f(x)的对称中心(kπ2−π12,54),k∈Z．(2)∵π12≤x≤π4，∴π3≤2x+π6≤2π3∴√32≤sin(2x+π6)≤1，∴5+√34≤12sin(2x+π6)+54≤74，故得函数f(x)在[π12,π4]上的值域是[5+√34,74]．【解析】本题主要考查对三角函数的化简能力和函数y=Asin(ωx+φ)的图象与性质的运用，利用三角函数公式将函数进行化简是解决本题的关键．属于中档题．(1)利用二倍角和辅助角公式基本公式将函数化为y=Asin(ωx+φ)的形式，再利用周期公式求函数的最小正周期，结合三角函数的图象和性质可求对称中心的坐标；(2)x∈[π12,π4]上时，求出内层函数的取值范围，结合三角函数的图象和性质，即得到f(x)的取值范围．23.【答案】解：f(x)=√32sin2x+12cos2x+32cos2x+3√32sin2x =2√3sin2x+2cos2x=4sin(2x+π6).(1)f(x)的最小正周期T=2π2=π，由π2+2kπ≤2x+π6≤3π2+2kπ，k∈Z，解得π6+kπ≤x≤2π3+kπ，k∈Z，所以f(x)的单调递减区间为[π6+kπ,2π3+kπ]，k∈Z.(2)由f(α2)=4sin(α+π6)=45知sin(α+π6)=15，因为α∈(0,π)，所以α+π6∈(π6,7π6)，又sin(α+π6)=15，所以α+π6∈(5π6,π)，所以cos(α+π6)=−2√65，则cosα=cos(α+π6−π6)=−2√65×√32+15×12=1−6√210．【解析】本题考查三角恒等变换以及三角函数的性质，属于中档题．化简得到f(x)=4sin(2x+π6).(1)根据周期公式求得周期，再解不等式得到单调递减区间；(2)运用同角三角函数关系以及两角和差的三角函数公式计算即可得到答案．24.【答案】解：(1)∵f(x)=cos2x+2√3sinxcosx−sin2x=cos2x+√3sin2x= 2sin(2x+π6)，∴函数f(x)的最小正周期T=2π2=π．(2)∵x∈[−π3,π3 ]，∴2x+π6∈[−π2,5π6]，∴sin(2x+π6)∈[−1,1]，f(x)=2sin(2x+π6)∈[−2,2]，∴f(x)在区间[−π3,π3]上的最大值为2，最小值为−2．【解析】(1)利用三角函数恒等变换的应用化简可得f(x)，由周期公式可得；(2)由x的范围逐步可得f(x)的范围，进而利用正弦函数的图象和性质可得最值．本题主要考查了三角函数恒等变换的应用，正弦函数的图象和性质的应用，涉及函数的周期的求解，属于基础题．25.【答案】解：(1)因为函数f(x)=(cosx+√3sinx)⋅sin(π2−x)+12=(cosx+√3sinx)⋅cosx+1 2=cos2x+√3sinxcosx+1 2=1+cos2x2+√32sin2x+12=sin(2x+π6)+1；∴函数f(x)最小正周期是T=π；当2kπ−π2≤2x+π6≤2kπ+π2，k∈Z，即kπ−π3≤x≤kπ+π6，k∈Z，函数f(x)单调递增区间为[kπ−π3,kπ+π6]，k∈Z；(2)x∈[712π,56π]⇒4π3≤2x+π6≤11π6；所以当2x+π6=32π时，即x=23π时，f(x)取得最小值0．【解析】(1)函数解析式利用二倍角的余弦函数公式化简，整理后利用两角和与差的正弦函数公式化为一个角的正弦函数，找出ω的值，代入周期公式即可求出函数f(x)的最小正周期，根据正弦函数的单调性即可确定出f(x)的单调递增区间；(2)由x∈[712π,56π]可得：43π≤2x+π6≤116π，所以当2x+π6=32π时，即x=23π时，f(x)取得最小值0．本题主要考查了三角函数的图象和性质，以及三角函数求最值，是中档题．26.【答案】解：(1)因f(x)的图象上相邻两个最高点的距离为π，所以f(x)的最小正周期T=π，从而ω=2πT=2，又因f(x)的图象关于直线x=π3对称，所以2×π3+φ=kπ+π2,k∈Z，因为−π2≤φ≤π2，得k=0，所以φ=−π6;(2)由(1)得f(α2)=√3sin(α−π6)=√34，所以sin(α−π6)=14，由，得，所以，因此sin(α+π3)=sin(α−π6+π2)=cos(α−π6)=√154．【解析】本题考查正弦型函数的图象性，考查诱导公式，属于中档题．(1)由函数图象上相邻两个最高点的距离为π求出周期，再利用公式T=2πω求出ω的值，然后由图象关于x=π3对称，求出φ;(2)由(1)及已知求出sin(α−π6)=14，利用同角关系式求出cos(α−π6)=√154，然后由sin(α+π3)=cos(α−π6)求解即可．27.【答案】解：(1)f(x)=12+12cos2x+√32sin2x−12=sin(2x+π6)，∴T=π；(2)依题意，令−π2+2kπ≤2x+π6≤π2+2kπ,k∈Z，解得−π3+kπ≤x≤π6+kπ,k∈Z，∴f(x)的单调递增区间为[−π3+kπ,π6+kπ],k∈Z；设A=[−π4,π4],B=[−π3+kπ,π6+kπ]，易知A∩B=[−π4,π6]，∴当x∈[−π4,π4]时，f(x)在区间[−π4,π6]上单调递增，区间(π6,π4]上单调递减．【解析】(1)化简可得f(x)=sin(2x+π6)，进而求得最小正周期；(2)先求得f(x)的单调递增区间为[−π3+kπ,π6+kπ],k∈Z，进而求得f(x)在区间[−π4,π4]上的单调性．本题考查三角函数的恒等变换，以及三角函数的图象及性质，考查运算化简能力，属于基础题．28.【答案】解：(1)由题意知，f(x)=2cosx(λsinx−cosx)+sin2x+1=(λ+1)sin2x−2cos2x+1=(λ+1)sin2x−cos2x=√(λ+1)2+1sin(2x−φ)，其中tanφ=1λ+1，由f(x)的最小值为−2，得−√(λ+1)2+1=−2，解得λ=√3−1或λ=−√3−1，∵λ<0，∴λ=−√3−1，∴f(x)=−√3sin2x−cos2x=−2sin(2x+π6 ).令2kπ−π2≤2x+π6≤2kπ+π2，k∈Z，解得kπ−π3≤x≤kπ+π6，k∈Z，故函数f(x)的单调递减区间为[kπ−π3,kπ+π6]，k∈Z.(2)∵g(x)=f(x)−k=−2sin(2x+π6)−k在[−π12,π2]上有且仅有一个零点，∴当x∈[−π12,π2]时，y=−k2与y=sin(2x+π6)的图象有且仅有一个交点．当x∈[−π12,π2]时，2x+π6∈[0,7π6]，令t=2x+π6，ℎ(t)=sint，t∈[0,7π6]，则y=−k2与ℎ(t)=sint，t∈[0,7π6]的图象有且仅有一个交点，数形结合可知当−k2∈[−12,0)或−k2=1时符合要求，即k∈(0,1]或k=−2时符合要求，故实数k的取值范围为{k|0<k≤1或k=−2}．【解析】本题主要考查二倍角公式、三角恒等变换、三角函数的图象与性质、函数的零点等知识，考查考生的化归与转化能力、运算求解能力，考查的数学核心素养是数学运算．(1)先根据二倍角公式及辅助角公式将函数f(x)化为Asin(ωx+φ)(A,ω,φ为常数，且A≠0，ω≠0)的形式，再根据函数f(x)的最小值求实数λ的值，最后根据正弦函数的单调性求函数f(x)的单调递减区间;(2)将g(x)在[−π12,π2]上有且仅有一个零点等价转化为当看答案x∈[−π12,π2]时，y=−k2与y=sin(2x+π6)的图象有且仅有一个交点，然后数形结合即可求解．29.【答案】解：(Ⅰ)由所给图像知：A=2,B=−1,T2=πω=7π−π12⇒ω=2，∴f(x)=2cos (2x+φ)−1，把点(π12,1)代入得：cos (π6+φ)=1，即π6+φ=2kπ,k∈Z，又∵|φ|<π2，∴φ=−π6，∴f(x)=2cos (2x−π6)−1；由图可知(π3,−1)是其中一对称中心，故所求对称中心坐标为：(π3+kπ2,−1),k∈Z．(Ⅱ)易知g(x)=12f(x−π6)+1=12{2cos [2(x−π6)−π6]−1}+1．化简得g(x)=sin (2x)+12，当x∈[π12,3π4]时，由−π2+2kπ≤2x≤π2+2kπ，k∈Z得增区间是：[π12,π4]，由π2+2kπ≤2x≤3π2+2kπ，k∈Z得减区间是：[π4,3π4]，故所求求区间为：[π4,3π4]，．当x=π12时，g(x)的值：sin(2×π12)+12=1，当x=π4时，g(x)的值32，当x=3π4时，g(x)的值：sin(2×3π4)+12=−12．故所求最大值为：32;最小值为−12．【解析】本题考查了函数y=Asin(ωx+φ)的图象与性质和余弦函数的图象与性质，是中档题．(Ⅰ)由图象可得A，B，周期T可得ω，代入点(π12,1)可得φ，即可得出f(x)的解析式，由图可知(π3,−1)是其中一对称中心，可得对称中心坐标；(Ⅱ)由三角函数图象变换可得g(x)=sin (2x)+12，由三角函数性质可得单调减区间和最值．30.【答案】解：(Ⅰ)由f(x)=2sinxsin(x+π2)，得f(0)=2sin0sinπ2=0；(Ⅱ)∵f(x)=2sinxsin(x+π2)=2sinxcosx=sin2x，∴f(x)的最小正周期为π；(Ⅲ)∵y=f(x+φ)=sin(2x+2φ)为偶函数，，∵0<φ<π2，∴φ=π4．【解析】本题考查三角函数的恒等变换应用，考查y=Asin(ωx+φ)型函数的图象与性质，是基础题．(Ⅰ)直接在函数解析式中取x=0求解；(Ⅱ)利用诱导公式及倍角公式变形，再由周期公式求周期；(Ⅲ)由y=f(x+φ)=sin(2x+2φ)为偶函数，可得，再结合φ的范围求解．。

题型特征及分值：[1]高考中对三角函数的考查一般有四大类型：（1）利用三角函数的定义与三角变换求值（如2008年卷3题）.（2）三角函数的图象、性质（单调性、奇偶性、周期性、对称性等）（如2008年卷5题）；（3）三角形相关的三角函数（以正余弦定理的运用为主）；（4）函数值域等综合问题（2008年卷17题）.[2]近几年对三角函数的考察中对三角变换的考查要求有所降低，同时对三角函数的图像与性质的考查有所加强，近几年每套试卷中一般有1至3道填空题或选择题(以三角变换求值、三角函数性质、图象为主，如卷2007年16题)和一个解答题（12分）（如卷2007年17题），总分值在20－26分左右。

同时三角函数具有工具性作用，近年也常和其他章节综合出题（如：2008年卷10题与导数结合）.§1.三角函数的求值知识网络：§2. 三角函数图象与性质§3.解斜三角形知识网络：§4.典型题型真题突破【例1】(2007年)若πtan 34α⎛⎫-= ⎪⎝⎭，则cot α等于（ ） A ．2- B ．12-C ．12D ．2 解题思路：π1tan 3cot tan()tan[()]42445πππαααα-⎛⎫-=⇒=-=++=⎪⎝⎭,选A. 【例2】(2007年)已知sin 5α=，则44sin cos αα-的值为（ ） A ．15-B ．35-C ．15D ．35解题思路：44222222sin cos (sin cos )(sin cos )sin cos αααααααα-=-+=-=22sin 1α-=35-.选B.【例3】(2005年) 若)20(tan cos sin παααα<<=+，则∈α( )A ．（0，6π） B ．（6π，4π） C ．（4π，3π） D ．（3π，2π）解题思路：sin cos tan cos ,2ααααα+=⇒=<<,故选C. 【例4】(2007年)已知11sin 225θ+=，且324θππ≤≤，则cos2θ的值是____．解题思路:1sin cos 5θθ+=,两边平方得: 11sin 225θ+=24sin 225θ-⇒=⇒cos2θ= 725-. 【例5】(2007年)若1cos()5αβ+=，3cos()5αβ-=，则tan tan αβ⋅=_____ 解题思路: 1cos()cos cos sin sin 5αβαβαβ+==⋅-⋅①, 3cos()5αβ-== cos cos sin sin αβαβ⋅+⋅②. ②-①得: 1sin sin 5αβ⋅=③, ②+①得: 2cos cos 5αβ⋅=.④, ③④:tan tan αβ⋅=12.【例6】(2006年)已知()33,,,sin ,45παβπαβ⎛⎫∈+=-⎪⎝⎭12sin()413πβ-=，则cos()4πα+=____.解题思路：cos()cos[()]cos(cos )444πππααββαββ+=+--=+--）（）（ 56sin(sin )465παββ+-=-）（.【例7】（2005年）已知α、β均为锐角，且αβαβαtan ),sin()cos(则-=+= 解题思路：cos()sin()cos()cos()2παβαβαβαβ+=-⇒+=--,2παβαβ++--=0, 4πα=,tan 1α=.【例8】(1996年全国)tan 20tan 4020tan 40++⋅。

三角函数复习教案整理一、教学目标1. 知识与技能：（1）掌握三角函数的定义及性质；（2）了解三角函数在各象限的符号；（3）熟练运用三角函数公式进行计算。

2. 过程与方法：（1）通过复习，巩固三角函数的基本概念；（2）通过例题解析，提高学生解决实际问题的能力；（3）培养学生运用三角函数解决几何问题的能力。

3. 情感态度与价值观：（1）激发学生对三角函数的学习兴趣；（2）培养学生的团队合作精神；（3）鼓励学生勇于探索，提高自主学习能力。

二、教学内容1. 三角函数的定义及性质（1）正弦函数、余弦函数、正切函数的定义；（2）三角函数的周期性；（3）三角函数的奇偶性；（4）三角函数的单调性。

2. 三角函数在各象限的符号（1）第一象限：正弦函数、余弦函数、正切函数均为正；（2）第二象限：正弦函数为正，余弦函数、正切函数为负；（3）第三象限：正弦函数、余弦函数、正切函数均为负；（4）第四象限：正弦函数为负，余弦函数、正切函数为正。

3. 三角函数公式（1）和角公式；（2）差角公式；（3）积化和差公式；（4）和差化积公式；（5）二倍角公式；（6）半角公式。

三、教学重点与难点1. 教学重点：（1）三角函数的定义及性质；（2）三角函数在各象限的符号；（3）三角函数公式的运用。

2. 教学难点：（1）三角函数公式的灵活运用；（2）解决复杂三角函数问题。

四、教学方法1. 采用讲解法，系统讲解三角函数的基本概念、性质和公式；2. 利用例题解析，让学生掌握三角函数公式的运用；3. 运用分组讨论法，引导学生合作探究，解决实际问题；4. 采用问答法，激发学生的思维，巩固所学知识。

五、教学过程1. 导入新课：回顾上节课的内容，引导学生进入本节课的学习。

2. 讲解三角函数的定义及性质：通过PPT展示，讲解三角函数的基本概念，让学生理解并掌握三角函数的性质。

3. 讲解三角函数在各象限的符号：引导学生通过绘制函数图像，观察并总结三角函数在各象限的符号。

三角函数图像与性质总复习教案一、教学目标1. 回顾和巩固三角函数的图像与性质，包括正弦函数、余弦函数、正切函数等。

2. 提高学生对三角函数图像与性质的理解和应用能力。

3. 培养学生的数学思维能力和解决问题的能力。

二、教学内容1. 复习正弦函数的图像与性质。

2. 复习余弦函数的图像与性质。

3. 复习正切函数的图像与性质。

4. 复习三角函数的周期性。

5. 复习三角函数的奇偶性。

三、教学方法1. 采用讲解法，通过教师的讲解，引导学生回忆和巩固三角函数的图像与性质。

2. 采用案例分析法，通过具体的例子，让学生理解和掌握三角函数的图像与性质。

3. 采用互动教学法，引导学生积极参与讨论和提问，提高学生的思维能力和解决问题的能力。

四、教学步骤1. 复习正弦函数的图像与性质。

a. 引导学生回忆正弦函数的定义和图像。

b. 讲解正弦函数的周期性和奇偶性。

c. 通过例子，让学生应用正弦函数的性质解决实际问题。

2. 复习余弦函数的图像与性质。

a. 引导学生回忆余弦函数的定义和图像。

b. 讲解余弦函数的周期性和奇偶性。

c. 通过例子，让学生应用余弦函数的性质解决实际问题。

3. 复习正切函数的图像与性质。

a. 引导学生回忆正切函数的定义和图像。

b. 讲解正切函数的周期性和奇偶性。

c. 通过例子，让学生应用正切函数的性质解决实际问题。

4. 复习三角函数的周期性。

a. 引导学生回忆三角函数的周期性定义。

b. 讲解三角函数的周期性性质。

c. 通过例子，让学生应用三角函数的周期性解决实际问题。

5. 复习三角函数的奇偶性。

a. 引导学生回忆三角函数的奇偶性定义。

b. 讲解三角函数的奇偶性性质。

c. 通过例子，让学生应用三角函数的奇偶性解决实际问题。

五、教学评价1. 课堂练习：布置相关的练习题，检查学生对三角函数图像与性质的理解和应用能力。

2. 课后作业：布置相关的作业题，巩固学生对三角函数图像与性质的记忆和理解。

3. 小组讨论：组织学生进行小组讨论，鼓励学生积极参与，提高学生的思维能力和解决问题的能力。

平面向量与三角函数综合习题1．已知→a ＝(cos40︒，sin40︒)，→b ＝(sin20︒，cos20︒)，则→a ·→b ＝（ ）A ．1B ．32C ．12D ．22 2．已知△ABC 中，AB →＝a →，AC →＝b →，若a →·b →＜0，则△ABC 是（ ）A ．钝角三角形B ．直角三角形C ．锐角三角形D ．任意三角形3．若向量→a ＝(cos α,sin α)，→b ＝(cos β,sin β)，则→a 与→b 一定满足（ ）A ．→a 与→b 的夹角等于α－βB ．→a ⊥→bC ．→a ∥→bD ．(→a ＋→b )⊥(→a －→b )4．设→a ＝(32,sin α)，→b ＝(cos α,13)，且→a ∥→b ，则锐角α为（ ）A ．30︒B ．45︒C ．60︒D ．75︒5．已知→a ＝(sin θ，1＋cosθ)，→b ＝(1，1－cosθ)，其中θ∈(π，3π2)，则一定有 （ ）A ．→a ∥→bB ．→a ⊥→bC ．→a 与→b 夹角为45°D ．|→a |＝|→b |6．已知向量a →＝(6，－4)，b →＝(0，2),c →＝a →＋λb →，若C 点在函数y ＝sin π12x 的图象上,实数λ＝（ ）A ．52 B ．32C ．－52D ．－327．设0≤θ≤2π时，已知两个向量OP 1→＝(cos θ，sin θ)，OP 2→＝(2＋sin θ，2－cos θ)，则向量P 1P 2→长度的最大值是（ ） A ． 2 B ． 3C ．3 2D ．2 38．已知向量→a ＝(cos25︒,sin25︒)，→b ＝(sin20︒,cos20︒)，若t 是实数，且→u ＝→a ＋t →b ，则|→u |的最小值为 （ ） A ． 2 B ．1C ．22D ．129．已知非零向量,22||||,0||||(,=⋅=⋅+BC AC BC AC BC AC AC AB AB BC AC AB 满足和则△ABC 为（ ）A ．等边三角形B ．等腰非直角三角形C ．非等腰三角形D ．等腰直角三角形10．已知向量→m ＝(1，1)，向量→n 与向量→m 夹角为3π4，且→m ·→n ＝－1.则向量→n ＝__________．11、已知向量→a ＝(3sin α,cos α)，→b ＝(2sin α，5sin α－4cos α)，α∈(3π2，2π)，且→a ⊥→b ．（Ⅰ）求tan α的值； （Ⅱ）求cos(α2＋π3)的值．12、已知向量→a ＝(cos α,sin α)，→b ＝(cos β,sin β)，|→a －→b |＝25 5.(Ⅰ)求cos(α－β)的值；(Ⅱ)若－π2＜β＜0＜α＜π2，且sin β＝－513，求sin α的值.13．已知A 、B 、C 的坐标分别为A （4，0），B （0，4），C （3cosα，3sinα）.（Ⅰ）若α∈(－π，0)，且|→AC|＝|→BC|，求角α的大小； （Ⅱ）若→AC ⊥→BC ，求2sin 2α＋sin2α1＋tanα的值．14、已知A 、B 、C 为三个锐角，且A ＋B ＋C ＝π.若向量→p ＝(2－2sinA ，cosA ＋sinA)与向量→q ＝(sinA －cosA ，1＋sinA)是共线向量.（Ⅰ）求角A ；（Ⅱ）求函数y ＝2sin 2B ＋cos C －3B2的最大值.15．已知向量→m ＝(sinA,cosA)，→n ＝(3,－1)，→m·→n ＝1，且A 为锐角.(Ⅰ)求角A 的大小；(Ⅱ)求函数f(x)＝cos2x＋4cosAsinx(x ∈R)的值域．16、设函数f(x)＝→a ·→b.其中向量→a ＝(m ，cosx)，→b ＝(1＋sinx ，1)，x ∈R ，且f( 2)＝2.（Ⅰ）求实数m 的值；（Ⅱ）求函数f(x)的最小值.17．已知→a ＝(cosx ＋sinx ，sinx)，→b ＝(cosx －sinx ，2cosx)，（Ⅰ）求证：向量→a 与向量→b 不可能平行；（Ⅱ）若f(x)＝→a ·→b ，且x ∈[－π4,π4]时，求函数f(x)的最大值及最小值．19、如图，函数2sin(),y x x R πϕ=+∈（其中02πϕ≤≤）的图像与y 轴交于点（0，1）。

题型特征及分值：[1]高考中对三角函数的考查一般有四大类型：（1）利用三角函数的定义与三角变换求值（如2008年卷3题）.（2）三角函数的图象、性质（单调性、奇偶性、周期性、对称性等）（如2008年卷5题）；（3）三角形相关的三角函数（以正余弦定理的运用为主）；（4）函数值域等综合问题（2008年卷17题）.[2]近几年对三角函数的考察中对三角变换的考查要求有所降低，同时对三角函数的图像与性质的考查有所加强，近几年每套试卷中一般有1至3道填空题或选择题(以三角变换求值、三角函数性质、图象为主，如卷2007年16题)和一个解答题（12分）（如卷2007年17题），总分值在20－26分左右。

同时三角函数具有工具性作用，近年也常和其他章节综合出题（如：2008年卷10题与导数结合）.§1.三角函数的求值知识网络：§2. 三角函数图象与性质§3.解斜三角形知识网络：§4.典型题型真题突破【例1】(2007年)若πtan 34α⎛⎫-= ⎪⎝⎭，则cot α等于（ ） A ．2- B ．12-C ．12D ．2 解题思路：π1tan 3cot tan()tan[()]42445πππαααα-⎛⎫-=⇒=-=++=⎪⎝⎭,选A.【例2】(2007年)已知sin α=，则44sin cos αα-的值为（ ） A ．15-B ．35-C ．15D ．35解题思路：44222222sin cos (sin cos )(sin cos )sin cos αααααααα-=-+=-=22sin 1α-=35-.选B.【例3】(2005年) 若)20(tan cos sin παααα<<=+，则∈α( )A ．（0，6π） B ．（6π，4π） C ．（4π，3π） D ．（3π，2π）解题思路：sin cos tan cos ααααα+=⇒=<<,故选C. 【例4】(2007年)已知11sin 225θ+=，且324θππ≤≤，则cos 2θ的值是____．解题思路:1sin cos 5θθ+=,两边平方得: 11sin 225θ+=24sin 225θ-⇒=⇒cos 2θ= 725-. 【例5】(2007年)若1cos()5αβ+=，3cos()5αβ-=，则tan tan αβ⋅=_____ 解题思路: 1cos()cos cos sin sin 5αβαβαβ+==⋅-⋅①, 3cos()5αβ-== cos cos sin sin αβαβ⋅+⋅②. ②-①得: 1sin sin 5αβ⋅=③, ②+①得: 2cos cos 5αβ⋅=.④, ③④:tan tan αβ⋅=12. 【例6】(2006年)已知()33,,,sin ,45παβπαβ⎛⎫∈+=-⎪⎝⎭12sin()413πβ-=，则cos()4πα+=____.解题思路：cos()cos[()]cos(cos )444πππααββαββ+=+--=+--）（）（ 56sin(sin )465παββ+-=-）（.【例7】（2005年）已知α、β均为锐角，且αβαβαtan ),sin()cos(则-=+= 解题思路：cos()sin()cos()cos()2παβαβαβαβ+=-⇒+=--,2παβαβ++--=0, 4πα=,tan 1α=.【例8】(1996年全国)tan 20tan 4020tan 40+⋅。