关于页码中出现多少个N这个数字这一系列问题的解答

小学奥数-页码问题页码问题就是根据书的页码而编制出来的一类应用题．编一本书的页码，一共需要多少个数码呢？反过来，知道编一本书的页码所需的数码数量，求这本书的页数．这是页码问题中的两个基本内容。

页码问题实际上是数论的问题。

一、页码问题的几种题型：(1)已知页码数，要求考生求出书中一共含有多少个数码。

(2)已知页码数，要求考生求此书中某个数码出现的次数。

(3)已知书中包含的数码数，要求考生求出该书的页码数。

(4)已知书中某个数码出现的次数，要求考生求出该书的页码数。

二、页码问题解题基本原理要想要想顺利解答页码问题，首先要弄明白“页码”与“组成它的数码个数”之间的关系。

1．一位数组成的页码共有9个(从1～9)，组成所有的一位数需要：（9-1+1）×1=9×1=9(个)数码。

2．两位数共有90个(从10～99)，组成所有的两位数需要：2×（99-10+1）=180(个)数码。

3．三位数共有900个(从100～999)，组成所有的三位数需要：3×（999-100+1）=2700(个)数码。

4．四位数共有9000个（从1000～9999），组成所有四位数需要：4×（9999-1000+1）=36000(个)数码。

5．9页的书共有：9个数码组成。

6．99页的书共有：9+180=189个数码组成。

7．999页的书共有：2700+180+9=2889个数码组成。

8．9999页的书共有：36000+2700+180+9=38889个数码组成。

三．例题：例1 一本书共204页，需多少个数码编页码？分析与解：1～9页每页上的页码是一位数，共需数码1×9＝9(个)；10～99页每页上的页码是两位数，共需数码2×90＝180(个)；100～204页每页上的页码是三位数，共需数码：(204－100＋1)×3＝105×3＝315(个)．综上所述，这本书共需数码：9＋180＋315＝504(个)．例2 一本小说的页码，在排版时必须用2211个数码．问：这本书共有多少页？分析：因为189＜2211＜2889，所以这本书有几百页．由前面的分析知道，这本书在排三位数的页码时用了数码(2211－189)个，所以三位数的页数有(2211－189)÷3＝674(页)．因为不到三位的页数有99页，所以这本书共有：99＋674＝773(页)．解：99＋(2211－189)÷3＝773(页)．答：这本书共有773页．例3 一本书的页码从1至62，即共有62页．在把这本书的各页的页码累加起来时，有一个页码被错误地多加了一次．结果，得到的和数为2000．问：这个被多加了一次的页码是几？分析与解：因为这本书的页码从1至62，所以这本书的全书页码之和为1＋2＋…＋61＋62＝62×(62＋1)÷2＝31×63＝1953．由于多加了一个页码之后，所得到的和数为2000，所以2000减去1953就是多加了一次的那个页码，是2000－1953＝47．例4 有一本48页的书，中间缺了一张，小明将残书的页码相加，得到1131．老师说小明计算错了，你知道为什么吗？分析与解：48页书的所有页码数之和为1＋2＋…＋48＝48×(48＋1)÷2＝1176．按照小明的计算，中间缺的这一张上的两个页码之和为1176－1131＝45．这两个页码应该是22页和23页．但是按照印刷的规定，书的正文从第1页起，即单数页印在正面，偶数页印在反面，所以任何一张上的两个页码，都是奇数在前，偶数在后，也就是说奇数小偶数大．小明计算出来的是缺22页和23页，这是不可能的．例5 将自然数按从小到大的顺序无间隔地排成一个大数：123456789101112…问：左起第2000位上的数字是多少？分析与解：本题类似于“用2000个数码能排多少页的页码？”因为(2000－189)÷3＝603……2，所以2000个数码排到第99＋603＋1＝703(页)的第2个数码“0”．所以本题的第2000位数是0．例6 排一本400页的书的页码，共需要多少个数码“0”？分析与解：将1～400分为四组：1～100，101～200，201～300，301～400．在1～100中共出现11次0，其余各组每组都比1～100多出现9次0，即每组出现20次0．所以共需要数码“0”例6、13/1995 化成小数后是一个无限小数，问在这个无限小数的小数点后面，从第一位到1995位，在这1995个数中，数字6共出现了多少次？解答：这是一个关于循环小数的周期问题。

第7讲页码问题本讲知识点汇总页码问题就是根据书的页码而编制出来的一类应用题，编一本书的页码，一共需要多少个数码呢?反过来，知道编一本书的页码所需的数码数量，求这本书的页数，这是页码问题中的两个基本内容。

页码问题实际上是数论的间题。

页码问题的几种题型:(1) 已知页码数，要求求出书中一共含有多少个数码。

(2) 已知页码数，要求求此书中某个数码出现的次数。

(3) 已知书中包含的数码数，要求求出该书的页码数。

(4) 已知书中某个数码出现的次数，要求求出该书的页码数。

页码问题解题基本原理:要想顺利解答页码问题，首先要弄明白“页码”与“组成它的数码个数”之间的关系。

1.一位数组成的页码共有9个(从1-9)，组成所有的一位数要:(9-1+1)⨯1=9⨯1=9 (个) 数码。

2. 两位数共有90 个(从 10-99)，组成所有的两位数需要:2⨯(99-10+1) =180(个)数码。

3.三位数共有900 个(从 100-999)，组成所有的三位数需要:3⨯(999-100+1) =2700(个) 数码。

4.四位数共有9000个(从1000-9999)，组成所有四位数要:4⨯ (9999-1000+1) =36000(个)数码。

5.9页的书共有:9个数码组成。

6.99 页的书共有:9+180=189 个数码组成。

7.999 页的书共有:2700+180+9=2889 个数码组成。

8.9999 页的书共有:36000+2700+180+9=38889 个数码组成。

解决与书本页码有关的计算问题的基本方法是:分类、分段分别计算，再求和。

按照印刷的规定;书的正文从第1页起，即单数页印在正面，偶数页印在反面，所以任何一张上的两个页码，都是奇数在前，偶数在后，也就是说奇数小偶数大。

范例解密例1、一本书共204 页，需多少个数码编页码?练习1一本书共 198页，需多少个数码编页码?例2、一本小说的页码，在排版时必须用2211个数码。

最新小学奥数页码问题一、考点、热点、重点、难点顾名思义，页码问题与图书的页码有密切联系。

事实上，页码问题就是根据书的页码而编制出来的一类应用题。

编一本书的页码，一共需要多少个数码呢？反过来，知道编一本书的页码所需的数码数量，求这本书的页数。

这是页码问题中的两个基本内容。

为了顺利地解答页码问题，我们先看一下“数”与“组成它的数码个数”之间的关系。

一位数共有9个，组成所有的一位数需要9个数码；两位数共有90个，组成所有的两位数需要2×90＝180（个）数码；三位数共有900个，组成所有的三位数需要3×900＝2700（个）数码……为了清楚起见，我们将n位数的个数、组成所有n位数需要的数码个数、组成所有不大于n位的数需要的数码个数之间的关系列表如下：由上表看出，如果一本书不足100页，那么排这本书的页码所需的数码个数不会超过189个；如果某本书排的页码用了10000个数码，因为2889＜10000＜38889，所以这本书肯定是上千页。

下面，我们看几道例题。

二、典型例题例1一本书共204页，需多少个数码编页码？分析与解：1～9页每页上的页码是一位数，共需数码1×9=9（个）；10～99页每页上的页码是两位数，共需数码2×90＝180（个）；100～204页每页上的页码是三位数，共需数码（204-100＋1）×3＝105×3＝315（个）。

综上所述，这本书共需数码9＋180＋315＝504（个）。

例2、编一本书的书页，用了270个数字（重复的也算，如页码115 用了2个1 和1个5共3个数字），问这本书一共有多少页？方法一：l--9 是只有9个数字，10--99 是2*90 =180个数字，那么剩下270-9-180= 81，剩下81/3 = 27页，则这本书是99+27-1=126 页。

方法二：假设这个页数是A页，则有A 个个位数，每个页码除了1--9 ，其他都有十位数，则有A-9个十位数，同理：有A-99个百位数。

奥数：页码问题（数论问题）页码问题编一本书的页码，一共需要多少个数码呢？反过来，知道编一本书的页码所需的数码数量，求这本书的页数．这是页码问题中的两个基本内容。

我们先看一下“数”与“组成它的数码个数”之间的关系．1、一位数的页码有9页，共1×9=9个数字；组成所有的一位数需要9个数码；2、两位数的页码有90页，共90×2=180个数字；需要180个数码3、三位数有900个，全部编上共用900×3=2700个数字，需要3×900＝2700(个)数码。

题目会出1、一本书有N页，求排版时用了多少个数字；或者反过来，一本书排版时用了N个数字，求这本书有多少页；2、已知一本N页的书中，求某个数字出现多少次；3、已知一本N页的书中，求含有某个数字的页码有多少页一本书排版时用了N个数字，求这本书有多少页，数字数<2889时，用公式：页码数=数字数/3+36；数字数>2889时,用添加0计算。

例1 一本书共204页，需多少个数码编页码？2.编一本书的书页，用了270个数字（重复的也算，如页码115 用了2个1 和1个5共3个数字），问这本书一共有多少页？N/3+36。

270/3 +36=126。

2．一本小说的页码，在排版时必须用2211 个数码。

问这本书共有多少页？A．773 B.774 C .775 D.7763 ．王先生在编一本书，其页数需要用6869 个字，问这本书具体是多少页？A.1999B.9999C.1994D.1995方法一：假设这个页数是A页，则：A+(A-9)+(A-99)+(A-999)=6869 ，求出A=1994方法二：6869>2889，所以，把所有的数字看作是4位数字，不足4位的添O补足4位，l , 2 , 3 , …9 记为0001 , 0002 , 0003 , ..0009 这样增加了3 * 9 = 27 个010 , 11 , 12 , …99 记为0010 , 0011 , 0012 ，..0099 增加了180 个0100 , 101 ，…999 记为0100 , 0101 ，…0999 增加了900 个O (6869+27+180+900)/4 =1994关于含“1”出现过多少次的问题，总结出的公式就是：总页数的1/10 乘以（数字位-1 )，再加上10 的（数字位数-l）次方。

页码问题常见的主要有三种题型：一、一本书有N页，求排版时用了多少个数字；或者反过来，一本书排版时用了N个数字，求这本书有多少页；二、已知一本N页的书中，求某个数字出现多少次；三、已知一本N页的书中，求含有某个数字的页码有多少页1．编一本书的书页，用了270个数字（重复的也算，如页码115 用了2个1 和1个5共3个数字），问这本书一共有多少页？A.117B.126C.127D.189方法一：l--9 是只有9个数字，10--99 是2*90 =180个数字，那么剩下270-9-180= 81，剩下81/3 = 27页，则这本书是99+27-1=126 页。

方法二：假设这个页数是A页，则有A 个个位数，每个页码除了1--9 ，其他都有十位数，则有A-9个十位数，同理：有A-99个百位数。

则：A+(A-9)+(A-99)=270 3A-110+2=270 3A=378 ， A=126方法三：公式法：公式：一本书用了N个数字，求有多少页：N/3+36。

270/3 +36=126。

2．一本小说的页码，在排版时必须用2211 个数码。

问这本书共有多少页？A．773 B.774 C .775 D.776解析：代入公式：N/3+36=737+36=7733 ．王先生在编一本书，其页数需要用6869 个字，问这本书具体是多少页？A.1999B.9999C.1994D.1995方法一：假设这个页数是A页，则：A+(A-9)+(A-99)+(A-999)=6869 ，求出A=1994 方法二：6869>2889，所以，把所有的数字看作是4位数字，不足4位的添O补足4位，l , 2 , 3 , … 9 记为0001 , 0002 , 0003 , ..0009 这样增加了3 * 9 = 27 个010 , 11 , 12 , … 99 记为0010 , 0011 , 0012 ，..0099 增加了180 个0 100 , 101 ，… 999 记为0100 , 0101 ，… 0999 增加了900 个O(6869+27+180+900)/4 =1994总结：一本书排版时用了N个数字，求这本书有多少页，N<2889时，用公式：N/3+36；N>2889时,用添加0计算。

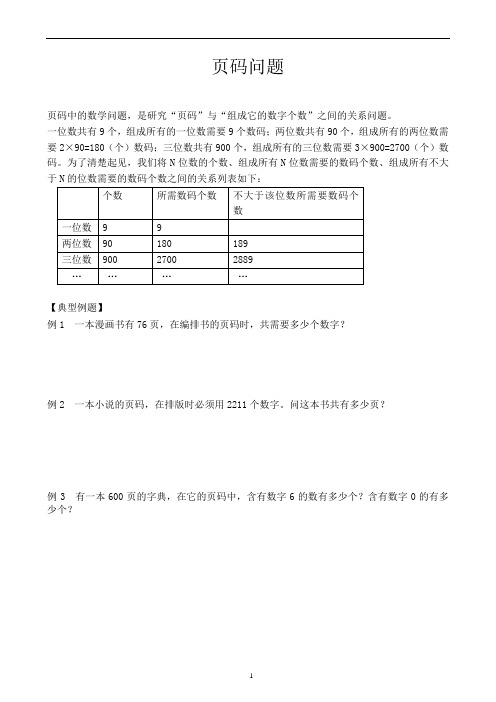
页码问题页码中的数学问题，是研究“页码”与“组成它的数字个数”之间的关系问题。

一位数共有9个，组成所有的一位数需要9个数码；两位数共有90个，组成所有的两位数需要2×90=180（个）数码；三位数共有900个，组成所有的三位数需要3×900=2700（个）数码。

为了清楚起见，我们将N位数的个数、组成所有N位数需要的数码个数、组成所有不大于N的位数需要的数码个数之间的关系列表如下：【典型例题】例1 一本漫画书有76页，在编排书的页码时，共需要多少个数字？例2 一本小说的页码，在排版时必须用2211个数字。

问这本书共有多少页？例3 有一本600页的字典，在它的页码中，含有数字6的数有多少个？含有数字0的有多少个？例4 甲、乙两册书的页码共用了777个数码，且甲册比乙册多7页。

甲册书有多少页？例5．一本书的页码里共含有88个数字“8”，这本书至少有多少页？至多有多少页？例6．一本书中间的某一张被撕掉了，余下的各页码数之和是1133，这本书有页，撕掉的是第页和第页。

随堂小测姓名成绩1．有一列数：1234567891011……887888889，各个数字是顺次从1至889，问第555个数字是几？2．一本书的页码中共用了3429个数字，这本书有多少页？3．一本英汉辞典有1034页，在这本辞典的页码中，数字0和5出现了多少次？4．一本书的页码一共含有100个数码5，则这本书至少有页，至多有页。

5．上、下两册书的页码共有687个数字，且上册比下册多5页，则上册书有页。

6．有一本书中间被撕掉了一张，余下各页码之和是1248，被撕掉的那一张上的页码是多少？课后作业姓名成绩家长签名1．一本书共有340页，在这本书的页码中共用了多少个数字？2．一本中篇小说的页码，在排版时必须用2211个数码，问这本书共有多少页？2．有7本竞赛书，书的页码刚好是7个连续的自然数，并且书的页码数的和是2002。

问：这7本书的页码数是哪7个自然数？3．一本英汉辞典有1034页，在这本辞典的页码中，数字0和数字5各出现了多少次？4．一本书的页码中，一共用了60个0，问这本书至少有多少页？5．一本书的页码是连续的自然数，1，2，3，…，当将这些页码加起来的时候，某个页码被加了两次，得到不正确的结果1997，则这个被加了两次的页码是哪一页？。

奥数：页码问题（数论问题）一、基本知识页码问题与图书的页码有密切联系。

事实上，页码问题就是根据书的页码而编制出来的一类应用题。

编一本书的页码，一共需要多少个数码呢？反过来，知道编一本书的页码所需的数码数量，求这本书的页数．这是页码问题中的两个基本内容。

页码问题是现在的奥数竞赛以及公务员考试中常见的、经常考试的知识点。

页码问题实际上是数论的问题。

页码问题涉及的应用题包含四个基本内容：(1)已知页码数，要求考生求出书中一共含有多少个数码；(2)已知页码数，要求考生求此书中某个数码出现的次数；(3)已知书中包含的数码数，要求考生求出该书的页码数；(4)已知书中某个数码出现的次数，要求考生求出该书的页码数。

为了顺利地解答页码问题，我们先看一下“数”与“组成它的数码个数”之间的关系:（1）一位数共有9个，1～9，组成所有的一位数需要9个数码；（2）两位数共有90个,10～99，组成所有的两位数需要2×90＝180(个)数码；（3）三位数共有900个，100～999，组成所有的三位数需要3×900＝2700(个)数码。

（4）四位数共有9000个，1000～9999，组成所有的三位数需要4×9000＝36000(个)数码。

...................为了清楚起见，我们将n位数的个数、组成所有n位数需要的数码个数、组成所有不大于n位的数需要的数码个数之间的关系列表如下：由上表看出，如果一本书不足100页，那么排这本书的页码所需的数码个数不会超过189个；如果某本书排的页码用了10000个数码，因为2889＜10000＜38889，所以这本书肯定是上千页。

二、举例说明例1 一本书共204页，需多少个数码编页码？分析与解：1～9页每页上的页码是一位数，共需数码1×9＝9(个)；10～99页每页上的页码是两位数，共需数码2×90＝180(个)；100～204页每页上的页码是三位数，共需数码(204－100＋1)×3＝105×3＝315(个)。

2019龙岩事业单位行测数量关系解题技巧：多位数问题【导读】多位数问题主要是事业单位录用考试，选调生考试等公职类的数量运算中时有出现的题，这类题的特点是考查比较细且往往难度也较大，通常都是选择放弃。

其实这类的问题并不难，掌握了解题的方法和规律后，能够快速解出这类题。

本文对多位数的定义、基础知识和常见考点与解题方法通过例题讲解进行了详细的阐述。

希望对大家备考行测能够有帮助,与各位共享。

一、定义多位数问题是针对“一个数及其个位、十位、百位等位置上的数字，以及小数点后一位、两位、三位等位置上的数字”的问题。

二、基础知识(一)多位数的算式表示(一)“数字”与“数”数字：多位数问题中“数字”表示多位数上的某一位数字，相同元素可重复计算。

数：多位数问题中的“数”表示组成这个多位数的元素，相同元素不可重复计算。

1位数从1到9共9个数，9个数字;2位数从10到99共90 个数，180个数字;3位数从100到999共900个，2700个数字;4位数从1000到9999共9000个数，36000个数字。

……另外一定要学会“直接代入法”法，这个方法在解决多位数问题时显得非常重要。

三、基本考点(一)多位数内部数字换序解题方法：1.利用多位数的算式表达式2.代入排除法【例1】一个三位数的各数字之和是16。

其中十位数比个位数小3。

如果把这个三位数的百位数字与个位数字对调，得到一个新的三位数，则新的三位数比原三位数大495，则原来的三位数是多少?A.169B.358C.469D.736【答案】B【中公解析】方法一：排除法。

由各位数之和是16排除C;由百位数与个位数字对调，得到一个新的三位数，则得到新的三位数，改数比原三位数大495，可排除A、D，故选B。

方法二：设原数个位数字为a，则十位数字为a-3，百位数字为19-2a。

由题意可得100a+10(a-1)+(19-2a)=100(19-2a)+10(a-1)+a+495，解得a=8,则a-3=5，19-2a=3，所以原数为358，故选择B。

统计数字问题（c/c++）：问题描述：一本书的页码从自然数1 开始顺序编码直到自然数n。

书的页码按照通常的习惯编排，每个页码都不含多余的前导数字0。

例如，第6页用数字6表示，而不是06 或006 等。

数字计数问题要求对给定书的总页码n，计算出书的全部页码中分别用到多少次数字0，1，2， (9)编程任务：给定表示书的总页码的10 进制整数n (1≤n≤109) 。

编程计算书的全部页码中分别用到多少次数字0，1，2， (9)数据输入：每个文件只有1 行，给出表示书的总页码的整数n。

结果输出:输出文件共有10行，在第k行输出页码中用到数字k-1 的次数，k=1，2， (10)代码一：最笨的方法，依次对每个数字进行统计#include<iostream>#include<memory.h>using namespace std;void count(int page);int num[10];void main(){int m,j;while(cin>>m){count(m);for(j=0;j<10;++j)cout<<num[j]<<endl;cout<<endl;}}void count(int page){int n,i;memset(num,0,sizeof(num));for(i=1;i<=page;++i){n=i;while(n!=0){++num[n%10];n/=10;}}}代码二：公式计算考察由0,1,2,……9组成的所有n位数,从n个0到n个9共有10n个n位数。

在这10n个n位数中，0,1,2,……9每个数字使用的次数相同，设为f(n)。

f(n)满足如下递归式：f(n)=n10n-1 (10f(n-1)=(n-1)10n-1)可从高位向低位进行统计，再减去多余的0的个数#include<iostream>#include<memory.h>#include<cmath>using namespace std;int weishu(int n);int zuigao(int n);int f(int n);void ff(int n);int num[10];void main(){int page,i;while(cout<<"请输入一个页码:"<<endl){cin>>page;memset(num,0,sizeof(num));int m=weishu(page);for(i=0;i<m;++i){ff(page);page=page%(int)pow(10,weishu(page)-1);}for(i=0;i<10;++i)cout<<num[i]<<' ';cout<<endl;}}int weishu(int n) //求位数{int i=1;while((int)(n/pow(10,i))!=0)i++;return i;}int zuigao(int n) //求最高位上的数{return n/(int)pow(10,weishu(n)-1);}int f(int n) //所有n位数中0-9出现的次数{return n*pow(10,n-1);}void ff(int n){int m=weishu(n),i;if(m==1){for(i=1;i<=n;++i)num[i]+=1;}else{for(i=0;i<10;++i)num[i]+=zuigao(n)*f(m-1);for(i=1;i<zuigao(n);++i)num[i]+=(int)pow(10,m-1);num[zuigao(n)]=num[zuigao(n)]+1+n%(int)pow(10,m-1);}}。

页码及相关问题( 1 ）答案与解析1 ．在1-5000 页中，出现过多少次数字3 ？含3 的页数有是多少？解析：对于3 出现了多少次这种题型，大家都不陌生，规律是：在页码1-99 中，l 、2 、3 、4 、5 、6 、7 、8 、9 均会出现20 次（0 不符合这一规律）。

在页码100 -999 中，l 、2 、3 、4 、5 、6 、7 、8 、9 均会出现20 *9+100 次。

那么，“含某个数字的页数有多少”这类题该怎么解呢？首先，在页码1-99 中，数字3 出现了20 次，即有19 个含3 的页码( 33 页要去掉一次）；在页码100-999 中，分两种情况考虑：( 1 ）首位数字是3 ，那么，后面两位就不用管了，一共有含3 的页码100 页；( 2 ）首位数字不是3 ，那么必须考虑后两位数字含3 ，而前面知道，1-99 中，有19 个含3 的页码，由于首位数字这时有l 、2 、4 、5 、6 、7 、8 、9 这么8 种可能性，所以应该是19 * 8 个含3 的页码。

在这里统计一下，在1-999 中，含3 的页码一共19 + 19 * 8 + 100 = 19 * 9 + 100 页，再引申到1000-5000 ，也分两种情况：( l ) 千位是3 ，则有1000 页：( 2 ）千位不是3 ，则只可能是l 、2 、4 ，只考虑后3 位，有（19*9+l00)*3 个含3 的页码。

所以，合计是：19 * 9 + 100 + ( 19 * 9 + 100 ) * 3 + 1000 =2084 页2 . 99999 中含有多少个带9 的页面？答案是40951 ，排列组合学的不是特别好的同学可以牢记公式:[ (19*9+100)*9+1000]*9+10000=40951规律很简单：19*9+100 ，代表l-999 里含l 、2 、3 、4 、5 、6 、7 、8 、9 的页码数；(19*9+100)*9+1000，代表1-9999 里含l 、2 、3 、4 、5 、6 、7 、8 、9 的页码数；（l9*9+100)*9+1000，代表l-99999 里含l 、2 、3 、4 、5 、6 、7 、8 、9 的页码数。