页码问题公式总结

第二讲页码问题我们的课本，每页上都有页码，页码都是由一列连续的自然数组成的，每个页码都是由一个或几个数字（数码）组成的。

页码问题就是根据图书的页码而编制出的一类应用题。

编一本书的页码，一共需要多少个数码呢？反过来，知道编一本书的页码所需的数码数量，求这本书的页数。

这是页码问题中的两个基本内容。

为了顺利地解答页码问题，我们先看一下“数”与“组成它的数码个数”之间的关系。

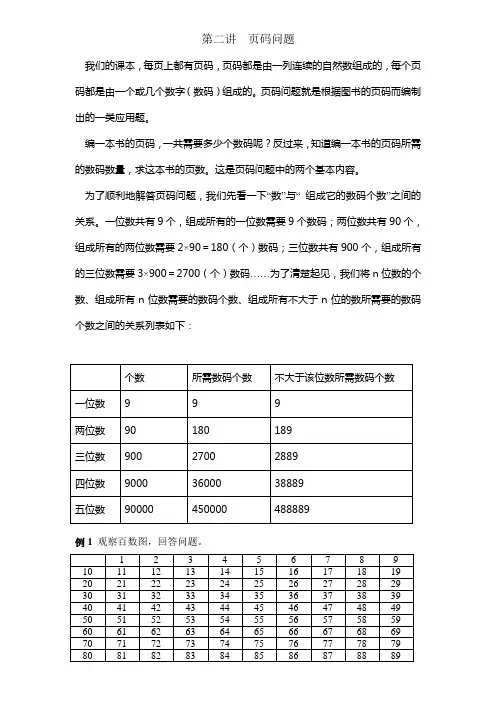
一位数共有9个，组成所有的一位数需要9个数码；两位数共有90个，组成所有的两位数需要2×90＝180（个）数码；三位数共有900个，组成所有的三位数需要3×900＝2700（个）数码……为了清楚起见，我们将n位数的个数、组成所有n位数需要的数码个数、组成所有不大于n位的数所需要的数码个数之间的关系列表如下：例1观察百数图，回答问题。

分析：将这100个数分成一位数、两位数、三位数三部分分别计算。

（结合此题分析表一）9+180+3=192（个）（2）数字“0”一共出现了多少次？数字“1”出现了多少次？其他的数字呢？分析： 0出现了11次，其他的数字分别出现了21次，追问：为什么0出现的次数与众不同？从而总结计算一个数字出现次数的方法是：将不同数位出现的次数进行累加。

例2一本科幻小说共320页，问：编印这本科幻小说的页码共要用多少个数字？分析：1～9页每页上的页码是一位数，共需数码1×9=9（个）；10～99页每页上的页码是两位数，共需数码2×90＝180（个）；100～320页每页上的页码是三位数，共需数码（320-100＋1）×3＝663（个）。

综上所述，这本书共需数码9＋180＋663＝852（个）。

例3 一本小说的页码，在排版时必须用2211个数码。

问：这本书共有多少页？分析：因为189＜2211＜2889，所以这本书有几百页。

由前面的分析知道，这本书在排三位数的页码时用了数码（2211-189）个，所以三位数的页数有（2211-189）÷3＝674（页）。

页码问题：例1一本书共204页，需多少个数码编页码？分析与解：1～9页每页上的页码是一位数，共需数码1×9=9（个）；10～99页每页上的页码是两位数，共需数码2×90＝180（个）；100～204页每页上的页码是三位数，共需数码（204-100＋1）×3＝105×3＝315（个）。

综上所述，这本书共需数码9＋180＋315＝504（个）。

例2一本小说的页码，在排版时必须用2211个数码。

问：这本书共有多少页？分析：因为189＜2211＜2889，所以这本书有几百页。

由前面的分析知道，这本书在排三位数的页码时用了数码（2211-189）个，所以三位数的页数有（2211-189）÷3＝674（页）。

因为不到三位的页数有99页，所以这本书共有99＋674＝773（页）。

解：99＋（2211——189）÷3＝773（页）。

答：这本书共有773页。

例3一本书的页码从1至62、即共有62页。

在把这本书的各页的页码累加起来时，有一个页码被错误地多加了一次。

结果，得到的和数为2000。

问：这个被多加了一次的页码是几？分析与解：因为这本书的页码从1至62，所以这本书的全书页码之和为1＋2＋…＋61＋62＝62×（62＋1）÷2＝31×63＝1953。

1．给一部百科全书编上页码需要6869个数字，那么，这部书共有多少页？2、上、下两册书的页码共有687个数字，且上册比下册多5页，则上册书有多少页？3、将自然数按从小到大的顺序无间隔地排成一个大数1234567891011121314........问：左起第1000位数是几？4、有一本科幻故事书，每四页中有一页为文字，其余三页为图画。

如果第一页为图画，那么第二、三页也是图画，第四页为文字，第五、六、七页又为图画。

以此类推。

如果第一页为文字，那么第二、三、四页为图画，第五页为文字，第六、七、八页又为图画。

数学运算典型题型及公式数学运算是行测中较难的一个模块，得分率较低，且考试做答题时普遍反映数学运算需要不少时间。

诚然，每年的数学运算都会有些新题出来，但大多数的题还是以往见过的类型，因此熟练掌握常规解法极其重要。

并且，如果能记住一些重要的公式和结论，遇到适用的题型能直接套用公式的话，能大大缩短解题时间，也会有很高的正确率。

因此考生一定要记住一些常用的公式结论。

在记忆这些常用公式的时候一定要注意适用的条件，最好是用典型例题进行训练；另外，公式结论的记忆准确性也极其重要，记错了当然得分就无从谈起了以下列举了一些常见公式和结论：一、三位数页码问题例1、编一本书的书页，用了270个数字（重复的也算，如页码115用了2个1和1个5共3个数字），问这本书一共有多少页？（）（2008年国家公务员考试行测试卷）A、117B、126C、127D、189结论：若一本书一共有N页（N为三位数，），用了M个数字，依上可知：M=9+180+3x（N-100+1），得出N=M÷3+36套用公式可得，这本书一共有270÷3+36=126页。

选B二、余数问题例2、一个三位数除以9余7，除以5余2，除以4余3，这样的三位数有几个（）（2006年国家公务员考试行测试卷）A、5B、6C、7D、8结论：余同取余，和同加和，差同减差，公倍数做周期根据结论，这个数除以20余7，和除以9余7又为余同问题，所以该数除以180余7，故可表示为180n+7（n为整数），这个数为三位数，所以共有5个。

选A三、星期日期问题例3、已知2008年的元旦是星期二，问2009年的元旦是星期几？（）A、星期二B、星期三C、星期四D、星期五结论：过多少年加几，其中经过多少个2月29日再加几由结论可得，2008年到2009年过了一年，所以星期数加1，其中经过了一个2月29日，即2008年2月29日，再加1，共加2，所以星期二到了星期四。

选C四、等距离平均速度题例4、一辆汽车以60千米/时的速度从A地开往B地，它又以40千米/时的速度从B地返回A地，则汽车行驶的平均速度为多少千米/时？（）A、50B、48C、30D、20套用公式可得，平均速度为2x60x40/（40+60）=48。

最新小学奥数页码问题一、考点、热点、重点、难点顾名思义，页码问题与图书的页码有密切联系。

事实上，页码问题就是根据书的页码而编制出来的一类应用题。

编一本书的页码，一共需要多少个数码呢？反过来，知道编一本书的页码所需的数码数量，求这本书的页数。

这是页码问题中的两个基本内容。

为了顺利地解答页码问题，我们先看一下“数”与“组成它的数码个数”之间的关系。

一位数共有9个，组成所有的一位数需要9个数码；两位数共有90个，组成所有的两位数需要2×90＝180（个）数码；三位数共有900个，组成所有的三位数需要3×900＝2700（个）数码……为了清楚起见，我们将n位数的个数、组成所有n位数需要的数码个数、组成所有不大于n位的数需要的数码个数之间的关系列表如下：由上表看出，如果一本书不足100页，那么排这本书的页码所需的数码个数不会超过189个；如果某本书排的页码用了10000个数码，因为2889＜10000＜38889，所以这本书肯定是上千页。

下面，我们看几道例题。

二、典型例题例1一本书共204页，需多少个数码编页码？分析与解：1～9页每页上的页码是一位数，共需数码1×9=9（个）；10～99页每页上的页码是两位数，共需数码2×90＝180（个）；100～204页每页上的页码是三位数，共需数码（204-100＋1）×3＝105×3＝315（个）。

综上所述，这本书共需数码9＋180＋315＝504（个）。

例2、编一本书的书页，用了270个数字（重复的也算，如页码115 用了2个1 和1个5共3个数字），问这本书一共有多少页？方法一：l--9 是只有9个数字，10--99 是2*90 =180个数字，那么剩下270-9-180= 81，剩下81/3 = 27页，则这本书是99+27-1=126 页。

方法二：假设这个页数是A页，则有A 个个位数，每个页码除了1--9 ，其他都有十位数，则有A-9个十位数，同理：有A-99个百位数。

页码问题常见的主要有三种题型：一、一本书有N页，求排版时用了多少个数字；或者反过来，一本书排版时用了N个数字，求这本书有多少页；二、已知一本N页的书中，求某个数字出现多少次；三、已知一本N页的书中，求含有某个数字的页码有多少页1．编一本书的书页，用了270个数字（重复的也算，如页码115 用了2个1 和1个5共3个数字），问这本书一共有多少页？方法一：l--9 是只有9个数字，10--99 是2*90 =180个数字，那么剩下270-9-180= 81，剩下81/3 = 27页，则这本书是99+27-1=126 页。

方法二：假设这个页数是A页，则有A 个个位数，每个页码除了1--9 ，其他都有十位数，则有A-9个十位数，同理：有A-99个百位数。

则：A+(A-9)+(A-99)=270 3A-110+2=270 3A=378 ， A=126方法三：公式法：公式：一本书用了N个数字，求有多少页：N/3+36。

270/3 +36=126。

2．一本小说的页码，在排版时必须用2211 个数码。

问这本书共有多少页？A．773 C .775解析：代入公式：N/3+36=737+36=7733 ．王先生在编一本书，其页数需要用6869 个字，问这本书具体是多少页？方法一：假设这个页数是A页，则：A+(A-9)+(A-99)+(A-999)=6869 ，求出A=1994 方法二：6869>2889，所以，把所有的数字看作是4位数字，不足4位的添O补足4位，l , 2 , 3 , … 9 记为0001 , 0002 , 0003 , ..0009 这样增加了3 * 9 = 27 个010 , 11 , 12 , … 99 记为0010 , 0011 , 0012 ，..0099 增加了180 个0 100 , 101 ，… 999 记为0100 , 0101 ，… 0999 增加了900 个O(6869+27+180+900)/4 =1994总结：一本书排版时用了N个数字，求这本书有多少页，N<2889时，用公式：N/3+36；N>2889时,用添加0计算。

一、一本书有N页，求排版时用了多少个数字；或者反过来，一本书排版时用了N个数字，求这本书有多少页；比如126页,1994页方法一：个位：1—9 ：只有9个数字；10位：10—99 ：是90×2 =180个数字百位：100—999，是900×3=2700个数字；如果页数超过1000页（1994页），数字总数就是总数字=9+180+2700+（1994-1000+1）×4=2889+3980=6869字如果页数大于100，但小于1000（126页），数字总数就是总数字=9+180+（126-100+1）×3=189+81=270方法二：假设这个页数是X页：因为每个页码都有个位数（比如第5的个位数是5, 第56页的个位数是6,第389的个位数是9，第1273的个位数是3），所以总计个位数的数字有X个。

在十位数上，除了（1,2,34,5,6,7,8,9）外，每个数字都有十位数，（比如第10页的十位数是1,第56的的十位数是5，第389的十位数是8，第1273的十位数是7），因此总计十位数的数字有X-9个；同理，在百位上，总计百位的数字数量就是有X-99个；计算公式就是X+（X-9）+（X-99）+（X-999）……如果页数超过1000页（1994页），数字总数就是总数字=1994+（1994-9）+（1994-99）+（1994-999）=1994×4-（10+100+1000-3）=7976-1107=6869字如果页数大于100，但小于1000（126页），数字总数就是总数字=126+（126-9）+（126-99）=126×3-（10+100-2）=378-108=270字反之，如果知道一本书有多少个字，比如270字，或者6869字，问有多少页，最简便的方法是如果字数小于2889（9+180+2700），也就是说页数在1000页以内的，按以下规则：总字数= X+（X-9）+（X-99）总字数= 3X-108页数X=总字数÷3+36，或者X=（总字数+108）÷3如果是4位数，那么就是以下规则。

页码问题知识点总结
页码问题通常指在文档或书籍中进行编号和标记页码的方法和规则。

以下是页码问题的一些常见知识点总结：
1. 页码的基本格式：页码通常以阿拉伯数字表示，并从文档或书籍的第一页开始，依次递增。

例如，第一页为1，第二页为2，以此类推。

2. 特殊页码：某些页面可能有特殊的页码，如封面、版权页、目录、前言等。

这些页面通常使用罗马数字或字母进行编号，例如i、ii、iii或I、II、III。

3. 页眉和页脚：页码通常位于页面的页眉或页脚中，以便读者可以方便地找到所在位置。

页眉和页脚通常包含其他信息，如章节标题、日期或作者名称。

4. 页面编号的位置：页码可以放置在页面的不同位置，如页眉的左侧、右侧或中间，或者页脚的左侧、右侧或中间。

不同出版物和文档可能有不同的偏好和规定。

5. 前言和序言：在一本书的开头通常有前言或序言部分，这些部分通常使用罗马数字进行编号（如i、ii、iii）。

6. 目录页面：在书籍或较长的文档中，目录页面通常列出各个章节的标题和对应的页码。

目录页面通常使用罗马数字进行编号，这些编号与章节页码相对应。

7. 章节编号：在书籍中，每个章节通常有自己的编号，以方便读者参考和引用。

章节编号可以使用阿拉伯数字、罗马数字或字母进行编号。

总的来说，页码问题涉及到文档结构和组织的方式，旨在为读者提供方便的导航和参考。

具体的页码规则会根据特定的出版物、学术领域或要求而有所不同。

奥数：页码问题（数论问题)页码问题与图书的页码有密切联系．事实上,页码问题就是根据书的页码而编制出来的一类应用题．编一本书的页码，一共需要多少个数码呢?反过来，知道编一本书的页码所需的数码数量，求这本书的页数．这是页码问题中的两个基本内容。

页码问题是现在的奥数竞赛以及公务员考试中常见的、经常考试的知识点.页码问题实际上是数论的问题。

为了顺利地解答页码问题，我们先看一下“数”与“组成它的数码个数”之间的关系．一位数共有9个，组成所有的一位数需要9个数码；两位数共有90个,组成所有的两位数需要2×90＝180(个)数码；三位数共有900个，组成所有的三位数需要3×900＝2700(个）数码。

现在我们来看几道例题．例1 一本书共204页，需多少个数码编页码？分析与解：1～9页每页上的页码是一位数，共需数码1×9＝9(个)；10～99页每页上的页码是两位数，共需数码2×90＝180(个);100～204页每页上的页码是三位数，共需数码(204－100＋1）×3＝105×3＝315(个)．综上所述，这本书共需数码9＋180＋315＝504（个）．例2 一本小说的页码，在排版时必须用2211个数码．问：这本书共有多少页？分析:因为189＜2211＜2889，所以这本书有几百页．由前面的分析知道,这本书在排三位数的页码时用了数码(2211－189）个，所以三位数的页数有(2211－189）÷3＝674(页)．因为不到三位的页数有99页,所以这本书共有：99＋674＝773(页）．解:99＋（2211－189）÷3＝773（页）．答：这本书共有773页．例3 一本书的页码从1至62，即共有62页．在把这本书的各页的页码累加起来时,有一个页码被错误地多加了一次．结果,得到的和数为2000．问：这个被多加了一次的页码是几？分析与解:因为这本书的页码从1至62,所以这本书的全书页码之和为1＋2＋…＋61＋62＝62×(62＋1）÷2＝31×63＝1953．由于多加了一个页码之后，所得到的和数为2000，所以2000减去1953就是多加了一次的那个页码,是2000－1953＝47．例4 有一本48页的书,中间缺了一张,小明将残书的页码相加,得到1131．老师说小明计算错了，你知道为什么吗?分析与解:48页书的所有页码数之和为1＋2＋…＋48＝48×(48＋1)÷2＝1176．按照小明的计算，中间缺的这一张上的两个页码之和为1176－1131＝45．这两个页码应该是22页和23页．但是按照印刷的规定，书的正文从第1页起，即单数页印在正面，偶数页印在反面,所以任何一张上的两个页码，都是奇数在前，偶数在后，也就是说奇数小偶数大．小明计算出来的是缺22页和23页，这是不可能的．例5 将自然数按从小到大的顺序无间隔地排成一个大数：123456789101112…问：左起第2000位上的数字是多少？分析与解:本题类似于“用2000个数码能排多少页的页码？”因为（2000－189)÷3＝603……2，所以2000个数码排到第99＋603＋1＝703(页）的第2个数码“0”．所以本题的第2000位数是0．例6 排一本400页的书的页码，共需要多少个数码“0”？分析与解:将1～400分为四组：1～100，101～200,201~300，301~400．在1～100中共出现11次0,其余各组每组都比1～100多出现9次0,即每组出现20次0．所以共需要数码“0”典型例题：例1、13/1995 化成小数后是一个无限小数，问在这个无限小数的小数点后面，从第一位到1995位,在这1995个数中，数字6共出现了多少次？解答：这是一个关于循环小数的周期问题。

页码及相关问题( 1 ）答案与解析1 ．在1-5000 页中，出现过多少次数字3 ？含3 的页数有是多少？解析：对于3 出现了多少次这种题型，大家都不陌生，规律是：在页码1-99 中，l 、2 、3 、4 、5 、6 、7 、8 、9 均会出现20 次（0 不符合这一规律）。

在页码100 -999 中，l 、2 、3 、4 、5 、6 、7 、8 、9 均会出现20 *9+100 次。

那么，“含某个数字的页数有多少”这类题该怎么解呢？首先，在页码1-99 中，数字3 出现了20 次，即有19 个含3 的页码( 33 页要去掉一次）；在页码100-999 中，分两种情况考虑：( 1 ）首位数字是3 ，那么，后面两位就不用管了，一共有含3 的页码100 页；( 2 ）首位数字不是3 ，那么必须考虑后两位数字含3 ，而前面知道，1-99 中，有19 个含3 的页码，由于首位数字这时有l 、2 、4 、5 、6 、7 、8 、9 这么8 种可能性，所以应该是19 * 8 个含3 的页码。

在这里统计一下，在1-999 中，含3 的页码一共19 + 19 * 8 + 100 = 19 * 9 + 100 页，再引申到1000-5000 ，也分两种情况：( l ) 千位是3 ，则有1000 页：( 2 ）千位不是3 ，则只可能是l 、2 、4 ，只考虑后3 位，有（19*9+l00)*3 个含3 的页码。

所以，合计是：19 * 9 + 100 + ( 19 * 9 + 100 ) * 3 + 1000 =2084 页2 . 99999 中含有多少个带9 的页面？答案是40951 ，排列组合学的不是特别好的同学可以牢记公式:[ (19*9+100)*9+1000]*9+10000=40951规律很简单：19*9+100 ，代表l-999 里含l 、2 、3 、4 、5 、6 、7 、8 、9 的页码数；(19*9+100)*9+1000，代表1-9999 里含l 、2 、3 、4 、5 、6 、7 、8 、9 的页码数；（l9*9+100)*9+1000，代表l-99999 里含l 、2 、3 、4 、5 、6 、7 、8 、9 的页码数。

页码问题一、页码问题的几种题型：(1)已知页码数，要求求出书中一共含有多少个数码。

(2)已知页码数，要求求此书中某个数码出现的次数。

(3)已知书中包含的数码数，要求求出该书的页码数。

(4)已知书中某个数码出现的次数，要求求出该书的页码数。

二、页码问题解题基本原理要想要想顺利解答页码问题，首先要弄明白“页码”与“组成它的数码个数”之间的关系。

1．一位数组成的页码共有9个(从1～9)，组成所有的一位数需要：(9-1+1)×1=9×1=9(个)数码。

2．两位数共有90个(从10～99)，组成所有的两位数需要：2×(99-10+1)=180(个)数码。

3．三位数共有900个(从100～999)，组成所有的三位数需要：3×(999-100+1)=2700(个)数码。

4．四位数共有9000个(从1000～9999)，组成所有四位数需要：4×(9999-1000+1)=36000(个)数码。

5．9页的书共有：9个数码组成。

6．99页的书共有：9+180=189个数码组成。

7．999页的书共有：2700+180+9=2889个数码组成。

8．9999页的书共有：36000+2700+180+9=38889个数码组成。

三、例题：例1、一本书共204页，需多少个数码编页码？分析与解：1～9页每页上的页码是一位数，共需数码1×9＝9(个)；10～99页每页上的页码是两位数，共需数码2×90＝180(个)；100～204页每页上的页码是三位数，共需数码：(204－100＋1)×3＝105×3＝315(个)．综上所述，这本书共需数码：9＋180＋315＝504(个)．例2、一本小说的页码，在排版时必须用2211个数码．问：这本书共有多少页？分析：因为189＜2211＜2889，所以这本书有几百页．由前面的分析知道，这本书在排三位数的页码时用了数码(2211－189)个，所以三位数的页数有 (2211－189)÷3＝674(页)．因为不到三位的页数有99页，所以这本书共有：99＋674＝773(页)．解：99＋(2211－189)÷3＝773(页)．答：这本书共有773页．例3、一本书的页码从1至62，即共有62页．在把这本书的各页的页码累加起来时，有一个页码被错误地多加了一次．结果，得到的和数为2000．问：这个被多加了一次的页码是几？分析与解：因为这本书的页码从1至62，所以这本书的全书页码之和为1＋2＋…＋61＋62＝62×(62＋1)÷2＝31×63＝1953．由于多加了一个页码之后，所得到的和数为2000，所以2000减去1953就是多加了一次的那个页码，是2000－1953＝47．例4、有一本48页的书，中间缺了一张，小明将残书的页码相加，得到1131．老师说小明计算错了，你知道为什么吗？分析与解：48页书的所有页码数之和为1＋2＋…＋48＝48×(48＋1)÷2＝1176．按照小明的计算，中间缺的这一张上的两个页码之和为1176－1131＝45．这两个页码应该是22页和23页．但是按照印刷的规定，书的正文从第1页起，即单数页印在正面，偶数页印在反面，所以任何一张上的两个页码，都是奇数在前，偶数在后，也就是说奇数小偶数大．小明计算出来的是缺22页和23页，这是不可能的．例5、将自然数按从小到大的顺序无间隔地排成一个大数：123456789101112…问：左起第2000位上的数字是多少？分析与解：本题类似于“用2000个数码能排多少页的页码？”因为(2000－189)÷3＝603……2，所以2000个数码排到第99＋603＋1＝703(页)的第2个数码“0”．所以本题的第2000位数是0．例6、排一本400页的书的页码，共需要多少个数码“0”？分析与解：将1～400分为四组：1～100，101～200，201～300，301～400．在1～100中共出现11次0，其余各组每组都比1～100多出现9次0，即每组出现20次0．所以共需要数码“0”例7、13/1995 化成小数后是一个无限小数，问在这个无限小数的小数点后面，从第一位到1995位，在这1995个数中，数字6共出现了多少次？解答：这是一个关于循环小数的周期问题。

页码问题解决页码问题的基本方法是：分段（或分类或分组）计算。

典型的页码问题有三类：1、计算页码中所用数字总数，或是根据已知的页码中所用数字总数来求页码。

2、计算页码中某个数字出现的次数。

3、计算页码中所有数字的和。

【例1】一本书有180页，在这本书的页码中共用了多少个数字解：1～9页：共1×9=9（个）；10～99页：共2×（99-1+1）=180（个）；100～180页：共3×（180-100+1）=243（个）；综上所述，共用9+180+243=432（个）。

【例2】一本童话书的页码在排版时需用1911个数字，这本童话书共有多少页解：1～9页：共1×9=9（个）；10～99页：共2×（99-1+1）=180（个）；100～999页：共3×（999-100+1）=2700（个）；因为189<1911<2899,所以这本书的页码在100～999页。

（1911-189）÷3+99=673（页）【例3】一本漫画共121页，在这本书的页码中数字一共出现了多少次解：1在个位上：1, 11，21,31，……，121，共出现了（121-1）÷10+1=13（次）；1在十位上：10～19,110～119，共出现了10+10=20（次）；1在百位上：100～121，共出现了（121-100）÷1+1=22（次）；共出现了13+20+22=55（次）。

【例4】一本漫画共200页，求页码中所有数字的和。

解：0～199分成100组，分组如下：（0，199），（1,198），（2,197），（3,196），……，（98,101）（99,100）每组数字的和=19，一共有100组，所用数字的和是19×100=1900，再加上“200”这三数之和为2，故200页中全部数字之和=1902【例5】将自然数从小到大的顺序无间隔的排成一列数121314……，在这个数的左起500位上的数字是多少解：这道题类似将500个数字排成多少页的页码。

一．页码问题对多少页出现多少1或2的公式如果是X千里找几，公式是1000+X00*3 如果是X百里找几，就是100+X0*2，X有多少个0 就*多少。

依次类推！请注意，要找的数一定要小于X ，如果大于X就不要加1000或者100一类的了，比如，7000页中有多少3 就是1000+700*3=3100（个）20000页中有多少6就是2000*4=8000 （个）友情提示，如3000页中有多少3，就是300*3+1=901，请不要把3000的3忘了二．页码问题(一)某数出现多少次问题99中，某数（不含0）出现20次。

999中，某数（不含0）出现20*9+120次。

(二)含某数的页数有多少问题（就是出现次数减去重复次数）99中，含某数（不含0）19页。

999中，含某数（不含0）19*9+100页。

9999中，含某数（不含0）(19*9+100)*9+1000页。

(三)A页的书需要多少字符数问题A+A-9+A-99=B(字符数)。

(四)页码数加减是否有误（等差求和公式的运用）等差求和公式是：Sn=（a1+an）×n/2，对于书本来说，页码是从第一页始，因此SN=（1+n）×n/2≈n^2/2【解析】例题：一本故事书共121页，在这本书的页码中数字“1”出现多少次？？A.70B.65C.60D.55选D。

0-99中 20个，100-121中 22+11+2=35个，20+35=55。

例题：老李有一本很旧的书，已知这本书最后一页页码的第一个数字是3，其它的页码数都已模糊不清。

这本书出现数字3的次数有180次。

求这本书由多少个铅字组成（1代表1个铅字，11，代表2个铅字）A.962B.965C.1057D.1089【解析】选B。

20+20+20+120，推出399页，399x3-9-99=1089。

例题：编一本书的书页，用了270个数字（重复的也算，如页码115用了2个1和1个5，共3个数字），问这本书一共有多少页？A.117B.126C.127D.189【解析】选B。

页码问题(一)精品文档页码问题（一）1、一本书共有40页，那么共需要多少个数码编页码?2、一本书共有200页，那么共需要多少个数码编页码?3、排一本小说的页码，需要用2202个数码，这本书共有多少页?4、一本书的页码为1至62，即共有62页。

在把这本书的各页的页码累加起来时，有一个页码漏加了。

结果，得到的和数为1939。

问：这个被漏加的页码是几?5、有一本96页的书，中间缺了一张。

如果将残书的所有页码相加。

那么可能得到偶数吗?6、有一本科幻故事书，每四页中，有一页为文字，其余三页为图画。

如果第一页为图画，那么第二、三页也是图画，第四页为文字，第五、六、七页又为图画，依此类推。

如果第一页为文字，那么第二、三、四页为图画，第五页为文字，第六、七、八页又为图画，依此类推。

试问：(1)假如这本书有96页，且第一页是图画，那么这本书多少页有图画?(2)假如这本书有99页，那么多少页有图画?7、将自然数按从小到大的顺序无间隔地排成一个大数：1234567891011121314……问：左起第7000位数是几?8、从“1”一直写到“701”123456789101112……699700701。

一共写了多少个阿拉伯数字？9、排一本小说的页码，需要用２9３3个数码，问：这本书共有多少页？10、设小数A = 0.1234567891011……998999，试问，小数点右边第1998位上的数字是几？11、一本数学用书的页码中共用297个数字，这本数学用书共多少页？12、一页书共380页，印刷厂的排版工人编排这本书，仅排页码一共要用多少个铅字？13．从“1”一直写到“801”：123456789101112……799800801。

共有多少个阿拉伯数字14．一本故事书，仅排页码就用去1392个铅字（数字）。

这本书有多少页？15．在2、4、6、……、396和398这些偶数的数列中，数字“2“一个有多少个？16．有一本书中间被撕掉一张，余下各页的页码数之和正好是1145。

总页码域公式
总页码域公式是指在文档编排过程中，计算总页码所使用的公式。

该公式通常以文档总页数为基础，再加上可能存在的封面、目录等前置页码和附录等后置页码，计算出最终的总页码。

具体公式如下：总页码 = 文档总页数 + 前置页码数 + 后置页码数
其中，文档总页数是指正文部分的页数，不包括前置页码和后置页码。

前置页码通常包括封面、扉页、版权页等内容，而后置页码则包括附录、参考文献、致谢等内容。

在实际应用中，总页码域公式可以通过Word等文档编辑软件的
页码设置功能进行自动计算和更新。

通过正确设置总页码域公式，可以保证文档页码的准确性和稳定性，方便读者查看和引用。

- 1 -。

页码问题主要有三种题型：欧阳歌谷（2021.02.01）一、一本书有N页，求排版时用了多少个数字；或者反过来，一本书排版时用了N个数字，求这本书有多少页；比如126页,1994页方法一：个位：1—9 ：只有9个数字；10位：10—99 ：是90×2 =180个数字百位：100—999，是900×3=2700个数字；如果页数超过1000页（1994页），数字总数就是总数字=9+180+2700+（19941000+1）×4=2889+3980=6869字如果页数大于100，但小于1000（126页），数字总数就是总数字=9+180+（126100+1）×3=189+81=270方法二：假设这个页数是X页：因为每个页码都有个位数（比如第5的个位数是5, 第56页的个位数是6,第389的个位数是9，第1273的个位数是3），所以总计个位数的数字有X个。

在十位数上，除了（1,2,34,5,6,7,8,9）外，每个数字都有十位数，（比如第10页的十位数是1,第56的的十位数是5，第389的十位数是8，第1273的十位数是7），因此总计十位数的数字有X9个；同理，在百位上，总计百位的数字数量就是有X99个；计算公式就是X+（X9）+（X99）+（X999）……如果页数超过1000页（1994页），数字总数就是总数字=1994+（19949）+（199499）+（1994999）=1994×4（10+100+10003）=79761107=6869字如果页数大于100，但小于1000（126页），数字总数就是总数字=126+（1269）+（12699）=126×3（10+1002）=378108=270字反之，如果知道一本书有多少个字，比如270字，或者6869字，问有多少页，最简便的方法是如果字数小于2889（9+180+2700），也就是说页数在1000页以内的，按以下规则：总字数=X+（X9）+（X99）总字数=3X108页数X=总字数÷3+36，或者X=（总字数+108）÷3如果是4位数，那么就是以下规则。

数学运算中近年来开始出现一些经典的题型，在此给各位考生介绍“页码问题”，此类题目初看有点无从下手的感觉，原因在于考生对页码问题中页码和数码之间的变化关系不了解，没有掌握。

事实上，页码问题就是根据书的页码而编制出来的一类应用题，只要灵活掌握了页码与数码的关系，此类试题就会迎刃而解。

一、页码问题常考细分题型：页码问题涉及的应用题包含四个基本内容：(1)已知页码数，要求考生求出书中一共含有多少个数码(2)已知页码数，要求考生求此书中某个数码出现的次数(3)已知书中包含的数码数，要求考生求出该书的页码数(4)已知书中某个数码出现的次数，要求考生求出该书的页码数二、页码问题解题基本原理要想要想顺利解答页码问题，首先要弄明白“页码”与“组成它的数码个数”之间的关系。

我们知道：一位数共有9个(从1～9)，组成所有的一位数需要9 个数码;两位数共有90个(从10～99)，组成所有的两位数需要2×90=180(个)数码;三位数共有90(从100～999)，组成所有的三位数需要3×900=2700(个)数码。

二、历年真题讲解例：编一本书的书页，用了270个数字(重复的也算，如页码115用了2个1和1个5共3个数字，问这本书一共多少页?答案及解析：本题是已知数码数，求页码数。

一共用了270个数字，其中一位数用9个数字，两位数用了180个数字，那么三位数用的数字就是270-9-180=81个数字。

81÷3=27，因此三位数的页码共27页，从100起算，到126页就是27页，因此这本书一共126页。

例：一本书共204页，需多少个数码编页码?答案及解析：本题是已知数码数，求页码数。

1～9页每页上的页码是一位数，共需数码1×9=9(个);10～99页每页上的页码是两位数，共需数码2×90=180(个);100～204页每页上的页码是三位数，共需数码(204-100+1)×3=105×3=315(个)。