连续传递函数离散化的方法与原理
- 格式:docx
- 大小:623.46 KB
- 文档页数:30
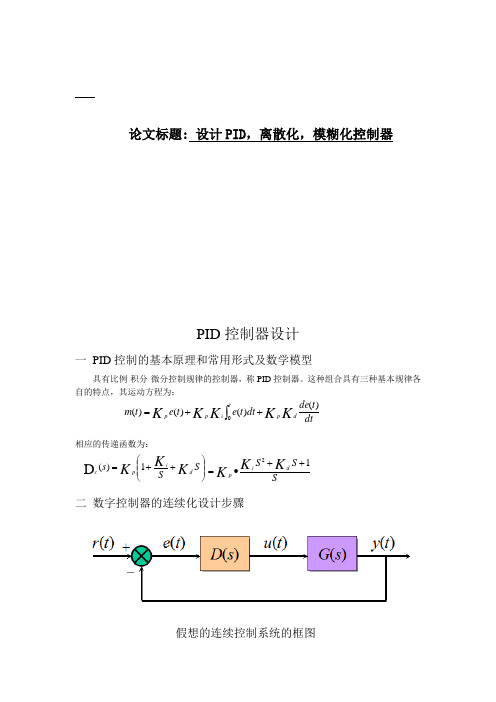
论文标题: 设计PID ,离散化,模糊化控制器PID 控制器设计一 PID 控制的基本原理和常用形式及数学模型具有比例-积分-微分控制规律的控制器,称PID 控制器。
这种组合具有三种基本规律各自的特点,其运动方程为:dt t de dt t e t e t m K K K K K dp ti p p )()()()(0++=⎰相应的传递函数为:⎪⎪⎭⎫ ⎝⎛++=S S s K K K d i p c 1)(D S S S K K K d ip 12++∙=二 数字控制器的连续化设计步骤假想的连续控制系统的框图1 设计假想的连续控制器D(s)由于人们对连续系统的设计方法比较熟悉,对由上图的假想连续控制系统进行设计,如利用连续系统的频率的特性法,根轨迹法等设计出假想的连续控制器D(S)。
2 选择采样周期T香农采样定理给出了从采样信号到恢复连续信号的最低采样频率。
在计算机控制系统中,完成信号恢复功能一般有零阶保持器H(s)来实现。
零阶保持器的传递函数为3将D(S)离散化为D(Z)将连续控制器D(S)离散化为数字控制器D(Z)的方法很多,如双线性变换法,后向差分法,前向差分法,冲击响应不变法,零极点匹配法,零阶保持法。
双线性变换法然后D(S)就可以转化离散的D(Z)三Matlab仿真实验直接试探法求PID根据这个框图,求出该传递函数的P=0.35 I=0 D=0根据⎪⎪⎭⎫ ⎝⎛++=S S s K K K d i p c 1)(D D (Z )=0.35 T=0.01数字连续话PID 控制器设计MA TLAB 仿真框图实验结果 没有经过调节的结果为结果分析一阶阶跃信号的幅值选择为5经过数字连续化PID控制器后,对比图形发现,结果变得非常稳定,没有发现超调量,而没有经过PID控制的图形发生了超调变化达到稳定的时间变得更长。
二离散化控制器的设计离散系统设计是指在给定系统性能指标的条件下,设计出控制器的控制规律和相应的数字控制算法。


§2.3 线性连续时间状态空间表达式的离散化如果用数字计算机对连续时间状态方程求解,或者对连续受控对象采用数字计算机进行在线控制,都要碰到一个将连续时间系统化为离散时间系统的问题。
本节将讨论线性连续时间状态空间表达式的离散化方法。
一、线性时变系统的离散化 设原线性系统的状态空间表达式为:).()t (u )t (D )t (X )t (C Y )t (u )t (B )t (X )t (A X612⎩⎨⎧+=+=离散化后状态空间表达式为:[]).()kT (u )kT (D )kT (X )kT (C )kT (Y )kT (u )kT (H )kT (X )kT (G T )k (X 6221⎩⎨⎧⋅+⋅=+=+式(2.61)、(2.62)之间的系数关系如下[][]).()t (D )kT (D )t (C )kT (C d )(B ,T )k ()kT (H kT ,T )k ()kT (G kTt kT t T)k (kT632111==+==+=+=⎰τττφφ式中[]kT ,T )k (1+φ表示)t ,t (0φ在kT t T )k (≤≤+1区段内的状态转移矩阵,而)t ,t (0φ则表示原连续系统(2.61)式的状态转移矩阵。
证明:由上节(2.60)式可知(2.61)式的解为:).(d )(u )(B ),t (X )t ,t ()t (X t t 642000ττττφφ⎰+=对上式离散化,令hT t ,T )k (t =+=01,T 为采样周期,则得[][][]).(d )(u )(B ,T )k (X hT ,T )k (T )k (X T )k (hT65211110ττττφφ+++=+⎰+再以hT t ,kT t ==0代入(2.64)式,则得 ).(d )(u )(B ),kT (X )hT ,kT ()kT (X kT hT 6620ττττφφ⎰+=将(2.66)式两边同左乘[]kT ,T )k (1+φ,得[][][][][]).(d )(u )(B ,T )k (X hT ,T )k (d )(u )(B ),kT (kT ,T )k (X )hT ,kT (kT ,T )k ()kT (X kT ,T )k (kT hT kT hT 6721111100ττττφφττττφφφφφ+++=++⋅+=+⎰⎰将(2.65)式减去(2.67)式得:[][][]).(d )(u )(B ,T )k ()kT (X kT ,T )k (T )k (X T )k (kT 6821111ττττφφ+++=+⎰+上式中,令[][]τττφφd )(B ,T )k ()kT (H kT ,T )k ()kT (G T)k (kT⎰+=+=+111设在区间[]T )k (,kT 1+内,)kT (u )(u =τ,则(2.68)式可简写成: [])kT (u )kT (H )kT (X )kT (G T )k (X ⋅+⋅=+1 同时,对(2.61)式输出方程离散化,则证明了)kT (u )kT (D )kT (X )kT (C )kT (Y ⋅+=二、线性时不变系统的离散化 对于线性时不变系统).(uD X C Y u B X A X692⎩⎨⎧+=+=离散化状态空间表达式为).()kT (u D )kT (X C )kT (Y )kT (u )T (H )kT (X )T (G T )k (X 7021⎩⎨⎧+=+=+其中D ,C ),T (H ),T (G 均为常数阵,且).(B)d e ()T (H e)T (G A T AT 7120⎪⎩⎪⎨⎧==⎰ττ证明:由于时不变系统是时变系统的一种特殊情况,所以只需要证明式(2.71)成立即可。


连续系统与离散系统的概念连续系统和离散系统是系统控制理论中两种基本的模型类型。
连续系统是指系统的输入和输出信号是连续变化的,并且系统的状态可以在任意时间点进行测量和控制。
而离散系统则是指系统的输入和输出信号是离散的,即只在离散的时刻进行测量和控制,而在两个离散时刻之间的信号变化是未知的。
首先,我们来详细介绍连续系统。
连续系统可以用微分方程来描述,通常采用微分方程的求解方法来求得系统的时域响应。
连续系统可以是线性的,也可以是非线性的。
线性连续系统的特点是具有叠加性质,即输入的线性组合对应于输出的线性组合。
而非线性连续系统则是具有非线性性质,输入的线性组合对应于输出的非线性组合。
连续系统的状态可以通过求解微分方程来得到,并且可以通过选择系统的控制输入来实现对系统状态的调节。
在连续系统中,我们可以利用传递函数来描述系统的频域特性,传递函数是输入和输出的拉普拉斯变换的比值。
传递函数可以用来分析系统的稳定性、频率响应、阻尼特性等。
接下来,我们来介绍离散系统。
离散系统可以用差分方程来描述,通过求解差分方程可以得到系统的时域响应。
离散系统也可以是线性的或非线性的,线性离散系统满足叠加性质,非线性离散系统则不满足叠加性质。
离散系统的状态可以通过迭代差分方程来得到,并且可以通过选择系统的控制输入来实现对系统状态的调节。
离散系统的频域特性可以用离散时间傅里叶变换(DTFT)或离散傅里叶变换(DFT)来描述,这些变换可以将系统的输入和输出信号从时域转换到频域。
离散系统的稳定性、频率响应等也可以通过这些变换来进行分析。
在实际应用中,连续系统和离散系统都有各自的优缺点。
连续系统具有高精度和高灵敏度的特点,适用于需要高精度控制和测量的应用,如机器人控制、飞行器导航等。
而离散系统则具有较低的复杂度和较好的实时性,适合于计算机控制、数字信号处理等应用。
此外,由于实际系统中往往存在传感器采样和控制执行的离散性,所以很多情况下需要将连续系统进行离散化,从而使用离散系统进行建模和控制。

matlab/simulink/simpowersystem中连续vs离散!1.连续系统vs离散系统连续系统是指系统状态的改变在时间上是连续的,从数学建模的角度来看,可以分为连续时间模型、离散时间模型、混合时间模型。
其实在simpowersystem 的库中基本所有模型都属于连续系统,因为其对应的物理世界一般是电机、电源、电力电子器件等等。
离散系统是指系统状态的改变只发生在某些时间点上,而且往往是随机的,比如说某一路口一天的人流量,对离散模型的计算机仿真没有实际意义,只有统计学上的意义,所以在simpowersystem中是没有模型属于离散系统的。
但是在选取模型,以及仿真算法的选择时,常常提到的discrete model、discrete solver、discrete simulate type等等中的离散到底是指什么呢?其实它是指时间上的离散,也就是指离散时间模型。
下文中提到的连续就是指时间上的连续,连续模型就是指连续时间模型。
离散就是指时间上的离散,离散模型就是指离散时间模型,而在物理世界中他们都同属于连续系统。
为什么要将一个连续模型离散化呢?主要是是从系统的数学模型来考虑的,前者是用微分方程来建模的,而后者是用差分方程来建模的,并且差分方程更适合计算机计算,并且前者的仿真算法(simulationsolver)用的是数值积分的方法,而后者则是采用差分方程的状态更新离散算法。
在simpowersystem库中,对某些物理器件,既给出的它的连续模型,也给出了它的离散模型,例如:离散模型一个很重要的参数就是采样时间sampletime,如何从数学建模的角度将一个连续模型离散化,后面会有介绍。
在simpowersystem中常用powergui这个工具来将系统中的连续模型离散以便采用discrete算法便于计算机计算。
2.连续模型的数学建模vs离散模型的数学建模Note:这里的连续和离散都是指时间上的连续和离散,无关乎现实世界的连续系统和离散系统。
控制系统各种传递函数离散化后的递推公式推导及结果一、凹口网络传递函数:上式中参数::凹口网络中心频率,;:二阶微分环节阻尼系数;:二阶振荡环节阻尼系数;采用双线性变换公式对上式离散化:代入H(S)表达式得到:迭代公式:;;*************************************************************** ********************** 二、PI调节器采用双线性变换公式对上式离散化:代入H(S)表达式得到:迭代公式:*************************************************************** ********************** 三、滞后-超前调节器采用双线性变换公式对上式离散化:代入H(S)表达式得到:迭代公式:*************************************************************** ********************** 四、PID 调节器(形式1)参数::一阶微分环节时间常数(第二转折频率);:一阶微分环节时间常数;:一阶惯性环节时间常数;K:PID调节器放大系数。
采用双线性变换公式对上式离散化:代入H(S)表达式得到:迭代公式:;;*************************************************************** ********************** 五、PID 调节器(形式2)采用双线性变换公式对上式离散化:代入H(S)表达式得到:迭代公式:;;*************************************************************** ********************** 六、I型系统期望特性假设一系统的原始开环传递函数为:它的波特图如下图:现对其增加串联迟后校正(近似PI控制器)环节:它的波特图如下:校正后的系统开环传递函数为:1.I型系统期望特性I型系统特点:系统的正向通道(即主通道)包含1个纯积分环节。
c2d函数离散方法
c2d函数是将连续时间系统的差分方程转换为离散时间系统的差分方程的方法。
c2d函数通常使用以下形式:
sys_d = c2d(sys_c, Ts, method)
其中,sys_c是连续时间系统的传递函数或状态空间模型,Ts 是采样时间,method是离散化方法。
常见的离散化方法有以下几种:
1. 零阶保持(Zero-order hold):该方法假设在两个连续时间采样点之间输入信号保持不变。
通过对连续时间系统进行零阶保持,得到离散时间系统的差分方程。
2. 一阶保持(First-order hold):该方法考虑了输入信号在两个连续时间采样点之间的线性变化。
通过对连续时间系统进行一阶保持,得到离散时间系统的差分方程。
3. 双线性变换(Bilinear transform):该方法通过将连续时间系统的传递函数进行双线性变换,在频域上将连续时间系统的频率响应映射到离散时间系统的频率响应。
4. 快速离散化(Fast discretization):该方法利用近似的方法快速计算离散时间系统的差分方程。
选择合适的离散化方法取决于具体的应用场景和要求。
在使用c2d函数进行离散化时,需要考虑采样时间、系统响应、稳定性等因素,并进行适当的验证和调整。
目录 第一章 模拟化设计基础 1 第一节 步骤 1 第二节 在MATLAB中离散化 3
第三节 延时e-Ts环节的处理 5 第四节 控制函数分类 6 第二章 离散化算法 10 摘要 10 比较 11 第一节 冲击响应不变法(imp,无保持器直接z变换法) 11 第二节 阶跃响应不变法(zoh,零阶保持器z变换法) 11 第三节 斜坡响应不变法(foh,一阶保持器z变换法) 11 第四节 后向差分近似法 12 第五节 前向差分近似法 14 第六节 双线性近似法(tustin) 15 第七节 预畸双线性法(prevarp) 17 第八节 零极点匹配法(matched) 18 第三章 时域化算法 19 第一节 直接算法1—双中间变量向后递推 19 第二节 直接算法2—双中间变量向前递推 20 第三节 直接算法3—单中间变量向后递推 21 第四节 直接算法4—单中间变量向前递推(简约快速算法) 21 第五节 串联算法 22 第六节 并联算法 23 第四章 数字PID控制算法 24 第一节 微分方程和差分方程 25 第二节 不完全微分 25 第三节 参数选择 26 第四节 c51框架 27 第五章 保持器 33 第一节 零阶保持器 33 第二节 一阶保持器 30 附录 两种一阶离散化方法的结果的比较 31 第一章 模拟化设计基础 数字控制系统的设计有两条道路,一是模拟化设计,一是直接数字设计。如果已经有成熟的模拟控制器,可以节省很多时间和部分试验费用,只要将模拟控制器离散化即可投入应用。如果模拟控制器还不存在,可以利用已有的模拟系统的设计经验,先设计出模拟控制器,再进行离散化。 将模拟控制器离散化,如果用手工进行,计算量比较大。借助数学软件MATLAB控制工具箱,可以轻松地完成所需要的全部计算步骤。如果需要的话,还可以使用MATLAB的SIMULINK工具箱,进行模拟仿真。
第一节 步骤 步骤1 模拟控制器的处理 在数字控制系统中,总是有传输特性为零阶保持器的数模转换器(DAC),因此,如果模拟控制器尚未设计,则应以下图
的方式设计模拟控制器,即在对象前面加上一个零阶保持器,形成一个新对象Ts1eGss(),然后针对这个新对象求模拟控制器D(s)。事实上,模拟控制器一般是已经设计好的,无法或不方便更改了,离散化后的系统只好作为近似设计了。 然而,按照上述思路,可否将已有的控制器除以一个零阶保持器再离散化呢?还没有这方面的实际经验。 以下假设选定的G(s),D(s)如下图,而且不对G(s)作添加保持器的预处理。 步骤2 离散化模拟控制器 离散化模拟控制器之前,先要确定离散化算法和采样时间。离散化算法有好几种,第二章中有详细的论述,现假定采用双线性变换法。确定采样时间,需要考虑被控对象的特性,计算机的性能,以及干扰信号的影响等,初步可按采样时间T<,Tp为被控对象时间常数,或T=~τ,为被控对象的纯滞后,初步确定后再综合平衡其它因素,当然这需要一定的经验,现在假定取秒。
假设模拟控制器为s2Ds8s15(),在MATLAB中,用c2d函数进行离散化,过程为:
转换结果为: 步骤3 检验数字控制器的性能 数字控制器的性能项目比较多,我们仅以直流增益,频率特性,零极点分布说明。 直流增益 dcgain(dz) 返回直流增益 频率特性 bode(ds,'r',dz,'g') 伯德图,见下页左图 零极点分布 pzmap(dz) 零极点分布图,见下页右图 步骤4 离散化控制对象 为了进行模拟仿真,需要对控制对象进行离散化,由于步骤1所说的原因,应把被控对象视为零阶保持器与原对象的串
连,即应对Ts1eGss()进行离散化,这时可在c2d函数中使用零阶保持器(zoh)方法,如果认为不需要添加零阶保持器,即直接对G(s)离散化,则应在c2d函数中使用冲击响应不变法(imp)。 借用零阶保持器(zoh)方法,将对象20Gsss2()()带一阶保持器离散化的过程如下:
转换结果为: 步骤5 模拟仿真 求离散系统的闭环传递函数和连续系统的闭环传递函数。
ds=zpk(-2,-15,8) %建立模拟控制器的s传递函数 dz=c2d(ds,,'tustin') %将模拟控制器按tustin方法转换为z传递函数的数
...... %模拟控制器D(s)转换为D(z)的过程见前 gs=zpk([ ],[0,-2],20) %建立对象的s传递函数 g1z=c2d(gs,,'zoh') %借用c2d函数进行带零阶保持器的对象的离散化 离散系统的闭环传递函数为:CZDzG1zTR1DzG1z()()()() 连续系统的闭环传递函数为:CSDsGsTR1DsGs()()()() 用MATLAB算TRCZ与TRCS:
结果为: 用MATLAB函数STEP画阶跃响应图形:
响应图形为: 步骤6 求数字控制器的时域表达式
上面已经求出, 连续传递函数s2Ds8s15()的tustin离散式为
11Uz61091z090486.1091-5.527zDzEzz04545104545z().(.)
()()..
,或 11Uz61091Ez5527Ezz04545Uzz().().().()。
对上式取z反变换,得时域表达式uk61091ek5527ek104545uk1().().().(),根据此式就可以写出计算uk()的程序代码来了。 除上述步骤之外,在编写程序代码时,还需要考虑几个问题: ① ADC位数 ADC位数是一个硬件问题,在系统设计时,就应该结合控制算法,仔细分析ADC位数对控制精度的影响。 ② 数据类型 在控制算法中有3种数据类型可以采用:无符号整数,定点数,浮点数。我们知道,无符号整数运算既是最简单和速度最快的运算,又是定点数运算和浮点数运算的基础。在数据动态范围比较小的情况下,应尽可能用无符号整数运算代替定点数运算和浮点数运算。 浮点数运算是一整套运算,包括加,减,乘,除,对阶,规格化,溢出处理等一系列子程序,使用浮点数的程序,将占用比较多的代码空间和比较长的运行时间。不论使用汇编语言还是c语言,对于是否使用浮点数运算,都应进行比较仔细的酌斟。 ③ 数值计算误差 数值计算引入的误差有3个方面,一是定点数字长不够或者浮点数有效数字过少,一是两个相近的数相减,一是加减乘除次数过多。在程序设计中,应优化算法以避免计算误差的引入。
trcz=dz*g1z/(1+dz*g1z) trcs=ds*gs/(1+ds*gs)
hold on %图形保持 step(trcs,'r',2) %画连续系统的阶跃响应图,红色,终止时间为2秒 step(trcz,'b',2) %画离散系统的阶跃响应图,兰色,终止时间为2秒 第二节 在MATLAB中离散化 1. 建立s降幂传递函数 ① 建立多项式型s降幂传递函数 方法1. sys = tf(num,den) 方法2. s = tf('s'),再令sys = f(s)
例: 已知03215s3G025s125ss...,用tf函数建立多项式型s降幂传递函数,0Gtf15302512510([.],[..]),
若G0以零极点形式给出,即已知0305s1Gss1025s1(.)()(.),仍可用tf函数建立多项式型s降幂传递函数,但需用多项式乘法函数conv配合,G0=tf(conv([3],[ 1]),conv(conv([1 0],[1 1]),[ 1])) ② 建立零极点型s传递函数 方法1. sys = zpk(z,p,k) 方法2. s = zpk('s'),再令sys = f(s)。 2. 传递函数的转换 ① 将任意形式的s传递函数转换为s降幂传递函数 sys = tf(sys) ② 将任意形式的s传递函数转换为s零极点传递函数 sys = zpk(sys) 3. 建立z传递函数 ① 将连续传递函数转换为离散传递函数 sysd = c2d(sysc,t,method)
② 建立多项式形式的z传递函数 方法1. sys = tf(num,den,?t) 方法2. z = tf('z',?t),再令sys = f(z)
③ 建立零极点z传递函数 方法1. sys = zpk(z,p,k,?t) 方法2. z = zpk('z',?t),再令sys = f(z)
4. 建立z-1格式的传递函数
直接根据分子和分母建立z-1格式的传递函数 sys_z = filt(num,den,?t) 当已有多项式形式的z降幂传递函数时,按以下步骤: ① 取z降幂传递函数a的分子多项式系数 [num,den] = tfdata(sys_s,'v') ② 建立z-1格式的传递函数 sys_z = filt(num,den,?t) 5. 将多项式形式的高阶z-1降幂传递函数转换为并联传递函数,按以下步骤: ① “手工”将z-1降幂传递函数a改写成多项式形式的z降幂传递函数b。 ② 取z降幂传递函数b的分子多项式系数num和分母多项式系数den。 ③ 利用residue函数取z降幂传递函数b的分项分式,[an ad ak]=residue(num,den)。