4-1连续系统模型的离散化处理方法

1-1 什么是计算机控制系统？画出一个实际计算机控制系统原理结构图，并说明一个计算机控制系统由哪些部分组成及各部分的作用。

利用计算机参与控制的系统称为计算机控制系统。

1-2 简述计算机控制系统的控制过程。

实时数据采样实时计算控制量实时控制实时管理1-3 实时、在线方式和离线方式的含义是什么？(1)实时：所谓“实时”，是指信号的输入、计算和输出都是在一定时间范围内完成的，超出了这个时间就会失去控制时机，控制也就失去了意义。

(2)“在线”方式：生产过程和计算机系统直接连接，并接受计算机直接控制的方式称为在线或联机方式。

(3)“离线”方式：若生产过程设备不直接与计算机相连接，其工作不直接受计算机的控制的方式叫做“脱机”方式或“离线”方式。

1-4 计算机控制系统的硬件由哪几部分组成？各部分的作用是什么？主机：这是微型计算机控制系统的核心，通过接口它可以向系统的各个部分发出各种命令，同时对被控对象的被控参数进行实时检测及处理。

输入输出通道：这是微机和生产对象之间进行信息交换的桥梁和纽带。

(3)外部设备：这是实现微机和外界进行信息交换的设备，简称外设，包括人机联系设备(操作台)、输入输出设备(磁盘驱动器、键盘、打印机、显示终端等)和外存贮器(磁盘)。

(4)生产过程装置a.测量变送单元：为了测量各种参数而采用的相应检测元件及变送器。

b.执行机构：要控制生产过程，必须有执行机构。

1.5 计算机控制系统的软件由哪几部分组成？各部分的作用是什么？就功能来分，软件可分为系统软件、应用软件及数据库。

系统软件：它是由计算机设计者提供的专门用来使用和管理计算机的程序。

系统软件包括：a.操作系统：即为管理程序、磁盘操作系统程序、监控程序等；b.诊断系统：指的是调节程序及故障诊断程序；c.开发系统：包括各种程序设计语言、语言处理程序(编译程序)、服务程序(装配程序和编辑程序)、模拟主系统(系统模拟、仿真、移植软件)、数据管理系统等；d.信息处理：指文字翻译、企业管理等。

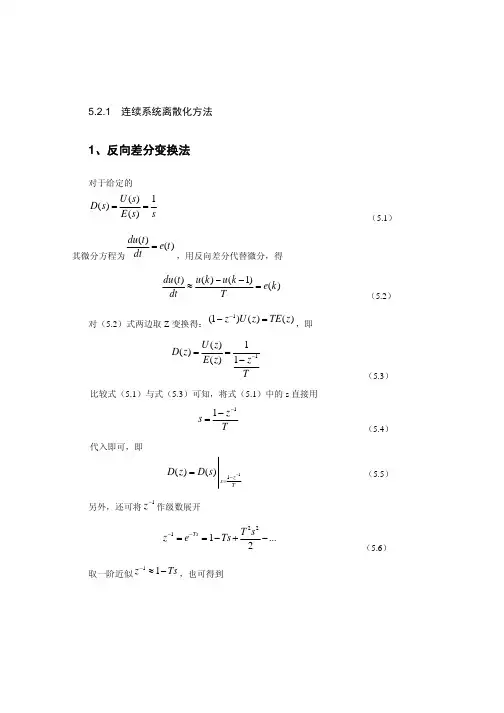
第6章连续系统的离散化方法及近似解在连续系统中，我们经常需要将其离散化为离散系统以便于分析和求解。

离散化方法能够将连续系统的微分方程转化为差分方程，从而得到近似解。

本章将介绍连续系统的离散化方法及近似解的计算。

连续系统的离散化方法有许多种，常见的有Euler方法、Runge-Kutta方法和有限差分方法等。

其中，Euler方法是最简单和最基础的离散化方法，其基本思想是将连续时间轴划分为若干个小时间间隔，并用差分逼近连续系统的导数。

具体地，对于一阶常微分方程：\[\frac{{dy}}{{dt}} = f(y, t)\]可以使用Euler方法将其离散化为：\[y_{n+1} = y_n + h \cdot f(y_n, t_n)\]其中，\(y_n\)是时间点\(t_n\)的近似解，\(h\)是时间步长。

Runge-Kutta方法是一种更精确的离散化方法，其基本思想是利用多个中间步骤来更准确地逼近连续系统的导数。

常见的是四阶Runge-Kutta 方法，其公式为：\[y_{n+1} = y_n + \frac{h}{6} \cdot (k_1 + 2k_2 + 2k_3 +k_4)\]其中\[k_1=f(y_n,t_n)\]\[k_2 = f(y_n + \frac{h}{2}k_1, t_n + \frac{h}{2})\]\[k_3 = f(y_n + \frac{h}{2}k_2, t_n + \frac{h}{2})\]\[k_4 = f(y_n + hk_3, t_n + h)\]这样可以得到更准确的近似解。

有限差分方法是一种常用的离散化方法，其基本思想是将连续的导数用差分逼近。

以二阶偏微分方程为例，该方程的一般形式为：\[\frac{{\partial^2u}}{{\partial x^2}} +\frac{{\partial^2u}}{{\partial y^2}} = f(x, y)\]可以使用中心差分公式将其离散化为：\[\frac{{u_{i+1,j} - 2u_{i,j} + u_{i-1,j}}}{{\Delta x^2}} + \frac{{u_{i,j+1} - 2u_{i,j} + u_{i,j-1}}}{{\Delta y^2}} =f_{i,j}\]其中，\(u_{i,j}\) 是近似解在网格点 \((i, j)\) 处的值，\(\Delta x\) 和 \(\Delta y\) 分别是网格在 \(x\) 和 \(y\) 方向的步长，\(f_{i,j}\) 是离散化后的右侧函数。

连续函数离散化 Prepared on 22 November 2020连续函数离散化替换法传递函数是控制系统应用最广泛的模型描述形式，连续系统为Ｓ域的传递函数G(S)，离散系统为Ｚ域的脉冲传递函数G(Z)。

替换法的基本思想：对给定的连续系统模型G(S)，设法找到Ｓ域到Ｚ域的某种映射关系，将Ｓ域的变量映射到Ｚ平面上，由此得到与连续系统G(S)相对应的离散系统的脉冲传递函数G(Z)。

然后，再由G(Z)通过Ｚ反变换得到系统的时域离散模型——差分方程，从而快速求解。

根据Ｚ变换理论，Ｓ域到Ｚ域的最基本的映射关系是：Ts e Z =或Z Ts ln 1= 其中Ｔ是采样周期若直接将这个映射关系代入G(S)得到G(Z)将会很复杂，不便于计算，实际应用中是利用Ｚ变换理论的基本映射关系进行简化处理，得到近似的离散模型。

简单替换法由幂级数展开式： +++++=!!212n x x x e nx取近似式：Ts e Z Ts +≈=1或：TZ s 1-= 用此式代入G(S)就得到G(Z)，这就是简单替换法，又称Euler 法。

例：二阶连续系统s s s U s Y s G 50400)()()(2+==，001.0=T 解：简单替换法TZ s 1-=代入G(s) 001.0=T 代入双线性替换法 取近似式：2121Ts Tse Z Ts -+==或)1()1(2+-=Z T Z s 用此式代入G(S)就得到G(Z)，这就是双线性替换法，又称Tustin 变换。

相当于数值积分法中的梯形法，有较好的性能。

例：二阶连续系统ss s U s Y s G 50400)()()(2+==，001.0=T 用双线性替换法建立差分方程。

解：双线性替换：)1()1(2+-=z T z s 代入G(s) 001.0=T 代入域离散相似法离散相似法将连续系统模型处理成与之等效的离散模型的一种方法。

设计一个离散系统模型，使其中的信息流与给定的连续系统中的信息流相似。

连续系统离散化方法连续系统离散化方法是一种常用的数值计算方法，它将连续系统转化为离散系统，从而使得计算机可以进行处理。

本文将从离散化方法的定义、应用、实现以及优缺点等方面进行介绍。

一、离散化方法的定义离散化方法是指将连续系统转化为离散系统的过程。

在计算机中，所有的数值都是离散的，而实际上很多系统是连续的，比如电路、机械系统、化学反应等等。

离散化方法就是将这些连续系统转化为可以在计算机中处理的离散系统。

离散化方法可以通过采样和量化来实现。

二、离散化方法的应用离散化方法在很多领域都有应用，比如电路设计、控制系统设计、信号处理等等。

在电路设计中，离散化方法可以将连续电路转化为数字电路，从而实现数字信号的处理。

在控制系统设计中，离散化方法可以将连续控制器转化为数字控制器，从而实现数字化自动控制。

在信号处理中，离散化方法可以将连续信号转化为数字信号，从而实现对信号的数字处理。

三、离散化方法的实现离散化方法的实现可以通过采样和量化来实现。

采样是指对连续信号进行离散化，将其转化为一系列的采样值。

量化是指对采样值进行离散化，将其转化为一系列的离散数值。

采样和量化的具体实现方式包括正弦采样、脉冲采样、最大值采样、平均值采样等等。

量化的具体实现方式包括线性量化、对数量化、非线性量化等等。

四、离散化方法的优缺点离散化方法的优点是可以将连续系统转化为离散系统，从而可以在计算机中进行处理。

离散系统具有稳定性、可控性、可观性等优点。

离散化方法的缺点是会引入误差，因为离散化过程中会丢失一些信息。

此外，离散化方法需要选取适当的采样周期和量化精度，否则会影响系统的性能。

离散化方法是一种常用的数值计算方法，它将连续系统转化为离散系统，从而使得计算机可以进行处理。

离散化方法的应用广泛，包括电路设计、控制系统设计、信号处理等等。

离散化方法的实现可以通过采样和量化来实现。

离散化方法既有优点，又有缺点，需要在具体应用中对其进行合理的选择和设计。

离散系统的分析1、连续系统的离散化功能：在离散控制系统中，会涉及到对模拟控制器的离散化，也会涉及到对系统的不可变部分的离散化问题，MATLAB对于离散化转换可采用相应的函数进行。

格式：[Ad,Bd]=c2d(A,B,ts)[Ad,Bd,Cd,Dd]=c2dm(A,B,ts,’method’)，[numz,denz]=c2dm(num,den,ts,’method’)说明：1) c2d命令使用离散化的零阶保持器方法，它只有状态空间形式；2) c2dm既有状态空间形式，又有传递函数形式；3) 参数ts是采样周期T；4) method指定转换方式，其中“zoh”表示采用零阶保持器；“foh”表示采用三角形近似；“tustin”表示采用双线性变换；“prewarp”表示采用指定转折频率的双线性变换，其转折频率Wc 由c2d （sysc ，T ，‘prewarp ’，Wc ）确定，系统默认为零阶保持器法。

5) A 、B 、num 、den 为连续域的数学模型，返回的是离散化以后的数学模型。

例已知系统的被控对象传递函数为：)5)(2(10)(++=s s s G采样周期T ＝0.1秒,试将其进行离散化处理。

解：将连续系统的传递函数G （s ）用零阶保持器法转换成离散系统的脉冲传递函数G(z)，并运行下面的程序。

num=10; den=[1,7,10]; ts=0.1; [n_zoh,d_zoh]=c2dm(num,den,ts) ; tf(n_zoh,d_zoh,ts)运行结果：Transfer function:0.0398 z + 0.03152 -------------------------- z^2 - 1.425 z + 0.49662、离散系统单位阶跃响应功能：对离散系统进行阶单位跃响应分析，给出一组阶跃响应的数据，并绘制其响应曲线。

格式： [y,x]=dstep(A,B,C,D,ui,n)[y,x]=dstep(num,den,n)说明：1) 若无左边的输出参数，则自动地绘制出响应曲线； 2) 参数ui 和n 为可选项，对于多输入系统是用于指定哪个输入通道，n 是指采样数； 3) 和连续系统中step 命令有关的所有命令都可以在离散系统中应用； 4) 其它时间响应命令是dimpulse 、dinitial 、dlsim 。

连续系统离散化方法一、概述连续系统离散化方法是一种将连续系统转化为离散系统的方法，常用于控制系统的设计和分析。

该方法可以将一个无限维度的连续系统转化为有限维度的离散系统，使得控制器设计和分析变得更加简单和可行。

二、连续系统模型在开始进行连续系统离散化的过程中，需要先建立一个连续系统模型。

通常情况下，这个模型可以由微分方程或者差分方程来表示。

三、离散化方法1. 时域离散化方法时域离散化方法是最基本的离散化方法之一。

它通过将时间轴上的信号进行采样，从而将一个连续时间信号转换为一个离散时间信号。

这个过程中需要确定采样周期以及采样点数目等参数。

2. 频域离散化方法频域离散化方法是一种利用傅里叶变换将一个连续时间信号转换为一个频域信号，然后再对该频域信号进行采样得到一个离散时间信号的方法。

这个过程中需要确定采样频率以及采样点数目等参数。

3. 模拟器法模拟器法是一种将连续系统转化为离散系统的方法。

这个方法的核心思想是利用一个数字模拟器来模拟连续系统的行为，从而得到一个离散时间信号。

4. 差分方程法差分方程法是一种将连续系统转化为离散系统的方法。

这个方法的核心思想是利用微分方程在离散时间点上进行近似，从而得到一个差分方程。

四、误差分析在进行离散化过程中，会产生一定的误差。

因此，需要对误差进行分析和评估，以确保离散化后的结果与原始连续系统相近。

五、应用实例1. 机械控制系统机械控制系统中通常需要对连续时间信号进行采样和处理。

通过使用离散化方法，可以将连续信号转换为数字信号，并且可以在数字域上进行控制器设计和分析。

2. 电力电子控制系统电力电子控制系统中通常需要对高频信号进行处理。

通过使用频域离散化方法，可以将高频信号转换为数字信号，并且可以在数字域上进行控制器设计和分析。

六、总结连续系统离散化方法是一种将连续系统转化为离散系统的方法。

通过使用不同的离散化方法，可以将连续时间信号转换为数字信号，并且可以在数字域上进行控制器设计和分析。