传递函数离散化之双线性转换
- 格式:pdf
- 大小:1.66 MB
- 文档页数:6

python 将传递函数转换为离散状态方程摘要:1.引言2.离散状态方程的定义3.使用Python 将传递函数转换为离散状态方程4.总结正文:1.引言在控制理论和工程领域中,离散状态方程是描述系统动态特性的重要工具。
传递函数是连续系统的数学模型,然而在实际应用中,很多系统是离散的。
因此,将传递函数转换为离散状态方程对于分析和设计离散控制系统至关重要。
Python 作为一种流行的编程语言,可以方便地实现这一转换过程。
2.离散状态方程的定义离散状态方程描述了系统状态随时间变化的规律。
它通常包括一组状态变量和一组输入变量,以及状态转移方程和观测方程。
状态转移方程描述了系统状态如何随时间变化,观测方程描述了如何从系统输出中观测到状态信息。
离散状态方程可以表示为:x[k+1] = A * x[k] + B * u[k]y[k] = C * x[k] + D * u[k]其中x[k] 是状态向量,u[k] 是输入向量,y[k] 是输出向量,A、B、C、D 是系统矩阵。
3.使用Python 将传递函数转换为离散状态方程传递函数是连续系统的数学模型,通常表示为:G(s) = A / (s^n * (s^2 + 2 * s * z + z^2))其中s 是复变量,n 是系统的阶数,z 是系统的零点。
为了将传递函数转换为离散状态方程,我们需要计算系统的零点和极点。
Python 可以通过调用第三方库,如scipy.roots,来实现这一计算过程。
以下是一个Python 代码示例,演示如何将传递函数转换为离散状态方程:```pythonimport numpy as npfrom scipy.special import gammafrom scipy.roots import realdef convert_to_discrete_state_equation(G, dt):"""Convert a continuous-time transfer function G(s) to a discrete-time state equation.:param G: Transfer function:param dt: Time step:return: Discrete state equation"""# Calculate the poles and zeros of the transfer functionpoles, zeros = real(G)# Calculate the A, B, C, and D matricesn = len(poles)A = np.diag(poles)B = np.zeros((n, n))C = np.zeros((n, n))D = np.zeros((n, n))for i in range(n):B[i, i] = -poles[i]C[i, i] = 1D[i, i] = zeros[i]# Convert the state equation to a discrete form A_discrete = np.diag(np.exp(-poles * dt))B_discrete = np.zeros((n, n))C_discrete = np.zeros((n, n))D_discrete = np.zeros((n, n))for i in range(n):B_discrete[i, i] = -np.exp(-poles[i] * dt)C_discrete[i, i] = np.exp(-poles[i] * dt)D_discrete[i, i] = zeros[i]return A_discrete, B_discrete, C_discrete, D_discrete ```该函数接受传递函数G(s) 和时间步长dt 作为输入参数,并返回离散状态方程的系数矩阵。

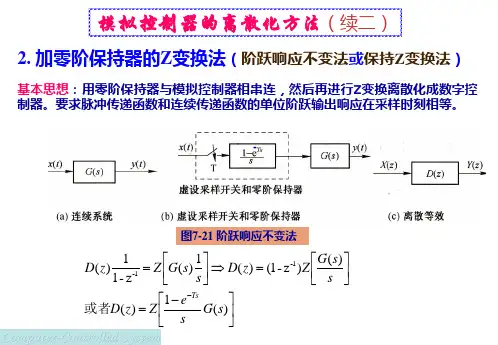
阶跃响应不变法
阶跃响应不变法是数字信号处理中一种常用的数字滤波设计方法。
它基于连续时间系统与离散时间系统之间的映射关系,将连续时间系
统的单位阶跃响应映射为离散时间系统的单位脉冲响应。
具体来说,阶跃响应不变法的步骤如下:
首先,将连续时间系统的传递函数H(s)通过双线性变换映射到离散时间系统的传递函数H(z)。
这里,双线性变换的公式为:
z = (1 + Ts/2)/(1 - Ts/2) * e^(sT/2)
其中,T为采样时间,s为连续时间复频域变量,z为离散时间复频域变量。
接着,根据连续时间系统的传递函数H(s)计算出其单位阶跃响应
h(t)。
此时,可以利用拉普拉斯反变换,或者直接通过求导等方法获
得h(t)的表达式。
然后,将h(t)离散化,得到离散时间系统的单位脉冲响应h[n]。
这里,将h(t)按照采样时间等间隔离散化即可。
最后,得到离散时间系统的传递函数H(z)的表达式,即可进一步计算出离散时间系统的频率响应、幅频特性、群延迟等性质。
需要注意的是,阶跃响应不变法存在一定的失真,导致映射后离
散时间系统的频率响应与连续时间系统的频率响应有所不同。
特别地,对于高频系统,采用阶跃响应不变法设计的数字滤波器易产生不稳定
性和失真。
因此,在实际应用中需要慎重选择滤波器设计方法,结合
具体的应用要求进行选择。

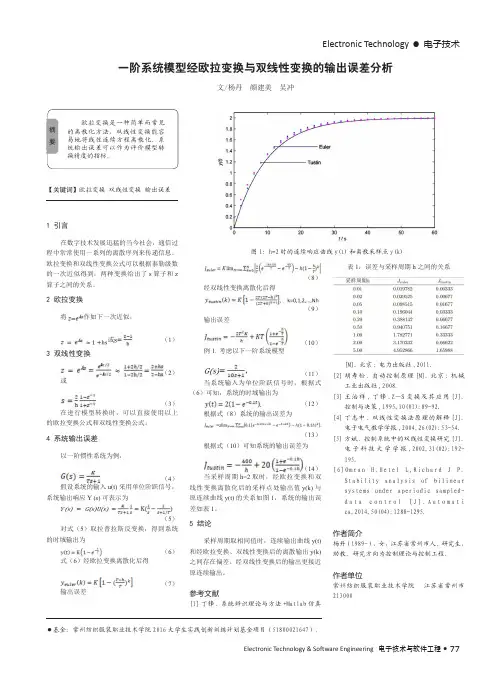
Electronic Technology •电子技术Electronic Technology & Software Engineering 电子技术与软件工程• 77【关键词】欧拉变换 双线性变换 输出误差1 引言在数字技术发展迅猛的当今社会,通信过程中常常使用一系列的离散序列来传递信息。
欧拉变换和双线性变换公式可以根据泰勒级数的一次近似得到,两种变换给出了s 算子和z 算子之间的关系。
2 欧拉变换将作如下一次近似,或(1) 3 双线性变换(2)或(3)在进行模型转换时,可以直接使用以上的欧拉变换公式和双线性变换公式。
4 系统输出误差以一阶惯性系统为例,(4)假设系统的输入u(t)采用单位阶跃信号,系统输出响应Y (s)可表示为(5)对式(5)取拉普拉斯反变换,得到系统的时域输出为(6)式(6)经欧拉变换离散化后得(7)输出误差一阶系统模型经欧拉变换与双线性变换的输出误差分析文/杨丹 颜建美 吴冲(8)经双线性变换离散化后得(9)输出误差(10)例1. 考虑以下一阶系统模型(11)当系统输入为单位阶跃信号时,根据式(6)可知,系统的时域输出为(12)根据式(8)系统的输出误差为(13)根据式(10)可知系统的输出误差为 (14)当采样周期h=2取时,经欧拉变换和双线性变换离散化后的采样点处输出值y(k)与原连续曲线y(t)的关系如图1,系统的输出误差如表1。
5 结论采样周期取相同值时,连续输出曲线y(t)和经欧拉变换、双线性变换后的离散输出y(k)之间存在偏差。
经双线性变换后的输出更接近原连续输出。
参考文献[1]丁锋.系统辨识理论与方法+Matlab 仿真[M].北京:电力出版社,2011.[2]胡寿松.自动控制原理[M].北京:机械工业出版社,2008.[3]王治祥,丁锋.Z ―S 变换及其应用[J].控制与决策,1995,10(01):89-92.[4]丁志中.双线性变换法原理的解释[J].电子电气教学学报,2004,26(02):53-54.[5]方斌.控制系统中的双线性变换研究[J].电子科技大学学报,2002,31(02):192-195.[6]O m r a n H ,H e t e l L ,R i c h a r d J P.Stability analysis of bilinear systems under aperiodic sampled-d a t a c o n t r o l [J ].A u t o m a t i ca,2014,50(04):1288-1295.作者简介杨丹(1989-),女,江苏省常州市人。




1电子科技大学网络教育考卷(A 卷)(20 年至20 学年度第 学期)考试时间 年 月 日(120分钟) 课程 机电一体化系统设计 教师签名 朱成华一、名词解释(每题2分,共10分) 1. 传递函数;答:于线性定常系统,在零初始条件下,系统输出量的拉氏变换与引起该 输出的输入量的拉氏变换之比,称为系统的传递函数2. 开发性设计;答:开发性设计是指在没有参照的情况下仅根据抽象的设计原理和要求设计出在质量和性能方面满足目的要求的产品。
3. PLC ;答:PLC 是指可编程逻辑控制器。
4.SSR ;答:SSR 是指固态继电器是一种带光电隔离的器的无触点开关。
5. D/A :答:D/A 是把数字量变成模拟量的装置。
二、判断正误(每题1分,共10分)1. 匹配Z 变换法适用于具有因式分解形式的传递函数。
( √ )2.双线性变换法就是突斯汀法,是控制系统中常用的一种离散化方法。
( × )3. 步进电机一般采用开环控制系统。
( × )4.滚珠丝杆具有自锁能力。
( × )5. 改变脉冲频率可以改变步进电机的转速。
( √ )6.改变直流电机电枢电压可以改变其转速。
( √ )7. 闭环控制系统是负反馈控制系统。
( √ )8. 光电隔离电路主要由光电耦合器的光电转换器组成,入端为光敏三极管,出端为发光二极管。
( × ) 9. 步进电动机的进给系统采用齿轮传动,不仅是为了求得所需的脉冲当量,还有满足结构要求和增大转矩的作用。
( × )10. 大惯量直流电动机的转子惯量大,小惯量直流电动机的转子惯量小。
( √ ) 三、填空(每题2分,共10分)1. 机电一体化对机械系统的基本要求是( 高精度、低惯性、高稳定性 )。
2. 传感器一般是由(敏感元件、传感元件和转换电路)三部分组成。
3. I/O 接口的编址方式,通常有两种编址方式,一种是(与存储器统一编址)另一种是(独立编址)。

第7章双线性变换下结构特性的映射7.1 导论在这一章中,我们要全面地给出一般的线性多变量系统在双线性和逆双线性变换下结构特性的映射。
我们将深入地探讨在双线性(逆双线性)变换下,一般的线性时不变多变量连续时间(离散时间)系统的有限和无限零点结构,以及可逆性结构是如何映射到离散时间(连续时间)系统的相应结构。
和这一章相似的内容已经包含在本书第一作者以前的专著[22]中,那里应用了双线性变换和它们的结构映射特性的结果来求一般的Riccati方程的解和离散时间控制问题。
但是在这一章中,我们要做的实际上是建立线性系统理论在连续时间域和离散时间域之间的桥梁。
在第8章就会看到这一章的结果对解决另一个线性系统问题也是有用的,即离散时间系统的分解。
双线性和逆双线性变换在数字控制和信号处理中得到广泛应用。
在[22]中已经证明双线性变换在离散时间控制的极优值计算,以及在寻找离散时间Riccati方程解中起着重要作用。
这一章的结果最早出现在Chen和Weller [30]中。
实际上,对连续时间到离散时间模型转换的需求出现在许多工程领域,包括采样数字控制系统设计,数字信号处理。
因此有许多离散化过程,包括输入的零阶和一阶保持器输入近似,脉冲不变变换,双线性变换(见[7]和[55])。
尽管双线性变换得到广泛应用,但是文献中关于连续时间系统的关键结构特性如何过渡到离散时间系统关键特性的全面研究却比较缺乏,如有限和无限零点结构,可逆特性。
我们知道无限和有限零点结构在控制系统设计中发挥重要作用,正确地理解双线性变换下的零点结构有助于设计采样数字控制系统,并且是对现有的零阶保持采样下的有限和无限零点结构映射的一种补充(参见[6]和[60])。
在这一章中,我们全面地研究在众所周知的双线性(逆双线性)变换下,一般的连续时间(离散时间)线性时不变系统的结构是如何映射到离散时间(连续时间)系统的,即有限和无限零点结构,可逆结构,以及几何子空间。

z变换形式离散化的几种方式
在连续系统离散化中,常用的有后向差分离散化方式和双向差分离散化方式。
下面以后向差分离散化为例进行说明,其曲线的斜率表示为:$\frac{T_s}{n}$,这种离散化表示成z变换形式就是:$Z[x(n)]=\frac{X(z)}{z^{nT_s}}$,其中,$T_s$为系统采样时间。
通过对连续系统表达式进行拉普拉斯变换,可以得到理想状态下的PID控制器表达式。
为了在控制器或者计算机系统中实现PID计算,必须将该表达式离散化为离散系统。
将后向差分Z变换表达式带入连续系统拉普拉斯变换表达式,得到增量式PID的差分表达式,其中$K_p$为比例系数、$T_i$为积分时间、$T_d$为微分时间、$T_s$为系统采样时间。
总之,z变换形式离散化的方式有很多种,在实际应用中需要根据具体情况选择合适的方法。
控制系统各种传递函数离散化后的递推公式推导及结果在控制系统中,传递函数描述了输入信号和输出信号之间的关系。
传递函数通常采用连续时间表示,但在实际应用中,为了能够在数字控制器中进行计算和实现,需要将传递函数离散化。
离散化是将连续时间信号转化为离散时间信号的过程,离散化后的控制系统可以方便地在数字控制器中进行实时计算和控制。
传递函数的离散化可以通过多种方法实现,其中最常见的是Z变换法。
在Z变换法中,将传递函数中的连续时间变量s替换为离散时间变量z,即进行变量替换s->z。
通过这种变换,将连续时间域的传递函数转化为离散时间域的递推公式。
对于一个一阶系统,其传递函数为G(s)=K/(Ts+1),其中K为增益,T为系统的时间常数。
将s替换为z,得到G(z)=K/(T(z-1)+z)。
为了将这个传递函数离散化为递推公式,可以使用Z变换的定义:X(z)=Σ[x(n)*z^(-n)],其中x(n)为离散时间输入信号。
将G(z)的分子和分母分别进行Z变换得到X(z)=K/(T(z-1)+z),Y(z)=X(z)*G(z)。
将X(z)代入Y(z)的表达式中,得到Y(z)=K/(T(z-1)+z)*X(z)。
对Y(z)进行逆Z变换,得到y(n+1)=K/T*[x(n)-x(n-1)]+y(n)。
以上就是一阶系统离散化后的递推公式。
通过递推公式可以实现对一阶系统的离散时间域模拟和控制。
对于高阶系统,可以使用相同的方法进行离散化。
将传递函数中的s替换为z,得到离散时间域的传递函数。
然后使用Z变换的定义计算输入信号和输出信号的Z变换,最后将Z变换后的表达式进行逆Z变换,得到系统的递推公式。
通过离散化后的递推公式,可以在数字控制器中进行实时计算和实现控制操作。
递推公式可以实现反馈控制、滤波器设计等。
总结起来,控制系统的传递函数离散化就是将连续时间域的传递函数转化为离散时间域的递推公式的过程。
通过Z变换法将传递函数中的s替换为z,然后通过逆Z变换得到递推公式。