(04)第4章 数据的概括性度量

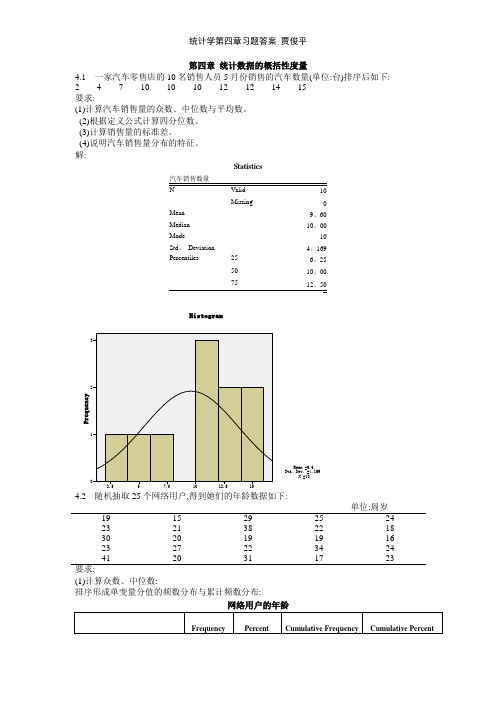
第四章统计数据的概括性度量4．1 一家汽车零售店的10名销售人员5月份销售的汽车数量(单位：台)排序后如下：2 4 7 10 10 10 12 12 14 15要求：（1）计算汽车销售量的众数、中位数和平均数。

(2)根据定义公式计算四分位数。

(3)计算销售量的标准差。

(4)说明汽车销售量分布的特征。

解：Statistics10Missing 0Mean 9.60Median 10.00Mode 10Std. Deviation 4.169Percentiles 25 6.2550 10.0075单位：周岁19 15 29 25 2423 21 38 22 1830 20 19 19 1623 27 22 34 2441 20 31 17 23要求；(1)计算众数、中位数：排序形成单变量分值的频数分布和累计频数分布：网络用户的年龄(2)根据定义公式计算四分位数。

Q1位置=25/4=6.25，因此Q1=19，Q3位置=3×25/4=18.75，因此Q3=27，或者，由于25和27都只有一个，因此Q3也可等于25+0.75×2=26.5。

(3)计算平均数和标准差；Mean=24.00；Std. Deviation=6.652(4)计算偏态系数和峰态系数：Skewness=1.080；Kurtosis=0.773(5)对网民年龄的分布特征进行综合分析：分布，均值=24、标准差=6.652、呈右偏分布。

如需看清楚分布形态，需要进行分组。

1、确定组数：()lg 25lg() 1.398111 5.64lg(2)lg 20.30103n K =+=+=+=，取k=6 2、确定组距：组距＝( 最大值 - 最小值)÷ 组数=（41-15）÷6=4.3，取53、分组频数表网络用户的年龄 (Binned)分组后的直方图：客都进入一个等待队列：另—种是顾客在三千业务窗口处列队3排等待。

第4章（数据的概括性度量）学习指导数据分布的特征可以从三个方面进行描述：一是分布的集中趋势，反映各数据向其中心值靠拢或聚集的程度；二是分布的离散程度，反映各数据远离其中心值的趋势；三是分布的形状，反映数据分布偏斜程度和峰度。

掌握计算、特点及其应用场合。

主要内容学习要点2．1 集中趋势的度量众数▶概念：众数。

▶众数的特点。

中位数和分位数▶概念：中位数，四分位数。

▶中位数和四分位数的特点。

▶中位数和四分位数的计算。

平均数▶概念：平均数，简单平均数，加权平均数，调和平均数，几何平均数。

▶简单平均数和加权平均数的计算。

▶用Excel中的统计函数计算平均数。

▶几何平均数的计算和应用场合。

众数、中位数和平均数的比较▶众数、中位数和平均数在分布上的关系。

▶众数、中位数和平均数的特点及应用场合。

异众比率▶概念：异众比率异众比率的计算和应用场合。

2．2离散程度的度量四分位差（内距）概念：四分位差。

四分位差的计算。

用Excel中的统计函数计算四分位差。

方差和标准差概念：极差，平均差，方差，标准差。

样本方差和标准差的计算。

用Excel计算标准差。

离散系数概念：离散系数。

离散系数的计算。

离散系数的用途。

2．3偏态与峰态的度量偏态及其测度概念：偏态，偏态系数。

用Excel计算偏态系数。

偏态系数数值的意义。

峰态及其测度概念：峰态，峰态系数。

用Excel计算峰态系数。

峰态系数数值的意义。

Excel统计函数的应用。

一）判断题1，各变量值与其平均数的离差之和为最小值。

( )2．当各组的变量值所出现的频率相等时，加权算术平均数中的权数就失去作用，因而，加权算术平均数也就等于简单算术平均数( )3．比较两总体的平均数的代表性，离散系数较小的总体，平均数代表性亦小。

( )4，平均数与次数和的乘积等于各变量值与次数乘积的和。

( )5．若两总体的平均数不同，而标准差相同，则离散系数也相同。

( )6．并非任意一个变量数列都可以计算其算术平均数、中位数和众数。

统计学各章计算题公式及解题方法第四章数据的概括性度量1.组距式数值型数据众数的计算：确定众数组后代入公式计算:下限公式：；上限公式：,其中，L为众数所在组下限，U为众数所在组上限，为众数所在组次数与前一组次数之差，为众数所在组次数与后一组次数之差，d为众数所在组组距2.中位数位置的确定：未分组数据为；组距分组数据为3.未分组数据中位数计算公式：4.单变量数列的中位数:先计算各组的累积次数（或累积频率）—根据位置公式确定中位数所在的组-对照累积次数（或累积频率）确定中位数（该公式假定中位数组的频数在该组内均匀分布)5.组距式数列的中位数计算公式:下限公式：；上限公式：，其中，为中位数所在组的频数，为中位数所在组前一组的累积频数,为中位数所在组后一组的累积频数6.四分位数位置的确定：未分组数据：；组距分组数据：7.简单均值：8.加权均值：，其中，为各组组中值统计学各章计算题公式及解题方法9.几何均值(用于计算平均发展速度）：10.四分位差（用于衡量中位数的代表性)：11.异众比率（用于衡量众数的代表性）:12.极差：未分组数据:；组距分组数据：13.平均差（离散程度)：未分组数据：；组距分组数据:14.总体方差：未分组数据：；分组数据:15.总体标准差：未分组数据：;分组数据:16.样本方差:未分组数据:；分组数据：17.样本标准差：未分组数据：;分组数据：18.标准分数:19.离散系数：第七章参数估计1.的估计值:置信水平α90％0.1 0。

05 1.65495% 0。

05 0.025 1.9699% 0.01 0。

005 2。

58统计学各章计算题公式及解题方法2.不同情况下总体均值的区间估计：总体分布样本量σ已知σ未知大样本（n≥30）正态分布小样本（n<30）非正态分布大样本(n≥30）其中，查p448 ，查找时需查n—1的数值3.大样本总体比例的区间估计：4.总体方差在置信水平下的置信区间为：5.估计总体均值的样本量：，其中，E为估计误差6.重复抽样或无限总体抽样条件下的样本量：，其中π为总体比例第八章假设检验1.总体均值的检验（已知或未知的大样本）[总体服从正态分布，不服从正态分布的用正态分布近似］假设双侧检验左侧检验右侧检验假设形式已知统计量未知拒绝域值决策，拒绝2.总体均值检验（未知，小样本，总体正态分布）假设双侧检验左侧检验右侧检验统计学各章计算题公式及解题方法假设形式已知统计量未知拒绝域值决策，拒绝注：已知的拒绝域同大样本3.一个总体比例的检验（两类结果，总体服从二项分布，可用正态分布近似）（其中为假设的总体比例）假设双侧检验左侧检验右侧检验假设形式统计量拒绝域值决策,拒绝4.总体方差的检验(检验）假设双侧检验左侧检验右侧检验假设形式统计量拒绝域值决策，拒绝5.统计量的参考数值0.1 0。

第四章数据的概括性度量一、填空题1.一组数据向某一中心值靠拢的倾向反映了数据的———————。

2. ————是一组数据中出现次数最多的变量值。

3.一组数据排序后处于中间位置上的变量值称——————。

4.不受极端值影响的集中趋势度量指标有————、————和————。

5.一组数据的最大值与最小值之差称————。

6. —————是一组数据的标准差与其相应的平均数之比。

7.数据分布的不对称性是——————。

8.数据分布的平峰或尖峰程度称——————9.计算比率的平均数一般用—————，它实际上是各变量值对数的—————。

二、单项选择题1.对于对称分布的数据，众数、中位数和平均数的关系是：A.众数＞中位数＞平均数B.众数＝中位数＝平均数C.平均数＞中位数＞众数D.中位数＞众数＞平均数2.可以计算平均数的数据类型有：A.分类型数据B.顺序型数据C.数据型数据D.所有数据类型3.顺序数据的集中趋势测度指标有：A.众数B.中位数C.四分位差D.标准分数4.数据型数据的离散程度测度方法中，受极端变量值影响最大的是：A.极差B.方差C.均方差D.平均差5.当偏态系数为正数时，说明数据的分布是：A.正态分布B.左偏分布C.右偏分布D.双峰分布三、多项选择题1.数据的分布特征可以从哪几个方面测度和描述：A.集中趋势B.分布的偏态C.分布的峰态D.离散程度E.长期趋势2.受极端变量值影响的集中趋势度量指标是A.众数B.中位数C.算术平均数D.调和平均数E.几何平均数3.加权算术平均数大小的影响因素有：A.变量值B.样本容量C.权数D.分组的组数E.数据的类型4.数据型数据离散程度的测度指标有：A.异众比率B.极差C.标准差D.四分位数E.离散系数5.离散系数的主要作用是：A.说明数据的集中趋势B.比较不同计量单位数据的离散程度C.说明数据的偏态程度D.比较不同变量值水平数据的离散程度E.说明数据的峰态程度四、简答题1.什么是数据的集中趋势？反映数据集中趋势的指标有哪些？2.什么是数据的离散程度？常用的测度离散程度的指标有哪些？3.怎样理解平均数在统计学中的地位4.简述众数、中位数和均值的特点和应用场合。

第四章 统计数据的概括性度量4.1 一家汽车零售店的10名销售人员5月份销售的汽车数量(单位:台)排序后如下: 2 4 7 10 10 10 12 12 14 15 要求:(1)计算汽车销售量的众数、中位数与平均数。

(2)根据定义公式计算四分位数。

(3)计算销售量的标准差。

(4)说明汽车销售量分布的特征。

解:Statistics汽车销售数量 10 Missing0 Mean 9、60 Median 10、00Mode10 Std 、 Deviation 4、169 Percentiles25 6、25 50 10、00 75单位:周岁19 15 29 25 24 23 21 38 22 18 30 20 19 19 16 23 27 22 34 24 41 20 3117 23要求;(1)计算众数、中位数:排序形成单变量分值的频数分布与累计频数分布:网络用户的年龄(2)根据定义公式计算四分位数。

Q1位置=25/4=6、25,因此Q1=19,Q3位置=3×25/4=18、75,因此Q3=27,或者,由于25与27都只有一个,因此Q3也可等于25+0、75×2=26、5。

(3)计算平均数与标准差;Mean=24、00;Std、Deviation=6、652(4)计算偏态系数与峰态系数:Skewness=1、080;Kurtosis=0、773(5)对网民年龄的分布特征进行综合分析:分布,均值=24、标准差=6、652、呈右偏分布。

如需瞧清楚分布形态,需要进行分组。

1、确定组数:()lg 25lg() 1.398111 5.64lg(2)lg 20.30103n K =+=+=+=,取k=6 2、确定组距:组距＝( 最大值 - 最小值)÷ 组数=(41-15)÷6=4、3,取53、分组频数表网络用户的年龄 (Binned)分组后的直方图::一种就是所有颐客都进入一个等待队列:另—种就是顾客在三千业务窗口处列队3排等待。

第四章数据的概括性度量第四章 数据的概括性度量一.填空题 1. 是一组数据中出现次数最多的变量值。

2.一组数据排序后处于中间位置上的变量值称 。

3.不受极端值影响的集中趋势度量指标有 . 和 。

4.一组数据的最大值与最小值之差称 。

5. 是一组数据的标准差与其相应的平均数之比。

6.Excel 中计算中位数时选用的函数为 。

7. 某工厂13名工人某日生产零件数分别为（单位：件）10.11.13.11.14.11.12.11.15.16.12.11.13 ，则中位数为 ；众数为 。

8.某百货公司连续几天的销售额如下：257.276.297.252.238.310.240.236.265，则其下四分位数是 。

9.若一组数据的e oX M M 〈〈，则其属于_______________分布（左偏.右偏）。

10.如果一组数据服从标准正态分布，则峰态系数为___________。

11.假定一个总体由5个数据组成：3.7.8.9.13，该总体的方差为。

13.某班共有25名学生，期末统计学课程的考试分数分别为：68.73.66.76.86.74.61.89.65.90.69.67.76.62.81.63.68.81.70.73.60.87.75.64.56，该班考试分数的下四分位数和上四分位数分别是和。

14.在某行业中随机抽取10家企业，第一季度的利润额（单位：万元）分别为72.63.1.54.7.54.3.29.26.9.25.23.9.23.20，该组数据的极差为。

二.单项选择题1.对于对称分布的数据，众数.中位数和平均数的关系是：（）。

A.众数＞中位数＞平均数B.众数＝中位数＝平均数C.平均数＞中位数＞众数D.中位数＞众数＞平均数2.可以计算平均数的数据类型有：（）。

A.分类型数据B.顺序型数据C.数据型数据D.所有数据类型3.数值型数据的离散程度测度方法中，受极端变量值影响最大的是（）。

A.极差B.方差C.均方差D.平均差4.当偏态系数为正数时，说明数据的分布是（）。

第4章数据的概括性度量4.1考点归纳【知识框架】【考点提示】（1）集中趋势、离散趋势的度量指标，包括每个指标的含义、计算公式、特点、意义、适用范围（选择题、简答题、计算题考点）；（2）众数、中位数和平均数三个指标的特点和应用场合，偏态分布下三个指标的关系（选择题、简答题、计算题考点）；（3）分布形状的测度指标：偏态系数和峰态系数的数值含义（选择题、简答题考点）。

（4）标准分数的计算公式及应用（选择题、简答题、计算题考点）；（5）经验法则、切比雪夫不等式的具体应用（选择题考点）。

【核心考点】考点一：集中趋势的度量表4-1集中趋势度量指标【注意】不同偏态程度的分布中集中趋势度量指标的关系：①对称分布中，众数、中位数和平均数相等；②左偏分布中，数据存在极小值，拉动平均数向极小值一方靠，而众数和中位数不受极值的影响，有＿x＜M e＜M o；③右偏分布中，数据存在极大值，必然拉动平均数向极大值一方靠，因此M o＜M e＜＿x。

【知识拓展】不同的教材分位数的计算公式不同，除了表中的计算公式，一种比较精确的计算公式：下四分位数Q L的位置＝（n＋1）/4，上四分位数Q U的位置＝（3n＋1）/4。

【真题精选】假定标志值所对应的权数都缩小1/10，则算术平均数（）。

[浙江财经大学2019研]A．不变B．无法判断C．缩小百分之一D．扩大十倍【答案】A【解析】假设标志值为x，其对应的权数为f，则算术平均数为＿x＝∑xf/∑f；若各权数都缩小1/10，则新的算术平均数为110110xf xf x x f f '===∑∑∑∑考点二：离散程度的度量数据的离散程度反映了各变量值远离其中心值的程度，离散程度越小，代表性就越好。

表4-2离散程度的度量指标【注意】①表中方差和标准差的计算公式均为样本数据的方差和标准差。

若为总体数据，则分母应为n。

②标准差系数，也称变异系数或离散系数。

③表中平均差、样本方差、样本标准差仅给出了未分组数据的计算公式，分组数据的计算公式实质是等于未分组数据的计算公式，会运用即可。

第4章数据的概括性度量一、单项选择题1．一组数据的峰度系数为3.5，则该数据的统计分布应具有的特征是（）。

[中央财经大学2018研]A．扁平分布B．尖峰分布C．左偏分布D．右偏分布【答案】B【解析】峰度系数用来度量数据在中心的聚集程度。

在正态分布情况下，峰度系数值是3。

大于3的峰度系数说明观察量更集中，有比正态分布更短的尾部；小于3的峰度系数说明观测量不那么集中，有比正态分布更长的尾部，类似于矩形的均匀分布。

2．某企业男性职工占80%，月平均工资为450元，女性职工占20%，月平均工资为400元，该企业全部职工的平均工资为（）。

[中央财经大学2015研] A．425元B．430元C．435元D．440元【答案】D【解析】企业全部职工的平均工资＝男性职工比例×男性月平均工资＋女性职工比例×女性月平均工资＝80%×450＋20%×400＝440（元）。

3．15位同学的某门课程考试成绩中，70分出现3次，80分出现4次，85分出现6次，90分出现2次，则他们成绩的众数为（）。

[华中农业大学2015研] A．80B．85C．81.3D．90【答案】B【解析】众数是一组数据中出现次数最多的变量值。

题中，85分出现次数最多，故成绩的众数为85分。

4．一组样本的变异系数（CV）等于10，样本均值为5，则样本方差为（）。

[厦门大学2014研]A．2B．4C．0.5D．2500【答案】D【解析】变异系数是一组数据的标准差与其相应的平均数之比，因而样本标准差＝样本均值×变异系数＝5×10＝50，样本方差＝50×50＝2500。

5．现抽取了10个同学，每个同学的月生活费数据排序后为：660，750，780，850，960，1080，1250，1500，1630，2000。

则中位数的位置为（）。

[重庆大学2013研]A．5.5B．5C．4D．6【答案】A【解析】中位数是将样本排序后处于中间位置的数据，总共有10个样本，因此中位数的位次＝（1＋10）/2＝5.5。