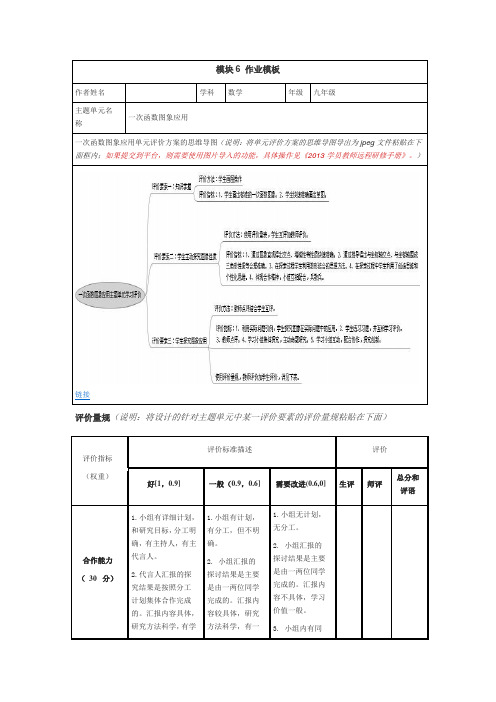
初中数学《一次函数》单元教学设计以及思维导图
- 格式:doc
- 大小:191.00 KB
- 文档页数:10

一元一次不等式和一元一次不等式组适用年八年级级所需时课内共用5课时,课外共用3课时间主题单元学习概述本章内容是在学生学习了一元一次方程、二元一次方程组和一次函数的基础上,进一步建立不等模型探究数量关系的重要内容,为学生建立不等模型解决一些实际问题“数学化”过程,为分析量与量之间的关系积累了一定的经验。
本章内容主要有三个方面:(1)通过具体实例建立不等式,探索不等式的基本性质,了解一般不等式的解、解集以及解不等式的概念。
(2)具体研究一元一次不等式和一元一次不等式组的解法,(3) 通过具体实例渗透一元一次不等式和一次函数的内在联系,一元一次不等式(组)在实际问题中的应用与探索。
本单元学习的重点:不等式的基本性质、一元一次不等式(组)的解法。
难点:一元一次不等式和一次函数的内在联系。
一元一次不等式(组)的实际应用在本主题单元中,我把3部分内容设计成2个专题来组织学习活动。
专题一:不等式的基本性质、一元一次不等式(组)的相关知识及解法。
专题二:一元一次不等式的应用与一次函数之间的关系,一元一次不等式(组)在实际问题中的应用与探索。
让学生通过观察、实验、归纳、类比、抽象概括和数学表示,自然过渡到“模型化”,通过一元一次不等式与一次函数的图象之间的结合,培养学生的数形结合意识. 通过一元一次不等式(组)在实际问题中的应用与探索,培养学生分析问题和解决问题的能力主题单元规划思维导图主题单元学习目标(说明:依据新课程标准要求描述学生在本主题单元学习中所要达到的主要目标)知识与技能:1.通过观察、对比和归纳,探索不等式的性质,能利用它们探究一元一次不等式的解法。
2.了解一元一次不等式(组)及其相关概念。
3.掌握解一元一次不等式(组)的一般步骤,并能在数轴上表示出解集,体会揭发中蕴含的化归思想。
4。
经历把实际问题抽象为不等式的过程,能够“列出不等式或不等式组表示的问题中的不等关系”,体会不等式(组)是刻画现实世界中不等关系的一种有效的数学模型。


七年级数学下册思维导图(超全)第一章:实数1. 实数的概念2. 实数的分类有理数整数正整数、负整数、零分数正分数、负分数无理数3. 实数的运算加法减法乘法除法乘方开方第二章:代数式1. 代数式的概念2. 代数式的分类单项式多项式3. 代数式的运算减法乘法除法乘方第三章:方程与不等式1. 方程的概念2. 一元一次方程求解方法3. 不等式的概念4. 一元一次不等式求解方法第四章:函数1. 函数的概念2. 函数的表示方法解析式法图象法3. 一次函数定义图象性质4. 二次函数定义图象第五章:几何图形1. 点、线、面2. 线段3. 角锐角、直角、钝角、平角、周角4. 三角形定义分类性质5. 四边形定义分类性质6. 圆定义性质第六章:概率与统计1. 概率的概念2. 概率的计算方法3. 统计的概念4. 数据的收集与整理5. 数据的表示方法表格法6. 数据的分析方法七年级数学下册思维导图(超全)第一章:实数1. 实数的概念实数是包括有理数和无理数在内的所有数的集合。
2. 实数的分类有理数整数正整数、负整数、零分数正分数、负分数无理数不能表示为两个整数比例的数,如根号2、π等。
3. 实数的运算加法将两个实数相加得到一个新的实数。
减法将一个实数减去另一个实数得到一个新的实数。
乘法将两个实数相乘得到一个新的实数。
除法将一个实数除以另一个非零实数得到一个新的实数。
乘方将一个实数乘以自身多次得到一个新的实数。
开方求一个实数的平方根或立方根等。
第二章:代数式1. 代数式的概念代数式是由数、字母和运算符号组成的表达式。
2. 代数式的分类单项式只有一个项的代数式。
多项式由多个项组成的代数式。
3. 代数式的运算加法将两个代数式相加得到一个新的代数式。
减法将一个代数式减去另一个代数式得到一个新的代数式。
乘法将两个代数式相乘得到一个新的代数式。
除法将一个代数式除以另一个非零代数式得到一个新的代数式。
乘方将一个代数式乘以自身多次得到一个新的代数式。

人教版八下第19章一次函数复习课(第1课时)教学设计教学内容解析教学流程图地位与作用函数是反映现实世界中数量关系和变化规律的常见数学模型之一,一次函数作为学生接触的第一种函数模型,是数学中最简单、最基本的函数,也是学生今后学习二次函数、反比例函数的基础.本章学习了函数与一次函数的定义和图象,结合图象研究了一次函数的性质,探讨了一次函数与一元一次方程、一元一次不等式、二元一次方程组之间的关系;其中,对一次函数的图象和性质的研究思路和方法,将对其他函数的研究起到很好的铺垫作用.一次函数是初中数学研究的一类最基本、最简单的函数,其中函数的定义、一次函数的定义、图象和性质是本章的主要基础知识;会根据问题的条件写出一次函数的解析式,会画一次函数的图象,是学习本章后应具备的基本技能.通过复习,加深学生利用函数观点对数学问题的理解.概念解析在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值都有唯一确定的y值与其对应,那么我们就说x是自变量,y是x的函数.函数的定义中包括了对应值的存在性和唯一性两重意思.单值对应是函数概念的关键词,是函数概念的核心所在.变量y要成为变量x的函数需满足两个条件:一是在同一变化过程中有两个变量x和y;二是对于变量x的每一个确定值,变量y都有唯一确定的值与之对应.一般地,形如y=kx+b(k,b是常数,k≠0)的函数,叫做一次函数.一次函数与正比例函数之间的关系是一般与特殊的关系,当一次函数中常数b=0时,一次函数就是正比例函数.思想方法本章从实际问题出发,研究变量与变量之间的一种对应关系,提出了函数的概念,给出了三种刻画函数的表示形式;学习了利用待定系数法求函数解析式的方法;结合函数图象研究了函数的性质,利用函数的性质也解释了函数的图象,接着研究了一次函数与一元一次方程、一元一次不等式、二元一次方程组之间的关系.这个过程不仅是知识的形成过程,更体现了数学建模、方程、数形结合、由特殊到一般等数学思想.知识类型本课时复习内容既有概念性知识,又有像正比例函数、一次函数的图象与性质等关于有理与规则的知识,更有数学抽象、数学建模、数形结合等关于数学思想方法的知识.由知识的类型决定,教学中应由具体事例出发,引导学生回顾知识,逐步完善知识结构,并注意对有关技能给予强化训练.教学重点一次函数的图象和性质,及三个“一次”之间的关系.教学目标解析教学目标1.掌握一次函数及其相关知识;并能运用这些知识解决相关的数学问题.2.通过具体实例,进一步体会数学中的数学建模、方程思想、数形结合、待定系数法等重要的数学思想和方法.目标解析达成目标1的标志是:能辨别函数及一次函数,会用描点法画函数的图象,能说出一次函数的性质,并能利用一次函数图象和性质解决相关的数学问题.达成目标2的标志是:能分析实际问题中变量之间的关系,将实际问题抽象为函数问题,能利用待定系数法求出一次函数解析式,能依据一次函数性质或图象解决有关问题.教学问题诊断分析具备的基础学生已经学完了本章的内容,对函数的定义、一次函数的图象和性质、一次函数与方程不等式的关系有了一定的理解,另外学生已掌握一元一次方程、二元一次方程组的解法,具备了一定的化归能力,积累了一定的数形结合解决问题的经验.与本课目标的差距分析学习本节内容,需要学生在学习过函数、一次函数相关知识的基础上,深入理解函数的概念,熟练准确调用一次函数的性质,并能结合函数的图象解决相关问题.在解决问题的过程中需要学生具备解方程的技能和较强的运算能力.存在的问题函数的概念较为抽象,掌握其本质——任给一x值都有唯一的y值和其对应,还需要一段时间消化;对一次函数的解析式中k≠0容易忽略,对一次函数与方程、不等式关系的理解和运用还需要进一步强化.应对策略(1)注意引导学生对相关概念、性质的理解;(2)通过呈现不同的题目,引导学生主动辨别概念和隐含条件;(3)通过解题反思和分享,引导学生熟练利用一次函数及其性质解决问题;(4)通过练习思考,逐步积累学习的经验,加深对相关概念和性质的理解.教学难点一次函数的图象及性质的综合应用.教学支持条件分析函数概念之中体现的是“变化与对应”的思想,教学中可以充分利用信息技术手段,用思维导图帮助学生完善本章的知识体系,运用几何画板、Geogebra等动态几何软件画出函数图象、利用其中的电子表格功能分析数量关系。