高中数学 2.2.1+2+3 恒等变换 伸压变换 反射变换课后知能检测 苏教版选修42(1)

苏教版高中数学章节目录(泰州地区)必修一第一章集合1.1 集合的含义及其表示1.2 子集、全集、补集1.3 交集、并集第二章函数概念与基本初等函数Ⅰ2.1 函数的概念和图象2.2 指数函数2.3 对数函数2.4 幂函数2.5 函数与方程2.6 函数模型及其应用必修二第一章立体几何初步1.1 空间几何体1.2 点、线、面之间的位置关系1.3 空间几何体的表面积和体积第二章2.1 直线与方程2.2 圆与方程2.3 空间直角坐标系必修三第一章算法初步1.1 算法的含义1.2 流程图1.3 基本算法语句1.4算法案例第二章统计2.1 抽样方法2.2 总体分布的估计2.3 总体特征数的估计2.4 线性回归方程第三章概率3.1 随机事件及其概率3.2 古典概型3.3 几何概型3.4 互斥事件必修四第一章三角函数1.1 任意角、弧度1.2 任意角的三角函数1.3 三角函数的图象和性质第二章平面向量2.1 向量的概念和表示2.2 向量的线性运算2.3 向量的坐标表示2.4 向量的数量积2.5 向量的应用第三章三角恒等变换3.1 两角和与差的三角函数3.2 二倍角的三角函数3.3 几个三角恒等式必修五第一章解三角型1.1 正弦定理1.2 余弦定理1.3 正弦定理、余弦定理的应用第二章数列3.1 数列2.2 等差数列2.3 等比数列第三章不等式3.1 不等关系3.2 一元二次不等式3.3 二元一次不等式与简单的线性规划问题3.4 基本不等式选修2-1第一章常用逻辑用语1.1 命题及其关系1.2 简单的逻辑联结词1.3 全称量词与存在量词第二章圆锥曲线与方程2.1 圆锥曲线2.2 椭圆2.3 双曲线2.4 抛物线2.5 圆锥曲线的统一定义2.6 曲线与方程第三章空间向量与立体几何3.1 空间向量及其运算3.2 空间向量的应用选修2-2第一章导数及其应用1.1 导数的概念1.2 导数的运算1.3 导数在研究函数中的应用1.4 导数在实际生活中的应用1.5 定积分第二章推理与证明2.1 合情推理2.2 直接证明与间接证明2.3 数学归纳法第三章数系的扩充与复数的引入3.1 数系的扩充3.2 复数的四则运算3.3 复数的几何意义选修2-3第一章计数原理1.1 两个基本计数原理1.2 排列1.3 组合1.4 计数应用题1.5 二项式定理第二章概率2.1 随机变量及其概率分布2.2 超几休分布2.3 独立性2.4 二项分布2.5 随机变量的均值和方差2.6 正态分布第三章统计案例3.1 独立性检验3.2 回归分析选修4-2 矩阵与变换2.1 二阶矩阵与平面向量2.1.1 矩阵的概念2.1.2 二阶矩阵与平面列向量的乘法2.2 几何常见的平面变换2.2.1 恒等变换 2.2.2 伸压变换 2.2.3 反射变换 2.2.4 旋转变换2.2.5 投影变换2.2.6 切变变换2.3 变换的复合与矩阵乘法2.3.1 矩阵乘法的概念2.3.2 矩阵乘法的简单性质2.4 逆变换与逆矩阵2.4.1 逆矩阵的概念2.4.2 二阶矩阵与二元一次方程组2.5 特征值与特征向量2.6 矩阵的简单应用选修4-4 坐标系与参数方程4.1 坐标系4.1.1 直角坐标系4.1.2 极坐标系4.1.3 球坐标系4.2 曲线的极坐标方程4.2.1 曲线的极坐标方程的意义4.2.2 常见曲线的极坐标方程4.3 平面坐标系中几种常见变换4.3.1 平面直角坐标系中的平移变换4.3.2 平面直角坐标系中的伸缩变换4.4 参数方程4.4.1 参数方程的意义4.4.2 参数方程与普通方程的互化4.4.3 参数方程的应用4.4.4 平摆线与圆的渐开线感谢您使用本店文档您的满意是我们的永恒的追求！（本句可删）------------------------------------------------------------------------------------------------------------。

旋转变换·温故：1恒等变换：恒等变换矩阵（单位矩阵）：2伸压变换：伸压变换矩阵：3反射变换：常见的反射变换矩阵：·知新~问题情境问题1：平面向量34⎡⎤⎢⎥⎣⎦1⎡⎤⎢⎥⎣⎦13⎡⎤⎢⎥⎣⎦4⎡⎤⎢⎥⎣⎦在矩阵0110-⎡⎤⎢⎥⎣⎦的作用下分别对应为怎样的向量？请在平面直角坐标系中画出上述向量．问题2：结合上图猜想矩阵0110-⎡⎤⎢⎥⎣⎦表示什么变换？·知新~建构数学旋转变换：，其中点O称为中心，角度θ称为 ．例如：当坐标原点为旋转中心，旋转角为 时，变换矩阵为 0110-⎡⎤⎢⎥⎣⎦． 问题3：非特殊角下的旋转变换矩阵该如何表示？故变换T 对应的矩阵为旋转变换的作用效果 ⎧⎨⎩几何图形的形状几何图形的相对位置关系·知新~数学运用【例1】设点P 的坐标为(1,2)-，T 是绕原点逆时针方向旋转3π的旋转变换，求旋转变换T 对应的矩阵，并求点P 在T 作用下得到的点P '的坐标．【例2】若点2222A ⎝⎭在矩阵cos sin sin cos αααα-⎡⎤⎢⎥⎣⎦对应的变换作用下得到的点为(1,0)，求α．·知新~学生活动【探究】已知()0,0A ，()0,2B ，()1,2C -，()1,0D -，求矩形ABCD 在矩阵0110M ⎡⎤=⎢⎥-⎣⎦作用下变换所得到的图形．小结提升1旋转变换矩阵对于 旋转变换同样适用2其中，若逆时针方向旋转，则记旋转角θ为“ ”（选填“”或“－”）；若顺时针方向旋转，则记旋转角θ为“ ”（选填“”或“－”） ．【例3】已知椭圆22:3C x y xy ++=，将曲线C 绕原点O 顺时针旋转4π，得到椭圆C '，求（1）椭圆C '的标准方程；（2）求C 的焦点坐标．巩固练习1若ABC ∆在矩阵M 对应的旋转变换作用下得到A B C '''∆，其中()0,0A ，(3B ，()0,2C ，()0,0A '，()3,1C '-试求矩阵M 以及点B '的坐标．2将抛物线2=绕它的顶点逆时针旋转60，得到曲线E'，求曲线E'的焦点坐标和准线E y x:4方程．·知新~回顾小结。

反射变换【学习目标】1. 反射变换2. 线性变换【学习过程】一、知识梳理1．_________________________________________________的变换矩阵称为反射变换矩阵，对应的变换称为反射变换，关于定直线或定点对称的反射又分别称为轴反射和中心反射，定直线称为反射轴，定点称为反射点．2．(1)变换T 使图形F 变成与F 关于x 轴对称的图形，则变换矩阵为________________；(2)变换T 使图形F 变成与F 关于y 轴对称的图形，则变换矩阵为________________；(3)变换T 使图形F 变成与F 关于原点对称的图形，则变换矩阵为________________；(4)变换T 使图形F 变成与F 关于直线y=x 对称的图形，则变换矩阵为____________．3.二阶非零矩阵对应变换把直线变为直线，把直线变为直线的变换叫做_____________． 一般地，12()M λλ+=αβ______________________________，其中12,λλ为任意实数．二、例题讲解1.求出曲线4y x =在矩阵0110⎡⎤⎢⎥⎣⎦作用下变换所得的图形．2.已知矩阵0101,1010M N -==⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦．在平面直角坐标系中，设直线2x - y + 1 = 0在变换T M ，T N 先后作用下得到曲线F ，求曲线的方程F ．3.计算0110x y --⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦，并说明其几何意义．三、巩固练习1.若曲线y = x 2（x ≥0）在矩阵M 对应的反射变换作用下得到的曲线为y = x 2（x ≤0），求矩阵M ．2.求出曲线y = sinx 在矩阵1001-⎡⎤⎢⎥⎣⎦作用下变换所得的图形．3.椭圆2219x y +=在经过矩阵0110⎡⎤⎢⎥⎣⎦对应的变换后所得的曲线是什么图形？4.利用矩阵变换的方法求曲线y = 10x 关于原点对称的曲线的方程．5.已知点P(3，1)在轴反射变换T 下的新坐标为Q(1，3)．(1)求反射变换所对应的变换矩阵M ；(2)求曲线y 2 = x 在变换T 作用下所得到的图形．。

旋转变换
·温故：
1恒等变换：
恒等变换矩阵〔单位矩阵〕：
2伸压变换：
伸压变换矩阵：
3反射变换：
常见的反射变换矩阵：
·知新~问题情境
问题1：平面向量在矩阵的作用下分别对应为怎样的向量？请在平面直角坐标系中画出上述向量．
问题2：结合上图猜测矩阵表示什么变换？
·知新~建构数学
旋转变换：，其中点O称为中心，角度θ称为．
例如：当坐标原点为旋转中心，旋转角为时，变换矩阵为．
问题3：非特殊角下的旋转变换矩阵该如何表示？
故变换对应的矩阵为
旋转变换的作用效果
·知新~数学运用
【例1】设点的坐标为，是绕原点逆时针方向旋转的旋转变换，求旋转变换对应的矩阵，并求点在作用下得到的点的坐标．
【例2】假设点在矩阵对应的变换作用下得到的点为，求．
·知新~学生活动
【探究】，，，，求矩形在矩阵作用下变换所得到的图形．
小结提升
1旋转变换矩阵对于旋转变换同样适用
2其中，假设逆时针方向旋转，那么记旋转角为“〞〔选填“〞或“－〞〕；假设顺时针方向旋转，那么记旋转角为“〞〔选填“〞或“－〞〕．【例3】椭圆，将曲线绕原点顺时针旋转，得到椭圆，求〔1〕椭圆的标准方程；〔2〕求的焦点坐标．
稳固练习
1假设在矩阵对应的旋转变换作用下得到，其中，，，，试求矩阵以及点的坐标．
2将抛物线绕它的顶点逆时针旋转，得到曲线，求曲线的焦点坐标和准线方程．
·知新~回忆小结。

高中数学2.4逆变换与逆矩阵章末综合检测苏教版选修421.求下列矩阵的逆矩阵. (1)A ＝⎣⎢⎡⎦⎥⎤1 12 3；(2)B ＝⎣⎢⎡⎦⎥⎤2 34 5. 【解】 法一 (1)∵|A |＝1×3－2＝1，∴A －1＝⎣⎢⎡⎦⎥⎤ 3 －1－2 1.(2)∵2×5－4×3＝－2，∴B －1＝⎣⎢⎢⎡⎦⎥⎥⎤－5232 2 －1. 法二 (1)设A －1＝⎣⎢⎡⎦⎥⎤ab cd ，则AA －1＝E ， 即⎣⎢⎡⎦⎥⎤1 12 3⎣⎢⎡⎦⎥⎤a b c d ＝⎣⎢⎡⎦⎥⎤ a ＋c b ＋d 2a ＋3c 2b ＋3d ＝⎣⎢⎡⎦⎥⎤1 00 1， ∴⎩⎪⎨⎪⎧a ＋c ＝1，b ＋d ＝0，2a ＋3c ＝0，2b ＋3d ＝1.∴⎩⎪⎨⎪⎧a ＝3，b ＝－1，c ＝－2，d ＝1.∴A－1＝⎣⎢⎡⎦⎥⎤ 3 －1－2 1. 同理求出B －1＝⎣⎢⎢⎡⎦⎥⎥⎤－52 32 2 －1.2.试从代数和几何角度分别求矩阵的乘积⎣⎢⎡⎦⎥⎤1201⎣⎢⎡⎦⎥⎤0 11 0的逆矩阵.【导学号：30650046】【解】 代数角度：⎣⎢⎡⎦⎥⎤1 20 1⎣⎢⎡⎦⎥⎤0 11 0＝⎣⎢⎡⎦⎥⎤2 11 0，⎪⎪⎪⎪⎪⎪2 11 0＝－1，∴⎣⎢⎡⎦⎥⎤2 11 0－1＝⎣⎢⎡⎦⎥⎤0 11 －2，∴(⎣⎢⎡⎦⎥⎤1201⎣⎢⎡⎦⎥⎤0 11 0)－1＝⎣⎢⎡⎦⎥⎤0 11 －2.几何角度：矩阵⎣⎢⎡⎦⎥⎤1201对应的变换是纵坐标不变，横坐标按纵坐标比例增加，即(x ，y )→(x ＋2y ，y )，又切变变换的逆变换为切变变换.∴该切变变换的逆变换是纵坐标不变，横坐标按纵坐标比例减小，即(x ，y )→(x －2y ，y )，故⎣⎢⎡⎦⎥⎤1 201－1＝⎣⎢⎡⎦⎥⎤1 －20 1.矩阵⎣⎢⎡⎦⎥⎤0 110对应的变换为关于直线y ＝x 的反射变换，其逆变换为其本身，故⎣⎢⎡⎦⎥⎤0 11 0－1＝⎣⎢⎡⎦⎥⎤0 11 0.∴(⎣⎢⎡⎦⎥⎤1 201⎣⎢⎡⎦⎥⎤0 11 0)－1＝⎣⎢⎡⎦⎥⎤0110－1⎣⎢⎡⎦⎥⎤1 20 1－1＝⎣⎢⎡⎦⎥⎤0110⎣⎢⎡⎦⎥⎤1 －20 1＝⎣⎢⎡⎦⎥⎤0 11 －2. 3.已知A ＝⎣⎢⎡⎦⎥⎤1 －10 1⎣⎢⎢⎡⎦⎥⎥⎤12－3232 12，求A －1.【解】 ⎣⎢⎡⎦⎥⎤1 －10 1－1＝⎣⎢⎡⎦⎥⎤1101，⎣⎢⎢⎡⎦⎥⎥⎤12 －3232 12－1＝⎣⎢⎢⎡⎦⎥⎥⎤ 1232－32 12，∴A－1＝⎣⎢⎢⎡⎦⎥⎥⎤12 －3232 12－1⎣⎢⎡⎦⎥⎤1 －10 1－1 ＝⎣⎢⎢⎡⎦⎥⎥⎤ 12 32－32 12⎣⎢⎡⎦⎥⎤1 10 1＝⎣⎢⎢⎡⎦⎥⎥⎤ 121＋32－32 1－32.4.用矩阵方法求二元一次方程组⎩⎪⎨⎪⎧2x －5y ＝4，3x ＋y ＝6的解.【解】 方程组可写为：⎣⎢⎡⎦⎥⎤2 －53 1⎣⎢⎡⎦⎥⎤x y ＝⎣⎢⎡⎦⎥⎤46， 令M ＝⎣⎢⎡⎦⎥⎤2 －53 1，则det(M )＝2×1－3×(－5)＝17，∴M－1＝⎣⎢⎢⎡⎦⎥⎥⎤ 117517－317 217， 所以⎣⎢⎡⎦⎥⎤x y ＝M －1⎣⎢⎡⎦⎥⎤46＝⎣⎢⎡⎦⎥⎤20，即方程组的解为⎩⎪⎨⎪⎧x ＝2，y ＝0.5.设A ＝⎣⎢⎡⎦⎥⎤ 1 2－2 3，B ＝⎣⎢⎡⎦⎥⎤1224.(1)计算det(A )，det(B )；(2)判断矩阵AB 是否可逆，若可逆，求其逆矩阵，若不可逆，说明理由. 【解】(1)det(A )＝1×3－2×(－2)＝7， det(B )＝1×4－2×2＝0. (2)矩阵AB 不可逆.理由如下：AB ＝⎣⎢⎡⎦⎥⎤ 1 2－2 3⎣⎢⎡⎦⎥⎤1 22 4＝⎣⎢⎡⎦⎥⎤5 104 8，det(AB )＝0，∴AB 不可逆.6.(福建高考)已知矩阵A ＝⎝⎛⎭⎪⎫2 14 3，B ＝⎝ ⎛⎭⎪⎫1 10 －1.求矩阵C ，使得AC ＝B .【导学号：30650047】【解】 由AC ＝B ，得(A －1A )C ＝A －1B ，故C ＝A －1B ＝⎝⎛⎭⎪⎪⎫32 －12－21⎝ ⎛⎭⎪⎫1 10 －1＝⎝ ⎛⎭⎪⎪⎫32 2－2 －3. 7.已知矩阵M ＝⎣⎢⎡⎦⎥⎤2 －31 －1所对应的线性变换把点A (x ，y )变成点A ′(13，5)，试求M 的逆矩阵及点A 的坐标.【解】 依题意，得det(M )＝⎪⎪⎪⎪⎪⎪2 －31 －1＝2×(－1)－1×(－3)＝1，故M －1＝⎣⎢⎡⎦⎥⎤－1 3－12，从而由⎣⎢⎡⎦⎥⎤2 －31 －1⎣⎢⎡⎦⎥⎤x y ＝⎣⎢⎡⎦⎥⎤135，得⎣⎢⎡⎦⎥⎤x y ＝M －1⎣⎢⎡⎦⎥⎤135＝⎣⎢⎡⎦⎥⎤－1 3－1 2⎣⎢⎡⎦⎥⎤135＝⎣⎢⎡⎦⎥⎤－1×13＋3×5－1×13＋2×5＝⎣⎢⎡⎦⎥⎤2－3，故⎩⎪⎨⎪⎧x ＝2，y ＝－3， 即A (2，－3)为所求.8.m 为何值时，二元一次方程组⎣⎢⎡⎦⎥⎤－1 7－2 3⎣⎢⎡⎦⎥⎤x y ＝m ⎣⎢⎡⎦⎥⎤2 10 －1⎣⎢⎡⎦⎥⎤x y 有惟一解？ 【解】 二元一次方程组即为⎩⎪⎨⎪⎧－x ＋7y ＝2mx ＋my ，－2x ＋3y ＝－my ， 即⎩⎪⎨⎪⎧（－1－2m ）x ＋（7－m ）y ＝0，－2x ＋（m ＋3）y ＝0， 即⎣⎢⎡⎦⎥⎤－1－2m 7－m －2 m ＋3⎣⎢⎡⎦⎥⎤x y ＝⎣⎢⎡⎦⎥⎤00. ∵⎪⎪⎪⎪⎪⎪－1－2m 7－m －2 m ＋3 ＝(－1－2m )(m ＋3)＋2(7－m ) ＝－2m 2－9m ＋11， 令－2m 2－9m ＋11＝0， 得m ＝1或m ＝－112，∴当m ≠1或m ≠－112时，方程组有惟一解.9.已知A ＝⎣⎢⎢⎡⎦⎥⎥⎤12 －3232 12，B ＝⎣⎢⎡⎦⎥⎤2 00 1，求圆x 2＋y 2＝1在(AB )－1变换作用下的图形的方程.【解】 (AB )－1＝B－1A －1＝⎣⎢⎡⎦⎥⎤2 00 1－1⎣⎢⎢⎡⎦⎥⎥⎤12 －3232 12－1＝⎣⎢⎢⎡⎦⎥⎥⎤1200 1⎣⎢⎢⎡⎦⎥⎥⎤ 12 32－3212＝⎣⎢⎢⎡⎦⎥⎥⎤ 14 34－32 12. 设圆x 2＋y 2＝1上任一点P ′(x ′，y ′)在(AB )－1作用下的点为P (x ，y )，则⎣⎢⎢⎡⎦⎥⎥⎤ 14 34－32 12⎣⎢⎡⎦⎥⎤x ′y ′＝⎣⎢⎡⎦⎥⎤x y ， 即⎣⎢⎡⎦⎥⎤x ′y ′＝⎣⎢⎢⎡⎦⎥⎥⎤ 1434－3212－1⎣⎢⎡⎦⎥⎤x y ＝⎣⎢⎢⎡⎦⎥⎥⎤1 －32312⎣⎢⎡⎦⎥⎤x y ， 所以⎩⎪⎨⎪⎧x ′＝x －32y ，y ′＝3x ＋12y ，因为点P ′(x ′，y ′)在圆x 2＋y 2＝1上，所以⎝⎛⎭⎪⎫x －32y 2＋⎝ ⎛⎭⎪⎫3x ＋12y 2＝1，化简得4x2＋y 2＝1.10.设a ，b ∈R ，若矩阵A ＝⎣⎢⎡⎦⎥⎤a0－1b ，把直线l ：2x ＋y －7＝0变换为另一直线l ′：9x ＋y －91＝0，求矩阵A 的逆矩阵.【导学号：30650048】【解】 设P (x ，y )为直线2x ＋y －7＝0上任意一点，则其对应点P ′(x ′，y ′)，且满足⎣⎢⎡⎦⎥⎤x ′y ′＝⎣⎢⎡⎦⎥⎤ a 0－1 b ⎣⎢⎡⎦⎥⎤x y ＝⎣⎢⎡⎦⎥⎤ ax －x ＋by ，即⎩⎪⎨⎪⎧x ′＝ax ，y ′＝－x ＋by ， ∵P ′在直线l ′： 9x ＋y －91＝0上， ∴9ax －x ＋by －91＝0， 即(9a －1)x ＋by －91＝0. ∵9a －12＝b 1＝－91－7＝13， ∴b ＝13，a ＝3，∴A ＝⎣⎢⎡⎦⎥⎤3 0－1 13.∵det(A )＝13×3－(－1)×0＝39，∴A－1＝⎣⎢⎢⎡⎦⎥⎥⎤1339 039139 339＝⎣⎢⎢⎡⎦⎥⎥⎤130139 113.。

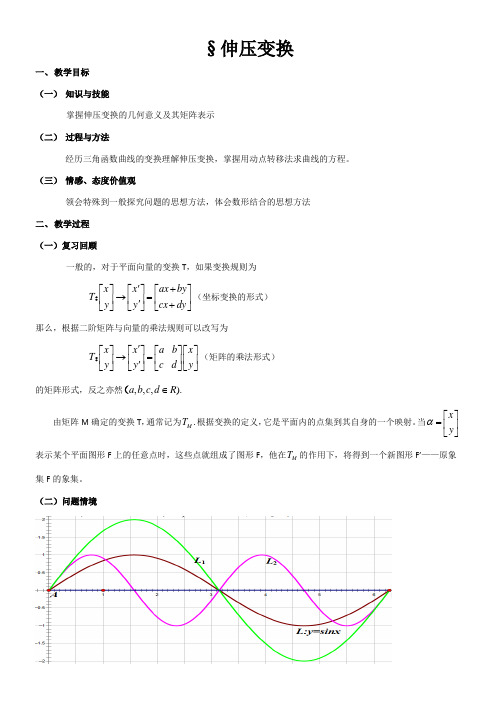
§伸压变换一、 教学目标（一） 知识与技能掌握伸压变换的几何意义及其矩阵表示（二） 过程与方法经历三角函数曲线的变换理解伸压变换，掌握用动点转移法求曲线的方程。

（三） 情感、态度价值观领会特殊到一般探究问题的思想方法，体会数形结合的思想方法二、 教学过程（一）复习回顾一般的，对于平面向量的变换T ，如果变换规则为x x ax by T y y cx dy '+⎡⎤⎡⎤⎡⎤→=⎢⎥⎢⎥⎢⎥'+⎣⎦⎣⎦⎣⎦：（坐标变换的形式）那么，根据二阶矩阵与向量的乘法规则可以改写为x x a b x T y y c d y '⎡⎤⎡⎤⎡⎤⎡⎤→=⎢⎥⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎣⎦⎣⎦：（矩阵的乘法形式）的矩阵形式，反之亦然,,,).a b c d R ∈（由矩阵M 确定的变换T ，通常记为.M T 根据变换的定义，它是平面内的点集到其自身的一个映射。

当x y α⎡⎤=⎢⎥⎣⎦表示某个平面图形F 上的任意点时，这些点就组成了图形F ，他在M T 的作用下，将得到一个新图形F’——原象集F 的象集。

（二）问题情境问题：曲线L 横坐标不变，纵坐标变为原来2倍得曲线L1的变换T1的坐标变换形式？问题：变换1T 对应的矩阵1M 是什么？问题：曲线L 纵坐标不变，横坐标变为原来一半得曲线L2的变换T2的坐标变换形式？问题：变换2T 对应的矩阵2M 是什么？问题3：曲线1L ，2L 的方程是什么？（三）数学建构1伸压变换：沿竖直方向或水平方向伸长或压缩的平面图形变换称为垂直伸压变换，简称伸压变换。

2伸压变化矩阵：像1100,20201⎛⎫⎛⎫ ⎪ ⎪ ⎪⎝⎭⎝⎭这样的矩阵，称为沿y 轴或x 轴的垂直伸压变换矩阵。

说明：伸压变换1T 不是简单的把平面上的点（向量）“向上”拉伸，它是沿y 轴方向拉伸，对于x 轴上方的点向上拉伸，对于x 轴下方的点向下拉伸，x 轴上的点变换前后原地不动。

同理，伸压变换2T 把平面上的点（向量）沿x 轴方向压缩。

(1)(2)(4)T 2T 1 2.2.2 《伸压变换》教学设计彭 成教学目标：1．理解可以用矩阵来表示平面中常见的几何变换。

2．掌握伸压变换的几何意义及其矩阵表示。

教学重点：伸压变换的矩阵表示。

教学难点：垂直伸压变换矩阵的产生过程。

教学过程 ：一．问题揭示上一节课，我们研究了一种特殊的平面图形变换—恒等变换，并对问题“该变换可用矩阵表示吗？”给予了一个肯定的回答：恒等变换矩阵单位矩阵1001E ⎡⎤=⎢⎥⎣⎦。

接下来，我们继续研究常见的平面图形的几何变换及其矩阵表示。

如图，现有根弹簧放在矩形ABCD 中，其中2根纵向，2根横向，在弹性限度内被分别挤压和拉伸的正视问题1：你对这两个变换有怎样初步的印象？问题2：能用矩阵来刻画这两个变换吗？如果可以又该怎样表示呢？二．自主学习垂直伸压变换：沿__________方向或__________方向__________或__________的平面图形变换，简称伸压变换。

问题2同样出现在上一节课的学习中，因此我们有必要回顾恒等变换矩阵E 的产生过程。

三．合作探究小组间相互合作对变换1T 与2T 作类似的探究，并分享你们的成果。

变换1T 的探究过程：变换2T 的探究过程：垂直伸压变换矩阵：四．精讲点拨例1．如图所示，已知曲线sin y x =经过变换作用后变为新的曲线C ，试求变换T 对应的矩 阵M ，以及曲线C 的解析表达式。

例2．验证圆C ：221x y +=在矩阵1002A ⎡⎤=⎢⎥⎣⎦对应的伸压变换下变为一个椭圆，并求此椭圆的方程。

问题3：能否从“矩阵”的角度分析例1与例2在题目设置上有何异同。

问题4：仔细观察前面的四个变换矩阵，试探究若将平面图形F 作沿x 轴方向的伸压变换，其对 应的变换矩阵的一般形式是什么？沿y 轴方向呢？五．当堂巩固求曲线2cos2y x =在矩阵10103M ⎡⎤⎢⎥=⎢⎥⎣⎦对应的变换作用下新曲线的方程。

第一课时恒等变换与伸压变换学习目标1、理解可以用矩阵来表示平面中常见的几何变换。

2、掌握恒等、伸压变换的几何意义及其矩阵表示。

学习过程：一、预习：〔一〕阅读教材，解决以下问题：问题：给定一个矩阵,就确定了一个变换,它的作用是将平面上的一个点向量变换成另外一个点向量反过来,平面中常见变换是否都可以用矩阵来表示呢如果可以,又该怎样表示呢如：1、△ABC, A2,0, B-1,0, C0,2, 它们在变换T作用下保持位置不变, 能否用矩阵M来表示这一变换2、将图中所示的四边形ABCD保持位置不变，能否用矩阵M来表示？〔二〕由矩阵M=确定的变换T M称为恒等变换，这时称矩阵M为恒等变换矩阵或单位矩阵，二阶单位矩阵一般记为E平面是任何一点〔向量〕或图形，在恒等变换之下都把自己变为自己〔３〕由矩阵M=或M=确定的变换T M称为〔垂直〕变换，这时称矩阵M=或M=变换矩阵．当M=时确定的变换将平面图形作沿轴方向伸长或压缩,当时伸长,确定的变换不是简单地把平面上的点向量沿轴方向“向下压〞或“向外伸〞,它是轴方向伸长或压缩,以为例，对于轴上方的点向下压缩，对于轴下方的点向上压缩，对于轴上的点变换前后原地不动．当M=时确定的变换将平面图形作沿轴方向伸长或压缩,当时伸长,当时压缩．在伸压变换之下，直线仍然变为直线，线段仍然变为线段．恒等变换是伸压变换的特例，伸压变换多与三角函数图象的变换联系起来研究．练习1、四边形ABCD的顶点分别为A〔-1，0〕，B〔1，0〕，C〔1，1〕，D〔-1，1〕，四边形ABCD在矩阵变换作用下变成正方形，那么＝2、假设直线=4-4在矩阵M对应的伸压变换下变成另一条直线=-1，那么M=__________3、求圆C：在矩阵对应的伸压变换下的曲线方程，并判断曲线的类型二、课堂训练：例1．求在矩阵M= 作用下的图形例2．曲线＝in经过变换T作用后变为新的曲线＝in2，画出相关的图象，并求出变换T对应的矩阵M。

【课堂新坐标】（教师用书）2013-2014学年高中数学 2.2 几种常见的平面变换综合检测 苏教版选修4-21．在平面直角坐标系xOy 中，设椭圆4x 2＋y 2＝1在矩阵A ＝⎣⎢⎡⎦⎥⎤2001对应的变换下得到曲线F ，求F 的方程．【解】 设P (x 0，y 0)是椭圆上任意一点，点P (x 0，y 0)在矩阵A 对应的变换下变为点P ′(x ′0，y ′0)，则⎣⎢⎡⎦⎥⎤x ′0y ′0＝⎣⎢⎡⎦⎥⎤2 001⎣⎢⎡⎦⎥⎤x 0y 0＝⎣⎢⎡⎦⎥⎤2x 0y 0， 即⎩⎪⎨⎪⎧x ′0＝2x 0，y ′0＝y 0，∴⎩⎪⎨⎪⎧x 0＝x ′02，y 0＝y ′0.又∵点P 在椭圆上，代入得 4x ′204＋y ′20＝1， 即x 2＋y 2＝1.∴曲线F 的方程为x 2＋y 2＝1. 2．若点A ⎝ ⎛⎭⎪⎫22，22在矩阵M ＝⎣⎢⎡⎦⎥⎤cos α －sin αsin α cos α对应的变换作用下得到点为B (1,0)，求α的值．【解】 由题意知⎣⎢⎡⎦⎥⎤cos α －sin αsin α cos α⎣⎢⎢⎡⎦⎥⎥⎤2222＝⎣⎢⎡⎦⎥⎤10， 所以⎩⎪⎨⎪⎧22cos α－22sin α＝1，22sin α＋22cos α＝0，解得⎩⎪⎨⎪⎧cos α＝22，sin α＝－22，从而可知，α＝2k π－π4，(k ∈Z )．3．已知直线l 与直线3x ＋5y ＋6＝0平行，且过点(5,6)，求矩阵⎣⎢⎢⎡⎦⎥⎥⎤1 00 15将直线l 变成了什么图形？并写出方程．【解】 由已知得直线l 的方程为3x ＋5y －45＝0，设P (x ，y )为l 上的任意一点，点P 在矩阵对应的变换下对应点P ′(x ′，y ′)．则⎣⎢⎡⎦⎥⎤x ′y ′＝⎣⎢⎢⎡⎦⎥⎥⎤1 00 15⎣⎢⎡⎦⎥⎤x y ＝⎣⎢⎢⎡⎦⎥⎥⎤ x 15y ，∴⎩⎪⎨⎪⎧x ′＝x ，y ′＝15y .∴⎩⎪⎨⎪⎧x ＝x ′，y ＝5y ′.代入3x ＋5y －45＝0，得3x ′＋25y ′－45＝0，∴直线l 变换成直线3x ＋25y －45＝0. 4．求直线y ＝2x 在矩阵⎣⎢⎡⎦⎥⎤1301确定的变换作用下得到的图形的表达式．【解】 设点(x ，y )为直线y ＝2x 上的任意一点，其在矩阵⎣⎢⎡⎦⎥⎤130 1确定的变换作用下得到的点为(x ′，y ′)，则⎣⎢⎡⎦⎥⎤x y →⎣⎢⎡⎦⎥⎤x ′y ′＝⎣⎢⎡⎦⎥⎤1301⎣⎢⎡⎦⎥⎤x y ＝⎣⎢⎡⎦⎥⎤x ＋3y y ，即⎩⎪⎨⎪⎧x ′＝x ＋3y ，y ′＝y ，所以⎩⎪⎨⎪⎧x ＝x ′－3y ′，y ＝y ′，将其代入y ＝2x ，并整理得2x ′－7y ′＝0，所以直线y ＝2x 在矩阵⎣⎢⎡⎦⎥⎤1301确定的变换作用下得到的图形的表达式是2x －7y ＝0.5．切变变换矩阵⎣⎢⎡⎦⎥⎤1101把直线x ＋y ＝1变成什么几何图形？【解】 设P (x ，y )在该变换下的象为P ′(x ′，y ′)，则⎣⎢⎡⎦⎥⎤x ′y ′＝⎣⎢⎡⎦⎥⎤1 10 1⎣⎢⎡⎦⎥⎤x y ＝⎣⎢⎡⎦⎥⎤x ＋y y ＝⎣⎢⎡⎦⎥⎤1y ，故⎩⎪⎨⎪⎧x ′＝1，y ′＝y ，所以切变变换矩阵⎣⎢⎡⎦⎥⎤1101把直线x ＋y＝1变成与y 轴平行的直线x ＝1.6．若曲线x 2＋4xy ＋2y 2＝1在矩阵M ＝⎣⎢⎡⎦⎥⎤1 a b1的作用下变换成曲线x 2－2y 2＝1，求a 、b 的值．【解】 设(x ，y )为曲线x 2＋4xy ＋2y 2＝1上的任意一点，其在矩阵M 的作用下变换成点(x ′，y ′)，则(x ′，y ′)在曲线x 2－2y 2＝1上，⎣⎢⎡⎦⎥⎤x ′y ′＝⎣⎢⎡⎦⎥⎤1a b1⎣⎢⎡⎦⎥⎤x y ＝⎣⎢⎡⎦⎥⎤x ＋ay bx ＋y ，即⎩⎪⎨⎪⎧x ′＝x ＋ay ，y ′＝bx ＋y ，将其代入x 2－2y 2＝1，并整理，得(1－2b 2)x 2＋(2a －4b )·xy ＋(a 2－2)y2＝1，比较系数得⎩⎪⎨⎪⎧1－2b 2＝1，2a －4b ＝4，a 2－2＝2，解得⎩⎪⎨⎪⎧a ＝2，b ＝0.7．点(2,2x )在旋转变换矩阵⎣⎢⎢⎡⎦⎥⎥⎤12 m 32 n 的作用下得到点(y,4)，求x ，y ，m ，n .【解】 因为矩阵⎣⎢⎢⎡⎦⎥⎥⎤12 m 32 n 是旋转变换矩阵，所以m ＝－32，n ＝12. 由题意知⎣⎢⎢⎡⎦⎥⎥⎤12 －3232 12⎣⎢⎡⎦⎥⎤22x ＝⎣⎢⎡⎦⎥⎤y 4， 所以⎩⎨⎧1－3x ＝y ，3＋x ＝4，解得⎩⎨⎧x ＝4－3，y ＝4－4 3 .8．二阶矩阵M 对应的变换T 将点(1，－1)，(－2,1)均变为点(1,1)． (1)求矩阵M ；(2)直线l ：2x ＋3y ＋1＝0在变换T 作用下得到什么图形？说明理由．【解】 (1)设M ＝⎣⎢⎡⎦⎥⎤ab c d ，则由题设得⎣⎢⎡⎦⎥⎤a b cd ⎣⎢⎡⎦⎥⎤ 1－1＝⎣⎢⎡⎦⎥⎤11，且⎣⎢⎡⎦⎥⎤a b c d ⎣⎢⎡⎦⎥⎤－2 1＝⎣⎢⎡⎦⎥⎤11， 即⎩⎪⎨⎪⎧a －b ＝1，c －d ＝1，－2a ＋b ＝1，－2c ＋d ＝1，解得⎩⎪⎨⎪⎧a ＝－2，b ＝－3，c ＝－2，d ＝－3.所以M ＝⎣⎢⎡⎦⎥⎤－2 －3－2 －3.(2)设P (x ，y )是l ：2x ＋3y ＋1＝0上任一点P ′(x ′，y ′)是对应的点，则由⎣⎢⎡⎦⎥⎤x ′y ′＝⎣⎢⎡⎦⎥⎤－2 －3－2 －3⎣⎢⎡⎦⎥⎤x y ＝⎣⎢⎡⎦⎥⎤－2x －3y －2x －3y ， 得⎩⎪⎨⎪⎧x ′＝－2x －3y ，y ′＝－2x －3y ，即2x ＋3y ＝－x ′＝－y ′.又2x ＋3y ＋1＝0，所以x ′＝y ′＝1. 故在l 在变换T 作用下变为点(1,1)．9．求直线y ＝－2x ＋1绕原点逆时针旋转45°后所得的直线方程． 【解】 ⎣⎢⎡⎦⎥⎤cos 45° －sin 45°sin 45° cos 45°＝⎣⎢⎢⎡⎦⎥⎥⎤22－222222. 设直线y ＝－2x ＋1上任意一点为(x 0，y 0)，其在旋转变换作用下得到点(x ′0，y ′0)，则⎣⎢⎢⎡⎦⎥⎥⎤22 －2222 22⎣⎢⎡⎦⎥⎤x 0y 0＝⎣⎢⎡⎦⎥⎤x ′0y ′0， 即⎩⎪⎨⎪⎧x ′0＝22 x 0－y 0，y ′0＝22x 0＋y 0，解得⎩⎪⎨⎪⎧x 0＝22 x ′0＋y ′0，y 0＝－22x ′0－y ′0.因为点(x 0，y 0)在直线y ＝－2x ＋1上，所以2x 0＋y 0－1＝0，所以2×22(x ′0＋y ′0)－22(x ′0－y ′0)－1＝0，整理得22x ′0＋322y ′0－1＝0. 所以直线y ＝－2x ＋1绕原点逆时针旋转45°后所得的直线的方程是22x ＋322y －1＝0.10．如图所示的是一个含有60°角的菱形ABCD ，要使只变换其四个顶点中的两个顶点后，菱形变为正方形，求此变换对应的变换矩阵M .该变换矩阵惟一吗？若不惟一，写出所有满足条件的变换矩阵．【解】 由题设知AC ∶BD ＝3∶1.若只变换A ，C 两个顶点，则应把A ，C 两个顶点的横坐标压缩为原来的33，纵坐标不变，于是变换矩阵为M ＝⎣⎢⎢⎡⎦⎥⎥⎤33 0 0 1；若只变换B ，D 两个顶点，则应把B ，D 两个顶点的纵坐标伸长为原来的3倍，横坐标不变，于是变换矩阵为M＝⎣⎢⎡⎦⎥⎤1 00 3.所以满足条件的变换矩阵M 为⎣⎢⎢⎡⎦⎥⎥⎤33 0 0 1或⎣⎢⎡⎦⎥⎤1 00 3.。

反射变换与旋转变换一、【知识回顾】1.反射变换的有关看法2.常用的几种反射变换矩阵3．旋转变换的看法二、【自学检测】x x′1. 关于x轴的反射变换的坐标公式为T：→＝，对应的二阶矩阵为；y y′2. 关于y x x′轴的反射变换的坐标公式为：→＝，对应的二阶矩阵为；Ty′y3. 旋转变换的坐标变换公式为x x′. T：→＝，对应的二阶矩阵为y y′4.已知直线ＡＢ过（２ , １），（－２，－２）两点 , 求 :10(1)直线AB在矩阵对应变换下的方程；0 10 1(2) 直线 AB在矩阵对应变换下的方程 .10（3）已知 A(0,0),B(2,0),C(2,1),D(0,1), 求矩形 ABCD绕原点逆时针旋转 900后所获取的图形，并求出其极点坐标 .三、【应用举例】研究 10 1求直线 y=4x 在矩阵作用下变换所得的图形.10研究 2求曲线 y= 1 0 x (x ≥ 0) 在矩阵 作用下变换所得的图形 .0 1研究 3若点 (2,2) 在矩阵 ＝ cos α － sin α 对应变换作用下获取的点为( － 2,2) ，求矩阵 ． A M sin α cos α B M.四、【检测反思】1. 将图形变换为关于 x 轴对称的图形的变换矩阵为 .将图形变换为关于 y 轴对称的图形的变换矩阵为 .将图形变换为关于原点对称的图形的变换矩阵为 .1 0 , 其中 A(1,1),B(4,2),C(3,0).2. 求△ ABC 在矩阵 M= 作用下变换获取的图形 0 13. 求出曲线 y= 1 (x>0) 在矩阵 M= 1 0 作用下变换获取的曲线 .x 0 14. 求曲线 y=lgx(x>0),0 1 在矩阵 M= 作用下变换获取的曲线 .1 0 5. 求曲线 y= 31 0 0 1 x 经 M= 和 M= 作用下变换获取的曲线 .1 12 00 1。